Ensayo científico

 

Minimización del riesgo de la rentabilidad de un portafolio de dos actividades agropecuarias o forestales

 

Risk minimization on the return of a portfolio of two agricultural or forestry activities

 

Eneas Arturo Caldiño García¹* y José Antonio Ávila Dorantes²

 

¹ Centro de Estudios Económicos, El Colegio de México, A. C. Camino al Ajusco 20. 10740, México, D. F. Tel. 5449-3000 ext. 4160. *Autor para correspondencia (eneas@colmex.mx)

² División de Ciencias Económico-Administrativas, Universidad Autónoma Chapingo. Km 38.5 Carretera México-Texcoco. 5630, Texcoco, Edo de México.

 

Recibido: 24 de Agosto de 2007.
Aceptado: 06 de Junio de 2009.

 

Resumen

En este trabajo se considera el caso de un productor agropecuario o forestal renuente al riesgo que desea invertir en dos actividades productivas simultáneas diferentes y en un instrumento financiero sin riesgo, mediante la formación de un portafolio que le dé el menor riesgo posible. La formación de este portafolio es una forma de auto-aseguramiento que le permite una reducción en el riesgo inherente a su actividad empresarial.

Palabras clave: Portafolio, programa de optimización convexo, riesgo.

 

Abstract

This paper examines the case of a risk-averse producer who wants to invest in two different simultaneous agricultural or forestry activities and in a risk-free security, by forming a portfolio that minimizes his risk. Putting together this portfolio is a way of self-insurance, allowing the producer a reduction in the risk inherent in his business activities.

Key words: Portfolio, convex optimization program, risk.

 

INTRODUCCIÓN

Como toda actividad productiva o empresarial, la producción agropecuaria y forestal está sujeta a riesgos en la tasa de rentabilidad obtenida. Estos riesgos pueden estar relacionados con el mercado, como los cambios en precios (Varangis y Larson, 1996), o con circunstancias ajenas al mercado, como las malas condiciones climáticas, plagas, enfermedades, etc. (Larson et al., 1998). Hay diferentes maneras de protegerse de estos riesgos. Una de ellas es la compra de un seguro contra desastres en la producción, que requiere el pago de primas (Quiggin, 1994; Miranda y Glauber, 1997; Vaughan y Vaughan, 2003; Barnett, 2004). El objetivo de este artículo es presentar y analizar una forma más de reducción del riesgo, que puede ser vista como una forma de auto-aseguramiento y que consiste en la formación de portafolios óptimos, mediante la distribución del capital disponible para inversión entre diferentes actividades agropecuarias o forestales simultáneas (siembra de diferentes cultivos, cría de diferentes animales, etc.) y un instrumento financiero sin riesgo (i.e., con tasa de interés fija), que en México puede ser una cuenta de inversión bancaria a tasa fija o CETES (Certificados de la Tesorería de la Federación), en forma tal que se minimice el riesgo enfrentado por el productor. La forma de auto-aseguramiento aquí propuesta tiene como objetivo minimizar la volatilidad (varianza) de la tasa de rentabilidad obtenida por el productor agropecuario o forestal.

Según la Teoría del Portafolio (Markowitz, 1952; Merton, 1972), para formar el portafolio óptimo el inversionista puede tener que pedir prestado a algunas de las tasas de rentabilidad de los activos incluidos en el portafolio. En lenguaje financiero, esta práctica se conoce como tomar "posiciones cortas", la cual está bien regulada y se usa en mercados financieros desarrollados (Newman et al., 1992; Woelfel, 1994). Sin embargo, en los países en desarrollo no todos los productores agropecuarios y forestales pueden alcanzar arreglos financieros que les permitan tomar posiciones cortas, por lo que en esta investigación se resuelve el problema de minimización de la varianza de la tasa de rentabilidad de los portafolios, sujeto a la restricción de que no hay posiciones cortas (Roberts, 2005). Se considera el caso de productores agropecuarios o forestales que no recurren al crédito, no toman posiciones cortas y pueden diversificar su producción entre dos actividades agropecuarias o forestales, además de poder invertir en un instrumento financiero con tasa de interés fija. Cuando se consideran tres o más actividades agropecuarias o forestales, se vuelve prácticamente imposible resolver algebraicamente el problema de minimización del riesgo, razón por la cual en este artículo solamente se estudia el caso de dos actividades productivas.¹

La importancia del estudio propuesto radica en que muchos productores agropecuarios y forestales del país se encuentran en condiciones de alta vulnerabilidad a los riesgos que enfrentan con respecto al clima, plagas, sequías, precios de productos, etc. En los países desarrollados existen arreglos financieros, instituciones y políticas para el campo, que contribuyen a reducir la vulnerabilidad de los productores agropecuarios y forestales (Makki, 2002; Kang, 2007). Dado que en México aún no están bien desarrollados ni extendidos estos sistemas de protección, la forma de auto-aseguramiento aquí estudiada, consistente en la diversificación de las actividades productivas, ofrece una alternativa de protección con el propósito de ayudar a satisfacer demandas y necesidades sociales como la protección del patrimonio de los productores, la posibilidad de contar con un flujo de ingreso menos volátil, la estabilidad económica que permita una mejor planeación del futuro y una mayor inversión en el campo.

 

PLANTEAMIENTO DEL PROBLEMA

Aquí se estudia el caso en que el productor agropecuario o forestal no puede tomar posiciones cortas. Como marco de referencia, conviene antes revisar el caso de un productor que sí puede tomar posiciones cortas y que considera invertir en dos actividades.

Sea un productor que dispone de un capital de W pesos que tiene dos opciones de inversión:

i) Invertir en un instrumento financiero con tasa de rentabilidad fija R₀. (i.e., CETES o una cuenta bancaria con tasa fija de interés).

ii) Invertir la parte restante en la producción y comercialización de dos productos agropecuarios o forestales, con tasas de rentabilidad R₁ y R₂.

La inversión a tasa de rentabilidad fija R₀ no tiene riesgo alguno, en el sentido de que el productor sabe desde el principio cuantos pesos va a recibir por peso invertido. La tasa de rentabilidad del producto agropecuario "i", R_i, se define como el ingreso bruto en pesos recibido al final del periodo de producción por la venta del producto "i", I_i, dividido por el costo de producción, Ci:

La tasa de rentabilidad R₁está sujeta a incertidumbre, porque depende de factores aleatorios como la cantidad producida del producto "i" que logra venderse, el precio de venta del producto, las condiciones climáticas, las plagas, los desastres naturales, los cambios en las políticas agropecuarias, el costo de los insumos requeridos durante la producción, como fertilizantes, combustible, mano de obra, plaguicidas, alimento, etc.

Así, R_i se puede considerar como una variable aleatoria, con valor esperado μi = E(R_i), i = 1, 2; varianza σ_ii = varianza(R₁), i = 1, 2; desviación estándar σ_i ≡ i = 1, 2 y σ₁₂ ≡ covarianza (R₁,R₂).

Sean ω₀ la fracción del capital W que se invierte a la tasa de rentabilidad fija R₀ y ω_i la fracción del capital W que se invierte en el producto "i", i = 1, 2.

Por construcción, la suma de las fracciones invertidas en las diferentes actividades es igual a 1:

La tasa de rentabilidad R del portafolio descrito es un promedio ponderado de las tasas de rentabilidad R₀, R₁ y R₂, donde los ponderadores son las fracciones del capital W invertidas en las diferentes actividades, ω₀, ω₁ ω₂:

 

R es a su vez una variable aleatoria, con valor esperado:

y varianza:

Si el productor desea obtener una tasa de rentabilidad esperada E; i.e., si desea satisfacer la condición:

puede obtenerla con una infinidad de diferentes portafolios o maneras de distribuir el capital W, pues hasta ahora sólo hay dos restricciones que cumplir (Ecs. 1 y 5), mientras que hay tres variables a escoger: ω₀, ω₁ ω₂. Un productor renuente al riesgo que pueda tomar posiciones cortas y esté interesado en encontrar el portafolio que le dé la tasa de rentabilidad esperada deseada, E, con el menor riesgo posible, debe resolver el siguiente problema de minimización de la varianza:

El problema de minimización anterior puede ser resuelto (Merton, 1972; Constantinides y Malliaris, 1995) para cualquier valor E ∈ R, al obtener la varianza mínima σ²(E) correspondiente a E ∈ R. El conjunto { (σ(E),E) ∈ R² | E ∈ R } se puede graficar sobre el plano R² para obtener así la Frontera de Media-Desviación Estándar generada por R₀, R₁ y R₂. En la Figura 1 se muestra la frontera correspondiente al Problema I, para E ≥ R₀, como la recta que parte del punto (0, R₀).

Para estudiar el efecto que tiene la exclusión del instrumento financiero sin riesgo, a continuación se considera un productor que puede tomar posiciones cortas y que quiere invertir únicamente en la producción y comercialización de dos productos agropecuarios o forestales con tasas de rentabilidad R₁ y R₂ (i.e. , no considera invertir en el instrumento financiero con tasa de rentabilidad fija). Este productor estaría interesado en resolver el siguiente problema de minimización:

 

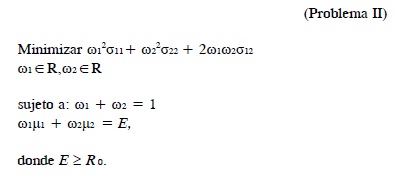
En la Figura 1 se muestra la frontera correspondiente al Problema II, para E ≥ R₀, como una hipérbola. El hecho de que esta hipérbola se encuentra a la derecha de la recta (salvo en el punto de tangencia) significa que si el productor decide no incluir el instrumento financiero con tasa de rentabilidad fija en su portafolio, incurre en un riesgo mayor al que incurriría si lo incluye junto con las dos actividades agropecuarias y forestales.

Además, en la Figura 1 ambas fronteras (la recta y la hipérbola) son tangentes en un único punto que corresponde a la tasa de rentabilidad esperada (Constantinides y Malliaris, 1995):

 

En el caso del productor que puede tomar posiciones cortas y que invierte en el instrumento financiero con tasa de rentabilidad fija y en las dos actividades productivas, en función de los valores de los parámetros R₀, μ₁, μ₂, σ₁₁, σ₁₂ y σ₂₂ y de la tasa de rentabilidad esperada E, puede ser que al resolver el Problema I encuentre que algún o algunos de los valores óptimos ω_i(E) sean negativos, i ∈ {0,1,2} (i.e., que el productor efectivamente tome posiciones cortas). La interpretación de estos valores negativos es como sigue. Supóngase que al resolver el Problema I se obtiene la solución: ω₀(E) = -0.20, ω₁(E) = 1.60 y ω₂(E) = -0.40 . Se observa que ω₀(E) + ω₁(E) + ω₂(E) = -0.20 + 1.60 -0.4 = 1. Entonces ω₀(E) = -0.20 significa que para formar el portafolio óptimo, el productor debe pedir prestados 0.20W pesos a la tasa de interés fija R₀; ω₂(E) = -0.40 significa que el productor debe pedir prestados 0.40W pesos a la tasa de interés variable R₂. Al sumar estos dos préstamos a su capital original W, el productor tendrá 1.60W pesos que invierte en el producto "1". Al final, el productor obtendrá 1.60WR₁ pesos, y deberá pagar a sus acreedores 0.20WR₀ y 0.40WR₂ pesos.

Para el caso de productores que no pueden tomar posiciones cortas, la actividad agropecuaria o forestal "1" será la que presente la mayor tasa de rentabilidad esperada (i.e., supóngase que μ₂ < μ₁). Por otra parte, se supone que la tasa de rentabilidad del instrumento financiero sin riesgo, R0, es menor que las tasas de rentabilidad esperadas de las dos actividades agropecuarias o forestales (R₀ < μ₂ < μ₁), ya que un productor renuente al riesgo jamás consideraría invertir en el campo, si aparte de enfrentar un riesgo la tasa de rentabilidad esperada fuese menor a la tasa sin riesgo R₀, pues invertiría todo su capital W en el instrumento financiero sin riesgo.

El incorporar la restricción de no posiciones cortas agrega tres restricciones adicionales al Problema I: Los ponderadores ω_i's no pueden tomar valores negativos (ω₀ ≥ 0, ω₁ ≥ 0, ω₂ ≥ 0). Una primera consecuencia de esta nueva restricción es que el productor no puede formar un portafolio con una tasa de rentabilidad esperada menor a Ro, ni mayor a μ1.² Así, el problema que aquí interesa resolver es el siguiente:

 

Sin embargo, antes de resolverlo, conviene reescribirlo de la siguiente manera³:

 

La solución del Problema IV son funciones ω₁(E) y ω₂(E), que para cada valor de la tasa de rentabilidad esperada E (R₀≤ E ≤ μ₁), indican las fracciones del capital W que se deben invertir en las actividades productivas "1" y "2", respectivamente. La fracción de W que se invierte en el instrumento financiero con tasa de rentabilidad fija R₀ es:

La varianza mínima de la tasa de rentabilidad del portafolio con la que se obtiene la tasa de rentabilidad esperada E, es por tanto:

Para cada tasa de rentabilidad esperada E y bajo el supuesto de que el vector aleatorio (R₁ R₂) tiene distribución normal bivariada, los intervalos de confianza de 99 %, 95 % y 90 %, I₉₉(E) I₉₅ e I₉₀(E), respectivamente, son:

 

La interpretación del intervalo de confianza I₉₉ (E) es como sigue: Si el productor forma el portafolio óptimo con tasa de rentabilidad esperada E, obtenido al resolver el Problema IV, con probabilidad (condicionada sobre los valores de los seis parámetros R₀, μ₁, μ₂, σ₁₁, σ₁₂ y σ₂₂) de 99 %, la tasa de rentabilidad obtenida al final del ciclo productivo será mayor o igual a E - 2.576σ(E) y menor o igual a E + 2.576σ(E). En otras palabras, con probabilidad de 1 %, la tasa de rentabilidad obtenida será menor a E - 2.576σ(E) o mayor a E + 2.576σ(E).

 

EL PORTAFOLIO ÓPTIMO

El Problema IV es un ejemplo de Programa Convexo Ordinario con restricciones de igualdad y de desigualdad, que en este trabajo se resolvió con el teorema de Kuhn-Tucker (Kuhn y Tucker, 1951; Rockafellar, 1997). El primer paso para su resolución es plantear el Lagrangiano:

Luego se derivó el Lagrangiano respecto a ω₁ y ω₂, se igualó a cero, y se obtuvo el sistema de dos ecuaciones simultáneas:

 

También se derivó con respecto al coeficiente λ₄, que corresponde a la única restricción de igualdad, y se igualó a cero para obtener la ecuación:

 

No se derivó con respecto a los coeficientes λ₁, λ₂ y λ₃ que están asociados a las tres restricciones de desigualdad, sino que se incorporó el siguiente conjunto de condiciones sobre ellos:

 

Al resolver el sistema de ecuaciones y desigualdades simultáneas (dado por las Ecs. 13 a 18) se encuentra que la solución del Problema IV depende en gran parte de lo que aquí se denomina "coeficientes cuadrados de variación de las tasas de rentabilidad R₁ y R₂" y "coeficiente de covariación de las tasas de rentabilidad R₁ y R₂", conceptos que se definen a continuación y que están muy relacionados con el concepto estadístico de "coeficiente de variación" (Spanos, 1999).

El coeficiente cuadrado de variación de la tasa de rentabilidad Ri, Cii, se define como:⁴

 

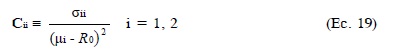
El coeficiente de covariación de las tasas de rentabilidad R₁ y R₂, C₁₂, se define como:⁵

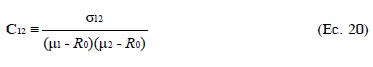
Se encuentra así que la composición del portafolio óptimo depende de la relación que guarden entre sí los coeficientes C₁₂, C₁₁y C₂₂, así como de la posición de la tasa de rentabilidad esperada deseada, E, en el intervalo [R₀ , μ1] . A continuación se presentan los resultados algebraicos que, para cada tasa de rentabilidad esperada E, muestran la composición del portafolio óptimo (ω₁(E), ω₂ (E) y ω₀(E)) y la varianza de su tasa de rentabilidad (σ²(E)).

Nótese primero que se cumple que C₁₂ < max{ C₁₁ , C₂₂}⁶. Esta desigualdad da origen a tres casos posibles para la colocación relativa de los tres coeficientes: C₁₂ < C₁₁ y C₁₂ ≤ C₂₂ ; C₂₂ ≤ C₁₂< C₁₁ ; C₁₁ ≤ C₁₂ < C₂₂. A continuación, para cada caso se presenta la composición del portafolio óptimo, así como la varianza de su tasa de rentabilidad.

Caso 1. Los valores de los parámetros R₀, μ₁, μ₂, σ₁₁, σ₁₂ y σ₂₂ son tales que C₁₂≤C₁₁ y C₁₂ ≤ C₂₂; i.e., los coeficientes cuadrados de variación C₁₁ y C₂₂ pueden ser iguales o diferentes, y C₁₂ es menor o igual a ambos.

En este caso la covarianza de los rendimientos de las dos actividades productivas es negativa (C₁₂ < 0), cero (C₁₂ = 0), o positiva pero pequeña (0 < C₁₂ < C₁₁ y 0 < C₁₂ < C₂₂). Cuando C₁₂ < 0, las actividades productivas "1" y "2" son complementarias, en el sentido de que si en alguna de ellas se obtiene una tasa de rentabilidad por debajo de su tasa de rentabilidad esperada, hay una tendencia para que en la otra actividad productiva se obtenga una tasa de rentabilidad por arriba de su tasa de rentabilidad esperada. Cuando C₁₂ = 0, las tasas de rentabilidad de las actividades productivas "1" y "2" no están correlacionadas. Cuando C12 es positiva pero pequeña se tiene que si en alguna de las actividades productivas se obtiene una tasa de rentabilidad por abajo (arriba) de su tasa de rentabilidad esperada, hay cierta tendencia para que en la otra actividad productiva también se obtenga una tasa de rentabilidad por abajo (arriba) de su tasa de rentabilidad esperada.

Si R₀≤ E ≤ E_T (E_T dado por Ec. 6), la composición del portafolio óptimo con tasa de rentabilidad esperada E es:

 

La varianza de la tasa de rentabilidad del portafolio óptimo con tasa de rentabilidad esperada E es:

Por otra parte, si E_T ≤ E ≤ μ1, la composición del portafolio óptimo con tasa de rentabilidad esperada E es:

 

La varianza de la tasa de rentabilidad del portafolio óptimo con tasa de rentabilidad esperada E es:

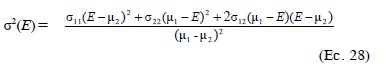
Caso 2. Los valores de los seis parámetros R₀, μ₁, μ₂, σ₁₁, σ₁₂ y σ₂₂ son tales que C₂₂≤C₁₂ < C₁₁; i.e., los coeficientes cuadrados de variación son diferentes (C₁₁≠ C₂₂) y C₁₂ es mayor o igual a C₁₁, que es el menor de ellos.

En este caso la actividad productiva "1", que tiene una tasa de rentabilidad esperada mayor que la de la actividad productiva "2" ( μ₂ < μ₁), presenta mayor volatilidad que la actividad "2" (C₁₁ ≤ C₁₂). Por otra parte, la covarianza de las tasas de rentabilidad de las dos actividades productivas es grande (C₁₁ ≤ C₁₂). Lo primero significa que la tasa de rentabilidad de la actividad "1" es muy volátil y lo segundo que la tasa de rentabilidad de la actividad productiva "1" tiene una alta correlación positiva con la tasa de rentabilidad de la actividad "2".

Si R₀ ≤ E ≤ μ₂, la composición del portafolio óptimo con tasa de rentabilidad esperada E es:

La varianza de la tasa de rentabilidad del portafolio óptimo con tasa de rentabilidad esperada E es:

 

Y si μ2 ≤ E ≤μ1 , la composición del portafolio óptimo con tasa de rentabilidad esperada E es:

 

 La varianza de la tasa de rentabilidad del portafolio óptimo con tasa de rentabilidad esperada E es:

Caso 3. Los valores de los parámetros R₀, μ₁, μ₂, σ₁₁, σ₁₂ y σ₂₂ son tales que C₁₁ ≤ C₁₂ < C₂₂; i.e., los coeficientes cuadrados de variación son diferentes (C₁₁ ≠ C₂₂) y C₁₂ es mayor o igual a C₁₁, que es el menor de ellos.

En este caso la actividad productiva "2", que tiene menor tasa de rentabilidad esperada que la actividad productiva "1" ( μ₁ < μ₂), presenta mayor volatilidad en su tasa de rentabilidad que la actividad "1" (C₁₁ < C₂₂). Por otra parte la covarianza entre las tasas de rentabilidad de las dos actividades productivas es grande (C₁₁ ≤ C₁₂). Lo primero significa que la tasa de rentabilidad de la actividad "2" es muy volátil, y lo segundo que la tasa de rentabilidad de la actividad productiva "2" tiene una alta correlación positiva con la tasa de rentabilidad de la actividad "1".

Para todo el rango R₀≤ E ≤ μ₁, la composición del portafolio óptimo con tasa de rentabilidad esperada E es:

La varianza de la tasa de rentabilidad del portafolio óptimo con tasa de rentabilidad esperada E es:

 

IMPLEMENTACIÓN DE LOS RESULTADOS

En esta sección, mediante un ejemplo se muestra como se usan las fórmulas algebraicas aquí obtenidas para encontrar el portafolio de mínima varianza con tasa de rentabilidad esperada E, la varianza de su tasa de rentabilidad y los intervalos de confianza.

Supóngase a un productor agropecuario o forestal que tiene el siguiente registro de las tasas de rentabilidad obtenidas en los últimos 16 ciclos productivos, donde cada ciclo tiene una duración de 122 d (4 meses)⁷:

 

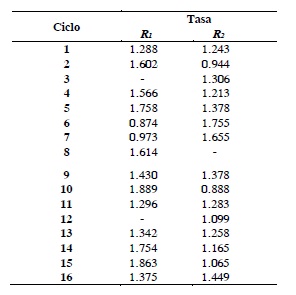
En los ciclos "3" y "12" no hay registro de R₁. En el ciclo "8" no hay registro de R₂. Por tanto, sólo hay registros simultáneos de R₁ y R₂ en 13 ciclos. Para poder utilizar las formulas presentadas anteriormente, que suponen μ₂ < μ₁, en la columna "R₁" aparece la serie de tasas de rentabilidad con mayor promedio⁸.

Supóngase también que la tasa de interés anualizada del instrumento financiero sin riesgo es r = 1.071 (7.1 %). Entonces la tasa de interés efectiva sobre el periodo de 122 d, R₀, es (Capinski y Zastawniak, 2004):

 

donde m es el número de días que dura el ciclo.

Las fórmulas obtenidas en la sección anterior para la composición del portafolio óptimo con tasa de rentabilidad esperada E, ω₀ (E), ω₁ (E), ω₂ (E) y su varianza σ²(E), están en función de R₀ y de los parámetros. Por ser desconocidos, estos cinco últimos deberán ser estimados a partir de los registros históricos de las tasas de rentabilidad.

Paso 1: Estimación de los parámetros μ₂, μ₁, σ₁₁, σ₁₂ y σ₂₂.

Las tasas de rentabilidad esperadas, μ₁ y μ₂, se estiman como el promedio simple de los Ni registros disponibles de las tasas de rentabilidad:

Las varianzas σ₁₁ y σ₂₂ y la covarianza σ₁₂ se estiman de la siguiente manera:

donde N₁₂ es el número de ciclos en los cuales existen registros simultáneos de R₁ y R₂ (N₁₂ = 13).

Paso 2: Cálculo de estimados de los coeficientes C₁₁, C₁₂ y C₂₂.

Al sustituir los valores y R₀ en Ecs. 19 y 20, se obtienen los estimados ^{^}C₁₁ = 0.4707, ^{^}C₁₂ = -0.5882 y ^{^}C₂₂ = 0.9040

Paso 3: Elección entre los Casos 1, 2 y 3.

Dado que para los datos analizados se cumple que 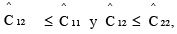, se está en el Caso 1. Al sustituir los valores y R₀ en Ec. 6, se obtiene el estimado de E_T, ^{^}E_T = 1.36. La composición del portafolio óptimo con tasa de rentabilidad esperada E, así como su varianza, están dadas por las Ecs. 21 a 24 (se usan los valores , y por las Ecs. 25 a 28 (se usan los valores ) si ^{^}E_T ≤ E ≤ ^{^}µ₁⁹.

Paso 4: Cálculo de los intervalos de confianza.

Para cada valor de E en el intervalo [R₀, μ₁], los estimados de los intervalos de confianza se calculan así:

 

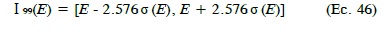
donde, según el caso y el valor de E, ^{^}σ (E) se obtiene de las Ecs. 24, 28, 32, 36 ó 40, al sustituir los valores de los parámetros μ₁, μ₂, σ₁₁, σ₁₂ por sus estimados

En la Figura 2 se presenta la Frontera de Media-Desviación Estándar correspondiente a este ejemplo.

  

Finalmente, al usar el valor de R₀ junto con los estimados en las ecuaciones correspondientes al caso (Caso 1, 2 ó 3), se puede construir el Cuadro 1 que registra para diferentes valores de la tasa de rentabilidad esperadas E, entre R₀ = 1.024 y ^{^}μ₁ = 1.473, la estimación de la composición del portafolio óptimo con tasa de rentabilidad esperada E (columnas "ω₀","ω₁","ω₂"), la desviación estándar estimada de la tasa de rentabilidad del portafolio óptimo (columna "σ"), y los estimados de los intervalos de confianza de 99 %, 95 % y 90 % de la tasa de rentabilidad del portafolio óptimo, para el siguiente ciclo productivo (columnas "99%", "95%" y "90%" respectivamente).

El Cuadro 1 indica que si el productor desea obtener una tasa de rentabilidad esperada de 30 % (E = 1.30) con el menor riesgo posible, deberá invertir 17.9 % de su capital en el instrumento financiero con tasa de rentabilidad fija R₀ (ω₀ = 0.179), 36 % de su capital en el producto "1" ((ω₁ = 0.360) y el restante 46.2 % en el producto "2" (ω₂ = 0.462). La desviación estándar de la tasa de rentabilidad de este portafolio es igual a 0.049 (σ = 0.049). Con una probabilidad de 99 %, la tasa de rentabilidad de este portafolio estará entre 1.174 (17.4 %) y 1.426 (42.6 %); con probabilidad de 95 %, la tasa de rentabilidad del portafolio estará entre 1.204 (20.4 %) y 1.396 (39.6 %), y con probabilidad de 90 %, la tasa de rentabilidad del portafolio estará entre 1.219 (21.9 %) y 1.381 (38.1 %).

Si el productor desea obtener un rendimiento esperado de 43 % (E = 1.43) con el menor riesgo posible, deberá invertir 78.6 % de su capital en el producto "1" (ω₁ = 0.786), y el restante 21.4 % en el producto "2" (ω₂ = 0.214), y no invertirá nada en el instrumento con tasa de rendimiento fija R₀ (ω₀ = 0.0). La desviación estándar de este portafolio es igual a 0.198 (σ = 0.198). Con probabilidad de 99 %, la tasa de rentabilidad de este portafolio estará entre 0.920 (pérdida de 8 %) y 1.940 (ganancia de 94 %). Así, el aumentar la tasa de rendimiento esperada E de 30 % a 43 % trae consigo un incremento de la desviación estándar de la tasa de rentabilidad del portafolio óptimo, de 0.049 a 0.198, y el consiguiente aumento en la longitud de los intervalos de confianza.

La construcción de un conjunto de datos como el Cuadro 1 es de utilidad, pues permite que el productor, dada su función de utilidad y su grado de aversión al riesgo, pueda elegir la tasa de rentabilidad esperada E que desee para su inversión y el portafolio óptimo correspondiente.

 

CONCLUSIONES

Se consideró un productor agropecuario o forestal renuente al riesgo, que no puede tomar posiciones cortas y desea invertir simultáneamente en dos actividades productivas diferentes mediante un portafolio óptimo que le dé el menor riesgo posible, medido este último como la varianza en la tasa de rentabilidad de su inversión. Para lograr este objetivo es conveniente que el portafolio contemple la inclusión de un instrumento financiero con tasa de rendimiento fija (por ejemplo CETES o una cuenta bancaria), pues de lo contrario se incurre en mayor riesgo.

El problema planteado de minimización de la varianza de la tasa de rendimiento de la inversión se resolvió algebraicamente con el método de Kuhn-Tucker. La principal aportación de este trabajo fue la obtención de 20 fórmulas (Ecuaciones 21 a 40) que le permiten al productor que no puede tomar posiciones cortas, encontrar para cada nivel posible de la tasa de rentabilidad esperada de la inversión, E, la composición del portafolio óptimo, la desviación estándar de la tasa de rentabilidad del portafolio óptimo y los intervalos de confianza de 99, 95 y 90 % de la tasa de rentabilidad del portafolio óptimo, a partir de registros históricos de las tasas de rendimiento obtenidas en varios ciclos productivos pasados¹⁰. A partir de esta información, que se puede presentar en forma de cuadro, cada productor, de acuerdo con su función de utilidad y grado de aversión al riesgo, puede elegir la tasa de rentabilidad esperada E que desea para su inversión y el portafolio óptimo correspondiente.

La formación del portafolio óptimo aquí estudiado es una forma de auto-aseguramiento al permitirle al productor una reducción notable en el riesgo inherente a su actividad empresarial. Esto puede contribuir a proteger el patrimonio de los productores, a tener la posibilidad de contar con un flujo de ingreso menos volátil, y en general a lograr una mayor estabilidad económica que permita una mejor planeación del futuro y una mayor inversión en el campo.

 

BIBLIOGRAFÍA

Barnett B J (2004) Agricultural index insurance products: strengths and limitations. Presented at Agricultural Outlook Forum, 19 February, Washington, USA. 40 p.         [ Links ]

Capiñski M, T Zastawniak (2004) Mathematics for Finance: An Introduction to Financial Egineering. Springer. London. 310 p.         [ Links ]

Constantinides G M, A Malliaris (1995) Portfolio Theory: In: Finance, Handbooks in Operations Research and Management Science, Vol. 9. North-Holland. Amsterdam. pp:1-30        [ Links ]

Kang M G (2007) Innovative agricultural insurance products and schemes. Agricultural Management, Marketing and Finance Occasional Paper 12. Food and Agriculture Organization of the United Nations. Rome. 49 p.         [ Links ]

Kuhn H W, and A W Tucker (1951) Nonlinear programming, In: Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability. Neyman J (ed). University of California Press, Berkeley, CA. pp:481-492        [ Links ]

Larson D F, P Varangis and N Yabuki (1998) Commodity risk management and development. Policy Research Working Paper, No. 1963, August. The World Bank. Washington, D.C. 35 p.         [ Links ]

Makki S S (2002) Crop Insurance: Inherent Problems and Innovative Solutions. In: Agricultural Policy for the 21st Century. L Tweeten, S R Thompson (eds). Blackwell Publishing Co. Ames, Iowa. pp:109-126.         [ Links ]

Markowitz H (1952) Portfolio Selection. J. Finance 7:77-91.         [ Links ]

Merton R C (1972) An analytic derivation of the efficient portfolio frontier. J. Financial Quant. Anal. 7:1151-1172.         [ Links ]

Miranda M J, J W Glauber (1997) Systemic risk, reinsurance, and the failure of crop insurance markets. Amer. J. Agric. Econ. 79:206-215.         [ Links ]

Newman P, M Milgate, J Eatwell (1992) The New Palgrave Dictionary of Money and Finance. Vol. 3. Macmillan Press, London. pp:445-446        [ Links ]

Quiggin J (1994) The optimal design of crop insurance. In: Economics of Agricultural Crop Insurance: Theory and Evidence. D L Hueth, W H Furtan (eds). Kluwer Academic Publishers. Boston. pp:115-134.         [ Links ]

Roberts R A J (2005) Insurance of crops in developing countries. FAO Agricultural Services Bulletin 159. Food and Agriculture Organization of the United Nations, Rome. 78 p.         [ Links ]

Rockafellar T R (1997) Convex Analysis. Princeton University Press, Princeton Landmarks in Mathematics and Physics, Princeton, New Jersey. 451 p.         [ Links ]

Spanos A (1999) Probability Theory and Statistical Inference: Econometric Modeling with Observational Data. Cambridge University Press, Cambridge. 815 p.         [ Links ]

Varangis P, D F Larson (1996) Dealing with Commodity Price Uncertainty. Policy Research Working Paper, No. 1667, October. World Bank.         [ Links ]

Vaughan E J, and T M Vaughan (2003) Fundamentals of Risk and Insurance. 9th ed. John Wiley & Sons. New York. 704 p.         [ Links ]

Woelfel Ch (1994) Encyclopedia of Banking & Finance, 10th ed. Probus Publishing Company, Chicago. 1219 p.         [ Links ]

 

Notas

¹ En una investigación en curso se está considerando el caso en que los productores pueden recurrir al crédito y diversificar su producción entre N actividades agropecuarias o forestales, con N ≥ 2, y el instrumento financiero sin riesgo. El problema de minimización de la varianza de la tasa de rentabilidad se resuelve con métodos computacionales, pues la complejidad del problema no permite una solución algebraica, a diferencia del caso de dos actividades agropecuarias o forestales estudiado en el presente artículo.

² Un promedio ponderado de tres números R₀, μ₂ y μ₁, con ponderadores ω₀, ω₂ y ω₁ no negativos, que suman la unidad, no puede ser menor que el menor de los números promediados (R₀), ni mayor que el mayor de los números promediados (μ₁).

³ Al despejar ω₀ de (III-a) y sustituir en (III-b) se tiene: ω₁ (μ₁ - R₀) + ω₂( μ₂ - R₀) = E - R₀. De (III-a) se tiene que ω₁+ ω₂ = 1-ω₀. Por (III-c), ω₁ + ω2 < 1. La ventaja de reescribir el problema en la forma (IV) es que se reduce el número de restricciones de cinco a cuatro y se reduce el número de variables de tres (ω₀, ω₁ y ω₂) a dos (ω₁ y ω₂)

⁴ El coeficiente cuadrado de variación representa la razón de la varianza de R_i (σii) a la tasa de rentabilidad esperada de R_i (μ₁) en exceso de la tasa de rentabilidad sin riesgo, R₀, al cuadrado y permite comparar la volatilidad de las dos tasas de rentabilidad R₁ y R₂, aún cuando éstas difieran en sus tasas de rentabilidad esperadas.

⁵ Este coeficiente representa la razón de la covarianza entre R₁ y R₂ (σ₁₂) al producto de las tasas de rentabilidad esperadas de R₁ y R₂ en exceso de la tasa de rentabilidad sin riesgo,R₀, y permite comparar la covarianza de las dos tasas de rentabilidad R₁ y R2, con las varianzas de las tasas de rentabilidad R₁ y R₂ aún cuando éstas difieran en sus tasas de rentabilidad esperadas.

⁶ Por ser Σ matriz positiva definida, σ_12² < σ₁₁σ₂₂, por lo cual C_12² < C₁₁C₁₂ < max{ C₁₁², C₂₂²}, y se obtiene que C₁₂ < max{C₁₁, C₂₂}.

⁷ Los datos de los rendimientos R₁ y R₂ presentados en el cuadro se generaron aleatoriamente al suponer una distribución normal bivariada del vector aleatorio (R₁ R₂) con E(R₁) = 1.5, E(R₂) = 1.3, var(R₁) = 0.09, var(R₂) = 0.13 y cov(R₁, R₂) = -0.03

⁸ El promedio de los datos de la columna "R₁" es 1.473, el promedio de los datos de la columna "R₂" es 1.272

⁹ Si para otro conjunto de registros se cumple que 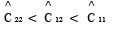(Caso 2), entonces la composición del portafolio óptimo y su varianza están dadas por las Ecs. 29 a 36. Si 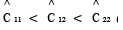(Caso 3), entonces la composición del portafolio óptimo y su varianza están dadas por las Ecs. 37 a 40.

¹⁰ Para el caso del inversionista que sí puede tomar posiciones cortas, las fórmulas de la composición del portafolio óptimo fueron derivadas por Markovitz (1952) y Merton (1972).