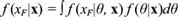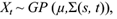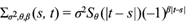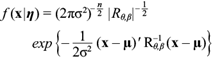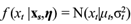1. Introduction
Direct and continuous measurements of carbon dioxide (CO2) in the atmosphere extend back only to the 1950s (British Antarctic Survey, 2014). However, scientists developed alternative ways of measuring greenhouse gases (GHG) concentrations in the earth’s atmosphere that prevailed far in the past. One of these techniques is based on ice core sampling. The core samples are cylinders of ice drilled out of an ice sheet or glacier (British Antarctic Survey, 2014), which contain small bubbles of air that trapped a sample of the atmosphere. The deepest ice cores extend to 3.26 km in depth, at only a few meters above bedrock. The oldest continuous ice core records to date extend back 800 000 years (Jouzel et al., 2007). To determine the date of the ice cores, scientists may use either snow accumulation and a mechanical flow model (Parrenin et al., 2007), or a firn densification model (Loulergue et al., 2007) to further compensate for differences in the age of the gas and the age of the surrounding ice.
The European Project for Ice Coring in Antarctica (EPICA) drilled two deep ice cores at Kohnen and Concordia. At the latter station, also called Dome C, the team of researchers produced climate records focusing on water isotopes, aerosol species and GHG. Temperature measurements are not observed but inferred from deuterium observations (Jouzel et al., 2007).
To estimate GHG concentrations in the earth beyond one million years ago, other techniques are required. Recently, Montanez-Boti et al. (2015) estimated CO2 levels from the Pliocene period (around three million years ago). These estimations were based on the boron isotopic composition of Globigerinoides ruber, a surface mixed-layer dwelling planktic foraminiferal species from the Ocean Drilling Program (ODP) site 999. The boron isotopic composition is a well-constrained function of seawater pH. It is well correlated with the aqueous concentration of CO2 (CO 2aq ). In the absence of major changes in surface hydrography, CO 2aq is largely a function of atmospheric CO2 levels.
On the other hand, for the late Paleozoic deglaciation (around 300 million years ago), Montanez et al. (2007) use the stable isotopic compositions of soil-formed minerals, fossil- plant matter, and shallow-water brachiopods to estimate atmospheric partial pressure of carbon dioxide (pCO2) and tropical marine surface temperatures.
The aim of this paper is to interpolate several paleoclimate datasets and make them available to the global community for further statistical analysis.
There are several interpolation methods for climate time series, which are mostly summarized in Mudelsee (2010). The most popular stochastic interpolation method is linear interpolation, which assumes a standard Brownian motion process (e.g., Chang, 2012; Eckner, 2012). More recently, Nieto-Barajas and Sinha (2015) proposed an interpolation method based on a Gaussian process model with a novel parameterization of the variance function. They compared their proposal with alternative models and showed that it is superior according to some specific fitting measures.
Interpolation of climate time series has been criticized by several authors (e.g., Schulz and Stattegger, 1997; Schulz and Mudelsee, 2002) arguing a loss of high-frequency variability and a spectral bias towards low frequencies. However, Bayesian stochastic interpolation methods account for the uncertainty in the estimation by means of the posterior predictive distribution, which allows to produce not only point predictions but posterior credible intervals for the interpolated series.
According to Rehfeld and Kurths (2014), paleoclimate time series are more challenging than the data in other disciplines since neither observation time nor the climatic variable are known precisely. Both have to be reconstructed, resulting in irregular and age-uncertain time series. To avoid interpolation these authors have studied the performance of dependence measures such as the Gaussian kernel based cross correlation and a generalized mutual information function. On the other hand, individual time series models have been proposed to account for the uneven time spacing. Robinson (1977) and Schulz and Mudelsee (2002) defined a first order autoregressive process where the autocorrelation parameter as well as the variance of the errors are functions of the time difference between two observed points. Alternatively, Polanco-Martínez and Faria (2015) estimate the wavelet spectrum of the time series.
The contents of the rest of the paper are as follows: In Section 2 we first present the datasets to interpolate. In Section 3 we recall the Bayesian thinking and describe the Gaussian process Bayesian model used for interpolation in Section 4. The actual interpolation of the series is presented in Section 5 and we conclude with some final remarks in Section 6.
2. Datasets
We will be using several datasets with different time scales. Variables measured are temperature, CO2 and methane (CH4). Actual temperatures are not usually provided. Instead, temperature anomalies with respect to a specific reference value are reported. The scale used is degrees centigrade (ºC). CO2 is usually reported in parts per million by volume (ppmv) and CH4 is measured in parts per billion by volume (ppbv). We start with the most recent information and progress backwards in time to approximately 300 million years ago.
The first dataset covers recent history from 1950 to 2013 for a period of 65 years and is shown in Figure 1. The top panel contains global land temperature anomalies with respect to the mean temperature in the years 1951-1980 (Hansen et al., 2010). The middle panel contains CO2 values from two different sources: atmospheric values derived from flask air samples collected at the South Pole (line) (Keeling et al., 2008), and Law Dome ice core records (dots) (MacFarling Meure et al., 2006). As can be seen, the dots follow the trend of the line, which confirms the ice core sample acts as an accurate measure of atmospheric gas concentrations. The bottom panel contains methane records from the law dome ice core (MacFarling Meure et al., 2006).
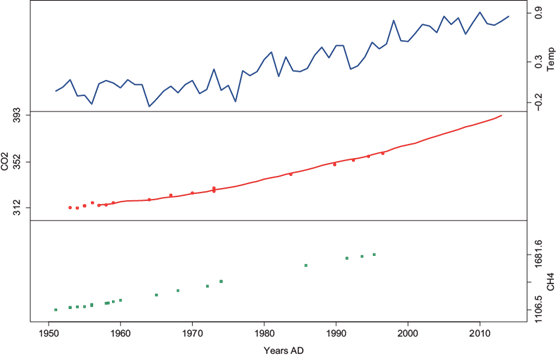
Fig. 1 Recent history data. Top: land temperature anomalies; middle: CO2, atmospheric values derived from flask air in the South Pole (line) and Law Dome ice core records (dots); bottom: CH4 Law Dome ice core records.
The second dataset covers the marine isotope stage, including a long range of 800 000 years before present. These data are shown in Figure 2. The top panel presents temperature anomalies with respect to the average temperature of the millennium (Jouzel et al., 2007). The middle panel includes carbon dioxide concentrations (Luthi et al., 2008), and the bottom panel contains methane values (Loulergue et al., 2008).
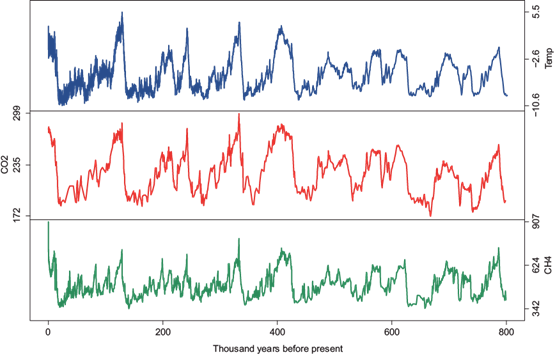
Fig. 2 EPICA dome C ice core 800 thousand years data. Top: Antarctic temperature anomalies; middle: CO2; bottom: CH4.
The third dataset covers the late Pliocene extending from 2.3 to 3.3 million years ago. The data are shown in Figure 3. The top panel contains interpolated relative mean annual sea surface temperature (SST) change (Montanez-Boti et al., 2015). The second panel presents the interpolated relative mean annual surface air temperature change (van de Wal et al., 2011). The bottom panel shows atmospheric CO2 reconstructions based on multi-site boron-isotope records (Montanez-Boti et al., 2015).
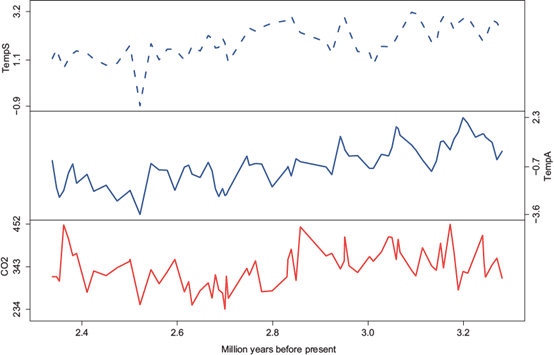
Fig. 3 Late Pliocene climate records extended from 2.3 to 3.3 million years ago. Top: Temperature anomalies in the sea surface; Middle: Temperature anomalies in the air; Bottom: CO2.
The fourth dataset covers the late Paleozoic deglaciation from 265 to 300 million years ago. The data are presented in Figure 4. The top panel shows paleotropical SSTs and the bottom panel presents estimated atmospheric pCO2. Both datasets were obtained from Montanez et al. (2007).
3. Bayesian thinking
Bayesian statistics is an alternative way of making inference about the unknown parameters in a probability model. It is based on decision theory, which establishes the foundations of inferential procedures by treating them as decision problems (DeGroot, 2004). As part of the inferential process, it is necessary to quantify the uncertainty about the unknown quantities (parameters or future observations) by using probability distributions. This quantification can reflect the beliefs of the statistician, or the lack of knowledge about the problem. As a consequence of this quantification, all observable variables, as well as the fixed parameters of the model, are described through probability distributions, simplifying so the inferential procedure. For a comprehensive exposition on the Bayesian foundations see Bernardo and Smith (2000) and references therein.
The methodology establishes how to formally combine an initial (prior) degree of belief of a researcher with currently measured or observed data in such a way that it updates the initial degree of belief. The result is called posterior belief. This process is called Bayesian inference since the updating process is carried out through the application of Bayes’ theorem. The posterior belief is proportional to the product of the two types of information, the prior information about the parameters in the model, and the information provided by the data. This second part is usually thought of as the objective portion of the posterior belief. We explain this process below. In what follows we denote by f (•) a density function of the argument inside the parenthesis, and a vertical bar “|” to denote conditional probabilities.
Let X = (X
1
, X
2
,..., X
n
) be a set of random variables whose joint distribution is denoted by f (x|θ), where θ is a parameter vector that characterizes the form of the density. In the case of independence, f (x|θ) = 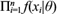 where the marginal distribution for each of the X
i
is coming from a probability model with density function f (x
i
|θ). Function f (x|θ) is usually referred to as the likelihood function. Prior available information on the parameter is described through a prior distribution f(θ) that must be specified or modeled by the researcher. Then formally, it follows that
where the marginal distribution for each of the X
i
is coming from a probability model with density function f (x
i
|θ). Function f (x|θ) is usually referred to as the likelihood function. Prior available information on the parameter is described through a prior distribution f(θ) that must be specified or modeled by the researcher. Then formally, it follows that
where f(x) is the marginal joint density of x defined as f(x) = ∫ f (x|θ) f (θ)dθ if θ is continuous, and f(x) = ∑ θ f (x|θ)f(θ) if θ is discrete. This is Bayes’ theorem that rules the updating of the information. Considering that f(x) is just a constant for θ, then the updating mechanism can be simply written as f(θ|x) ∝ f(x|θ)f(θ), where “∝” indicates proportionality. In other words, the posterior distribution of the parameters, conditional on the observed data, is proportional to the product of the likelihood function and the prior degree of belief. Any inference on the parameters is now carried out using the posterior distribution f(θ|x).
As can be proved (DeGroot, 2004), the only criterion for optimal decision making, consistent with the axiomatic system, is the maximization of the expected utility. Alternatively, this criterion is equivalently replaced by the minimization of a loss function. Therefore, in the Bayesian framework, parameter estimation is done by minimizing the expected value of a specified loss function l( , θ) with respect to
, θ) with respect to  , where the expected value is taken with respect to the posterior distribution of the parameter θ given the data y. In particular, a quadratic loss function l(
, where the expected value is taken with respect to the posterior distribution of the parameter θ given the data y. In particular, a quadratic loss function l( , θ) = (
, θ) = ( - θ)2 leads to the posterior mean
- θ)2 leads to the posterior mean  = E(θ|x) as an optimal estimate for the parameter. On the other hand, a linear loss function l(
= E(θ|x) as an optimal estimate for the parameter. On the other hand, a linear loss function l( , θ) = |
, θ) = | - θ| yields the median of the posterior distribution as an optimal estimate
- θ| yields the median of the posterior distribution as an optimal estimate  for θ.
for θ.
When the main purpose of modeling is prediction, then the observed data x are used to predict future observations X F by means of the posterior predictive distribution. In the continuous case the predictive distribution is defined as
where f (x
F
| θ,
x
) becomes f (x
F
|θ) in the case that X
F
and X are conditionally independent given the parameter θ. In (2) the parameters have been marginalized (integrated out). Therefore, only information in the observed data is used in the prediction. Finally, the optimal point predictor  F, assuming a quadratic loss function, is the mean of the predictive distribution, i.e. E(XF|x).
F, assuming a quadratic loss function, is the mean of the predictive distribution, i.e. E(XF|x).
For the interested reader, we suggest Renard et al. (2006), who provide an excellent review of the Bayesian thinking applied to environmental statistics.
4. A Gaussian process model for interpolation
The model of Nieto-Barajas and Sinha (2015) aims to produce equally spaced observations via stochastic interpolation. It assumes a Gaussian process with a correlation function parameterized in terms of a parametric survival function and allows for positive or negative correlations. For parameter estimation they follow a Bayesian approach. Once posterior inference on the model parameters is done, interpolation is carried out by using the posterior predictive conditional distributions of a new location given a subset of size m of neighbors, in a sliding windows manner. The number of neighbors m is decided by the user. This procedure is similar to what is done in spatial data known as Bayesian kriging (e.g. Handcook and Stein, 1993; Bayraktar and Turalioglu, 2005).
4.1 Model
In time series analysis, the observed data are a result of an evolving process in time where independence in the observations is no longer hold. The probability law that generates the data is typically described in terms of a stochastic process which characterizes all dependencies among the observations. A stochastic process can be thought of as a family of random variables linked via a parameter (usually time) which takes values on a specific domain (usually the real numbers).
Let {Xt} be a continuous time stochastic process defined for an index set t ∈ T ⊂ ℝ and which takes values in a state space χ ⊂ ℝ. We will say that Xt1, Xt2..., Xtn is a sample path of the process at possible unequal times t1,t2,...,tn with n > 0. In a time series analysis we only observe a single path that is used to make inference about the model. This is possible since the likelihood is defined as the joint distribution of the observed path, which depends on the n observed times. This will later be given in (5) for our particular model.
It is assumed that Xt follows a Gaussian process with constant mean E(Xt) = µ and covariance function Cov(Xs, Xt) = Ʃ(s, t). In notation
this assumption implies that the joint distribution of the path (X t1 , X t1 ..., X tn ) is a multivariate normal with mean vector (µ,...,µ) of dimension n, and variance-covariance matrix of dimension n × n with (i, j)th element Ʃ(t i , t j ).
It is further assumed that the covariance is a function only of the absolute times difference |t - s|. In this case it is said that the covariance function is isotropic (Rasmussen and Williams, 2006). By assuming a constant marginal variance for each X t , the covariance function can be expressed in terms of the correlation function R(s,t) as Ʃ(s,t) = s2 R(s,t). Nieto-Barajas and Sinha (2015) noted that isotropic correlation functions behave like survival functions as a function of the absolute time difference |t - s|. In particular, they considered two alternatives: A Weibull survival function S θ (t) = exp(-λt α ), and a log-logistic survival function S θ (t) = (1 + λt α )-1, with θ = (λ, α) in either case. Therefore, the covariance function they proposed is
with β ∈ {1, 2} in such a way that β = 1 implies a negative/positive correlation for odd/even time differences |t - s|, and it is always positive regardless |t - s| being odd or even, for β = 2. Note that |t - s| needs to be an integer since the power of a negative base becomes imaginary.
4.2 Prior distributions
Let x = (X t1 , X t2 ,...,X tn ) be the observed unequally spaced time series at times t 1 , t 2 ,...,t n , and η = (µ, σ2, θ,β) the vector of model parameters. The joint distribution of the data x i nduced by model (3) is a n-dimensional multivariate normal distribution of the form
where µ = (µ,...,µ) is the vector of means, R θ,β = R ij θ,β is the correlation matrix with (i, j) term R ij θ,β = Ʃ σ2,θ,β (t i , t j )/σ2 and Ʃ σ2,θ,β is given in (4).
The proposed priors for η are conditionally conjugate for µ, σ 2 and β, but unfortunately there is no conjugate prior for the vector θ = (λ,α). A priori all parameters are independent and the specific choices are: µ~N(µ 0 , σ µ 2 ), i.e., a normal distribution with mean µ 0 and variance σ µ 2 ; σ 2 ~IGa(a σ ,b σ ), i.e., an inverse gamma distribution with mean b σ /(a σ -1) and whose density can be found in Bernardo and Smith (2000: 431); β - 1~Ber(p β ), i.e., a Bernoulli distribution with probability of success p β ; λ~Ga(a λ , b λ ), i.e., a gamma distribution with mean a λ /b λ ; and α~Un(0,A α ), i.e., a continuous uniform distribution on the interval (0,A α ).
Posterior inference is obtained by implementing a Gibbs sampler (Smith and Roberts, 1993), which is a particular case of the Markov chain Monte Carlo (MCMC) algorithms frequently used in Bayesian analysis. The Gibbs sampler is an algorithm that generates a Markov chain whose stationary distribution is the posterior distribution of η , f( η | x). The algorithm is based on iteratively sampling from each of the conditional distributions of the elements of η , say µ, σ2 , θ, and β given the most recent values of the other parameters. The posterior distribution of η is obtained via the Bayes' Theorem (1), and the conditional distributions for each of the elements of η are simply proportional to the joint distribution. For example, the conditional distribution of µ is f(μ|x,σ 2 ,θ,β) ∝ f(μ,σ 2 ,θ,β|x), where f(η | x) is only seen as a function of μ. For the other parameters the conditional distributions are obtained in a similar way. The set of conditional distributions as well as the details of the simulation strategy can be found in Nieto-Barajas and Sinha (2015).
4.3 Interpolation
Once posterior inference is done, as a result of running a Gibbs sampler, the output consists of a series of samples from the posterior distribution of η = (μ, σ 2 , θ, β). Let ( η (1) ,…, η (L) ) denote this sample of size L from f( η | x). Posterior summaries can then be obtained with this sample such as posterior means and credible (probability) intervals.
Our most important inference goal is the interpolation of unequally spaced series, to produce equally spaced series. Within the Bayesian paradigm, this inferential procedure is done via the posterior predictive distribution. Nieto Barajas and Sinha (2015) propose to interpolate using the posterior predictive conditional distribution given a subset of neighbours. Their procedure is as follows. Let x s = x s1 ,...,x sm be a set of size m of observed points, such that s = (s 1 ,…,s m ) are the m observed times nearest to time t, with s j ∈ {t 1 ,…,t n }. If m = n, x s = x is the whole observed time series. Therefore, the conditional distribution of the unobserved data point X t given its closest m observations and model parameters is a univariate distribution given by
with scalars μ t = μ + Σ(t, s)Σ(s, s)−1(x s − μ) and σ t 2 = σ 2 − Σ(t, s) Σ(s, s)−1 Σ(s, t), where, as before, Σ(t, s) = Σ(s, t)' = Cov(X t , X s ) and Σ(s, s) = Cov( X s , X s ).
We need to integrate out the parameter vector η from (6) using its posterior distribution, that is, f(x t | x s , x) = ∫ f(X t | xs, η ) f ( η | x) dη . This marginalization process is usually done numerically via Monte Carlo as
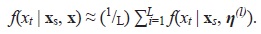
The interpolation procedure is better understood if we consider the specific case when m = 2, so that x s = (x s1 ,x s2 ) consists of the two closest observations to time t. Then, from (6) we obtain that E(X t | x s , η ) becomes
where ρ t,s = Cor(X t , X s ) = Σ(t, s)/σ 2 . The conditional expected value (7) is a linear function representing a weighted average of the neighbour observations xs where the weights are given by the correlations among x t , x s1 and x s2 . Finally, the marginal posterior predictive expected value E(X t | x s , x) = E η|x {E(X t |x s , η )} is the estimated interpolated point under a quadratic loss. This is usually approximated via Monte Carlo.
In general, for any m > 0, the estimated interpolated point at time t will be a weighted average of the closest m observed data points, as sliding windows, with weights determined by their respective correlations with the interest point X t . As will be seen by the examples in Section 5, the larger the value of m, the smoother the interpolated series becomes.
5. Data analysis
In Section 2 we described several datasets that contain earth climate measurements at different ages. The recent history dataset (Fig. 1) that contains measurements from the years 1950 to 2013; the marine isotope stage dataset (Fig. 2) obtained from the EPICA dome C ice core which contains measurements up to 800 000 years ago; the Pliocene dataset (Fig. 3) that extends from 3.3 to 2.3 million years ago; and the Paleozoic dataset (Fig. 4) covering from 300 to 265 millions years ago. Recorded variables include temperature anomalies, carbon dioxide, and in some cases methane.
Apart from the records from recent history, in the rest of the datasets the available variables are measured at unequally spaced times. Additionally, apart from the Paleozoic dataset, the observation times are different from one variable to another, so causal or simple association studies are not possible to perform.
We therefore proceed to interpolate the different time series to produce equally spaced observations. We start with the Pliocene dataset, move on with the Paleozoic dataset and finish with the marine isotope era dataset.
The reason we start analyzing the Pliocene dataset is because it has very interesting interpolation properties, which need some comment and explanation first. There are three variables available in this dataset, temperature anomalies in the sea surface, temperature anomalies in the air, and CO2. These three variables are measured at the same, but unequally spaced, times. Figure 5 shows three graphs. The first one corresponds to the time series of temperatures anomalies in the air. The middle panel includes the observed time differences (t i − t t-1 ) versus the final observed time t i and the last panel corresponds to a histogram of the time differences. Most of the observations were made at a frequency of less than 0.02 million years, with the largest gap of slightly more than 0.05 million years. The median frequency (time difference) is 0.01 million (10 000) years.
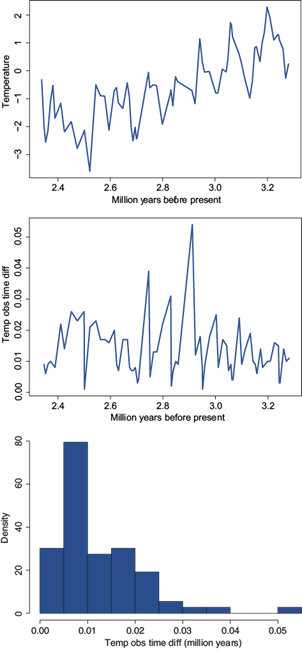
Fig. 5 Late Pliocene climate records. Temperature anomalies in the air. From top to bottom: data, observed time differences versus time, and histogram.
We implemented the interpolation methodology described in Section 4. According to Nieto-Barajas and Sinha (2015) the log-logistic survival function to define the covariance matrix has better performance than the Weibull due to its flexibility to capture slower and faster decays, so the log-logistic will be our choice for all cases considered here. Prior specifications of the Bayesian model are those considered in Nieto-Barajas and Sinha (2015), which are: μ 0 = 0, σ µ 2 = 100, a σ = 2, b σ = 1, a λ = b λ = 1, A α = 2 and p β = 0.5. The value of A α is particularly important since it constrains the support of parameter α. Larger values of A α would make the posterior exploration unstable. The Gibbs sampler was run for 20 000 iterations with a burn in of 2000 and keeping one of every 10th iteration. In the end, posterior inferences including interpolation, are based on 1800 samples.
The interpolation process, as described in Section 4, is done via the posterior predictive distribution based on the closest m neighbours. The choice of this parameter plays an important role in the smoothness of the interpolation series. The larger the value of m the smoother the interpolated series becomes. The best value of m depends on the specific data at hand and its impact is highly dependent on the estimated correlation function. For the pliocene data, the correlation functions for the three variables (air temperature, SST, and CO2) are included in Figure 6. From the graphs we can see that the correlation function for the air temperature variable (left panel) decays fairly fast reaching the value of zero at around one million years. The correlation for SST (middle panel) also presents a very fast decay in the first 0.1 million years but remains almost constant with a very slow rate of decay afterwards. On the other hand, the estimated correlation for CO2 (right panel) has almost no decay, remaining very close to one even after one million years.
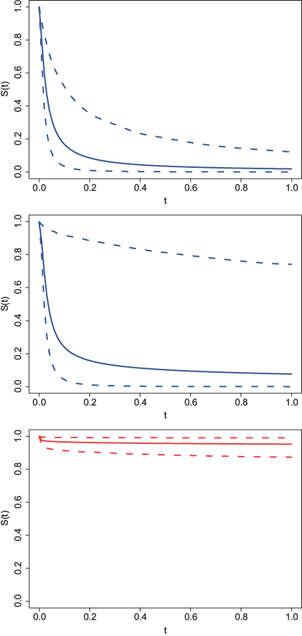
Fig. 6 Late Pliocene climate records. Correlation function estimates. From top to bottom: air temperature, SST, and CO2.
When the correlation function has a fast decay, as is the case of the two temperature variables, the choice of m for interpolation has almost no impact. Figure 7 shows the interpolated series for the two temperature variables with m = 10 closest neighbors and an equal spacing of one and five thousand years, respectively. In all cases the dots correspond to the observed data and the lines to the interpolated data. The shadows correspond to a 95% pointwise credible interval (CI). As can be seen from the graphs the shadows become larger between two observed data points due to the higher uncertainty in the prediction. The interpolated series at every one thousand years (left column) follows closely the path of the observed points whereas the interpolated series at every five thousand years (right column) has a smoother path, sometimes not reaching the observed points.
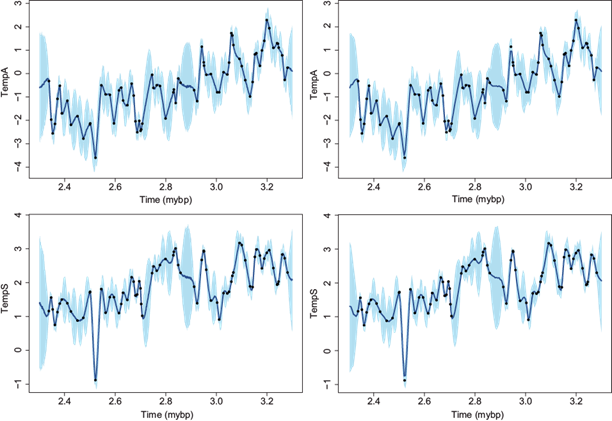
Fig. 7 Late Pliocene climate records. Interpolated temperature data using m = 10 closest neighbors at every one (first column) and five (second column) thousand years. Air temperature (top row) and SST (bottom row). Full dots correspond to observed data, lines to interpolated series, and shadows to 95% CI.
As was mentioned before, the estimated correlation function for the CO2 variable is very high. In this case the choice of m has a large impact in the interpolated series. Figure 8 presents the interpolated series using m = 2 (top row) and m = 10 (bottom row) closest neighbors at every one (left column) and five (right column) thousand years, respectively. From this graph the impact of m is clear. For the case of m = 10 at every five thousand years (bottom left panel), the interpolated series follows the path of the observed data but for the non observed times the interpolated series quickly goes down/up to an average value. However this over smoothing effect is not present when m = 2 for the same spacing of five thousand years (top left panel). Given the large correlation in this CO2 variable, it is preferable to interpolate using the smaller value of m = 2 neighbors to avoid over smoothing.
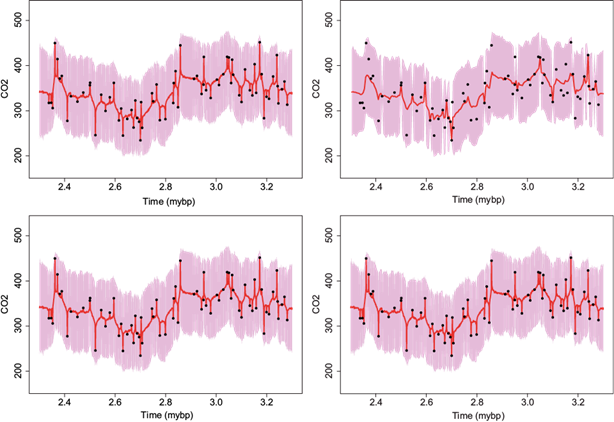
Fig. 8 Late Pliocene climate records. Interpolated CO2 data at every one (first column) and five (second column) thousand years using m = 2 (top row) and m = 10 (bottom row) closest neighbors. Full dots correspond to observed data, lines to interpolated series, and shadows to 95% CI.
We move on to the Paleozoic data. There are two variables available, temperature anomalies and CO2. These two variables have not been measured at the same times and are not equally spaced. Moreover, the temperature was recorded from 265 to 303.5 million years before the present, whereas CO2 was measured from 273.3 to 300.2 million years before the present. The observation time for the CO2 variable has a shorter span and its range lies within that of the temperature. See also the two panels in the first column of Figure 9. The frequency with which these two variables were measured is also shown in Figure 9 (middle and right columns) where we plot the observed time differences. For the CO2 variable (bottom row), most of its observations were measured at a frequency less than 0.5 million years, whereas temperature (top row) was measured at more dispersed frequencies with most of the observations made at time differences larger that 0.5 million years.

Fig. 9 Late Paleozoic deglaciation data. From left to right: data, observed time differences versus time, and histogram. From top to bottom: temperature anomalies, CO2.
The estimated correlation functions for these two variables have a fast decay (not shown), so we decided to use m = 10 closest neighbors for interpolation. The interpolated series for both variables at every 0.1 and 0.5 million years are shown in Figure 10, respectively. Something to note in these graphs is the interpolation uncertainty obtained for the CO2 variable. Within the observed time range the 95% credible intervals are very narrow and are almost indistinguishable from the point estimate (solid line in the graph). However, if we go beyond the observed time range, which is below 273.3 and above 300.2 million years, the predicted series shows a huge uncertainty that increases as we move away. Strictly speaking, for these times beyond the observed time range we are doing an extrapolation of the time series, and going far beyond the limits produces a huge uncertainty. The shadows in the two bottom panels for the times beyond the observed range increase in size very fast as we go away. Note that in the graph the shadows were only included for the closest extrapolated times to avoid increasing the scale of the graph. For the further away time points we decided to report only the point predicted values and are shown as dashed lines in the graphs.
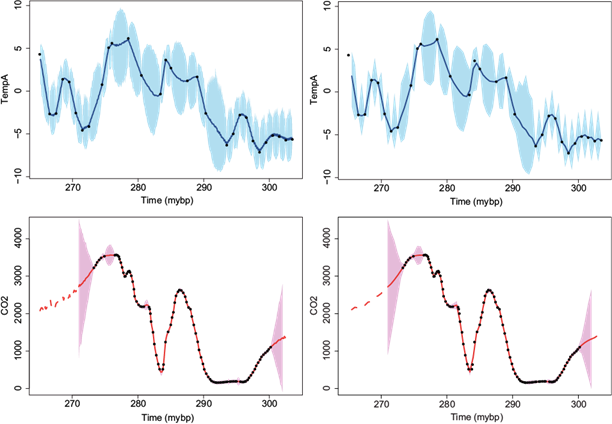
Fig. 10 Late Pliocene climate records. Interpolated data using m = 10 closest neighbors at every 0.1 (first column) and 0.5 (second column) million years. Temperature (top row) and CO2 (bottom row). Full dots correspond to observed data, lines to interpolated series, and shadows to 95% CI.
Finally, we analyze the marine isotope stage dataset. There are three variables available: temperature anomalies, carbon dioxide, and methane. Figure 11 includes the observed time series for these three variables (first column). The middle and right panels report the observed time differences vs. time and a histogram, respectively for the three variables. Broadly speaking, temperature and CH4 variables were measured at an increasing frequency, that is, they were measured very frequently close to present and less frequent as we go back in time up to 800 thousand years. The CO2 variable, on the other hand, has a reversed path in terms of frequency it was not measured very often close to present time, but was measured more frequently as we go back in time. The maximum gap between measurements is 1.36 thousand years for temperature, 6.02 for the CO2 variable, and 3.46 for the CH4 variable. The median observed time differences are 0.06, 0.58 and 0.31 thousand years, respectively for the three variables.
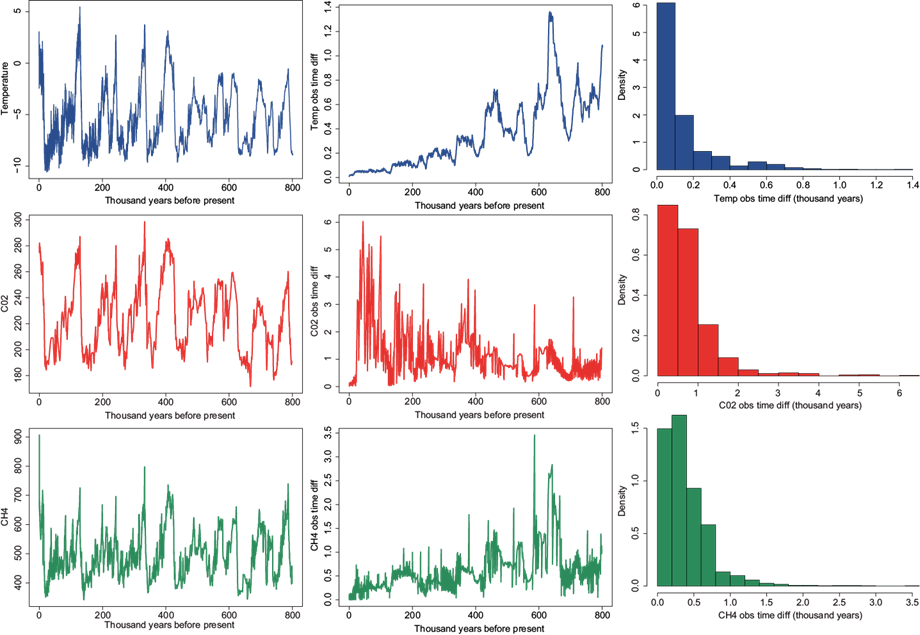
Fig. 11 EPICA dome C ice core 800 thousand years data. From left to right: data, observed time differences versus time, and histogram. From top to bottom: temperature anomalies, CO2, CH4.
We implemented the methodology of Section 4 and produced interpolated series using the m = 10 closest neighbors for the three variables at every 0.1 and 0.5 thousand years. The interpolated series together with a 95% credible interval are presented in Figure 12. Note that the credible intervals are larger in regions were the observed data are more spaced (less frequently measured), that is, closer to 800 thousand years for the temperature (top row) and methane (bottom row) variables, and closer to zero for the carbon dioxide (middle row) variable.
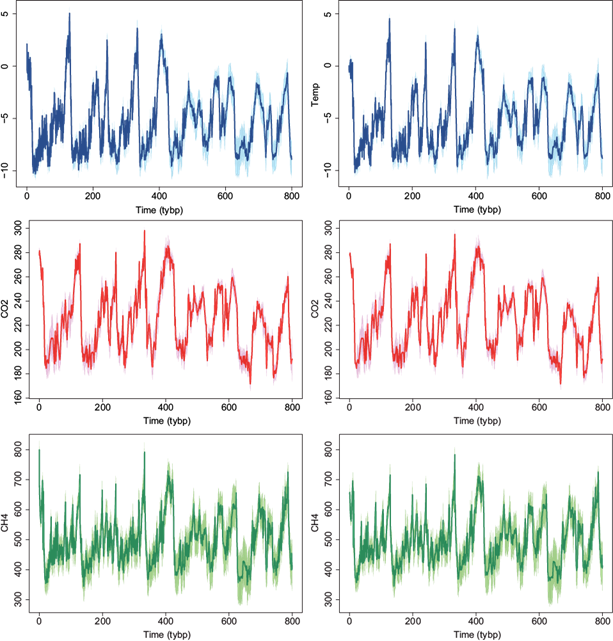
Fig. 12 EPICA dome C ice core 800 thousand-years data. Interpolated data using m = 10 closest neighbors at every 100 (first column) and 500 (second column) years. Temperature (top row), CO2 (middle row) and CH4 (bottom row). Lines correspond to interpolated series and shadows to 95% CI.
We implemented the methodology of Section 4 and produced interpolated series using m = 10 closest neighbors for the three variables at every 0.1 and 0.5 thousand years. The interpolated series together with a 95% CI are presented in Figure 12. Note that CIs are larger in regions where the observed data are more spaced (less frequently measured), that is, closer to 800 000 years for the temperature (top row) and methane (bottom row) variables, and closer to zero for the CO2 (middle row) variable.
6. Concluding remarks
In this article we collected four important data sets for climate change study. Three of these datasets are representative of the paleoclimate covering periods from marine isotope stage, passing by the late Pliocene up to the late Paleozoic deglaciation.
We used a Bayesian statistical method to interpolate the datasets and produced equally spaced observations in the observed range. The original data as well as the interpolated values are available as supplementary material.
Interpolated values include point predictions (predictive means) and quantiles of order 2.5% and 97.5%. The latter two can be used as the lower and upper limits, respectively, to produce 95% CIs as those shown in Figures 7, 8, 10 and 12.
One important challenge that is worth exploring in paleoclimate statistical research is to consider the age-uncertainty into the model, that is, to produce a joint modeling of the climatic variable as well as the observation time. This would produce a better model since all sources of uncertainty would be taken into account.











 text new page (beta)
text new page (beta)