Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Atmósfera
versión impresa ISSN 0187-6236
Atmósfera vol.25 no.3 Ciudad de México jul. 2012
Sensitivity of simulated convection to soil moisture in a region in central Amazon
M. Mendina and R. Terra
Instituto de Mecánica de los Fluidos e Ingeniería Ambiental, Universidad de la República, Julio Herrera y Reissig 565 - Código Postal 11300 - Montevideo - Uruguay. Corresponding author-mail: mmendina@fing.edu.uy
Received June 7, 2011; accepted March 28, 2012
RESUMEN
Se estudia la sensibilidad de la precipitación convectiva a variaciones de la humedad del suelo en una región continental del Amazonas en simulaciones con un modelo de circulación general de la atmósfera (MCGA) y se analizan los procesos físicos que establecen dicha sensibilidad, en particular aquellos relacionados con el ciclo diario. Se utilizó el MCGA de la Universidad de California-Los Angeles (UCLA) para simular condiciones de enero perpetuo. Surge del análisis de dichas simulaciones el interés por una región ubicada en el centro del Amazonas, con un comportamiento uniforme -y diferenciado de las regiones circundantes- en el ciclo diario de la convección, fuertemente asociados a procesos de superficie y en fase opuesta al movimiento ascendente de gran escala. Se eligió dicha región para explorar la sensibilidad a la variación de la humedad del suelo, siendo el parámetro de control un factor multiplicativo (entre 0 y 1) de la evaporación. Los resultados muestran que la mayor sensibilidad se tiene para situaciones relativamente secas, confirmando estudios anteriores. Si bien la evaporación es monótona decreciente con la disminución de la humedad del suelo, el leve aumento de la convergencia de humedad mantiene la precipitación en casi los mismos valores hasta niveles de 0.3 del parámetro multiplicativo. Los máximos de convergencia de humedad (excluyendo el caso extremo de evaporación nula), precipitación convectiva y movimiento ascendente en 500 mb se dan para un valor de 0.4 en el parámetro de control. Las temperaturas del suelo y del aire en superficie aumentan con el parámetro de control, con máximos diarios que se retrasan y ciclos diarios de mayor amplitud. Igual comportamiento muestran el calor sensible y la altura de la capa límite planetaria (CLP). Estos efectos, sumados a la variación de la concentración del vapor de agua, se conjugan en un ciclo diario de la humedad relativa al tope de la CLP que varía gradualmente, sobre todo en su comportamiento durante la mañana, donde acaba revertiendo la tendencia creciente, lo cual inhibe el inicio de la actividad convectiva en las primeras horas de la tarde. La sensibilidad de la convección a la humedad del suelo no puede ser comprendida sin considerar también la retroalimentación de la circulación de gran escala. En los casos húmedos, la convección es responsable principal del calentamiento en la troposfera media. En los casos secos el calentamiento convectivo es insuficiente, generándose un movimiento descendente diferencial cerca de la troposfera media. En el caso extremo la circulación cambia drásticamente, instalándose en capas bajas una celda somera con gran convergencia de humedad que explica el incremento en la precipitación de gran escala.
ABSTRACT
We study the sensitivity of convective precipitation to soil moisture in a continental region in Central Amazon based on Atmospheric General Circulation Model (AGCM) simulations and further analyze the physical processes involved, in particular those related to the diurnal cycle. The region was selected based on the analysis of perpetual January simulations with the University of California at Los Angeles AGCM. It shows a uniform and differentiated behavior in the diurnal cycle of convection, which is strongly associated to surface forcing and in opposite phase to large scale ascending motion. Sensitivity to ground wetness was explored based on a control parameter (which varies between 0 and 1) that multiplies evaporation. Results show that the largest sensitivity appears for relatively dry conditions, confirming previous studies. Although evaporation decreases monotonically as the control parameter is reduced, a slight increase in moisture convergence maintains precipitation almost unchanged up to a value of 0.3 of the parameter. The daily maxima in moisture convergence (excluding the extreme case with no evaporation within the region), convective precipitation, and large scale ascending motion at 500 mb are reached in the simulation with a value of 0.4 of the control parameter. Soil and surface temperature increase with decreasing sensitivity parameter, and show retarded daily maxima and larger diurnal amplitude. The same behavior is observed in the sensible heat flux and planetary boundary layer (PBL) height. These effects combine with the variations in PBL water vapor mixing ratio to produce a gradual sensitivity in PBL top relative humidity, in particularly during the morning hours when the humidification observed in the control simulation is gradually reverted, eventually inhibiting early afternoon convection. However, sensitivity of moist convection to ground wetness can not be fully explained without also considering large scale circulation feedbacks. In the more humid cases, deep convection is responsible for mid tropospheric warming. In the drier cases, convective induced warming is insufficient and a differential large scale subsiding motion is induced in the mid troposphere. In the extreme case, with the control parameter equal to zero, the large scale circulation changes drastically with the development of a shallow direct convergent cell that explains the notorious increase in large scale precipitation.
Keywords: Soil moisture, convection, sensitivity.
1. Introduction
The south american continent exhibits a wide range of surface climate conditions including an extensive area of tropical forest, the Amazon, where land-atmosphere energy and water exchanges are intense. It is well know that large changes in land cover have taken place during the last decades in the region (INPE, 2005; Silva Correia et al., 2006). Several studies have focused on the general impact of such land use changes within the Amazon basin. Moisture transport to and from the basin has been analyzed through numerical modeling and based on field data, especially from the LBA (Large-Scale Biosphere-Atmosphere Experiment in Amazonia). Marengo (2006) reviewed the most relevant studies on the hydrological cycle in the basin since the 70s and presents different changes in the water budget depending on the subregion, with long term statistically significant tendencies of different sign within the basin. In some cases, these tendencies have been associated with global natural variations rather than deforestation (Chang Chen et al., 2001).
Other studies have shown that changes in ecosystems can affect moisture fluxes and thus the hydrological cycle in South America. In the South American Monsoon Region, soil moisture has been signaled -together with sea surface temperature- as the main source of predictability for the atmosphere in intraseasonal to interannual timescales (Lenters and Cook, 1999; Fu et al., 2001). Grimm et al. (2007), analyze the development of the rainy season in central east Brazil as it relates to the forcing of local springtime soil moisture and remote SST.
As for future climate scenarios, several studies agree in some key tendencies for the Amazon basin: significant reduction in precipitation and evapotranspiration (Hahmann and Dickinson, 1997; Zeng and Neeling, 1999; Sampaio et al., 2006; Silva Correia et al., 2006), while there is less agreement on the changes in moisture convergence.
The large majority of these analyses are inevitably based on climate models forced by different land use scenarios. Soil moisture directly affects turbulent surface fluxes and in turn the thermodynamic conditions of the Planetary Boundary Layer (PBL). Betts et al. (1996) offers an observational and model-based review of the key role of the PBL -its depth and intensive properties- on land atmosphere interactions. Betts and Viterbo (2005) find that low cloud cover, net longwave radiation at the surface and low level relative humidity are strongly related to soil moisture, while high cloud cover and precipitation are more associated to large scale dynamics, in particular low level convergence and ascending motion. Derbyshire et al. (2004), Kuang and Bretherton (2006) and Chaboureau et al. (2004) confirm, through cloud resolving modeling, the strong association of deep convection with tropospheric humidity. In particular, Derbyshire et al. (2004) determine the sensitivity of deep convection to a wide range of values of environmental humidity. A dry environment inhibits penetrative convection since lateral entrainment of dry air enhances evaporative cooling reducing buoyancy.
The sensitivity of convection to changes in ground wetness is mediated by a series of complex physical processes that are difficult to capture in theoretical or simplified numerical models. Atmospheric general circulation models (AGCM) are the main tools to understand the interaction between the atmosphere and the rest of the climate system. However, the broad spectrum of spatial scales involved -from turbulent eddies in the PBL to the large scale circulation- poses an important challenge that forces AGCM to explicitly resolve part of the spectrum and parametrize the rest.
Many of the parameterized physical process are, indeed, those that directly address the interaction between the atmosphere and the underlying surface. Therefore, it is not surprising that land-atmosphere coupling presents model dependence, as the studies on climate scenarios mentioned before suggest. Moreover, the intensity of the coupling between the surface and the atmosphere also varies spatially, being dominant in specific regions (Koster et al., 2004; Dirmeyer et al., 2006; Guo et al., 2006). Guo et al. (2006) and Koster et al. (2006), globally evaluate land-atmosphere coupling with an ensemble of various AGCM. They analyze how surface anomalies (i.e. soil moisture) affect precipitation and other atmospheric processes during the boreal summer, emphasizing the need of a robust coupling with surface fluxes and precipitation processes to achieve a significant impact. The sensitivity of evaporation is larger for drier soils, as compared to more humid conditions, a result consistent with the work of Dirmeyer et al. (2000) and Collini et al. (2008). Again, the impact of soil moisture on precipitation showed large intermodel variability. Dirmeyer et al. (2006) carried an observational evaluation within regions with available data of the findings by Guo et al. (2006) and show discrepancy with models regarding the relation between soil moisture and surface fluxes. Xue et al. (2006) study the role of vegetation on the evolution of the South American Monsoon using two different models for surface fluxes, with and without the explicit representation of vegetation. They find that, although vegetation modulates water and energy surface budgets, changes in precipitation are largely controlled by associated circulation changes.
One of the salient characteristics of warm season continental convective systems relates to the strong associated diurnal forcing with an early afternoon peak (Kikuchi and Wang, 2008). Simplified modeling studies (Figueroa et al., 1995) have proposed that the daily divergence pulse associated with deep convection in the Amazon was required to generate a South American Convergence Zone (SACZ) with an intensity as observed. The importance of the daily cycle has also been emphasized as related to the Bolivian Altiplano convection, which shows variability in diverse frequencies (Garreaud, 1999) and is believed to be associated to SACZ (Lenters and Cook, 1999). However, AGCM have generally failed to appropriately represent the diurnal cycle over the continent (Chien-Ming-Mu et al., 2009). Krishnamurti et al. (2006) analyze the amplitude and phase of the diurnal cycle of precipitation using different parameterizations of cloud radiative transfer and show differences in both phase and amplitude with observations in all cases. In addition, Collini et al. (2008) show the shortcomings of the NCEP regional model in the simulation of the timing of maximum precipitation in a region in central Brazil. Betts and Jacobs (2002) find that the ECMWF forecasts over Rondonia tend to produce precipitation too early in the day, and suggest that it is caused by the inappropriate representation of shallow clouds. Bechtold et al. (2004) try different cumulus mass flux representations to study the effect of the convective parameterization on the diurnal cycle of precipitation. Adjustments in the convective triggering tend to improve the timing of maximum convection, although it continues to occur hours before observed. The escalation in computing power has enabled the use of global cloud resolving models, which have the potential to explicitly resolve both the mesoscales and the feedback with the large scale flow. With such an approach, Sato et al. (2009) find that the timing of peak precipitation over tropical land is still very sensitive to horizontal resolution for 3.5, 7 and 14 km grids.
As we can see, the simulation of the continental diurnal cycle in convective regimes -closely related to the question of the dependence of precipitation on soil moisture- has proved a difficult task for the modeling community. Approaches have included single column, AGCM, regional and cloud resolving models. There is always a compromise when choosing a model. Since one of our main focus is the feedbacks between column physics and the large scale flow involved in the sensitivity of convection to soil moisture, the use of an AGCM is required, even considering its inability to simulate the mesoscale organization of convection.
In summary, the objective of this study is to fully analyze and understand the sensitivity of convective precipitation to changes in ground wetness for a specific region in the continental Amazon in a large scale model with a simplified land surface scheme. In section 2 we present a brief description of the model used while section 3 shows some of the most relevant simulated fields, including the diurnal phase of precipitation which can be compared against observations. Based on this initial exploration, a specific region of interest (Central Amazon Region - CAR) is defined. Section 4 analyzes the model sensitivity to ground wetness in terms of daily mean energy and water balances and its impact on deep convection. Section 5 looks at the diurnal cycle of the relevant processes and their sensitivity to soil moisture changes. Finally, a summary of the results and main conclusions are presented in section 6.
2. Model and experiments configuration
All simulations were performed with version 6.95 of the UCLA (University of California at Los Angeles) AGCM. A detailed description of the model can be found in Arakawa (2000) or Mechoso et al. (2000). Horizontal discretization is based on a finite difference scheme on the Arakawa C grid (Arakawa and Lamb, 1977) with 4° x 5° resolution. Vertical discretization is performed in 16 sigma levels as in Suárez et al. (1983). PBL consists on the lowest model layer where processes are parameterized following Suárez et al. (1983). Convective parameterization, including its interaction with the PBL, follows the prognostic version of Arakawa and Shubert (1974) implemented by Pan and Randall (1998). Surface fluxes are computed based on Deardorff (1972) with the scheme presented in Suárez et al. (1983). Long and shortwave radiation parameterization follows Harshvardhan et al. (1987, 1989). Surface albedo is prescribed as a function of land cover type and surface emissivity is set to one. Ground temperature is computed based on the ground energy budget with a prescribed heat capacity (C). Soil moisture is represented by the b factor, the rate between evapotranspiration and potential evapotranspiration. This coefficient, that represents the availability of water, is prescribed as a function of soil and vegetation type following Mintz and Serafini (1981) climatological annual cycle. Therefore, while the effect of b on the evaporation is direct, there is no feedback from precipitation to ground wetness in this simple model.
The AGCM was run for 100 days in a perpetual summer mode (date fixed at January 15) to filter all variability but that associated with the diurnal cycle. The analysis of this simulation serves as the basis for the selection of the precise location of the region of the sensitivity study. The sensitivity analysis on ground wetness is performed affecting the coefficient b by a multiplicative parameter (GW) in the equation that determines latent heat flux (Eq. 1) only within the area selected.
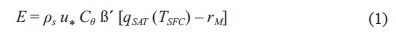
where E is the evaporation rate, ρs surface air density, u* friction velocity, qSAT saturation mixing ratio, TSFC surface temperature, rM total water mixing ratio, Cθ transfer coefficient from Deardorff (1972) and ß' = GW x β. With this simplified representation, the dynamics associated with the stomatal resistance of vegetation are eliminated, focusing only on the direct effect of ground wetness on evaporation. Other effects that ground wetness may have on ground physical properties (i.e. heat capacity) are also ignored.
A set of 50-day-long simulations (statistics on the diurnal cycle proved insignificantly different beyond that length) in identical conditions to the control one, were performed for a series of values of the control parameter GW: 1.0, 0.8, 0.6, 0.2 and 0. We will hereafter name these sensitivity simulations as S1.0, S0.8, S0.6, S0.4, S0.2 and S0 respectively. It is noted that the mean original value of b over the selected region is 0.82 and that the S0 implies that the evaporation is suppressed in the region of study. As it has been repeatedly suggested (Dirmeyer et al., 2000; Koster et al., 2004; Guo et al, 2006; Collini et al, 2008), it was found that the sensitivity was much stronger in the drier cases. Therefore, a complementary set of simulations was performed in the range of the control parameter GW that showed the most sensitivity: S0.3, S0.1 and S0.05.
3. Selection of the region of study
Figure 1 shows the diurnal cycle of precipitation accumulated in one hour over South America for the control simulation (perpetual January). Precipitation maximum over the Amazon appears around 16 to 20 h GMT.
Figure 2 shows the diurnal cycle of large scale vertical velocity at 500 mb (oo500) which is out of phase with precipitation in the CAR. Maximum ascendant motion (minimum ω500) takes place around 2 to 6 h GMT. In the coastal Atlantic region, on the other hand, diurnal cycles of both fields are approximately in phase.
In order to better appreciate the relative phase of each variable in the diurnal cycle, the following clock-plots are constructed for precipitation, oo500 and potential temperature at 500 mb (e500). The local time of the daily maximum of each variable is computed at each grid point, together with the standard deviation of the diurnal cycle. Figure 3 shows the phase and amplitude -position and length of the arrow respectively- of the diurnal cycle of each variable (normalized by the mean in the case of e500). Precipitation diurnal phase is largely coincident with TRMM (Tropical Rainfall Measurement Mission) observations (Nesbitt and Zipster, 2003).
It stands out from Figure 3 that the CAR (12° S - 4° N; 285° E - 310° E) has a uniform and distinctive behavior. Minimum large scale upward motion (maximum w500) takes place close to midnight, almost have a day later than the precipitation peak that occurs two to three hours after noon. In contrast, these two variables are almost in phase in the Atlantic coastal region. Maximum temperature at 500 mb in the CAR occurs at around 18:00 h local time (LT), after the peak in precipitation.
To better visualize the relative timing and phase of the different variables in the CAR, Figure 4 shows the diurnal evolution of variables averaged in the region, along with surface temperature.
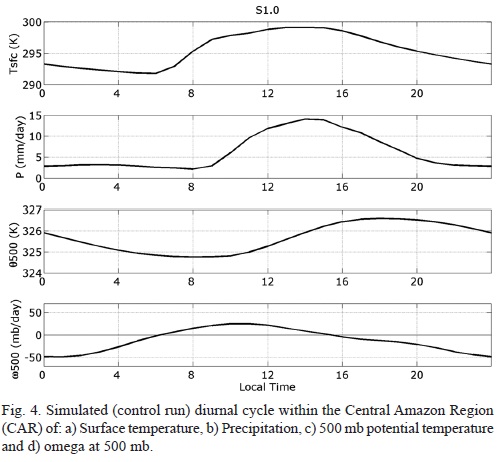
Diurnal cycle of surface temperature and precipitation are approximately in phase, with a slight lag of the latter. This suggests that the dominant precipitation mechanism is due to the convective activity forced by surface heating (as will be shown later). Maximum simulated precipitation takes place around 15:00 LT, compatible with observations (Betts and Jacob, 2002; Bechtold et al., 2004) with a slight lead. Maximum temperature at 500 mb is lagging the precipitation (and convective) maximum by approximately a quarter of a day. Tropospheric heating -as represented by the evolution of 500 mb temperature- takes place during the convective period and the maximum temperature is attained once the precipitation peak subsides, all of which suggests that convection is the dominant mechanism for tropospheric heating and stabilization. Maximum destabilization (500 mb cooling) occurs during the maximum in large scale ascending motion, as represented by omega at 500 mb. Anomalous (respect to the daily mean) upward motion -and associated low level convergence- is not simultaneous with precipitation but rather responds to the tropospheric warming and lags the maximum in 500 mb temperature by approximately a quarter of a day. Therefore, there is an almost total out of phase relation between the maximum in precipitation (of convective origin) and the maximum in large scale upward motion (as indicated by w500). The paradigm that the dominant balance in convective regions is between adiabatic cooling and moist convective induced warming still holds for daily mean values, but the simulations show that these processes are in opposite phase during the day in this region.
The following findings for the CAR make it appropriate for the proposed sensitivity studies:
A large region where the simulations show a uniform behavior that differentiates from the surrounding regions in aspects that are of interest for the present study.
In contrast to what the simulations show for more coastal regions, the diurnal cycle of convection is closely associated with surface processes (Cook, 1994; Fu et al, 2001), a characteristic that has emerged in the preliminary analyses.
It is a region of great interest for the scientific community and society at large AGCM tend to have problems representing the diurnal cycle of convection in the region.
4. Sensitivy of daily mean variables to ground wetness
Energy and water budgets to the ground and atmospheric column over the region of study (CAR) were computed and are presented next; Figure 5 illustrates the fluxes involved.
Since the ground surface is modeled as a closed system it cannot accumulate energy for long periods of time and therefore the energy fluxes exchanged necessarily add up to zero. This is not the case with water fluxes, since the simple model introduced before does not conserve water in the ground. The atmospheric column, on the other hand, can exchange energy and water with the surrounding regions (Fig. 5b). Resulting energy budget equation for the ground and water budget equation for the atmospheric column are:
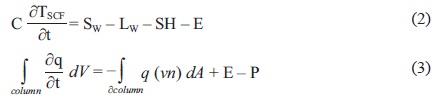
where q is water vapor mixing ratio and v wind velocity. The temporal derivative of the surface temperature in equation (2) is approximately zero for long enough periods, in particular for the 50-day long simulations to be analyzed.
Evaporation is the process most directly affected by the sensitivity parameter. It shows a behavior that is monotonously decreasing with the reduction in ground wetness -as expected- although the decrease is extremely modest for values of the control parameter larger than 0.2. The reduction in evaporation directly implies an increase in sensible heat and surface temperature which is also reflected in a larger upward longwave flux from the surface, further increasing the energy loss from the surface.
The resulting increase in net short and longwave flux loss at the surface suggests that the atmospheric column loses humidity and cloudiness as the ground becomes drier, results that can be verified both at the surface (Fig. 6) and at the top of the atmosphere (Fig. 7).


Associated with the enhanced sensible heat flux there is an increase in the maximum height reached by the PBL in its diurnal cycle, therefore both variables -together with the maximum surface temperature- show a similar response to the control parameter (Fig. 8).
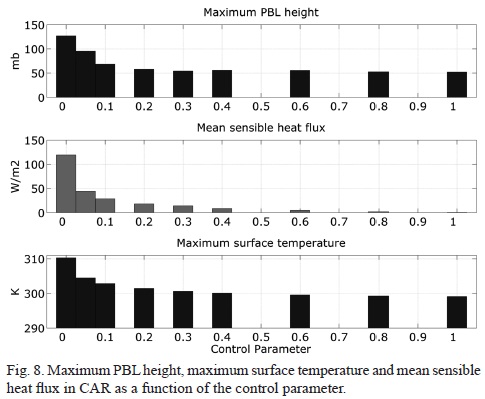
Surface heating is the dominant convective destabilization mechanism and convection responds quickly in the model (Fig. 4). For this reason, key parameters indicative of the PBL behavior are next evaluated at the time when surface temperature reaches its daily maximum (Fig. 8).
Temperature at PBL top (at the time of maximum surface temperature) shows an evolution that is not monotonous with the control parameter; in relatively wet conditions it increases with decreasing control parameter (responding to a general PBL warming) but for dry conditions (S0 and S0.05) the effect of PBL deepening dominates and the temperature at its top decreases with decreasing parameter (Fig. 9). The reduction of evaporation, which in the dry cases is associated with PBL drying, however, seems to play a dominant role. Unlike the case with temperature, relative humidity at the PBL top (also at the time of maximum surface temperature) decreases monotonically with the control parameter, even in the dry range when PBL top temperature (and therefore saturation mixing ratio) diminishes.
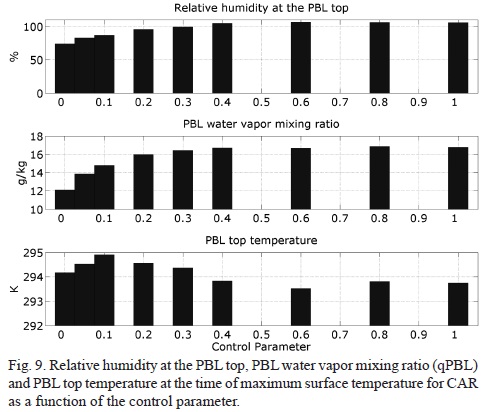
Convective precipitation (Fig. 10) and 850 mb cumulus mass flux (not shown) have a similar dependence with the control parameter than the one shown by PBL top relative humidity, which suggest the importance of the latter parameter to maintain moist convection.
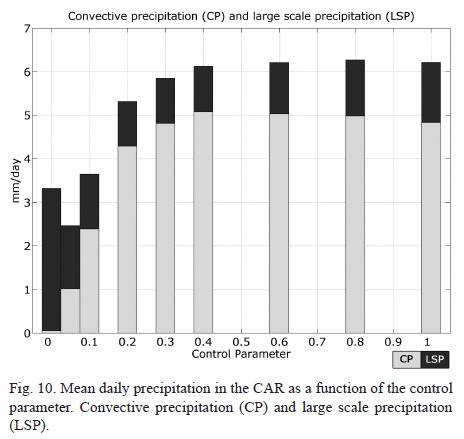
Convective activity decreases drastically for values of the control parameter smaller than 0.2 and is essentially suppressed in S0. These results indicate that deep convective conditions are lost around a value 0.2 of the control parameter.
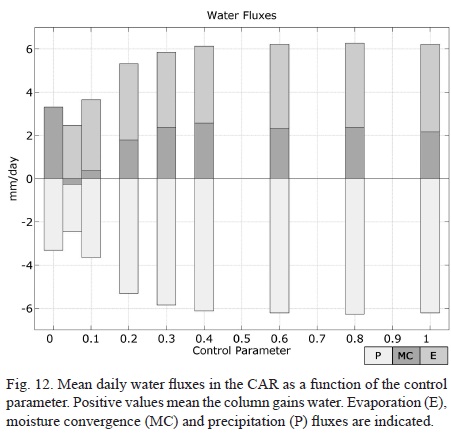
For values of the sensitivity parameter larger than 0.4, precipitation is essentially constant, while evaporation decreases monotonically as the ground dries. This implies an enhanced moisture convergence to the region, a fact that is later verified (Fig. 12).

For the driest conditions, after the weakening of convection in S0.2, large scale precipitation gain dominance, suggesting that new precipitation mechanisms emerge. It can be seen that mid-troposphere large scale upward motion (w500) peaks at S0.4 parameter (Fig. 11), after which it decreases sharply, collapsing (and even changing sign) in the driest conditions when convective precipitation has lost dominance.
The net variation of water vapor content in the entire column through the simulation is neglected and, therefore, so is the time derivative term in the water budget (Eq. 3) resulting in (Eq. 4):
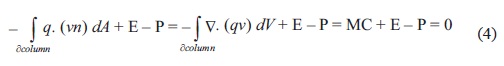
being MC the integral term that represents the net moisture convergence to the column. Figure 12 shows the column water budget for CAR for the different values of the control parameter.
Moisture convergence increases with decreasing control parameter in the 0.8 to 0.4 range, enabling the slight increase in precipitation, considering that evaporation steadily decreases. Previous studies under deforestation scenarios show similar results (Zeng and Neeling, 1999; Silva Correia et al., 2006; Silva Días, 2006). The hypothesis that a decrease in ground wetness conditions may deepen the thermal low and enhance mass and moisture convergence has been previously posed (Grimm et al., 2007).
The drastic decrease in soil moisture forced with values of the control parameter smaller than 0.3 reduces moisture convergence. This situation is not sustainable in the real world, neither in a model which simulates the ground water budget, and therefore the results have theoretical interest only in those cases. In the extreme case when evaporation is completely suppressed (S0), the water balance is between precipitation and MC, which suffers an abrupt increase for reasons that will later be analyzed.
5. Sensitivity of the diurnal cycle
The importance of the diurnal cycle of PBL physical processes in determining the sensitivity of convection in CAR to the control parameter was already implicit in the previous section; we next examine it explicitly.
5.1 Precipitation and evaporation
Figure 13 shows the diurnal cycle of precipitation and evaporation in CAR as a function of the control parameter. In the reference case (S1.0) the primary precipitation maximum occurs in the early afternoon with a secondary maximum at night and the minimum in the morning, at around 8:00 LT. These results are consistent with TRMM observations in the Amazon region (Lin et al., 2000). As was the case with the daily mean, sensitivity is most significant for values of the control parameter smaller than 0.2. The amplitude of the maximum decreases with the control parameter, first slowly up to S0.2 and then much faster. Although the evaporation is the variable most directly affected by the control parameter, it shows a weak sensitivity which reflects the existence of strong compensatory mechanisms.
5.2 Surface and planetary boundary layer
Figure 14a shows the daily cycle of surface temperature, whose amplitude increases with decreasing control parameter. Similar behavior is found in surface air temperature (not shown) with smaller thermal amplitude and a slight lag. The timing of the surface temperature maximum slightly delays as the conditions get drier.
Analogous results (decrease in amplitude and delay of daily maximum as ground wetness is reduced) are found in the response of sensible heat flux -which is closely coupled to the evaporation through the ground energy budget- and PBL height which in turn responds to surface forcing (Figure 14b and c).
The response of the PBL top temperature depends on the relative importance of two competing effects: PBL warming and deepening. Of particular importance is the response of PBL top temperature to the control parameter (Fig. 14d) at noon and early afternoon, when moist convection takes over. While in the driest cases (S0 and S0.05) temperature decreases indicating the dominance of the PBL deepening effect, in all other cases it increases.
The sensitivity of PBL humidity (Fig. 14e) is gradual up to S0.4. Changes become apparent around S0.3-S0.2, when all the results indicate that simulations are shifting away from a deep convective regime. Moreover, water vapor sensitivity does not follow the pattern observed in the other variables. In particular, beyond the 0.2 threshold in the control parameter, the shape of the diurnal cycle is notoriously distorted compared to the humid cases (S1.0 up to S0.3). As conditions get drier, PBL humidity cannot overcome the morning minimum, skips the maximum at noon and only reaches the second maximum in the late afternoon. As the ground gets even drier, PBL humidity diminishes through the day until the diurnal cycle is completly reversed, with a maximum in the morning and a minimum in the afternoon. These results confirm the importance of the processes that regulate PBL humidity to understand the sensitivity of convection to ground wetness.
The diurnal cycle of PBL top relative humidity (Fig. 14f), that more directly relates to the occurrence of moist convection in reality and in the model's cumulus parameterization, shows the most gradual sensitivity to the control parameter of all variables examined. At around S0.4, the cycle begins to show double maxima. The early afternoon maximum (present in the humid cases) decreases in amplitude and delays, while a second maximum -of larger amplitude- develops in the early morning. In the extreme dry case (S0), the shape of the diurnal cycle resembles that of the humid cases, but with significantly lower values -which do not reach the threshold to sustain moist convection- and a considerable delay in the timing of the maximum.
In the case S1.0 the daily cycles of convective precipitation (Fig. 15a) and large-scale precipitation (Fig. 15b) behave qualitatively similar to the daily cycles observed in the Amazon (Lin et al, 2000; Yang and Smith, 2008); convective precipitation is the dominant component, whereas large scale precipitation shows a double-peaked behavior. Convective precipitation decays significantly for values of the control parameter smaller than 0.2, as had been shown in the daily means, together with a delay in the timing of the afternoon maximum. The behavior of large scale precipitation is entirely different. In most conditions, humid and intermediate, there is a double maxima, at night and in the afternoon, the latter one of larger amplitude. For values of the control parameter smaller than 0.1, the night maximum tends to come later and the afternoon one earlier. In the extreme dry case, they join for a single maximum at noon. In this case, the large scale precipitation is dominant and convective precipitation negligible.
5.3 Vertical motion
Daily cycle of vertical motion at 850, 500 and 200 mb is shown in Figure 16. Humid cases show positive values of oo500 occurring during the morning and early afternoon and ascending motion the rest of the day. The cycle is not symmetric; the diurnal maximum in oo500 comes 10 hours after the nocturnal minimum, which in turn leads the following maximum by 14 hours.
Large scale vertical motion at 200 mb is completely in phase, though naturally with smaller amplitudes, than at 500 mb. On the contrary, oo850 presents double maxima diurnal cycle in the humid cases. The first nighttime minimum and morning maximum of ω850 are approximately in phase with the upper levels. The second minimum takes place soon after midday and the second relative maximum, which is still negative (upward), after midnight.
As the control parameter is reduced, the ω500 minimum (upward motion) shifts forward in time (as much as two hours) and slightly decreases in magnitude. The sensitivity of the maximum (downward motion) is larger, presenting delays of up to 4 hours in S0.2 and even 6 hours in the drier cases and a large increase in magnitude that approximately duplicate the amplitude compared to the humid cases. Changes at 200 mb are in the same direction but much smaller.
Simulated ω850 diurnal cycles do not show a large sensitivity, although in the driest conditions the second maximum reaches positive values and therefore descendant motion. In the extreme case (S0), there are major changes in low level large scale vertical velocity, which is upward through the day and twice as strong as in the rest of the simulations.
At night (2:00 h LT) simulations show upward large scale motion through the atmospheric column with maximum intensity at 500 mb in all cases except S0 where it is found at 850 mb.
This means that at this time, all simulations present low level convergence and upper level divergence.
Transition to a situation with one subsiding cell takes place around 6:00 h LT in the humid cases and is completely established by 8:00 h LT local time. Starting at 10:00 h LT, with daytime surface heating, subsidence recedes, divergence shift from the low levels to somewhere between 850 and 500 mb, below which an upward cell develops. By 14:00 h LT the double cell circulation, descending motion on top of a shallow ascending cell, is fully established. It is not until 18:00 h LT that the upward motion reaches the entire troposphere creating a single ascending cell through the column that will last until the next day. In the dry cases, the transition from the double cell circulation to the single cell upward motion shifts from the afternoon, as in the humid cases, to late in the evening, approximately at 22:00 h LT. In S0, the transition to the double cell regime occurs much earlier in the day, it is already established by 8:00 h LT, and lasts most of the day. Only at night does it rapidly change into the one cell ascending pattern that is common to all simulations at that time of the day. These results are summarized in Figure 17.
We next analyze the physical mechanisms associated with the sensitivity of the diurnal cycle of large scale vertical motion. The analysis is based on the same line of reasoning introduced in Section 3. Figure 18 (analogous to Fig. 4) shows the daily cycle of surface temperature, convective precipitation, potential temperature and oo500. Mid tropospheric potential temperature in the tropics is highly constrained by the planetary scale circulation and therefore it does not vary significantly among simulations. In all cases except S0, surface warming initiates convection and therefore the cycles of surface temperature and convective precipitation are in phase. Convective induced warming (Wmc) is the main mechanism that heats the mid troposphere during the morning and afternoon, while adiabatic cooling (Cl) associated with large scale upward motion takes place mainly during the evening and night.
In the dry cases, deep convection is not strong enough to maintain the tropospheric thermal structure and a differential subsident motion is generated to compensate for the decrease in convective induced warming. In the extreme case (S0), where convection is almost inexistent, the mid tropospheric subsident motion is maintained throughout most of the day, since it is the only warming mechanism (Wma) to balance radiative cooling.
The stabilizing effect of 500 mb downward motion together with the destabilizing surface heating result, in the dry and extreme cases, in the formation of a shallow direct circulation that is present through most of the day and that is particularly intense in S0. Enhances moisture convergence (Fig. 12) feeds an intensified shallow circulation (strong large scale upward motion at 850 mb that does not reach 500 mb) which is responsible for the notable increase in the large scale precipitation (Fig. 10).
6. Summary and conclusions
Based on a perpetual January simulation with the UCLA AGCM, the diurnal cycle of precipitation and other selected variables were analyzed over the tropical south american continent. A characteristic and differentiated behavior was detected over a continental region in Central Amazon. Unlike what happens in the surrounding regions, the diurnal cycles of precipitation and large scale motion are in opposite phase in CAR. Low level convergence and large scale ascending motion are maximum at local night and minimum when the convective precipitation peaks in the early afternoon. Maximum temperature at 500 mb follows the period of maximum precipitation. Even if the dominant balance between adiabatic cooling and convective induced warming -characteristic of moist convective regions- holds in the daily means, the mechanisms are out of phase within the day in CAR. This suggest that the dominant destabilizing effect is due to the daily surface warming which motivated the selection of this region for the analysis of the sensitivity of convection to ground wetness.
The sensitivity analysis was based on nine additional simulations in the same conditions than the previous one, perpetual January. A parameter multiplicative of the b factor, that regulates the ratio between evaporation and potential evaporation, was introduced in the latent heat flux equation. Simulations were performed varying the control parameter in the range from 1.0 to 0. The sensitivity proved larger for small values of the control parameter and therefore more simulations were performed in that range.
The reduction in ground wetness directly decreases latent heat flux and consequently generates an increase in surface temperature and sensible heat flux, and therefore PBL height. The small sensitivity of evaporation with respect to the control parameter, considering it is the process being affected in the first place, illustrates the strength of the feedback mechanisms that increase potential evaporation, predominantly surface warming. Of course a model that enforces a ground water budget will eventually show a reduction in evaporation due to lack of water; this feedback is purposely excluded in our surface model.
The analysis of the diurnal cycle of key variables confirm that the range with larger sensitivity to the control parameter is for values smaller than 0.2. As the mean surface temperature increases with decreasing control parameter, so does the daily maximum, whose timing slightly delays. The same results (larger amplitude and delayed maximum) are observed for sensible heat and PBL height diurnal cycles.
PBL humidity shows sensitivity to the control parameter, especially during the daytime, starting at S0.3-S0.2, range at which all the results agree that the transition out of the convective regime is occurring. PBL top relative humidity, which combines the effect of PBL height, temperature and water vapor mixing ratio, shows the most gradual sensitivity to the control parameter, starting already at S0.4. The pattern in the diurnal cycle changes as the control parameter decreases is different for PBL top relative humidity than from other variables. One key aspect is the ability to maintain sufficiently high relative humidity at the PBL top during the early afternoon, when convection is triggered. The results show that this ability is gradually and monotonically lost as the ground dries through the combined effect of PBL top warming and drying in S0.3-S.01 and the dominant drying effect in S.05 and S0, in spite of a PBL top cooling (due to the large increase in its depth).
Regarding the diurnal cycle of large scale vertical motion, results show a slight reduction and delay of the upward nightly maximum in the mid troposphere (500 mb) for the humid range of simulations (S1.0-S0.2). For the drier cases (S0.3-S0), on the other hand, there is an important increase and delay of the diurnal downward maximum at 500 mb. At 200 mb, changes are in the same direction although with smaller amplitude than at 500 mb. No significant sensitivity is observed in the large scale vertical motion at 850 mb, except for the extreme case S0. In this particular case, the large scale vertical velocity at 850 mb is upward through the day and much more intense than in the other simulations, reflecting a strong convergent circulation with little vertical development.
To gain an overall idea of the adjustment of the large scale motion to ground wetness conditions, we aggregate the analyses of large scale velocity in three groups: humid cases (S1.0-S0.3), dry cases (S0.2-S0.05) and the extreme case S0. In the humid and dry cases, destabilization by surface heating initiate convection and thus surface temperature and convective precipitation are in phase. Convective induced warming is the main mechanism that heats the mid troposphere during the morning and afternoon, while adiabatic cooling associated with large scale upward motion takes place mainly during the evening and night. In the dry cases, deep convection is not strong enough to maintain the tropospheric thermal structure and a differential subsident motion is generated to compensate for the decrease in convective induced warming. In the extreme case (S0), where convection is almost inexistent, the mid troposheric subsident motion is maintained throughout most of the day, since it is the only warming mechanism to balance radiative cooling. This stabilizing mid-tropospheric subsident motion combines with the surface heating to generate an intense shallow circulation responsible for the increased moisture convection and large scale precipitation.
We highlight as main conclusions:
• Perpetual January simulations performed enabled the identification of a region in Central Amazon of characteristic and uniform behavior with regard to the diurnal cycle of convection and its association with large scale, PBL and surface processes. In particular, the strong connection of convective activity with surface forcing rendered the region appropriate for the proposed study.
• In the region of study, the simulated diurnal cycle of large scale vertical motion is in opposite phase to that of precipitation (mainly convective), in contrast to what it is generally observed in longer time scales.
• Consistent with previous studies, the sensitivity of the simulations to changes in ground wetness -as represented by the control parameter- is much larger for the drier cases, with control parameters smaller than 0.2.
• Sensitivity of convection to ground wetness in the region can not be understood without fully considering the large circulation feedback and in particular the induced changes in vertical velocity as described earlier.
• However, the mechanisms that control PBL top relative humidity are critical to explain the ability of the system to maintain moist convection in the region. The sensitivity of this parameter in the simulations is gradual and monotonous, resulting from the combined effect of PBL warming, drying and deepening.
References
Arakawa A. and W. H. Schubert, 1974. Interaction of a cumulus cloud ensemble with the large-scale environment, Part I. J. Atmos. Sci. 31, 674-701. [ Links ]
Arakawa A. and V.R. Lamb, 1977. Computational design of the basic dynamical processes of the UCLA general circulation model. In: Methods in Computational Physics (B. Alder, Ed.). Academic Press, New York, 173-265. [ Links ]
Arakawa A., 2000. A personal perspective on the early years of general circulation modeling at UCLA. Book Chapter In: General Circulation Model Development. Past, Present, and Future. (D. A. Randall, Ed.). Academic Press, 1-65. [ Links ]
Bechtold P., J. P. Chaboureau, A. Fljaars, A. K. Betts, M. Kohler, M. Miller and J. L. Redelsperguer, 2004. The simulation of the diurnal cycle of convective precipitation over land in a global model. Q. J. Roy. Met. Soc, 130, 3119-3137. [ Links ]
Betts A. K, J. H. Ball, A. C. M. Beljaars, M. J. Miller and P. A. Viterbo, 1996. The land surface-atmosphere interaction: A review based on observational and global modeling perspectives. J. Geophys. Res. 101, 7209-7226. [ Links ]
Betts A. K and C. Jakob, 2002. Evaluation of the diurnal cycle of precipitation, surface thermodynamics, and surface fluxes in the ECMWF model using LBA data. J. Geophys. Res., 107, 8045-, doi:10.1029/2001JD000427. [ Links ]
Betts A. K and P. Viterbo 2005. Land-surface, boundary layer, and cloud-field coupling over the southwestern Amazon in ERA-40. J. Geophys. Res, 110, D14108, doi: 10.1029/2004JD005702. [ Links ]
Chaboureau J. P., F. Guichard, J. L. Redelsperger and J. P. Lafore, 2004. The role of stability and moisture in the diurnal cycle of convection over land. Q. J. Roy. Met. Soc. 130, 3105-3117. [ Links ]
Chang Cheng T., J. Yoon, K. J. St. Corix and E. S. Takle, 2001. Suppressing impacts of the Amazonian deforestation by the global circulation change. B. Am. Met. Soc. 82, 2209-2216. DOI: 10.1175/1520-0477 [ Links ]
Chien-Ming-Mu, B. Stevens and A. Arakawa et al., 2009. What controls the transition from shallow to deep convection? J. Atmos. Sci. 66, 1793-1806. [ Links ]
Collini E. A., E. H. Berbery, V. R. Barros and M. E. Pyle, 2008. How does soil moisture influence the early stages of the South American Monsoon?. J. Climate 21, 195-213. [ Links ]
Cook K. H., 1994. Mechanisms by which drying perturbs tropical precipitation fields. J. Climate, 7, 400-413. [ Links ]
Deardorff J.W., 1972. Parameterization of the planetary boundary layer for use in general circulation models. Mon. Wea. Rev. 100, 93-106. [ Links ]
Derbyshire S. H., I. Beau, P. Bechtold, J. Y. Grandpeix, J. M. Piriou J. L. Redelsperger and P. M. M. Soares, 2004. Sensitivity of moist convection to environmental humidity. Q. J. Roy. Met. Soc. 130, 3055-3080. [ Links ]
Dirmeyer F., J. Zeng, A. Ducharne, J. Morrill, and R. D. Koster, 2000. The sensitivity of surface fluxes to soil water content in three land surface schemes. J. Hydrometeor. 1, 121-134. [ Links ]
Dirmeyer F., R. D. Koster and Z.Guo, 2006. Do global models properly represent the feedback between land and atmosphere? J. Hydrometeor. 7, 1177-1198. [ Links ]
Figueroa S. N., P. Satyamurty and P. L. da Silva Días, 1995. Simulations of the summer circulation over the South American region with an Eta coordinate model. J. Atmos. Sci. 52, 1573-1584. [ Links ]
Fu R., R. E. Dickinson, M. Chen, and H. Wang, 2001. How do tropical sea surface temperatures influence the seasonal distribution of precipitation in the equatorial Amazon? J. Climate 14, 4003-4026. [ Links ]
Garreaud R., 1999. A multi-scale analysis of the summertime precipitation over the Central Andes. Mon. Wea. Rev. 127, 901-921. [ Links ]
Grimm A. M., J. S. Paland and F. Giorgi, 2007. Connection between spring conditions and peak summer monsoon rainfall in South America: role of soil moisture, surface temperature, and topography in eastern Brazil. J. Climate 20, 5929-5945. [ Links ]
Guo Z, P. A. Dirmeyer, R. D. Koster, G. Bonan, E. Chan, P. Cox, C. T. Gordon, S. Kanae, E. Kowalczyk, D. Lawrence, P. Liu, Cheng-Hsuan Lu, S. Malyshev, B. Mcavaney, J. L. McGregor, K. Mitchell,D. Mocko, T. Oki, K. W. Oleson, A. Pitman, Y. C. Sud, C. M. Taylor, D. Verseghy, R. Vasic, Y. Xue, and T. Yamada, 2006. GLACE: The Global Land-Atmosphere Coupling Experiment. Part II: Analysis. J. Hydrometeor. 7, 611-625. [ Links ]
Hahmann A. N. and R. E. Dickinson, 1997. TCCM2/BATS model over tropical South America: Applications to tropical deforestation. J. Climate 10, 1944-1964. [ Links ]
Harshvardhan R. Davies D. A. Randall and T. G. Corsetti, 1987. A fast radiation parameterization for atmospheric circulation models. J. Geophys. Res. 92, 1009-1016. [ Links ]
Harshvardhan D. A. Randall T. G. Corsetti and D. A. Dazlich, 1989. Earth radiation budget and cloudiness simulations with a general circulation model. J. Atmos. Sci. 46, 1922-1942. [ Links ]
INPE, 2005. Monitoring the Brazilian Amazon forest by satellite: 2002-2003 Instituto Nacional de Pesquisas Espaciais. São José dos Campos, Brazil. [ Links ]
Kikuchi K. and B. Wang, 2008. Diurnal precipitation regimes in the global tropics. J. Climate 21, 2680-2696. [ Links ]
Koster R. D., P. A. Dirmeyer, Z. Guo, G. Bonan, E. Chan, P. Cox, C. T. Gordon, S. Kanae, E. Kowalczyk, D. Lawrence, P. Liu, Cheng-Hsuan Lu, S. Malyshev, B. McAvaney, K. Mitchell, D. Mocko, T. Oki, K. Oleson, A. Pitman, Y. C. Sud, C. M. Taylor, D. Verseghy, R. Vasic, Y. Xue and T. Yamada, 2004a. Regions of strong coupling between soil moisture and precipitation. Science 305, 1138-1140. doi: 10.1126/science 1100217. [ Links ]
Koster R. D., Z. Guo, P. A. Dirmeyer, G. Bonan E. Chan, P. Cox, H. Davies, C. T. Gordon, S. Kanae, E. Kowalczyk, D. Lawrence, P. Liu, Cheng-Hsuan Lu, S. Malyshev, B. McAvaney, K. Mitchell, D. Mocko, T. Oki, K. Oleson, A. Pitman, Y. C. Sud, C. M. Taylor, D. Verseghy, R. Vasic, Y. Xue and T. Yamada, 2004b. GLACE: The Global Land-Atmosphere Coupling Experiment. Part I: Overview. J. Hydrometeor. 7, 590-610. [ Links ]
Krishnamurti T. N., C. Gnanaseelan and A. Chakraborty, 2006. Prediction of the diurnal change using a multimodel superensemble. Part I: Precipitation. Mon. Wea. Rev. 135, 3613-3632. [ Links ]
Kuang Z. and C. Bretherton, 2006. A mass-ux scheme view of a high-resolution simulation of a transition from shallow to deep cumulus convection. J. Atmos. Sci. 63, 1895-1909. [ Links ]
Lenters J. D. and K. H. Cook, 1999. Summertime precipitation variability over South America: Role of the large-scale circulation. Mon. Wea. Rev. 127, 409-431. [ Links ]
Marengo J. A., 2006. On the hydrological cycle of the Amazon basin: A historical review and current satate of the art. Brazilian J. Meteorology 21, 1-19. [ Links ]
Mechoso C. R., J.-Y. Yu and A. Arakawa, 2000. A coupled GCM pilgrimage: From climate catastrophe to ENSO simulations. In: General Circulation Model Development: Past, Present, and Future. (D. A. Randall, Ed.). Academic Press, NY, 539-575. [ Links ]
Mintz Y. and Y. Serafini, 1981. Global fields of soil moisture and land-surface evapotranspiration. NASA Tech. Memo. 83907, Research Review-1980/81, NASA Goddard Space Flight Center, Greenbelt, MD, 178-180. [ Links ]
Nesbitt S.W. and E. J. Zipster, 2003. The diurnal cycle of rainfall and convective intensity according to three years of TRMM Measurements. J. Climate 16, 1456-1475. [ Links ]
Pan D. M., and D. A. Randall, 1998. A cumulus parameterization with a prognostic closure. Q. J. Roy. Met. Soc. 124, 949-981. [ Links ]
Sampaio G., C. Nobre and P. Satyamurty, 2006. Projected Amazonian deforestation in the 21th century and possible regional climatic impacts. Proceed. of 8 ICSHMO. INPE, 939-944. [ Links ]
Sato T., H. Miura, M. Satoh and Y. N. Takayabu, 2009. Diurnal cycle of precipitation in the tropics simulated in a global cloud-resolving model. J. Climate 22, 4809-4826. [ Links ]
Silva Correia F. W, R. C. Dos Santos Avalá and A. O. Manzi, 2006. Brazilian J. Meteorology 21, 153-167. [ Links ]
Silva Días P., 2006. Background sobre otros aspectos regionales: cambios en el uso del terreno, aerosoles y traza de gases. El cambio climático en la cuenca del plata. (V. Barros, R. Clarke and P. Silva Días, Eds.). 1ª edición, Buenos Aires: Consejo Nacional de Investigaciones Científicas y Técnicas - CONICET, 135-148. [ Links ]
Suárez M. J., A. Arakawa and D. A. Randall, 1983. Parameterization of the planetary boundary layer in the UCLA general circulation model: Formulation and results. Mon. Wea. Rev. 111, 2224-2243. [ Links ]
Xue Y., F. de Sales, W.-P. Li, C. R. Mechoso, C. A. Nobre and H.-M. Juang, 2006. Role of land surface processes in south American Monsoon Development. J. Climate 19, 741-762. [ Links ]
Yang S. and E. A. Smith, 2008. Convective-stratiform precipitation variability at seasonal scale from 8 yr of TRMM Observations: Implications for multiple modes of diurnal variability. J. Climate 21, 4087-4114. [ Links ]
Zeng N. and J. D. Neeling, 1999. A land atmosphere interaction theory for the tropical deforestation problema. J. Climate 12, 857-872. [ Links ]














