Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Atmósfera
versión impresa ISSN 0187-6236
Atmósfera vol.25 no.2 Ciudad de México abr. 2012
Turbulence integral length and footprint dimension with reference to experimental data measured over maize cultivation in Po Valley, Italy
D. Masseroni, G. Ravazzani, C. Corbari and M. Mancini
Dipartimento di Ingegneria Idraulica, Ambientale, Infrastrutture viarie, e Rilevamento, Politecnico di Milano Piazza Leonardo da Vinci, 32, 20133 Milano, Italia
Corresponding author: D. Masseroni; e-mail: daniele.masseroni@mail.polimi.it
Received March 3, 2011; accepted November 23, 2011
RESUMEN
La turbulencia atmosférica en la capa límite planetaria (PBL, por sus siglas en inglés) gobierna el intercambio de masa y energía en el sistema suelo-vegetación-atmósfera. Actualmente existen estaciones micrometeorológicas basadas en la técnica de covarianza turbulenta para la evaluación de los flujos de calor latente y sensible a través de la medición de las fluctuaciones de la componente vertical de la velocidad del viento, de la temperatura y del vapor de agua en la PBL. La interpretación correcta de estas mediciones requiere de la correcta evaluación del área de origen donde se generan los flujos turbulentos. Se han desarrollado muchos enfoques diferentes para calcular esta área de origen, pero no existe ningún consenso general sobre la precisión y la aplicabilidad de esos métodos. El objetivo de este trabajo es demostrar que existe una relación entre el área de origen típica que afecta al instrumental y los torbellinos que son responsables del transporte de la energía cinética turbulenta (TKE, por sus siglas en inglés). Se realizó una serie de mediciones con una estación micrometeorológica situada en un campo de maíz en Landriano, en el valle del Po, Italia. Los resultados demuestran que la dimensión de los torbellinos está en estrecha relación con la dimensión del área de origen, proponiendo un nuevo enfoque para el estudio de la covarianza turbulenta con base en en las dimensiones de los torbellinos.
ABSTRACT
The atmospheric turbulence in the planetary boundary layer (PBL) governs the mass and energy exchange over the soil-vegetation-atmosphere system. Micrometeorological stations based on the eddy-covariance technique have been recently developed for the assessment of latent and sensible heat fluxes through high frequency measurements of the fluctuating component of wind velocity, temperature and air water content in the PBL. Correct interpretation of such measurements requires assessment of the actual source area (footprint) contributing to the eddy fluxes (latent and sensible heat). Many different approaches have been developed to estimate the source area function but there is no general consensus on the accuracy and applicability of these methods. The objective of this work is to demonstrate the existence of a relationship between the representative source area for eddy covariance measurements, and the large eddies responsible for the transport of turbulent kinetic energy (TKE). Moreover, the energy balance closure was used to analyze the possible effects of the different lengths of the source area on the heat fluxes. A series of measurements were carried out in a micrometeorological eddy covariance station located in a maize field in Landriano in Po Valley (PV), Italy. The results show that the dimension of the large eddies is tightly bound to the footprint size, leading to a new approach to study the eddy covariance measure based on the assessment of the turbulence scale.
Keywords: Footprint, integral length, energy balance, autocorrelation function.
1. Introduction
Planetary boundary layer (PBL) delimits the fraction of the troposphere in direct contact with the terrestrial surface that is characterized by the accumulation of the atmospheric pollution (Stull, 1989). The upper boundary of the PBL can be represented by the height of the thermal inversion from sounding measurements (Fig. 1a, b).
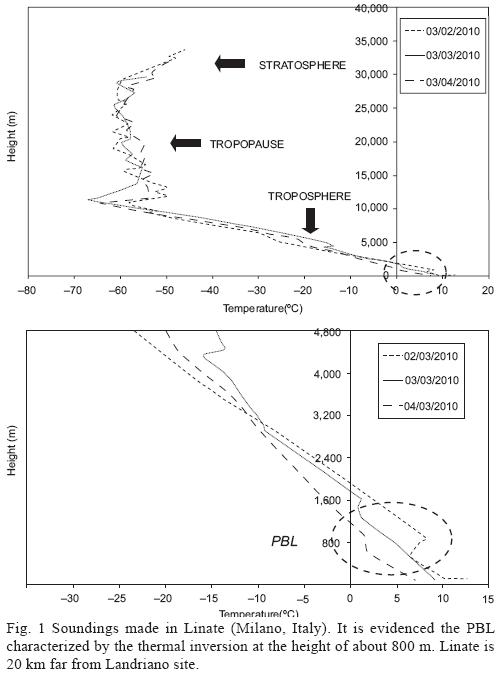
The PBL can be considered as an enormous thermal machine that converts solar energy in air mass movement (Sorbjan, 1989). The characteristics of the air in the PBL can be assimilated to that of a turbulent viscous fluid. The turbulence of the air flow can be described using the Reynold's hypothesis (Garrat, 1999) subdividing a generic turbulent parameter in a mean component and in a fluctuating component. Another way to study the turbulence is based on the overlap of harmonic signals (sine and cosine) characterized by different periods. It is possible to define the eddies sizes that characterize the turbulent structure using frequency analysis (Dias et al., 2004). In particular, using the autocorrelation function it is possible to calculate the size of the large eddies that are responsible for the transport of most of the turbulent kinetic energy (TKE) (Teleman et al., 2008).
The source area of a turbulent flux measurement defines the spatial context of the measurement. It is something akin to the field of view of the measurement of surface atmosphere exchange. When turbulent flux sensors are deployed, the objective is usually to measure signals that reflect the influence of the underlying surface on the turbulent exchange. The measured signal depends on which part of the surface has the strongest influence on the sensor, and thus on the location and size of its footprint (Schmid, 2002). The footprint size can be considered like a representative area of the sensor detector. Generally the footprint can be represented like a distance from the tower (where sensors are located) upwind the preferential direction of the wind velocity. Many models are available to calculate the footprint dimension, for example the Lagrangian, Eulerian and LES (large eddy simulation) models try to represent the conditions of the atmospheric turbulence in a realistic way (Dyer, 1963; van Ulden, 1978; Hsieh et al., 1997; Kljun et al., 2002; Markkanen et al., 2009; Mao et al., 2007). One of the problems of these models is the computational cost required to solve equations. A simple model based on the combination of Lagrangian stochastic model and dimensional analysis is represented by the Hsieh's (2000) hybrid model. The advantage of this model is that it can be applied in neutral, stable and unstable conditions and compared with Gash's Eulerian model (1985) and Thomson's (1978) Lagrangian model results, produces a correct assessment of the footprint size.
The eddy covariance method is used to estimate turbulence fluxes of mass and energy to and from the surface. A difficult but important issue is to quantify the uncertainty in the flux measurements. These fluxes are in fact complex processes, and the estimates result from various measurements and calculations as well as numerous explicit and implicit assumptions. One simple measure of internal consistency is to check for the conservation of energy. The sum of the turbulence fluxes of latent and sensible heat should balance the available energy (net radiation-soil heat flux). Experience has indicated that closure values are generally significantly lower than 1 (Wilson et al., 2002). There are several reasons because the balance closure value is not perfectly 1, but the two main problems are: the dimension of source area for eddy fluxes measurements and the stability conditions of the atmosphere (Massman et al., 2002).
The objective of this work is to find a relationship between the footprint dimension, calculated by the Hsieh and Gash models, and the turbulence integral length that represent the dimension of the large eddies. The energy balance closure improvement, using only flux measurements with a source area equal to the field size is shown, and the effect of the stability conditions of the atmosphere (unstable, neutral and stable conditions) on energy balance closure and footprint length is calculated. The experimental data used in the analysis are measured by a micrometeorological station located in a maize field in Landriano in Po Valley (PV), Italy.
2. Theoretical background
2.1 Eddy covariance technique
The turbulence of the air flow can be described, using the Reynold's hypothesis, subdividing wind speed and the scalar temperature in a mean component and in a fluctuating component:

U, V, W are the instantaneous three-dimensional components of the wind speed and T is the scalar temperature;  , represents the mean components and the u', v', w', T' represents the fluctuation, which are all functions of the spatial position (x, y, z) and time (t).
, represents the mean components and the u', v', w', T' represents the fluctuation, which are all functions of the spatial position (x, y, z) and time (t).
The turbulence scales of the instantaneous wind speed are the measure of the representative dimensions of the vortices induced by the turbulence inside the mean stream of the flow (Teleman et al., 2008). The determination of the turbulence scale starts computing the autocorrelation function for all the fluctuation components (longitudinal, transversal, vertical) of the wind speed. Generally only the component that represents the prevalent direction of the wind wave is used. The correlation in time, about the U component of the wind speed, is defined as:

Where ρuu(τ) defines the autocorrelation function, Ruu(τ) represents the covariance function of the u(t) variable determined in two different instant of time t and τ and  defines the average. According to the Taylor's hypothesis of the frozen turbulence (Foken, 2008) and assuming that the turbulence is homogeneous and isotropic, the integral length (Lx) is represented by (Sozzi et al., 2002):
defines the average. According to the Taylor's hypothesis of the frozen turbulence (Foken, 2008) and assuming that the turbulence is homogeneous and isotropic, the integral length (Lx) is represented by (Sozzi et al., 2002):

The eddy covariance method determines the surface fluxes as the sum of turbulent eddy-fluxes, measured above the surface, and the flux divergence between the surface and the eddy covariance measurement level (Barr et al., 2006). The basic equations to estimate latent (LE) and sensible heat (H) fluxes, are comparatively simple:

λ is the latent heat of evaporation, ρ the air density and 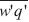 the covariance between vertical wind velocity component and scalar concentration of vapor in the air. Cp is the specific heat at constant pressure and
the covariance between vertical wind velocity component and scalar concentration of vapor in the air. Cp is the specific heat at constant pressure and  is the covariance between vertical wind velocity component and the scalar temperature.
is the covariance between vertical wind velocity component and the scalar temperature.
The surface energy balance may be written as:

Where Rn is the net radiation flux and G is the soil heat flux.
In a perfect world, under theoretical conditions, measurements would be perfect and the closure value would be close to 1.
2.2 The Hsieh model
The Hsieh model (2000) is based on:

where x represents the distance from the tower, k is the von Karman constant (0.4), D and P are called similarity constants and depend on stability conditions of the atmosphere (Hsieh et al., 2000). zu is a length scale and zm represents the height where sensors are installed.  is the ratio between the flux measured by the sensors and the flux emitted by the total field. S0 quantity is not known, but it is not important because the ratio is always between 0 and 1 (Hsieh et al., 2000). L is the Monin-Obukov length (Calder, 1965) and can be calculated as:
is the ratio between the flux measured by the sensors and the flux emitted by the total field. S0 quantity is not known, but it is not important because the ratio is always between 0 and 1 (Hsieh et al., 2000). L is the Monin-Obukov length (Calder, 1965) and can be calculated as:

Where u* is the friction velocity (Eq. 9),  is the mean air temperature, g is the gravity constant and w'T' is the covariance between vertical wind velocity component and the scalar temperature.
is the mean air temperature, g is the gravity constant and w'T' is the covariance between vertical wind velocity component and the scalar temperature.

Where 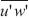 and
and  are the covariance between vertical velocity component and planar (longitudinal and transversal) components of the wind, and zu is defined by (Eq. 10) where z0 represents the surface roughness.
are the covariance between vertical velocity component and planar (longitudinal and transversal) components of the wind, and zu is defined by (Eq. 10) where z0 represents the surface roughness.

Diuring the growing period of a crop, it is necessary to change the measurement height zm in (zm–d) where d is called displacement and it is about 2/3 of hv (Foken, 2008), where hv is the vegetation height. The roughness is calculated by the approximate relation (Foken, 2008).

2.3 The Gash model
The Gash model for estructing the distance from the tower, x, is defined as:

where  is the mean wind velocity along the prevalent direction. The Gash model (1985) can be applied only in neutral conditions of the atmosphere and it is derived from one approximate solution of the diffusion equation (Calder, 1952).
is the mean wind velocity along the prevalent direction. The Gash model (1985) can be applied only in neutral conditions of the atmosphere and it is derived from one approximate solution of the diffusion equation (Calder, 1952).
More information about the models and methods used in this work can be founded in Gash (1985), Hsieh et al. (1999) and Teleman et al. (2008).
3. Study site and instruments
Experimental data were obtained by a micrometeorological station utilized to measure evapo-transpiration fluxes in a maize field in Landriano at the valley of Po, Italy (45.19 ºN, 9.16 ºE, 87 m.a.s.l) (Fig. 2). A Three-dimensional sonic anemometer (Young 81000 by Campbell Scientific), to measure the wind velocity components, and a gas analyzer (LI-COR 7500), to measure the concentrations of CO2 and H2O in the atmosphere, were installed at the top of the station (5 m). The anemometer is able to measure wind velocity to a maximum frequency of 20 Hz. A radiometer (CNR 1 by Kipp and Zonen) which measures the four components of net radiation, was positioned at about 4 m height. Two thermocouples (by ELSI) and a heat flux plate (HFP01 by Hukseflux) for the measurements of soil ground heat flux were positioned, respectively, at 6-10 cm and 8 cm.

Data were collected during the year 2010 from Julian day 152 (1 June) to 283 (10 October), by a Campbell Scientific data logger (CR 5000) and stored every 30 min. High frequency measurements were carried out during some days in this period, in particular on 173 julian day (22 June), 203 (22 July), 215 (3 August) and 216 (4 August) Julian day. Generally, the high frequency measurements were carried out during daytime (from 12:00 to 13:00), but on Julian day 215 the experiment was carried out during the night (from 23:00 to 24:00). For these experiments (day time and night) the anemometer was set to 10 Hz.
Energy fluxes have been corrected applying the Webb correction for density fluctuations (Webb et al., 1980) and the correction for buoyancy flux due to sonic temperature measurements (Liu et al., 2001). Tilt correction has been applied to take into account that the assumption of a negligible mean vertical velocity is not always verified (Tanner and Thurtell, 1969). Frequency response correction has been applied for the attenuation of eddy covariance fluxes due to sensor response, path-length averaging, sensor separation, signal processing, and flux averaging period (Massman, 2000). The data during periods of rainfall were discarded. The database, after these corrections, is composed of 4163 half hourly data.
4. Method
The first step was to identify the prevalent direction of the wind speed. During the experiments the prevalent direction of the wind speed in the field was east-west, in agreement with the general behavior observed during 2010. From the anemometric configuration the east-west component is represented by the planar component U.
The second step was to calculate the autocorrelation function using Eq. (2) and the integral length (Eq. 3). The (2) is integrated only up to the first zero-crossing (Katul and Parlange, 1995).
The third step was to calculate the footprint size (x), for each value of  , using Eqs. (7) and (12).
, using Eqs. (7) and (12).  is an independent variable, and x was calculated for 99 different values of
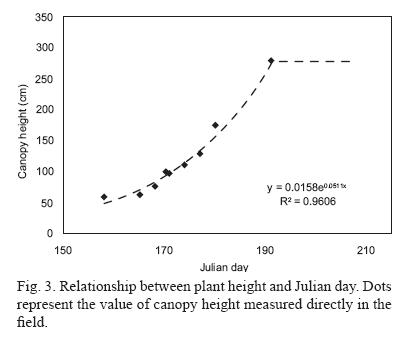
is an independent variable, and x was calculated for 99 different values of  (i.e. 0.01, 0.02,…, 0.99). The parameters in (Eq. 8) and (Eq. 9) were calculated from experimental data measured by the eddy covariance tower. To calculate the footprint size using Eq. (7) it was necessary to determine the parameter zu (10), which is a function of vegetation height hv. The plant height is a function of the Julian day, for the Landriano field in 2010, represented by Eq. (13), which is obtained from canopy height measured directly in the field, as showed in Figure 3.
(i.e. 0.01, 0.02,…, 0.99). The parameters in (Eq. 8) and (Eq. 9) were calculated from experimental data measured by the eddy covariance tower. To calculate the footprint size using Eq. (7) it was necessary to determine the parameter zu (10), which is a function of vegetation height hv. The plant height is a function of the Julian day, for the Landriano field in 2010, represented by Eq. (13), which is obtained from canopy height measured directly in the field, as showed in Figure 3.

Where JD is the Julian day and the hv is expressed in cm. The quantity  is called stability parameter. If:
is called stability parameter. If:
 the atmosphere is unstable (convective conditions);
the atmosphere is unstable (convective conditions);
 the atmosphere is neutral;
the atmosphere is neutral;
 the atmosphere is stable.
the atmosphere is stable.
This classification is important to define the value of D and P in Eq. (7) (Hsieh et al., 2000).
The fourth step was to show some experimental data of heat fluxes of the cornfield and to analyze the different lengths of the source area and their possible effect on the heat fluxes. The energy balance closure was calculated using the relation in section 2.1 and the footprint of latent and sensible heat fluxes was analyzed in order to understand which was its role into the energy balance closure. Landriano field was divided in four different sectors (Fig. 4) along the geographic directions, so that the data are subdivided in four classes of 90º each depending on wind direction. For each sector a radius of a source area which included at least for 95% in the field was defined. The radius in sector I is 160, in sector II is 100, in sector III is 120 and sector IV is 200 m.
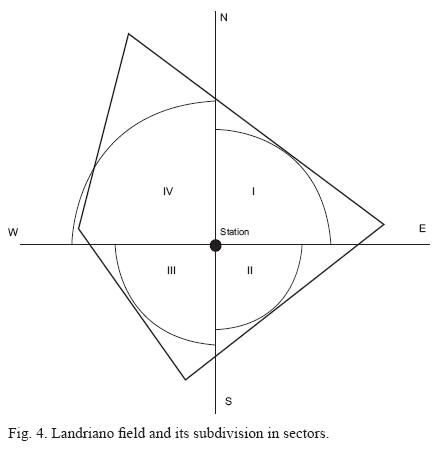
For each measurement of latent and sensible heat fluxes, the footprint size (7), assuming that  was equal to 0.8, was calculated and the energy balance closure was calculated using only the data of latent and sensible heat fluxes which had a footprint size less than field dimension.
was equal to 0.8, was calculated and the energy balance closure was calculated using only the data of latent and sensible heat fluxes which had a footprint size less than field dimension.
In the fifth step the latent and sensible heat fluxes were classified as a function of the atmospheric stability conditions. The slope values of the linear regression and linear correlation coefficients for energy closure balance in unstable, neutral and stable atmospheric conditions are presented. Moreover, a statistic of the footprint sizes for the different atmospheric stability conditions is calculated.
The data stored every 30 min were used to calculate the energy balance closure (fourth and fifth steps) whereas the high frequency data set was used to study the integral length (from first to third steps).
5. Results and discussions
In Table I the stability conditions of the atmosphere which are in correspondence with the data measured in high frequency way, are represented. On Julian days 173 and 203 the atmosphere was unstable and the convective forces were prevalent, on Julian day 216 the atmospheric conditions were neutral, on day 215 during the night the atmospheric conditions were stable.
The form of the autocorrelation function (Fig. 5) is such that it generally decreases rapidly to its first zero, after which it may become negative and proceed to oscillate about zero. Yaglom (1987) founded that the shape of the autocorrelation function may contain information about the structure of the turbulence. The oscillation of the autocorrelation values tends to zero with time because the characteristics of the turbulence change moving away from the fixed station.

Integral length scales of the velocity are represented in Figure 6. If the PBL is in stable conditions the turbulence is formed by eddies that have small dimension and are originated by the mechanical forces of the wind shear. If the atmosphere is unstable, in addition to the small isotropic eddies, there are large eddies that have a circular structure (isotropic hypothesis) (Wyngaar, 1990). The integral length for stable conditions is greater than in unstable conditions as shown in Table I. This is due to the presence of small self-similar vortices, and the velocity of the particles in two more distant points in the spatial domain tends to be correlated. For unstable conditions the integral length is smaller than in stable conditions because the turbulence structures are more defined.
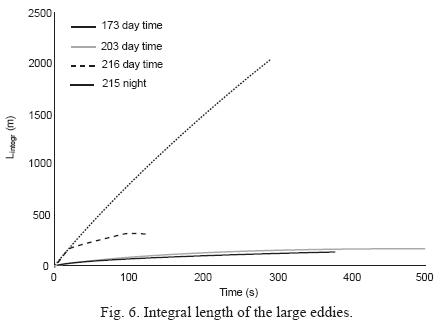
Note that the integral length in convective conditions increases and after 300 s becomes constant, defining the time and spatial domain of the eddy covariance measures. In contrast for stable conditions, the integral length tends to infinity and due to poorly mixed conditions. In this case the PBL is not well defined and there is no clear line that characterized the top of the boundary layer.
The footprint cumulated curves calculated by (Eq. 7) and (12), are presented in Figure 7.
Comparing the footprint size, for the different stability conditions, and the integral lengths, we note that the integral lengths are about the 90% to the footprint size (Table I). This result shows that the footprint size and the integral lengths are correlated and the footprint size depends on the turbulence structure of the atmosphere and in particular on the size of the large eddies.
In Figure 8a the energy balance closure with all data (4163) are presented. The slope value (m) of the linear regression forced thought the origin is equal to 0.6433, while the linear correlation coefficient (R2) is equal to 0.8715. In Figure 8b the energy balance closure using only the data which have a footprint size compatible with the field dimension (section 4) are presented. A small improvement in terms of m and R2, respectively, of about 0.6 and 4.4% was obtained. In Table II the values of m and R2 for different atmospheric stability conditions are shown. In the column Total data the energy balance closure was calculated using the total data set whereas in Fluxes with compatible footprint size the energy balance closure was calculated using the data which had a representative source area less than the field dimension.

The atmospheric stability conditions play a relevant role on eddy covariance measurements. In fact, during stable conditions, the fluxes measured by the tower are not corrected because the turbulence in the PB is low. The stable stratification of the atmosphere causes a quasi laminar flow (Foken, 2008) and this phenomenon generates very small values of m and R2, respectively, 0.1415 and 0.0744. It is not possible to use the eddy covariance method during stable conditions, only during unstable and neutral conditions the data are corrected because the turbulence in the PBL is high.
The footprint lengths for different atmospheric stability conditions are presented in Figure 9. For each atmospheric conditions the footprint lengths from minimum to maximum value were stored in 20 classes and the percentage of data for each class was calculated. The results show that 1980 data points (47.6% of the total set) are in unstable conditions, 977 data (23.5%) are in neutral conditions and 1206 (29%) are in stable conditions. Figure 9a (unstable conditions) shows that the most characteristic range of values of the footprint size is from 34 to 43 meters with a frequency of about 16%; in neutral conditions (Fig 9b) the range is from 128 to 147 meters with a frequency of about 37% and in stable conditions (Fig. 9c) the range is from 173 to 264 meters with a frequency of about 24%. From unstable to stable conditions the footprint size increases from 43 to 264 m, the dimension of the representative source area for latent and sensible heat fluxes, for unstable conditions, is smaller than in stable conditions and the number of data points with a footprint size compatible with the field dimension is higher than in stable conditions: In fact, during unstable and neutral conditions the fluxes which have a source area compatible with the field dimension are, respectively, 1840 and 774, while in stable condition only 12 (Table II).

6. Conclusions
In this paper we have shown how the eddy covariance technique and high-frequency measurements can be used to assess the footprint size. In particular the footprint models depend on height, roughness, stability conditions and wind speed. However, a correspondence between the footprint sizes and large eddies exists. The turbulence structure plays a fundamental role determining the representative area of the eddy covariance instruments. The integral length under different atmospheric situations (stability, unstability and neutral) is about 90% of the footprint size (Table I). The integral length in the convective situations tends to be constant from t > 300 s (>5 min). This value of t, when multiplied by the mean wind velocity, represents the maximum spatial domain of the eddy covariance station that is the area where the flux exchange between soil-vegetation and atmosphere influenced the measure of the sensors. This study demonstrates that it is possible to assess the footprint dimension of the eddy covariance sensors from the turbulence atmospheric characteristic parameters using the spatial-temporal autocorrelation function from high frequency data.
The representative source area for eddy fluxes has been studied and the influence of a footprint size compatible with the field dimension on the energy balance closure has been shown. The slope value of the linear regression (m) and the linear correlation coefficient (R2) increase respectively, about 0.6 and 4.4%. A decrease in dispersion and the process of eliminating some spikes around the linear regression curve in the energy balance closure was noticed. The slight improvement of m value is caused because the Landriano field is surrounded on three sides (north, east, south) by other maize fields so that if the footprint size is larger than the field dimension, the latent and sensible fluxes do not change in a substantial way. The footprint size changes with atmospheric stability conditions and in unstable conditions the source area is smaller than in stable conditions as a consequence of the atmospheric turbulence structure as presented in section 5. The most representative values for footprint size are 43 m for unstable, 147 for neutral and 264 for stable conditions.
Acknowledgements
This work was funded in the framework of the ACQWA EU/FP7 project (grant number 212250) "Assessing Climate impacts on the Quantity and quality of WAter", the framework of the ACCA project funded by Regione Lombardia "Misura e modellazione matematica dei flussi di ACqua e CArbonio negli agro-ecosistemi a mais" and PREGI (Previsione meteo idrologica per la gestione irrigua) founded by Regione Lombardia. The authors thank the University of Milan-Dipartimento di Idraulica Agraria for the collaboration given in managing Landriano eddy covariance station.
Reference
Barr A., K. Morgenstern, T. Black, J. McCaughey and Z. Nesic, 2006. Surface energy balance closure by the eddy-covariance method above three boreal forest stands and implications for the measurement of CO2 flux. Agr. Forest Meteorol. 140, 322-337. [ Links ]
Calder K., 1952. Some recent british work on the problem of diffusion in the lower atmosphere, air pollution. Mc Graw-Hill, New York, 787 pp. [ Links ]
Calder K., 1965. Concerning the similarity theory of A. S. Monin and A. M. Obukhov for the turbulent structure of the thermally stratified surface layer of the atmosphere. Q. J. R. Meteorol. Soc. 92, 141-146. [ Links ]
Dias N., M. Chamecki, A. Kan and C. Okawa, 2004. A study of spectra, structure and correlation functions and their implications for the surface-layer turbulence. Bound.-Lay. Meteorol. 110, 165-189. [ Links ]
Dyer A., 1963. The adjustament of profiles and eddy fluxes. Q. J. R. Meteorol. Soc. 89, 276-280. [ Links ]
Foken T., 2008. Micrometeorology. Springer, Berlin, 306 pp. [ Links ]
Garratt J., 1999. The atmospheric boundary layer. Cambridge University Press, Cambridge, USA, 316 pp. [ Links ]
Gash J., 1985. A note on estimating the effect of a limited fetch on micrometeorological evaporation measurements. Bound. -Lay. Meteorol. 35, 409-413. [ Links ]
Hsieh C., G. Katul, J. Schieldge, J. Sigmon and K. Knoerr, 1997. The Lagrangian stochastic model for fetch and latent heat flux estimation above uniform and nonuniform terrain. Water Resour. Res. 33, 427-438. [ Links ]
Hsieh C., G. Katul and T. Chi, 2000. An approximate analytical model for footprint estimation of scalar fluxes in thermally stratified atmospheric flows. Adv. Water. Resour. 23, 765-772. [ Links ]
Katul G. and M. Parlange, 1995. Analysis of land surface heat fluxes using the orthonormal wavelet approach. Water Resour. Res. 31, 2743-2749. [ Links ]
Kljun N., M. Rotach and H. Schmid 2002. A 3D backward Lagrangian footprint model for a wide range of boundary layer stratifications. Bound.-Lay. Meteorol. 103, 205-226. [ Links ]
Liu H., G. Peters and T. Foken, 2001. New equations for sonic temperature variance and buoyancy heat flux with an omnidirectional sonic anemometer. Bound. -Lay. Meteorol. 100, 459-468. [ Links ]
Mao S., Z. Feng and E. Michaelides, 2007. Large-eddy simulation of low-level jet-like flow in a canopy. Environ. Fluid. Mech. 7, 73-93. [ Links ]
Markkanen T., G. Steinfeld, N. Kljun, S. Raasch and T. Foken, 2009. Comparison of conventional Lagrangian stochastic footprint models against LES driven footprint estimates. Atmos. Chem. Phys. 9, 5575-5586. [ Links ]
Massman W., 2000. A simple method for estimating frequency response corrections for eddy covariance systems. Agr. Forest Meteorol. 104, 185-198. [ Links ]
Massman W. and X. Lee, 2002. Eddy covariance flux corrections and uncertainties in long-term studies of carbon and energy exchanges. Agr. Forest Meteorol. 113,121-144. [ Links ]
Schmid H., 2002. Footprint modeling for vegetation atmosphere exchange studies: a review and prospective. Agr. For. Meteorol. 113, 159-184. [ Links ]
Sorbjan Z., 1989. Structure of the atmospheric boundary layer. New Jersey, Prentice Hall, 316 pp. [ Links ]
Sozzi R., M. Valentini and T. Georgiadis, 2002. Introduzione alla turbolenza atmosferica, concetti stime e misure. Pitagora, Milano, 544 pp. [ Links ]
Stull R., 1989. An introduction to boundary layer meteorology. Dordrecht, Kluwer Academic Publishers, 671 pp. [ Links ]
Tanner C. and G. Thurtell, 1969. Anemoclinometer measurements of Reynolds stress and heat transport in the atmospheric surface layer. Department of Soil Science, Wisconsin University Madison. Defense Technical Information Center. Madison, USA, 200 pp. [ Links ]
Teleman E., S. Radu, E. Axinte and R. Pescaru, 2008. Turbulence scales simulations in atmospheric boundary layer wind tunnels. Buletinul Institutului Politehnic Din Iaşi. Publicat de Universitatea Tehnica "Gheorghe Asachi" din Iasi Tomul LIV (LVIII), Fasc. 2, Sectia Constructii. Architectura, Romania, 13 pp. [ Links ]
Thomson D., 1978. Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J. Fluid Mech. 180, 529-556. [ Links ]
van Ulden A., 1978. Simple estimates for vertical diffusion from sources near the ground. Atmos. Environ. 12, 2125-2129. [ Links ]
Webb E., G. Pearman and R. Leuning, 1980. Correction of the flux measurements for density effects due to heat and water vapour transfer. Bound. -Lay. Meteorol. 23, 251-254. [ Links ]
Wilson K., A. Goldstein, E. Falge, M. Aubinet, D. Baldocchi, P. Berbigier, C. Bernhofer, R. Ceulemans, H. Dolman, C. Field, A. Grelle, A. Ibrom, B. E. Law, A. Kowalski, T. Meyers, J. Moncrieff, R. Monson, W. Oechel, J. Tenhunen, S. Verma and R. Valentini, 2002. Energy balance closure at FLUXNET sites. Agr. Forest Meteorol. 113, 223-243. [ Links ]
Wyngaar J., 1990. Scalar fluxes in the planetary boundary layer. Bound.-Lay. Meteorol. 50, 49-79. [ Links ]
Yaglom A., 1987. Correlation theory of stationary and related random functions. Vol. 1, Springer Verlag, New York, 526 pp. [ Links ]














