Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Atmósfera
versión impresa ISSN 0187-6236
Atmósfera vol.24 no.3 Ciudad de México jul. 2011
May the NAO index be used to forecast rain in Spain?
A. CASTRO, M. I. VIDAL
Departamento de Física, Facultad de Ciencias Biológicas y Ambientales, Universidad de León, 24071 León, España
A. I. CALVO
Centro de Estudos do Ambiente e do Mar (CESAM), Universidade de Aveiro, Aveiro, Portugal
M. FERNÁNDEZ–RAGA and R. FRAILE
Departamento de Física, Facultad de Ciencias Biológicas y Ambientales, Universidad de León, 24071 León, España. Corresponding author: R. Fraile; e–mail: roberto.fraile@unileon.es.
Received February 2, 2010; accepted September 15, 2010
RESUMEN
Este trabajo estudia la influencia de la Oscilación del Atlántico Norte (NAO) en el régimen de precipitaciones mensuales, estacionales y anuales de la España Peninsular. Para ello se han utilizado los datos mensuales de precipitación de 325 estaciones pluviométricas repartidas homogéneamente y los índices mensuales del índice NAO desde 1961 a 1998; se han usado un total de 5525 series de precipitación. El estudio se ha realizado mediante correlaciones lineales simples o múltiples entre estas variables utilizando diferentes combinaciones. Se trata de ver si se podría predecir la precipitación mensual, estacional o bien anual a partir de datos previos de precipitación y del índice NAO. Se han representado espacialmente las zonas geográficas cuyos observatorios manifiestan una correlación estadísticamente significativa. Los resultados difieren del tipo de correlación elegido, pero en general los mejores resultados se encuentran en los meses de invierno. Por último, se ha aplicado esta metodología al Valle del Ebro y se ha observado que una combinación del índice NAO de primavera y verano, junto con la precipitación registrada en esas dos estaciones podría ser útil para predecir la precipitación de otoño.
ABSTRACT
This paper studies the influence of the North Atlantic Oscillation (NAO) on monthly, seasonal and annual precipitation regimes in continental Spain. The data used for this study include the monthly rain series of 325 meteorological stations distributed homogeneously over the study zone, and the monthly NAO indices from 1961 to 1998. A total of 5525 rain series were employed for the analysis. Simple and multiple linear correlations were established between these variables in different combinations. The main aim was to check whether monthly, seasonal or annual precipitation data could be predicted using earlier precipitation data and the NAO index. The geographical areas where the stations have shown a statistically significant correlation have been represented on maps. The results differ depending on the correlation, but, in general, the best results have been found in the fall and winter months. Finally, a practical application of the method was carried out in the Ebro Valley and it was observed that the combination of the NAO index for spring and summer and the precipitation registered in those two seasons may be useful to forecast rain in the fall.
Keywords: North Atlantic Oscillation (NAO), precipitation, forecasting, Spain, Ebro Valley.
1.Introduction
In the past few years the number of studies on the NAO index has increased considerably. This index influences the climate in Western Europe in particular (Wanner et al., 2001). The strong positive trend of the NAO detected over the past 30 years has been the focus of many scientific analyses. The most outstanding anomalies were registered in the winter of 1989 (Hurrell, 1995; Walsh, 1996; Thompson and Wallace, 1998; Watanabe and Nitta, 1999). One of the climatic consequences observed are regional changes in the precipitation patterns (Hurrell, 1995; Hurrell and van Loon, 1997; Dai et al., 1997; García et al., 2005).
Studies on global climatic change carried out by the IPCC (2001) show that during the 20th century the average annual rainfall has increased between 7 and 12% in regions between 30 and 85 °N, while it tends to decrease in latitudes under 30 °N. The most recent report (IPCC, 2007), comments that the annual precipitation has increased in most of northern Europe and decreased in most of the Mediterranean area, where there was a decrease also in the annual number of precipitation days. In addition, southern Europe and parts of central Europe as well as North Africa are characterized by a drier winter during the positive phase of the NAO, while the reverse is true in the British Isles, Fennoscandia and northwestern Russia. Changes in the precipitation regimes have also been detected in the past few decades in continental Spain (Mossmann et al., 2004; del Río et al., 2005). Bearing in mind these data, the questions that arise are the following: Is the NAO the cause of these changes in the rainfall in Western Europe? Is there a way to forecast the amount of rain that will fall using the NAO index?
The aim of this paper is to analyze the influence of the NAO on the rainfall regime in Spain. Linear correlations have been established between monthly rainfall data and monthly NAO indices for different months. Several combinations have been considered. Similar correlations have been established with seasonal rainfall data and seasonal NAO values, again in various combinations.
In those cases where the correlations are statistically significant, it will be possible to forecast the monthly or seasonal precipitation by using the variables it correlates well with (precipitation data in the previous months or seasons and NAO values). As an example, one of these linear models will be applied onto the rainfall regime in the Ebro Valley, Spain.
2. Databases
2.1 Precipitation
This study has been carried out in the Spanish part of the Iberian Peninsula, i.e. continental Spain (Fig. 1). Monthly rainfall series from 325 meteorological stations were used (a density of one rainfall station per 2000 km²). The data were provided by the National Institute for Meteorology in Spain for the period between 1961 and 1998.

The methodology and working procedure used were the following:
2.1.1 Filling gaps
The normal–ratio interpolation method was used for filling the gaps in those stations where there were missing data in some series (Paulus and Kohler, 1952). Among the various gap–filling methods available, this particular one has proved to work adequately for rain series (Tang et al., 1996).
2.1.2 Series homogeneity
Once the series were complete, the series with climatic variations or trends were distinguished from those series that presented non–climatic variations. The methodology employed for this study did not take into account non–climatic variations. The non–parametric Kruskal–Wallis homogeneity test was applied (Essenwanger, 1986) for a significance level of 5% (α = 0.05). Each series consisted of 38 data. The threshold value of the H statistic for accepting the null hypothesis was of 52.16 for 37 degrees of freedom (Lindey and Scott, 1984). The results showed that there were 325 weather stations with homogeneous monthly rainfall series.
2.1.3 Rainfall series
Apart from the monthly rainfall series, the four seasonal series were also added (spring, summer, fall and winter), as well as the annual series. Thus, 17 rain series were analyzed for each meteorological station (12 monthly series, 4 seasonal series and 1 annual series). March, April and May have been grouped together as spring; June, July and August as summer; September, October and November as fall; and December, January and February as winter months. All in all, 5525 series were used for this study. Mossmann (2002) describes further details on the databases.
2.2 North Atlantic Oscillation
The NAO index is traditionally defined as the normalized pressure difference at sea level between a station on the Azores and one on Iceland. This index takes on different values depending on the stations used to calculate it. Stykkisholmur (Iceland) is the most widely used northern weather station, although Akureyri is sometimes chosen. On the other hand, Ponta Delgada (Azores), Lisbon or Gibraltar may be used as southern stations. In this study the NAO index has been calculated using the data from Ponta Delgada and Stykkisholmur.
The necessary data to establish the NAO index have been kindly provided by James W. Hurrell (Climate Analysis Section from the National Center for Atmospheric Research, in Boulder, Colorado). These data were also used to establish the average seasonal and annual NAO. The units used for the NAO index are hPa.
3. Methodology
Two procedures were followed to obtain the results: on the one hand, the linear regressions between the rainfall series and the NAO were processed; on the other hand, contour maps were drawn for every individual study in order to represent the spatial correlations and facilitate the interpretation of the results.
3.1 Linear regressions between rainfall series and NAO
Linear regressions of four types were carried out depending on the number of variables involved:
a) linear regressions type y = ax + b between:
NAO for a particular month (variable x) and rainfall in that month (variable y);
NAO for a particular season (variable x) and rainfall in that season (variable y);
NAO for a particular year (variable x) and rainfall in that year (variable y);
NAO for a particular month (variable x) and rainfall in the following month (variable y);
NAO for a particular season (variable x) and rainfall in the following season (variable y).
b) multiple linear regressions type z = ax + by + c between:
NAO for two consecutive seasons (variables x and y) and rainfall in the following season (variable z);
NAO for a particular month (variable x) and rainfall in that month (variable y) and in the following one (variable z);
NAO for a particular season (variable x) and rainfall in that season (variable y) and in the following one (variable z).
c) multiple linear regressions type w = ax + by + cz + d between:
NAO for three consecutive seasons (variables x, y, z) and rainfall in the following season (variable w).
d) multiple linear regressions type v = ax + by + cz + dw + e between:
NAO for two consecutive seasons (variables x, y) and rainfall in these two consecutive seasons (variables z, w) in order to forecast the precipitation in the following season (variable v).
Once the constants that define the linear equation have been calculated (a, b, c, d or e) what we have is, depending on the case, a sort of ‘rainfall forecast’ for the following month, season or year, if the NAO values are known (and the rainfall in previous months or seasons are known, if they were also taken into account).
In each linear regression, simple or multiple, the correlation coefficient R was calculated with an explained variance of R2. The significant correlations for α = 0.05 were selected when the Pearson R threshold (with N–1 degrees of freedom, and N=38) to accept the null hypothesis was of 0.3165, 0.3206, 0.3246 and 0.3444, for the cases a), b) c) and d), respectively. The meteorological stations that fulfill this condition were represented on maps.
The R2 corresponding to the above mentioned values are about 0.10. Consequently, the contour maps will show positive or negative significant correlations when the squared correlation coefficient exceeds 0.10.
A whole of 325 correlations were studied in each analysis, one for each meteorological station. R2 data are available in 325 places over continental Spain. These data were used to draw the contour maps that represent the spatial distributions of the correlations.
3.2 Spatial distribution of rainfall–NAO correlations
The R2 values obtained in the different linear regressions for each of the 325 weather stations and the NAO index in each of the 17 monthly, seasonal and annual series from 1961 to 1998 were used to draw contour maps. The aim was to identify relationships between rainfall and NAO and extract relevant conclusions.
Areas with a similar R2 were represented on maps drawing contour lines with the same correlation between rainfall data and NAO. The Kriging interpolation method was used to draw the maps (Isaaks and Srivastava, 1989). The lines in the figures are the boundaries of the geographical areas affected in the same way by the North Atlantic Oscillation in their monthly, seasonal and annual rainfall rates. The correlations are represented using a range of colors, but only so in the case of significant correlation coefficients. Non–significant R2 have not been represented, in order to highlight the significant geographical areas.
But what exactly does R2 measure? There is an algebraic relationship between R and the regression variance: R2 (determination coefficient) is the part of the variation of the variable y that is explained by the regression. Thus, R2 accounts for the explanatory power of the linear model. In this case, it indicates whether the precipitation forecasts using NAO data are statistically acceptable or not, and the explanatory force of the NAO in these forecasts.
The sections below describe the most important results found in continental Spain with respect to the relationship between each of the 17 time series analyzed and the NAO index from different points of view.
4. Results
Only the linear correlations with statistically significant relationships will be commented here.
4.1 Correlation between monthly NAO and monthly rainfall
The analysis indicates that:
• in October and November (first row in Fig. 2) there is a significant correlation in wide areas of Spain. However, in October there is a considerable lack of correlation in the eastern part of the country as well as in part of the southern border of the Peninsula. In November there is no significant correlation in the Mediterranean zones and the north of the Peninsula. It can be noted that the areas with good correlations grow gradually every month until they reach their maximum in the winter months;
• there is a very significant correlation in the winter months (December, January, February), and also in March, in practically the whole of the study zone, except in the Mediterranean areas and in the north. It is precisely during these months that the effect of the NAO is most clearly observable on the north Atlantic coasts. Therefore, its influence on the Iberian Peninsula can also be felt more intensely during the winter. It may be pointed out that there is no significant correlation in any coastal areas of Spain (see rows 2 and 3 in Fig. 2);
• a significant correlation can also be observed during the spring, but the areas affected by the NAO are smaller. The correlation tends to be less strong as the season advances;
• in July and August the correlation between rainfall and NAO is significant in only very few small areas scattered over the country. September shows a correlation in isolated areas mainly in the south of the Peninsula. In these months most of the precipitation is of convective origin and we cannot establish a correlation between the likelihood of storms with rain and the NAO in these months.
Summing up, it can be stated that the correlation between rainfall in a particular month and the NAO index in that month varies greatly along the year. There is a good correlation in winter months and in March, whereas the correlation is poor in summer. The correlation decreases as convective precipitation increases, since this type of precipitation is highly localized and does not depend on Atlantic pressures. This ties in with the observations carried out by Muñoz–Díaz and Rodrigo (2003), who have also found a good correlation between precipitation and the NAO index in Spain.
4.2 Correlation between seasonal NAO and seasonal rainfall
The results in Figure 3 indicate that:
• there is a good significant correlation in winter over the whole of continental Spain, but not in the northern and eastern coasts;
• in spring the geographical areas with significant correlations are smaller, but they still cover the center of the Peninsula. The areas with lack of correlation grow larger in the north and the east;
• in summer there is hardly any significant correlation, apart from small isolated areas scattered over the Peninsula;
• the correlation increases in fall, but in general it is still not significant in continental Spain. Only a few isolated areas in the center and the south show good correlations between the NAO and fall precipitation.
Summing up, the NAO indices for winter and spring correlate very well (although with negative correlation) with the precipitation regime found in those two seasons, but the same cannot be said for the summer and fall.
4.3 Correlation between annual NAO and annual rainfall
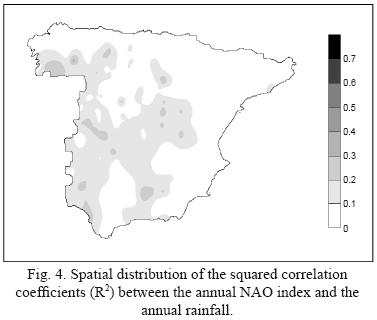
It has been found that the annual rainfall correlates significantly with the annual NAO index in some isolated zones of the Peninsula (Fig. 4).
4.4 Correlation between seasonal NAO and rainfall in the following season
The authors considered the possibility of forecasting the rainfall in a particular season using the NAO index for the previous season. However, no clear relationship between these two variables was found, indicating that the NAO index is not a good rainfall forecaster in this sense.
4.5 Correlation between the NAO of two consecutive seasons and the rainfall in the following season
Forecasting the rainfall of a particular season by using the NAO indices of the two previous seasons is only acceptable in the case of the fall by using NAO indices for spring and summer. However, this was only found to be applicable to a small part of the Iberian Peninsula.
4.6 Correlation between the NAO indices of three consecutive seasons and the rainfall in the following season
The correlations of the NAO indices of three consecutive seasons to forecast the rainfall in the following season are not good in most of the meteorological stations in Spain. There are only significant correlations in a few small areas. This means that the NAO indices of the three previous seasons do not generally help in forecasting the rainfall in the following season.
4.7 Correlation between monthly NAO and the rainfall in the following month
As in the case of seasons, no significant correlations were found between the monthly NAO index and the rainfall in the next month. This means that the monthly rain forecast by using the NAO index of the previous month is not useful, except in the months of February, March, November and January in small isolated zones.
In any case, the best correlations occur again in the winter months.
4.8 Correlation between monthly rainfall + monthly NAO and the rainfall of the following month
For example, the rainfall in May would be forecast using the NAO index and the rainfall in April. It has been found that (see Fig. 5):
in January and February there is a significant correlation stretching from the north–east to the south–west of the Peninsula. It must be pointed out that there is no significant correlation in the Mediterranean coast or in the northern coast;
• the correlation used to forecast the rainfall in March was significant in the northern half of the Peninsula. The northern coast shows a particularly good correlation.
The spatial representation of the correlations for the rainfall forecast in April, May, June, July, August and September showed that:
• from April on the significant correlations occur only in isolated zones;
• there is no good correlation in April, it improves in May with a higher number of zones, and it keeps the same in June, July, August and September;
• the reason may be the fact that – especially in the summer months – precipitation is mainly convective. This type of precipitation is highly localized and does not depend on Atlantic pressures;
• in October there is an increase in the significant correlations, which continues in November and December;
• in October the best correlations are located in isolated zones of the southern plateau;
• in November, the correlation spreads over the Peninsula, and the isolated zones are larger. The long line between the northeast and the southwest shows a good correlation, together with additional zones in the northern plateau;
• the significant correlations found to forecast the rainfall in December are located in small isolated areas in the south–west of the Peninsula;
It may be concluded that the forecasts that can be made using precipitation data and the NAO index for a particular month, to forecast the rainfall in the following month are relatively good in several months of the year, especially in January, February and March. The correlations are not good in spring and summer months, especially in the summer, due to the presence of convective precipitation.
4.9 Correlation between seasonal rainfall + seasonal NAO and the rainfall in the following season
In general, there are no significant correlations in enough places to produce a reliable forecast of the rainfall in a particular season.
4.10 Correlation between rainfall for two seasons + NAO for two seasons and rainfall in the following season
It has been observed that:
The top left–hand side map (Fig. 6) shows that there is a high number of isolated zones scattered all over the Peninsula with significant correlations, which indicates that summer precipitation can be forecasted. However, the spatial discontinuity of these areas reduces the reliability of any forecast.
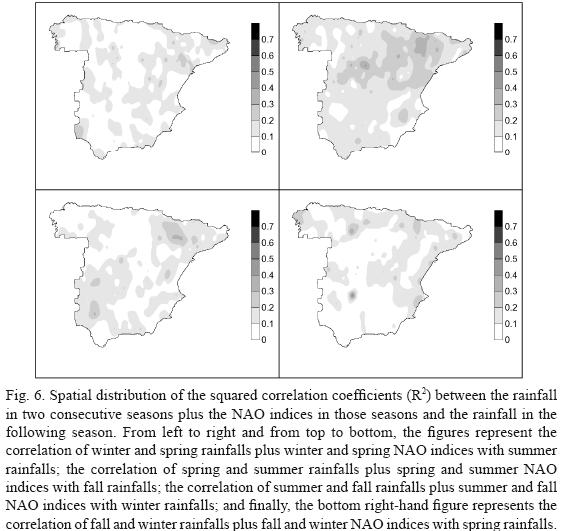
In the case of forecasts for fall rain (top right–hand side map), it was found that there was a very significant correlation in the whole Peninsula. The different areas are not isolated anymore, but rather form a continuum. However, the correlation decreases in most of the Peninsula when winter rain is forecasted, the only exception being the south–west, where the correlation increases somewhat. The rainfall rates in fall and winter, together with the NAO index for fall and winter, have been found to be relatively poor for forecasting spring rainfalls (bottom right–hand side map). Summing up, the rainfall forecasts in a particular season based on rainfall rates and NAO indices of the two previous seasons are good, especially in the fall.
Bearing in mind these results, it was decided to carry out a detailed analysis in the Ebro Valley to confirm the possibility of forecasting rain during the fall. The present study may be considered complementary to the one published by Trigo et al. (2004) on the influence of NAO on the precipitation regime in the main Atlantic basins of the Iberian Peninsula.
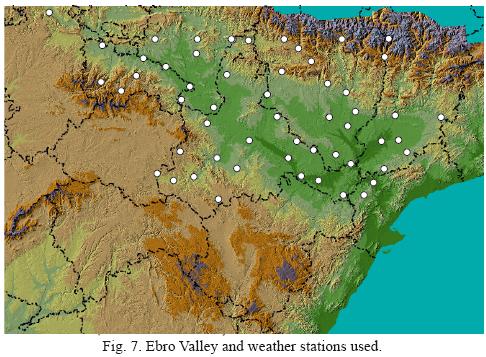
The Ebro Valley is the main Mediterranean basin in the Peninsula. Fig. 7 is a map of the valley and the 54 weather stations used in the study. Fig. 6 shows that in the north–east the best correlation for rain forecast is registered in the fall. This was confirmed numerically while analyzing the data of the 54 stations in the Ebro Valley.
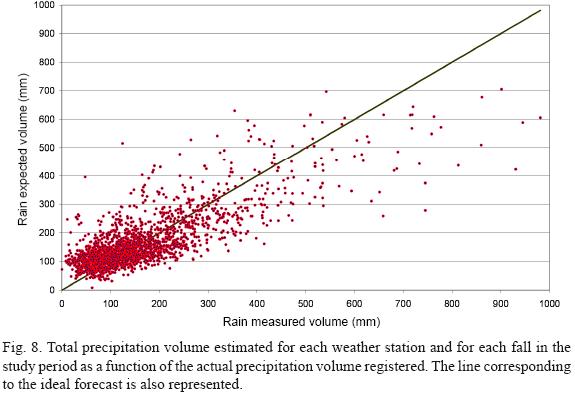
Using the linear correlation described above, the total rain volume was calculated for each station and each fall in the study period. Thus, the study included 38 falls × 54 stations = 2052 figures of estimated rain. Fig. 8 compares these data with the real measurement. The line corresponding to the ideal forecast is also represented (y = x). It can be noted that there is a certain dispersion of the expected amount of rain, but most of the dots are grouped along the line of ideal forecast. Calculating the residual variance (Essenwanger, 1986), it may be established that the percentage of variance accounted (or percentage reduction) is 42.8%. Even though this is not a very high value, it must be taken into account that:
• similar and even smaller values have been found for the explained variance in correlations between NAO and the precipitation in the same month (Romero et al., 1998, 1999; Muñoz–Díaz and Rodrigo, 2003);
• the present paper does not deal with the correlation NAO–precipitation in the same month, but rather aims at setting up a simple forecast model, which is clearly much more complicated. Therefore, the explained variance enables us to consider the forecast model a useful tool in the case of the Ebro Valley.
5. Conclusions
The correlations found between monthly rainfalls and the NAO index of the same month show that the NAO considerably affects rainfalls in the Iberian Peninsula, especially in winter and spring. It affects annual rainfalls as well.
On the other hand, the correlation between the NAO indices and the rainfall of the following month is not significant in most of the Peninsula, except in some winter months. As a result, there are generally few possibilities of forecasting monthly rainfalls with linear models in Spain using the NAO index of the previous month. The same happens when using seasonal NAO indices and seasonal rainfall rates.
However, in the months of January, February and March it is possible to forecast the monthly rainfall using the NAO index and the rainfall rate of the previous month.
In addition, the NAO index may be used, together with data from recent rainfalls, to suggest reliable forecasts of seasonal precipitation, especially fall precipitation. For example, in the Ebro Valley it is possible to use the data for the NAO in spring and summer plus the precipitation registered in those two seasons in order to forecast the amount of rain that will be falling between September and November.
Acknowlegements
The authors are grateful to Dra. Noelia Ramón for translating the paper into English. The study was supported by the Consejería de Educación y Cultura, Junta de Castilla y León (Grants LE014A07 and LE039A10–2).
References
Dai A., I. Y. Fung and A. D. Del Genio, 1997. Surface observed global land precipitation variations during 1900–88. J. Climate 10, 2943–2962. [ Links ]
del Río S., A. Penas and R. Fraile, 2005. Analysis of recent climatic variations in Castile and Leon (Spain). Atmos. Res. 73, 69–85. [ Links ]
Essenwanger O. M., 1986. Word survey of climatology, Vol. 1B: Elements of statistical analysis. Elsevier Science Publising Company, Ing., Amsterdam, 532 pp. [ Links ]
García N. O., L. Gimeno, L. de la Torre, R. Nieto and J. A. Añel, 2005. North Atlantic Oscillation (NAO) and precipitation in Galicia (Spain). Atmósfera 18, 25–32. [ Links ]
Hurrell J. W., 1995. Decadal trends in the North Atlantic Oscillation: regional temperatures and precipitation. Science 269, 676–679. [ Links ]
Hurrell J. W. and H. van Loon, 1997. Decadal variations in climate associated with the North Atlantic Oscillation. In: Climate Change. Proceedings International Workshop on Climatic Change at High Elevation Sites, Wengen, Switzerland, pp. 302–326. [ Links ]
IPCC, 2001. Climate Change 2001. The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Pannel on Climate Change (J. T. Houghton, Y. Ding, D. J. Griggs, M. Noguer, P. J. van der Linden, X. Dai, K. Maskell, and C.A. Johnson, Eds.). Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA. [ Links ]
IPCC, 2007. Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Four Assessment Report of the Intergovernmental Pannel on Climate Change (S. Solomon, D. Quin, M. Manning, Z. Chen, M. Marquis, K. B. Averyt and H. L. Miller, Eds.). Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA. [ Links ]
Isaaks E. H. and R. M. Srivastava, 1989. An introduction to applied geostatistics. Oxford University Press, NY, 592 pp. [ Links ]
Lindey D. V. and W. F. Scott, 1984. New Cambridge elementary statistical tables. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 96 pp. [ Links ]
Mossmann V. L. F., 2002. Análise especial e temporal das tendêncies das precipitações na Espanha Peninsular. Ph. D. Thesis. Universidad de León, León, Spain, 342 pp. [ Links ]
Mossmann V. L. F., A. Castro, R. Fraile, J. Dessens and J. L. Sánchez, 2004. Detection of statistically significant trends in the summer precipitation of mainland Spain. Atmos. Res. 70, 43–53. [ Links ]
Muñoz–Díaz D. and F. S. Rodrigo, 2003. Effects of the North Atlantic Oscillation on the probability for climatic categories of local monthly rainfall in southern Spain. Int. J. Climatol. 23, 381–397. [ Links ]
Paulus J. L. H. and M. A. Kohler, 1952. Interpolation of missing precipitation records. Mon. Wea. Rev. 80, 129–133. [ Links ]
Romero R., J. A. Guijarro, C. Ramis and S. Alonso, 1998. A 30 years (1964–1993) daily rainfall data base for the Spanish Mediterranean regions: first exploratory study. Int. J. Climatol. 18, 541–560. [ Links ]
Romero R., G. Sumner, C. Ramis and A. Genovés, 1999. A classification of the atmospheric circulation in patterns producing significant daily rainfall in the Spanish Mediterranean area. Int. J. Climatol. 19, 765–785. [ Links ]
Tang W. Y., A. H. M. Kassim and S. H. Abubakar, 1996. Comparative studies of various missing data treatment methods – Malaysian experience. Atmos. Res. 42, 247–262. [ Links ]
Thompson D. W. J. and J. M. Wallace, 1998. The Arctic Oscillation signature in the wintertime geopotential height and temperature fields. Geophys. Res. Lett. 25, 1297–1300. [ Links ]
Trigo R. M., D. Pozo–Vázquez, T. J. Osborn, Y. Castro–Diez, S. Gámiz–Fortis and M. J. Esteban–Parra, 2004. North Atlantic Oscillation influence on precipitation, river flow and water resources in the Iberian Peninsula. Int. J. Climatol. 24, 925–944. [ Links ]
Walsh J. E., 1996. Recent decrease of sea level pressure in the central Arctic. J. Climate 9, 480–486. [ Links ]
Wanner H., S. Brönnimann, C. Casty, D. Gyalistras, J. Luterbacher, C. Schmutz, D.B. Stephenson and E. Xoplaki, 2001. North Atlantic Oscillation – Concepts and studies. Surveys in Geophysics 22, 321–382. [ Links ]
Watanabe M. and T. Nitta, 1999. Decadal changes in the atmospheric circulation and associated surface climate variations in the Northern Hemisphere winter. J. Climate 12, 494–510. [ Links ]














