Services on Demand
Journal
Article
Indicators
Related links
Share
Atmósfera
Print version ISSN 0187-6236
Atmósfera vol.21 n.1 Ciudad de México Jan. 2008
Spatial estimation of mean temperature and precipitation in areas of scarce meteorological information
J. D. GÓMEZ
Departamento de Suelos, Universidad Autónoma Chapingo,
Km 38.5 Carretera México–Texcoco, Chapingo, México
Corresponding author; e–mail: dgomez@correo.chapingo.mx
J. D. ETCHEVERS
Instituto de Recursos Naturales, Colegio de Postgraduados,
Km. 36.5 Carretera México–Texcoco, Montecillo Edo. de México
A. I. MONTERROSO
Departamento de Suelos, Universidad Autónoma Chapingo,
Km 38.5 Carretera México–Texcoco, Chapingo, México
C. GAY
Centro de Ciencias de la Atmósfera, Universidad Nacional Autónoma de México,
Circuito Exterior, Ciudad Universitaria, México, D. F. 04510 México
J. CAMPO
Instituto de Ecología, Universidad Nacional Autónoma de México,
Circuito Exterior, Ciudad Universitaria, México, D. F. 04510 México
M. MARTÍNEZ
Instituto de Recursos Naturales, Colegio de Postgraduados,
Km. 36.5 Carretera México–Texcoco, Montecillo Edo. de México
Received August 9, 2006; accepted June 15, 2007
RESUMEN
En las regiones de relieve complejo y con escasa información meteorológica se dificulta la aplicación de las diferentes técnicas y modelos de interpolación numéricos para elaborar mapas de variables climáticas confiables, indispensables para realizar estudios de los recursos naturales, con la utilización de las nuevas herramientas de los sistemas de información geográfica. En este trabajo se presenta un método para la estimación de la temperatura y la precipitación media anual y mensuales, tomando elementos de los métodos de interpolación simple complementándolo con análisis estadísticos. Para la determinación de la temperatura se generaron ecuaciones de regresión lineal simple relacionando la temperatura con la altura de las estaciones meteorológicas en la región de estudio, haciendo previamente una subdivisión de la zona de acuerdo a las condiciones de humedad y aplicando dichas ecuaciones a los modelos de elevación digital de la zona. La estimación de la precipitación se basó en las propuestas del método gráfico a través del análisis de los sistemas meteorológicos que afectan a cada una de las regiones de la zona de estudio a lo largo del año y en el impacto que pueden tener las barreras montañosas en el movimiento del viento. En las estaciones meteorologicas con información de las zonas aledañas se analizaron los valores de precipitación de acuerdo a su posición en el paisaje, la exposición a los vientos con humedad y el falso color que se asocia con los tipos y condición de la vegetación. Estos sitios fueron usados como referencia para asociar los valores de precipitación con sitios semejantes sin información dentro del área de estudio y posteriormente se realizó la interpolación usando analogías con las imágenes de falso color a las que se les superpuso un modelo de elevación digital para trazar las isolíneas con valores similares de precipitación.
ABSTRACT
In regions of complex relief and scarce meteorological information it becomes difficult to implement techniques and models of numerical interpolation to elaborate reliable maps of climatic variables essential for the study of natural resources using the new tools of the geographic information systems. This paper presents a method for estimating annual and monthly mean values of temperature and precipitation, taking elements from simple interpolation methods and complementing them with some characteristics of more sophisticated methods. To determine temperature, simple linear regression equations were generated associating temperature with altitude of weather stations in the study region, which had been previously subdivided in accordance with humidity conditions and then applying such equations to the area's digital elevation model to obtain temperatures. The estimation of precipitation was based on the graphic method through the analysis of the meteorological systems that affect the regions of the study area throughout the year and considering the influence of mountain ridges on the movement of prevailing winds. Weather stations with data in nearby regions were analyzed according to their position in the landscape, exposure to humid winds, and false color associated with vegetation types. Weather station sites were used to reference the amount of rainfall; interpolation was attained using analogies with satellite images of false color to which a model of digital elevation was incorporated to find similar conditions within the study area.
Keywords: Spatial interpolation, temperature modeling, terrain analysis, lapse rate, geographic information systems.
1. Introduction
In many regions of the planet it is not always possible to incorporate climatic factors into ecological analysis due to the scarcity of weather stations. Therefore, it becomes necessary to develop procedures for extrapolating a small amount of available climatic data to a whole region. The statistical validity of the interpolation procedure and how accurately it permits climatic variables to be mapped across a landscape is a critical and limiting consideration.
Reports on climatic change (IPCC, 2001) have pointed to the importance of having a detailed description of current climate in the different areas in order to forecast with greater accuracy the impact of climatic change on terrestrial ecosystems. According to Price et al. (2000), improved methods of climatic data interpolation will enhance our knowledge about natural and managed ecosystems, including the possible effects of climatic change.
The development of methods to interpolate climatic data from networks of few stations has been the focus of several research projects (Thiessen, 1911; Peck and Brown, 1962; Schermerhorn, 1967; Hutchinson and Bischof, 1983; Dingman et al., 1988; Phillips et al., 1992; Daly, 1994; Nalder and Wein, 1998; Price et al., 2000). Interpolation procedures must incorporate the effects of physical processes which determine the climate spatial distribution. Some authors have used simple procedures, which include the latitude and longitude of weather stations (MacIver and Whitewood, 1990) without providing estimates of the predicted error. Because of the strong influence of topography on temperature lapse rates and orographic rains, Hutchinson (1987) showed that the inclusion of elevation was critical to generating reliable data for precipitation and mean temperature through interpolation.
In general, temperature patterns on the earth's surface are determined by the combination of certain geographic factors which include latitude, altitude, patterns of atmospheric circulation, local conditions, the effect of continentality and the characteristics of ocean currents (Aguado and Burt, 2001). Other factors having an influence on surface temperature are exposure to the sun, the physical properties of the effective surface, air moisture content, the water supply of vegetation and the actual surface–atmosphere exchange characteristics (Wörlen et al., 1999).
Ortiz–Solorio (1987) described three estimation methods of temperature in areas of scarce weather stations: standard analysis, the simple or empirical method and that of median lapse rate. Standard analysis implies the participation of one person with great experience in climatology that sets the desired value, a situation considered to be highly subjective. The simple method estimates temperature as an elevation function by using a simple regression equation between these two variables. Finally, the median lapse rate method includes the elevation and geographical location of the point whose temperature will be estimated (García–Benavides, 1979).
For spatial estimations of temperature in mountainous environments, Lookinbill and Urban (2003) focused on a series of regression models that start with the simple elevation model and later incorporate more complex models which include relative radiation and the slope aspect. Local topography can substantially modify the relationship between elevation and temperature (Barry, 1992).
Precipitation shows great spatial variation as a result of the different types and scales of the processes generating clouds and precipitation (Aguado and Burt, 2001). Basically, the mechanisms responsible for the development of clouds are surface heating and free convection, topography, widespread ascent due to the convergence of surface air and the uplift along weather fronts (Ahrens, 2003). The spatial variation of precipitation is strongly influenced by local and regional factors, such as topography and the dominant direction of humid winds (Phillips et al., 1992).
The methods used to estimate precipitation are classified into three major groups: graphical, topographical, and numerical (Daly et al., 1994). Graphical methods involve the mapping of precipitation data, sometimes in combination with precipitation–elevation analysis, and include isohyets mapping (Reed and Kincer, 1917; Peck and Brown 1962) and Thiessen's polygon estimation (Thiessen, 1911). Topographical methods include the correlation of point precipitation data with an array of topographic and synoptic parameters such as slope, exposure, elevation, the location of barriers, and wind speed and direction (Spreen, 1947; Burns, 1953; Schermerhorn, 1967; Houghton, 1979). Numerical methods have been the most commonly used in the analysis of precipitation distribution over the last decades. Particular attention has been given to the development of sophisticated statistical methods which, given certain assumptions, generate optimality criteria and guarantees of unbiased predictions. Some examples are optimal interpolation (Gandin, 1963), kriging and its variants (Phillips et al., 1992), and smoothing splines (Hutchinson and Bischof, 1983). Several studies have compared various of these sophisticated methods to simple ones and among them, in the context of the areal distribution of rainfall (Creuting and Obled, 1982; Tabios and Salas, 1985; Phillips et al., 1992; Nalder and Wein, 1998; Price et al., 2000). This comparison has had surprising results. Some studies do not reveal significant differences between sophisticated and simple methods; others consider sophisticated methods substantially inferior to simple ones (Tabios and Salas, 1985), but in general statistical methods are for the most part more accurate than the simple methods, though not entirely satisfactory. Based on these results, Thornton et al. (1997) suggested that an effective, efficient interpolation method could be developed by taking elements from the simple methods and addressing some characteristics of the statistical methods that give a better performance. Daly et al. (1994) generated what can be considered a hybrid approach for precipitation distribution, combining geographical and statistical elements. They demonstrated this approach to be both more flexible and more accurate than kriging or some of its variants.
The use of numerical methods in México has been difficult because of the country's complex relief and the scantiness of weather stations, especially in mountainous regions. The previous procedure demands having observation points on site as elements to establish relations with the climatic variables for attaining an acceptable margin of reliability. In the conditions described above, regions with very scarce weather information, the best choice is to use simple methods. Although numerical methods may be marginally more appropriate, their implementation requires much more time and money (Price et al., 2000).
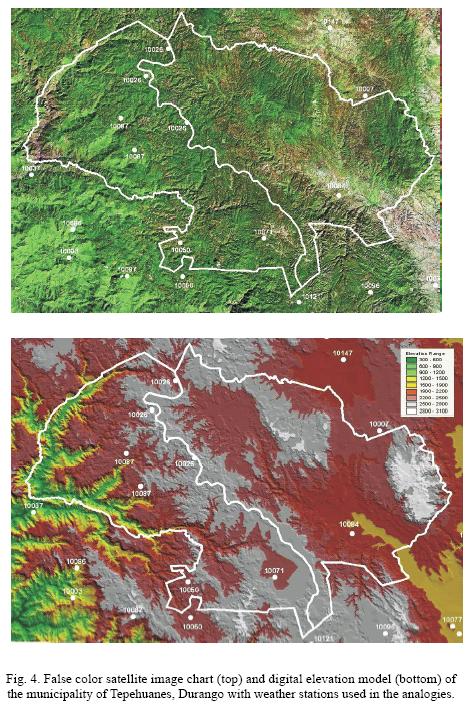
The objective of this paper is to develop simple methodologies to estimate monthly and annual mean temperature and precipitation in areas with scarce weather information and complex relief. On this account, elements from previous proposals were selected, incorporating the use of geographical information systems in the preparation of isotherm and isohyet maps. The case study was located in the municipality of Tepehuanes, Durango, México, characterized by huge contrasts in altitude, where the influence of orography on the distribution of precipitation is evident, and the humidity conditions of the different zones affect temperature. In addition, within its vast area only four communities have weather stations.
2. Methods
2.1 Study area
The municipality of Tepehuanes is located in northwestern state of Durango, at 25° 12' and 26° 25' N and 105°23'to 106°40'W (Fig. 1), covering an area of 6401.5 km2. Elevations in the municipality range from 600 to 3200 m. Topography is mostly mountainous; the territory can be divided by differences in climate and vegetation into four regions or strips, which are more or less parallel, oriented northwest to southeast (Fig. 2). The region of the Quebradas is located in the western part of the municipality; this area is characterized by rivers descending rapidly from the high plateaus of the Sierra forming canyons. The mountainous region of the Sierra Madre Occidental is divided into two by the region of Valleys, that emerges between the two Sierra regions.
2.2 Data
In this study, data from 41 weather stations were used (Table I). These data were obtained through the Rapid Extractor of Weather Information (Extractor Rápido de Información Climática–ERIC) version 2 (IMTA, 2000). Since only four communities in this municipality have weather information, it was necessary to expand geographical coverage in order to have information analogous to the municipality's different climatic conditions (Fig. 2). This meant that 37 new weather stations were included.
2.3 Spatial estimation of temperature
The process of temperature estimation and the elaboration of isotherm maps is detailed as follows:
1. Regionalization of the study area according to conditions that affect the temperature gradient.
These conditions are latitude, altitude, patterns of atmospheric circulation, local conditions, continental effects and characteristics of ocean currents, exposure to the sun in the regional mountainous systems, and air moisture content throughout the year (Ahrens, 2003).
For this particular study, the area was divided into two large portions: the western, or windward, and part of the high plateau of the mountainous region, and the leeward. The windward portion is affected by the humid winds of the Pacific Ocean blowing from June to October, known as the Mexican Monsoon (Douglas et al., 1993; Stensrud et al., 1995) and, in general, is more humid. The leeward portion comprises part of the high plateau, with less rainfall, and the valley zone which is the Tepehuanes River watershed, as well as the eastern side of the Sierra, which is drier (Monterroso–Rivas and Gómez–Díaz, 2003) (Fig. 2).2. Selection of the meteorological stations with complete data set in the study area.
In the example shown here, the municipality was delimited using the regional digital elevation model and the four weather stations with reliable data were located within the municipal boundaries.3. Expansion of the data collection area in order to have more data.
As the number of meteorological stations was not sufficient, it was necessary to increase coverage considering the characteristics that affect the temperature gradient defined in the initial delimitation of the different areas. The location and altitude of the meteorological stations were verified and corrections were introduced where necessary. Therefore, thirty–seven weather stations were incorporated into the analysis.4. Estimation of temperature on areas with complex landscape with simple regression equations. To estimate temperature within a landscape characterized by mountains, the simple or empirical method described by Ortiz–Solorio (1989) was used. This method calculates regional lapse rates for each month and the annual mean, establishing simple regression equations between temperature and elevation.
Twenty–four weather stations for the windward portion and twenty–three for the leeward were chosen, while six stations from the high plateau were used for both zones (Table II).
For each group of stations, a simple linear regression analysis was performed, obtaining twelve monthly models and one annual model. To determine whether the models were satisfactory, the statistical estimators of each were calculated: determination coefficient (R2), standard error, and probability of F distribution.
5. Creating isotherm maps with the simpler regression equations.
The simple regression models were applied to each of the areas defined above. Thus, twelve monthly and one annual isotherm maps had to be constructed for each area. The maps were drawn using a digital topographic map and the site's digital elevation model, and detailed with the Arc View geographic information System (ESRI, 2004).
In each one of the areas in which the municipality was divided the simple regression models were incorporated for the monthly and annual reports to calculate the temperature corresponding to each interval of altitude above sea level. Temperatures calculated for the different altitudes within the municipality were arranged in accordance with one Celsius degree intervals. This procedure was applied separately to the windward and leeward portions. The isotherm maps were structured using an interval of one degree, starting from the lowest part of the territory to the highest. Polygons were established for each temperature interval, associated with meters above sea level of that temperature; values are expressed in whole numbers.6. Isotherm maps for relatively flat areas.
In this study there were no flat areas, but in nearly flat areas with relatively small variations in altitude and with an acceptable number of meteorological stations, the monthly and annual isotherms maps are constructed with interpolation models such as kriging, or its variants, using Arc View Geographic Information System (ESRI, 2004).7. Combination of the isotherm maps of the windward and leeward portions.
Monthly and annual isotherm maps of the different areas were combined, making adjustments in the areas where temperature range values differed. In the parts with lower temperature values, adjustments were made by using the same temperature intervals and reducing altitude intervals. In the parts where temperatures were higher, with the same temperature intervals, altitude intervals were increased until their values matched.
In this particular exercise, the monthly and annual isotherm maps of both portions were combined, making adjustments in the areas where temperature range values differed. The adjustments were made by increasing temperature ranges on the windward portion at small altitude differences, and on the leeward portion temperature ranges were decreased until their values matched. In this case, the largest difference between the temperature ranges in some parts of the junction zone was of two degrees.8. Digital edition of monthly and annual mean temperature maps.
The monthly and annual maps of temperature are kept in digital format, assigning colors to each of the temperature ranges, based on the Instituto Nacional de Estadística, Geografía e Informática (INEGI) proposal for the colors on its annual mean temperature maps of México, at 1:1 000 000 scale (SPP, 1981).
2.4 Elaboration of precipitation maps
2.4.1 Mean annual isohyet maps
The process of precipitation map construction is detailed as follow:
1. Location of weather stations on a digital elevation model map.
The location of each of the weather stations must be identified geographically and the annual amount of rainfall reported.2. Analysis of the relationship between the amount of rainfall and global and regional wind circulation systems.
For each weather station the amount of rainfall reported and its annual distribution must be analyzed, and a possible explanation must be given. To do this, it is necessary to have a general knowledge of the influence of the different meteorological systems throughout the year for each of the regions in which the amount of precipitation will be estimated.
In this study the data from two weather stations for rainfall distribution throughout the year in each portion (windward and leeward) were compared. One reported the highest annual amount of precipitation and the other the lowest value (Fig. 3a for windward and 3b for leeward). It is clear that all the stations have very similar patterns of rainfall distribution. The rainy season is in summer, but there is also a small but significant winter rainfall. The summer rainfall over the windward slopes of the Sierra Madre Occidental and western high plateaus was associated with elements of the Monsoon of North America (Barlow et al., 1998; Berbery, 2001; Higgins et al., 2003), specifically, the component known as the Mexican Monsoon (Douglas et al., 1993; Stensrud et al., 1995; Berbery, 2001; Higgins et al., 2003) (Fig. 3a). In this system the prevailing winds blow mainly southwest to northeast. For the zone of valleys and the leeward part of the municipality, the rainy season was associated with the influence of moisture coming from the Gulf of México (Tang and Reiter, 1984) as well as with the effect of the Mexican Monsoon (Fig. 3b). In this system the prevailing winds blow east to west. The winter rainfall in both areas was associated to the impact of vortexes and cold fronts (Mosiño and García, 1974), where the prevailing winds blow from west to east.3. Analysis of impacts of the climate–modifying factors in the amount of rainfall.
The monthly amount of rainfall in each meteorological station must be analyzed, identifying the impact of the climate modifying factors, such as bodies of water, distance from the ocean, and orography including form of the mountain ridges, their orientation and aspect (Ahrens, 2003).
In this study, once the phenomena causing different amounts of precipitation were identified, the impact of orography of the areas where the weather stations were located was examined.
The amount of precipitation was explained as a result of the direction of moisture–carrying winds throughout the year, and whether they arrive directly to those areas or bypass orographic units that may divert them or force them to ascend and lose moisture. Other factors also considered were the form and dimension of the mountain ridge, slope aspect, winds conducted through a canyon, the shadow effect of mountain barriers and other elements that contribute to explaining the magnitude of the rainfall reported in areas having weather information, and surrounding zones.4. Search for relationships between the amount of rainfall and the color associated with vegetation on a false color satellite image.
All the meteorological stations were located in two different false color satellite images, one taken in the dry season and the other during the wet season. The meteorological stations must be situated in their place and the amount of annual rainfall reported. A relationship was sought between the amount of rainfall reported in each meteorological station and the false color associated with the natural vegetation and also with the position in the landscape, emphasizing the forms of the terrain and how they influence prevailing winds that carry rainfall–producing moisture.
In this study the satellite image chart colors were reviewed to associate them with the vegetation and soil moisture so as to find a connection with the rainfall present in the sites having weather information. In general, a more intense color associated with vegetation was translated as a higher amount of rainfall. In this assumption, slope orientation has an enormous effect on soil moisture retention. At the latitude of the study site vegetation on the northern slope differs considerably from that of the southern slope even when the amount of rainfall is the same (Fig. 4) as consequence of the amount of radiation received and its impact on availability of water to the vegetation (Ahrens, 2003).
5. Search for analogies between sites with meteorological information and areas without meteorological stations.
These analogies were established by analyzing the prevailing wind direction and the modifying effect of this flow by the different elements of the landscape. Tentative values of mean annual precipitation were assigned to sites with similar land form conditions and similar location relative to the direction of prevailing winds. Values must be assigned matching the false color associated with condition of the natural vegetation.6. Drawing the isohyet map on the digital elevation model.
Annual isohyets must be drawn manually on the digital elevation model based on the mean annual precipitation values assigned by analogy in the previous analysis and those values taken directly from weather stations. The process starts with the identification of the analogies that are easiest to locate; these, in general, correspond to the extreme values of precipitation. Intermediate isohyets are then drawn manually by joining the points defined after analyzing the effect of the different precipitation–modifying factors and the local circulation of winds.7. Edition of the mean annual isohyet map in digital format.
The manually–drawn isohyet map of annual mean precipitation was reproduced digitally using the Arc View Geographic Information System (ESRI, 2004), generating areas defined by precipitation ranges.
2.4.2 Mean monthly isohyet maps
Monthly precipitation maps are based on the annual precipitation maps. The steps in this work are detailed as follows:
1. Estimation of mean monthly values of precipitation for each annual range of rainfall.
For each of the areas, monthly precipitation data from the meteorological stations were previously subdivided according to the portion in which they are located (windward or leeward). The monthly data from the different stations located in a given area (defined by annual means) were averaged to obtain monthly precipitation values.2. Estimation of mean monthly precipitation ranges.
The mean monthly precipitation ranges for each area defined by annual ranges were assigned according to the variation in mean precipitation reported for each month by the different groups of stations. Making sure that the monthly values add up to annual range be covered proportionally and that the adjacent sections of the two portions have the same precipitation range.
In the months of less precipitation the ranges established are narrow and in those months of heavy rains these ranges are considerably broader.3. Estimation of proportional values of monthly precipitation.
The median of each monthly range was used as the estimation of monthly precipitation. It was verified that the sum of the monthly precipitation estimates was within the corresponding annual mean precipitation range.4. Correlation of mean monthly precipitation estimates and averages reported by the meteorological stations.
For each annual precipitation range a simple linear regression analysis was performed between the mean precipitation calculated from data obtained from the groups of weather stations and the median values of the monthly ranges. To determine whether the models were satisfactory, their statistics estimators –coefficient of determination (R2), standard error, and the probability of F distribution– were calculated for each linear regression model.5. Edition of the mean annual isohyet map in digital format.
Monthly precipitation maps were constructed using the areas delimiting annual average precipitation ranges using the Arc View Geographic Information System (ESRI, 2004).
3. Results and discussion
3.1 Isotherm maps
Tables II and III show the results of regional temperature models with statistical diagnoses.

There was a clear difference in the study area temperature ranges between the extreme values on the leeward portion (Table III) as a consequence of less moisture in the air, and the smaller variations on the windward portion (Table III) at the same heights (Arhens, 2003).
In both cases the determination coefficients (R2) were satisfactory, above 0.9 on the windward and 0.8 on the leeward. The standard errors on the windward portion were in all cases below 1 °C (0.43 to 0.70 °C); on the leeward portion these values were higher, ranging from 0.83 to 1.47 °C. In both cases the calculated F distribution was considerably higher than F from tables, with a 0.001 level of significance. Forthe windward portion, F from tables was 14.4, and forthe leeward it was 15.1, which shows that the regression coefficients in the models representing elevation lapse rates of temperature variation are highly significant. The windward regressions are better defined and this is probably due to the broad elevation range used.
For the estimation of monthly and annual mean temperatures in areas of complex relief and scarce weather stations it is critical to establish a relationship between elevation and temperature variation ranges (Hutchinson, 1987). Moreover, interpolation methods must include objective techniques together with statistical diagnoses that have previously quantified predicted errors (Mackey et al., 1996).
According to literature, in the construction of monthly and annual models it is necessary to delimit areas with similar temperature elevation lapse rates in each region, considering such factors that might affect such lapse rates, as the following:
1. The modifying effect of water bodies on temperature changes (Arhens, 2003).
2. Moisture conditions of the area, which are generally associated with the effect of mountain ridges on rainfall distribution.
Thus, attention is given to the effect of air moisture on the vertical temperature lapse rate, which is lower in humid zones (Stull, 2000; Arhens, 2003).3. The orientation of mountain ridges, which separates the effect of incoming solar radiation on temperature (Aguado and Burt, 2001); the northern slope in subtropical regions of México tends to be cooler.
The moisture condition factor of this exercise was taken into account due to the specific conditions of the area under study.
There are considerable differences between the windward and leeward portions in terms of annual and monthly temperature lapse trends as altitude increases. On the leeward slope temperature lapse rates were higher than on the windward. At similar altitudes, there are considerable differences in mean temperature between the two portions, especially at lower elevations; however, as elevation increases, the temperature ranges become more similar. This is due to the cooling trend of humid air rising from the windward portion of the Sierra, which leaves part of its moisture in this zone and releases latent heat in the condensation of water vapor to then descend as dry air towards the region of valleys (Ahrens, 2003). The release of latent heat of the water vapor on the windward side warms the air, and the cooling rate of ascending air range diminishes. The trends in rapid temperature change with changes in altitude on the leeward portion can be explained by the dry adiabatic lapse rate that can be up to 1 °C for each 100 m (Aguado and Burt, 2001) because the air is drier than on the windward portion, especially during the hottest months. The elevation range of the weather stations on the leeward portion was between 1660 to 2690 m and, due to the high temperature lapse rate in each model, the hypothetical mean monthly values at sea level of the hottest and also driest months were very high (40.55 and 41.32 °C for May and June, respectively).
Figure 5 shows the maps of monthly mean temperatures in January (5b) and May (5c) and Figure 5a shows the map of annual mean temperature, after combining the windward and leeward portions. The finest detail in the different temperature range areas is clear as a result of the use of the digital elevation model.
3.2 Isohyet maps
Figure 6 clearly shows the influence of moist winds from the Pacific Ocean on mean precipitation, especially on the windward portion of the Sierra, which is associated with the Mexican Monsoon (Douglas et al., 1993, Stensrud, et al., 1995; Berbery, 2001; Higgins et al., 2003), and the orographic rainshadow in the region of valleys. On the leeward portion of the Sierra it is possible to detect the influence of winds with a lower content of moisture which travels at a greater height from the Gulf of México (Barlow et al., 1998); these winds are usually associated with lower amount of precipitation.
The relation between precipitation measured in weather stations and elevation can vary from one mountain to another since rainfalls are influenced by such factors as the dimension of the mountain barrier, slope differences and land form, mountain ridges orientation, their position in relation to the prevailing winds, whether winds come directly or have passed by other mountain systems, which side of the mountain winds rise or descend, whether they have been diverted or conducted through a canyon (Mosiño and Garcia, 1974). All this makes it difficult to establish reasonable relationships between elevation and precipitation since there are few stations in the region registering the differences associated with the factors mentioned above (Daly et al., 1994).
Due to the specific conditions of the study area –similar to a large part of the mountain regions in México where the lack of meteorological information is frequent– the proposed method for the elaboration of isohyet maps can be classified as graphic, in which an analysis was made of the factors influencing the distribution of precipitation and of the information on the atmosphere's local circulation throughout the year.
Monthly ranges were set so that the mean precipitation estimated would fall within annual ranges; this was the case for most of the situations. There were few cases in which this did not occur due to the criterion that the larger the amount of annual precipitation, the larger the amount of monthly precipitation must be.
The estimated values of monthly precipitation for each annual range were the median of the interval. The sum of all the estimated monthly mean precipitations was within the expected annual range.
Table IV shows the linear regression models between the statistical parameters on the windward portion and Table V presents those for the leeward. In both cases R2 values were satisfactory, above 0.96, most of them between 0.98 and 0.99. The standard errors were between 1.4 to 6.1 mm and from 1.0 to 7.0 mm of monthly rainfall for the windward and leeward portion, respectively. These are acceptable, based on the values of monthly rainfall reported in the weather stations. The F distribution calculated was considerably higher than F from tables with a 0.001 level of significance. For the different monthly levels, F from tables was 21.0 for the general model; 11.7 for the windward model and 11.8 for the leeward. This shows that the regression coefficients in models representing the relationship between the average precipitation calculated for the different weather stations and the value of precipitation estimated by the procedure indicated in this paper of the different groups of stations (by annual precipitation ranges) are highly significant.


The monthly mean precipitation maps elaborated in accordance with the ranges established are presented in Figure 6b and c. They also show the great influence of orography on the distribution of precipitation throughout the year.
4. Conclusions
The methodology proposed to estimate temperature and monthly and annual mean precipitation in areas of complex relief and little meteorological information served to draw detailed maps of these variables.
In the case of temperature, the models estimated by applying the simple method, previously subdividing the zone according to moisture conditions, resulted in highly satisfactory statistical estimators; thus, it can be concluded that the methodology fulfills its purpose.
The application of the Arc View Geographical Information System (ESRI, 2004) provides a clear image of the relation between the location elevation and temperature.
The estimation procedure for precipitation, based on the graphic method, produces detailed maps of this variable, although it requires considerable knowledge of local circulation of the atmosphere in the region throughout the year and also of the effect of orography on the processes causing precipitation. For the analogies established to enable the estimations, the different reports given by the weather stations, the specific conditions in which these stations are located and the vegetation reflectance shown in the false color satellite images (satellite image chart) through differences in colors are all essential.
The monthly precipitation estimated for each of the annual ranges established correlates highly with the mean precipitation obtained as averages from the stations grouped within each annual precipitation range on both portions of the Sierra.
This technique has great potential in the drawing of maps of monthly and annual mean temperature and precipitation at local and regional level in areas with little meteorological information and complex relief.
References
Ahrens C. D., 2003. Meteorology today: an introduction to weather, climate, and the environment. 7th Ed. Brooks Cole. Pacific Grove, CA, USA, 594 pp. [ Links ]
Aguado E. and J. E. Burt, 2001. Understanding weather and climate. 2nd ed. Prentice Hall, Upper Saddle River, New Jersey, USA, 505 pp. [ Links ]
Barlow M., S. Nigam and E. H. Berbery, 1998. Evolution of the North American monsoon system. J. Climate. 11, 2238–2257. [ Links ]
Barry R. G., 1992. Montain weather and climate. 2nd Ed. Routledge, London, 402 pp. [ Links ]
Berbery E. H., 2001. Mesoscale moisture analysis of the North American monsoon. J. Climate. 14, 121–137. [ Links ]
Burns J. I., 1953. Small–scale topographic effects on precipitation distribution in San Dimas Experimental Forest. Trans. Am. Geophys. Union 34, 761–768. [ Links ]
Creutin J. D. and C. Obled, 1982. Objective analysis and mapping techniques for rainfall fields: an objective comparison. Water Resour. Res. 18, 413–431. [ Links ]
Daly C., R. P. Nielson and D. L. Phillips, 1994. A statistical–topographic model for mapping climatological precipitation over mountainous terrain. J. Appl. Meteorol. 33, 140–158. [ Links ]
Dingman S. L., D. M. Seely–Reynolds and R. C. Reynolds III, 1988. Application of kriging to estimating mean annual precipitation in a region of orographic influence. Water Resources B. 24, 329–339. [ Links ]
Douglas M. W., R. A. Maddox, K. Howard and S. Reyes, 1993. The Mexican monsoon. J. Climate 6, 1665–1667. [ Links ]
ESRI, 1996. Environmental Systems Research Institute, Inc., 380 New York Street. Redlands, CA. 92373 USA. [ Links ]
Gandin L. S., 1963. Objective analysis of meteorological fields. Israel Programme for Scientific Translation (translated from Russian, 1965), Jerusalem. [ Links ]
García Benavides J., 1979. Estructura metodológica para la caracterización agroecológica de áreas por procedimientos cuantitativos de análisis y su posterior zonificación. Tesis de Doctor en Ciencias. Colegio de Posgraduados, Chapingo, México, 401 pp. [ Links ]
Higgins R. W., A. Douglas, A. Hahmann, E. H. Berbery, D. Gutzler, J. Shuttleworth, D. Stensrud, J. Amador, R. Carbone, M. Cortez, M. Douglas, R. Lobato, J. Meitin, C. Ropelewski, J. Schemm, S. Schubert and C. Zhang, 2003. Progress in Pan American CLIVAR research: The North American Monsoon System. Atmósfera 16, 29–65. [ Links ]
Houghton J. G., 1979. A model for orographic precipitation in the North–Central Great Basin. Mon. Wea. Rev. 107, 1462–1475. [ Links ]
Houghton J. T., L. G. Meiro Filho, B. A. Callander and N. Harris 1996. Climate Change 1995: The science of climate change. (A. Kattenburg and K. Maskell, Eds.). Cambridge University Press, Cambridge, 584 pp. [ Links ]
Hutchinson M. F., 1987. Methods of generation of weather sequences. In: Agricultural environments: Characterizaction, classification and mapping. A. H. Bunting, Ed.), CAB International, Wallingford, UK, 335 pp. [ Links ]
Hutchinson M. F. and R. J. Bischof, 1983. A new method of estimating mean seasonal and annual rainfall forthe Hunter Valley, New South Wales. Aust. Meteorol. Mag. 31, 179–184. [ Links ]
IMTA, 2000. Extractor Rápido de Información Climatológica. Instituto Mexicano de Tecnología del Agua, ERIC CD–ROM. Cuernavaca, Mor. México. [ Links ]
INEGI, 1993. Espaciomapas Hojas G13 – 4, G13 – 5, G13 – 7, G13 – 8, G13 – 10 G13 –11. Instituto Nacional de Estadística, Geografía e Informática. Dirección General de Geografía. Aguascalientes, México. [ Links ]
IPCC, 2001. Climate Change 2001: Synthesis report. Contribution of Working Groups I, II, and III to the Third Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, New York, 33 pp. [ Links ]
Kleinbaum D. G., L. L. Kupper and K. E. Muller, 1988. Applied regression analysis and other multivariable methods. 2nd Edition. PWS–Kent Publishing, Boston, MA, 718 pp. [ Links ]
Lookingbill T. R. and D. L. Urban, 2003. Spatial estimation of air temperature differences for landscape–scale studies in montane environments. Agr. For. Meteorol. 114, 141–151. [ Links ]
MacIver D. C. and R. D. Whitewood, 1992. Forest climates of Ontario. Part I. Bioclimate profiles 1968–1988. Environment Canada, Atmospheric Environment Service, Ontario Ministry of Natural Resources, Toronto. [ Links ]
Mckey B. G., D. W. Mckenney, Y. Q. Yang, J. P. McMahon and M. F. Hutchinson, 1996. Site regions revisited: a climatic analysis of Hill's site regions for the province of Ontario using a parametric method. Can. J. For. Res. 26, 333–354. [ Links ]
Monterroso–Rivas A. I and J. D. Gómez–Díaz, 2003. Escenarios climatológicos de la República Mexicana ante el cambio climático. Comisión Nacional de las Zonas Áridas y Universidad Autónoma Chapingo. Chapingo, Méx. 170 pp. [ Links ]
Mosiño P. A. and E. García, 1974. The climate of México. In: World Survey of Climatology. (R.A. Bryson and F. K. Hare, Eds.) Vol. II, Climates of North America, Elsevier, 373–404. [ Links ]
Nalder I. A. and R. W. Wein, 1998. Spatial interpolation of climatic normals: test of a new method in the Canadian boreal forest. Agr. For. Meteorol. 9, 211–225 [ Links ]
Ortiz Solorio C. A., 1987. Elementos de agrometeorología cuantitativa: con aplicaciones en la República Mexicana. Departamento de Suelos, Universidad Autónoma Chapingo, Chapingo, México, 327 pp. [ Links ]
Peck E. L. and M. J. Brown, 1962. An approach to the development of isohyetal maps for mountainous areas. J. Geophys. Res. 67, 681–694. [ Links ]
Phillips D. L., J. Dolph and D. Marks, 1992. A comparison of geostatistical procedures for spatial analysis of precipitation in mountainous terrain. Agric. For. Meteorol. 58, 119–141. [ Links ]
Price D. T., D. W. McKenney, I. A. Nalder, M. F. Hutchinson and J. L. Kesteven, 2000. A comparison of two statistical methods for spatial interpolation of Canadian monthly climate data. Agr. For. Meteorol. 101, 81–94. [ Links ]
Reed W. G. and J. B. Kince, 1917. The preparation of precipitation charts. Mon. Wea. Rev. 45, 233–235. [ Links ]
Schermerhorn V. P., 1967. Relations between topography and annual precipitation in western Oregon and Washington. Water Res. Res. 3, 707–711. [ Links ]
SPP, 1981. Cartas de temperatura media anual de la República Mexicana escala 1: 1000000. Dirección General de Geografía del Territorio Nacional. México. (8 cartas). [ Links ]
Spreen W. C., 1947. A determination of the effect of topography upon precipitation. Trans. Am. Geophys. Union 28, 285–290. [ Links ]
Stensrud D. J., R. L. Gall, S. L. Mullen and K. W. Hoeard, 1995. Model climatology of the Mexican Monsoon. J. Climate 8, 1775–1794. [ Links ]
Stull R., 2000. Meteorology for scientists and engineers. 2nd Ed. Brooks Cole. Pacific Grove, CA, USA, 502 pp. [ Links ]
Tabios G. O. and J. D. Salas, 1985. A comparative analysis of technique for spatial interpolation of precipitation. Water Resour. B. 21, 365–380. [ Links ]
Tang M. and E. R. Reiter, 1984. Plateau monsoons of the Northern Hemisphere: A comparison between North America and Tibet. Mon. Wea. Rew. 112, 617–637. [ Links ]
Thiessen A. H., 1911. Precipitation averages for large areas. Mon. Wea. Rev. 39, 1082–1084. [ Links ]
Thornton P. E., S. W. Running and M. A. White, 1997. Generating surfaces of daily meteorological variables over large regions of complex terrain. J. Hydrol. 190, 214–251. [ Links ]
Wörlen C., K. Schulz, B. Huwe and R. Eiden, 1999. Spatial extrapolation of agrometeorological variables. Agr. For. Meteorol. 94, 233–242. [ Links ]