Introducción
El recurso agua es limitante del desarrollo de la vegetación e impone serias restricciones a la producción de alimentos para la humanidad. En el caso de México, los escenarios climáticos proyectados para el Noroeste plantean un incremento en las temperaturas y una reducción en las precipitaciones (Seager et al., 2007), por lo que es necesario generar estrategias de adaptación al cambio climático que permitan un uso más eficiente del agua. En el caso de la agricultura, es necesario el desarrollo de tecnologías que permitan estimar los requerimientos de agua de los cultivos, en espacio y tiempo, para permitir que los agricultores hagan un uso racional del recurso en función de las necesidades de las plantas.
Las estimaciones de requerimientos de agua, evapotranspiración (ET) de los cultivos, ha sido planteada bajo esquemas operativos simples como el de FAO (Allen et al., 1998) que puede ser muy útil con fines de planeación o de estimaciones regionales, pero con errores importantes cuando se aplica a escala de predios agrícolas. Para realizar estimaciones locales asociadas a distritos o zonas de riego se ha planteado el uso de sensores remotos, junto con modelos de balances de energía, para el desarrollo de esquemas de estimación de la ET cuando se usan imágenes satelitales (Bastiaanssen et al., 1998; Roerink et al., 2000; Allen et al., 2007). Este tipo de desarrollos han resultado en estimaciones más o menos razonables (tendencias), con algunos problemas todavía sin resolver. Los modelos de balance de energía han sido calibrados y validados con el uso de estimaciones directas de los flujos de energía y materia a través de lisímetros (solo ET) o técnicas micrometeorológicas.
Las técnicas micrometeorológicas permiten la medición de flujos de energía y materia en forma directa a través de la técnica de Covarianza de Vórtices (EC, por sus siglas en inglés) (Verma, 1990). Con esta técnica, las mediciones de flujos y de materia se realizan a través de la covarianza de la velocidad del viento (medida con un anemómetro sónico) y la temperatura (para el cálculo del calor sensible (H) o vapor de agua (para calcular el calor latente (λET, donde λ es el calor de vaporización del aire). La radiación neta (Rn) y el flujo de calor del suelo (G) son medidas con instrumentación relacionada y las cuales no son dependientes de la velocidad y dirección del viento. Un problema asociado a la técnica de covarianza de flujos es que el cierre del balance de energía (Rn - G = λET + H) muestra errores que oscilan entre un 10 y 30 % (Wilson et al., 2002); aunque hay muchas situaciones donde los errores son más grandes. Una posible explicación del no cierre del balance de energía es que λET y H son mediciones dinámicas donde el área de influencia de éstas cambia en función de la dirección e intensidad del viento y las mediciones de Rn y G son estáticas y con áreas de influencia fijas.
Los flujos de calor latente y sensible tienen áreas de influencia (footprints, en inglés) dinámicas que varían en función de la altura de los sensores, velocidad y dirección del viento, rasgos morfo-estructurales de la vegetación y condiciones de estabilidad de la atmósfera (Leclerc y Thurtell, 1990; Schmid, 2002). Por otro lado, Rn tiene un footprint constante, dependiendo del ángulo de visión del sensor y altura de observación y G tiene una configuración geométrica de distribución de sensores (placas de calor en el suelo) fija, definiendo un footprint constante. Esta situación, más la consideración de que los sensores remotos tienen footprint constantes, plantea la necesidad de escalar las mediciones de flujos para que sean intercomparables con los sensores remotos (Chen et al., 2009). El escalamiento (agregación/desagregación) de las mediciones de flujo ha sido aproximado bajo diferentes esquemas (Chehbouni et al., 2000; Anderson et al., 2008), con resultados aceptables; pero difíciles de reproducir en forma operativa por la complejidad de sus parametrizaciones.
Para poder intercomparar (cierre del balance) los flujos de energía y materia es necesario hacer que las mediciones tengan un mismo footprint. Al respecto, es posible desarrollar dos enfoques: hacer que las mediciones de Rn y G (sensores estáticos) tengan el mismo footprint que las de λET y H (sensores dinámicos). El otro camino es cambiar el footprint de los sensores dinámicos para hacerlos comparables con los estáticos. Esta situación no es viable ya que esta modificación implica un cambio en las condiciones de estabilidad atmosférica, como se discute más adelante, y genera flujos diferentes a los reales. Así, desde la perspectiva de modificar el footprint de Rn (sus componentes), el objetivo en este trabajo fue presentar el desarrollo de un modelo general basado en la dualidad de mediciones con geometría sol-sensor diferente y su contraparte de escala (cambio en las dimensiones de las áreas de influencia). El modelo introducido fue calibrado parcialmente en función del footprint de los sensores de radiación neta semi-hemisféricos a una altura dada.
Materiales y métodos
Modelo del Footprint de Flujos (Sensores Dinámicos)
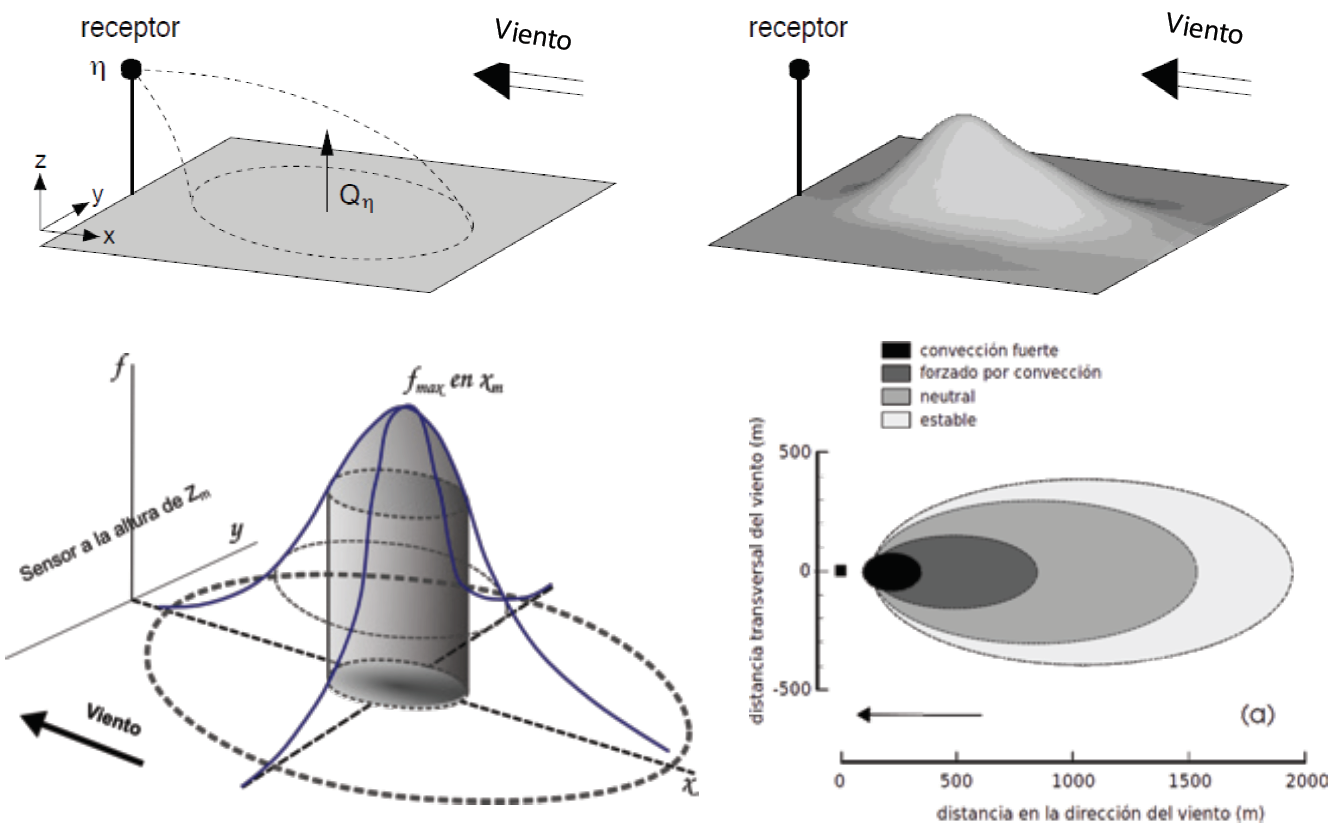
La Figura 1 muestra el concepto del footprint de flujos (Qɳ) medidos por un sensor a la altura zm, donde estos son promediados con el uso de la función f que define la proporción de un flujo individual del medio en relación con el total medido por el instrumento (ɳ).
Aunque existen diferentes esquemas de modelación del footprint de los flujos (Schmid, 2002), en esta sección solo se discute el desarrollo de un modelo analítico, el cual es dependiente de la altura del sensor (zm), de la longitud de rugosidad (z0), de la velocidad del viento (u) y su dirección, de la desviación estándar de la velocidad del viento lateral (σv), de la velocidad de fricción (u*) y de la estabilidad atmosférica (L o longitud de Obukhov). A diferencia de otros modelos analíticos, el modelo usado (Kormann y Meixner, 2001) es aplicable a todas las condiciones de estabilidad atmosférica. Los desarrollos siguientes están basados en Chen et al. (2009), con adaptaciones.
Con el uso de un sistema coordenado donde el eje X corresponde a la dirección longitudinal del viento frontal y Y a la dirección transversal (centrada en X; es decir y = 0 en la línea longitudinal a la dirección del viento, Figura 1), el footprint de un flujo representado por la función f(x,y,zm), en m-2, puede ser modelado por la función de distribución de la concentración transversal a la dirección del viento Dy(x,y), en m-1, y el fooprint integrado transversalmente a la dirección del viento fy(x,zm), en m-1, (Pasquill y Smith, 1983; van Ulden, 1978):
La dispersión en la dirección transversal y puede ser estimada con el uso de una función de distribución Gausiana (Pasquill, 1974):
donde: σ y es la desviación estándar de la pluma de dispersión en la dirección y, la cual depende de la estabilidad atmosférica y la distancia viento arriba x. Bajo consideraciones del límite de corto rango de la teoría estadística de la turbulencia (Pasquill y Smith, 1983; Schmid, 1994), σ y puede ser aproximada como:
donde: up(x) es la velocidad efectiva de la pluma de dispersión y σv es la desviación estándar de las fluctuaciones laterales del viento.
Con el uso de perfiles potenciales de la velocidad del viento y de la difusividad de los vórtices (K):
donde: u0, k0, m y n son constantes empíricas, podemos estimar la velocidad efectiva de la pluma (van Ulden, 1978):
donde: Г( ) es la función gama.
El footprint en la dirección longitudinal al viento puede ser estimado de (Kormann y Meixner, 2001):
El modelo de Kormann y Meixner (2001) está basado en una modificación de la solución analítica de la ecuación de advección-difusión de van Ulden (1978) y Horst (1979) desarrollada para los perfiles potenciales definidos por las relaciones (4).
Para considerar la estabilidad atmosférica en la modelación del footprint, Kormann y Meixner (2001) ajustaron las relaciones (4) a las funciones de similitud de Monin-Obukov para parametrizar las constantes de estas relaciones, lo que permite el desarrollo de un modelo analítico general.
Si se considera que el footprint de una medición de flujos tiene teóricamente un rango de influencia de -∞ a +∞, una estimación de la región de la superficie que más está contribuyendo a la medición de un flujo puede realizarse al considerar el área de la fuente al nivel P (peso relativo, 0-1) caracterizada por la isopleta f(x´,y, zm) = fP (Schmid, 1994):
donde: ΨP es la integral del footprint sobre el área de la fuente ΩP.
Modelo del Footprint de la Radiación Neta (Sensores Estáticos)
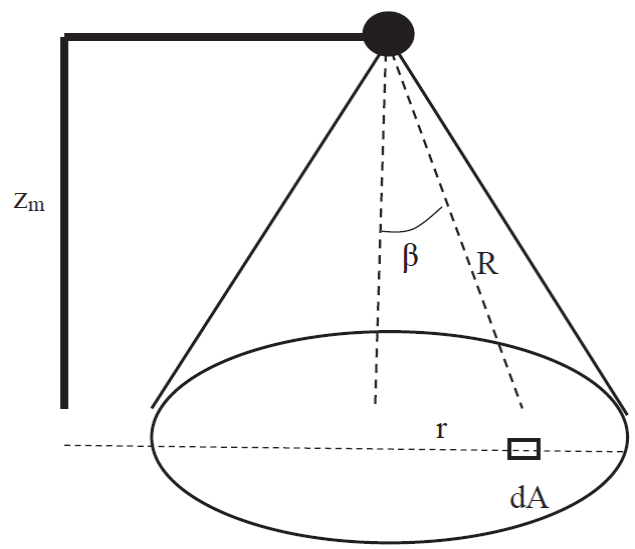
Los radiómetros netos tienen campos de visión semi-hemisféricos (hacia arriba y hacia abajo) con ángulo de semi-campo (field of view) de 90°; es decir, el footprint se extiende hacia el infinito (Figura 2).
Con el uso de la ley del coseno de Lambert para la radiación, Schmid (1997) definió el footprint asociado al radio R como (se ha normalizado para tener valor máximo igual a 1.0):
La estimación del área de la fuente al nivel P puede ser estimada como equivalente al factor de visión discutido por Reifsnyder (1967):
El modelo del footprint de la radiación neta es independiente de la altura del sensor zm, dado su ángulo de campo semi-hemisférico, por lo que su uso es limitado para sensores con ángulos de visión menores.
Resultados y discusión
Desarrollo de un Modelo Generalizado del Footprint para Sensores Estáticos
Para el desarrollo de un modelo generalizado del footprint para sensores estáticos con ángulos de visión oblicuos y ángulos de semi-campo menores a 90°, es necesario el desarrollo de tres elementos: la geometría de visión (envolvente del footprint), la función de ponderación o de footprint y los componentes de la mezcla suelo-vegetación observadas.
Geometría de Visión y Envolvente del Footprint
Al considerar solo la geometría de visión de un sensor pasivo, el área de influencia de las observaciones puede definirse de acuerdo con la Figura 3, donde θv es el ángulo de visión del sensor y α es el ángulo de semi-campo. Así, la geometría de la envolvente del footprint puede ser estimada de:
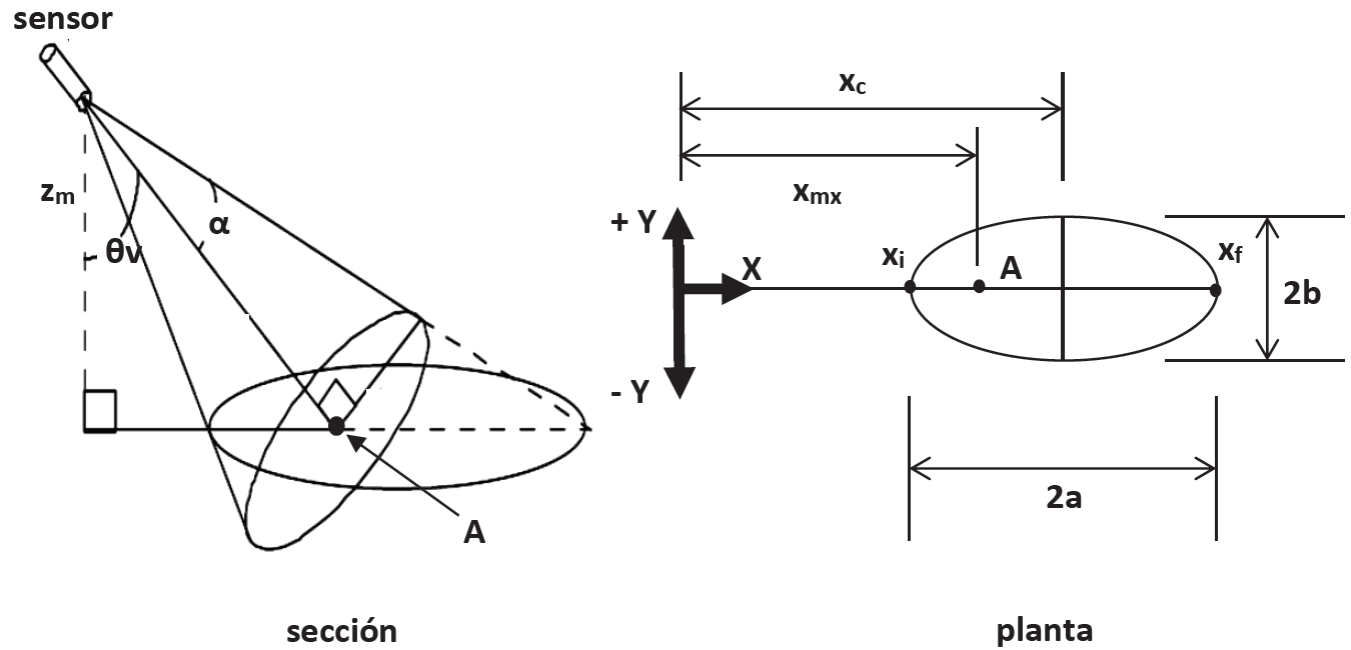
Figura 3 Geometría de visión de un sensor pasivo con ángulo de visión oblicuo y envolvente del footprint de las observaciones. El punto A es común entre las figuras, permitiendo establecer relaciones entre la geometría en perfil (izquierda) y planta (derecha). θv es el ángulo de visión del sensor y α es el ángulo de semi-campo.
Función del Footprint del Sensor
En el caso de sensores remotos, mediciones de reflectancias o temperaturas radiativas, la función de respuesta espacial (point spread function) define el footprint de las mediciones (Schowengerdt, 1997; Cracknell, 1998). Con el uso de funciones separables (Schwengerdt, 1997), válidas para este caso, el footprint de las observaciones satelitales puede aproximarse de las funciones lineales en las direcciones x,y (Cracknell, 1998):
De la argumentación anterior, el uso de la función de distribución Gausiana bidireccional es típicamente usada para definir el footprint (no dependencia de la geometría de visión):
donde: ax define la dimensión en la dirección longitudinal a la órbita del sensor y ay en la transversal.
El modelo bi-Gausiano establece límites del footprint de -∞ a +∞, además de suponer no efectos geométricos relacionados con el ángulo de visión, por lo que resulta inconveniente con el desarrollo mostrado en la sección anterior. En general, el modelo de la Figura 3 delimita un footprint que es dependiente de la tecnología usada por el sensor, por lo que puede usarse la aproximación de que la envolvente definida caracteriza entre el 90 al 95% del área de influencia total.
En el caso del modelo de la Figura 3 es necesario considerar que el footprint es distorsionado en relación a su proyección sobre una superficie plana, por lo que si se considera rayos de visión del sensor dependientes de intervalos fijos de dθv, entonces se tendrán áreas con rayos más densos y áreas con rayos más dispersos (ver sección en Figura 3). Una forma empírica de aproximar esta situación es el uso de la función (parámetros definidos en la Figura 3):
donde: fx es un parámetro que define la forma de la curva. La función de la Ecuación (13) incluye el caso de un footprint simétrico x mx - x i = x f - x mx y toma valores entre 0 y 1, inclusive.
La Figura 4 muestra el efecto del parámetro de forma fx, el cual al reducirse asigna mayores pesos a los limites inferior y superior del footprint.
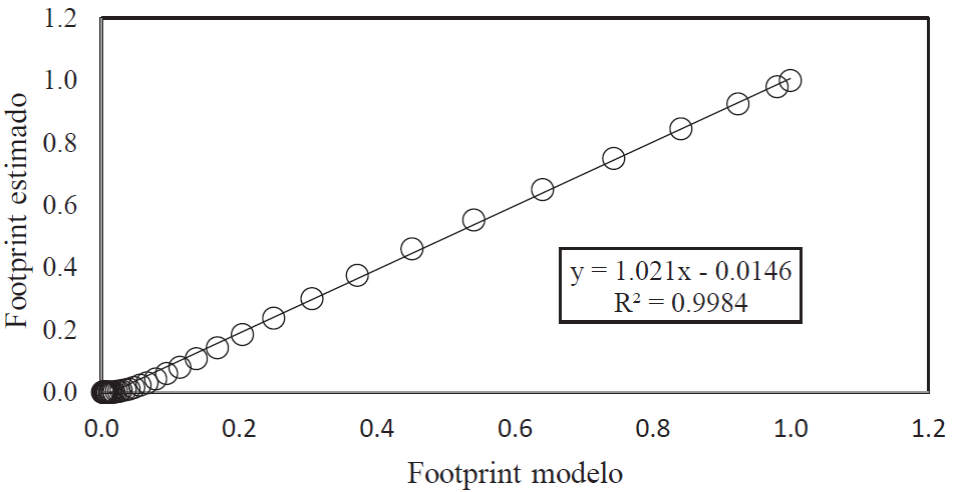
Con el uso del modelo validado de footprint para la radiación neta, Ecuación (8), como referencia para calibrar fx, se parametrizó con fx = 4. Los resultados del modelo de la Ecuación (8) en relación con el modelo de la Ecuación (13) con fx = 4 están mostrados en la Figura 5. La parametrización introducida fue realizada bajo el supuesto que un modelo de footprint genérico debe cumplir la condición específica (sensor a nadir) asociada a la Ecuación (8).
De la relación (11), el modelo propuesto del footprint de un sensor estático estará dado por:
donde de acuerdo con el sistema coordenado mostrado en la Figura 3, ymx = 0; con yi negativo y yf positiva.
De la ecuación de la elipse centrada en (xc, 0), los valores de yi y yf se estiman de:
Para el caso de rotaciones o traslaciones, solo hay que modificar el sistema coordenado con el uso de transformaciones de ejes, las cuales se discuten en cualquier libro de geometría analítica.
Conclusiones
-El modelo desarrollado en este trabajo permite aproximar el footprint de los sensores estáticos, por lo que es posible analizar los cierres de balances de energía en un marco homogéneo de comparación (interoperabilidad), al evaluar el footprint equivalente para los footprints dinámicos de calor sensible y latente.
-La parametrización introducida, formato analítico, es suficientemente simple para ser integrada en software de medición de flujos de sistemas de covarianza de vórtices, permitiendo así realizar balances de energía en periodos de integración de los datos, pudiendo contribuir a la discusión de si los cierres de balance de energía son producto de footprints diferentes o de advección del viento.











 nueva página del texto (beta)
nueva página del texto (beta)