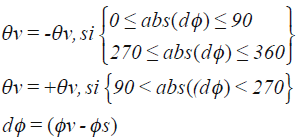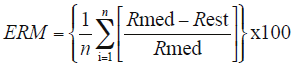INTRODUCCIÓN
Los sensores remotos a bordo de plataformas espaciales brindan una oportunidad para caracterizar y clasificar la vegetación natural en forma espacialmente continua y con tiempos de visita al mismo sitio, que van de horas hasta menos de un mes. De esta forma, la tecnología satelital ofrece un enorme potencial para obtener productos cartográficos de la vegetación a costos muy bajos y con la ventaja de obtener actualización en periodos cortos. No obstante lo anterior, las clasificaciones de vegetación realizadas con sensores remotos todavía muestran problemas serios de estabilidad temporal y de confusión entre clases. Esta situación es mayormente producto de la utilización de enfoques empíricos de clasificación basados en supuestos, generalmente implícitos, que no son viables: homogeneidad espacial, temporal, angular y espectral; principalmente.
El sensor Advanced Very High Resolution Radiometer (AVHRR) ha sido ampliamente utilizado con la finalidad de clasificar vegetación, con resolución espacial a nadir de 1.1 km, disponible en diferentes versiones desde 1978. Actualmente, el sensor Moderate Resolution Imaging Spectroradiometer (MODIS), con una resolución a nadir de 250, 500 y 1000 m, en operación desde 2000, es usado intensivamente en el mapeo de la vegetación a escalas locales y globales. Ambos sensores son de barrido ancho, por lo que los píxeles en una escena son vistos con diferentes ángulos cenitales de visión e iluminación solar, lo que genera un problema de geometría sol-sensor.
Debido al sistema de barrido de la superficie terrestre, los sensores AVHRR y MODIS introducen un efecto simultáneo de geometría sol-sensor y escala (el tamaño de los píxeles se incrementa con el ángulo de visión; esto es, los píxeles que se alejan de la línea orbital ortogonal a la superficie incrementan sus dimensiones producto de vistas oblicuas del sensor). En el otro extremo, el sensor Multi-Angle Imaging SpectroRadiomer (MISR) mantiene fijas las dimensiones de los píxeles a través de un muestreo de barrido temporal a lo largo de su línea orbital.
Un enfoque teórico de clasificación de la vegetación, actualmente operacional usando los sensores MODIS y MISR, es el desarrollado por el grupo de la Universidad de Boston (Lotsch et al., 2000; Zhang et al., 2002a y b), cuya base parte de una clasificación de tipos de vegetación usando propiedades radiativas y geométricas típicas de la mezcla suelo-vegetación para seis biomas distintivos en esos términos (Myneni et al., 1997). Los biomas radiativamente definidos son usados para condicionar la estimación de parámetros biofísicos usando información espectral (Knyazikhin et al., 1998a y b). Aunque resulta atractivo, este enfoque usa simplificaciones (biomas tipo y propiedades asociadas con poca variación) que limitan su uso en términos operacionales a escalas locales o regionales.
Se ha argumentado que la información espectral multi-angular mejora la clasificación de la vegetación (Bicheron et al., 1997; Asner, 2000; Diner et al., 1999 y 2005). Barnsley et al. (1997) y Hyman y Barnsley (1997) muestran que el utilizar información multi-angular en una sola banda espectral, en la clasificación de la vegetación, da resultados similares a utilizar información de múltiples bandas espectrales con un solo ángulo de visión; aunque estos autores reconocen que la separación de clases de vegetación está fuertemente influenciada por las diferencias a nivel espectral y, en menor medida, a nivel angular. Gerard (2003) plantea que el uso de un ángulo de visión relacionado con la información a obtener, da resultados similares al uso de dos ángulos de visión.
En una perspectiva teórica y estadística, Zhang et al. (2002a y b) argumentan que la clasificación de la vegetación debe basarse en principios de consistencia entre las propiedades radiativas de las clases y sus firmas espectrales distintivas, manteniendo fija la resolución espacial (problema de mezclas). Estos autores utilizan espacios espectrales (rojo o R e infrarrojo cercano o IRC, por ejemplo) y muestran que las clases de vegetación (radiativamente diferentes) están diferenciadas en función de su localización en el espacio espectral y tres métricas: inclinación, longitud e intercepción de los patrones cuasi-lineales en ese espacio. Con ello se favorece la hipótesis de firmas espectrales multi-angulares únicas para las clases de vegetación (los seis biomas definidos por Myneni et al., 1997).
En este trabajo, se utilizó un modelo de la geometría sol-sensor de un parámetro único para analizar los patrones angulares de diferentes arquetipos de vegetación, contrastantes entre sí y se revisó si la información espectral angular puede diferenciar las clases estudiadas.
MATERIALES Y MÉTODOS
Modelos espectrales multi-angulares
Los objetos terrestres generalmente reflejan la energía solar en forma anisotrópica, de tal forma que esta señal angular puede ser usada para distinguir o clasificar los diferentes objetos en una escena con un satélite multi-angular. La caracterización de las mezclas suelo-vegetación ha sido estudiada experimentalmente por muchos autores (Kimes, 1983; Ranson et al., 1985; Bolaños et al., 2007) y ha servido de base para plantear que la información espectral multi-angular puede ser usada para una mejor discriminación y caracterización de los cultivos y ecosistemas.
En la actualidad, los modelos de la función de distribución de la reflectancia bidireccional (BRDF, por sus siglas en inglés) más usados, son los basados en kernels (funciones matemáticas) que combinan modelos de medios turbios y de óptica geométrica (Wanner et al., 1995). Estos modelos semi-empíricos de kernels pueden ser lineales (Roujean et al., 1992; Wanner et al., 1995; Lucht y Roujean, 2000) o no lineales (Staylor y Suttles, 1986; Rahman et al., 1993). Un modelo de la BRDF requiere de, al menos, tres parámetros (Engelsen et al., 1996): uno relacionado con la amplitud de la señal, otro con la dependencia con respecto a los ángulos cenitales solares y de visión y, un último con las variaciones acimutales. Si se requiere modelar en forma más fina los rasgos de la BRDF (pico de retro-iluminación o Hot Spot y el pico especular) es necesario incorporar más parámetros al modelo (Engelsen et al., 1996). En un caso de pixel por pixel de una imagen satelital, los requerimientos de datos de los modelos actuales de la BRDF deben utilizar hipótesis restrictivas (homogeneidad temporal o espacial) para contar con información para caracterizar las BRDF.
La clasificación de la vegetación natural mediante modelos de la BRDF ha sido realizada a través de los parámetros ajustados en dichos modelos. En el caso de los kernels lineales (isotrópicos, volumétricos y geométricos), los coeficientes ajustados han sido utilizados para buscar relaciones con la cobertura aérea y estructura de la vegetación (altura, composición, etc.) para diferentes tipos de vegetación (Gerard y North, 1997; Lovell y Graetz, 2002; Gao et al., 2003). Aunque los resultados muestran relaciones congruentes entre los parámetros de los modelos de kernels lineales de la BRDF y la estructura de la vegetación, éstos muestran confusión en las clasificaciones y errores de estimación altos en las variables asociadas a las clases de vegetación.
Una alternativa al uso de los coeficientes de los modelos de kernels de la BRDF es el uso de índices espectrales angulares de la vegetación (Sandmeier et al., 1998; Sandmeier y Deering, 1999; Lacaze et al., 2002; Zhang et al., 2002a y b), que en algunos casos son construidos a partir de los coeficientes de los kernels (Gao et al., 2003). Este tipo de enfoque presenta los mismos problemas que el caso de los coeficientes directos de los modelos de kernels.
Modelación del ángulo cenital de iluminación y visión
Recientemente se ha introducido una nueva familia de modelos de la BRDF que simplifica fuertemente el problema de modelación, ya que solo requieren de un parámetro para su caracterización (Bolaños et al., 2007; Bolaños y Paz, 2010). Este tipo de modelación es discutida en lo siguiente y constituye la base del análisis de los experimentos mostrados en este trabajo.
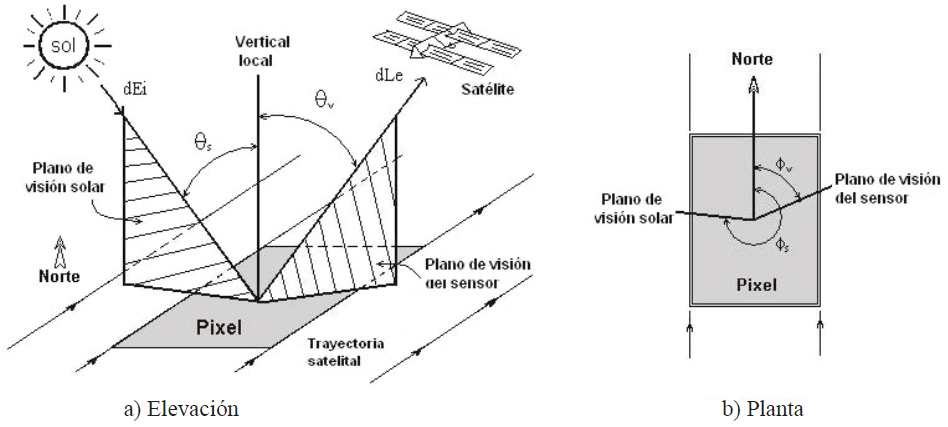
La BRDF de una pequeña superficie de área δA está definida como la razón de la radianza incremental dejando la superficie a través de un ángulo sólido infinitesimal, en la dirección definida por el vector de visión Ω(θv,Øv), sobre la irradianza incremental de la dirección definida por el vector de iluminación, Ω’(θs,Øs), (Nicodemus et al., 1977), tal como se define en la Ecuación 1 y se muestra en la Figura 1.
donde: dLe es la radianza incremental reflejada desde la superficie en la dirección del ángulo de visión Ω (Wm-2 sr-1), dEi es la irradianza incremental que llega desde la dirección de iluminación Ω’ (Wm-2 sr-1), θs es el ángulo cenital solar, ϕs es el ángulo acimutal solar, θv es el ángulo cenital de visión y ϕv el ángulo acimutal de visión.
El modelo de Bolaños et al. (2007) utiliza un plano de simetría para el IRC, de tal forma que los patrones angulares de la reflectancia se simplifican y pueden modelarse con un solo parámetro. Este modelo no fue aplicable a la banda del R.
Para desarrollar un modelo general de la BRDF aplicable a todas las bandas espectrales, se utilizó un plano de simetría genérico propuesto por Paz y Bolaños (2006)1 y Bolaños y Paz (2010). El plano de simetría seleccionado fue χ = 90 - θv + θs, donde θv no tiene signo. Las reflectancias normalizadas están definidas como Rn = Rcos (χ) (más adelante se utiliza R para referirse a solo la banda del rojo). El modelo propuesto para todas las bandas del espectro electromagnético de onda corta es un modelo lineal simple:
donde se utiliza un valor de a = 90 para obtener un punto adicional y poder estimar b usando un esquema similar al del IRC del modelo de Bolaños et al. (2007). El uso de la función cos(χ) como factor multiplicativo de R permite definir un punto del espacio Rn-χ, ya que cos(90°) = 0, por lo que Rn = 0 en χ = 90° (θv = θs; es decir, el plano del Hot Spot).
Experimentos bajo condiciones controladas
La discriminación de clases de vegetación que utiliza información espectral multi-angular fue analizada en un experimento bajo condiciones controladas de laboratorio, donde se simularon diferentes configuraciones geométricas de especies vegetales con arquetipos contrastantes. Para esto se utilizaron plantas pequeñas de especies arbóreas y arbustivas y, plantas adultas para pastizales, después de podarse. En el Cuadro 1 se muestran las características principales de las plantas usadas en los experimentos, donde están consideradas especies con diferentes tipos de hoja.
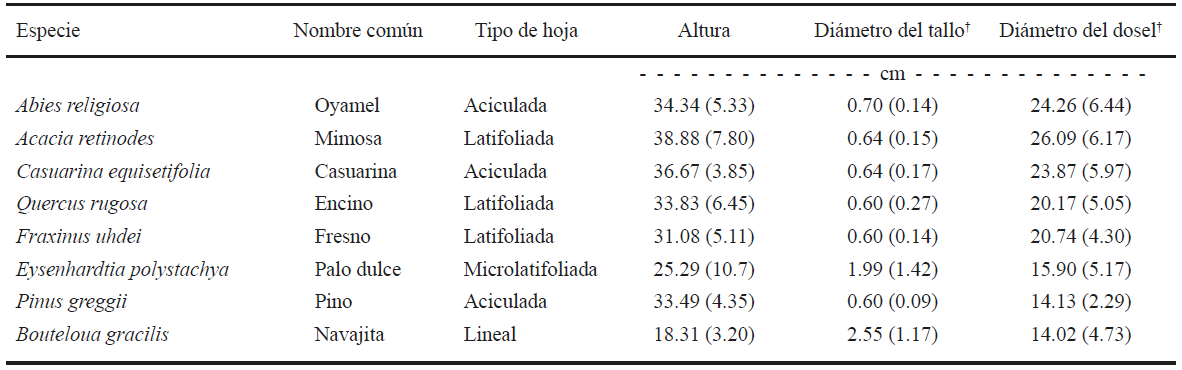
† Los datos entre paréntesis son las desviaciones estándar.
Cuadro 1: Características de las especies vegetales usadas en el experimento.
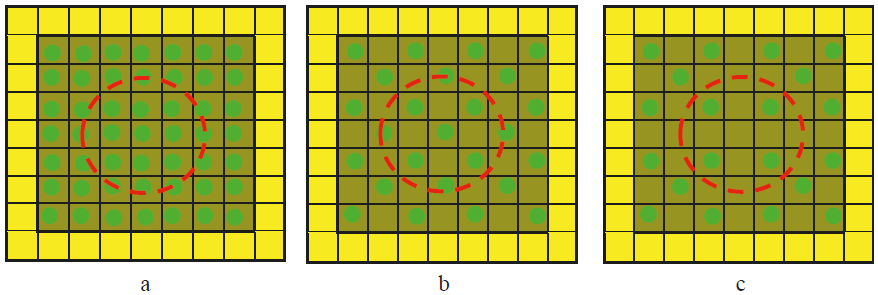
Las plantas individuales de cada especie, empacadas en bolsas de plástico abiertas y sin estrés aparente, fueron acomodadas en tres densidades de acuerdo con los arreglos mostrados en la Figura 2. Los arreglos de plantas fueron colocados en un cajón de madera de dimensiones de 1.5 m × 1.5 m, con un sistema de mallas de 15 cm × 15cm para la colocación de las plantas individuales dentro de bolsas de plástico abiertas, de tal manera que no se inclinaran al apoyarse sobre el fondo del cajón y se mantuvieran verticales. Para analizar el efecto del fondo de los arreglos de plantas, arriba de la malla superior del cajón se colocaron tiras de madera a la altura del inicio de los tallos de las plantas y sobre estas tiras, selladas en los tallos, se colocó suelo previamente seleccionado y con una granulometría menor a 2 mm.
Cada circulo relleno representa la posición de una planta y los cuadros perimetrales más claros solo contienen suelo. El círculo que se ubica al centro de los cuadros es el área de visión del sensor hiperespectral con un ángulo de visión a nadir. El cajón de madera conteniendo los arreglos de plantas forma parte del sistema goniométrico (SIGO-CP) de medición de reflectancias multi-angulares diseñado (Cano et al., 2014).
A nadir, el radiómetro hiperespectral (350 a 2500 nm) udaso (modelo FR Jr de ASDMR) observó un área circular de diámetro 0.41 m. El radiómetro tiene un campo instantáneo de visión de 25º (α = 12.5º, ver Figura 3). Adicionalmente al radiómetro, se montó en el SIGO-CP una cámara fotográfica digital (Cybershot DSC-V1 de SonyMR) y un termómetro radiativo (modelo ITRS de ApogeeMR). Estos instrumentos fueron usados para realizar mediciones cenitales a intervalos de 10º, desde 0º a 60º, y en las direcciones acimutales de 0º a 360º, con intervalos de 10º. La dirección acimutal de 0/360º de medición coincide con el acimut de la fuente de iluminación, por lo que las direcciones acimutales representan en realidad diferencias acimutales en la convención de 0-360º. La fuente de iluminación utilizada fue un reflector de aluminio de cuerpo negro de la marca Tecno LiteMR equipado con una lámpara de halógeno de cuarzo de 500 watts de la marca OsramMR (modelo 64706). Los filamentos de estas lámparas son de tungsteno y el vidrio que recubre el filamento está hecho de cuarzo, siendo el halógeno el gas que rellena el tubo o bombilla. La lámpara se montó en una base telescópica elevada a 3 m y su ángulo cenital (θs) fue de 38º. Estas condiciones de iluminación se mantuvieron constantes para todas las mediciones de las especies analizadas.
Las propiedades ópticas de los fondos de los arreglos de plantas contribuyen a la BRDF del sistema suelo-vegetación. Por ejemplo, en los bosques, el fondo varía estacionalmente (Miller et al., 1997) y tiene su propia función BRDF (Peltoniemi et al., 2005). Así, en cada arreglo de plantas por especie vegetal se consideró el uso de dos fondos: suelo claro (franco arenoso) y oscuro (franco arcilloso). Los suelos fueron colocados sobre las tiras de madera a la altura del inicio de los tallos de las plantas, con un espesor de 1cm. En cada suelo se consideraron dos condiciones de humedad: suelo secado a la intemperie y suelo húmedo producto de un evento de precipitación. Para este último caso se utilizó un simulador de lluvia (Morin et al., 1967), donde el cajón del SIGO-CP con el arreglo de plantas se transportó a la base del simulador, en la misma área experimental, y se sometió a un evento de precipitación con un disco de 75 mm durante 5 min con la llave del simulador abierta al máximo, lo cual aporta una lámina de precipitación de 8.3 mm. El evento de precipitación fue utilizado para analizar el efecto de la lluvia en el suelo del fondo de la vegetación, inmediatamente después del evento. La reflectancia del suelo después del evento de precipitación se incrementó en proporción a la energía de las gotas de lluvia (Goldshleger et al., 2002). El agua residual en las hojas de las plantas introduce errores en las mediciones del sistema suelo-vegetación, por lo cual los patrones de su BRDF resultan más erráticos que los de suelo seco.
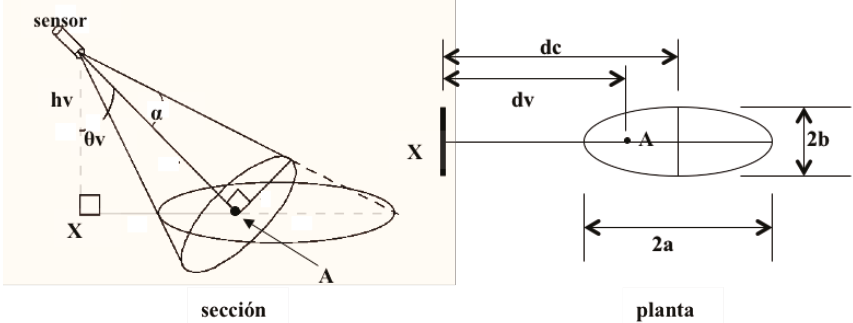
En la Figura 3 se muestra la geometría de medición para el radiómetro montado en el arco cenital del SIGO-CP (Cano et al., 2014), donde el área de visión para ángulos cenitales oblicuos forma una elipse, cuyo centro esta desplazado del centro del cajón una distancia dpc = dc - dv.
En el Cuadro 2 se muestran las configuraciones geométricas asociadas a las mediciones cenitales de visión del arreglo de plantas.
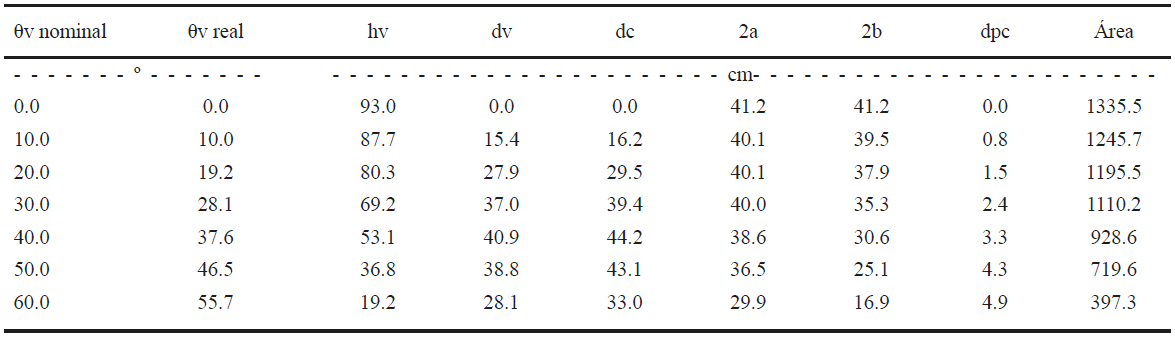
Cuadro 2: Configuraciones geométricas asociadas a los ángulos cenitales de visión (ver Figura 3 para la definición de las variables).
Debido a que el SIGO-CP tiene un grado de libertad adicional al acimutal y cenital, relacionado con el desplazamiento radial del sensor del radiómetro, se diseñó una estrategia de adquisición de datos dentro del área global de medición de 41.2 × 41.2 cm (2a × 2b del Cuadro 2). En el caso de θv = 60º, el sensor quedó muy cerca de la vegetación, produciendo errores de medición, por lo cual este ángulo no fue considerado en la modelación de la función BRDF asociada a cada arreglo de plantas y fondo usado.
El área del experimento fue aislada con paños de tela negra y el techo pintado de negro, para evitar contribuciones de radiación difusa y aproximar una fuente de iluminación con un ángulo cónico de solo radiación directa.
El procedimiento general de determinación de los factores de reflectancia para cada especie en particular consistió de los siguientes pasos: a) colocación del arreglo de densidad alta de plantas en el cajón de madera del SIGO-CP; b) colocación del suelo (oscuro o claro) del fondo de los arreglos de plantas; c) optimizar el radiómetro con el panel de referencia colocado a nadir (ASD, 1999); d) realizar el conjunto de mediciones acimutales y cenitales; e) aplicar evento de precipitación al suelo usando el simulador de lluvia; f) optimizar el radiómetro con el panel de referencia colocado a nadir; g) realizar el conjunto de mediciones acimutales y cenitales; h) retirar el suelo mojado y colocar el otro suelo; i) repetir todo el proceso para el nuevo suelo; j) retirar el nuevo suelo; k) retirar plantas de acuerdo con la Figura 2 para establecer la densidad media; l) colocar el suelo inicial y repetir todo el proceso; m) retirar plantas para establecer la densidad baja; y n) repetir todo el proceso. Adicionalmente, se realizaron conjuntos completos de mediciones para el caso de suelo desnudo (suelos claro y oscuro, en condiciones secas y mojadas, al aplicar un evento de precipitación con el simulador de lluvias). En cada conjunto de medición del arreglo de plantas de las especies se tomaron fotografías digitales para estimar la cobertura aérea (COB) usando un proceso de clasificación supervisada.
RESULTADOS Y DISCUSIÓN
En términos de la definición de la BRDF (Nicodemus et al., 1977), ésta implica ángulos sólidos infinitesimales, por lo que no puede ser medida en la práctica. El arreglo de medición de reflectancias en condiciones de laboratorio discutido anteriormente implica la caracterización de los factores de reflectancia bi-cónicos o cónico-cónico (CCRF, por sus siglas en inglés) (Nicodemus et al., 1977; Schaepman-Strub et al., 2006), donde el término cónico es usado para el ángulo sólido (iluminación y visión), similar al mostrado en la Figura 3. Las mediciones de reflectancia del radiómetro hiperespectral se refieren en realidad a factores de reflectancia, los cuales son calculados en función de las propiedades ópticas de un panel de referencia (ASD, 1999).
En la Figura 3 y el Cuadro 2, la CCRF medida incorpora factores de escala (áreas de medición diferentes en función del ángulo cenital de visión), por lo que debe usarse una definición generalizada que considere la parte espacial del área de medición (Di Girolamo, 2003). Los cambios en las dimensiones de los píxeles con los ángulos de visión se presentan en los sensores AVHRR y MODIS, por lo que es importante considerar en forma explícita esta situación. En este caso, usaron la relación exponencial entre las reflectancias y los índices de área foliar (Ross, 1981), como elementos de escala, se utilizó en una nueva definición de reflectancias normalizadas: Rn = ln(R) cos(χ), dejando igual el modelo de la BRDF (CCRF).
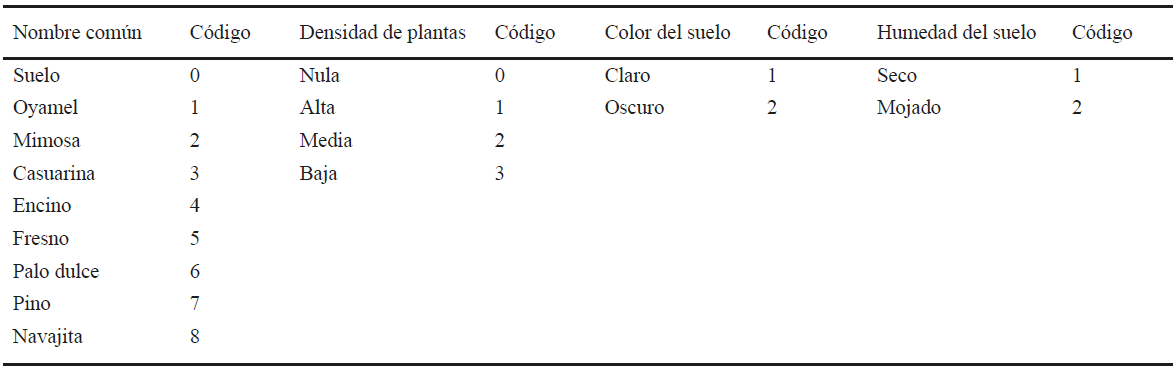
Las mediciones de reflectancia generadas (archivo de 350 a 2500 nm, muestreado a intervalos de 2 nm) fueron convertidas a las reflectancias de las bandas del sensor Landsat 5 utilizando las funciones de respuesta correspondientes. Por problemas relacionados con efectos de la atmósfera del área del experimento (vapor de agua) y de estabilidad del radiómetro, las bandas del azul y del infrarrojo medio no fueron analizadas y solo los resultados de las bandas del verde (V), rojo (R) e infrarrojo cercano (IRC) son presentados en el presente trabajo. Los datos generados en el experimento fueron guardados en archivos etiquetados con 4 dígitos: primer dígito = especie vegetal, segundo dígito = densidad del arreglo de plantas; tercer dígito = color del suelo y cuarto dígito = humedad del suelo. El Cuadro 3 muestra la codificación usada, donde, por ejemplo, un código 2121 significa planta Mimosa, densidad alta de plantas, color oscuro del suelo y estado de humedad seco.
Patrones angulares de la CCRF de los experimentos
Con fines de visualización se construyeron diagramas de reflectancias en función de los ángulos cenitales y acimutales de observación. En el caso de los ángulos cenitales se utilizó la convención de que los ángulos son negativos en la dirección de iluminación y positivos en la contraria (ángulos acimutales de visión positivos en el sentido contrario a las manecillas del reloj):
Para el caso del acimut relativo el signo positivo es para los cuadrantes a la derecha acimutal (diferencia de 0º a 180º) y el negativo para la dirección contraria, en una convención de diferencias de 0º a 90º
La Figura 4 muestra el efecto del tipo de suelo (claro y escuro) y su condición de humedad (seco y mojado) para las reflectancias de la banda del R e IRC para las plantas de Acacia. Se observa que las propiedades ópticas del suelo de fondo de la vegetación generan algunos cambios en los patrones multi-angulares de las reflectancias. En la Figura 5 se muestra el efecto en la reflectancia del R del cambio en la humedad del suelo para el caso de un suelo claro y la cobertura aérea (densidad de plantas) para el pasto Navajita, donde resulta claro que la CCRF es dependiente de estos factores. Finalmente, en la Figura 6 se muestra la CCRF de la reflectancia de la banda del R para todas las especies analizadas, dentro de un rango de cobertura aérea local a nadir de 18 al 28%. Los gráficos muestran diferencias entre las especies (mismo suelo: claro y seco), que permiten clasificarlas a priori.
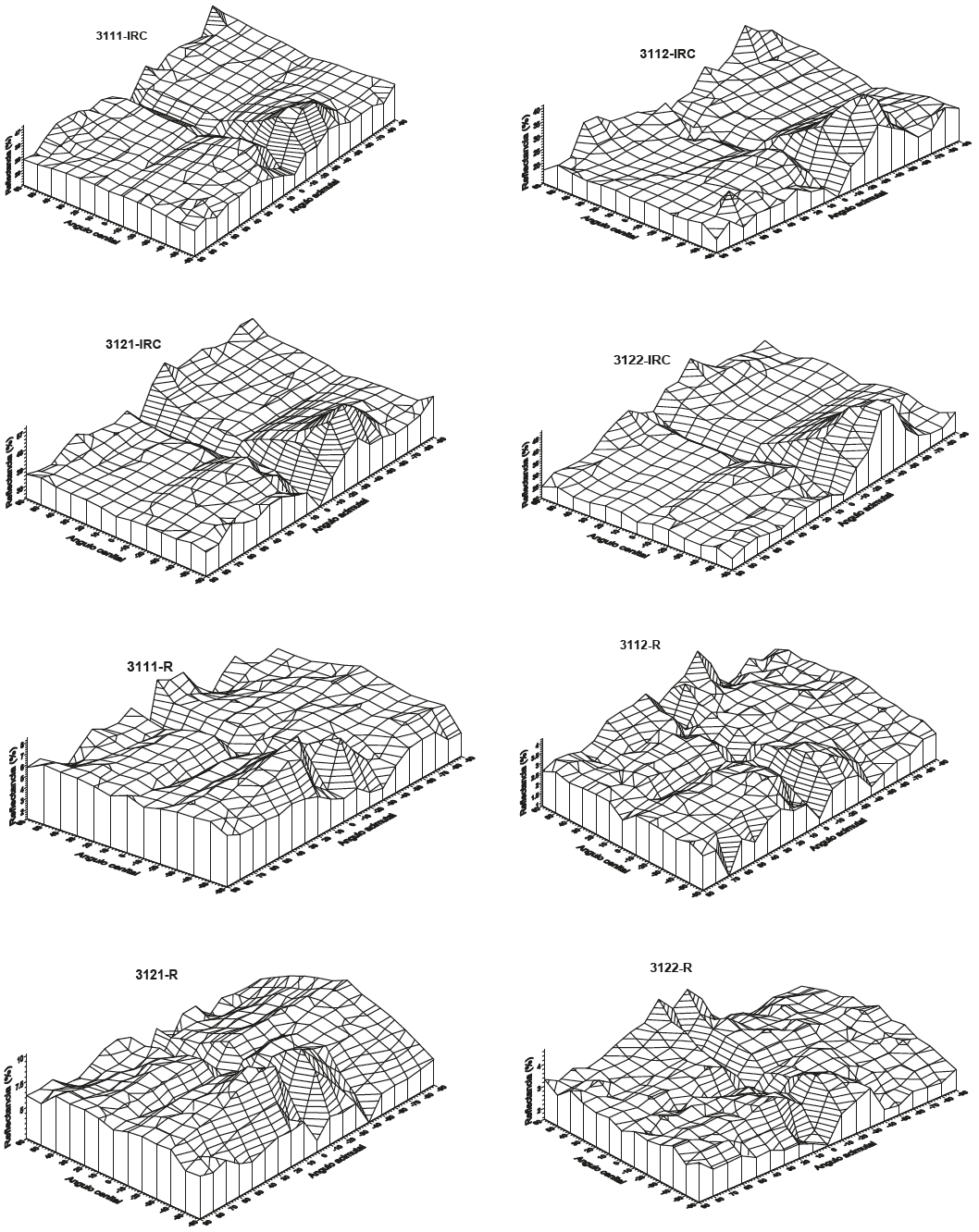
Figura 4: CCRF para las reflectancias de las bandas del R e IRC para diferentes propiedades ópticas del suelo de Acacia retinodes.

Figura 5: CCRF para las reflectancias del R para un suelo claro seco y mojado, para diferentes coberturas aéreas (densidad de plantas) para el pasto Navajita.
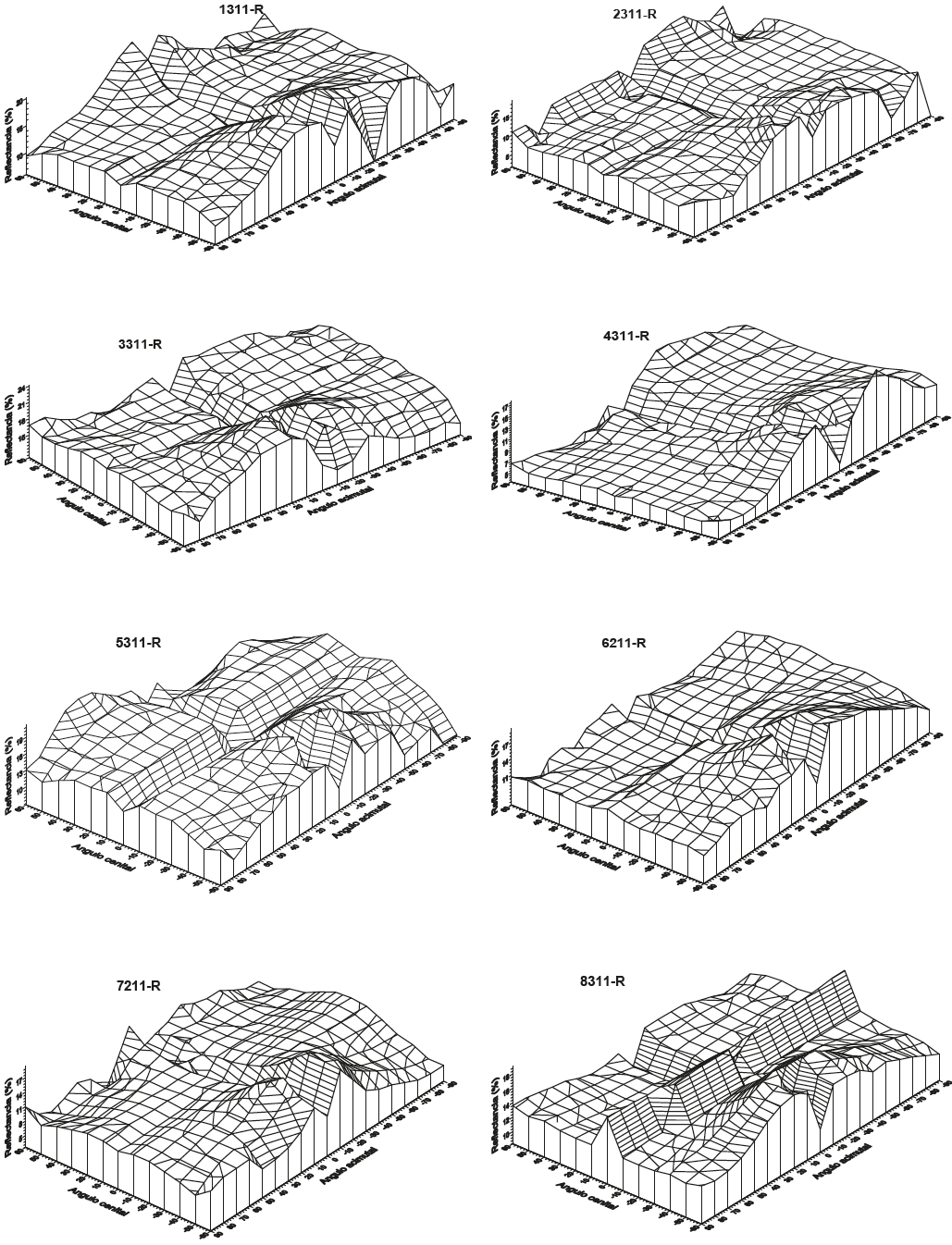
Figura 6: CCRF para las reflectancias del R para un suelo claro seco para todas las especies analizadas, dentro de una cobertura aérea del 18 al 28%.
En el caso de las coberturas aéreas, el Cuadro 4 muestra las estimaciones realizadas en las fotografías digitales, donde COB (cobertura aérea) global se refiere a la cobertura de todo el cuadro de medición (sin los cuadros del borde) del cajón del SIGO-CP y COB local nadir es la cobertura del área del círculo de medición del radiómetro a nadir (41.2 × 41.2 cm).
De las Figuras 4 a 6 (5) resulta claro que para discriminar las especies es necesario definir una diferencia acimutal particular, así como un fondo específico y una cobertura aérea o índice de área foliar. Para poder compactar la información multi-angular de las reflectancias, se ajustó el modelo de la Ecuación (2) con a = 90 y la transformación logarítmica para el efecto de escala.
La Figura 7 muestra los resultados obtenidos para las bandas del V, R e IRC. El error relativo medio (ERM), en %, está definido por:
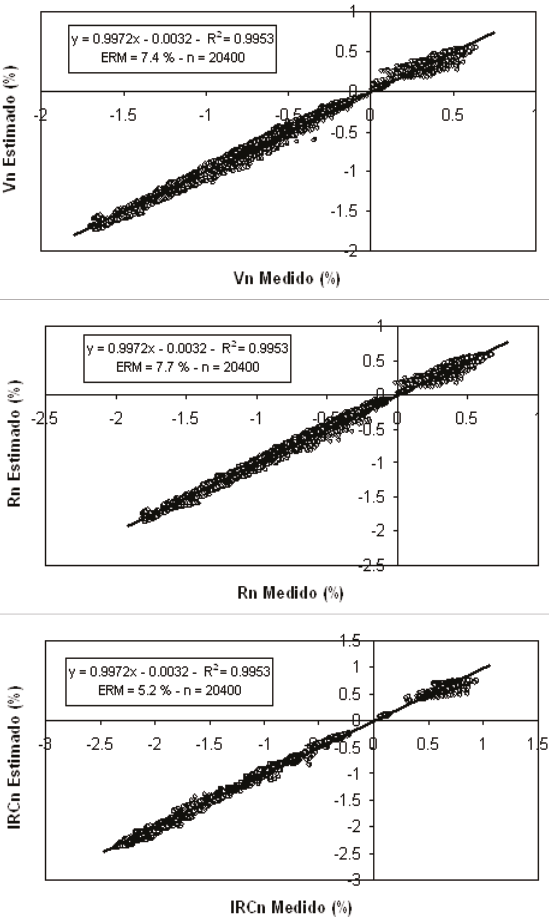
Figura 7: Ajuste del modelo multi-angular para los efectos de los ángulos cenitales de visión e iluminación para todas las especies analizadas, incluyendo los suelos.
donde: med se refiere a medida, est a estimada y R a reflectancia de la banda del V, R e IRC.
Los resultados de la Figura 7 muestran que el modelo multi-angular de la reflectancia por efecto de los ángulos cenitales de iluminación y visión resulta en ajustes buenos para las 8 especies y suelos analizados, con errores relativos menores al 8%.
Los ajustes del modelo multi-angular fueron hechos sin considerar el ángulo de visión a 60º, por problemas de representatividad y de cercanía a los arreglos de plantas.
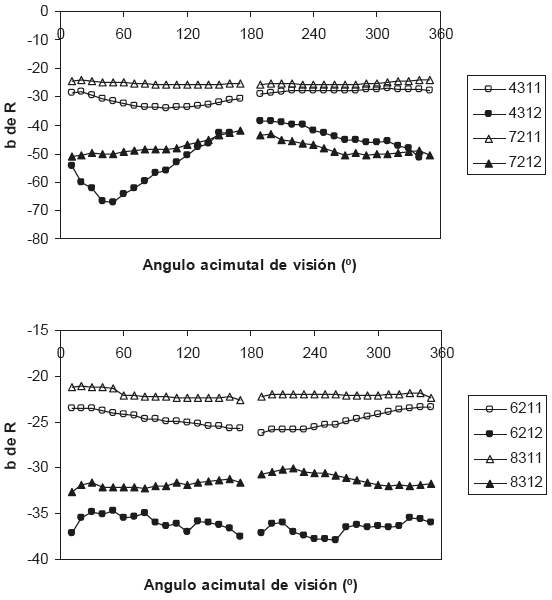
La Figura 8 muestra un gráfico polar para el parámetro b de la reflectancia del rojo para las especies con arquetipos contrastantes de plantas de Encino y Pino, con fondos de suelos claro y oscuro, cada uno en condición seca y húmeda, para tres densidades de arreglos de plantas.
Una forma de visualizar el efecto del fondo de la vegetación para especies contrastantes es el uso de un gráfico acimutal de b. La Figura 9 muestra esta situación para un suelo claro en condición seca y mojada para las especies Encino-Pino y Palo Dulce-Navajita. En esta figura se omitieron el acimut de 0º y 180º, dado que el radiómetro sombrea el área de visión. Del análisis de la Figura 9, es claro que los cambios en las propiedades ópticas (humedad, en este caso) del fondo de la vegetación pueden resultar en confusión en la discriminación de especies tan contrastantes como las mostradas, dejando en claro que la información multi-angular, sin una referencia común, no es suficiente para clasificar la vegetación natural.
CONCLUSIONES
- El enfoque de utilizar biomas con propiedades geométricas tipo, incluyendo los fondos de la vegetación (Myneni et al., 1997), parte de que se pueden obtener firmas espectrales multi-angulares características de éstos (Zhang et al., 2002a y b), para discriminarlos. Los resultados de este trabajo muestran que los cambios en las propiedades ópticas de los suelos de fondo pueden producir confusiones en las clasificaciones basadas en la información espectral multi-angular.
- Aunque la modelación presentada permite compactar en forma paramétrica los efectos del ángulo cenital de visión e iluminación, los efectos del ángulo acimutal relativo, además de los fondos y densidades de plantas, hacen difícil una discusión de la factibilidad de clasificar la vegetación natural usando información espectral multi-angular. Si se deja fijo el fondo y la cantidad de follaje de la vegetación, la discriminación de especies es factible. No obstante, esto, en condiciones operacionales la variación de los fondos de la vegetación, así como del follaje de la vegetación está garantizada, por lo que la utilización de hipótesis de invarianza (propiedades típicas) puede conducir a grandes errores.











 nova página do texto(beta)
nova página do texto(beta)