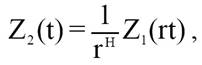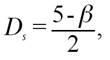Data

The original data were long-term records of monthly evaporation and precipitation. We acquired those data sets from 32 meteorological stations located within the territory of the Mexico's State of Zacatecas. Generalities for each station and series are presented in Table 1. Data were kindly provided by the Comisión Nacional del Agua, the national official institution in charge of registration of climatic and meteorological data in Mexico. For the analysis, we considered stations with at least 30 years of records, within a period from January 1943 to May 2006. In other words, we involved time series without missing data.

Table 1 Generalities of meteorological stations and time series. 

Linear Trends

Experimental series are often affected by non-stationarity and fractality (^{Ming, 2010}). Climate time series are in general non-stationary, and frequently present long-term trends. Among several methods to calculate the trend of a climatological time series, the simplest and broadly used one is the interpretation of the time series as a superposition of a linear trend (^{Tromel and Schonwiese, 2008}). This technique has been used by ^{Muhlbauer et al. (2009)}, ^{Guerreiro et al. (2010)}, ^{Nickl et al. (2010)}, Xie et al. (2010), and Xie et al. (2011). Therefore, linear trends were estimated through least squares linear regression analyses, taking into account the following simple model (^{Draper and Smith, 1966}).

(1)

The presence of a trend can make it more difficult to analyze other components of interest, such as the cycle or the seasonal (^{White and Granger, 2011}). Thus, the purpose of removing a trend is then simplifying the analysis of those other components (^{White and Granger, 2011}). In other words, removing the trend is an important issue in order to avoid that non-stationary behavior accompanying these data which will give spurious results (^{Peng et al., 1994}; ^{Hausdorff and Peng, 1996}).

Then, the series' precipitation and evaporation linear trends were removed following the Eq. 2:

(2)

where Ŷ _di is the detrended monthly precipitation or evaporation. When the above step is performed, the new time series is known as anomaly time series (i.e. monthly precipitation anomaly or monthly evaporation anomaly), which is the time series of deviations of a quantity from some mean (Wilks, 2011).

Fractal Analysis

Temporal variation of natural phenomena has been difficult to characterize and quantify. To solve these problems, fractal analysis was introduced by ^{Mandelbrot (1982)}. Time series can be characterized by a noninteger dimension (fractal dimension), when treated as random walks or self-affine profiles (^{Valdez-Cepeda et al., 2003}). Self-affine systems are often characterized by roughness, which is defined as the fluctuation of the height over a length scale (^{Moreira et al., 1994}). For self-affine profiles, the roughness scales with the linear size of the surface by an exponent called the roughness or Hurst exponent (^{Valdez-Cepeda et al., 2003}). However, this exponent gives limited information about the underlying distribution of height differences (^{Evertsz and Berkner, 1995}). There is the fact that the Hurst exponent, as well as the fractal dimension, measures how far a fractal curve is from any smooth function which one uses to approximate it (^{Moreira et al., 1994}). There are a lot of approaches to estimate fractal dimension for self-affine profiles, but we only used the power spectrum technique, because it is sensitive and a good exploratory tool for real data (^{Weber and Talkner, 2001}).

Power spectrum approach. Self-affine fractals are generally treated quantitatively using spectral techniques. The power spectrum variation P(f) with frequency f appears to follow a power law (^{Turcotte, 1992}):

(3)

The power spectrum P(f) is defined as the square of the magnitude of the Fourier transform of the monthly precipitation anomaly data. Denoting anomaly data as a function of time by Z(t), we have

(4)

where t₀ and t₁ are the limits oftime over which the series extend. Regarding such precipitation or evaporation anomalies record, which is sampled at discrete time intervals, we should use the discrete version of Eq. 4:

(5)

The next step is to obtain a relationship between the power b and the fractal dimension (D). By considering two time series Z₁(t) and Z₂(t) separated by the distance r, and related by

(6)

it can be observed that Z₁(t) has the same statistical properties as Z₂(t), and since Z₂ is a properly rescaled version of Z₁, their power spectral densities must also It follows that be properly scaled. Thus, we can write

(7)

It follows that.

(8)

(9)

and

(10)

where D_s is the fractal dimension estimated from the power spectrum and H is the Hurst exponent. The Hurst exponent provides a measure for long-term memory and fractality of a time series; it quantifies the relative tendency of a time series to either regress to a long-term mean value in certain direction.

Since the periodogram is a poor estimate of the power spectrum because the estimate of power at any frequency is very noisy, with the amplitude of the noise being proportional to the spectral power, we followed the strategy proposed by ^{Valdez-Cepeda et al. (2007)}, that is, we rather use the Welch's method of averaging periodograms in order to obtain 50 regular logarithmic intervals of the two records (complete series and partial series); in addition, we used the 'running sum' transformation to shift, by a factor of + 2, the slope, and thereby the Hurst exponent and the D_s because data trace had a slope between -1 and 1 on the log-log plot.

In practice, with the aim of obtaining an estimate of the fractal dimension D_s, one calculates the power spectrum P(f) (where f = 2π/l, f is the wave-number, and l is the wavelength), and plots the logarithm of P(f) versus the logarithms off If the profile is self-affine, this plot should follow a straight line with a negative slope -β.

Correlation

In addition, in order to find possible bivariate associations between geographical coordinates of the stations and the estimated self-affinity statistics, as well as trends in Zacatecas territory, correlation coefficients were estimated. Pearson's correlation coefficient (r), sometimes also called the cross-correlation coefficient, is a quantity that gives the quality of a least squares fitting to the original data. This value allowed the authors to analyze the relationship among self-affinity statistics of the monthly evaporation and precipitation anomaly time series, and geographic coordinates of the stations.

(11)

where X _i is the geographic coordinate latitude or longitude, and Y _di. is the monthly precipitation or evaporation anomaly.

Evaporation Anomaly Time Series

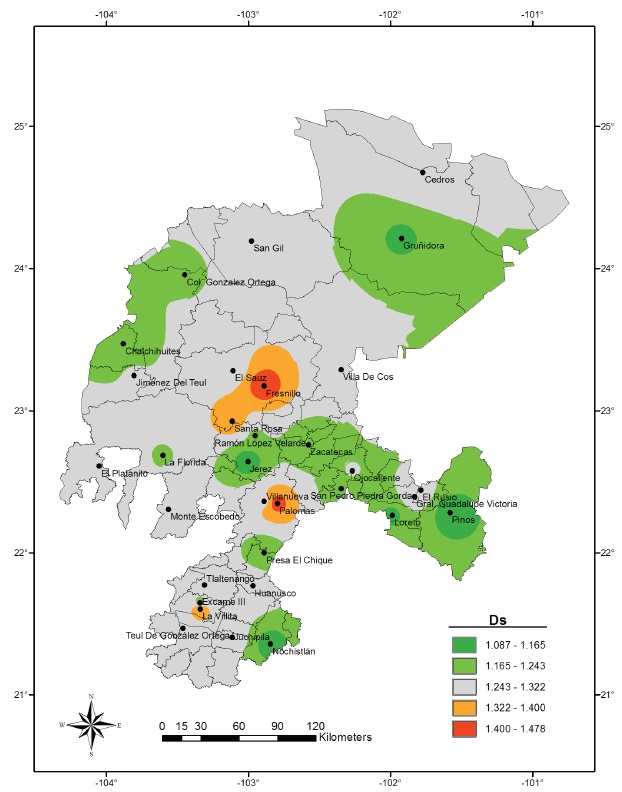
Most of the spectral fractal dimension (D_s) values varied from 1.087 to 1.478, and H values changed from 0.521 to 0.913 (Table 2); consequently, the behavior of estimated D_s values throughout Zacatecas State territory is very irregular (Figure 1), although noise in most of the evaporation anomaly time series tends to have persistent (long-term memory) behavior. Notably, most of the D_s values fall in the 1.243-1.322 range, and they represent an area that may be covering almost 62.60% of the State area (Figure 1). On the other hand, time series with D_s values in the range of 1.4-1.478 represent only 0.67% of the State area. These results indicate most of the monthly evaporation anomaly time series showed long-term positive autocorrelation, which means that a high value in these series will probably be followed by another high value. In addition, a few monthly evaporation anomaly series (those with D_s near to 1.5) tend to have a behavior like the Brownian movement or random walk.

Figure 1 Evaporation time series anomalies fractal dimension (Ds) through Zacatecas State territory. 

Precipitation Anomaly Time Series

Spectral fractal dimension (D_s) values varied from 1.411 to 1.791, and H values changed from 0.209 to 0.589 with a mean of 0.47. Most of the D_s values are in the range of 1.486 to 1.562; so their corresponding area in the map could be covering 49.08% of the State area (Figure 2). In addition, a time series (El Sauz) showed D_s ≈ 1.5. Hence noise in that monthly precipitation anomaly time series tend to be like the Brownian movement or random walk. Results for these series suggest that autocorrelations at small time lags can be positive or negative, but where the absolute values of the autocorrelations decay exponentially quickly to zero.

Figure 2 Precipitation time series anomalies fractal dimension (Ds) through Zacatecas State territory. 

On the other hand, high D_s values are in the range of 1.638 to 1.796. However, they may represent as much as 0.16% of the State area. Therefore, noise in the corresponding monthly precipitation anomaly series tends to have anti-persistent (short-term memory) behavior. As a consequence, prediction of these time series values is not an easy task since a single high value will probably be followed by a low value or vice versa.

Yet oddly enough, there is a recent report (^{Velásquez-Valle et al., 2013}) about the H spatial variability of the daily rainfall series for almost all the same stations considered by us. ^{Velásquez-Valle et al. (2013)} presented a map and a figure showing a close positive relationship (r = 0.57) between H and Longitude (westwards). By carefully looking that map, anybody may be able to identify that H value diminishes from Northeast to Southwest and from Northwest to Southeast in the upper half of the territory (the driest); in such a map, H values also diminishes from Southwest to Northeast in the lower half of the State. Thus, it might seem eerie but our results partially match those of the map from these authors, although used rainfall scales were different (monthly versus daily). In the present case, Ds values appear to decrease toward the Northwest and Northeast, in the upper half of the State, and toward small areas in the Southwest, South and Southeast in the lower half of the territory (Figure 2). It is worth pointing out that both maps (Figures 1 and ²) were developed using a digital elevation model in order to correct a potential orographic influence.

Correlation Analysis

Monthly evaporation or precipitation anomaly time series self-affinity statistics and the stations' geographic coordinates were used in order to estimate correlation coefficients. Results can be appreciated in Tables 3 and ⁴. High correlations between fractal statistics mean a great interdependence, whereas these significant correlations between geographical coordinates and central tendency or dispersion statistics suggest the strong influence of orography on the precipitation case.

Table 3 Correlation matrix among geographic coordinates and fractal statistics for monthly evaporation anomaly time series at Zacatecas State. 

^†Correlations are significant at P ≤ 0.05; n = 32; Ds = fractal dimension; H = Hurst exponent; SD standard deviation.

Table 4 Correlation matrix among geographic coordinates and fractal statistics for monthly precipitation anomaly time series at Zacatecas State. 

^†Correlations are significant at P ≤ 0.05; n = 32; Ds = fractal dimension; H = Hurst exponent; SD standard deviation.

There, significant correlations between each fractal statistic and latitude were estimated; for instance, a significant negative correlation (r = -0.41) between Ds values for the precipitation anomaly time series and latitude. In addition, significant positive correlations (r = 0.41) between H and P values of the precipitation anomaly time series and latitude were evidenced. The present findings strongly suggest that Ds values of the monthly precipitation anomaly decrease as latitude increase, and H and P values of the monthly precipitation anomaly increase as latitude does within Zacatecas State territory. In order to test such possible associations, linear relationships were estimated. Results showed clearly that the model was significant (P = 0.019) for monthly precipitation anomalies Ds against latitude, as can be appreciated in Figure 3. Thus, such results are compelling evidence that monthly precipitation anomalies behavior may be more regular toward North of Zacatecas State territory, that is, toward driest areas.

Figure 3 Linear model and Pearson correlation between geographic latitude and fractal dimension (Ds = 2.4354 - 0.04 Latitude; P = 0.0191; R² = 0.1699) for Zacatecas State monthly precipitation anomaly time series. 

Future research to gain knowledge about the behavior of the monthly evaporation and precipitation time series for each station (punctual) or area should take into account their fractal level and their possible association with periodic phenomena, such as the sun cycle and El Niño Southern Oscillation. This might be possible when using other techniques, such as wavelet cross spectrum and wavelet coherency analyses (^{Maraun and Kurths, 2004}; ^{Hartmann et al., 2008}), among others.