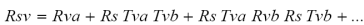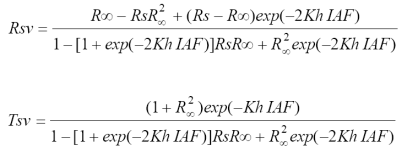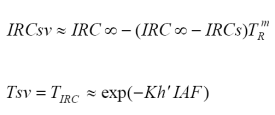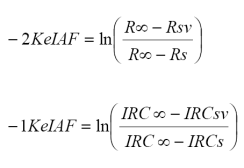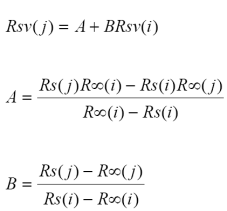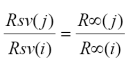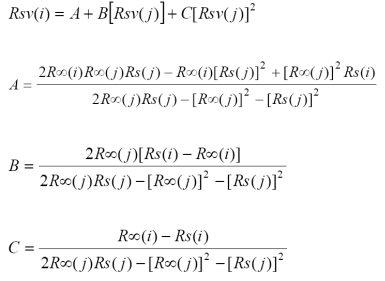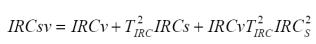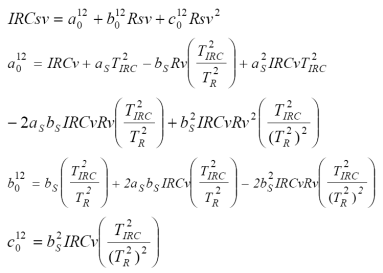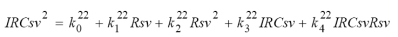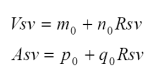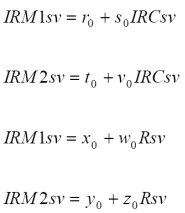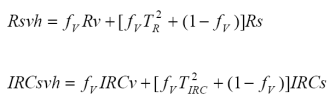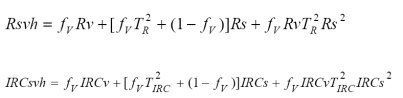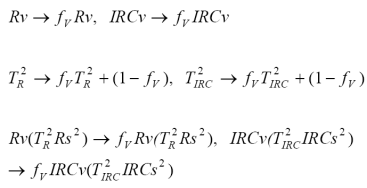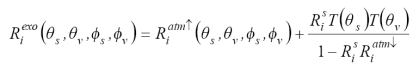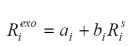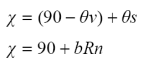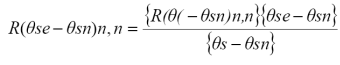Introducción
Los índices de vegetación (IV) espectrales han sido utilizados en el campo de los sensores remotos desde los inicios de esta tecnología como una forma indirecta de estimar variables biofísicas de la vegetación (índice de área foliar o IAF y cobertura de la vegetación o fv, principalmente). Estos índices con base en datos captados por sensores remotos explotan el alto contraste entre la banda del rojo (R) e infrarrojo cercano (IRC) de la vegetación (Tucker, 1979), para caracterizarla y diferenciarla de otros objetos terrestres; esto fundamentalmente con bases empíricas, pero con sustento biofísico genérico.
Los valores de IV basados en datos espectrales son función de factores internos: propiedades ópticas de las hojas, arquitectura de los fitoelementos y suelo o sustrato (fondo) principalmente. Adicionalmente influyen factores externos, como la condición de la atmósfera y la geometría sol-sensor. El efecto combinado de los factores internos y externos en las estimaciones de IV han sido analizados por varios autores (Baret y Guyot, 1991; Jackson y Huete, 1991; Myneni y Asrar, 1994; Bannari et al., 1995). La optimización de los IV para efectos externos combinados ha sido explorada con poco éxito (Chehbouni et al., 1994; Liu y Huete, 1995; Verstraete y Pinty; 1996; Steven, 1998; Gao et al., 2002). Paz et al. (2007) han planteado un esquema general para su análisis, mostrando que muchos de ellos son incompatibles con la teoría radiativa y la evidencia experimental.
Este trabajo analiza las bases teóricas de los IV al generalizar la propuesta de Paz et al. (2007) y establece el marco teórico-conceptual para revisar si los índices son congruentes con la teoría de la transferencia radiativa en la vegetación (Ross, 1981). Los desarrollos que se muestran parten del efecto del suelo (fondo de la vegetación) y después se enfocan en los problemas atmosféricos. Finalmente se discute el caso de la geometría sol-sensor. En todos los análisis se mantiene una perspectiva global; es decir, de efectos combinados suelo, atmósfera y geometría sol-sensor.
Es importante enfatizar, que el punto de discusión de este trabajo no es cuestionar que la gran mayoría de los IV publicados en el literatura no tienen relaciones estadísticas significativas con variables biofísicas, dado el uso de las bandas del rojo y del infrarrojo cercano o bandas relacionadas con éstas, sino la generación de un marco general de análisis de los IV para entender sus alcances y limitaciones, y poder hacer los análisis interoperables cuando se usan distintos IV, además de definir los requerimientos teóricos y experimentales, para el diseño de índices de vegetación generales. Los argumentos teóricos mostrados han sido planteados usando múltiples simplificaciones para enfatizar patrones, que no son diferentes de los generados usando enfoques más complejos dada la ecuación tridimensional de transferencia radiativa en la vegetación, permitiendo de esta manera discutir sus implicaciones en un esquema matemático relativamente simple.
Teoría de transferencia radiativa en el sistema suelo-vegetación
Se utiliza en lo siguiente la aproximación de medio "turbio" para analizar la mezcla suelo-vegetación. Se parte del supuesto que este medio turbio se compone de elementos diferenciales y fitoelementos distribuidos aleatoriamente en forma infinitamente horizontal (sin efecto de borde), continua y homogénea, sin auto-sombreado.
Transferencia Radiativa
De acuerdo a la ley de conservación de la energía: R+T+A=1, donde R es la reflectancia, T la transmitancia y A la absortancia. En adelante, se usa la reflectancia genérica R para referirnos a cualquier banda espectral y también para la banda del rojo, aclarando cuando esto suceda. Bajo la perspectiva de un medio turbio, se puede analizar el patrón de reflectancias de la mezcla suelo-vegetación al usar el método aditivo (Cooper et al, 1982). Primero es conveniente analizar los dos casos extremos de esta mezcla:
-
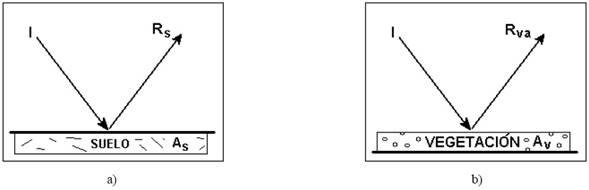
Suelo desnudo (antes de la siembra o emergencia de vegetación). En la Figura 1a se muestra el balance de energía que establece que Rs+As=1, la s se refiere a suelo, el cual se supone como un medio semi-infinito (absorbe todo lo que se transmite). La irradianza I se supone como unitaria en todas las descripciones siguientes.
Vegetación densa (cobertura total del suelo). El balance está dado por Rva+Av=1, v significa vegetación y a denota una trayectoria de reflectancia que sale de la parte superior del follaje (Figura 1b). La transmitancia del follaje se consideró nula (medio ópticamente denso o infinito), por lo que la reflectancia de este medio también se le denomina como de infinito (R( = Rva).
Los escenarios anteriores son los correspondientes a un solo medio (sin interacción) y sirven para definir los extremos de la mezcla suelo-vegetación. Para el caso general de la interacción de la vegetación y el suelo (medio turbio), la Figura 2 muestra las trayectorias de la reflectancia en este medio, donde la letra b se refiere a las trayectorias que llegan al follaje desde la parte de abajo. Esto es necesario para diferenciar la transmitancia del follaje en función del haz y el envés de las hojas. La absortancia de las hojas se consideró igual para las dos trayectorias y no tiene mayor repercusión en el análisis, puesto que el interés es en la reflectancia que emerge del medio combinado (lo que captan los sensores remotos).

Figura 2 Balance de energía para el caso la mezcla suelo-vegetación, donde I es la irradianza, R se refiere a reflectancias, T a transmitancias y A a absortancias; con s = suelo, v = vegetación, con direcciones a hacia arriba y b hacia abajo.
Las trayectorias de la reflectancia mostradas en la Figura 2 se describen como:
La irradianza del sol (I), trayectoria A, de arriba hacia abajo, es reflejada por el follaje (Rva), trayectoria B, y el resto es absorbido (Av) o transmitido (Tva) por el follaje, trayectoria C. Estas trayectorias representan interacciones simples de la mezcla suelo-vegetación.
La reflectancia de arriba hacia abajo que llega al suelo (Tva) una parte se refleja (Rs × Tva), trayectoria D, y el resto es absorbido por el suelo (As). La radianza reflejada por el suelo, trayectoria D, de abajo hacia arriba, una parte es reflejada por el envés del follaje hacia el suelo (Rs × Tva × Rvb), trayectoria F, y el resto es absorbido (Av) por el follaje o transmitido hacia fuera del mismo (Rs × Tva × Tvb), trayectoria E. Estas trayectorias representan interacciones múltiples de primer orden de la mezcla suelo-vegetación.
El proceso se repite para las interacciones múltiples de segundo, tercer, ..., n orden; hasta que la radianza se extingue por proceso de absorción en el follaje o en el suelo.
Si sumamos las radianzas normalizadas (reflectancias) hacia fuera del medio representando a la mezcla suelo-vegetación (Figura 2) se tiene que:
donde: Rsv se refiere a la reflectancia de la mezcla suelo-vegetación.
Simplificando términos, se tiene que:
Haciendo uso de la identidad de la serie matemática:
Se puede simplificar la Ecuación 1 como:
La Ecuación 4 representa el resultado clásico de la transferencia radiativa 1-D (unidimensional) (Chandrasekhar, 1960) y se interpreta como producto de dos componentes (Knyazikhin, 1998): el asociado a Rva, que es la reflectancia relacionada solo con la vegetación ("suelo negro"), que supone que los fotones que llegan al suelo son absorbidos totalmente por éste; y el asociado al segundo término de la derecha, que constituye al componente del "suelo", donde el numerador representa las contribuciones de primer orden de las interacciones múltiples (solo "ven" al suelo una vez) y el denominador a las contribuciones de orden mayor de las interacciones múltiples ("ven" más de una vez al suelo).
Usando rangos de valores extremos de las reflectancias del suelo y de las transmitancias y absortancias de la vegetación, el error al no considerar interacciones de orden mayor a uno, Ecuación 1, para las bandas del visible es menor al 1% y menor al 10 % para las bandas del infrarrojo cercano.
En la discusión previa se ha supuesto un régimen de reflectancia total (reflectancia directa más difusa) en los análisis. La solución de la Ecuación 4 de transferencia radiativa, bajo esta condición, es compleja y requiere de soluciones numéricas. Adicionalmente, esta ecuación está en función de la reflectancia y transmitancia únicamente de la vegetación (componentes va y vb), por lo que es conveniente replantearla en función de la reflectancia total accesible a los sensores remotos. Aunque es posible utilizar diferentes acercamientos para resolver la ecuación de transferencia radiativa, la solución de la ecuación del transporte de fotones en el follaje de la vegetación se puede aproximar usando el esquema de Kubelka y Munk (1931) para el caso de dos flujos difusos en un medio turbio compuesto por hojas horizontales (Figura 3).
Una solución del problema de transferencia radiativa definido en la Figura 3 es parametrizar los flujos de la radianza en función del albedo foliar ω (reflectancia más transmitancia foliar) para resolverla (Bonhomme y Varlet-Grancher, 1977; Goudriaan, 1977; Ross, 1981; Price y Bausch, 1995):
donde: Kh es el coeficiente de extinción para hojas negras horizontales. El término K se usa en forma genérica para definir un coeficiente de extinción.
Para el caso de las bandas visibles, RsR(, RsR2 ( y R 2 ( son despreciables, por lo que la Ecuación 5 se puede simplificar a:
donde: T es la transmitancia. La relación exponencial definida por la ley de Beer-Lambert para la transmitancia solo es válida para el caso de hojas negras.
En el caso de la banda del IRC, la simplificación es más complicada y puede aproximarse como:
donde: Kh' es función de Kh y ω (mKh' < 2Kh). El exponente m (< 2) está definido por la transmitancia foliar en el IRC. En el caso general, hojas no negras y no horizontales, usando simulaciones radiativas del modelo SAIL (Verhoef, 1984) y de evidencia experimental (Rodskjer, 1972; Huete, 1988), una aceptable aproximación es usar m = 1 (KIRC = 0.5 KR ), que considera en forma implícita las propiedades de hojas no negras.
En un suelo negro, las Ecuaciones 5, 6 y 7, usando la notación donde R se refiere a la banda del rojo, se reducen a (Paz et al., 2011):
Aunque los desarrollos de las aproximaciones de radianza difusa y hojas horizontales negras solo son aplicables a este caso, la estructura matemática definida en las Ecuaciones 6, 7 y 8 es válida para el caso de radianza total, y de hojas no horizontales y no negras; ya que la radianza total es una relación lineal de la radianza difusa y directa, ponderadas por las fracciones de éstas en la iluminación (Ross, 1981).
Invarianza Espectral
De las Ecuaciones 6 y 7, las relaciones 8 pueden ser puestas como:
donde: Ke es un coeficiente de extinción efectivo que considera la distribución angular y espacial de los fitoelementos de la vegetación (Ross, 1981); es decir, es un término puramente estructural de la vegetación, el cual es independiente de la longitud de onda (banda) espectral, lo mismo que el IAF. Así, los términos a la izquierda de las relaciones 9 son invariantes espectralmente; aunque el factor 2 o 1(m) depende de la región espectral en análisis.
Considerando una región espectral de manera separada, visible (VIS) o IRC, para un par de bandas, anchas o angostas, se pueden emplear las relaciones 9 para cada banda e igualarlas en los términos estructurales (IAF y Ke), dando como resultado (R puede ser cualquier banda del VIS o del IRC):
La Ecuación 10 implica un patrón lineal entre un par de bandas espectrales de la misma región espectral, donde la banda Rsv(j) (con suelo Rs(j)) es sustituida por Rsv(i) (con suelo Rs(i)), usando una transformación lineal con las constantes A y B. Esto implica que, dentro de regiones espectrales radiativamente similares (dejando fijo todo lo demás), una banda espectral por sí misma no tiene nada de particular y se puede sustituir por cualquier otra.
Para relacionar la escala de las hojas con la del follaje de la vegetación, es conveniente establecer una función entre las reflectancias en el infinito y el albedo foliar. La reflectancia en el infinito para hojas no horizontales y no negras, puede aproximarse razonablemente de la siguiente manera (Goudriaan y van Laar, 1994):
donde: K es un coeficiente de extinción (efectivo), dir es radianza directa, dif es radianza difusa, n es hojas no negras y h es hojas con distribución angular horizontal.
Goudriaan (1977) y Ross (1981) propusieron una serie de simplificaciones para estimar la reflectancia en el infinito para hojas horizontales. Así, para hojas horizontales no negras y bi-lambertianas (reflectancia igual a transmitancia), la reflectancia en el infinito está dada por:
Usando la relación 12 en las relaciones 10, por región espectral, la relación entre un par de bandas puede ser puesta en función de solo el albedo foliar de estas bandas (y las reflectancias de los suelos), definiendo una relación espectral invariante; es decir, una transformación que hace que la relación (ponderada por los albedos foliares y reflectancias del suelo) entre las bandas sea constante (caso general). Esto queda más claro si analizamos el caso del "suelo negro".
Haciendo Rs(i) y Rs(j) igual a cero en la relación 10, se tiene:
o, usando las relaciones 11 y 12:
La relación 14, suelo negro, implica que las diferencias entre un par de bandas (todas las bandas, por generalización) de una región espectral radiativamente similar son producto solamente de las diferencias entre sus albedos foliares (o reflectancias en el infinito) y una banda, ancha o angosta, se puede transformar en cualquier otra cuando se conoce el albedo foliar. Esto es válido para todas las condiciones de crecimiento de la vegetación (todos los IAF, analizando las relaciones invariantes entre bandas para cada IAF en forma independiente).
Para el caso de la relación entre una banda del VIS, Rsv(i), y una del IRC, Rsv(j), al usar el mismo procedimiento discutido anteriormente se puede establecer que:
y en forma alternativa:
Saturación de las Bandas Espectrales
En el desarrollo de IVs empíricos se ha discutido cual banda espectral es la que se satura (no cambia de valor) menos rápido, para usarla como una banda de referencia o estándar de comparación. Para entender esta problemática, es conveniente analizar las firmas espectrales típicas de hojas de cultivos agrícolas (Figura 4).
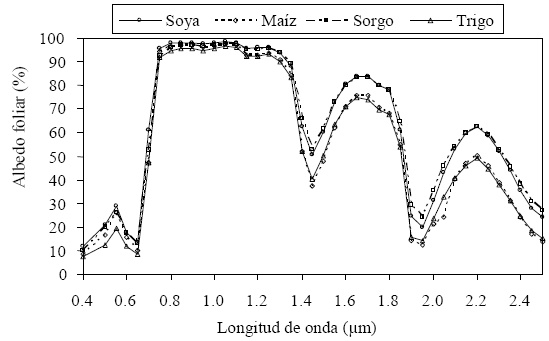
Figura 4 Firmas espectrales típicas de hojas de cultivos agrícolas (adaptada de Gausman et al.,1973).
Dejando fija la geometría y propiedades ópticas del medio, entre mayor sea la reflectancia o albedo foliar de las hojas menor será la saturación y viceversa (Ross, 1981). La banda del R es generalmente la de menor reflectancia (debido a la absorción por pigmentos foliares) y es la que más rápido se satura (Figura 4). La banda del IRC es la de mayor reflectancia o albedo foliar (dada la estructura del mesófilo esponjoso foliar). Esto establece un criterio biofísico sólido sobre la discusión de cuales bandas son mejores para analizar la vegetación. Las bandas del R e IRC tienen la característica de ser contrarias en su saturación, por lo cual son usadas en forma conjunta para desmezclar las señales y definir índices de vegetación óptimos. Cualquier otra banda que se seleccione no cumple estos criterios y no brinda información adicional a la que se puede extraer del espacio R-IRC.
Usando el modelo radiativo 1-D SAIL (Verhoef, 1984), en la Figura 5 se muestra la variación de las reflectancias en las bandas del sensor ETM+ del satélite LANDSAT 7 (azul o A, centrada en 480nm; verde o V, centrada en 570nm; R centrada en 660nm; IRC centrada en 840nm; infrarrojo medio 1 o IRM1 centrada en 1650nm; infrarrojo medio 2 o IRM2 centrada en 2200nm), en relación al IAF (caso de suelo negro). A continuación la discusión estará en función de las bandas del sensor ETM+ como referencia.

Figura 5 Patrones de saturación de las bandas espectrales del sensor ETM+. A = azul; V = verde; R = rojo
Las bandas del espectro electromagnético visible o VIS (A, V y R) se saturan (no cambian de valor) a partir de valores de IAF entre 2 y 3 (caso del suelo negro) (Figura 5). Las bandas del infrarrojo medio (IRM1 e IRM2) muestran un patrón de saturación similar, aunque para valores de IAF mayores.
Curvas Espectrales iso-IAF y sus Patrones Dinámicos
En la Figura 6 se muestra el patrón temporal de crecimiento de un cultivo de maíz en el espacio espectral R e IRC, representado por curvas de igual IAF (iso-IAF), misma cantidad de vegetación y suelos ópticamente diferentes, el cual se generó usando seis tipos de suelos (S2, S5, S7, S9, S11 y S12; del más oscuro al más claro). Paz et al. (2005) detallan las simulaciones radiativas mostradas en la Figura 6.
El análisis de la Figura 6 define varios patrones importantes para entender el comportamiento de la reflectancia y de los IV durante el desarrollo de los cultivos:
Si se unen los valores de igual IAF (iso-IAF) correspondientes a cada curva de igual suelo (iso-Suelo), se obtiene un patrón cuasi-lineal. Así, el estado de crecimiento de un cultivo (IAF) se refleja en una línea recta, independientemente del tipo de suelo de fondo en el cultivo. Este patrón ha sido verificado experimentalmente (Huete et al., 1985; Price, 1992 con datos de Huete y Jackson, 1987; Baush, 1993; Gilabert et al., 2002; Meza Diaz y Blackburn, 2003; Romero-Sánchez et al., 2009; Odi-Lara et al., 2010) y por modelos de transferencia radiativa (Richardson y Wiegand; 1991, Baret y Guyot, 1991; Qi et al., 1994; Yoshioka et al., 2000; Gao et al., 2000).
La pendiente (b0 ) e intersección (a0 ) de las líneas rectas de iso-IAF varían con el valor del IAF. La inclinación (pendiente) de las rectas de iso-IAF parte desde una pendiente igual a la de la línea del suelo (IAF = 0) y aumenta, en el sentido contrario a las manecillas del reloj, hasta alcanzar un ángulo de 90°. Esta última condición corresponde al caso de saturación de la reflectancia de la banda del R, representada en la Figura 6 como los valores de reflectancia arriba del ápice del "sombrero de tres picos" (IAF > 5). Los patrones de los espacios espectrales IRC-VIS son similares para todas las bandas del espectro visible, dado que hay una relación lineal entre estas bandas.
Todas las curvas de iso-Suelo convergen al mismo punto de saturación de las bandas visibles. En realidad la convergencia es hacia una línea recta (ápice en la Figura 6), ya que cuando una banda visible se satura, el IRC no lo hace y sigue creciendo hasta su propio punto de saturación. El punto de saturación, llamado también de reflectancia infinita o de medio denso, es función de las propiedades ópticas de las hojas y de su distribución angular.
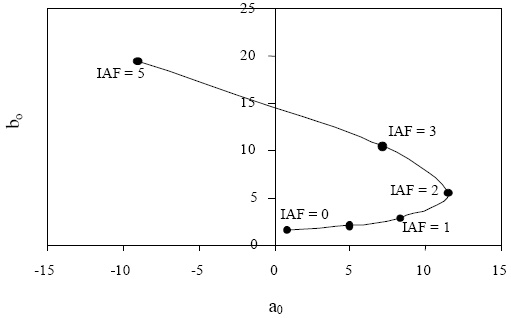
En la Figura 7 se muestra la relación entre los parámetros a0 y b0 de las líneas rectas iso-IAF, para el ciclo de crecimiento del cultivo que va desde el suelo desnudo hasta la condición de cubrimiento completo del suelo por la vegetación. Se observa también que en la etapa inicial hay un patrón de comportamiento tipo exponencial, hasta un punto donde la banda R se satura (aparentemente). Después del punto de saturación aparente de la banda R, el patrón es de tipo lineal. El punto inicial de la curva a0 -b0 representa el caso de suelo desnudo (a0 = as y b0 = bs ). El punto donde a0 alcanza su valor máximo (punto de transición del patrón exponencial al lineal), representa el término de la fase de crecimiento exponencial e inicio de la fase lineal de la etapa de crecimiento vegetativo. El punto final del patrón lineal de la curva a0-b0 representa la situación donde la banda del IRC se puede o no saturar, lo cual ocurre cuando el IAF alcanza su valor máximo.
Curvas Espectrales iso- IAF en el Espacio R-IRC
Al usar solo las interacciones hasta primer orden (Huete, 1987) de la serie definida en (2) o haciendo una expansión de Taylor de la relación 4 (Yoshioka et al., 2000), suponiendo Rva = Rvb y usando (Tv)2 = TvaTvb, para las bandas del rojo y del infrarrojo cercano tenemos:
La línea del suelo (Figura 6) está definida por:
Poniendo las relaciones 17 en función de Rs e IRCs y substituyéndolas en la relación 18, después de manipulación algebraica, tenemos (Yoshioka et al., 2000):
donde: el superíndice 11 se usó para denotar interacciones de primer orden en la banda del R e IRC, respectivamente.
Una formulación similar a las relaciones 19 ha sido desarrollada por Xia (1994) y Price y Bausch (1995), pero usando las relaciones 5.
En el caso de las bandas visibles, la relación 17 tiene un error muy pequeño (generalmente menor al 1%), pero para el caso del IRC y un suelo muy claro, el error está alrededor del 10%. Price y Bausch (1995) realizaron un análisis teórico-empírico de la aproximación (17), formulada en términos de las relaciones 5.
Para aproximar en forma más precisa el caso de la banda del IRC, se puede considerar el caso de interacciones hasta de orden 2:
Siguiendo un procedimiento similar al caso de las interacciones de orden uno, se puede definir una curva espectral iso-IAF como:
Las relaciones entre a0 y b0 de las aproximaciones de segundo y primer orden están dadas:
Las relaciones 19 y 21 se reducen a aS y bS de la línea del suelo para el caso de suelo desnudo (IAF = 0, Rv = IRCv = 0, TR = TIRC = 1). Ahora bien, usando las relaciones 8 para poner las curvas espectrales iso-IAF (19) y (21) en función de las reflectancias en el infinito, en el caso de una vegetación ópticamente densa (IAF = ?, TR = TIRC = 0), las curvas iso-IAF degeneran en un punto (reflectancias en el infinito), tal como se muestra en la Figura 6. La ventaja de formular las relaciones 19 o 21 en función de las reflectancias en el infinito es que estos valores son accesibles del espacio espectral del R-IRC (Figura 6).
El caso de interacciones de orden dos para las bandas del R e IRC; aunque innecesario para el caso de las bandas del visible, establece una relación tipo polinomio de segundo grado con interacciones:
Un punto muy importante para enfatizar es que si las curvas iso-IAF son lineales, con interacciones de primer orden del R e IRC, entonces los modelos de mayores interacciones se ajustan estadísticamente igual o mejor a los datos experimentales, dado que un polinomio de mayor orden aproxima siempre a uno de menor orden (la línea recta es un polinomio de orden 1); aunque las constantes asociadas a los términos de mayor orden son despreciables si la relación es lineal. No obstante lo anterior, para el caso de datos experimentales con dispersión en relación a la línea recta, los ajustes de polinomios de orden mayor a uno generan inestabilidad numérica en los patrones de sus parámetros que enmascaran los reales (Romero-Sánchez et al., 2009).
Curvas Espectrales iso-IAF en otros Espacios
En el desarrollo analítico de las curvas espectrales iso-IAF se utilizó la simetría impuesta por la línea del suelo, relación 19; esto es, las curvas iso-IAF mantienen el patrón matemático de la línea del suelo. En el caso de las bandas del R e IRC, el patrón lineal de la curva del suelo se mantiene razonablemente lineal para el caso de suelos diferentes (Baret et al., 1983), por lo que los desarrollos mostrados anteriormente se pueden generalizar a nivel de zonas agrícolas más o menos uniformes. En el caso de bandas espectrales diferentes al R e IRC, las líneas del suelo tienen mayor dispersión y en algunos pares de bandas espectrales la relación es claramente no lineal y con mucha dispersión.
En los espacios espectrales del visible (R-A, R-V y V-A), las curvas del suelo son aproximadamente lineales (Gitelson et al., 2002; Paz et al., 2005) y están altamente correlacionadas (Clevers, 1999). La Figura 8 muestra simulaciones radiativas, mismo caso de la Figura 6, para el espacio V-R.
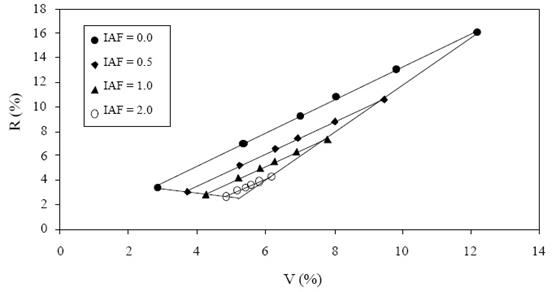
Figura 8 Espacio espectral V-R para las simulaciones del cultivo maíz. V = verde; IAF = índice de área foliar.
En la Figura 8 las curvas iso-IAF e iso-Suelo son lineales; aunque el contraste de las líneas iso-IAF es pequeño, por lo que resulta difícil de usar en aplicaciones satelitales (particularmente con resoluciones numéricas de 8 bits de la información espectral).
De la Figura 8, generalizándola al espacio del azul, se puede establecer que:
La parametrización de las relaciones 24 sigue los mismos pasos que en el caso de las relaciones 19 para interacciones de primer orden.
Ahora bien, para el caso de interacciones de primer y segundo orden, las relaciones 19 y 21 siguen siendo válidas al sustituir el R por A o V (una línea recta o un polinomio de segundo orden mantienen sus patrones matemáticos bajo una transformación lineal). Así, el uso de la banda del V o del A mantiene la estructura mostrada en las Figuras 6 y 7; donde su ventaja relativa es en relación a la rapidez de saturación de estas bandas (reflectancias en el infinito).
En el caso de los espacios espectrales del infrarrojo medio 1 o IRM1 (centrada en 1650 nm) e infrarrojo medio 2 o IRM2 (centrada en 2200 nm), en relación a las bandas del visible o entre ellas, las curvas del suelo generalmente no pueden ser aproximadas por patrones de curvas matemáticas simples, por lo que resulta sumamente difícil evaluar sus formas. No obstante lo anterior, las bandas del infrarrojo medio están altamente correlacionadas linealmente con las del visible (Kaufman et al., 1997; Karnieli et al., 2001; Jiang et al., 2008), por lo que pueden ser usadas en términos intercambiables. Al considerar un espacio espectral de un par de bandas, en la Figura 9 se muestra un ejemplo donde las curvas del suelo para el espacio del R-IRM1 y R-IRM2 fueron aproximadas por un polinomio, de tal manera que las simulaciones radiativas (misma situación que la Figura 6) muestran curvas iso-IAF con estos mismos patrones (simetría en relación a la línea del suelo).

Figura 9 Espacio espectral R-IRM1 (rojo - infrarrojo medio 1) y R-IRM2 (rojo - infrarrojo medio 2) para las simulaciones del cultivo de maíz. R = rojo.
La conservación del patrón matemático de la curva del suelo por las curvas iso-IAF es consecuencia de que la ecuación tridimensional de transferencia radiativa en la vegetación es una ecuación integro-diferencial lineal (Ross, 1981; Myneni et al., 1990; Myneni, 1991).
La Figura 10 muestra simulaciones radiativas para el espacio del IRM2-IRM1 e IRM1-IRC (mismo caso de la Figura 6), donde los patrones de las curvas iso-IAF son similares a los de la Figura 9. De los análisis de las Figuras 9 y 10 resulta claro que las curvas iso-IAF presentan patrones no lineales difíciles de parametrizar en forma razonablemente simple.
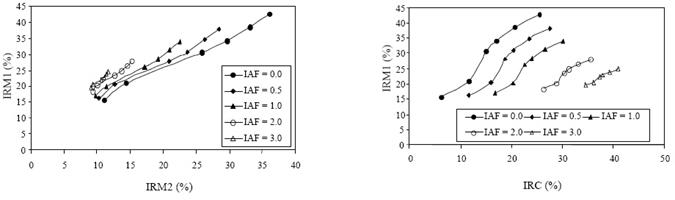
Figura 10 Espacio espectral IRM2-IRM1 (infrarrojo medio 2 - infrarrojo medio 1) e IRM1-IRC (infrarrojo medio 1 - infrarrojo cercano) para las simulaciones del cultivo de maíz.
En el mejor de los casos, la relación de las curvas del suelo (e iso-IAF) pueden ser aproximadas por un polinomio de segundo grado para el caso de una zona agrícola o zona de vegetación homogénea.
Considerando la situación de un predio agrícola o pixel de vegetación homogéneo, las reflectancias de los suelos (cambio de humedad, rugosidad o prácticas de labranza) en todos los espacios espectrales se pueden aproximar por relaciones lineales (dependiendo de la hipótesis de a qué región espectral pertenecen ambas reflectancias):
En relación a otros espacios espectrales diferentes del R-IRC es necesario enfatizar varios puntos:
El máximo contraste (separabilidad) entre las curvas iso-IAF se da entre las bandas donde el albedo foliar es máximo y mínimo (IRC y R). Esto es importante para las aplicaciones con base en sensores remotos en plataformas espaciales.
Las curvas del suelo introducen una simetría (mismos patrones matemáticos) en las curvas iso-IAF, de tal manera que el más simple es el patrón lineal definido en los espacios del VIS-IRC y entre las bandas del VIS. Así, usando el principio de parsimonia, la solución más simple para extraer información biofísica es el espacio del R-IRC (o del V-IRC o A-IRC).
El albedo foliar (reflectancia en nuestro caso), define las relaciones entre los espacios espectrales de la vegetación. En la discusión anterior se ha supuesto que el albedo foliar (propiedades ópticas de las hojas) y la arquitectura de las hojas (distribución angular y espacial) permanecen constantes durante la etapa vegetativa del crecimiento. Esta aproximación es razonablemente válida en la fase exponencial (IAF < 2) de los cultivos (Ranson et al., 1985); aún para el caso de cultivos bajo estrés nutrimental o hídrico (Duke y Guérif, 1998). Para el caso de IAF > 2, las propiedades ópticas y la arquitectura de las hojas generalmente cambia (Ranson et al., 1985; Duke y Guérif, 1998); aunque esto no invalida los desarrollos mostrados (patrones de a0-b0 de las curvas iso-IAF, ver Figura 6 y 7). Paz et al. (2007) y Casiano et al. (2012) muestran esta situación para el caso de experimentos con diferentes cultivos, validando el enfoque generalizado mostrado en la Figura 7.
Aun suponiendo que una banda espectral sea superior a otra para extracción biofísica, se ha demostrado teórica y experimentalmente (Huang et al., 2007), ver sección de invarianza espectral para una formulación alternativa, para el caso del problema del suelo negro, que con la información de los albedos foliares entre un par de bandas y con la reflectancia de una banda, es posible determinar la reflectancia de una banda desconocida. Así, los invariantes espectrales asociados a la ecuación de transferencia radiativa permiten estimar cualquier banda espectral a partir de una banda de referencia, conocidos los albedos foliares. Para el caso de las reflectancias, generalmente la relación entre pares de bandas es un polinomio de segundo grado (Huang et al., 2007), ver sección de invarianza espectral para una formulación alternativa.
Para el caso de un espacio espectral IRC-cualquier otra banda que no sea del VIS, la aproximación de interacciones de segundo orden se pueden generalizar a esa otra banda; aunque persiste el problema de la complejidad y dispersión de las curvas del suelo.
Curvas Espectrales iso- IAF para Medios Heterogéneos
En la sección anterior se utilizó la aproximación de un medio turbio (homogéneo) para el desarrollo de las curvas iso-IAF. En situaciones reales en la agricultura (o vegetación natural con algunas consideraciones), los cultivos tienen una dinámica que va desde el suelo desnudo hasta la cobertura máxima del suelo y son sembrados en patrones geométricos. La Figura 11 muestra el caso de un cultivo sembrado en surcos, donde al principio de la etapa de crecimiento se observa un patrón de plantas individuales, donde las plantas no se tocan entre sí (caso 3-D). Al avanzar el crecimiento, las plantas en un mismo surco se tocan entre sí y forman un cultivo en hileras o surcos (caso 2-D). Cuando las plantas de diferentes surcos se alcanzan entre sí, tenemos la situación de cobertura total del suelo (caso 1-D). Así la dinámica del crecimiento de un cultivo va desde un suelo desnudo (1-D), siguiendo una mezcla suelo vegetación con plantas individuales (3-D) hasta que las plantas dentro de un mismo surco se cubran entre sí (2-D), llegando hasta la cobertura total del suelo cuando las plantas de diferentes surcos se tocan (1-D). Esta dinámica de crecimiento requiere de una estrategia genérica de modelación que tome en cuenta, razonablemente, la complejidad geométrica de los cultivos en parcelas.
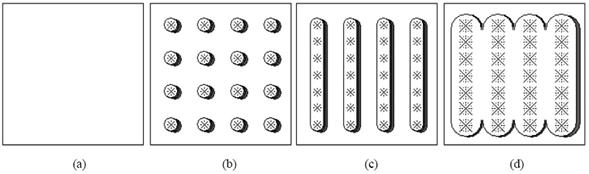
Figura 11 Geometría de la relación suelo - cultivo sembrado en surcos: (a) sin cultivo (suelo desnudo); (b) plantas individuales sin traslape; (c) plantas traslapadas en surcos; y, (d) vegetación densa traslapada.
Un esquema simplificado para modelar un medio heterogéneo es considerar el caso 2-D y analizarlo en un formato 1-D, donde el medio está compuesto de vegetación (mezcla suelo-vegetación) y suelo desnudo (entre hileras o surcos):
donde: la h se ha agregado para denotar medio heterogéneo, ƒv y ƒs son las fracciones (coberturas) de la mezcla suelo-vegetación (caso homogéneo) y suelo desnudo, respectivamente. En la relación 26, R se refiere a las reflectancias de cualquier banda espectral.
Para el caso de la aproximación de interacciones de primer orden, se puede sustituir las relaciones 17 en la Ecuación 26 (Yoshioka et al., 2000):
En forma similar, para el caso de interacciones de segundo orden tenemos que:
De las relaciones 27 y 28, la aproximación usada de un medio heterogéneo implica un cambio de valores:
Puesto que las relaciones 29 implican una transformación lineal del medio homogéneo ya discutido, las curvas iso-IAF mantienen los mismos patrones mostrados en las Figuras 6 y 7.
Es importante señalar que en las aproximaciones discutidas, medio homogéneo y heterogéneo, las variables utilizadas asociadas al medio analizado son diferentes al caso 3-D, por lo que deben considerarse como "radiativamente equivalentes" (Pinty et al., 2004). No obstante esto, los patrones de las curvas iso-IAF del caso 3-D son similares a los presentados (Gao et al., 2000).
Curvas Espectrales iso-IAF Bajo Efectos Atmosféricos
Para eliminar los efectos atmosféricos en las señales espectrales los métodos se agrupan en dos alternativas: directas e indirectas (Kaufman y Tanré, 1996). En los métodos directos se busca la corrección atmosférica directamente en las reflectancias espectrales y en los indirectos las correcciones son efectuadas sobre los índices de vegetación.
La corrección atmosférica indirecta de los índices de vegetación ha sido analizada con diferentes enfoques. Myneni y Asrar (1994) describen a detalle el efecto atmosférico sobre los índices de vegetación (IV) más comunes y concluyen que es importante su corrección, ya que la atmósfera (principalmente aerosoles) cambia el contraste entre la banda del R e IRC, la cual es usada en los IV. Así, los efectos atmosféricos dan como resultado que a medida que su intensidad es mayor, los índices muestran que la vegetación (fv o IAF, o biomasa) disminuye, como artefacto de los cambios atmosféricos (Figura 12a); aunque los patrones entre a0-b0 se mantienen, Figura 12b.
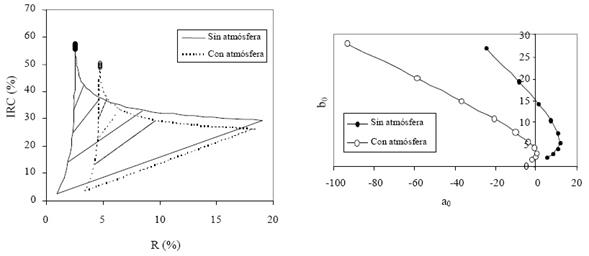
Figura 12 Patrones espectrales de la mezcla suelo-vegetación, con y sin atmósfera. R = rojo; IRC = infrarrojo cercano.
El efecto atmosférico se puede modelar, para una banda espectral i, por un sistema de capas en paralelo usando una aproximación de medio turbio semi-infinito unidimensional (Chandrasekhar, 1960; Vermote et al., 1997) como (reflectancias en proporciones):
donde:
Ri exo = Reflectancia exo atmosférica
Ri atm↑ = Reflectancia de trayectoria o reflectancia atmosférica hacia arriba.
Ri s = Reflectancia de la superficie terrestre
Ri atm↓ = Albedo esférico o reflectancia atmosférica hacia abajo.
T = Transmitancia atmosférica
θs = Ángulo cenital solar
θv = Ángulo cenital de visión del sensor
ϕs = Ángulo acimutal solar
ϕv = Ángulo acimutal de visión
Considerando solo interacciones hasta orden uno, la Ecuación 30 se puede simplificar:
La Ecuación 30 o 31 puede ser puesta, quitando los argumentos angulares, como:
La constante a es la radianza de trayectoria (efectiva) y b es una constante multiplicativa (efectiva) que considera la segunda parte del término de la derecha de la Ecuación 30 o 31.
Los efectos atmosféricos en las reflectancias se pueden aproximar en forma lineal (Steven, 1998). Así, la relación entre las reflectancias con atmósfera (letra a) con las reflectancias terrestres, para las bandas espectrales del R y del IRC, estará dada por:
donde: los parámetros a y b están definidos en función del modelo atmosférico y de aerosol usado, para una visibilidad atmosférica (espesor óptico de la atmósfera), ángulo cenital solar y altitud dada. En la Ecuación 33, R e IRC se refieren a los casos homogéneos y heterogéneos discutidos anteriormente. Así, al usar argumentos similares al caso del medio heterogéneo, las relaciones 33 implican que las curvas iso-IAF, mantienen sus patrones matemáticos bajo efectos atmosféricos (Yoshioka, 2004; Figura 12).
Efecto de la Geometría sol-sensor
Al igual que en los efectos atmosféricos, el efecto de la geometría sol-sensor (función de distribución bidirecccional de la reflectacia o BRDF por sus siglas en inglés) se puede corregir estandarizando las reflectancias a una geometría sol-sensor de referencia o directamente en los IV (Chehbouni et al., 1994). La corrección del efecto de la geometría sol-sensor en los IV ha sido aproximada bajo diferentes formatos para IV específicos (Huete et al., 1992; Chehbouni et al., 1994; Gao et al., 2002).
Aunque los modelos de la geometría sol-sensor son relativamente complejos y requieren de estimar varias constantes, este enfoque de estandarizar las reflectancias es genérico e independiente del IV particular a usar o analizar.
El modelo de la geometría sol-sensor de Bolaños et al. (2007), generalizado en Bolaños y Paz (2010) usa un solo parámetro:
donde: Rn representa una reflectancia, R e IRC, normalizada [multiplicada por cos(χ)] y χ es una variable angular de posición que reduce la complejidad de la geometría sol-sensor al usar simetrías angulares.
La ventaja del modelo de la relación 34 es que solo requiere un dato, por lo que la constante b se puede estimar de la reflectancia medida. La relación 34 permite estimar la reflectancia a nadir, para cualquier ángulo de visión. Para un ángulo de visión a nadir, el efecto atmosférico de la anisotropía de la mezcla suelo-vegetación es menor al 1% en relación al caso isotrópico (Thome et al., 1998).
Ahora bien, partiendo de la estandarización del ángulo de visión a un ángulo a nadir, para un ángulo cenital solar dado, el siguiente paso es estandarizar el ángulo cenital solar. Partiendo de que para cada día del año existe un ángulo cenital solar mínimo que es posible, θsn (se conoce para cada localización geográfica del centro de un píxel de una imagen satelital, para cualquier día del año), el modelo establece:
donde: Ps es una constante y n,n significa reflectancias normalizadas a nadir (R e IRC). La relación 35 solo asegura que R(θs - θsn)n,n = 0 cuando (θs - θsn) = 0.
Así, de la relación 35 se determina Rn,n a un ángulo estandarizado cualquiera (θse - θsn):
Al estandarizar la geometría sol-sensor (ángulo de visión y de iluminación solar), el análisis de los patrones de las curvas iso-IAF se hace independiente de este efecto, permitiendo un análisis generalizado de los efectos combinados de la geometría sol-sensor y cualquier otro efecto, como los analizados en este trabajo. En la perspectiva de que las transformaciones lineales no cambian los argumentos desarrollados en este trabajo, el modelo de la BRDF es simplemente una transformación lineal de las reflectancias por lo que no afecta los desarrollos.
Aunque los desarrollos presentados en este trabajo utilizan como referencia el caso de cultivos monoespecíficos, el marco teórico es aplicable al caso de policultivos o vegetación multiestrato (Sinoquet et al., 2000), ya que estos casos son transformaciones lineales del caso monoespecífico.
Conclusiones
En este trabajo se presentó una aproximación teórica, interacciones de primer y segundo orden, para la parametrización de las curvas iso-IAF (misma cantidad de área foliar por unidad de superficie) para medios homogéneos y heterogéneos. Asimismo, se planteó que el uso de bandas espectrales diferentes de las del R e IRC deja invariantes los patrones matemáticos de las curvas iso-IAF.
Se analizó el caso de los efectos atmosféricos y se concluyó que este efecto también deja invariantes los patrones matemáticos de las curvas iso-IAF.
Para el caso de los efectos de la geometría sol-sensor, se esbozó un modelo que permite estandarizar estos efectos, evitando así su consideración en las curvas iso-IAF.
En términos generales, el análisis de los índices de la vegetación o IV (así como su formulación correcta), debe basarse en los patrones mostrados en la Figura 6, así como en los de la Figura 7 (caso de interacciones de primer orden). Los IV que no reproduzcan los patrones señalados no son válidos como IV con bases teóricas y experimentales.











 nova página do texto(beta)
nova página do texto(beta)