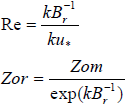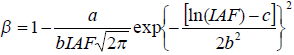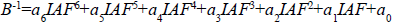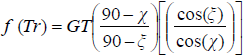Introducción
La disponibilidad de agua en el planeta es el principal factor para el crecimiento de la vegetación en alrededor de dos terceras partes de la superficie terrestre (Nemani et al., 2003). Esta disponibilidad es producto de los intercambios de energía y masa entre la superficie de la tierra y la atmósfera. Un proceso crítico en estos intercambios es la evapotranspiración (ET) (Sellers et al., 1996), ya que ocupa alrededor del 76% de la energía neta disponible (Chapin et al., 2002), la cual puede estar en forma de calor sensible o de energía radiante (Allen et al., 2006). En lo que concierne al calor sensible (H), se han desarrollado diferentes métodos para su aproximación, algunos requieren datos de la temperatura aerodinámica de la superficie (To), cuya medición es complicada, por lo que se dificulta su aplicación. En contraparte, Chehbouni et al. (1996), plantearon una propuesta que utiliza datos de temperatura radiativa de la superficie (Tr) en lugar de To. Este esquema facilita el cálculo de H, ya que la Tr puede ser obtenida con instrumentos de campo o con sensores remotos a bordo de satélites, a partir de mediciones en la región espectral del infrarrojo térmico (8-14 μm).
Las mediciones de Tr no solo arrojan información esencial para el cálculo H, sino también para el cálculo de la radiación neta (Rn), por lo que su modelación en forma simple y operativa es indispensable. Es importante considerar que la evidencia experimental indica que el valor de la Tr de un objeto en la superficie varía en función del ángulo de visión del sensor y del ángulo de incidencia de la fuente de iluminación, es decir, es dependiente de la geometría sol-sensor (Jackson et al., 1977; Kimes, 1980; Sobrino y Caselles, 1990; Lagourde et al., 1995). Se han desarrollado diferentes modelos para caracterizar Tr en función de la geometría sol-sensor (Kimes, 1983; Mathias et al, 1987; McGuire et al., 1989; Smith y Ballard, 2001), no obstante, son poco útiles en la práctica ya que dependen de un conjunto más o menos grande de parámetros.
Un modelo simple (dependiente de un solo parámetro) de la geometría sol-sensor fue desarrollado por Bolaños y Paz (2010) con aplicación a mediciones de reflectancia en cualquier banda espectral de onda corta. Los autores obtuvieron buenos ajustes del modelo, por lo que en el presente trabajo se evalúa su desempeño con mediciones radiativas de onda larga (temperatura radiativa). Así, este modelo presenta una aproximación a la función de distribución bidireccional de la Tr, que además tiene la ventaja de capturar de forma intrínseca la variación de las áreas de influencia o footprints de las mediciones, ya que de argumentos geométricos estos footprints son una función solamente del ángulo de visión y de la altura del sensor.
En este punto, vale la pena mencionar que la modelación del footprint ha cobrado gran importancia, en especial en estudios micrometeorológicos que abordan el problema del cierre del balance de energía (Masseroni et al., 2012). Como se verá más adelante, algunos autores han atribuido este problema a diferencias en los footprints de los componentes del balance de energía (radiación neta, calor sensible, calor latente y calor en el suelo), por lo que es necesario desarrollar esquemas que permitan re-escalar los footprints de estos componentes y obtener mediciones interoperables.
En propuestas como la de Chehbouni et al. (1996) para el cálculo del flujo de calor sensible, la Tr es el componente que captura la variabilidad espacial (footprint) de las mediciones, lo que confirma la importancia de modelar esta variable.
Con base en los elementos antes mencionados, se planteó como objetivo principal de este trabajo modelar la función de distribución bidireccional de la temperatura radiativa de superficies agrícolas, a partir del modelo uni-paramétrico introducido por Bolaños y Paz (2010), a fin de obtener elementos básicos que incidan en el cálculo de H y en la modelación del footprint asociado.
Parametrización del Flujo de Calor Sensible en Función de la Temperatura Radiativa
El flujo de calor sensible (H) sobre la vegetación está definido, para el caso de esquemas de una sola fuente (medios “turbios” en términos radiativos o de “gran hoja” para ET), por:
donde: ρ = densidad del aire (kg m-3), Cp = calor específico del aire a presión constante (J kg-1 K-1), Ta = temperatura del aire (K), To = temperatura aerodinámica de superficie (K) y Ra = resistencia aerodinámica de la superficie (s m-1).
Ra se estima con ecuaciones clásicas de correcciones de estabilidad por viento y temperatura (Brutsaert, 1982), donde pueden usarse las funciones de estabilidad de Paulson (1970), así como las parametrizaciones de la longitud de rugosidad (Zo) y altura del plano de desplazamiento cero (d) de Choudhury y Monteith (1988). La temperatura aerodinámica (To) no se mide directamente, sino que se obtiene de extrapolar el perfil logarítmico de la temperatura del aire a la longitud de rugosidad para el transporte de calor (Zoh), o de forma más precisa a d + Zoh (Norman y Becker, 1995). Debido a lo anterior, es difícil usar To en la parametrización de la relación (1). Por otro lado, el uso de Tr en lugar de To puede generar diferencias importantes en el cálculo de H en función de la condición de estabilidad de la atmósfera (Choudhury et al., 1986) o de las características estructurales de la vegetación (Chehbouni et al., 1996). Kustas et al. (1989) encontraron diferencias de hasta 10 °C entre ambas temperaturas. Para poder considerar el uso de Tr en la relación (1) Stewart et al. (1994) y Lhomme et al. (1997) han propuesto el uso de una resistencia de exceso (Re), para compensar las diferencias:
donde: Ψ define la geometría sol-sensor de las mediciones de Tr, por lo que Ψ = f(θv, φv, θs, φs) donde θv y φv son los ángulos cenital y acimutal de visión, respectivamente, en tanto que θs y φs son los ángulos cenital y acimutal de la iluminación solar; B-1 es un parámetro relacionado con la altura de rugosidad para el calor, k es la constante de von Karman y u* es la velocidad de fricción.
El parámetro kB-1 fue definido por Garrat y Hicks (1973):
donde: Zom = longitud de rugosidad para el momento. Matsushima (2005) revisó diferentes formulaciones para la relación To y Tr, diferenciando el uso de parámetros aerodinámicos de los radiativos, por lo que la resistencia en exceso al usar temperaturas radiativas debe establecerse, para evitar confusión, como:
donde: el subíndice r se refiere a mediciones de temperaturas radiativas.
La longitud de rugosidad en términos radiativos (Zor) depende de la geometría sol-sensor (Vining y Blad, 1992; Matsushima y Kondo, 1997). Para relacionar To y Tr se han utilizado tres enfoques: i) usar nuevas funciones de estabilidad o definir nuevo coeficiente de intercambio radiométrico/altura de rugosidad radiométrica (Sun y Mahrt, 1995); ii) usar la Re y parametrizarla empíricamente (Kustas et al., 1989) y iii) desarrollar una relación entre ambas temperaturas y parametrizarla empíricamente (Chehbouni et al., 1996; Troufleau et al., 1997). En el primer enfoque, el uso de la temperatura radiativa en la teoría de similaridad de Monin-Obukov no se aplica, por lo que es necesario realizar mediciones adicionales para hacer correcciones (Sun y Mahrt, 1995), lo que resulta poco práctico. Para el tercer caso, su planteamiento utiliza el parámetro β (Chehbouni et al., 1996):
Los parámetros B-1 y β son función de las características estructurales de la vegetación (índice de área foliar -IAF-, altura y distribución angular de los fitoelementos y sus dimensiones, principalmente), de las condiciones climáticas (estabilidad atmosférica y radiación solar), del nivel de estrés hídrico y humedad del suelo y de la geometría sol-sensor, generalmente representada solamente por θv (Lhomme et al., 2000; Mahrt y Vickers, 2004; Kustas et al., 2007; Boulet et al., 2012). Los resultados de mediciones y simulaciones han mostrado que el IAF es el mejor predictor de estos parámetros.
La formulación del parámetro β desarrollado por Boulet et al. (2012) está dada por:
donde: a, b y c son constantes empíricas.
La formulación del parámetro B-1 desarrollado por L homme et al. (2000) está dada por:
donde: a0, a2, …, a6 = constantes empíricas.
En las relaciones mostradas, las constantes empíricas muestran un fuerte nivel de dependencia de la geometría sol-sensor, más marcado en el caso de las constantes de B-1, por lo que es necesario separar estos efectos de medición y de iluminación, de los estructurales de la vegetación y clima, para el desarrollo de relaciones genéricas. El punto de cómo varia la geometría sol-sensor en las mediciones por la técnica de covarianza de vórtices se discute enseguida, poniendo en perspectiva la necesidad de modelar la función de distribución bidireccional de la temperatura radiativa (FDBT).
Balances de Energía y el Problema de Cierre
Las técnicas micrometeorológicas, en especial la de covarianza de vórtices, son de las pocas que miden los flujos de energía y masa en forma directa (Baldocchi et al., 1988; Verma, 1990). Empleando la formulación del balance de energía en una superficie, se puede establecer el cierre como:
donde: Rn es la radiación neta, λE es el flujo de calor latente, H es el flujo de calor sensible y G el flujo de calor de suelo, todos en Wm-2.
Los errores asociados al cierre de flujos de energía usando técnicas de EC oscilan entre el 10 y el 30% (Aubinet et al., 2000; Wilson et al., 2002), aunque pueden ser mayores en algunos casos, lo que cuestiona la utilidad de las mediciones de flujos turbulentos en forma sesgada, ya que el uso de la técnica EC está basada en hipótesis de que ciertas condiciones son satisfechas para su aplicación (por ejemplo homogeneidad horizontal, estado estacionario, advección cero, etc.) (Gökede et al., 2004).
Dejando aparte los problemas de homogeneidad de la superficie, coordenadas de referencia, correcciones y control de calidad de datos e instrumentos, se ha argumentado que la falta de cierre del balance de energía se debe a diferencias en las áreas de influencia (footprints en inglés) de las mediciones, a condiciones de estabilidad de la atmósfera (Massman y Lee, 2002), así como a problemas de advección horizontal/vertical (Aubinet et al., 2000; Oncley et al., 2007).
Los flujos de vapor de agua y calor (λE, H), numerador del cierre en la relación (8), tienen footprints que varían dinámicamente. La orientación y dimensión de estos footprints dependen de la altura del sensor, la longitud de rugosidad de la superficie, la velocidad y dirección del viento y la estabilidad atmosférica (Leclerc y Thurtell, 1990; Schmid, 2002) (Figura 1).
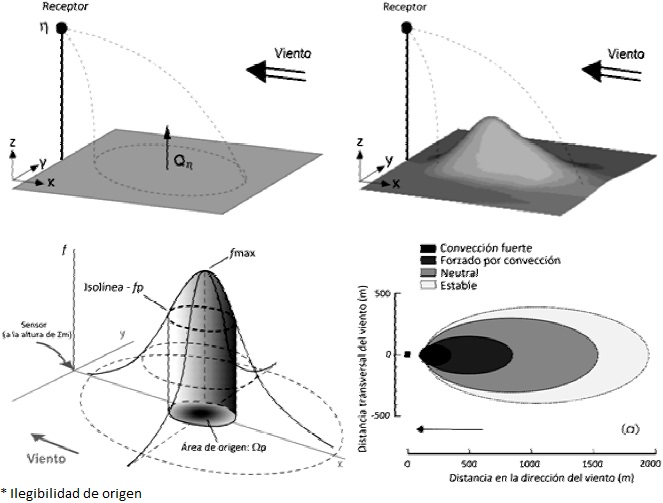
Figura 1 Concepto del footprint de los flujos de vapor de agua y calor, y su variación en función de la condición de la estabilidad atmosférica. Adaptado de: Kljun, 2002 y Schmid, 2002, donde: x, y, z = coordenadas de posición espacial, η = señal o valor medido en la ubicación r del sensor, Qη= tasa de emisión del origen (o fuerza del sumidero) en r + r', r' = separación entre la medición y el forzado, f = función de transferencia (función de footprint) , P = área pequeña posible responsable de una contribución relativa.
El denominador del cierre en la relación (8), Rn es representativo de una superficie circular fija (footprint constante) (Figura 2). Aunque esta superficie es teóricamente infinita, al usar un ángulo de visión e iluminación semi-hemisférico el área de influencia se vuelve finita. Así, las dimensiones del footprint de Rn dependen del ángulo de visión del sensor y de la altura de medición (Masseroni et al., 2011).
Los intentos de incluir los footprints en el análisis del cierre del balance de energía, solo han considerado mediciones cuyos footprints caen dentro de las parcelas homogéneas de estudio, resultando en una leve mejoría del cierre (Masseroni et al., 2011 y 2012). Este enfoque supone una homogeneidad fuerte del área de estudio y considera que bajo esta situación no hay efecto de escala al combinar footprints con diferentes dimensiones.
Para analizar en forma apropiada el cierre del balance de energía es necesario que sus componentes sean representativos de un mismo footprint, particularmente para el caso de cultivos en hileras o surcos, donde la componente geométrica-direccional es importante. De esta forma, si se toma como referencia el footprint (dinámico) de λE, se debe convertir el footprint de los otros componentes (H, G y Rn) a esta referencia. En la actualidad no existen modelos para realizar estos escalamientos (o los que existen son muy complicados de parametrizar), por lo que se requiere explorar esquemas simples que proporcionen elementos para realizar este tipo de desarrollos.
En el caso del componente H, el problema de escalamiento se puede abordar a partir de la modelación del footprint de la temperatura radiativa (considerando que esta última captura la variabilidad espacial del footprint de H, como se plantea en las relaciones 2 y 5). Así, se definió como objetivo de este trabajo modelar la función de distribución bidireccional de la Tr, a fin de generar elementos para el posterior desarrollo de modelos de escalamiento del footprint de H. Para lograr este objetivo, se introdujo un modelo uni-paramétrico que considera de forma intrínseca el footprint de la Tr (considera en forma implícita la geometría y propiedades ópticas del cultivo y del suelo). Este modelo fue desarrollado inicialmente por Bolaños et al., (2007) para el caso de reflectancias y generalizado por Bolaños y Paz (2010). El modelo puede ser parametrizado en forma simple, por lo que en este trabajo se extiende su uso al caso de temperaturas radiativas.
Materiales y métodos
Modelo uni-paramétrico de la Función de Distribución Bidireccional de la Temperatura Radiativa
Este modelo (en lo siguiente referido como MUPT) plantea un esquema con simetría especial (Hot Spot o coincidencia de ángulos cenitales del sol y visión) que simplifica la modelación de la función de distribución bidireccional de la Tr a un solo parámetro. Así, se necesita sólo un dato y puede aplicarse a nivel de pixel (para el caso de una imagen satelital) o a una medición única de campo, y para una fecha cualquiera, de la siguiente forma:
donde: θv es el ángulo cenital de visión y θs el ángulo cenital solar (ambos en grados), Tr es la temperatura radiativa de cualquier banda térmica (°C), Tn es la temperatura normalizada (°C, sin efecto de escala), gt es el parámetro de la función de distribución bidireccional de la temperatura radiativa y a es una constante con valor igual a 90°. χ en conjunto con Rn determinan el espacio de análisis propuesto por este esquema de modelación. La función f(Tr) es igual a ln(Tr), ln(°C), para el caso de considerar efecto de escala de las mediciones (el área cambia en función del ángulo cenital de visión) o igual a Tr para no efecto de escala.
El MUPT definido por las relaciones (9) se puede extender al caso de los ángulos acimutales, bajo los mismos argumentos, como:
donde: ϕv es el ángulo acimutal de visión, ϕs es el ángulo acimutal solar, GT es el parámetro de la función de distribución bidireccional que captura las variaciones angulares cenitales y acimutales, y A es una constante con valor igual a 90°.
El MUPT se parametriza con un solo parámetro: gt para el caso de considerar sólo ángulos cenitales (visión a nadir) o GT para el caso general (considerando ángulos cenitales y acimutales). Las constantes a y A son iguales a 90°, producto de la simetría introducida por las variables de posición χ y ξ.
El sistema de ecuaciones (9) y (10) puede replantearse como (a = 90, A = 90):
Una definición generalizada de temperaturas radiativas normalizadas (Tn), a ser usada en lo siguiente, se expresa como:
Para evaluar el ajuste empírico del MUPT a los datos de campo, se empleó la raíz cuadrada del error cuadrático medio (RECM) y el error relativo medio (ERM):
donde: Tn,med corresponde a los valores medidos de Tn, en tanto que los valores estimados se representan como Tn,est.
Adicionalmente, se realizó una regresión lineal simple entre los valores de Tn,med y Tn,est de la siguiente forma:
Los parámetros c y d, además del R2 del ajuste, fueron calculados para todos las fechas de medición de la Tr bajo diferentes geometrías sol-sensor.
Área de Estudio
La fase experimental del presente trabajo se llevó a cabo en el estado de Sonora, en un bloque agrícola ubicado en el distrito de riego 041-Río Yaqui, entre las coordenadas: 27° 14’ 24” y 27° 16’ 48” N y 109° 52’ 12” y 109° 54’ 36” O (Figura 3).
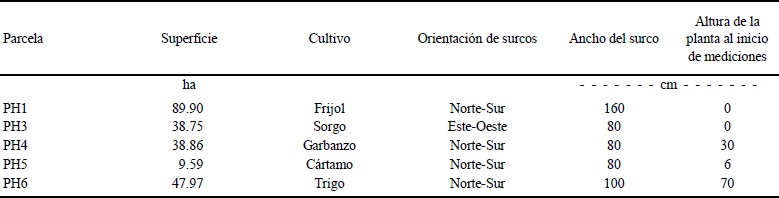
Se seleccionaron cinco parcelas homogéneas (PH) para llevar a cabo las mediciones. La condición de “homogeneidad” indica que en la parcela se estableció un solo cultivo, con una sola densidad de siembra, un mismo espaciamiento y dirección de los surcos y una misma fecha de siembra. La condición inicial de cada parcela de estudio se describe en el Cuadro 1.
Equipo e Instrumentación
Para poder medir la Tr empleando diferentes configuraciones de la geometría sol-sensor, se diseñó un sistema que consta de las siguientes partes:
a) Una estructura de fierro (mástil extensible) para el posicionamiento de la altura de los sensores, con mecanismos de sujeción a 2.5, 4 y 5.5 m.
b) Una estructura de policarbono con base plana (para sostener al sensor de Tr). Esta estructura posee un mecanismo electrónico con servomotores que permiten posicionar el sensor de 0 a 90° en el plano cenital (Figura 4a) y de 0 a 180° en el plano acimutal (Figura 4b).
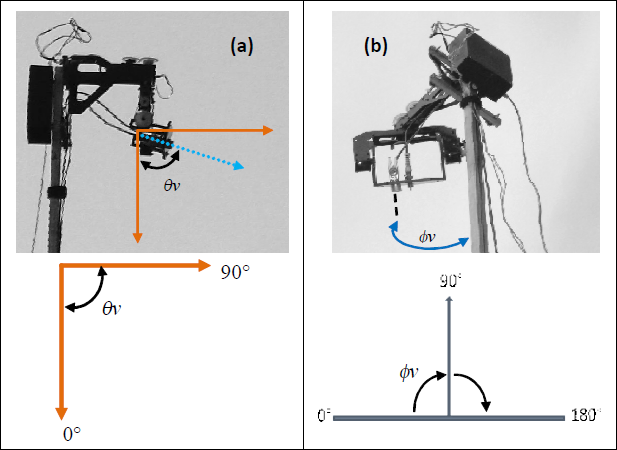
Figura 4 Geometría del sistema para la medición de la Tr. (a) plano cenital de visión, (b) plano acimutal de visión.
c) Tarjeta de control y programa para la operación de la estructura de policarbono.
d) Un sensor de la temperatura radiativa del cultivo. Se utilizó un termómetro infrarrojo modelo IRTS de la marca ApogeeMR con ángulo de visión de 18.4° (3:1).
e) Computadora portátil para la operación del sistema y el almacenamiento de datos.
La forma de ensamblar el equipo se muestra en la Figura 5a, éste se montó sobre un tripie adaptado con un soporte central para mantener la estabilidad del sistema. Para asegurar que el tripie estuviera nivelado se empleó un nivel de burbuja, lo que garantizo que en el día de medición la posición vertical estuviera asegurada (al terminar el día de medición se desmontó el equipo y al siguiente día se volvío a montar). En la Figura 5b se muestra la ubicación del sitio de mediciones, en este sitio se montó el sistema orientando el ángulo acimutal 90° (del equipo) de forma paralela a la dirección de los surcos. Se buscó que el sitio de mediciones fuera representativo de la condición predominante del cultivo y que no presentara rasgos de perturbación, sin embargo para fines prácticos (traslado, montaje y desmontaje continuo de equipo), se ubicó hacia un extremo (varios metros adentro) de la parcela, dejando un margen de cultivo suficiente para evitar que las mediciones fueran afectadas por la superficie contigua de suelo desnudo (en el caso de sensores pasivos el efecto de borde no es importante si se está a varios metros de las orillas).
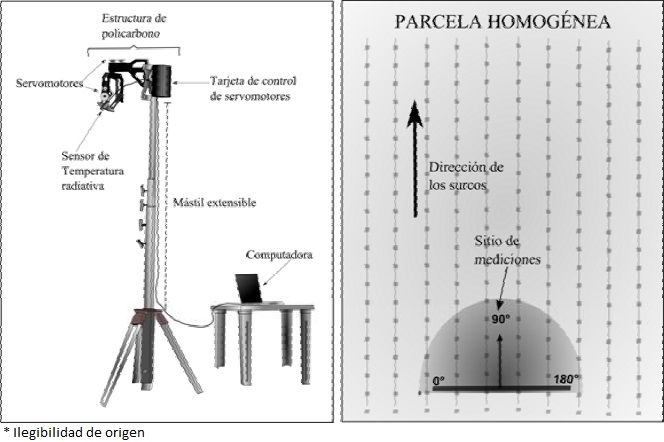
Figura 5 (a) Equipo para la medición de la temperatura radiativa,(b) ubicación del sitio de mediciones.
En cada parcela se dejó una marca para ubicar fácilmente este sitio en las visitas semanales subsecuentes. La condición inicial de las parcelas de estudio se muestra en el Cuadro 1.
Estrategia de Medición
Las mediciones se realizaron a lo largo del ciclo de crecimiento de los cultivos (entre los meses de febrero a mayo). Cada parcela se visitó una vez por semana y en cada visita se ejecutaron tres ciclos de mediciones de la Tr. Las mediciones de cada ciclo se realizaron empleando las alturas y los ángulos de visión (ϕv, θv) que se especifican en el Cuadro 2.
Para una misma altura y posición acimutal del sensor, se tomaron diferentes mediciones de la Tr (diferente posición cenital del sensor). Así, por ejemplo, con el sensor a 2.5m de altura y posición acimutal en 15° se tomaron 4 lecturas de Tr (según las inclinaciones cenitales: 40, 60, 70 y 75°). En total, por cada ciclo de mediciones se obtuvieron 70 lecturas (Cuadro 2).
Es importante considerar que el plano acimutal del sistema (Figura 4b) difiere de la convención normal de los acimut (positivos en la dirección de las manecillas del reloj a partir del N). La correspondencia entre los acimut del sistema y los acimut reales depende de la ubicación del sitio de mediciones en cada PH. En el Cuadro 3 se indican las correspondencias en todos los casos.

ϕv = ángulo acimutal de visión
Cuadro 3 Correspondencia entre ángulos acimutales del sistema y ángulos acimutales reales.
Los ciclos de mediciones se realizaron a diferente hora del día para obtener datos con diferente ángulo solar (cenital y acimutal). El primer ciclo se realizó cerca del amanecer, el segundo alrededor del mediodía solar y el tercero cercano a la puesta de sol. La programación del horario para la ejecución de cada ciclo se hizo previamente, considerando dos aspectos importantes: 1) horarios representativos de tres ángulos cenitales solares distintos y 2) que entre los ángulos seleccionados existiera una diferencia de al menos 10 grados.
Áreas de Influencia (footprints) de las Mediciones
El esquema de las áreas de influencia o footprints de las mediciones de Tr, según la altura y el ángulo cenital de visión del sensor se muestra en la Figura 6. Las dimensiones de las elipses representativas de estos footprints se resumen en el Cuadro 4.
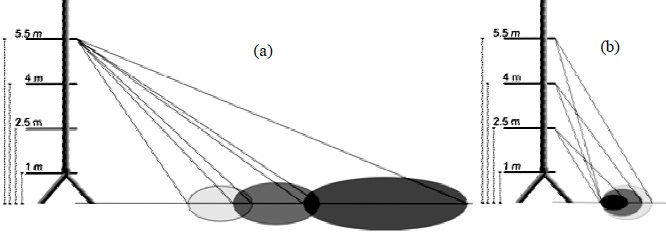
Figura 6 Áreas de influencia o footprints de las mediciones de temperatura radiativa, (a) para una altura fija y cambiando el ángulo cenital de visión, (b) para mismo ángulo cenital de visión y diferentes alturas.
Resultados y discusión
Con la información generada se revisó la variación de Tr en función de la geometría sol-sensor. Los datos de la PH1 del primer día de mediciones (día juliano 58) y con los tres tiempos de condiciones de iluminación solar, así como los datos levantados en todo el periodo de estudio, muestran diferencias de hasta 15 °C en los valores de Tr (Figura 7).
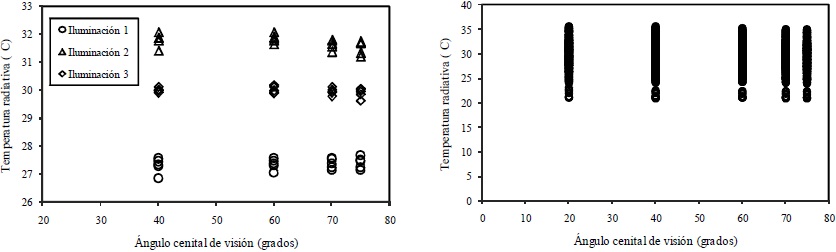
Figura 7 Medición de Tr en la PH1. (a) Mediciones del día juliano 58 y (b) mediciones en todo el periodo de estudio.
Como siguiente paso, se revisó el ajuste del MUPT obteniendo los resultados que se muestran en la Figura 8.
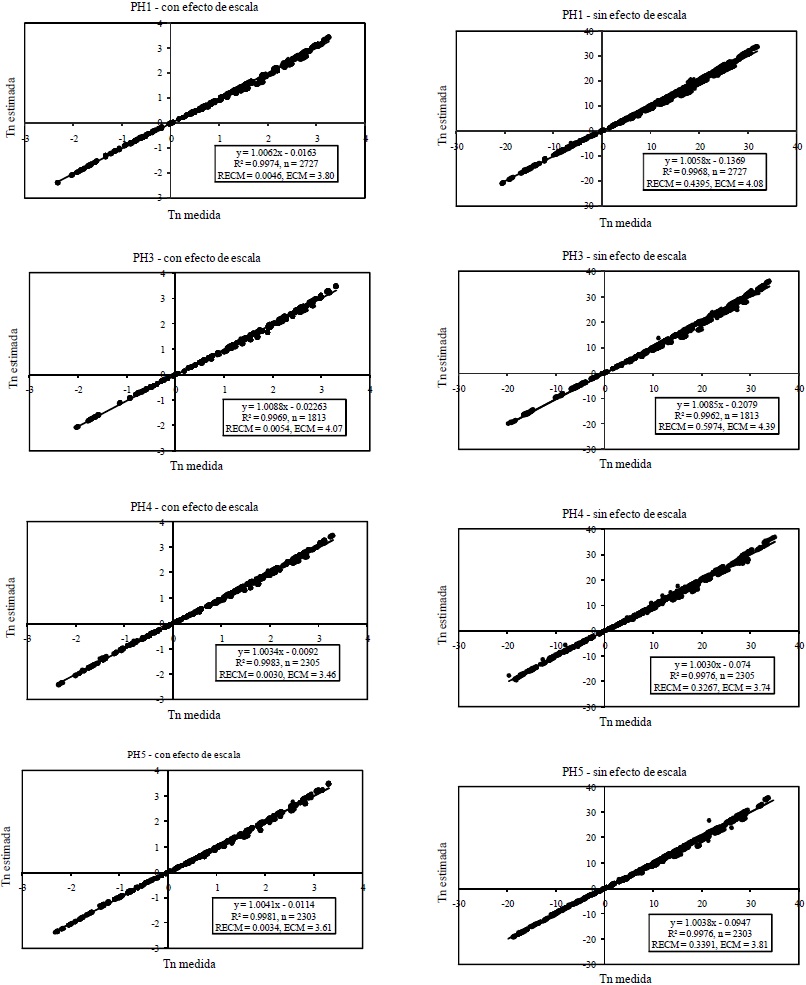
Figura 8 Ajustes de Tn para las diferentes parcelas de estudio (PH1, PH3, PH4, PH5 y PH6), con efecto de escala (transformación logarítmica) donde Tn está en ln(° C), y sin éste (con Tn en °C).
Los cálculos de la temperatura radiativa normalizada (Tn) que se muestran en la Figura 8 sólo consideran la geometría cenital de las observaciones (relaciones 9). Las gráficas del lado izquierdo muestran los ajustes del MUPT considerando el efecto de escala (transformación logarítmica de la Tr en la Ecuación 9) y las gráficas del lado derecho no consideran este efecto en los cálculos de Tn. Se puede ver que los ajustes del MUPT con y sin efecto de escala son muy similares, por lo que en la estimación de gnt (reflectancia normalizada por efecto de ángulos cenitales y acimutales) de las relaciones (10) sólo se consideraron los resultados de la no transformación logarítmica de Tn. Los ajustes del MUPT en los cálculos de gnt se muestran en la Figura 9.
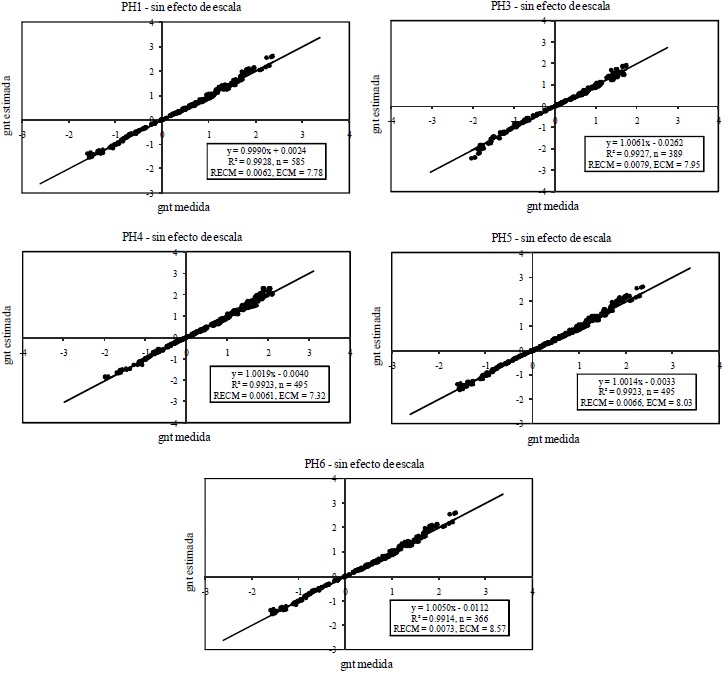
Figura 9 Ajustes de gnt para todas las parcelas de estudio (PH1, PH2, PH3, PH4, PH5 y PH6) para el caso de no efecto de escala.
El MUPT presenta buenos ajustes (R2 > 0.99), ya sea considerando sólo la geometría cenital de las observaciones (Figura 8) o evaluando el caso general que considera tanto la geometría cenital como la acimutal (Figura 9), por lo que puede usarse de forma confiable para estandarizar los efectos de la geometría sol-sensor en mediciones de Tr. El modelo planteado implica que la curva de las figuras discutidas debe pasar por origen, no obstante, para el análisis estadístico se revisó el sesgo (constante aditiva) introducido en los datos experimentales. Aun así, los resultados muestran que este sesgo es despreciable.
La principal ventaja del modelo aquí propuesto es que se puede usar en términos operativos, ya que sólo requiere información conocida, ésta es: la geometría sol-sensor de las mediciones (ángulos cenitales y acimutales de visión e iluminación) y el valor de Tr del sitio muestreado. En mediciones satelitales el sitio muestreado corresponde a un píxel de la imagen, mientras que en mediciones de campo cada observación tiene una área de influencia asociada (también conocida como footprint).
Una limitante del MUPT es que los resultados se generan en un espacio normalizado (como se puede apreciar en las Figura 8 y 9), de tal forma que para poder usar los datos de Tn en cálculos como el flujo de calor latente o la radiación neta, se requiere reformular las ecuaciones correspondientes para su uso en este nuevo espacio. Aun así, a diferencia de otros modelos que se han desarrollado para caracterizar la Tr en función de la geometría sol-sensor y que dependen de diferentes parámetros (Kimes, 1983; Mathias et al., 1987; McGuire et al., 1989; Smith y Ballard, 2001), generalmente no accesibles en las aplicaciones, el MUPT tiene la ventaja de que depende de un solo parámetro (el parámetro gt si se usa el caso simple o GT si se usa el caso general) el cual se calcula con la información conocida de las mediciones. En relación a los ajustes empíricos del MUPT a datos experimentales, aun con el requerimiento de usar un solo dato, el modelo introducido se comporta mejor en términos estadísticos.
Para el caso del albedo, es práctica común el uso de modelos semi-empíricos basados en funciones matemáticas con bases físicas (kernels) (Wanner et al., 1995), donde para aplicar estos modelos se requiere estimar al menos tres parámetros. La evaluación de la precisión que podría ser alcanzada en las estimaciones de albedo y reflectancias a partir del muestreo angular ofrecido por los sensores MODIS y MISR considerando condiciones ideales de observación (ausencia de nubes, atmósfera y ruido) fue realizada por Lucht (1998). Puesto que las estimaciones de albedo son obtenidas mediante la integración de la BRDF, tanto en el hemisferio de observación como en ambos hemisferios, un factor importante evaluado fue la capacidad del modelo para reproducir el comportamiento de la reflectancia en geometrías donde no se realizaron mediciones, principalmente en el hemisferio de iluminación. Los resultados obtenidos fueron satisfactorios (Lucht, 1998), pero bajo los requerimientos de contar con información multitemporal para parametrizar los modelos de kernels. Por otro lado, Hu et al. (1997) realizaron una validación de las expresiones matemáticas (kernels) contenidas en los modelos semi-empíricos a partir de datos obtenidos con sensores remotos aéreos multi-angulares. La información fue colectada con diferentes instrumentos bajo distintas configuraciones de la geometría sol-sensor. Los resultados obtenidos muestran niveles de concordancia entre los valores de reflectancia medidos y estimados superiores al 90%. En el caso de estimaciones de la temperatura radiativa también se han empleado los modelos de kernels con resultados aceptables (Snyder y Wan, 1998).
No obstante los resultados aceptables relacionados con el uso de los modelos de kernels, una crítica a este paradigma de modelación procede de los requerimientos para su calibración; es necesario contar con información capturada con diferente geometría sol-sensor, lo cual demanda utilizar periodos de composición entre 10 y 16 días (Huete et al. 1999) y suponer condiciones de homogeneidad en el sistema suelo-vegetación-atmósfera.
Si bien los modelos de kernels aproximan razonablemente la temperatura radiativa y albedo en su dependencia angular de los objetos terrestres, su uso demanda información no disponible en mediciones uni-temporales, tal como las discutidas en este trabajo. En un trabajo en proceso de publicación del grupo de investigación (Medrano et al., 2013), se demuestra que el modelo introducido genera resultados similares al uso de modelos de kernels, sin la necesidad de contar con información multi-temporal, que bajo el principio de parsimonia permite utilizar el modelo uni-paramétrico como un substituto de modelos más complejos y con necesidad de mayores datos para su parametrización.
Finalmente, una vez que se ha evaluado el desempeño del MUPT para modelar la función de distribución bidireccional de la temperatura radiativa y el albedo, la contribución más importante del esquema es que provee elementos para modelar el footprint de las mediciones a partir de argumentos geométricos como la altura de observación y el ángulo de visión del sensor (Figura 6). El desarrollo de un modelo que acople las variaciones de la temperatura radiativa y albedo, y los footprints, es importante en el contexto del cierre del balance de energía, pues para poder revisar el cierre se requiere ajustar los componentes del balance a un mismo footprint.
Conclusiones
- La necesidad de modelar en forma simple y operativa la temperatura radiativa (Tr) de la superficie se justifica desde la perspectiva de estimar los flujos de calor sensible y la radiación neta en la vegetación y desde la necesidad de explicar las diferencias en los cierres del balance de energía, principalmente, en mediciones con la técnica de covarianza de vórtices, donde se comparan flujos con diferentes áreas de influencia o footprint.
- Para modelar las variaciones de Tr con relación a la geometría sol-sensor, y los footprints implicados, se introdujo un modelo uni-paramétrico de la función de distribución bidireccional de las temperaturas radiativas (MUPT), el cual fue originalmente desarrollado para el caso de reflectancias. El MUPT fue validado con mediciones de campo, para un conjunto grande de mediciones de diferentes geometrías sol-sensor, diferentes cultivos y estados del crecimiento de éstos. Los resultados muestran buenos ajustes (R2 > 0.99), lo que permite la utilización del MUPT en forma operativa para la estandarización de las mediciones de Tr.











 nueva página del texto (beta)
nueva página del texto (beta)