División III

Nota de investigación

 

Análisis multifractal del carbono en los suelos. 1. Función universal de escalamiento*

 

Multifractal Analysis of Soil Organic Carbon. 1. Universal Scaling Function

 

Fernando Paz Pellat^1‡, Claudio Balbontín Nesvara¹, Jorge Etchevers Barra¹, Mario Martínez Menez¹ y Carlos Ortiz Solorio¹

 

¹ Colegio de Postgraduados, Campus Montecillo. 56230 Montecillo, Estado de México. ^‡Autor responsable (pellat@colpos.mx)

 

Recibido: junio de 2005.
Aceptado: abril de 2008.

 

RESUMEN

En este trabajo se discuten los requerimientos de los inventarios de carbono orgánico en los suelos (COS) y las comunicaciones nacionales, compromisos contraídos por México ante la Convención Marco de las Naciones Unidas sobre el Cambio Climático. Dos problemas que enfrentan esos estudios son los efectos de escala y la variabilidad del COS. Para realizar estimaciones del COS a diferentes escalas de observación se propone introducir la teoría de procesos multifractales, conservativos o no, como una estrategia para caracterizar funciones universales multi-escalantes. La estimación de la función de estructura espacial del COS se hizo con base en los datos de 4583 muestras de suelo colectadas en el periodo 2001 -2002. Se describió el problema de estimación desde la perspectiva de la divergencia de los momentos estadísticos de procesos multifractales y se estimaron los parámetros de la función universal de escalamiento del COS.

Palabras clave: inventarios de carbono en suelos, funciones de escalamiento, procesos conservativos y no conservativos.

 

ABSTRACT

In this paper, the requirements of soil organic carbon (SOC) inventories are discussed under the perspective of the national communications commitment to the United Nations Framework Convention on Climate Change. Using considerations of scale effect and spatial variability of SOC, the theory of multifractal processes, conservative or not, is introduced as a strategy for characterizing universal multiscaling functions in order to estimate SOC at different scales of observation. The estimation of the multifractal function of SOC was performed using a data base of 4583 samples gathered over the period 2001-2002. The SOC universal scaling function parameters were estimated and the estimation problem was reviewed from the perspective of the divergence of statistical moments of multifractal processes.

Keywords: soil carbon inventories, scaling functions, conservative and non conservative processes.

 

INTRODUCCIÓN

Una de las obligaciones contraídas por México ante la Convención Marco de las Naciones Unidas sobre el Cambio Climático (CMNUCC) es la presentación de comunicaciones nacionales sobre el inventario de emisiones de gases de efecto invernadero. Uno de estos gases es el dióxido de carbono (CO₂), estrechamente relacionado con el cambio de uso del suelo, la silvicultura y la pérdida de carbono desde el suelo. La tarea en relación con este tema es compleja, dada la escasa información con que se cuenta en México y el alto grado de incertidumbre que tiene asociada.

Las metodologías desarrolladas por el Panel Intergubernamental sobre Cambio Climático (IPCC por sus siglas en inglés) para realizar estos inventarios establecen tres niveles de aproximación (IPCC, 1997, 2000, 2006). El Nivel 1 es el más general y utiliza valores de emisiones en función de clases de uso del suelo o taxonómicas por defecto, aceptados internacionalmente. El Nivel 2 propone la utilización de factores estimados a partir de la información generada a nivel de país, a escala regional o nacional. El Nivel 3, el más detallado, considera estimaciones espacialmente explícitas de los factores de emisiones hacia donde se debe tender en los inventarios nacionales y es el nivel de mayor complejidad.

Actualmente, México ha elaborado tres comunicaciones nacionales (INE-SEMARNAP, 1997; INE-SEMARNAT, 2001) usando el Nivel 1 de aproximación en las dos primeras y en la tercera (INE-SEMARNAT, 2006) una mezcla de Niveles 1 y 2.

En la segunda comunicación (INE-SEMARNAT, 2001) se estableció que el sector de cambio de uso del suelo y silvicultura generaba 199 mil Gg de CO₂, de los cuales los suelos contribuían con 89 mil Gg (44.8%). El recientemente publicado Inventario Nacional de Gases de Efecto Invernadero 1990-2000 (INE-SEMARNAT, 2006), en el cual se empleó el Nivel 2, con menor incertidumbre que los cálculos anteriores, modifica algunas de estas cifras, asignando al sector (manejo de bosques, conversión de bosques, abandono, suelo) un total de 86 877 Gg de CO₂, de los cuales 30 344 Gg corresponden a emisiones de los suelos.

El potencial de secuestro global de carbono en los suelos en los ecosistemas terrestres es alrededor de tres veces el de la vegetación (Post et al., 1990). Lo anterior resalta la importancia de implementar políticas de adaptación, mitigación y conservación nacionales en dichos ambientes. Así, los suelos son los mayores reservorios de carbono, dentro de los ecosistemas terrestres, y generan emisiones asociadas a los cambios de uso del suelo de alrededor de la mitad del total del sector cambio de uso de suelo y silvicultura. Para evaluar las emisiones de CO₂ en los suelos es necesario primero estimar sus reservorios (carbono secuestrado), para años base, y del análisis de los patrones de cambio de uso del suelo, estimar las emisiones de CO₂ asociadas a éstos. Para la presentación de la tercera comunicación de México ante la CMNUCC se estableció utilizar como año base 1993 y un periodo que comprendió hasta 2002, coincidentes con la disponibilidad de planos de uso del suelo actualizados por el Instituto Nacional de Estadística, Geografía e Informática (INEGI).

Desde la perspectiva del carbono secuestrado en los suelos, en el mencionado ejercicio para la CMNUCC se decidió emplear el Nivel 2 recomendado por IPCC, para lo cual fue necesario desarrollar un marco metodológico que permitiese realizar estimaciones espaciales en forma confiable, además de cuantificar, en forma explícita, las incertidumbres asociadas a dichas estimaciones (IPCC, 2000), lo cual mejoraría sustancialmente el inventario preliminar de carbono orgánico de los suelos a nivel de país realizado por Etchevers et al. (2006). El método de estimación espacial utilizado en este trabajo fue el del inverso de la distancia.

En las ciencias del suelo es cada vez una práctica más común la utilización de las técnicas geoestadísticas (Matheron, 1971; Journel y Huijbregts, 1978; Goovaerts, 1997); éstas usan hipótesis implícitas muy restrictivas que generalmente producen sobreestimaciones. El denominado método kriging usado en geoestadística es un estimador óptimo lineal no sesgado sólo en el caso de procesos gaussianos (Isaaks y Srivastava. 1989) (en términos más técnicos, la geoestadística supone que las medidas son regulares en relación con las medidas de Lebesgue). Íntimamente ligado a la variabilidad espacial de las propiedades de los suelos está el efecto de escala, el cual es de relevancia en los inventarios nacionales, ya que con información de unas pocas decenas de metros cúbicos de material se pretende realizar estimaciones de miles de millones de metros cúbicos. Existe evidencia experimental que establece que las concentraciones de algún elemento en el suelo dependen de la escala de muestreo (Hassan et al., 1983; Starr et al., 1995). Para acotar esta variabilidad en función de la escala de muestreo se ha propuesto el concepto de Volumen Elemental Representativo o VER (Dagan, 1986) o Área Elemental Representativa o AER (Wood et al., 1988). Así, usando un gráfico de la varianza en función de la escala (volumen o área de la muestra), el VER o AER, se obtiene un punto donde la variación es prácticamente constante (en procesos cíclicos la varianza reduce sus amplitudes al incrementar la escala) definiendo una escala de trabajo donde el suelo tiene propiedades más o menos constantes, en términos estadísticos. Esta interpretación de la variabilidad de escala espacial, establece que a nivel micro las variaciones observadas son producto de la heterogeneidad del medio (estructura definida por la geometría de los elementos constitutivos del suelo; donde se encuentra la situación de variables dicótomas: grano o poro) y que a una escala meso (valores promedio) esta variabilidad está limitada, pudiéndose usar un enfoque jerárquico de escalas acotado en una escala superior (Miller, 1994; Lin, 2003). Esta visión restringida del concepto de escala (sesgada por una visión geométrica y no de medidas que son singulares en relación con las medidas de Lebesgue) es la que prevalece actualmente en las estimaciones geoestadísticas y en las clasificaciones taxonómicas o funcionales de los suelos. Con relación a la escala superior de la reducción de la varianza es generalmente producto del número reducido de muestras utilizadas (usando una hipótesis de ergodicidad), que implica simplemente una divergencia en la estimación de los momentos estadísticos. Así, los inventarios de carbono en los suelos son estimados después de agrupar clases de comportamiento "homogéneo" (estratificación) y de la asociación de valores promedio del contenido de carbono en estas clases (IPCC, 1997; Post et al., 2001).

En este trabajo se desarrolla una propuesta de metodología de modelación del efecto de escala y de la variabilidad espacial, usando la teoría de procesos multifractales, y se ejemplifica en la evaluación de la función universal de escalamiento del contenido de carbono orgánico en los suelos de México; la cual se utiliza para definir los errores de estimación de los inventarios de carbono bajo diferentes escalas de muestreo.

 

CASCADAS MULTIPLICATIVAS

Para introducir los procesos multifractales, se utilizará la fenomenología de las cascadas multiplicativas, ampliamente utilizada en el estudio de la turbulencia. Considérese el caso de una cascada unidimensional, donde la escala más externa (mayor) está dada por L y ésta es dividida en segmentos iguales de longitud l en cada paso de la cascada. La razón de escala λ = L/l, λ > 1, está dentro del rango 1 ≤ λ ≤ Λ, donde Λ = L/1_min , y 1_min es la escala mínima del proceso de cascada (disipación de la energía por viscosidad en el caso de turbulencia). Sin pérdida de generalidad, se puede hacer L = 1 (Figura 1).

Ahora bien, si se considera una variable Z (densidad = concentración/espacio), a la escala L con λ = L/L = 1, la podemos normalizar para que su promedio sea uno:

De esta manera, a la escala L (= 1) se tiene que el área de la Figura 1 en λ = 1 es unitaria. La densidad (tasa de disipación de energía cinética por unidad de masa en turbulencia) a la escala λ es transferida multiplicativamente a la escala inferior siguiendo un proceso binomial conservativo, de tal forma que el promedio se conserva (el área en la Figura 1 es la misma para todos los pasos de la cascada):

La escala superior modula en forma multiplicativa la transferencia de densidad a la escala inferior a través de generadores estocásticos:

donde: γ es el generador u orden de singularidad del proceso. Las γ caracterizan las singularidades en relación con las medidas de Lebesgue y son invariantes a escala.

De la Ecuación 3 el orden de singularidad está dado

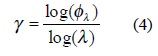
La cascada descrita se denomina el modelo a (Schertzer y Lovejoy, 1983) y tiene la propiedad que el límite de la cascada (cuando el número de pasos tiende al infinito) está dado por:

donde: Pr es la probabilidad y el signo ≈ significa igualdad dentro de factores constantes o variando lentamente (como la función logarítmica). La función C(γ) es la codimensión del proceso y está dada por:

donde: d es la dimensión del proceso (d = 1 en el caso unidimensional) y D(γ) es la dimensión fractal asociada al orden de singularidad y.

Las propiedades de una distribución de probabilidad de una variable aleatoria pueden ser especificadas en forma equivalente como:

donde: K(q) es la función escalante de los momentos estadísticos de orden q.

La relación entre C(γ) y K(q) se reduce a la transformada de Legendre (Parisi y Frisch, 1985) para razones de escala grandes (λ >>1):

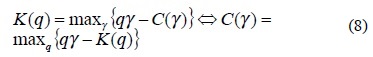
Esta ecuación implica que hay una correspondencia uno a uno entre las singularidades y los órdenes de los momentos: a cualquier orden q hay asociada una singularidad λ que maximiza qλ - C(λ) y es la solución C' (λ_q) = q_λ En forma similar, para cualquier singularidad λ hay asociado un orden de momento q que maximiza qλ - K(q) y es la solución de K'(q_λ) = λ_q La única restricción en C(λ) y K(q) es que deben ser convexas.

La cascada mostrada en la Figura 1 genera una función de codimensión con un número infinito de dimensiones fractales asociadas a las singularidades del proceso (dentro de un valor mínimo y máximo definido). Por esta razón, la cascada multiplicativa descrita es un multifractal. De la Ecuación 5, un multifractal tiene asociadas probabilidades que dependen de la escala de observación, por lo que para un valor dado de γ (o de ø), por ejemplo, el contenido de materia orgánica en un suelo, su probabilidad de excedencia (o momentos estadísticos) estará en función de la escala en que está integrado (promediado) el proceso.

Para caracterizar un proceso multifractal (con un número infinito de grados de libertad) es necesario definir un número infinito de dimensiones fractales, lo que hace poco práctico este análisis. Para solucionar este inconveniente, asociado a cascadas multiplicativas discretas, es necesario plantear el proceso como una cascada continua y analizar sus límites para determinar funciones universales.

PROCESOS MULTIPLICATIVOS UNIVERSALES CONSERVATIVOS

Si se usan generadores de variables aleatorias Levy estables en un proceso continuo de cascada multiplicativa, es posible definir funciones universales escalantes, que lo caracterizan en forma completa (Schertzer y Lovejoy, 1987, 1989, 1991; Brax y Peschanski, 1991; Kida, 1991):

donde: C₁ = la codimensión de la singularidad media del proceso que mide la fractalidad promedio (0 ≤ C₁ ≤ d), α = el índice de Levy (0 ≤ α ≤ 2), el cual define que tan rápido se incrementa la fractalidad con singularidades cada vez más grandes. Para α = 2, el proceso es log normal.

En procesos conservativos (E[ ø _λ ] = 1) se tiene que K(1) = 0, lo que corresponde, por la transformada de Legendre, al hecho de que la singularidad media del proceso C₁ = K'(1) es un punto fijo de C(γ) en y₁ = C(γ₁) = C₁, por lo que C'(C₁) = 1.

La función universal de escalamiento que caracteriza las propiedades probabilísticas de un multifractal, con un número infinito de dimensiones fractales, depende de sólo dos parámetros: α y C₁.

PROCESOS MULTIFRACTALES UNIVERSALES NO CONSERVATIVOS

En procesos multifractales no conservativos es necesario introducir un nuevo parámetro en las funciones universales:

donde: H es el parámetro de Hurst, el cual mide el grado de no conservación del proceso (0 ≤ H ≤ 1); donde H = 0 implica un proceso estacionario y H = 1 uno fuertemente no estacionario.

Las funciones universales introducidas, conservativas o no, requieren contar con información muestral a diferentes escalas de observación, lo que hace extremadamente difícil la caracterización de los parámetros de estas funciones, dada la información en general disponible (excepto del campo de sensores remotos). Un enfoque alternativo es utilizar diferencias de variables, para un escala fija muestral, como una forma equivalente de caracterizar las relaciones de escala.

En el fenómeno de turbulencia, una cascada multiplicativa modula un proceso donde los vórtices grandes transmiten su energía de disipación a los más pequeños hasta llegar a la escala de Kolmogorov, donde la energía es disipada por viscosidad. Considerando la hipótesis de similaridad débil de turbulencia (Kolmogorov, 1962) (análisis dimensional):

donde: ΔV es el cortante de velocidad turbulenta (x es una coordenada espacial o temporal y h es una distancia elapsada) y ε es la tasa de disipación de energía cinética por unidad de masa. El cortante de velocidad es una variable no conservada que está relacionada con la tasa de disipación, la cual es una variable conservada. De acuerdo con la Ecuación 11, es posible estimar la variable conservada por una diferenciación fraccional de orden -1/3 de la variable no conservada.

De la Ecuación 11 se puede establecer una relación genérica del tipo:

donde: a puede ser igual a uno, como primera aproximación, si no se conoce su valor (un cambio en a implica sólo un cambio en el parámetro C₁) y H es el parámetro de Hurst previamente consignado. La Ecuación 12 es utilizada en forma empírica en este trabajo por no contar con las ecuaciones (sistema no lineal de derivadas parciales) que definen la génesis del contenido de materia orgánica en el suelo. No obstante esto, es posible realizar un análisis dimensional que permita establecer una relación similar al de turbulencia utilizando estas técnicas en los suelos (Tillotson y Nielsen, 1984).

De las Ecuaciones 7 y 12 con a = 1:

donde: E[(ΔZ_λ)^q] es llamada función de estructura (Monin y Yaglom, 1975) y ζ(q=1) = H.

Definiendo λ = h_max /h, h ≈ λ ¹ y h_max es la escala exterior L, para una escala fija, por lo que:

En geoestadística, al caso q = 2 se le llama variograma (Goovaerts, 1997) y es la función básica de correlación espacial (o temporal) utilizada en esta teoría, la cual tiene un dominio de atracción gaussiano (varianza finita). La función de estructura mencionada anteriormente es más general que la usada en geoestadística (generalizada a momentos estadísticos de orden q), además de relacionar las variaciones espaciales en función de la escala de observación λ. Journel (1988) propuso la utilización de q = 0.5 y q = 1 como una forma de evitar la gaussianidad implicada en las estimaciones geoestadísticas usando el método del kriging, pero lo planteó como un método ad hoc sin explorar sus bases escalantes.

Un proceso monofractal (aditivo) tiene ζ(q) = qH (α = 0 en la perspectiva multifractal), por lo que la función de estructura multifractal mide el grado de desviación de la monofractalidad.

FUNCIÓN ESCALANTE DEL CARBONO ORGÁNICO DE LOS SUELOS DE MÉXICO

Para la tercera comunicación ante la CMNUCC de México fue necesario realizar el inventario de carbono orgánico en los suelos y su asociación con los diferentes tipos de uso de suelo para la estimación de los factores de emisión de CO₂. Para realizar un inventario, se requiere que los muestreos de carbono orgánico sean realizados en un periodo de tiempo relativamente corto; aunque los cambios de carbono orgánico asociados a los cambios del uso del suelo son significativos; en general, después de un periodo de 5 a 10 años (Paul et al., 1997; Post y Kwon, 2000). Garten y Wullschleger (1999) usaron técnicas estadísticas convencionales) y concluyeron que se requieren de al menos 100 muestras en un sitio para detectar un cambio de 2 a 3% en el carbono orgánico de los suelos y que un cambio de 10 a 15% sólo requiere de 16 muestras. Así, considerando las limitaciones de los muestreos disponibles (incluyendo los límites de detección de las técnicas de laboratorio utilizadas) y la tasa de cambio asociada a un cambio en el uso del suelo, resulta suficiente una base de datos muestral que cubra un periodo de dos a cuatro años para nuestro objetivo.

La aplicación de multifractales a los suelos se ha intentado previamente (Kravchenko et al. , 1999; Eghball et al. , 2003), aunque utilizando un marco teórico muy restrictivo y sin estimar funciones universales. En estos trabajos se utilizó la caracterización de multifractales en espacios de fase asociados a dinámicas no-lineales (Parisi y Frisch, 1985; Halsey et al., 1986) que utiliza una notación relacionada con la usada en este trabajo:

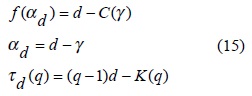
donde: el subíndice d es utilizado para enfatizar su dependencia del espacio de análisis. Las funciones multifractales f(α_d) y τ_d(q) son usadas para caracterizar a los multifractales y no tienen comportamientos universales. Las dimensiones y órdenes de momentos de la Ecuación 15 son aplicables a la enumeración de eventos (determinísticos) en un espacio de fase; a diferencia de los multifractales universales introducidos que se definen para frecuencias de eventos estocásticos. Las densidades de los procesos multifractales universales:

están referenciadas a un soporte muestral espacial (o temporal) para una resolución l de muestreo (d = 1 para una longitud o unidad de tiempo, d = 2 para un área o d = 3 para un volumen). En el caso de las Relaciones 15, éstas son sólo aplicables a concentraciones acumuladas y no a densidades; de allí su dependencia del espacio d de análisis y su no universalidad.

Para evaluar la función escalante (de estructura) del carbono orgánico en los suelos de México, se analizó la base de datos del "Estudio de la Evaluación de la Degradación de los Suelos Causados por el Hombre" (SEMARNAT-CP, 2001-2002) que cuenta con información de localización geográfica y contenido de carbono orgánico (kg m^-2 C) del periodo 2001-2002. El soporte muestral es un volumen aproximado de 20 cm x 20 cm en área y 20 cm de profundidad (0.008 m³). El número de muestras es de 4583 y el rango de la distancia de separación entre las muestras es 524.5 m ≤ h ≤ 3 274 751.0 m.

Para evaluar la función E[(ΔZ_λ)^q] para la escala fija de muestreo, después de un análisis del número de datos en cada distancia elapsada h, se utilizó el rango 5000 m ≤ h ≤ 200 000 m. La Figura 2 muestra la evaluación de la función de estructura, en una gráfica log-log de la función de la Ecuación 14, para los momentos q = 0.5, 1.0, 1.5, 2.0 y 2.5, donde se observa que el comportamiento multi-escalante está bien definido (para un monofractal se tendría curvas con igual pendiente). La dispersión observada para los órdenes de momentos grandes es debida al número finito de muestras usado. La Figura 3 muestra el coeficiente de determinación para diferentes órdenes de momento analizados, donde, para q > 3, las estimaciones no son tan buenas.

La Figura 4 muestra la función ζ(q) estimada, donde se observa un comportamiento lineal para momentos de orden aproximadamente q ≤ q_min≈ 0.6 y q ≤ q_max ≈ 2.8, asociados a la divergencia de los momentos estadísticos. El valor de H se estimó directamente de H = = 0.1196.

 

DISCUSIÓN

En este trabajo se presenta un marco teórico para la caracterización del comportamiento del contenido orgánico de los suelos, definiendo metodologías de estimación de la función multi-escalar universal empírica que caracteriza la variabilidad de escala (espacial) del proceso. La teoría de los procesos multifractales ha servido de fundamento de la modelación y está basada en una fenomenología que utiliza cascadas multiplicativas como un medio de disipación de las densidades del proceso.

La teoría de los procesos universales no conservativos se aplicó a una base de datos del COS en México, usando funciones de estructura para caracterizar los parámetros de la función universal multi-escalar ζ(q). Los resultados del proceso de estimación dieron como resultado de H = ζ(1) 0.1196, que hace al proceso ligeramente no conservativo. En las modelaciones realizadas se observó una divergencia de momentos estadísticos (mínimo y máximo), caracterizada por un comportamiento lineal de la función universal de estructura, que puede ser interpretada en forma errónea como evidencia de un proceso fractal. Este comportamiento será analizado en un trabajo complementario, el segundo de una serie de tres.

Es importante enfatizar que el marco teórico introducido, multifractales universales, permite utilizar una función general (universal) que relaciona los parámetros de los procesos analizados. Así, la universalidad se refiere a la función multi-escalar y no necesariamente a los parámetros de ésta. El siguiente paso consiste en determinar si los parámetros de la función universal multi-escalar espacial del COS son universales, por lo que se requiere del análisis de otras bases de datos. En primera instancia, los resultados de los análisis realizados en este trabajo muestran que el modelo multifractal universal es compatible con la evidencia experimental.

Definida la función universal multi-escalante, después del análisis de la divergencia de los momentos estadísticos, entonces es posible estimar los momentos estadísticos (promedios, por ejemplo) asociados a cambios de escala de muestreos del COS y asi poder realizar inventarios objetivos que consideren en forma explícita la escala de muestreo y la de agregación. Esta temática es tratada en el tercer artículo de la serie.

 

LITERATURA CITADA

Brax, Ph. and R. Peschanski. 1991. Levy stable law description of intermittent behaviour and quark-gluon plasma phase transitions. Phys. Lett. B. 253: 225-230.         [ Links ]

Dagan, G. 1986. Statistical theory of groundwater flow and transport: pore to laboratory, laboratory to formation, and formation to regional scale. Water Resour. Res. 9: 120-134.         [ Links ]

Eghball, B., J. S. Schepers, M. Negahban, and M. R. Schlemmer. 2003. Spatial and temporal variability of soil nitrate and corn yield: multifractal analysis. Agron. J. 95: 339-346.         [ Links ]

Etchevers, J. D., O. Masera, C. Balbontin, D. Gomez, A. Monterroso, R. Martinez, M. Acosta, M. Martinez, and C. Ortiz. 2006. Soil carbon sequestration in Mexico and Central America (Biome A). Part II. Chapter 7. In: R. Lal, C. C. Cerri, M. Bernoux, J. Etchevers, and C. E. Pellegrino Cerri (eds.). Carbon sequestration in soils of Latin America. The Haworth Press. Binghamton, NY, USA.         [ Links ]

Garten, C. T. and S. D. Wullschleger. 1999. Soil carbon inventories under a bioenergy crop (Switchgrass): measurement limitations. J. Environ. Qual. 28: 1359-1365.         [ Links ]

Goovaerts, P. 1997. Geostatistics for natural resources evaluation. Oxford University Press. New York, NY, USA.         [ Links ]

Halsey, T. C., M. H. Jensen, L. P. Kadanoff, I. Procaccia, and B. Shraiman. 1986. Fractal measures and their singularities: the characterization of strange sets. Phys. Rev. A. 33: 1141-1151.         [ Links ]

Hassan, H. M., A. W. Warrick, and A. Amoozegar-Fard. 1983. Sampling volume effects on determining salt in a soil profile. Soil Sci. Soc. Am. J. 47: 1265-1267.         [ Links ]

INE-SEMARNAP (Instituto Nacional de Ecología-Secretaría de Medio Ambiente, Recursos Naturales y Pesca). 1997. México: Primera comunicación nacional ante la Convención Marco de las Naciones Unidas sobre cambio climático. México, D. F.         [ Links ]

INE-SEMARNAT (Instituto Nacional de Ecología-Secretaría de Medio Ambiente y Recursos Naturales). 2001. México: Segunda comunicación nacional ante la Convención Marco de las Naciones Unidas sobre cambio climático. México, D. F.         [ Links ]

INE-SEMARNAT (Instituto Nacional de Ecología-Secretaría de Medio Ambiente y Recursos Naturales). 2006. México: Tercera comunicación nacional ante la Convención Marco de las Naciones Unidas sobre cambio climático. México, D. F.         [ Links ]

IPCC (Intergovernmental Panel on Climate Change). 1997. Revised 1996 IPCC guidelines for national gas inventories. Reference Manual. Volume 3. IPCC/OECD/IEA. Paris, France.         [ Links ]

IPCC (Intergovernmental Panel on Climate Change). 2000. Good practice guidance and uncertainty management in national greenhouse gas inventories. IPCC/OECD/IEA/IGES. Hayama, Japan.         [ Links ]

IPCC (Intergovernmental Panel on Climate Change). 2006. 2006 IPCC guidelines for national greenhouse inventories. Volume 4. IGES. Hayama, Japan.         [ Links ]

Isaaks, E. H. and R. M. Srivastava. 1989. Applied geostatistics. Oxford University Press. New York, NY, USA.         [ Links ]

Journel, A. G. 1988. New distance measures: the route towards truly non-Gaussian geostatistics. Math. Geol. 20: 459-475.         [ Links ]

Journel, A. G. and C. Huijbregts. 1978. Mining geostatistics. Academic Press. New York, NY, USA.         [ Links ]

Kida, S. 1991. Log-stable distribution and intermittency of turbulence. J. Phys. Soc. Japan 60: 5-8.         [ Links ]

Kolmogorov, A. N. 1962. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mechanics 13: 82-85.         [ Links ]

Kravchenko, A. N., C. W. Boast, and D. G. Bullock. 1999. Multifractal analysis of soil spatial variability. Agron. J. 91: 1033-1041.         [ Links ]

Lin, H. 2003. Hydropedology: bridging disciplines, scales, and data. Vadose Zone J. 2: 1-11.         [ Links ]

Matheron, G. 1971. The theory of regionalized variables and its applications. Fasc. 5. Paris School of Mines. Paris, France.         [ Links ]

Miller, R. D. 1994. Intrinsic mesoscopic spatial variability in macroscopically uniform soils. Soil Sci. Soc. Am. J. 58: 1364-1367.         [ Links ]

Monin, A. S. and A. M. Yaglom. 1975. Statistical fluid mechanics: mechanics of turbulence. MIT Press. Boston, MA, USA.         [ Links ]

Parisi, G. and U. Frisch. 1985. A multifractal model of intermittency. pp. 84-88. In: M. Ghil, R. Benzi, and G. Parisi (eds.). Turbulence and predictibility in geophysical fluid dynamics and climate dynamics. North Holland Press. Amsterdam, The Netherlands.         [ Links ]

Paul, E. A., K. Paustian, E. T. Elliot, and C. V. Cole. 1997. Soil organic matter in temperate agroecosystems: long-term experiments in North America. CRC Press. Boca Raton, FL, USA.         [ Links ]

Post, W. M. and K. C. Kwon. 2000. Soil carbon sequestration and land-use change: processes and potential. Global Change Biol. 6: 317-327.         [ Links ]

Post, W. M., J. Pastor, A. W. King, and W. R. Emanuel. 1990. Aspects of the interaction between vegetation and soil under global change. pp. 345-363. In: J. Wisniewski and A. E. Lugo (eds.). Natural sinks of CO₂. Kluwer Academic Publishers. Palmas del Mar, Puerto Rico.         [ Links ]

Post, W. M., R. C. Izaurralde, L. K. Mann, and N. Bliss. 2001. Monitoring and verifying changes of organic carbon in soil. Clim. Change 51: 73-99.         [ Links ]

Schertzer, D. and S. Lovejoy. 1983. The dimension and intermittency of atmospheric dynamics. pp. 7-33. In: B. Launder (ed.). Turbulence shear flows 4. Springer-Verlag. Karlsruhe, Germany.         [ Links ]

Schertzer, D. and S. Lovejoy. 1987. Physically based rain and cloud modeling by anisotropic multiplicative turbulent cascades. J. Geophys. Res. 92: 9693-9714.         [ Links ]

Schertzer, D. and S. Lovejoy. 1989. Nonlinear variability in geophysics: multifractal analysis and simulation. pp. 49-63. In: L. Pietronero (ed.). Fractals: physical origin and consequences. Plenum. New York, NY, USA.         [ Links ]

Schertzer, D. and S. Lovejoy. 1991. Nonlinear geodynamical variability: multiple singularities, universality and observables. pp. 41-82. In: D. Schertzer and S. Lovejoy (eds.). Non-linear variability in geophysics: scaling and fractals. Kluwer. Dordrecht, The Netherlands.         [ Links ]

SEMARNAT-CP (Secretaría de Medio Ambiente y Recursos Naturales-Colegio de Postgraduados). 2001-2002. Evaluación de la degradación de los suelos causada por el hombre en la República Mexicana, a escala 1:250 000, Memoria Nacional. México, D. F.         [ Links ]

Starr, J. L., T. B. Parkin, and J. J. Meisinger. 1995. Influence of sample size on chemical and physical soil measurements. Soil Sci. Soc. Am. J. 59: 713-719.         [ Links ]

Tillotson, P. M. and D. R. Nielsen. 1984. Scale factors in soil science. Soil Sci. Soc. Am. J. 48: 953-959.         [ Links ]

Wood, E. F., M. Sivapalan, K. Beven, and L. Band. 1988. Effects of spatial variability and scale with implications to hydrologic models. J. Hydrol. 102: 29-47.         [ Links ]

 

NOTA

* Publicado como nota de investigación en Terra Latinoamericana 26: 183-191.