Introducción

La modelación de curvas de mortalidad es bastante antigua y se tiene como primera propuesta la de ^{Moivre (1725)}. Posteriormente son de destacar las elaboradas por ^{Gompertz (1825}; ¹⁸⁶⁰; ¹⁸⁶²) y ^{Makeham (1867}; 1890). Asimismo, se fueron afinando las propuestas de modelaje de la mortalidad donde sobresale la incorporación de patrones cada vez más específicos y característicos de las distintas etapas de la vida humana, como se hace originalmente en ^{Thiele (1871)}, idea que se retoma tiempo después en los modelos desarrollados por ^{Heligman y Pollard (1980)}. En ^{Forfar (2006)} se hace un amplio recorrido cronológico de las diversas propuestas existentes en la literatura en cuanto a curvas (leyes) de mortalidad.

El modelo de ^{Heligman y Pollard (HP) (1980)}, además de ser útil para la graduación, entre varias aplicaciones, también ha sido empleado para analizar o predecir el comportamiento de la mortalidad futura. Por ejemplo, en ^{Felipe, Guillen y Pérez-Marín (2002)} se realiza un estudio de la evolución de sus parámetros con modelos ARIMA y se pronostica su comportamiento para la población española. También se ha recurrido al modelo para detectar los cambios en la mortalidad en edades jóvenes, la joroba, debido a los efectos del VIH en África (^{Sharrow, Clark, Collinson, Kahn y Tollman, 2013)}. En ^{Hartmann (1987)} y ^{Yuen (1997)} se lleva a cabo una comparación entre diferentes modelos para ajustar la mortalidad y se concluye que ^{Heligman y Pollard (1980)} proporciona un mejor ajuste. Por otra parte, ^{Kostaki (1991)}, ^{Irnawati (2008)} y ^{Syahmi, Md Yusuf, Suhaylah y Yazis (2015)} han utilizado esta herramienta para crear tablas de mortalidad a partir de datos agregados.

El modelo de HP tiene diferentes formas de ser estimado: una posibilidad es por medio de optimización no lineal, donde es fundamental utilizar valores iniciales, y otra es a través de técnicas bayesianas. Se considera que, en ambos casos, se requiere del conocimiento de herramientas teóricas que permitan su estimación con el fin de facilitar la convergencia del modelo, al igual que tener acotados intervalos y la distribución para los parámetros. Por ejemplo, en ^{Sharrow, Clark, Collinson, Kahn y Tollman (2013)} se propone el uso de distribuciones uniformes continuas para sus parámetros de la siguiente manera: A ~ U [0,0.25 ], B y C ~ U [0,1 ], D ~ U [0,0.25 ], E ~ U [0,20 ], F ~ U [15,55 ], G ~ U [0,0.01 ] y H ~ U [1,1.5 ]. La relevancia de los rangos de referencia de dichos parámetros resulta orientativa para intentar la estimación del modelo, sin embargo, puede no resultar atractivo por las exigencias técnicas que más adelante se implican.

En este trabajo se tienen por objetivos: 1) ilustrar la aplicación de un método para estimar tendencias con suavizamiento controlado (método propuesto por ^{Guerrero, 2008}), es decir, en el presente contexto, curvas de mortalidad donde se impone la suavidad por medio de un índice (o porcentaje); así como 2) proponer un método para medir la suavidad inducida, sujeta a funciones de pérdida, ejemplificado para estimaciones previas citadas en la literatura con el modelo HP. El índice de suavizamiento se sustenta en el llamado filtro de ^{Hodrick y Prescott (1997)}, mismo que ha tomado una gran aceptación en el campo de la economía en el marco de series de tiempo. En este documento se puede concebir a los valores de las q _x como una serie de tiempo.

Se tienen entonces como preguntas centrales de investigación: ¿desde la perspectiva de suavizamiento, con una técnica no paramétrica, es posible aproximar de mejor manera curvas de mortalidad en comparación con otros métodos?, ¿qué tan factible es medir la suavidad inducida en curvas de mortalidad estimadas con el modelo HP, para que con esa información se pueda orientar en cómo poder fijar la suavidad y luego se puedan estimar curvas de mortalidad en general?, y ¿resulta satisfactoria la propuesta para todas las edades de las curvas de mortalidad?

Es importante reconocer que en la propuesta existen problemas al aproximar la curva de HP en las colas, esto es, no se logra un ajuste “idóneo” tanto al inicio como al final de la curva de mortalidad, como se verá más adelante; sin embargo, para edades centrales es notable su potencial. Adicionalmente, se entiende en el trabajo como términos equivalentes la tendencia en estadística y la curva de mortalidad en demografía. Se emplean estimaciones provenientes de HP (1980), ^{Kostaki (1991)}, ^{Felipe, Guillen y Pérez-Marín (2002)} y ^{Jos (2014)}.

Se considera que la relevancia de este trabajo radica en que algún analista interesado en estimar curvas de mortalidad, con no mucha holgura de tiempo y con una formación estándar en la profesión demográfica, pueda realizarlo de una manera sencilla y expedita, en términos de la aproximación aquí propuesta, con los beneficios agregados que más abajo se enuncian. En principio, este tipo de herramientas no sólo es útil para analizar series económicas, sino que por su objetividad, que se verifica en este trabajo, también es útil en tópicos demográficos. Como se menciona en ^{Guerrero (2008)}, la necesidad de estimar la tendencia para fines informativos de una serie de tiempo es de suma importancia para cualquier tipo de análisis, y puede ser apoyada desde la gráfica de los datos.

El trabajo está organizado como sigue. En la primera sección (Introducción) se describe el tema de investigación. En la segunda se enmarca el modelo HP, así como algunas de sus variantes. En la tercera se aborda la estimación de tendencias de mortalidad con suavizamiento controlado. En el cuarto apartado se exponen ejemplos y comparativos en la aplicación del llamado índice de suavidad, con estimaciones previamente elaboradas, y se señala la manera de aproximar las curvas generadas mediante HP de los artículos seleccionados. Posteriormente se exponen aplicaciones diversas con la presentación de los patrones observados en funciones de pérdida, y el comportamiento del parámetro de suavizamiento, donde se hace una ilustración de las aproximaciones y se presentan cuadros resumen de los resultados obtenidos. Finalmente se señalan las principales conclusiones a partir de los hallazgos encontrados en el presente trabajo.

El modelo de Heligman y Pollard (HP)

El modelo HP es utilizado en la literatura demográfica para estimar la mortalidad de una población. En el artículo seminal de 1980 se presentan distintas expresiones matemáticas que generan las correspondientes curvas de mortalidad basadas en la siguiente propuesta:

donde q _x es la probabilidad de morir durante un año de una persona a edad x ,px=1-qx y los parámetros a estimar resultan ser A, B, C, D, E, F, G y H. La naturaleza de la ecuación no permite valores mayores a 1 ni menores que 0. La curva está compuesta por tres términos que poseen interpretaciones demográficas. El primer sumando representa la caída rápida de la mortalidad infantil y requiere tres parámetros. El segundo término ajusta una curva que se asemeja a la distribución log-normal. En tanto que el último sumando está basado en la función de Gompertz. En ^{Heligman y Pollard (1980)} y ^{Sharrow, Clark, Collinson, Kahn y Tollman (2013)} se proporciona una descripción detallada de la interpretación de cada uno de los parámetros desde un punto de vista demográfico.

De la ecuación previa, en ^{Heligman y Pollard (1980)} se proponen otras expresiones de la curva de mortalidad, que se presentan de manera reducida y en donde sólo se expresa el valor de q _x . Sus expresiones son las siguientes:

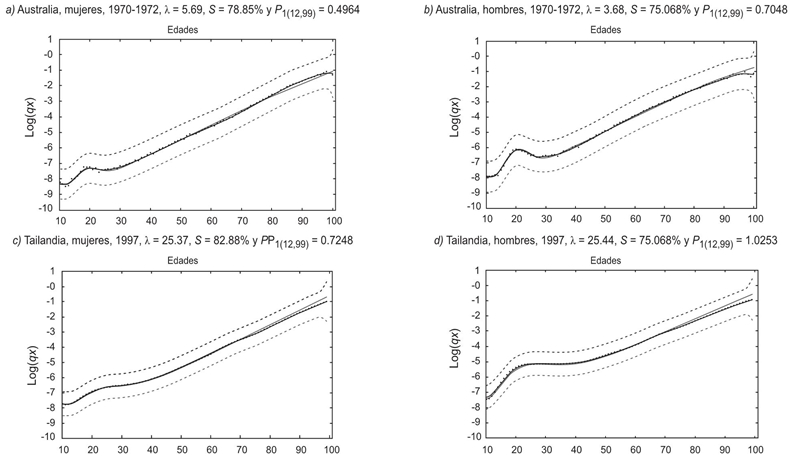
Las ecuaciones anteriores muestran una diferencia en el tercer sumando. Como lo mencionan ^{Heligman y Pollard (1980)}, ambas formas presentan un mejor ajuste en la joroba de accidentes y en edades avanzadas. En este trabajo se utiliza la respectiva expresión, en función de lo que fue elegido en cada una de las fuentes bibliográficas seleccionadas y consultadas para este fin. Algunos ejemplos de las curvas estimadas con sus valores observados de q _x , en escala de logaritmo natural, se muestran en la Gráfica 1.

Fuente: Elaboración propia.

Gráfica 1 Mortalidades varias 

De acuerdo con ^{Dellaportas, Smith y Stavropoulos (2001)}, ^{Debón, Montes y Sala (2006)} y ^{Congdon (1993)}, el modelo HP tiene algunos inconvenientes: los errores estándar para las estimaciones de los parámetros son muy grandes, ya que cuentan con una alta correlación entre ellos; se tienen dificultades cuando se estima el parámetro K, que en muchas ocasiones resulta insignificante y que imposibilita la estimación del modelo; no siempre se logra la convergencia en rutinas iterativas de estimación no lineal; las correlaciones entre los parámetros del modelo HP son altas, especialmente entre A y B, A y C, B y C, G y H, en ambos sexos, así como entre G y K, H y K para hombres. Todas estas desventajas que presenta el modelo HP son significativamente superadas con la propuesta que se realiza en el presente documento.

Estimación de curvas de mortalidad con suavizamiento controlado

Al analizar series de tiempo se puede llegar a distintas formas de interpretar los datos. Una de ellas es considerar una serie de tiempo cualquiera, como la suma de una tendencia no observable, pero sí subyacente, que varía dinámicamente a lo largo del tiempo, adherida a un componente aleatorio, es decir,

donde τ _t es la tendencia, η _t es el componente aleatorio y N el número de datos.

Existen otras técnicas para calcular la tendencia de una serie de tiempo, como pueden ser, por ejemplo, promedios móviles, suavizamiento exponencial, regresión no paramétrica, entre varias. Todos los métodos anteriores funcionan aplicando filtros a las series yt dando como resultado otra serie τ^t es decir la tendencia estimada. Este tipo de filtros utilizan operaciones que involucran retrasos de la forma ∇=1-Β en donde B está dado por ΒΧt=Χt-1 .

El llamado filtro de ^{Whittaker (1923)} ha tenido extensiones como las elaboradas por ^{Knorr (1984)} y ^{Nocon y Scott (2012)}. Con los parámetros de orden de diferenciación d = 2 y la matriz de pesos idénticos en las observaciones, W = I, el método de Whittaker se utilizó por ^{Hodrick y Prescott (1997)} para estimar tendencias y ciclos económicos y se le conoce en el ámbito de la econometría como filtro de Hodrick y Prescott. En él se reduce gradualmente el componente aleatorio, induciendo a una suavidad, y a través de éste se estiman valores suavizados que representan mejor a los valores verdaderos no observables. En el filtro se considera además un parámetro de suavizamiento, λ, mismo que simultáneamente pondera tanto la bondad del ajuste como la suavidad. En este filtro se sustenta el método de ^{Guerrero (2008)}. Es importante mencionar que, en general, cuando se realizan estimaciones de manera automática, es decir, utilizando herramientas implementadas en los softwares estadísticos, no se puede decidir qué valor otorgarle al parámetro λ; por lo tanto, se ignora la suavidad alcanzada y no se tienen elementos válidos, desde el punto de vista estadístico, para hacer comparativos con otras estimaciones.

El filtro es relativamente sencillo de aplicar para cualquier serie de datos y, como lo menciona y demuestra ^{Guerrero (2008)}, produce resultados idénticos a otros métodos de suavizamiento. En ^{Kaiser y Maravall (2001)} se proporciona una explicación más detallada de la teoría matemática detrás del filtro. La estructura del filtro Hodrick y Prescott proviene de la siguiente expresión:

donde λ es el parámetro que penaliza la ausencia de suavidad. El primer término tiene como propósito el ajuste de la tendencia con los datos observados, en tanto que el segundo a la inducción de la suavidad. Puede apreciarse que cuando λ→0 la tendencia estimada τ^t converge a los valores observados y _t , debido a que el segundo parámetro se vuelve cero y el valor τ^t de la serie que minimiza es el mismo yt . Por otro lado, cuando λ→0 el valor que minimiza la serie sería el modelo lineal ∇2τt=0 . La expresión anterior, escrita en forma matricial está dada por

donde y=y1,…,yN´,τ=τ1,…,τN´ , y K ₂ es la matriz de N-2×N de segundas diferencias. Es decir, es la matriz tridiagonal

La solución al problema que se propone es alcanzable tras aplicar mínimos cuadrados generalizados, con lo que se obtiene el resultado

La serie τ^t representa la tendencia estimada dado un valor de λ, que en el presente trabajo se refiere a la curva de mortalidad. Nótese que el valor de λ se establecerá, bajo este enfoque, con base en la necesidad del análisis que se requiera y, en general, de la naturaleza de los datos. También, como fue mencionado anteriormente, la varianza de τ^ en términos del error cuadrático medio, está dada por Varτ^=IN+λΚ2´K2-1ση-2 (para conocer los detalles, véase ^{Guerrero, 2008}). Debe tenerse presente que por medio de Varτ^ se obtienen los intervalos de las respectivas estimaciones, elemento que no proporciona el modelo HP per se.

Dada la solución anterior a la tendencia τ^ , ^{Guerrero (2008)} propone medir la suavidad por medio de la siguiente expresión, que es un índice,

en donde tr(.) representa la traza de la matriz. Puede notarse que la suavidad no depende de los datos, sino exclusivamente del valor del parámetro λ y del número total de datos N. De hecho, a mayor cantidad de datos se requerirá un índice más alto para suavizar. Es claro que cuando λ→0 la suavidad Sλ;N→0, en tanto que cuando λ→∞ la suavidad Sλ;N→1; este índice se puede representar en términos porcentuales como Sλ;N% .Es demostrable que el máximo del índice de suavidad alcanzable para un conjunto de N datos está dado por 1 - 2/N. Con ello, por ejemplo, con 100 datos la máxima suavidad a la que se puede aspirar es de S = 98%. Sin embargo, este orden de índice de suavidad podría ser demasiado alto y ello generaría la ausencia de sentido demográfico en el contexto de suavizado de curvas de mortalidad. Asimismo, el índice cuenta con algunas propiedades deseables, como lo son: linealidad, adherencia a la unidad y no alteración ante transformaciones lineales de los datos. En el contexto estadístico, se deduce que el índice es una reparametrización de lo que se conoce, en el marco del suavizamiento o graduación, como grados de libertad (df = degree of freedom).

Una crítica que existe a esta propuesta de índice radica en cómo justificar la imposición de determinado porcentaje de suavidad, aun cuando se argumenta que es relevante para hacer comparativos. Por ejemplo, en ^{Alba y Gómez (2012)} se abona al respecto desde la perspectiva bayesiana y se propone un método para tal fin. En este trabajo, justamente, la propuesta para imponer la suavidad pertinente se resume en realizar mediciones de suavidades inducidas en aplicaciones previamente construidas. Otras opciones podrían ser ejercicios de simulación o a través de indicadores de cobertura. Para esto último, dada una determinada suavidad impuesta, el indicador de cobertura podría indicar cuántas observaciones están contenidas dentro del intervalo de estimación e imponer aquella en la que se tengan coberturas de órdenes específicos como: 90, 95 o 99%.

Desde una óptica usual, para suavizar datos, se podría obtener un valor del parámetro de suavizamiento λ óptimo mediante criterios automáticos como el Akaike, Schwarz, validación cruzada generalizada (VCG) o el de validación cruzada ordinaria (VCO). En ^{Cortés-Toto, Guerrero y Reyes (2017)} se mide la suavidad alcanzada cuando el parámetro de suavizamiento λ es elegido a través de esta clase de criterios. En tal trabajo se concluye que en principio el analista depende de la cantidad de datos y del tipo de tendencia subyacente a los mismos, y que son menos relevantes la eventual presencia de estacionalidad y la varianza existente. Además, se dimensiona la suavidad inducida y se evidencia que escapa la misma de la decisión del analista. En la Gráfica 2 se presentan algunos ejemplos y comparativos que ponen de manifiesto la necesidad y la ventaja de imponer suavidades como es factible con el uso de la propuesta aquí expuesta.

Fuente: Elaboración propia.

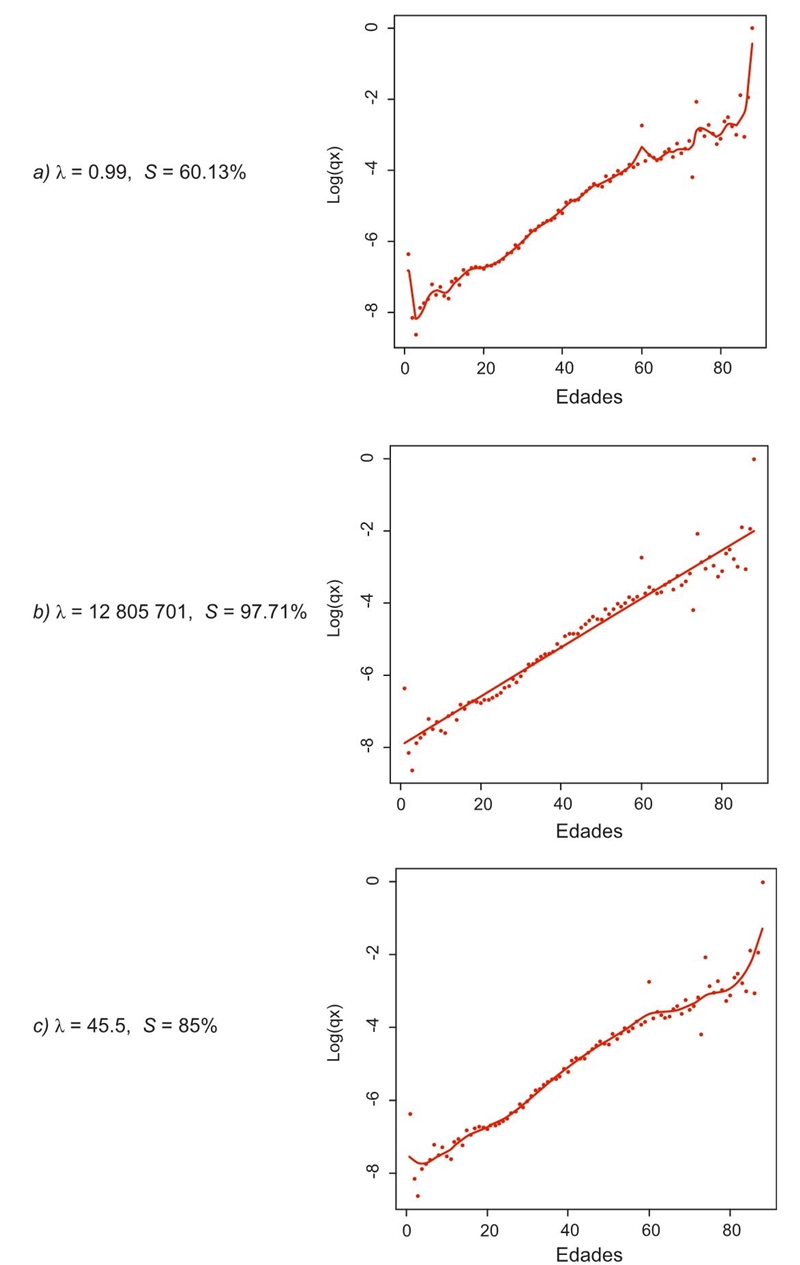
Gráfica 2 Estimaciones de tendencias con criterios automáticos e impuesto 

Con el software estadístico R, con la librería pspline, los criterios VCG y VCO están disponibles (véase el código genérico en los Anexos). Al emplearlo con datos de ^{Mendoza, Madrigal y Gutiérrez-Peña (2001)}, con el criterio VCG se obtiene de manera automática λ = 0.99, lo cual implica un índice de suavidad de aproximadamente el S = 60.13% y grados de libertad de 35.09. Se observa cómo la tendencia se dispone próxima a los datos. Con el criterio VCG se obtiene λ = 12 805 701, un índice de suavidad de S = 97.71% y grados de libertad de 2.01, lo cual hace que la tendencia sea prácticamente una recta. En ambos casos queda sin sentido demográfico la estimación de la curva de mortalidad. Por un lado, es demasiada rugosa la estimación, y por el otro, en principio la curvatura de la mortalidad en edades jóvenes es ignorada y se evoca a la añeja propuesta de Moivre.

Es claro que para un mismo conjunto de datos, dos criterios automáticos estadísticos ad hoc generan estimaciones totalmente distintas. Si se impone un índice de suavidad, por ejemplo de S = 85% como el sugerido en ^{Ovin y Silva (2016a}; ^2016b), con λ = 45.5 y grados de libertad de 13.18, se obtienen resultados con más sentido demográfico. En términos operativos, para obtener determinado índice de suavidad, en la ecuación para S(λ; N), se calibra dando distintos valores de λ, hasta que de manera heurística se obtiene la suavidad deseada.

Con la finalidad de sensibilizar al usuario de la presente propuesta, en la Gráfica 3 se muestra un ejemplo con diferentes valores de λ, con datos simulados. Se puede observar cómo con valores pequeños de λ, como en la Gráfica 3a, la tendencia estimada se aproxima bastante a los valores observados. En cambio, cuando λ crece la suavidad se vuelve más evidente como muestra el hecho de que los datos quedan alrededor de la curva suavizada, y para λ mayores a 1000 la tendencia comienza a parecerse a una recta, como en la Gráfica 3d.

Fuente: Elaboración propia.

Gráfica 3 Tendencias estimadas con diferentes valores de λ 

Comparativo con otras curvas de mortalidad y funciones de pérdida

En esta sección se contrastan resultados desde la perspectiva aquí propuesta con algunas curvas de mortalidad obtenidas en ^{Vargas (2014)} y comparables con aquellos estimados por medio de índices de suavidades impuestas del S = 85% y S = 90%, respectivamente. En todos los casos se utiliza el logaritmo natural de las q _x y sin pérdida de generalidad se ilustra con una población selecta; la lógica de la ilustración sería la misma para cualquier otra población que cuente con estimaciones de curvas de mortalidad. Se eligen los que ahí se refieren como tablas de mortalidad mexicana ajustada mediante el modelo de: a) CNSF, b) Makeham, c) extrapolación polinomial, y d) Gompertz. En particular, el modelo HP empleado no resultó ser comparable pues en casi todas las edades se tiene una estimación constante hasta casi los 75 años (véase ^{Vargas, 2014, p. 88}). Debe tenerse presente que cada estimación hecha de a a d, así como las de otros modelos de mortalidad, tienen una complejidad superior a lo que sencillamente se realiza con la estimación y/o medición de tendencias y suavidades respectivamente, pues tienen el común denominador de emplear criterios matemáticos de optimización lineal o no lineal con sus respectivos valores iniciales.

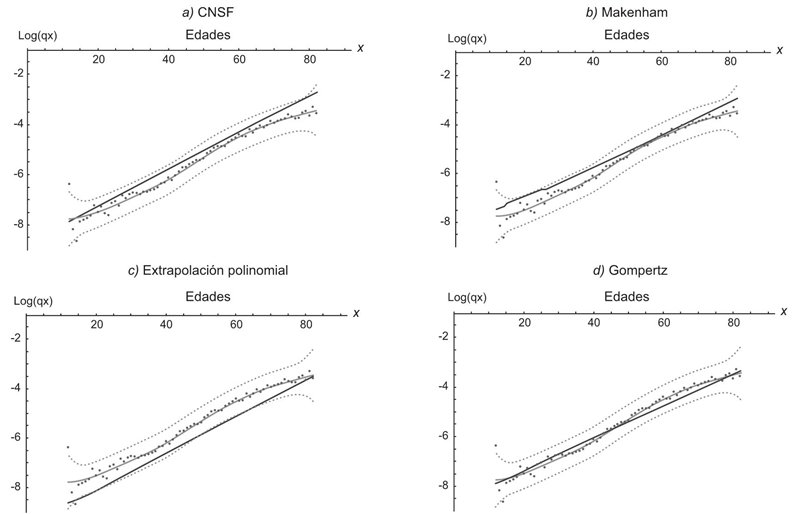
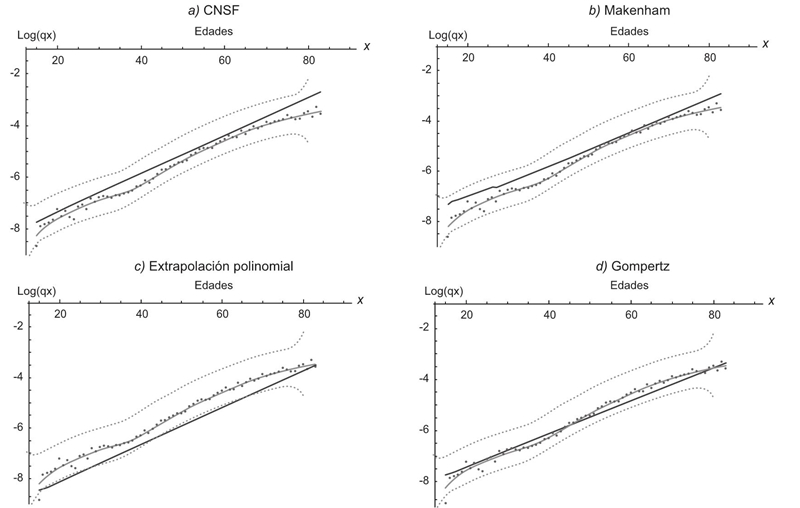
En general, con base en las Gráficas 4 y 5, se aprecia cómo las estimaciones seleccionadas y realizadas por la autora están comprendidas dentro del intervalo de estimación de la tendencia o en algunos casos cercanos a alguna de las fronteras del mismo. También se tiene un mejor patrón en la estimación de la respectiva curva de mortalidad con la propuesta no paramétrica sobre todas las propuestas paramétricas expuestas por la autora. Es probable que en términos numéricos la diferencia parezca insignificante, pero deja de serlo si se consideran indicadores demográficos como esperanza de vida, que considera todas las q _x .

Fuente: Elaboración propia.

Gráfica 4 Comparativos de estimaciones de curvas de mortalidad con intervalos de estimación de dos desviaciones estándar (líneas sólidas tenues), con λ = 293.7 y S = 90% (líneas sólidas): CNSF, Makeham, Extrapolación polinomial y Gompertz 

Fuente: Elaboración propia.

Gráfica 5 Comparativos de estimaciones de curvas de mortalidad con intervalos de estimación de dos desviaciones estándar (líneas sólidas tenues), con λ = 49.25 y S = 85% contra (líneas sólidas): CNSF, Makeham, Extrapolación polinomial y Gompertz 

Dado que uno de los propósitos del trabajo es estimar la suavidad necesaria para aproximar lo mejor posible la curva de mortalidad que proporciona el modelo de HP, y así tener un parámetro de referencia en cuanto a la suavidad necesaria para estimar una curva de mortalidad, se propone conseguirlo a través de medir la diferencia punto a punto que hay entre la tendencia estimada y los valores de la mortalidad estimados por el modelo HP. Por medio de dos de las funciones de pérdida propuestas en ^{Carriere (1992)}, se logra el objetivo. Sin pérdida de generalidad, sean {q _x } los valores observados, y q^x los valores estimados mediante HP. Sean τ^t los valores suavizados con el logaritmo aplicado a los qx dado un valor de λ. Al compararlos con los valores estimados mediante HP q^x se necesita aplicar el inverso del logaritmo para manejarlos en la misma escala (como probabilidades); a esta serie se le llamará t^x . Las funciones de pérdida elegidas dependen exclusivamente del valor de λ, y son:

Ahora se realizan las siguientes tareas. La primera, encontrar el valor de λ que minimiza las expresiones anteriores. Después, encontrar el porcentaje de suavidad logrado para cada uno de los dos valores de λ obtenidos mediante la expresión que se define para S(λ; N). Por último, se analiza el valor mínimo obtenido por las funciones de pérdida para poder comparar las distintas series de datos entre sí. Este valor representará la distancia total que existe entre la serie suavizada t^x y la serie estimada por HP q^x .

Resultados con el modelo de Heligman y Pollard (HP)

Se utilizan estimaciones realizadas en los trabajos de ^{Heligman y Pollard (1980)}, ^{Kostaki (1991)}, ^{Felipe, Guillen y Pérez-Marín (2002)} y ^{Jos (2014)}, en donde se encuentran los valores de los respectivos parámetros para el modelo de HP. Los valores observados de HP y Kostaki se encuentran en los anexos correspondientes; los de ^{Jos (2014)} en Asian Mortality Table, ubicados en la página web de la sociedad actuarial de Hong Kong. Los datos observados de ^{Felipe, Guillen y Pérez-Marín (2002)} fueron obtenidos de la página HumanMortality.com. El número total de series, es decir tablas de mortalidad utilizadas, es de 42. Los cálculos de este apartado se elaboraron con el software de R versión 3.4.1 y Mathematica de Wolfram, versión 10 (véase el código genérico en los Anexos).

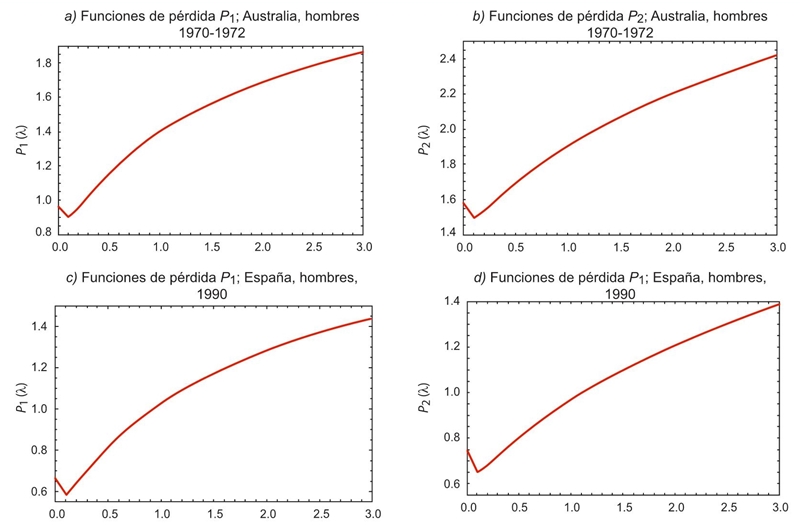
Cuando se busca la minimización de las funciones de pérdida, se obtienen valores pequeños de λ que están entre 0.07 y 0.08 en los dos casos, siendo prácticamente el mismo resultado para todas las series analizadas. Usando este valor de λ, la suavidad alcanzada está en el rango de S = 23% a S =25%, con lo cual se tienen estimaciones demasiado rugosas. Los patrones de comportamiento de las funciones de pérdida se muestran a continuación. Nótese que en las series el mínimo se localiza relativamente pronto y luego hay un crecimiento de manera aparentemente cuadrática. El mecanismo utilizado para construir las gráficas de las funciones de pérdida fue a través de asignar paulatinamente distintos valores crecientes del parámetro de suavizamiento λ (véase la Gráfica 6).

Fuente: Elaboración propia.

Gráfica 6 Comportamiento de funciones de pérdida P₁ y P₂ ; Australia, hombres, 1970-1972, y España, hombres, 1990  

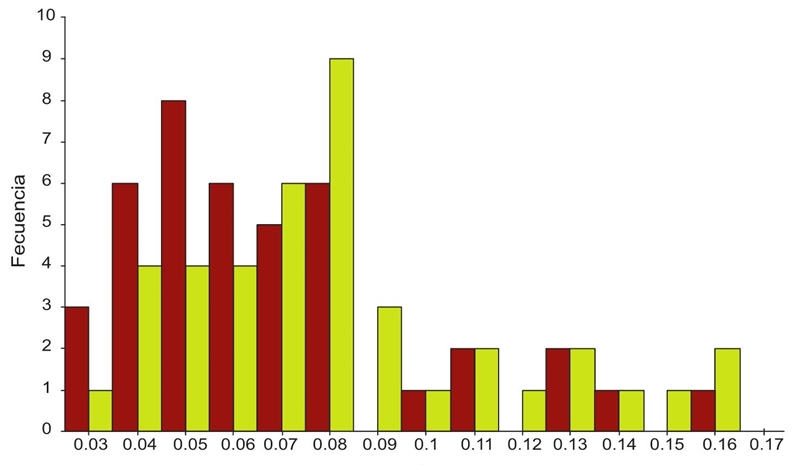
Al realizar este procedimiento de análisis para todas las series mencionadas, se tienen los siguientes resultados, mostrados en los histogramas de la Gráfica 7. La descriptiva de los mismos, así como los demás hallazgos, aparecen más adelante en el Cuadro 2. En ambos casos se aprecia una asimetría a la derecha, con una cola pesada.

Fuente: Elaboración propia.

Gráfica 7 Distribución de los valores de λ que minimizan P₁ versus P₂ (rojo obscuro y verde claro, respectivamente)  

Para P₁ los valores más frecuentes se ubican entre 0.04 y 0.08; para P₂ los valores más comunes estuvieron alrededor de 0.08. En la Gráfica 8 se tienen dos segmentos de la serie suavizada de España 1990 con un parámetro de suavizamiento de λ = 0.07. Así, el índice de suavidad en este caso es de S = 23.47%. Se observa claramente cómo la tendencia estimada se aproxima a casi todos los valores observados de la serie; esto debido al valor pequeño del parámetro λ, lo cual se manifiesta prácticamente con la totalidad de las series utilizadas. El problema no es tan evidente, pues el desbalance (o desajuste) generado en las colas de los datos hace que el valor de la función de pérdida crezca con gran rapidez conforme el valor de λ crece por apenas valores mayores a 0.1, lo cual ocurre para los primeros valores observados y para los últimos. La falta de precisión en los primeros datos hace que las funciones de pérdida crezcan rápidamente, haciendo que el valor de λ que minimiza dichas funciones sean valores muy pequeños. El problema se presenta en menor escala en los valores finales de la serie (entre 90 y 99 de los valores observados) y sólo en algunos casos de las 42 series.

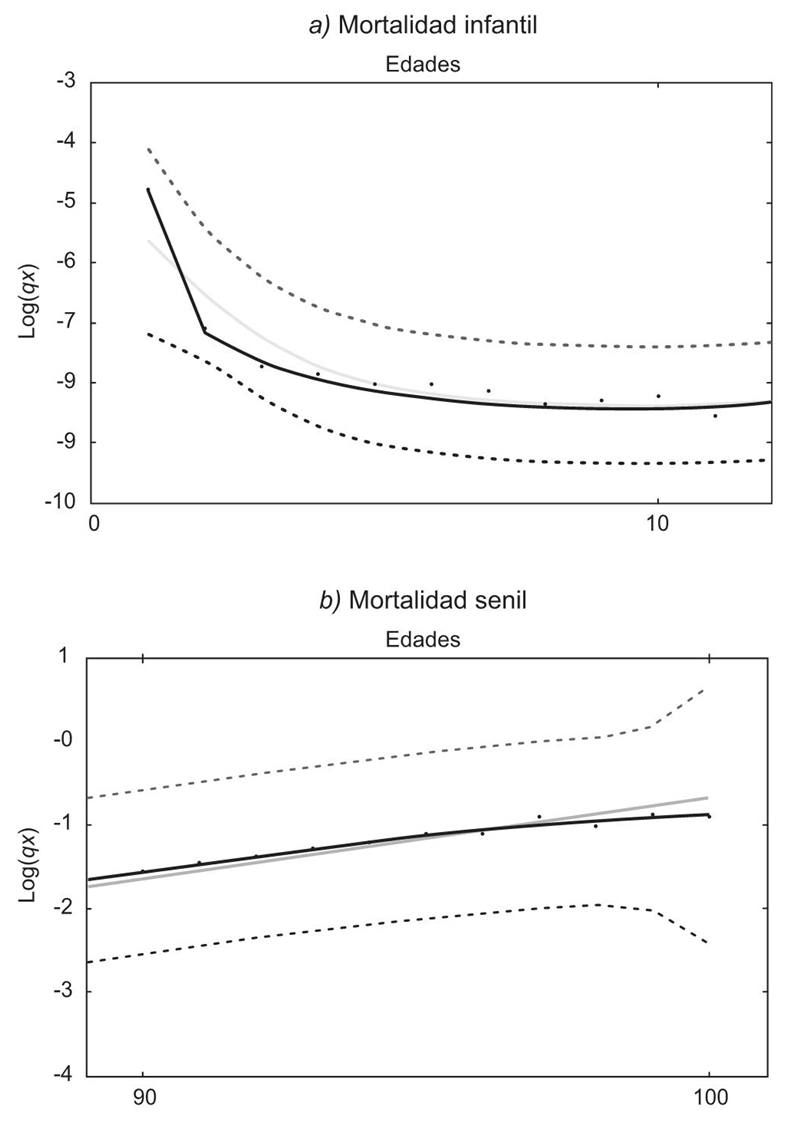
Datos observados: puntos; curva estimada (tendencia) con el modelo HP: línea gris; tendencia estimada: línea negra. Fuente: Elaboración propia.

Gráfica 8 España, hombres, 1990, con λ=0.07. Mortalidad infantil y mortalidad senil 

En el Cuadro 1 se presenta la evolución del comportamiento de las funciones de pérdida, con distintos valores del parámetro de suavizamiento λ, pero considerándolas en dos partes. De esta manera las funciones de pérdida se reescriben como sigue:

y con un razonamiento similar se tiene:

Se puede observar cómo para valores pequeños del parámetro de suavizamiento λ, entre 0.03 y 0.5, P_1(0,11) alcanza su mínimo y se incrementa rápidamente cuando λ crece, mientras P_1(12,99) alcanza su mínimo para valores entre 4 y 20, pero el total de P₁ es fuertemente influenciado por el crecimiento rápido de P_1(0,11). Un escenario similar ocurre en la función de pérdida P₂. De hecho, también se aprecia cómo el valor P_2(0,11) para valores entre 8 y 20 es considerablemente mayor que P_2(12,99), donde su mínimo se encuentra de modo aproximado. Se debe recalcar que P_2(0,11) contiene solamente 12 de los 100 datos, mientras P_2(12,99) el resto. La presente situación se manifiesta análogamente en las demás series analizadas en el documento.

Dado que el desajuste empieza a crecer más significantemente en la parte de la mortalidad infantil, se decide omitirles y así la propuesta, en relación a la curva de la mortalidad del modelo HP, como se notará más adelante, crea un ajuste casi perfecto en el resto de los datos. Con esta restricción del número de datos a emplear, la máxima suavidad a la que se puede aspirar es de S = 97.7%. Las funciones de pérdida quedan como sigue:

(11)

(12)

En la Gráfica 9 se presentan los comportamientos de las funciones P_1(12,99), y P_2(12,99). Cabe notar que el patrón a continuación expuesto es similar en el resto de las series elegidas y, una vez localizado el mínimo, el patrón de las funciones de pérdida, a diferencia de los anteriores, crece de manera menos acelerada. Al igual que con las otras funciones de pérdida, se tiene una distribución asimétrica a la derecha.

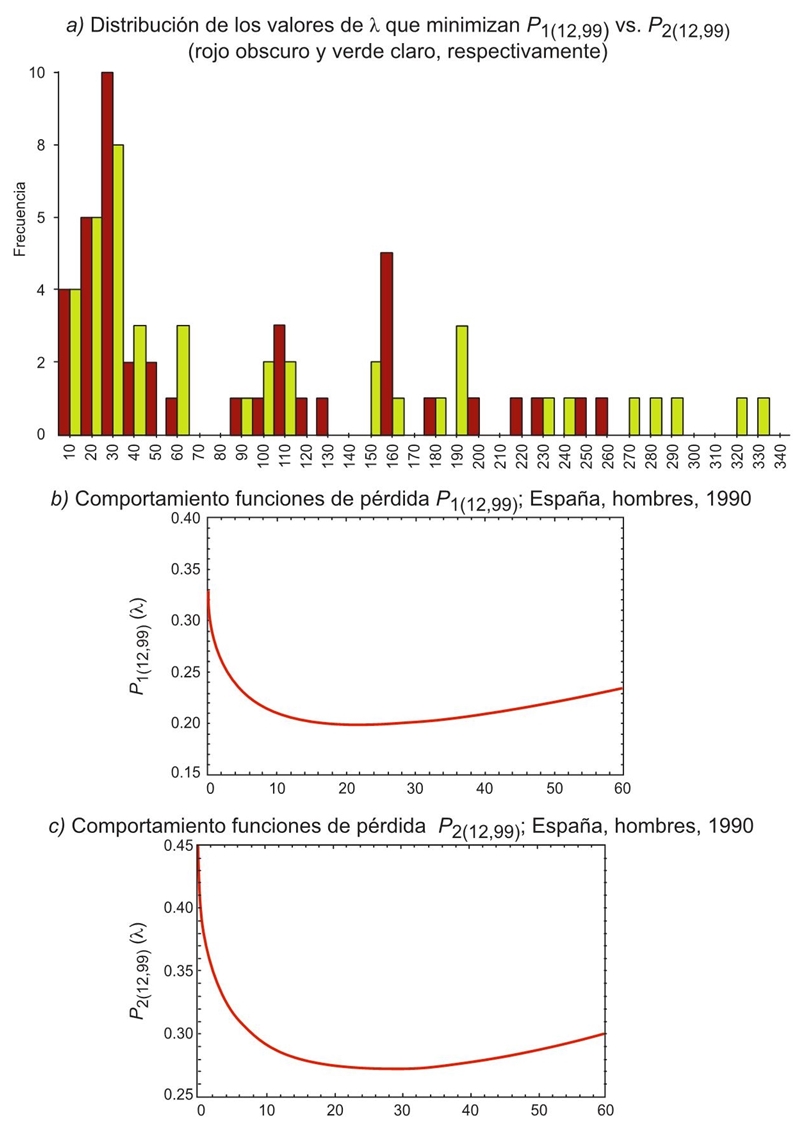
Fuente: Elaboración propia.

Gráfica 9 Distribución de los valores de λ que minimizan P_1(12,99) vs. P_2(12,99); y comportamiento funciones de pérdida. España, hombres, 1990  

Ahora el valor que minimiza la función P_1(12,99) es λ = 23.12, que implica una suavidad de S= 82.5%, y para P_2(12,99) el valor obtenido es λ = 28.36 con una suavidad alcanzada de S = 83.25%. En otras palabras, los dos valores de λ fueron muy similares para las dos funciones de pérdida. La mayor discrepancia fue encontrada en la última parte de las series.

Se aprecia, con base en la Gráfica 10, que existe una mejora sustantiva en el ajuste para casi todos los valores. Al eliminar los primeros valores de la serie de las funciones de pérdida se logra que el método proporcione resultados más consistentes e interpretables en función de los valores de λ y de la suavidad S. El resumen de todos los valores de λ obtenidos para las 42 series se presenta en el Cuadro 2; en él se realiza una comparativa de las funciones P₁, P₂, P_1(12,99) y P_2(12,99), así como su media y desviación estándar. La información está organizada tanto por décadas como por sexo.

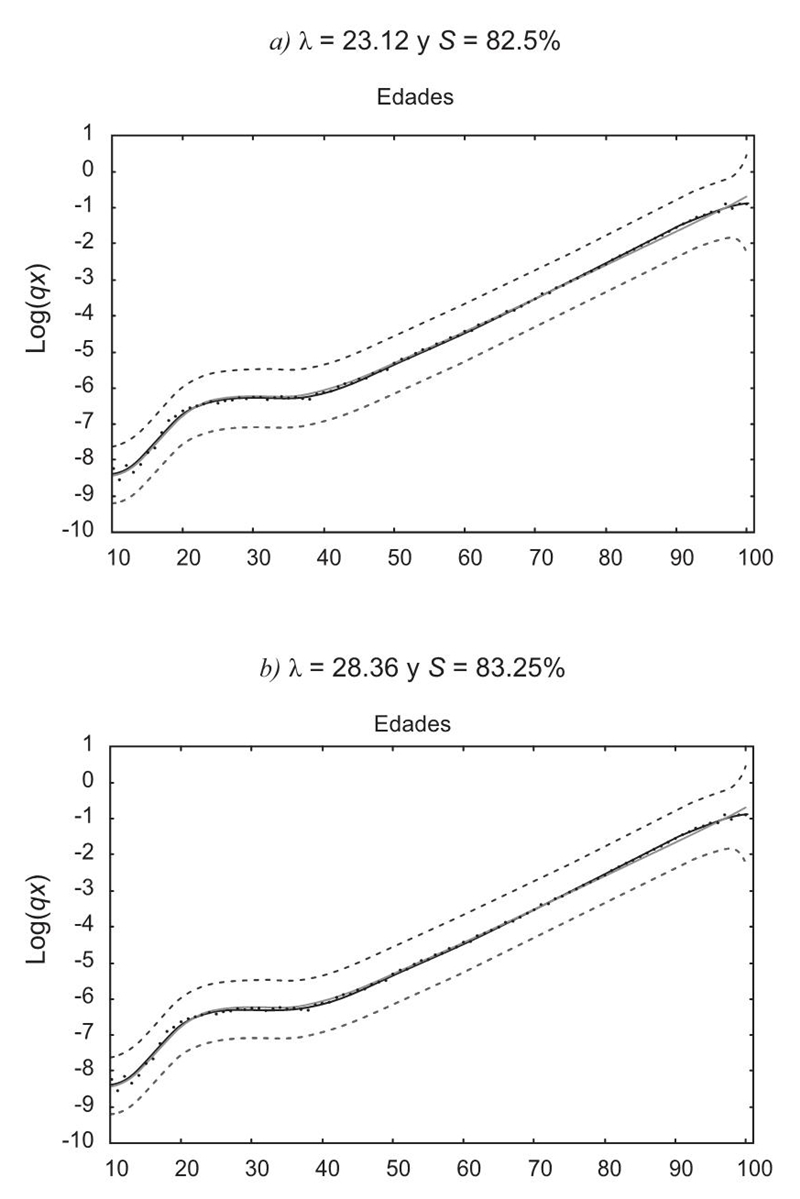
Datos observados: puntos; curva estimada (tendencia) con el modelo HP: línea gris; tendencia estimada: línea negra. Fuente: Elaboración propia.

Gráfica 10  España, hombres, 1990, con: a) λ = 23.12 y S = 82.5%; b) λ = 28.36 y S = 83.25%  

En la Gráfica 11 se presentan ejemplos de los resultados obtenidos con sus respectivos valores de λ. Aunque otra vez la falta de ajuste se da en los últimos valores, se observa en general un aumento en el ajuste por medio de la aplicación del método no paramétrico propuesto; además, adicionalmente a las estimaciones puntuales, ahora se tienen intervalos de estimación de dos desviaciones estándar de tamaño. Así pues, una buena guía para el analista es seleccionar el valor de la media de valores de λ (o su equivalente medido en suavidad alcanzada) presentados en el Cuadro 2.

Datos observados: puntos; curva estimada (tendencia) con el modelo HP: línea gris; tendencia estimada: línea negra. Fuente: Elaboración propia.

Gráfica 11 Ejemplos de los resultados obtenidos con sus respectivos valores de λ  

Conclusiones

Con base en los resultados comparativos con curvas de mortalidad previamente elaboradas, se tiene con la aplicación expuesta, una estimación altamente acertada en relación con las que se estimaron en ^{Vargas (2014)}. Con el valor agregado de que el proceso para la generación de tales estimaciones es expedito y satisfactorio para los rangos de edades establecidos. Con ello queda de manifiesto lo que al menos con los comparativos mostrados aquí se aprecia: se cuenta con una estimación apropiada.

Se encontró que el valor de la función de pérdida para las series de ^{Felipe, Guillen y Pérez-Marín (2002)} de hombres es bajo, comparado con el de las mujeres, lo cual se puede observar en el Cuadro 1. Aunque se resolvió el problema del mal ajuste para los primeros datos de la serie, no se puede observar un patrón de distribución que siga los valores de λ. Es evidente que los resultados sugieren que el estudio de la suavidad inducida a través del modelo HP es perfectible para abarcar toda la experiencia de mortalidad.

Los resultados son más convincentes cuando se omite de las estimaciones la mortalidad infantil y para menores de 12 años. Ahora se puede afirmar un rango adecuado de índices de suavidades para obtener curvas de mortalidad similares a aquellas que se obtendrían con la aplicación del modelo HP. En cada uno de los casos se encontró un valor de λ que aproxima lo suficientemente bien las estimaciones del modelo HP y además se proporciona un intervalo de dicha estimación.

Los porcentajes de suavidad dependen claramente de la cantidad de datos. Por ejemplo, para el rango de edades de 12-99 años, ellos están entre S = 85.26% y S = 89.29%, y S = 75% y S = 87.71% para mujeres y hombres, respectivamente. Es posible encontrar casos en los cuales los valores de las funciones de pérdida sean altos con respecto a lo que se espera, lo cual sugiere que no hay un valor de λ que se aproxime lo suficiente a la tendencia estimada con la curva de mortalidad objetivo.

Se detectó homogeneidad en los resultados si se agrupan las estimaciones por décadas. De hecho, en muchos casos el índice de suavidad requiere ser más alto para el caso de las mujeres que para el de los hombres. Así pues, se tienen dos conclusiones sustantivas: cuando sólo se tiene una serie con tendencia lineal ascendente, es decir, cuando se omite la mortalidad infantil y de menores de 12 años, el índice de suavidad es alto, en tanto que cuando hay una tendencia no lineal en un segmento y otra tendencia lineal en el otro, es decir, cuando se toman todas las edades, entonces el índice de suavidad es más bajo.

Se puede afirmar que con la perspectiva del suavizamiento controlado se aproximan de manera más sencilla curvas de mortalidad en comparación con otros métodos que exigen al analista más herramientas técnicas que no necesariamente se traducen en mejores estimaciones: aquí es sólo un índice que genera tendencias. También queda evidenciado que sí es factible medir la suavidad inducida en curvas de mortalidad estimadas con el modelo HP con funciones de pérdida, con lo que el analista ahora tiene información útil para poder estimar curvas de mortalidad en general; es decir, se tiene la suavidad que se puede imponer para obtener resultados satisfactorios. La limitante se tiene para las edades iniciales de la vida, así como en igualar la calidad de las estimaciones para los dos sexos.

Una futura línea de investigación justamente consiste en realizar la aproximación no paramétrica a través de tres segmentos, por medio de la propuesta de ^{Guerrero y Silva (2015)}, con lo que se podría replicar y adecuar el procedimiento aquí señalado, pero para cada una de las tres etapas de la vida, a saber: mortalidad infantil, mortalidad en edades jóvenes-adultas y mortalidad senil. Se considera que bajo dicha óptica se podría superar la limitante de la estimación que se manifiesta para la primera etapa de la vida.

El enfoque no paramétrico se puede utilizar en cualquier otro modelo de mortalidad, siguiendo el mismo criterio aquí expuesto. Aun cuando la mortalidad es un fenómeno que se va transformando por lo general lentamente en el tiempo y que los niveles pueden variar de contexto a contexto, es verdad que los patrones son sistemáticos en muchos países del mundo. Es meritorio recalcar que ésta es una primera aproximación a resultados derivados de la aplicación del modelo HP y que también es factible realizar pronósticos de la tendencia, es decir, de la edad máxima estimada a partir de propuestas ya existentes en torno al suavizamiento controlado.