Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Contaduría y administración
versão impressa ISSN 0186-1042
Contad. Adm vol.63 no.4 Ciudad de México Out./Dez. 2018
https://doi.org/10.22201/fca.24488410e.2018.1256
Articles
The dependence of the Price and Quotation Index of the Mexican Stock Exchange (IPC) with respect to the main Latin American stock market indices
1Instituto Tecnológico y de Estudios Superiores de Monterrey, México.
2Universidad Juárez del Estado de Durango, México.
3Instituto Politécnico Nacional, México.
The intensity and speed with which the effects of monetary and fiscal policy are transmitted from one financial market to another is of paramount importance to accurately calibrate the decisions of the responsible authorities. Similarly, the effects caused by unexpected shocks in a given market on the behavior of financial asset prices in other markets requires a better understanding of the nature of the response. However, the bulk of published studies on this subject have employed methodologies that assume a normal distribution of the yields and, for that reason, its results are questionable. Although in recent years robust non-normality methodologies have been used, there is still much work to be done. This article contributes to the study of the dependency between the indices of four Latin American stock exchanges (the CPI for Mexico, the IPSA for Chile, the IBOVESPA for Brazil, and the MERVAL for Argentina) through a Copula Analysis methodology. The main contribution of this study with respect to previous work is to obtain the level of dependence on the queues for the pairs of indices formed by the CPI of Mexico and each of the other three Latin American indices of the sample.
Keywords: Latin American capital markets; bivariate copulas; relations of dependence
JEL classification: C58; F65; G15
La intensidad y velocidad con la cual se transmiten los efectos de la política monetaria y fiscal de un mercado financiero a otro es de primordial importancia para calibrar con precisión las decisiones de las autoridades responsables. De manera similar, los efectos provocados por shocks inesperados en un mercado sobre el comportamiento de los precios de los activos financieros de otros mercados requieren una mejor comprensión de la naturaleza de la respuesta. Sin embargo, la mayoría de los estudios publicados sobre este tema han empleado metodologías que asumen normalidad en la distribución de los rendimientos y, por esa razón, sus resultados son cuestionables. Aunque en años recientes se han comenzado a utilizar metodologías robustas a la no-normalidad, aún falta mucho trabajo por realizar. Este artículo contribuye al estudio de la dependencia entre los índices de cuatro bolsas de valores latinoamericanas (el IPC de México, el IPSA de Chile, el IBOVESPA de Brasil, y el MERVAL de Argentina) mediante la metodología de Análisis de Cópulas. La principal contribución de este estudio con respecto a trabajos anteriores es la obtención del nivel de dependencia de las colas para los pares de índices formados por el IPC de México y cada uno de los otros tres índices latinoamericanos de la muestra.
Palabras clave: Mercados de capital latinoamericanos; cópulas bivariadas; relaciones de dependencia
Códigos JEL: C58; F65; G15
Introduction
In recent decades, increasingly higher cross-correlations have been observed in different financial markets. For this reason, various authors have begun to study the phenomenon and documenting its characteristics (e.g., Licht, 1997; Forbes and Rigobon, 2002; Climent and Meneu, 2003; Aggarwal and Kyaw, 2005; Darrat and Zhong, 2005). The background of the discussion has to do with the idea that, as globalization advances and financial integration between countries and regions becomes more in-depth, the integration of diversified portfolios has grown more difficult. Another concern lies in the observation of events that cause an exacerbated volatility in a determinate national market, which transmit to other markets. In fact, this is the very same phenomenon, the difference being just a matter of intensity; however, in one case it is associated with a gradual tendency and, in the second, with a sudden increase in the correlation between the yields of two or more national markets.
Different factors have contributed to global financial integration. One example is the strengthening of trade agreements between countries and the decision of the governments of the main industrial powers to coordinate their economic policies to moderate the volatility of the economic cycles. Another example is the “International Fisher Effect”, by virtue of which interest rate fluctuations act as a mechanism to attract financial flows between countries and influence on the valuation of financial assets (Choudhry, 1997). And even one more is the favorable influence attributable to financial deregulation, economic globalization and technological advancement, because they contribute to greater market efficiency.
Most reference studies assume a normal distribution of yields, although there is ample evidence to the contrary, and it is precisely this reality that allows the use of statistically more robust techniques that, in addition to the possible linear relations, can also capture the nonlinear relations. Such is the case of the copulas methodology, which has seen increased usage in the study of financial phenomena, such as in the works by Calvo and Reinhart (1996), ChanLau, Mathieson and Yao (2004), Bekaert et al. (2014), and Sosa, Bucio and Cabello (2015), to mention a few authors who have been recently published.
This work empirically examines the structure of the dependency relationships of the heavytailed distribution of yields for the indices of the four Latin American stock markets, using the bivariate copulas technique. The choice of the sample of studied countries followed a simple logic: Argentina, Brazil, and Mexico are the largest economies in Latin America, while Chile is probably the country with the greatest development relative to its capital market with regard to the size of its economy in the region.
The daily yields of the stock market indices of the countries in the sample were obtained from Yahoo Finance for the period of January 21, 2015, to January 20, 2016, comprising a total of 2,524 observations. The characteristics of the series suggest that the most adequate copulas to model dependency are of the Joe-Clayton (BB7) and Survival (BB7) types, characterized for having different dependency values in the upper and lower tails. With the proposed methodology it is possible to interpret the interaction of the indices and the higher-order structures present in the yields and conclude that the marginal distributions that best characterize Latin American stock market indices approximate logistics distribution similar to normal, but with heavy tails and more pronounced kurtosis, and, that Mexico and Brazil present the strongest dependency relationships, both in the upper and lower tails.
A brief review of studies is presented in the second part of this work, regarding the transmission of effects between financial markets, highlighting the main methodological approaches and the most frequently used tools. Following this, a few studies that have used the copulas methodology to solve the “non-normality” problem of financial yields are mentioned. The third part presents most relevant methodological aspects of this proposal, as well as the results obtained from the econometric analysis. Finally, the fourth section summarizes the findings and suggests future lines of research.
Review of the literature
LUnderstanding of the processes underlying Financial Globalization has garnered the interest of several researchers. In this work, only a few of the most relevant are mentioned. First of all, the works related to the “contagion” effect ought to be mentioned, the empirical evidence of which is made manifest when the financial asset prices quoted in different sized markets-with dissimilar structures and different geographical locations-react simultaneously to disturbances generated either in any of them or in remote and unrelated markets (Forbes and Rigobon, 2002; Gurgul and Machno, 2016). An example is the Subprime Mortgage Crisis1 of 2007-2012-considered the first global crisis since the Great Depression of the 1930s-, which had significant influence on the behavioral pattern of the stock yields worldwide and increased the levels of correlation between markets (e.g., Ffrench-Davis, 2001; Aloui et al., 2013; Schwert, 2011; Slimane et al., 2013; Bekaert et al., 2014).
Given the range and depth of the crises, the study on how the events that affect a national market are transmitted beyond its borders has made it a topic of great interest in finance (Rigobon, 2002; Mollah and Hartman, 2012). This interest is justified because such dependent relationships affect decisions of international diversification, risk management, asset valuation, and portfolio development (Boubaker and Sghaier, 2014). On an ad hoc basis, Gurgul and Machno (2016) maintain that the study on the transmission of the effects caused by extraordinary events or phenomena beyond borders is important not only for investors, but also for the governments. In the case of the latter, the transmission of effects at the international level is relevant due to how economic policy must respond to the impact of international investment decisions on the exchange rate and inflation. In turn, investors and fund managers also react to the information on the joint behavior of prices, modifying their investment decisions or the offer of their products.
Main approaches to the transmission of financial effects
Algunos ejemplos de estudios sobre la propagación de efectos entre mercados financieros inclSome studies on the propagation of effects between financial markets include the works of Calvo and Reinhart (1996), Rigobón (2002), Forbes and Rigobon (2002) and Ning (2008), among others.
For example, according to Calvo and Reinhart (1996), most studies on the topic of financial contagion can be grouped as: a) those with a main interest focused on the “herd behavior” of the economic agents; and b) those interested in understanding the transmission channels of the contagion. This last group includes studies that highlight the level of integration of the capital markets, trade agreements, institutional practices, developed market bias, technological factors and political instability as determinants of the intensity of the contagion.
Rigobon (2002) indicates that the measurement of the contagion is one of the most complex tasks in international finance; he analyzes the classic definition of contagion2: “Contagion is the propagation of shocks among markets in excess of the transmission explained by fundamentals”, arguing that it is ambiguous3, and cannot be proven. He argues that the statistical properties of the financial series-heteroscedasticity, autocorrelation, and lack of normality-prevent the use of traditional tools to capture the contagion. However, although such tools (i.e., correlation coefficients, main components, linear regressions, and conditional probabilities) can be adjusted to solve said limitations, the existence of non-observable common factors in the joint dynamic of the yields complicates the analysis. He classifies the efforts to define and capture the contagion into two groups: a) shift contagion; and b) pure contagion. The first reflects changes in the intensity of the shocks and covers the changes in the propagation mechanisms during a financial crisis. In contrast, pure contagion refers to the mechanism through which the effects spread. The key is to identify the proportion of the shock that transmits through the major channels; thus, the non-identified part will comprise the contagion itself. Transmission, more than a short-term contingency that responds to periods of focalized crisis, is a more or less stable process. Therefore, contagion presents itself only when the magnitude of the transmission is unusually large. Based on the foregoing, it can be argued that the short-term economic policy strategies only serve to delay the adjustment or reception of the external shock.
Throughout the 1990s, various emerging countries experienced episodes of crisis and “contagion” not attributable to changes in the macroeconomic fundamentals towards other economies (Ffrench-Davis, 2001). Calvo and Reinhart (1996) find that contagion in emerging markets is more driven by regional factors. Chan-Lau, Mathieson and Yao (2004) also document the contagion effect and conclude that it is greater when there are bear markets, than when there are bull markets. Furthermore, they present evidence that contagion differs in intensity between regions; for example, Latin American markets are more propense to contagion, than what occurs with Asian economies.
A work of great significance is that of Bekaert et al. (2014), who study the effects of the subprime mortgage crisis and the way it quickly transmitted from the United States to practically all the economies in the world. Using a factor model to analyze the effect of the crisis on the yield of 415 portfolios integrated with financial assets of different countries, the residual correlations and unexplained increases in the factor loads were identified, confirming contagion. Additionally, the analysis reveals that the crisis was not transmitted uniformly, but rather had a greater impact on markets with macroeconomic imbalances and a low credit score.
Despite the abundant evidence in validation of the existence of contagions, some studies indicate disadvantages and limitations in its conception or even, as suggested by Lorenzo and Massa (2013), contagion is confused with dependency relationships. Also Rigobon (2002), addressing the theoretical and empirical implications of contagion, highlights a few inconveniences on its measurement, such as: a) the tests ignore the effects of heteroscedasticity, and as a result present bias and tend to exaggerate the normal interactions between markets; b) there are transmissions following the unexpected shocks that are perfectly normal and that, sometimes, are confused with contagion; c) although trade explains almost half of the transmission of shocks, a significant ratio is due to the fact that the financial instruments object of the analysis quote simultaneously in the same capital markets. For his part, by indicating that the Pearson correlation coefficient, vector autoregressive (VAR) models, and stimuli-response functions assume a multivariate normal behavior-an unrealistic assumption in financial series-Uribe (2011) ascertains that they lack inferential utility.
Contagion vs Dependency
In an analysis on the transmission of effects between financial markets, Rigobon (2002) reviews a couple of the financial crises of recent decades4, and proves that they had an echo on the behavior of global financial markets, which can be interpreted as a clear manifestation of contagion. Nevertheless, the author indicates that said interpretation could be erroneous, as contagion is more than just the presence of a high level of correlation between markets, even when this increases after a period of crisis in one of them. At the end of the study, Rigobon (2002) proposes the term “interdependency” to define such relationships.
Hu (2003) indicates that most studies on dependency have focused on capturing the “level” of dependency but have not concerned themselves with isolating the “structure” of the same. In his study, he documents that even when the levels of correlation are identical between determined markets, it is possible to identify different dependency structures. Lorenzo and Massa (2013) analyze dependency between the capital markets of emerging Latin American economies and coincide with previous studies in that said structures are not stable. More specifically, they conclude that said relationships have increased over time, especially after the subprime mortgage crisis. The authors maintain that the financial asset yields of Latin American economies show heavy tails, that is, they have greater probabilities of presenting large losses, and the dependency links strengthen in periods of crisis, reducing the benefits of diversification. Ning (2008) recognizes that during periods of crisis the links between markets can grow closer and analyzes the dependency relationships in international equity markets. The analysis reveals the presence of asymmetric dependency and direct relationships with the state of the economy. Similarly, greater levels of dependency are reported in Europe and Southeast Asia than in the Americas.
The studies of Boubaker and Sghaier (2014), and Sosa, Bucio and Cabello (2015) are two recent studies that document significant regional differences in the dynamic dependency relationships between capital markets. The former addresses the study of the relationships in the United States, Japan, the United Kingdom, Germany and France, while the latter studies the magnitude of the dependency relationships between the capital markets that are a part of BRIC+M (Brazil, Russia, India, China and Mexico). Both studies suggest that the assets of the analyzed capital markets offer possibilities for diversification. Similarly, both cases highlight that the most common approach to quantify the dependency phenomenon is using the Pearson correlation coefficient.
Measurement difficulties: correlation coefficient and lack of normality
One of the most used measurements to evaluate the transmission of financial effects is the correlation coefficient, however, various authors suggest that it has significant limitations. For example, the works of Forbes and Rigobon (2002), Hu (2003), Chan-Lau, Mathieson and Yao (2004), Lorenzo and Massa (2013), Sosa, Bucio and Cabello (2015) have taken care to deepen the analysis. Forbes and Rigobon (2002) indicate that the high dependency regarding volatility is a significant weakness of the correlation coefficient, thus, during periods of crisis, when this tends to increase, the parameter often overestimates the association between markets. Hu (2003) shows that the level of dependency captured in a bivariate normal distribution from the correlation coefficients can generate results that offer a misconception on the modeled relationships. Sosa, Bucio and Cabello (2015) also criticize the use of correlation as a dependency measurement, highlighting the inability for the correlations to capture nonlinear relations and extreme events; coinciding with Chan-Lau, Mathieson and Yao (2004) and Lorenzo and Massa (2013).
Heteroscedasticity on the behavior of the yields of financial series is another aspect to consider. Rigobon (2002), when studying the transmission of financial effects, highlights the heteroscedasticity, autocorrelation, and non-normal behavior of the yields. Hu (2003) and Chan-Lau, Mathieson and Yao (2004) agree that the modeling of joint distributions to capture the relationships between the yields of assets exchanged in different markets, by assuming a normal behavior, produce incorrect results. Ning (2008) criticizes the methods that utilize conditional correlations to capture dependency, and agrees with Boubaker and Sghaier (2014), Ortiz, Bucio and Cabello (2016), and Oh and Patton (2017).
Advantages of the copula analysis methodology
Among the proposed alternatives to solve the methodological limitations of the Gaussian approaches, two closely related concepts stand out: extreme value theory5 and copula analysis. In this study only the second is addressed. In particular, copula analysis represents a robust alternative to analyze dependency relationships. For this, it relies on nonparametric correlation measurements such as the Spearman’s Rho (ρ) and Kendall’s Tao (τ) (Hu, 2003; Chan-Lau, Mathieson and Yao, 2004).
Hu (2003) claims to be the pioneer on presenting evidence of the dependency relationships between international markets through a mixed copulas approach, which favors the dependency structure patterns, but not its intensity. His analysis reveals that there are greater possibilities of joint “falls” versus bullish behaviors.
Alternatively, Chan-Lau, Mathieson and Yao (2004) measure dependency with extreme values and the use of copulas. These authors conclude that the contagion effect is greater when there are bear markets and they present negative yields than when there are positive yields. Furthermore, said effect differs from one region to another.
Ning (2008) also proposes the use of copulas as a tool that allows capturing, in a more robust manner, the dependency relationships between financial markets in light of the presence of extreme values, whose analysis reveals the presence of asymmetric dependency in the tails. Aloui et al. (2013) analyze extreme interdependencies through copulas that allow analyzing the dynamic patterns of the heavy-tailed distributions and linear and non-linear interdependencies, and report variant dependency in time between BRIC markets and the American market. It is worth highlighting that said relationships are more intense in those markets that are sensitive to the price of commodities, while being less intense in economies that export manufactured products. Boubaker and Sghaier (2014) document significant regional differences in the dynamic dependency relationships between the capital markets of the United States, Japan, the United Kingdom, Germany and France, for which they use the copulas methodology, generating the marginal distributions through the extreme value theory and adjusting the dependency in mean and conditional variance. In a recent study, Oh and Patton (2017) use new time-varying conditional copula models to link the conditional marginal distributions.
Studies in emerging markets
Ortiz, Bucio and Cabello (2016) assure that most published studies on dependency relationships between financial markets report empirical evidence generated in developed economies, with there being few studies done in the context of emerging markets and fewer still in Latin American markets.
Among the published works on the dependency relationships in Latin America is that of Christofi and Pericli (1999), who research the short-term dynamic and analyze the joint distributions using a VAR model with innovations that follow an exponential GARCH process.
The results reveal a dependency between the studied countries, as well as greater spillover problems than in other regions of the world. Another work that addresses dependency between Latin American markets is that of Edwards and Susmel (2001), who answer the question of whether during high volatility periods the markets correlate in a differentiated manner and focus their attention on the codependency regimes of volatility. The analysis reveals statechanging volatility. In the same vein, Arouri et al. (2010) study the structural ruptures in the trajectory of the conditional correlations of the capital markets in the region and find that the intensity of co-movements between markets has changed over time, nevertheless, opportunities for international portfolio diversification persist. One last example of this approach is the work of Lorenzo and Massa (2013), who analyze the case of Mexican and Brazilian markets and propose copula as an alternative that considers asymptotic dependency and solves the issue of a lack of linearity of the simple correlation. In addition to making an appeal to not confuse dependency with contagion, the authors claim that the financial asset yields of Latin American economies are heavy-tailed.
As an example of a line of research that addresses the dependency relationships between Latin American markets and markets from other regions is the work of Uribe (2011), which studies the impact of the behavior of the American market on the Colombian economy. The use of copulas and extreme values in the analysis reveals that, in general terms, the evidence on contagion is incipient, thus the inclusion of financial assets of the Colombian market can contribute to the diversification of North American portfolios. According to the author, the aforementioned can be explained as the result of the Colombian economic policy, which conscientiously regulates the transit of capital towards the domestic market. In the context of the study of credit risk, Uribe and Ulloa (2012) also document the importance of considering the information contained in the heavy-tailed distributions in order to enhance the results provided by the traditional VaR (Value at Risk), through the application of the GARCH methodology and the estimation of parameters using maximum likelihood. Said study compares the main Latin American markets (Argentina, Brazil, Mexico, Chile, and Colombia) with some from developed economies and other from emerging markets. In the case of Valenzuela and Rodríguez (2015), the existence of interdependencies between the main six Latin American stock markets and the United States is analyzed, using the estimator of Garman and Klass (1980) to analyze the volatility of the stock yields. The results reported by these authors suggest that there is a strong relationship between volatility and the positive correlations of the market yields. Sosa, Bucio and Cabello (2015) study the magnitude of the dependency relationships between the capital markets of BRIC+M (Brazil, Russia, India, China, and Mexico) using copulas, and present evidence on the existence of moderate dependency levels. In other words, they suggest that assets of the analyzed markets offer benefits to portfolio diversification. Similarly, Ortiz, Bucio and Cabello (2016) analyze the yields observed in economies of the Americans: Canada, the United States, Mexico, Venezuela, Colombia, Peru, Brazil, Chile and Argentina, and estimate potential losses through the Value at Risk (VaR) methodology with a copulas approach. The analysis allowed concluding that, among other aspects, the dependency relationships are stronger in the countries that comprise the NAFTA, while in the rest of the economies such a dependency relationship is limited and thus the region-the authors assure-offers interesting possibilities of diversification. Finally, the work of Bucio, De Jesús and Cabello (2016) reports that a VaR supported by copula analysis more precisely captures the extreme values typically observed in the dynamic of the financial assets. The authors highlight the importance of addressing the analysis of the financial asset yields, respecting the inherent quality of said information, that is, considering its asymmetric and leptokurtic behavior.
An interesting finding from the previous literature review is confirmation on the increasing use of the copula analysis methodology to model dependency patterns between financial variables. Without relying on previous assumption on the distribution followed by the series of financial yields, the copula theory allows to include the observed extreme values in the dependency modelling, using the relationships observed in the heavy-tailed distributions (Hu, 2003; Chan-Lau, Mathieson and Yao, 2004; Kostadinov, 2005; Ning, 2008; Boubaker and Sghaier, 2014; Uribe and Ulloa, 2012; Ortiz, Bucio and Cabello, 2016; Bucio, De Jesús and Cabello, 2016).
Methodology used, and results obtained
A copula associates a multivariate distribution function to its uniform marginal distributions, which makes it an adequate tool to model and simulate random, correlated variables. The main appeal of the copulas is that they allow capturing the dependency structure and the marginal distributions separately; for this reason, they are also known as dependency functions (Yan, 2007).
Given that in all cases the marginal distribution of copulas is uniform, its probability distribution is found within the [0,1] interval, and given a random U vector of p-dimensions on the unitary cube [0,1]n x [0,1], copula C can be defined as follows:
According to Sklar’s Theorem (1959), there is a C copula of p-dimensions so that for every x in domain F:
In the particular case that F1
,...,Fp are continuous, then
C is unique, that is, C is
unequivocally determined by the marginal distributions. Sklar’s Theorem
allows establishing the relationship between copulas and random variable
distribution functions. Similarly, it not only allows considering copulas as
joint distribution functions, but the inverse argument is also true. In this
manner, based on the inverse of the marginal distributions
There is a wide variety of copulas, but the most used are the elliptical and Archimedean6 copulas. With F being the Cumulative Distribution Function (CDF) of an elliptical distribution, Fi the CDF of the marginal ith and
The Gaussian copula is included in the elliptical copulas, and presents a normal distribution, as follows:
Where F is the normal joint distribution and ф-1 is the quantile of the univariate normal distribution. Similarly, the t-Student copula is among the elliptical copulas and presents a t distribution:
Where tν,R is the joint t-Student distribution
and
Where φ(t) is the generating function and φ-1(t) is the inverse. Unlike elliptical copulas, Archimedean copulas present broad ranges of dependency properties from the generating function. The most widely used are known as Clayton, Gumbel and Frank as they allow modeling different dependency patterns through simple functional forms. Said dependency pattern is indicated by parameter θ, which represents the strength or level of dependency.
In the case of this research, bivariate copulas are used, adjusted to the yields of market pairs. In this sense, the three most used Archimedean copulas have the following form:
Table 1 Archimedean copula families and generating function.
| Familia | Función Cópula | Función generadora | Parámetros |
|---|---|---|---|
| Clayton |
|
|
α ≥ |
| Frank |
|
|
α ≥ 0 |
| Gumbel |
|
|
α ≥ 1 |
Source. Own elaboration.
For the purposes of this study, three bivariate copulas are estimate that link the Mexican IPC with each of the other three Latin American stock markets (IBOVESPA, MERVAL, and IPSA).
Figure 1 shows the behavior of the stock market reference indices, highlighting that the data were homogenized considering their matching quote days. A similar behavior is observed with regard to IPC and IBOVESPA, thus some form of correlation between said indices can be assumed in advance. However, this is not easily perceptible in the case of the MERVAL and IPSA indices.
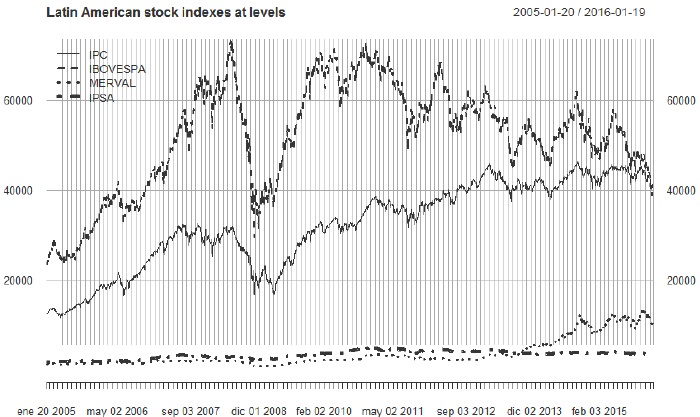
Source: Own elaboration based on Ryan J, Ulrich, J and Thielen, W. (2016): Quantitative Financial Modelling. R package version 0.4-10
Figure 1 Behavior of the Latin American stock market indices from 21/01/2005 to 20/01/2016
Figure 2 shows the yields of the reference indices during the analyzed period, allowing to observe that the periods of greater volatility manifested during the last quarter of 2008 as a result of the financial crisis that originated in the real estate sector of the United States. It should be mentioned that in the case of IPSA, turbulence is observed during a shorter period. Similarly, the figure shows that the Chilean index presents less volatility throughout the entire period. For Mexico and Brazil, the yields show greater instability towards the end of 2006 and during 2008 and 2012. Meanwhile MERVAL, in addition to the mentioned years, presents an episode of high volatility in 2015, which as of January 2016 has not been completely mitigated, that is explained to some measure by the political problems caused by the Kirschner-Marcri change of government in Argentina.
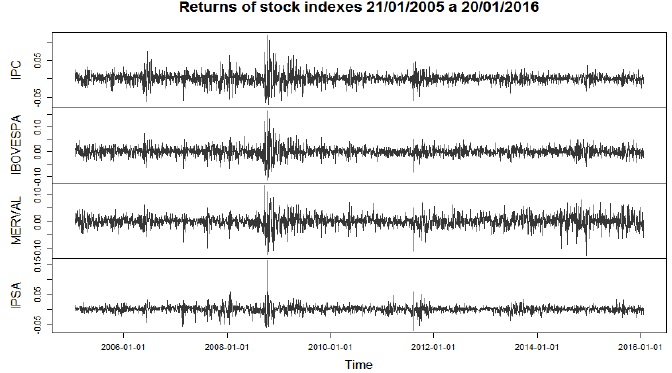
Source: Own elaboration based on Royal J, Ulrich, J and Thielen, W. (2016): Quantitative Financial Modeling. R package version 0.4-10.
Figure 2 Yield of the stock market indices from 21/01/2005 to 20/01/2016.
Figure 3 is a quantile graph of the yield series and corroborates that none of the indices adjusts to a normal distribution. This fact is evident from the previous figures since, due to the presence of volatility clusters, there are heteroscedasticity problems in the graphed series.

Source: Own elaboration based on R Core Team (2013): The R Stats. R package version 3.3.0.
Figure 3 Graph Q-Q with normal distribution.
To model the dependency structure, an all a Chi-plot graph is used, representing the local
dependency7 between the
variables. Proposed by (Fisher &
Switzer, 1985), this representation indicates that if
yi is a strictly growing
function of xi, then χ=1, and in the
opposite case χ=-1. In turn, if the random variables are
independent, when n → ∞ the asymptotic distribution of
λi is uniformly distributed
in a range of
Similar to the Pearson correlation case, when there is independence between yi and xi, then χi is randomly distributed with a value close to zero. Positive correlation occurs when λ > 0 and, in the opposite case, λ < 0. Figure 4 shows the Chi-plots associated to the stock market indices, taking IPC as the contrast variable. In all three cases-IPC-IBOVESPA.
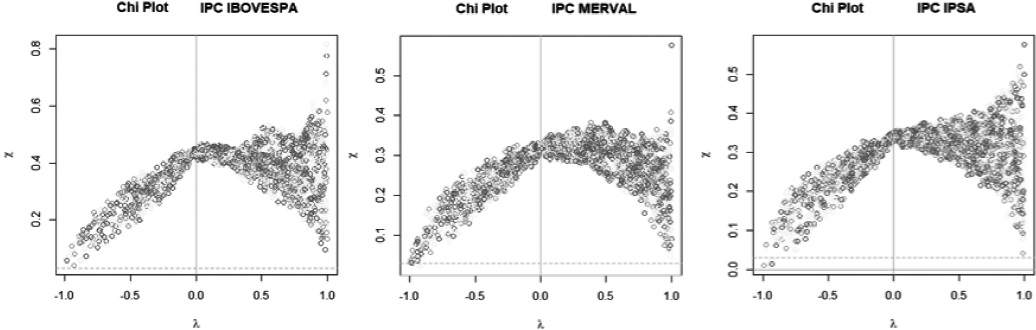
Source: Own elaboration based on Statistical Inference of Vine Copulas (2015): Schepsmeie. Ulf. R package version 1.6-1
Figure 4 Chi-plot
Similar to the Pearson correlation case, when there is independence between yi and χi, then χi is randomly distributed with a value close to zero. Positive correlation occurs when λ > 0 and, in the opposite case, λ < 0. Figure 4 shows the Chi-plots associated to the stock market indices, taking IPC as the contrast variable. In all three cases-IPC-IBOVESPA, IPC-MERVAL, and IPC-IPSA-a negative dependency is observed, although it is worth noting the dispersion of the data when λ > 0 (positive correlation), as well as the positive dependency structures.
Table 2 reports the correlation between the IPC and the other stock market indices of the sample with the Spearman correlation coefficient and Kendall’s Tau.
Table 2 Correlation coefficients between the IPC and the different Latin American stock markets: Kendal’s Tau and Spearman’s Rho.
| Stock market index / Test | Kendall’s Tau | p Value | Spearman’s Rho | p Value |
|---|---|---|---|---|
| IPC | IPC | |||
| IBOVESPA | 0.459 | 0.000 | 0.630 | 0.000 |
| MERVAL | 0.346 | 0.000 | 0.489 | 0.000 |
| IPSA | 0.355 | 0.000 | 0.500 | 0.000 |
Source: Own elaboration based on McLeod, A. (2015): Kendall rank correlation and Mann-Kendall trend test. R package version 2.2.
Although said correlation measures have different values for the same sample, if the significance tests are based on their sampling distributions, the same p values8 are obtained (Siegel and Castellan, 1988). Even if both tests are used to measure the level of correlation of the non-parametric data between two variables, the most adequate for the samples with correlated tails is Kendall’s Tau (Gilpin, 1993), which is denoted as follows:
This means that it is a function of the copula. To estimate the corresponding parameters, the maximum likelihood methodology is implemented. Retaking Equation (2), it can be deduced that
The maximum likelihood estimator is given by:
With θ being the space of the parameters.
Marginal distribution selection
To select the marginal distributions, an asymmetry-kurtosis graph proposed by (Cullen & Frey, 1999) is used, based on a re-sampling or bootstrap to approximate the empirical distribution of a sample (in this case, of each of the stock market indices). Both the asymmetry and kurtosis values corresponding to the bootstrap are represented by a circle in Figure 5, as follows:

Source: Own elaboration based on Delignette-Muller et al. (2017): fitdistrplus: Help to Fit of a Parametric Distribution to Non-Censored Data. R package version 1-0-9
Figure 5 Cullen & Frey graph for each of the stock market indices
Figure 5 suggest that, in all cases, the marginal distributions approximate more to a logistic distribution. It is worth noting that the logistic distribution is similar to the normal distribution, but it presents heavier tails and more pronounced kurtosis, thus it has the advantage of being comparatively more robust. The density function of a logistic distribution is given by:
Where α is the localization parameter (-∞≤α≤∞) and β is the scale parameter (0<β). Once the marginal distributions have been obtained, the pseudo observations of the stock market indicators are used, that is, the observations of the transformed samples on interval [0,1] based on the empirical marginals to differentiate between the different possible copula families through the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC). The results of the selection process are shown in the table below.
According to Table 3, the family that best adjusts to the dependency relationship between IPC-IBOVESPA and IPC-MERVAL is BB7; the same copula was obtained for the IPC-IPSA relationship, but rotated 180 degrees (that is, it is a survival copula), and whose properties are shown in Table 4.
Table 3 Bivariate copula selected for the Latin American indices
| Relation of the indices | Copula |
|---|---|
| IPC, BVSP | Joe-Clayton (BB7) |
| IPC, MERV | Joe-Clayton(BB7) |
| IPC, IPSA | Survival Joe-Clayton (BB7) |
Source: Own elaboration.
Table 4 Properties of the Joe-Clayton (BB7) copula
| Copula | Generating Function | Parameters |
|---|---|---|
| BB7 y cópula de supervivencia BB7 | (1 - (1 - t)θ)-δ -1 | θ ≥ 1, δ > 0 |
Source: Own elaboration.
θ and δ refer to the parameters associated to copula BB7, characterized by having different dependency values in the upper and lower tails. It is worth remembering that the Clayton family does not allow dependency in the upper tail, while the Joe copula has the restriction of impeding dependency in the lower tail9. For this reason, the use of the copula BB7 allows modeling both dependency structures.
Based on the use of copula BB7 and survival copula BB7, Table 5 shows the parameters associated with the stock market indices, the theoretical value of Kendal’s Tau for bivariate copulas, and the dependency coefficients of the tails, given the estimated parameters.
Table 5 Properties of the Joe-Clayton copula (BB7)
| Relation of the indices | Parameter 1 | Parameter 2 | Kendall’s Tau | Uper tail | Lowel tail |
|---|---|---|---|---|---|
| IPC BVSP | 1.6347 | 1.0906 | 0.4615 | 0.4719 | 0.5296 |
| IPC, MERV | 1.3250 | 0.7002 | 0.3430 | 0.3127 | 0.3716 |
| IPC, IPSA | 1.5407 | 0.5682 | 0.3646 | 0.4318 | 0.2953 |
Source: Own elaboration.
Table 5 shows the correlation estimated with copula BB7 and the marginal logistic distributions. It is important to note that the results obtained are similar to those show in Table 2, which suggests that the adjustment of the copula is adequate to model the dependency structure. Furthermore, the dependency level of the tails is presented for each copula. For example, the IPC-BVSPA relationship-copula observed to have greater dependency-depends 47% on the upper tail and 53% on the lower tail. The IPC-MERVAL relationship has a dependency of 37% on the upper tail, and of 31% on the lower tail. Finally, the IPC-IPSA relationship has a dependency structure of 31% on the upper tail and of 29% on the lower tail. For the cases of Brazil and Argentina, the interaction has a greater effect in the lower tail, while the IPC relationship with IPSA concentrates mainly in the positive yields.
Conclusions
The transmission of information between financial markets contributes to the formation of prices. Thus the advances in information technology and computing, financial deregulation, and the growing transparency in the management of financial information are positive factors. In addition to the solely financial factors, there are behavioral elements of the markets that are difficult to classify and that manifest in the way they react to the deepening of the trade and contractual relations between national markets, but also and in a particularly intense manner, as a response to difficult prognostic events and which are, occasionally, visibly dangerous for stability. The literature on the growing long-term financial integration between countries is complemented with those studies that propose to show the contagion phenomena that result as a response to unexpected events in order to configure a growing body of knowledge and of greater relevance for financial and monetary authorities, but also particularly relevant to portfolio managers and investors in general. It is worth mentioning that the incursion into this topic is still in the early stages and the variety of published studies do not exactly agree in their conclusions, thus a notable development in the research on this topic is expected to occur in the near future.
This study uses the analysis of copulas to study the dependency relationships between the IPC of the Mexican stock market and the Argentinian, Brazilian, and Chilean markets. The approach is innovative from a methodological point of view and comprises an interesting contribution for the better understanding of the dynamic of the financial markets of the region.
A significant difference with regard to other works that address the issue is obtaining the dependency level of the tails for the index pairs formed by the Mexican IPC and each of the other three Latin American indices. The most important findings are the following:
The relationship between IPC and IBOVESPA presents the strongest dependency, both in the upper and lower tails (52.96% and 46.15%, respectively).
The marginal distributions that best characterize the Latin American stock market indices approximate a logistic distribution, similar to the normal but with heavier tails and a more pronounced kurtosis.racterizan la distribución conjunta de los índices son las arquimedianas. Específicamente, la Cópula Joe-Clayton BB7, permite modelar ambas estructuras de dependencia con buena precisión.
The bivariate copula families that best characterize the joint distribution of the indices are the Archimedean ones. Specifically, the Joe-Clayton BB7 copula, which allows to model both dependency structures with good precision.
A better understanding of the dependency relationships between the Latin American stock markets contribute to improving the investment and financing decision-making of the companies in the region, portfolio managers, and investors in general. It can also contribute valuable information for the design of public policies, regulatory schemes, and supervisory authorities. The diversity of topics associated to dependency and, in exceptional cases, contagion between markets, represents a fertile field of great interest for future researches.
REFERENCES
Aggarwal, R., & Kyaw, A.N (2005). Equity Market Integration in the NAFTA Region: Evidence from Unit Root and Cointegration Tests. International Review of Financial Analysis. 14(4): 393-406. https://doi.org/10.1016/j.irfa.2004.10.008 [ Links ]
Aloui, R., M. S., Aïssa Ben & Nguyen, D. K. (2013). Conditional Dependence Structure between Oil Prices and Exchange Rates: A Copula-GARCH Approach. Journal of International Money and Finance. 32(2), 719-738. https://doi.org/10.1016/j.jimonfin.2012.06.006 [ Links ]
Arouri, M. E. H., Bellalah, M., & Nguyen, D. K. (2010). The Comovements in International Stock Markets: New Evidence from Latin American Emerging Countries. Applied Economics, 17(13): 1323-1328. https://doi.org/10.1080/13504850902967449 [ Links ]
Bekaert, G., Ehrmann, M., Fratzscher, M., & Mehl, A. (2014). The global crisis and equity market contagion. The Journal of Finance, 69(6), 2597-2649. https://doi.org/10.1111/jofi.12203 [ Links ]
Boubaker, H., & Sghaier, N. (2014). On the dynamic dependence between US and other developed stock markets: An extreme-value time-varying copula approach. Ipag Business School Working Paper No. 2014-094. Disponible en: http://www.ipagcn.com/wp-ontent/uploads/recherche/WP/IPAG_WP_2014_281.pdf ; consultado el 21/08/2018 [ Links ]
Bucio, C., De Jesús, R., & Cabello, A. (2016). Valor en riesgo anual de los mercados accionarios de México y Estados Unidos: VaR tradicional vs VaR cópulas elípticas. Estocástica: finanzas y riesgo, 6(1), 83-114. Disponible en: http://estocastica.azc.uam.mx/index.php/re/article/viewFile/38/35 , consultado el 21/08/2018 [ Links ]
Calvo, S., & Reinhardt, C. (1996). Capital flows to Latin America: Is There Evidence of Contagion Effects? Policy Research Working Paper 1619.The World Bank, International Monetary Fund. https://doi.org/10.1596/1813-94501619 [ Links ]
Christofi, A., & Pericli, A. (1999). Correlation in Price Changes and Volatility of Major Latin American Stock Markets. Journal of Multinational Financial Management, 9(1): 79-93. https://doi.org/10.1016/s1042-444x(98)00047-4 [ Links ]
Chan-Lau, J. A., Mathieson, D. J., & Yao, J. Y. (2004). Extreme contagion in equity markets. IMF staff papers, 51(2), 386-408. https://doi.org/10.2139/ssrn.382502 [ Links ]
Climent, F., & Meneu, V. (2003). Has 1997 Asian Crisis Increased Information Flows between International Markets? International Review of Economics and Finance, 12(1): 111-143. https://doi.org/10.1016/s1059-0560(02)00140-5 [ Links ]
Choudry, T. (1997). Stochastic Trends in Stock Prices: Evidence from Latin American Markets. Journal of Macroeconomics, 19(2): 285-304. https://doi.org/10.1016/s0164-0704(97)00016-5 [ Links ]
Cullen, A.C. and H.C. Frey, H.C. (1999). Probabilistic Techniques in Exposure Assessment, Plenum Publishing Corp., New York, USA [ Links ]
Darrat, A. F., & Zhong, M. (2005). Equity Market Linkage and Multinational Trade Accords: The Case of NAFTA. Journal of International Money and Finance, 24(5): 793-817. https://doi.org/10.1016/j.jimonfin.2005.04.006 [ Links ]
Edwards, S., & Susmel, R. (2001). Volatility Dependence and Contagion in Emerging Equity Markets. Journal of Development Economics, 66(2): 505-532. https://doi.org/10.1016/s0304-3878(01)00172-9 [ Links ]
Ffrench-Davis, R. (2001). Crisis financieras en países exitosos. CEPAL. McGraw-Hill Interamericana. [ Links ]
Fisher, N., & Switzer, P. (1985). Chi-plots for assessing dependence. Biometrika, 72, 253-265. https://doi.org/10.1093/biomet/72.2.253 [ Links ]
Forbes, K. J., & Rigobon, R. (2002). No Contagion, Only Interdependence: Measuring Stock Market Co-movements? Journal of Finance, 57(5): 2223-2261. https://doi.org/10.1111/0022-1082.00494 [ Links ]
Garman, M. B., & Klass, M. J. (1980). On the Estimation of Security Price Volatilities from Historical Data. The Journal of Business, Vol. 53, No. 1 (Jan. 1980), pp. 67-78. https://doi.org/10.1086/296072 [ Links ]
Gilpin, A. R. (1993). Table for conversion of Kendall’s Tau to Spearman’s Rho within the context of measures of magnitude of effect for meta-analysis. Educational and Psychological Measurement, 53(1), 87-92. http://dx.doi.org/10.1177/0013164493053001007 [ Links ]
Gurgul, H., & Machno, A. (2016). Modeling dependence structure among European markets and among Asian-Pacific markets: a regime switching regular vine copula approach. Central European Journal of Operations Research, 24(3), 763-786. https://doi.org/10.1007/s10100-015-0411-x [ Links ]
Hu, L. (2003). Dependence Patterns Across Financial Markets: Methods and Evidence. Mimeo. Department of Economics. Ohio State University. USA. [ Links ]
Kostadinov, K. (2005). Non-parametric estimation of elliptical copula with application to credit risk. Research paper, Munich University of Technology. Disponible en: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.61.3953&rep=rep1&type=pdf ; consultado el 21/08/2018 [ Links ]
Licht, A. N. (1997). Stock Market Integration in Europe. Program on International Financial Systems, Harvard Law School. Disponible en: http://pdf.usaid.gov/pdf_docs/PNACH173.pdf ; consultado el 21/08/2018 [ Links ]
Lorenzo, Valdés A., & Massa Roldán, R. (2013). Measuring Dependence in Financial Crisis A Copula Approach for Mexico and Brazil. Economía Mexicana. Nueva Época, 22(2) 341-355. Disponible en: http://www.economiamexicana.cide.edu/indice_articulos.html ; consultado el 21/08/2018 [ Links ]
Mendoza, Velázquez A., López, Herrera F. y Watkins, Fassler K. (2011), Reflexiones sobre las crisis financieras, Centro de Investigación e Inteligencia Económica CIIE-UPAEP y División de Investigación de la Facultad de Contaduría y Administración, UNAM. Coordinadores. [ Links ]
Mollah, S., & Hartman, T. (2012). Stock Market Contagion, Interdependence and Shifts in Relationship due to Financial Crisis-A Survey. International Review of Business Research Papers, 8(1), 166-195. Disponible en: https://www.bizresearchpapers.com/10.%20Sabur.pdf ; consultado el 21/08/2018 [ Links ]
Ning, C. (2008). Extreme dependence of international stock market. Working paper, Ryerson University. Disponible en: http://digital.library.ryerson.ca/islandora/object/RULA:182/datastream/OBJ/download/Extreme_Dependence_in_International_Stock_Markets.pdf , consultado el 21/08/2018 [ Links ]
Oh, D. H., & Patton, A. J. (2017). Time-varying systemic risk: Evidence from a dynamic copula model of CDs spreads. Journal of Business & Economic Statistics, 1-15. https://doi.org/10.1080/07350015.2016.1177535 [ Links ]
Ortiz, E., Bucio, C., & Cabello, A. (2016). Dependence and Value at Risk in the Stock Markets from the Americas: A Copula Approach. Journal of Research in Business, Economics and Management, 5(5), 761-780. Disponible en: http://www.scitecresearch.com/journals/index.php/jrbem/article/view/734 ; consultado el 21/08/2018 [ Links ]
Rigobon, Roberto (2002). International Financial Contagion: Theory and Evidence in Evolution, CFA.The Research Foundation Publications. Disponible en: https://www.cfainstitute.org/en/research/foundation/2002/international-financial-contagion-theory-and-evidence-in-evolution ; consultado el 21/08/2018 [ Links ]
Santillán Salgado, R.J. (2015). La Gran Recesión (2007-2012): Lecciones y Oportunidades para México. EGADE Business School-Instituto Mexicano de Ejecutivos de Finanzas, PWC. Roberto J. Santillán-Salgado, Coordinador. [ Links ]
Sosa, M., Bucio, C., & Cabello, A. (2015). Mercados de Capitales del Bloque Bric+ México: Dependencia Estimada con un Enfoque de Cópulas. Investigación Administrativa, 44 (115), 70-86. Disponible en: http://www.sepi.escasto.ipn.mx/Revista/Paginas/articulos115.aspx; consultado el 21/08/ [ Links ]
Schwert, G. W. (2011). Stock Volatility during the Recent Financial Crisis. European FinancialManagement, 17(5):789-805. https://doi.org/10.1111/j.1468-036x.2011.00620.x [ Links ]
Siegel, S., & Castellan, N. J. (1988). Nonparametric statistics for the behavioral sciences (2nd ed.) New York: McGraw-Hill. [ Links ]
Sklar, A. (1959). Fonctions de répartition à n dimensions et leurs marges, Vol. 8, pp. 229-231, Publications de l’Institut de Statistique de L’Université de Paris. [ Links ]
Slimane, F., Mehanaoui, M. & Kazi, I. (2013). How Does the Financial Crisis Affect Volatility Behavior and Transmission Among European Stock Markets? International Journal of Financial Studies, 1(3): 81-101. https://doi.org/10.3390/ijfs1030081 [ Links ]
Uribe, J. (2011). Contagio financiero: una metodología para su evaluación mediante coeficientes de dependencia asintótica. Lecturas de Economía, (75), 29-57. Disponible en: http://www.redalyc.org/pdf/1552/155222750002.pdf , consultado el 21/08/2018. [ Links ]
Uribe, J. & Ulloa, I. (2012). La medición del riesgo en eventos extremos. Una revisión metodológica en contexto. Lecturas de Economía, No. 76, 87-117. Disponible en: http://www.scielo.org.co/scielo.php?pid=S0120-25962012000100004&script=sci_abstract&tlng=fr ; consultado el 21/08/2018. [ Links ]
Valenzuela, G. & Rodríguez, A. (2015). Interdependencia de mercados y transmisión de volatilidad en América Latina. Innovar, 25(55): 157-170. https://doi.org/10.15446/innovar.v25n55.47231 [ Links ]
Yan, Jun (2007). Enjoy the Joy of Copulas: With a Package copula. Journal of Statistical Software. October 2007, Volume 21, Issue 4. Disponible en: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.610.7783&rep=rep1&type=pdf ; consultado el 21/08/2018. [ Links ]
1For a detailed review of the fnancial crises, see Calvo and Reinhardt (1996), Rigobon (2002), Mendoza, López and Watkins (2011), and Santillán (2015).
2For an ample review on contagion refer to Calvo and Reinhart (1996), Rigobon (2002), and Mollah and Hartman (2012).
3Asking questions such as: when are yields considered to be in excess? And, what is understood as fundamentals?
4For example: The United States stock market crash in 1987, the devaluation of the Mexican peso in 1994, the Hong Kong stock market crash in 1997, among others.
5The extreme value theory studies the transmission of effects between financial markets. It has been strengthened in light of the evidence that, through different mechanisms, financial markets react and transmit shocks or financial crises, considering that said transmission is asymmetric, in function of the magnitude of the disturbances (see, for example, Hu, 2003; Chan-Lau, Mathieson and Yao, 2004; Uribe and Ulloa, 2012).
6In the field of finance, elliptical copulas are widely used due to their easy implementation, their symmetric multivariate distribution function, and their advantages in obtaining conditional distributions for their prediction (Sosa, Bucio & Cabello, 2015).
7Local dependency refers to the fact that certain subsets of the random variables are independent of those outside their respective neighborhoods, thus not all the values recorded in the observations have an influence on the others.
9This is due to its generating function, for example, for the Clayton copula ψ(t) = (1+t), t ∈ [0, ∞] where θ ∈ (0, ∞). Whereas for the Joe copula the generating function is 1 - (q-exp(t))1/θ where θ ∈ (1,∞).
Received: October 06, 2016; Accepted: January 19, 2018











 texto em
texto em 


