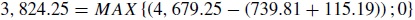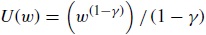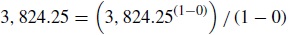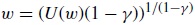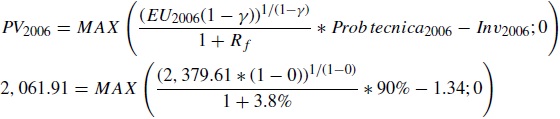Códigos JEL: G3; G17; G30; G39
Introducción
La metodología de valoración por medio de discounted cash flow (DCF, «flujos de caja descontados») es uno de los procedimientos más utilizados para valuar todo tipo de activos; incluso se extiende hasta aquellos que se consideran intangibles. Por medio de ella, se determina el valor del proyecto, descontando sus flujos de caja a una tasa ajustada por riesgo, la cual se calcula, por lo general, mediante un modelo de capital asset pricing model (CAPM, « valoración de activos de capital»). Este ajuste por riesgo sigue un proceso de selección que depende de las preferencias por liquidez, las cuales están sujetas a las tasas de interés (Tobin, 1958). Este modelo predice que el retorno de equilibrio de los activos financieros es función de la covarianza del retorno del activo con el del mercado (Maya Ochoa y Pareja Vasseur, 2014).
Para la definición de este portafolio óptimo se asumen los supuestos que han sido planteados por Sharpe (1964), Lintner (1965) y Rubinstein (1973), quienes demuestran que: (1) cada inversionista podrá invertir su capital en activos libres de riesgo, los cuales pagan una tasa de interés positiva; (2) el inversionista podrá invertir cualquier proporción de su capital en uno o varios activos riesgosos; (3) los activos riesgosos son negociados en mercados competitivos, en donde no hay impuestos ni costos de transacción, y (4) cualquier inversionista podrá pedir prestado fondos para invertir en activos riesgosos. En la teoría de portafolios, el principal problema se centra en definir las cantidades óptimas que se deben mantener de cada activo, con el fin de obtener la máxima tasa de retorno esperada, asociada al menor riesgo posible (Lintner, 1965).
Estas teorías, que están enmarcadas en el plano de toma de decisiones tanto de los individuos como de las organizaciones, tienen como objetivo fundamental maximizar la utilidad, dada una cantidad limitada de recursos. Por lo tanto, la inclusión del riesgo en la teoría de portafolios se hace indispensable para estimar adecuadamente este tipo de modelos. Esta teoría está fundamentada principalmente por autores como Markowitz (1952) y Roy (1952), quienes a través de sus modelos han contribuido a la selección de portafolios que cumplan con el objetivo que espera un inversionista a un determinado nivel de riesgo. Posteriormente, Sharpe (1964), basándose en este modelo, plantea el CAPM, el cual, como se mencionó anteriormente, es utilizado para valorar no solo activos, sino también portafolios.
Son varias las investigaciones y extensiones que han surgido a partir de su construcción; por ejemplo, Roll (1977) discute sobre los test para validar el CAPM, los cuales considera incompletos y con errores de inferencia, además de realizar un análisis sobre ambigüedades en los mismos; por su parte, Fama y French (1992) han extendido su aplicación a lo largo de modelos dinámicos en los activos y sus betas, mostrando cómo la influencia permanente del riesgo en las transacciones financieras ha forzado a las investigaciones en esta área a incorporar modelos de comportamiento de precios que sean un poco más asertivos, tal como lo hacen en su trabajo publicado en 1995, donde muestran la relación que tiene la ratio book-to-market y el tamaño de la empresa sobre el retorno de las acciones (Fama y French, 1995).
A pesar de todas las críticas que se han hecho alrededor del CAPM y de todas las extensiones que han surgido en un intento por refutar la validez del mismo, hoy sigue siendo el método de valoración más empleado (Nawalkha y Schwarz, 2006). Este modelo, como bien se ha mencionado, permite obtener una tasa ajustada por riesgo con la cual se descuentan los flujos de caja y se obtiene el net present value (NPV, «valor presente neto»); si este criterio resulta positivo, significa que vale la pena emprender la inversión, de lo contrario, debería abandonarse (Westerfield, Jaffe y Ross, 1999).
A pesar de su manejo sencillo y de su amplia aceptación, la metodología DCF deja vacíos importantes, ya que excluye elementos que se deben tener en cuenta en los activos intangibles, como, por ejemplo, el riesgo de ocurrencia de eventos contingentes, la volatilidad y el riesgo presente en los flujos de caja (Trigeorgis, 1996). Estos elementos permiten generar un valor adicional, que cuando se incluye en la metodología de valoración facilita una mejor toma de decisiones (Borison, 2005; Amram y Kulatilaka, 1998), pues las reglas convencionales de valoración fallan al capturar este tipo de complejidades (Kulatilaka, 1988).
Como un método alternativo de valoración ante las limitaciones expuestas, surge la teoría de real options approach (ROA, «opciones reales») (Myers y Turnbull, 1977), enfoque que complementa el tradicional DCF y que permite incluir la flexibilidad del negocio mediante decisiones como, por ejemplo, diferir, expandir o abandonar, entre otras. Incluso es posible encontrar proyectos con opciones reales compuestas, cuya sinergia no solo podría afectar el valor de estos, sino también los límites en los cuales el ejercicio de la opción empieza a ser óptimo (Kulatilaka, 1995). No obstante, a pesar de su amplia difusión, esta metodología se ha caracterizado por tener una alta tasa de deserción en cuanto a su uso, explicada por su complejidad técnica (Copeland y Tufano, 2004).
En el presente artículo se desarrolló una propuesta metodológica utilizando ROA, que se fundamenta en equivalentes de certeza y en funciones de utilidad; se adaptó dicho método al caso de estudio de Serono International S. A. de valoración de una patente planteado por Borissiouk y Peli (2002). Los autores aplicaron para tal fin la metodología tradicional ROA y calcularon el valor de la opción de abandono del proyecto, pero mediante la metodología propuesta se encontró que el valor de dicha opción podría variar de acuerdo con las preferencias del inversionista frente al riesgo, utilizando para ello la función de utilidad de tipo constant relative risk aversion (CRRA, «aversión relativa al riesgo constante»).
El artículo se compone de 5 secciones; en la primera se revisan de modo sucinto los conceptos básicos de los activos intangibles y, en específico, las patentes; la segunda refiere los fundamentos teóricos de la propuesta metodológica; en la tercera se presenta la clasificación de las patentes en el contexto de ROA; en la sección 4 se enumeran las etapas para la obtención de una patente y se hace una breve referencia al caso de aplicación; y en la quinta y última sección se expone al detalle la metodología propuesta adaptada al caso de estudio; por último, se presentan las conclusiones.
Conceptos sobre la valoración de los activos intangibles
La diferencia entre el valor del mercado y el valor expresado en libros da origen a los activos intangibles. Su importancia en cuanto a la determinación del valor de una empresa ha cobrado vigencia entre los diferentes actores del mercado y ha impulsado el desarrollo y la implementación de diferentes metodologías, en búsqueda de su verdadero valor; sin embargo, la condición etérea y abstracta de los mismos hace, por lo general, compleja esta labor.
Múltiples son las definiciones utilizadas para describir este tipo de activo; una buena aproximación es: un activo no monetario, sin sustancia física, que es mantenido para su uso en la producción o suministro de bienes o servicios, alquiler o similares, o con propósitos administrativos [...] este activo es un recurso controlado por una empresa como resultado de sucesos pasados, y del que se esperan futuros beneficios económicos (Acosta Molina, Correa Rodríguez, Barrios del Pino y González Pérez, 2003, p. 3).
Diversos son los propósitos por los cuales se considera necesaria una valoración de este tipo de activos, entre los que podemos contar: soporte de transacciones, procesos de quiebra, licenciamientos, alianzas estratégicas, entre otras (Smith y Parr, 2005).
Dentro del concepto de activo intangible se encuentra de manera prioritaria la propiedad intelectual, que potencia el desarrollo de las «creaciones de la mente» que tienen un fin de lucro comercial. La propiedad intelectual presenta 2 clasificaciones: derechos de autor y propiedad industrial; en la última se agrupan las patentes, las marcas, los diseños industriales, los modelos de utilidad y las indicaciones geográficas.
Clasificación de la propiedad intelectual
En esta clasificación es posible encontrar lo siguiente: la propiedad industrial, que son los derechos de propiedad más utilizados debido a su importancia estratégica y económica para la actual sociedad del conocimiento (WIPO, 2015); las marcas, que son signos distintivos como letras, números, fotos, formas y colores o combinación de los anteriores (Fawcett, 2014); los diseños industriales, que se catalogan en un aspecto ornamental o estético del artículo (Olsen y Halliwell, 2007), los modelos de utilidad, que hacen referencia a un título de protección de una invención y, por lo general, se denominan «pequeñas patentes» o «patentes de innovación»; las indicaciones geográficas, que hacen referencia a un distintivo, utilizado en productos que tienen un origen geográfico determinado (WIPO, 2015), y finalmente, las patentes, cuya importancia incide de manera meritoria en el desarrollo científico y tecnológico de un país; además, es importante tener en cuenta el abordaje de los derechos monopolísticos que se otorgan por el solo hecho de innovar (Rubio Martín y López-Cózar Navarro, 2007). Según la Superintendencia de Industria y Comercio, «la patente es un título de propiedad otorgado por el gobierno de un país, que da a su titular el derecho de explotar e impedir temporalmente a otros la fabricación, venta o utilización de la invención protegida» (SIC, 2010, p. 3), mientras que autores como Smith y Parr (2005) la definen como: «un proceso legal por el cual, la tecnología o los métodos patentados pueden convertirse en propiedad con derechos asociados para el propietario» (Smith y Parr, 2005, p. 27).
La clasificación de las patentes en términos generales se puede hacer de la siguiente forma: métodos tradicionales que se refieren a los modelos basados en el mercado, en costos e ingresos (Smith y Parr, 2005), y los no tradicionales, como los econométricos y las opciones reales (Olsen y Halliwell, 2007). Para los primeros, se refiere a un enfoque contable de medición, que ha sido insuficiente para determinar un valor que se ajuste más a las características reales y de efectos prácticos para dicho tipo de activos. Así mismo, esta tipificación incluye también una de las herramientas financieras más comúnmente utilizadas: el DCF. En la segunda clasificación, la no tradicional, se destaca el uso creciente del ROA. En esta metodología se resalta el empleo de algunos aspectos relacionados de modo directo con las patentes, como son la incertidumbre y la volatilidad sobre los ingresos, costos e inversiones, y la contingencia, entre otros (Reyck, Degraeve y Gustafsson, 2004). Además, existe una característica importante según Pindyck (1988): cuando una inversión es irreversible y la demanda futura o las condiciones relacionadas con la estructura de costos son inciertas se hace necesario introducir la opción de ejercicio o de abandono dentro de los gastos relacionados con la inversión. Cuando se tiene en cuenta esta condición, el valor de la empresa podrá estar influido en gran medida por las posibilidades de crecimiento, que a su vez son vistas como opciones Call (Myers, 1977).
El problema cuando se tiene una oportunidad de inversión es la baja probabilidad de encontrar una opción Call lo suficientemente parecida a la oportunidad de inversión con el fin de traducir el valor de la oportunidad (Luehrman, 1998). Desafortunadamente, para el caso de las patentes, estas oportunidades son escasas y la única forma de encontrar una opción similar es construirla a partir del enfoque ROA, el cual sirve como complemento importante a la valoración por DCF, puesto que se aproxima de mejor manera al valor que podría tener una patente cuando se introduce una invención al mercado (Trigeorgis, 1996).
La importancia de la utilización del ROA para valorar patentes es que permite incluir una mayor flexibilidad en la toma de decisiones de inversión y de renovación, como también para realizar solicitudes internacionales de patentabilidad o de abandonar (Smith y Nau, 1995). Del mismo modo, se incluye la incertidumbre que se da antes, durante y después del proceso de concesión de la patente y de la introducción de la invención al mercado, eventos que no se tienen en cuenta en la metodología DCF (Dixit y Pindyck, 1994; Luehrman, 1998; Bernardo y Chowdhry, 2002; Mun, 2004; Álvarez Echeverría, López Sarabia y Venegas-Martínez, 2012). Además, las opciones reales son útiles no solo para valorar proyectos de negocio estratégicos, sino también como herramienta funcional en las decisiones de inversión de capital (Mun, 2004).
Bajo el anterior contexto se define la opción como un derecho a obtener beneficios generados por el activo subyacente, que equivalen a los flujos futuros de la invención o a las regalías del licenciamiento de la patente, que tienen, como contraprestación, las inversiones de capital (Sereno, 2010).
Fundamentos teóricos de la propuesta metodológica: árboles binomiales, equivalentes de certeza y funciones de utilidad
Árboles binomiales
El método de árboles n-nomiales fue planteado por Cox, Ross y Rubinstein y se basa, según sus autores, en operaciones algebraicas elementales que permiten estimar el precio del activo subyacente en tiempo discreto (Cox, Ross y Rubinstein, 1979). El supuesto que se asume para el activo subyacente es que sigue una caminata aleatoria o random walk (Hull, 2005).
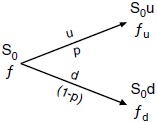
La representación de un árbol binomial para 2 periodos se puede observar en la figura 1.
Fuente: Adaptada de Hull (2005, p. 248).
Figura 1 Representación de un árbol binomial en un periodo.
Donde S0 es el valor inicial del activo subyacente, que se incrementa y decrece de acuerdo con los factores u y d, respectivamente, los cuales dependen de la volatilidad del subyacente. Por su parte, la variable fu indica el valor de la opción en el escenario con incremento y fd es su símil en el contexto decrecido; ambos valores se han evaluado con la función MAX(ST − X ; 0), lo que permite calcular el valor de la opción f en el momento cero, teniendo en cuenta que este método asume una valoración neutral ante el riesgo, es decir, que el cálculo de las probabilidades p y 1−p, estarán en función de la siguiente fórmula:
Donde: p es la probabilidad para el valor de la opción en el escenario creciente, e es la función exponencial, u es el factor de crecimiento del valor del activo subyacente, y d es el factor de decrecimiento del valor del activo subyacente.
Este método ha sido generalmente empleado para valorar proyectos de las industrias minera, petrolera y tecnológica, ya que según Kulatilaka (1988, 1995) y Brandão, Dyer y Hahn (2005) permite aproximar la incertidumbre asociada a los cambios que puede tener el valor del proyecto durante su ejecución y en donde el uso de la programación dinámica para resolver árboles binomiales permite el análisis de escenarios factibles, característica que no es posible incorporar en otros modelos de valoración (Borison, 2005).
El presente artículo se fundamenta en la anterior metodología, pero se enfoca en utilizar una opción de abandono, en la cual usualmente los inversionistas se comprometen a invertir determinada cantidad de dinero, lo que suelen hacer por etapas, pues les permite mantener viva la opción de abandonar el proyecto (es decir, la patente) cuando se visualiza un futuro bastante oscuro (Mascareñas, 2015), es decir, cuando los costos y gastos son mayores a los ingresos que generaría el proceso de explotación y comercialización del producto patentado, lo que ocurre específicamente para el caso de la presente investigación.
Equivalentes de certeza
Un certainty equivalent (CE, «equivalente de certeza») es la cantidad que se obtiene con certidumbre y que deja indiferente a un inversionista, en relación con el valor esperado de una situación aleatoria; en otras palabras, es la suma de dinero que un individuo necesitaría con certeza en un determinado momento con el fin de hacer que sea impasible entre una cantidad segura y otra que espera recibir con riesgo en un determinado instante del tiempo (Van Horne y Wachowicz, 2002); la diferencia entre el valor esperado y el CE es la prima de riesgo. Cuando se aplica la metodología de CE es preciso determinar un flujo de caja cierto que ofrezca la misma utilidad que uno riesgoso, la cual, descontada a la risk free (Rf, «tasa libre de riesgo»), es tan deseable como la distribución de probabilidad del flujo de caja para el año t (Mukherjee, van Belle y Baker, 2003).
El método CE hace ajustes separados para el tiempo y el riesgo; para el primero se emplea la Rf como ajuste de descuento, y para el segundo, se convierten los flujos de caja riesgosos en ciertos; además, con el fin de evitar suponer que el riesgo se incrementa a través del tiempo, la toma de decisiones se soporta en CE para que esta sea más realista (Beedles, 1978).
Funciones de utilidad
La teoría de la utilidad esperada, que se caracteriza por la aversión relativa y absoluta que posee un inversionista frente al riesgo (Pratt, 1964; Arrow, 1964), ha permitido desarrollar una amplia bibliografía sobre las diferentes funciones de utilidad que sirven para modelar dichas preferencias. Esta teoría está enmarcada en el plano de las finanzas neoclásicas (Shefrin, 2010), ya que se basa en fundamentos sistemáticos y rigurosos, y no incluye ningún tipo de supuesto que esté apoyado por las finanzas comportamentales que están soportadas por hallazgos desde la psicología. Adicionalmente, durante varios años, el análisis de decisiones bajo riesgo ha sido generalmente aceptado como un modelo normativo de selección racional aplicado a diferentes comportamientos económicos (Kahneman y Tversky, 1979).
Lo primero por considerar en las funciones de utilidad es que muestren un comportamiento de aversión relativa y absoluta tanto constante como decreciente en su orden, es decir, el agente debe preferir más que menos, lo que significa que deberá seleccionar la opción dominante, en el sentido estocástico, entre un conjunto de alternativas riesgosas, y en segundo lugar, deberá incorporar su nivel de aversión al riesgo (Maya Ochoa y Pareja Vasseur, 2014).
Arrow (1964) y Pratt (1964) plantearon el uso de las funciones de utilidad exponencial y lineal, y demostraron que solo ellas tienen aversión absoluta al riesgo constante; además, sustentan que las únicas funciones de utilidad continuas que muestran CRRA son la logarítmica y la de potencia. Adicionalmente, se tiene la familia de funciones con aversión absoluta al riesgo hiperbólica, de la cual se desprende la función de utilidad generalizada de potencia, que permite obtener con facilidad las funciones de utilidad exponencial negativa, logarítmica y cuadrática (Merton, 1992).
Algunas funciones deben desecharse, como la cuadrática y la cúbica, por presentar aversión absoluta al riesgo creciente, y la exponencial negativa, porque presenta un comportamiento de tipo aversión absoluta al riesgo constante y aversión relativa al riesgo creciente (Maya Ochoa y Pareja Vasseur, 2014).
Para explicar la selección anterior, los autores se basan en los coeficientes de Arrow-Pratt que comprenden los siguientes elementos:
Aversión absoluta al riesgo: mide la tasa a la cual la utilidad marginal decrece cuando la riqueza aumenta en una unidad.
Donde: A(w) es la aversión absoluta al riesgo, u′′(w) es la segunda derivada de la función de utilidad, y u′(w) es la primera derivada de la función de utilidad.
Aversión relativa al riesgo: mide la tasa a la cual la utilidad marginal decrece cuando la riqueza aumenta en un 1%.
Donde: R(w) es la aversión relativa al riesgo, w representa la riqueza del inversionista, u′′(w) es la segunda derivada de la función de utilidad, y u′(w) es la primera derivada de la función de utilidad.
Sin embargo, a efectos de esta investigación es importante proponer la función que permita modelar de modo adecuado el comportamiento del inversionista en condiciones particulares, razón por la cual se optó por la CRRA, puesto que cumple una serie de condiciones deseadas, tales como una aversión absoluta al riesgo decreciente y CRRA, además de que permite diferenciar las preferencias de los agentes de acuerdo con distintos niveles de concavidad y porque, según la literatura, es una función deseada para ajustar datos de utilidad. Fuera de lo anterior, se encontró que la expo-power es una función de utilidad también apropiada y que cumple las características anteriores; además de su flexibilidad, que permite modelar casi cualquier tipo de comportamiento frente al riesgo (Saha, 1993). Se puntualiza por parte de los autores que la última función referenciada no se utilizó en la metodología propuesta dado que existe poca bibliografía al respecto, vacío de conocimiento que podrá abordarse en investigaciones futuras.
Aversión relativa al riesgo constante
Su forma estructural es (Azar, 2010; Wakker, 2008):
Donde: U(w) representa la utilidad en función de la riqueza, w es la riqueza del inversionista, y γ es el coeficiente de aversión al riesgo (parámetro gamma).
La CRRA cumple las propiedades de tener una aversión absoluta al riesgo decreciente y poseer CRRA.
La teoría argumenta que γ fluctúa entre −1 y +1 (Pratt, 1964); sin embargo, según diferentes trabajos empíricos, la calibración del coeficiente depende de forma exclusiva de las características del individuo, por lo cual también puede oscilar desde −0.5, que significa moderadamente amante del riesgo, hasta 1.25, que equivale a muy adverso; debe quedar claro que el valor de cero corresponde a neutralidad (Harrison, Johnson, McInnes y Rutstrom, 2005).
Con el fin de utilizar la función CRRA en el modelo, conviene referirse a un artículo que expone un experimento de laboratorio en el cual se utilizó un γ = 0.45, lo que permitía que los individuos analizados fueran indiferentes frente a elegir entre diversas loterías (Harrison et al., 2005). En otro trabajo, realizado con el fin de medir el comportamiento frente al riesgo de los inversionistas en Dinamarca, se encontraron diferentes valores para γ; el estudio gira en torno a la riqueza actual y la riqueza esperada y se concluye que el valor medio para este parámetro fue de 0.67, muy cercano al anterior, que reveló que los individuos, en efecto, son adversos al riesgo, resultado que es congruente y consistente con el que se obtuvo en Estados Unidos con una muestra de estudiantes (Harrison, Lau y Rutstrom, 2007). Otro experimento similar empleó un γ = 0.536, lo que permitió modelar una aversión al riesgo moderada por parte de los agentes que participaron en el estudio; además, este valor resultó comparable con los obtenidos en otros experimentos del mismo tipo y con métodos estadísticos en países desarrollados (Harrison, Humphrey y Verschoor, 2009).
En muchos de los anteriores estudios referenciados se empleó la función de utilidad CRRA para caracterizar las actitudes frente al riesgo y conocer la correlación de dicha prueba con el comportamiento de los individuos en un mundo real; se encontró que, en este último contexto, la media del parámetro fue de 0.63, mientras que en la prueba de laboratorio fue de 0.79; ambos resultados exhibieron aversión al riesgo (Andersen, Harrison, Lau y Rutstrom, 2010).
En la figura 2 es posible percibir que los individuos de ambos experimentos son adversos al riesgo, ya que un valor positivo en la media del parámetro γ indica dicha condición. Es importante mencionar también que, a pesar de que los autores indican que no existe una diferencia significativa entre las medias de ambos grupos, es decir, 0.63 para el primero y 0.79 para el segundo, es importante indicar que las distribuciones sí difieren tanto en dispersión como en forma, lo que indica que no se tienen las mismas preferencias por parte de los agentes en pruebas de laboratorio que en la vida real.
En último lugar, los autores también plantean que es posible construir, a partir de la información suministrada, intervalos de confianza del 95% para el coeficiente mencionado, así: para el grupo de campo se define entre −0.49 y 1.87, y para el de laboratorio, entre −0.02 y 1.85.
Finalmente, y como complemento de los trabajos anteriores, Harrison, Lau, Rutstrom y Tarazona-Gomez (2013) plantearon un caso de estudio realizado en la Universidad de Oxford, en el que estimaron el parámetro γ para diferentes grupos sociodemográficos y alcanzaron datos más específicos teniendo en cuenta diferentes especificaciones de la población. De acuerdo con la información que contiene, es posible inferir que el valor del coeficiente γ cambia por efectos de dichas variables.
Clasificación de patentes mediante utilización de opciones
Los principales modelos de opciones reales utilizados en la determinación de aspectos relacionados con características en las patentes (Sereno, 2010) son los que podemos observar en las tablas 1 y 2.
Tabla 1 Clasificación de tipos de opciones en patentes
| Tipo | Definición |
|---|---|
| Opciones de renovación | Otorga el derecho, mas no la obligación, al poseedor de la patente (patentee), de renovar la obtención de beneficios generados por la explotación de la invención a partir del pago de unos importes periódicos. Esta tiene una protección de 20 años y es denominada europea, ya que el patentee puede en cada etapa decidir el pago de una cuantía, fija o variable, o abstenerse de hacerlo (Baudry y Dumont, 2006) |
| Opciones de licenciamiento | Da el derecho al patentee de vender la patente, de manera que pueda ser explotada, a través de los derechos que se otorguen a terceros (Sereno, 2010) |
| Opciones de aplicar una solicitud de patente en el extranjero | Se asemeja a una opción de expansión de un proyecto. Se refiere a la posibilidad de extender la protección de la invención a otros países, en los que se espera obtener beneficios sobre ella. De esta manera, el patentee puede ejercer una opción de compra de una parte adicional del mercado, incurriendo con ello en unos costos de expansión, o abstenerse de hacerlo (Mascareñas Pérez-Íñigo, 1999) |
| Opción de abandonar la patente | Esta opción, denominada americana de venta, que tiene como precio de ejercicio el valor residual de la patente, también contiene los retornos actuales generados por la invención y una opción permanente de abandonar el proyecto (Sereno, 2010) |
| Opción de litigio | El elemento esencial que se resalta para esta opción se origina por la decisión de demandar por el uso desautorizado de una invención (litigar). Por lo anterior, da el derecho de vender los beneficios actuales por regalías derivadas del proceso de disputa (Marco, 2005) |
Fuente: Elaboración propia.
Tabla 2 Modelos de opciones utilizadas en patentes
| Modelos que estudian patentes como inversiones secuenciales y su valor se modela a través de opciones compuestas | Modelos en los cuales la patente se compone de opciones reales múltiples y su valor se expresa en portafolios de activos tangibles e intangibles |
| Modelos que utilizan procesos estocásticos complejos para simular las principales fuentes de incertidumbre | Modelos que combinan el ROA y la teoría de juegos para analizar el efecto de la competencia y las decisiones de patentar |
Fuente: Elaboración propia.
Este artículo se sustenta en la utilización de la metodología ROA, donde se aplica el método que considera dos o más opciones reales (Puran, 2005). Por lo general, la primera de ellas está relacionada con el proceso de concesión y las diferentes fases de la patente, y la segunda se erige de manera exclusiva cuando se ejerce la primera y consiste en comercializar la invención patentada con el fin de obtener los beneficios después de ejecutar la inversión. Es importante considerar que en ambas opciones se incluyen costos hundidos.
Valoración de patentes farmacéuticas a través de opciones reales. Un caso de estudio de Serono International S. A.
Las compañías biofarmacéuticas deben su valor en el mercado a los beneficios que generan los productos que comercializan y a las patentes que desarrollan, las cuales les aportan una ventaja competitiva frente al resto de las empresas del sector (Rubio Martín y Lamothe Fernández, 2010). El poder de patentar para este tipo de empresas se refiere, en la gran mayoría de los casos, al descubrimiento de una nueva molécula, al desarrollo de un medicamento o fármaco, que más tarde tendrá el privilegio de comercializar (Kellogg y Charnes, 2000; Borissiouk y Peli, 2002; Rubio Martín y Lamothe Fernández, 2010). En general, se pueden distinguir 2 componentes o etapas en los proyectos de biotecnología, que se muestran a continuación (Sereno, 2010; Puran, 2005; Piñeiro Groba y León Valle, 2004; Kellogg y Charnes, 2000; Rubio Martín y López-Cózar Navarro, 2007).
Etapas en los proyectos de biotecnología
Etapa uno: investigación y desarrollo
a. Descubrimiento.
b. Fase preclínica: comprende pruebas de laboratorio y experimentos en animales para detallar los posibles efectos secundarios. La duración de esta fase es difícil de estimar.
c. Fase clínica: comprende:
•. Fase I: pruebas clínicas sobre sujetos sanos (entre 20 y 80 personas) que acuden de forma voluntaria bajo autorización. Por lo general tiene una duración entre uno y 2 años.
•. Fase II: se desarrolla en pacientes (entre 3,000 y 4,000 personas) que presentan la enfermedad específica. Se evalúa la eficacia del fármaco, a la vez que se recopila información sobre los efectos secundarios y la obtención de la dosis. Su duración oscila entre uno y 2 años.
•. Fase III: se efectúan pruebas a gran escala en todo tipo de pacientes con el fin de estimar su seguridad y eficacia. Su duración es el doble de la de las 2 fases anteriores.
d. Fase regulatoria: una vez se pasa el periodo de prueba de cada una de las fases, se recopila la información y se envía al gobierno para su aprobación. La duración de este trámite es de uno a 2 años.
Etapa dos: comercialización
Cada fase puede entenderse como una opción real que va surgiendo de manera secuencial, donde el activo subyacente es el present value (PV, «valor presente») de los ingresos y el precio de ejercicio es el agregado de los egresos, imputables de manera directa a cada una de las fases, sobre las que se toma la decisión de continuar con el proyecto o de desistir de él.
Aplicación de la propuesta metodológica al caso de una patente. Caso Serono International S. A.
Con el fin de aplicar la propuesta metodológica que se presenta en esta investigación, se decidió adaptarla al caso de estudio presentado por Borissiouk y Peli (2002), en el que se evaluó un proyecto del sector biotecnológico que recibió el nombre de «Proyecto X» debido a la necesidad de confidencialidad de las cifras. El proyecto presentó y alcanzó de forma exitosa la etapa de investigación y desarrollo, la fase preclínica y la fase I, y estaba a la espera de continuar con la fase clínica II o de detenerse.
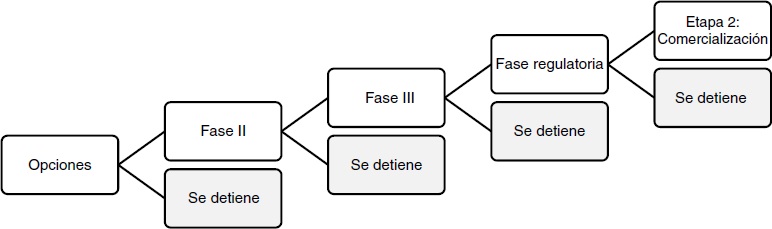
En este caso de estudio, las opciones de inversión fueron las siguientes: opción uno) consistió en la decisión de entrar a la fase clínica II; opción 2) fue la decisión de entrar a la fase clínica III; opción 3) se constituyó como la decisión de entrar a la fase de aprobación regulatoria, y opción 4) se definió como el lanzamiento del medicamento al mercado. Lo anterior se representa de manera gráfica en la figura 3.
Fuente: Elaboración propia con base en Sereno (2010).
Figura 3 Árbol de decisión del caso de Serono International S. A.
El activo subyacente que se consideró en las opciones primera y segunda, equivalente a la decisión de entrar en la fase siguiente, correspondió a los flujos de caja futuros; en la tercera se incluyó el valor del derecho del gerente de proceder con el lanzamiento del medicamento «X», solo si el valor del proyecto excedía las inversiones en esta fase, y en la cuarta opción emergió del valor generado por la comercialización del fármaco.
La valoración de patentes y otros tipos de proyectos que incluyen el concepto de flexibilidad se deberían llevar a cabo con el método tradicional ROA, que se fundamenta en argumentos de no arbitraje y probabilidades neutrales frente al riesgo, en lugar de tasas de descuento ajustadas por riesgo (Smith, 2005). Pero a diferencia de lo anterior, se propone para el caso una valoración alternativa que utiliza el método ROA pero con el uso de CE, a través de funciones de utilidad, en el cual la ausencia de neutralidad ante el riesgo es el elemento más predominante. En este enfoque de CE, el ajuste por riesgo está en la distribución de probabilidad de los flujos de caja, y no en la tasa de descuento (Schwartz, 2013).
Dados los razonamientos anteriores se decidió aplicar la propuesta metodológica de valoración de opciones reales a una patente colombiana, de preferencia del sector biofarmacéutico, porque, a diferencia de los métodos tradicionales de valoración de activos intangibles y de otros modelos no tradicionales, como el de lógica difusa y los econométricos, el método ROA incluye una característica importante para el desarrollo de un medicamento sujeto a protección a través de una patente: la flexibilidad administrativa. Sin embargo, dada la complejidad en la consecución de la información necesaria para la aplicación de la metodología seleccionada, se decidió adaptar el caso de Serono International S. A. y en él aplicar la propuesta metodológica, con el fin de detallar que se pueden adicionar nuevos e importantes elementos en torno al tema de enfoques y modelos de valoración de activos intangibles, en especial lo referente a las patentes.
En primera instancia se desarrolló la aplicación de la opción real a una patente farmacéutica; a esta metodología se le realizó una modificación sustancial, que se basó en la utilización de una nueva propuesta presentada por Maya Ochoa, Mongrut, Pareja Vasseur y Salazar (2011) y Maya Ochoa y Pareja Vasseur (2014), que se fundamenta en la utilización de CE (Mukherjee et al., 2003) para descontar los flujos con la tasa libre de riesgo, con lo que se supera una de las críticas más importantes que se le hacen a la metodología tradicional ROA en torno al supuesto de neutralidad ante el riesgo (Beedles, 1978).
Para este propósito, el desarrollo de la valoración se ejecutó en 3 etapas, que se presentan a continuación:
Etapa uno: se encuentra el valor del proyecto patentable sin incluir la flexibilidad mediante el método tradicional DCF, excluyendo del mismo todo lo referente a costos e inversiones necesarias para ejecutar y completar de manera exitosa todas y cada una de las fases del proyecto; el criterio de evaluación utilizado en este caso fue el PV.
Etapa 2: se estipula la volatilidad, tanto del PV como de la porción de costos de lanzamiento -que equivalen a los de mercadeo-. Para ello se utilizó la volatilidad implícita que posee cada una de estas variables y se empleó un proxy: la desviación estándar.
Etapa 3: se construye un árbol binomial a partir del PV y en cada una de las ramas finales del mismo se evalúa la diferencia entre el valor mencionado y los costos; los últimos son tanto estocásticos como fijos; finalmente, al valor resultante se le calculó su respectivo CE. Para tal fin se debe utilizar la función de utilidad en cada rama del árbol, por lo cual se hace necesario determinar la particular para cada inversionista. Las utilidades resultantes se ponderaron luego por las probabilidades asignadas (p y [1−p]), lo que generó una utilidad esperada ponderada.
A continuación, se convirtió a flujo de caja cierto la utilidad esperada ponderada mediante el cálculo de la función de utilidad inversa, cuyo valor resultante se descontó a la Rf, con lo que se subsanó la dificultad planteada de encontrar una tasa adecuada para los flujos de caja concernientes a la patente. Vale la pena indicar que este proceso se debe repetir cada año mediante el uso de las etapas 2 y 3, hasta encontrar un único valor, que corresponda al proyecto estratégico, del cual más tarde se podrá sustraer el valor del proyecto estático, cantidad resultante que equivale al valor de la opción.
Los autores estimaron el valor del «Proyecto X» con el criterio NPV mediante la metodología DFC; se incluyeron, además, los ingresos y los diferentes costos calculados con los precios esperados y los volúmenes pronosticados para 3 mercados: la Unión Europea, Japón y Estados Unidos. Todos los flujos de caja previstos se estimaron en millones de dólares (USD) debido a que las ventas vigentes se concentraron en el último de dichos mercados.
Los estudios arrojaron como resultado las probabilidades de éxito tecnológico del «Proyecto X» en cada una de las fases; estas, a su vez, se determinan con base en las tasas promedio en la industria de la biotecnología y, por último, las ajustan expertos clínicos para reflejar de mejor manera las características específicas que otorga el proyecto. Por lo tanto, la probabilidad de resultados positivos en el medicamento «X» en la fase II fue del 66%; la probabilidad de eficiencia significativa en el tratamiento de los pacientes durante la fase III fue del 50%; al final, la fase de aprobación por parte de la Agencia Europea de Evaluación Médica, en el caso de Europa, y para el caso de Estados Unidos, la Administración de Alimentos y Medicamentos, fue del 90%. Si este organismo aprueba el medicamento, este también será certificado para Japón (Sereno, 2010).
La empresa posee un costo de capital promedio ponderado cercano al 11% anual, de lo que se obtiene un NPV de 212.2 millones USD en el año 2002. Este valor se da si, y solo si, todos los estudios clínicos tuvieran un éxito del 100%. Con posterioridad, Borissiouk y Peli (2002) optaron por utilizar el expected net present value (ENPV, «valor presente neto esperado») que permite, en su estructura, incluir las probabilidades técnicas de ocurrencia de las fases, para ajustar de este modo la cifra inicial a un valor cercano a 53.1 millones USD.
Sin embargo, cuando se utiliza la metodología NPV tradicional complementada con árboles de decisión para cada una de las fases, la cifra resultó ser de 39.22 millones USD; en otras palabras, el valor de la flexibilidad que tuvieron los gerentes para ajustar la evolución que se incluye en el desarrollo y en el proceso de mercadeo del medicamento «X» asociado con el comportamiento del riesgo tecnológico correspondió a la diferencia de las 2 últimas cifras, es decir, 13.9 millones USD.
Hasta este momento, los autores concluyeron que el enfoque de árbol de decisión refleja en mejor forma la situación real en el proceso de toma de decisiones y proporciona un valor «correcto» del proyecto de I + D. Además, concluyen que el ENPV clasifica mejor los proyectos de biotecnología disponibles en términos de su rentabilidad, ya que aprovecha la parte positiva de los riesgos tecnológicos inherentes a los mismos.
No obstante, también reconocen y resaltan el hecho de que el anterior modelo presentó 2 grandes problemas: el primero, utilizaron una tasa constante de descuento, lo cual se presume como un error, ya que no se debe derivar de los mercados financieros, sino que, por el contrario, debe tener relación con los riesgos a los cuales están expuestos el proyecto y el inversionista; y el segundo, no se tuvo en cuenta el impacto de la incertidumbre económica, lo que implica subestimar en la mayoría de los casos el verdadero valor de la flexibilidad.
En vista de los anteriores problemas, los autores tomaron la decisión de emplear la metodología tradicional ROA para determinar el cálculo de la opción; para realizar este proceso excluyeron todo lo referente a las inversiones y los costos.
A partir del PV y los costos que se volverán estocásticos es posible construir el árbol binomial para la propuesta metodológica de la investigación. En tal sentido, los autores plantean que para el año 2002 representaban un valor de 69.4 millones USD, con la siguiente composición: variables en un 80% y fijos en un 20%.
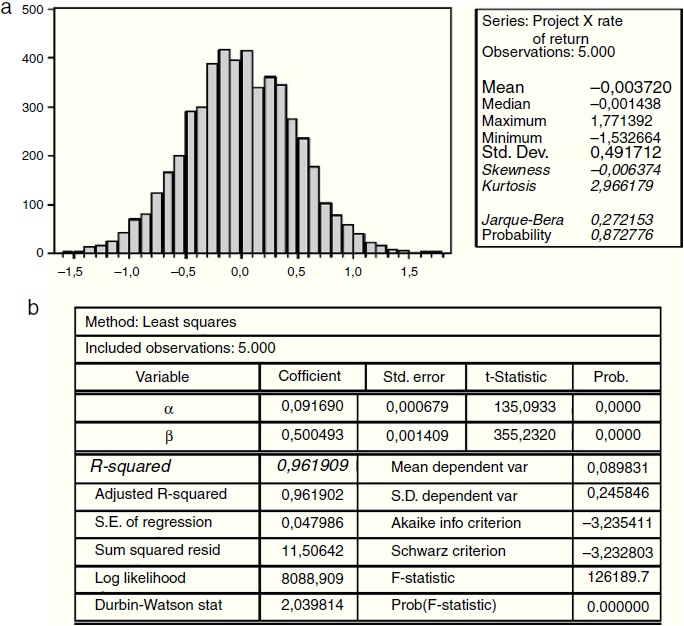
Para obtener una medida consolidada de la volatilidad, los autores modelaron de forma separada las distribuciones de precio y participación de mercado, caracterizadas en cada caso por su valor esperado, volatilidad, bandas de confianza y autocorrelación. Se capturó el efecto de la correlación entre las variables estocásticas y por medio de la simulación de Monte Carlo se generó la distribución de los retornos del «Proyecto X» con el fin de encontrar la media y la desviación estándar para este caso. Durante la realización del proceso se detectó que los principales impulsores de la volatilidad del proyecto fueron la incertidumbre de los precios y la participación en el mercado, la cual correspondió a un 49.17% anual, como se puede visualizar en la figura 4a, seguida de la volatilidad de los retornos de los costos, con un 47.33% anual, proceso en el cual se percibió una correlación entre estas 2 variables de 0.9619. Por último, y al incluir todas las condiciones anteriores, se procedió a estructurar la flexibilidad del proyecto por medio de la metodología tradicional ROA.
Fuente: Tomada de Sereno (2010).
Figura 4 (a) Simulación de los retornos del «Proyecto X», caso de Serono International S. A. (b) Regresión lineal entre los retornos del proyecto y los retornos de los costos.
El anexo 1 representa parte de la metodología propuesta en la investigación, aplicada al caso específico, y se explica al detalle de la siguiente manera: primero se parte del PV inicial ubicado en el año 2002, que corresponde al precio del subyacente, S0, que otorga el modelo DCF (400.37 USD). Después se proyectan 2 ramas que equivalen a los valores futuros estimados a partir del monto inicial, utilizando para ello los factores u y d, a partir de las siguientes ecuaciones:
Utilizando la volatilidad del proyecto (que corresponde a 49.17%), se obtienen así los valores de 654.65 y 244.86 millones USD (ver anexo 1); el mismo procedimiento se utilizó para la porción de costos que son variables, pero substituyendo la volatilidad por 47.33% anual (ver anexo 2).
El cálculo del valor del proyecto con flexibilidad supone, en un primer paso, el cálculo de los pagos en el último año de evaluación (MAX2007) (ver anexo 3); este valor se obtiene de S2007 , que corresponde al PV estimado para ese año, menos el valor X2007 , es decir, el precio de ejercicio, que equivale a los costos e inversiones requeridas para ejecutar el proyecto.
Debido a que los mismos pueden tomar valores negativos, la empresa tiene el derecho de abandonar el proyecto, situación en la cual los costos de lanzamiento no se harían efectivos. Esta oportunidad de abandono es lo que corresponde al valor de la opción que se evalúa en cada nodo a través de la función:
Por ejemplo, el último valor para el año 2007 en USD, que está ubicado en la parte superior del anexo 3, se calculó de la siguiente forma utilizando la ecuación anterior:
La segunda etapa implicó calcular la utilidad para el inversionista de los valores obtenidos con anterioridad, mediante la función de utilidad apropiada, que para la presente investigación correspondió a la función isoelástica tipo CRRA debido a que es fácil de manipular, entender y calibrar; de acuerdo con lo anterior, fue posible comparar las 2 metodologías (tradicional y propuesta), de modo que si se utiliza la última para el caso de un inversionista neutral al riesgo, es decir, con γ = 0, el valor de la opción real valorada en estas condiciones deberá ser igual a la que se obtiene por el método tradicional (ver anexo 3). Para esta fase se recurre a la ecuación (1.3).
Por ejemplo, el valor equivalente en utilidad utilizando γ = 0 y que está ubicado en la parte superior del anexo 3 para el año 2007 se calculó de la siguiente forma utilizando la ecuación anterior:
Más tarde, en una tercera fase, se calculó la utilidad esperada ponderada, multiplicando cada utilidad por su respectiva probabilidad.
Utilizando la ecuación (1.1) es posible encontrar los valores de p y 1−p, y aplicando la fórmula (1.7) se estima el valor de la utilidad esperada ponderada, utilizando para ello las utilidades que se estiman en la fase anterior, de esta forma:
A continuación, se encontró su respectivo equivalente de certeza a través de la función de utilidad inversa (ver anexo 3).
Al tratarse de equivalentes de certeza, este valor fue posible descontarlo a la tasa Rf para obtener el valor de la flexibilidad, pero antes de hacerlo, el valor resultante se multiplica por la probabilidad técnica de aprobar la fase, y por último, se le restó el valor de la inversión inicial. Los cálculos a partir de la ecuación (1.8) fueron los siguientes:
Para calcular el valor de NPV estratégico se repitió todo el proceso desde la segunda hasta la última etapa, con el fin de determinar el valor del proyecto con flexibilidad, que como era de esperar, al utilizar el mismo valor de parámetro γ habría de obtenerse el mismo valor reportado por los autores.
La opción de abandono se dedujo de la diferencia entre el NPV estratégico (55.09 millones USD) y el ENPV estático (53.1 millones USD), obteniéndose un valor de 2 millones USD.
En el anexo 4 se puede observar cómo a través de la manipulación del parámetro γ, es decir, de la variable que representa las preferencias, es posible modelar un agente más propenso al riesgo (es decir, equivale a valores negativos de γ) y, por ende, mayor será el valor de la opción; para este caso específico se tiene que el valor del parámetro γ debe tomar valores entre −1 y 0.02, aproximadamente, para que sea viable la opción de abandono. La diferencia anterior se puede explicar de acuerdo con la función de utilidad empleada para el estudio, la cual a través del método CE castiga las preferencias del inversionista y la exposición que el mismo muestra frente al riesgo, eliminando así por completo el concepto de neutralidad.
Conclusiones
La importancia de las patentes dentro del portafolio de activos intangibles se debe a que son indicadoras de la productividad y la creatividad de un país; por lo tanto, se consideran una fuente de valor agregado, no solo para la producción científica, sino también para la tecnología mundial.
Aunque el enfoque tradicional basado en DCF ha sido el más utilizado en finanzas para la valoración de diferentes activos, cuando se tienen en cuenta activos intangibles, como por ejemplo las patentes, se generan resultados poco realistas, pues no se incluyen los efectos de la incertidumbre y la flexibilidad, elementos que reflejan el riesgo de éxito o fracaso en cada etapa de desarrollo y que están incluidas en la metodología ROA.
La metodología propuesta permitió, a través del uso de CE y de forma específica mediante la función de utilidad CRRA, en razón a que esta última posee características relacionadas con el tipo de preferencias de los agentes, modelar a través del uso del coeficiente de aversión a aquellos inversionistas que no están diversificados por completo y que por lo general subyacen en mercados incompletos. La metodología empleada, además de generar resultados que son consistentes con la literatura, le permite al lector apropiarse de ella a pesar de su alto contenido matemático, y se considera fácil de implementar.
La propuesta metodológica proporcionó diferentes valores para los que existiría la opción de abandono, cuya vigencia en el escenario de un inversionista adverso frente al riesgo oscila entre un rango de 0 y 0.02; lo anterior quiere decir que, para otros valores positivos, no cabría la posibilidad de opción, y en ese caso se debería tomar el ENPV estático como el mejor predictor. Por lo anterior, el mayor valor agregado de esta investigación es poder utilizar este enfoque como adecuado para determinado tipo de inversionistas, ya que les presenta un amplio abanico de resultados de acuerdo con sus respectivas preferencias ante el riesgo.
Existe también la opción en circunstancias de preferencia o propensión frente al riesgo; lo anterior ocurre cuando al coeficiente γ se le asignan valores negativos. Es importante resaltar, como se demostró en el artículo, que en el caso de utilizar un valor de parámetro igual a cero se obtiene un resultado igual al de la metodología tradicional, en la cual subyace el concepto de neutralidad ante el riesgo.
La función de utilidad seleccionada, CRRA, permitió calibrar y modelar el parámetro γ gracias a sus propiedades y características ideales. Sin embargo, se exhorta a los lectores en futuras investigaciones a apropiarse del uso de otras funciones de utilidad, como puede ser la expo-power, ya que, gracias a su atractiva flexibilidad, podría generar otro tipo de aportes interesantes.











 nova página do texto(beta)
nova página do texto(beta)