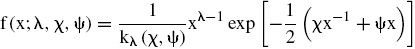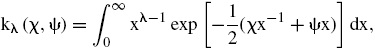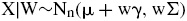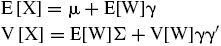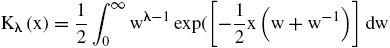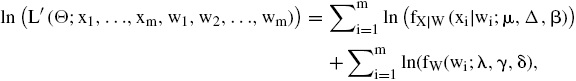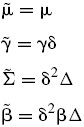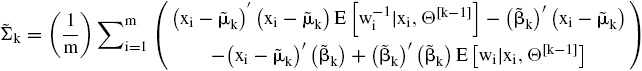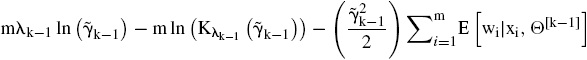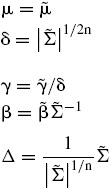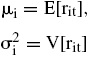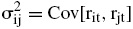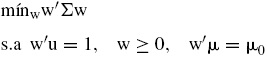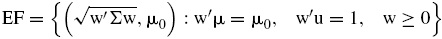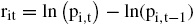Códigos JEL: G11; G15
Introducción
La matriz de covarianzas de un conjunto de rendimientos es un parámetro relevante en la construcción de portafolios de inversión. No obstante, resulta difícil determinar una matriz de covarianzas empírica confiable Laloux, Cizeau y Bouchaud (1999), ya que las series de tiempo disponibles pueden contener ruido y este elemento estocástico ocasiona indirectamente que se sobrestimen o subestimen las covarianzas y varianzas poblacionales.
Específicamente, Burda y Jurkiewicz (2004) señalan que la matriz de covarianzas muestral puede no reflejar la correcta asociación poblacional entre los diferentes rendimientos porque las condiciones del mercado cambian con el tiempo y la covarianza existente entre un par de activos no necesariamente es permanente. El tamaño de la muestra, la longitud de las series de tiempo y el conjunto de activos que se hayan considerado pueden arrojar observaciones con ruido. En este caso, la varianza muestral estimada traería consigo un componente asociado a la variable aleatoria del ruido, pero que no se puede distinguir directamente (Laloux et al., 1999). Análogamente, las covarianzas muestrales podrían presentar el mismo problema y sesgar los cálculos relacionados con la matriz de covarianzas muestral (Mata, 2013).
Idealmente se desearía utilizar la matriz de covarianzas poblacional de los rendimientos en un portafolio específico, pues se eliminarían las posibles complicaciones que presenta el estimador muestral de la matriz de covarianzas. En este sentido, la función de densidad de probabilidad multivariada que mejor se ajuste a la muestra de información disponible es un punto clave (Alayón, 2014), ya que sería posible emplear un estimador más consistente de la matriz de covarianzas poblacional en el procedimiento de Markowitz (Mata, 2013).
En este trabajo se emplea la distribución hiperbólica generalizada (GH), pues es una familia de funciones altamente flexibles para ajustarse según los hechos estilizados de los rendimientos financieros (Breymann y Lüthi, 2013). La distribución multivariada GH permite capturar el sesgo y las colas pesadas que se observan usualmente (Prause, 1999), y que la distribución normal multivariada pasa por alto (Hu, 2005).
Esta familia de distribuciones multivariadas GH fue introducida para describir situaciones complejas de la naturaleza, como por ejemplo el estudio de los granos de arena (Barndorff-Nielsen, 1977). No obstante, pasaron muchos años antes de las implementaciones numéricas consistentes en el ámbito financiero. Eberlein y Keller (1995) ajustaron la distribución hiperbólica univariada para diversos rendimientos de acciones en el mercado alemán, obteniendo ajustes razonables sobre las muestras de datos, donde se modelaba satisfactoriamente el sesgo y la alta curtosis. Años más tarde, Protassov (2004) empleó el algoritmo expectation-maximization (EM) para estimar una GH multivariada de dimensión 5 sobre un conjunto de tipos de cambios de la OCDE, y es el primer autor en reportar una estimación superior a la presentada por Blæsild y Sørensen (1992). Sin embargo, Protassov (2004) no presenta una prueba de hipótesis para verificar la bondad de ajuste de la distribución GH a la muestra de datos.
Si bien es cierto que uno de los obstáculos para la implementación de la familia GH es la dificultad numérica para calibrar los parámetros de la distribución (Hu, 2005), existen diferentes propuestas numéricas para ajustar la familia GH (Breymann y Lüthi, 2013), donde usualmente se asume que el parámetro de la función de Bessel de tercer orden es fijo. Recientemente, Alayón (2014) emplea algunos casos particulares de la familia GH para calibrar portafolios, al igual que Mina (2010) presenta algunos ejercicios para el caso mexicano mediante casos específicos de la familia GH. Similarmente, Mata (2013) comenta aspectos teóricos y numéricos para estimar la familia GH e implementar algunas aplicaciones financieras. Adicionalmente, Erickson, Ghysels y Wang (2009) muestran que uno de los miembros de la familia GH puede utilizarse para valuar opciones y otros derivados.
En este documento se realiza la estimación de los parámetros bajo el algoritmo de Protassov (2004), en conjunto con algunos aspectos numéricos señalados en la especificación propuesta por McNeil, Frey y Embrechts (2005), salvo que el parámetro de la función de Bessel de tercer orden no se asume fijo (Mata, 2013). Adicionalmente, se implementa una prueba de hipótesis reciente (McAssey, 2013) para evaluar la bondad de ajuste de la distribución GH.
De esta forma es posible valorar la relevancia del estimador de la matriz de covarianzas y utilizarlo como un insumo dentro del procedimiento de construcción de portafolios de Markowitz (1959). Los resultados obtenidos se comparan con el portafolio tradicional que emplea la matriz de covarianzas muestral. Este comparativo muestra que el coeficiente de variación se reduce al emplear el estimador de la matriz de covarianzas GH, lo cual sugiere que la distribución multivariada GH puede servir como una herramienta complementaria en la elaboración de portafolios bajo el método de Markowitz, siempre y cuando exista evidencia de que la distribución de probabilidad multivariada de los rendimientos se ajuste razonablemente a la familia GH.
El contenido de este trabajo se divide en 6 secciones. La primera es la introducción, la segunda discute aspectos teóricos de la familia GH y del algoritmo EM. En la tercera sección se hace una revisión de la prueba de bondad de ajuste (McAssey, 2013) utilizada en el artículo y en la cuarta se presenta el proceso de formación de portafolios eficientes de Markowitz. Finalmente en el quinto apartado se presentan los resultados y en la sexta las conclusiones de este estudio.
Familia hiperbólica generalizada
La familia de distribuciones de probabilidad GH puede obtenerse como la mezcla de una distribución normal multivariada y una distribución gaussiana inversa generalizada (GIG). Esta especificación queda en términos de los parámetros λ, χ y ψ de la distribución GIG y los parámetros de la normal multivariada μ y Σ, así como de un vector γ (McNeil et al., 2005).
La función de densidad de probabilidad GIG está dada por:
donde kλ (χ,ψ) es una especificación alternativa para la función de Bessel de tercer orden (Paolella, 2007) y se define como:
El m-ésimo momento queda caracterizado por los parámetros λ, χ, ψ y determinan la media y varianza correspondientes, ver Abramowitz y Stegun (1972) y Paolella (2007).
Los parámetros λ, χ, ψ definen conjuntamente a los momentos de la variable aleatoria GIG, la cual es un elemento importante para establecer la especificación de la función de densidad GH. El papel que desempeñan estos parámetros dentro de la familia se puede esbozar, según Hu (2005), como sigue:
a). El parámetro λ∈ℝ determina el integrando de la función de Bessel de tercer orden y por ende define a los miembros de la familia GH. Una función de densidad clásica en la literatura (Paolella, 2007) es la función de densidad normal inversa gaussiana y corresponde a λ = −1/2. Manteniendo fijos χ, ψ ≥ 0, se observa que mientras más pequeño sea |λ| la función de densidad presenta colas más pesadas y conforme aumenta en su magnitud en valor absoluto las colas se vuelven más delgadas; asimismo la función de densidad tiende a ser simétrica.
b). Los parámetros χ, ψ ≥ 0 influyen sobre la magnitud de los momentos; dejando fijo λ∈ℝ se aprecia que conforme los parámetros tienden a cero se converge a la función varianza gamma (Prause, 1999), y conforme aumentan en magnitud se presentan colas más pesadas.
Ahora bien, un vector aleatorio X dimensión n × 1 de la familia GH se puede expresar como una mezcla normal media-varianza
donde W ∼ GIG(λ, χ, ψ), A, γ, μ son vectores n × y Z sigue una distribución normal estándar (McNeil et al., 2005). Bajo esta especificación se cumple que:
siendo Σ = AA′ la matriz de covarianzas de la normal multivariada y μ el vector de medias. En este caso, γ puede interpretarse como el sesgo que presenta X, con relación a la normal multivariada, cuando se presenta la perturbación realizada w. Si γ = 0, la distribución GH es simétrica.
El valor esperado y la varianza del vector aleatorio X que sigue una distribución multivariada GH son:
Alternativamente, Protassov (2004) define la distribución de probabilidad GH mediante los parámetros α, δ ≥ 0 tal que χ = δ2 y α2 = ψ − β′Δβ con γ = Δ β. La matriz Δ = Σ/|Σ| posee determinante igual a uno, y bajo ese caso, la función de densidad de probabilidad para un vector aleatorio X de tamaño n × es:
donde
es la función de Bessel de tercer orden modificada para x > 0. Esta distribución de probabilidad multivariada resulta más sencilla de calibrar que la especificación original (Protassov, 2004), y es altamente versátil para capturar los hechos estilizados usuales de los rendimientos financieros (Hu, 2005), que usualmente la distribución normal multivariada pasa por alto.
En el caso particular de la distribución de probabilidad normal inversa gaussiana se puede tener una caracterización más amplia de los momentos de la variable aleatoria y del significado de los parámetros. Erickson et al. (2009) muestran que los parámetros α, β, μ, δ se relacionan con la media M , la varianza V , el sesgo S y el exceso de curtosis K de la población como:
donde ρ=3KS-2−4 y signo se define como:
En ese caso es posible establecer una relación directa entre los parámetros de la distribución y los momentos de la variable aleatoria.
Por otra parte, dado que existen problemas de calibración bajo el método de máxima verosimilitud directo (Hu, 2005), entonces se utiliza el algoritmo EM (Protassov, 2004) para estimar los parámetros de la función de densidad GH, pues se ha demostrado como una alternativa plausible para evitar problemas numéricos (McNeil et al., 2005). En términos sucintos, este algoritmo considera una muestra aleatoria de tamaño m de variables aleatorias U1, U2, ..., Un cuyos vectores Xi = [Ui1, Ui2, ..., Uin], i = 1, 2, .., m, provienen de una distribución multivariada GH con parámetros Θ = (λ, γ, δ, β, μ, Δ). La expresión Uij representa la i-ésima realización de la variable aleatoria j , para j = 1, 2, .., n.
La función de log-verosimilitud GH es:
El algoritmo EM no maximiza directamente la función de log-verosimilitud sino que introduce variables latentes w1, w2, ..., wm, cuya distribución de probabilidad GIG implica una función log-verosimilitud aumentada
pues se cumple que X|W ∼ Nn(μ + wΔβ, wΣ), cada vector xi denota un vector de observaciones de las variables aleatorias Uj, j = 1, 2, .., n.
Dada una aproximación inicial Θ0, el algoritmo EM estima los parámetros de la distribución GH mediante un método recursivo que consiste básicamente en 2 pasos:
a). Se calcula el valor esperado de la función de verosimilitud aumentada mediante alguna aproximación inicial Θ0 y la muestra de datos observada x1, x2, ..., xm.
b). Luego se maximiza el valor esperado de la función obtenida en el inciso a) para obtener la siguiente aproximación del conjunto de parámetros Θ.
En la k-ésima iteración se obtendría el valor esperado
cuya maximización implicaría encontrar el vector Θ[k+1].
En este documento, la elección de la aproximación inicial para Θ0 toma Δ0 = I (matriz identidad), μ0 = β0 = 0 y el resto de puntos iniciales (λ0, γ0, δ0) se colocan en las medianas muestrales de las estimaciones univariadas llevadas a cabo sobre las variables aleatorias U1, U2, ..., Un (Mata, 2013). Esta elección de los puntos iniciales se apoya en la propiedad de invarianza que presenta la familia GH ante combinaciones lineales, ver McNeil et al. (2005). La especificación univariada para cada uno de los elementos del vector aleatorio corresponde a la función GH empleada por Paolella (2007), pues evita problemas de convergencia ante los casos límite de los parámetros de la función de densidad GIG cuando χ o ψ tienden a cero.
Asimismo, para facilitar el proceso de calibración de los parámetros en la distribución GH, se realiza el cambio de variable señalado por Protassov (2004),
De esta manera se tiene que wi|xi,Θ[k+1]∼GIG
lo cual implica que los momentos condicionales que se calculan de acuerdo a GIG
Entonces se calcula
y se maximiza la función
que permite actualizar los parámetros λk−1 y
Utilizando los parámetros estimados de la distribución de probabilidad multivariada ajustada GH se encuentra un estimador para la matriz de covarianzas de los rendimientos, pues se cumple que VX=E[W]Σ+V[W]γγ′.
En la siguiente sección se presenta el algoritmo discutido en McAssey (2013) para verificar la bondad de ajuste de la distribución ajustada GH, luego se emplea el estimador de la matriz de covarianzas como insumo en el procedimiento de Markowitz y se discuten los resultados obtenidos.
Prueba de bondad de ajuste para la distribución hiperbólica generalizada
En general, existe poca literatura que abarque la bondad de ajuste de distribuciones de probabilidad multivariadas no normales. Loudin y Hannu (2003) extienden la prueba clásica de Kolmogorov al caso bidimensional al igual que Justel, Peña y Zamar (1997), pero la implementación al caso n dimensional no es una aplicación directa. Análogamente, existen propuestas no paramétricas mediante estimadores kernel (Gábor y Rizzo, 2004), pero hay problemas de calibración para el caso de dimensiones superiores a 3.
En este trabajo se emplea la prueba de McAssey (2013) para distribuciones de probabilidad multivariadas continuas, donde la hipótesis nula afirma que la muestra de datos sigue la distribución de probabilidad propuesta. Mediante esta prueba se valora la bondad de ajuste de la distribución de probabilidad multivariada GH a la muestra aleatoria y se refuerza la utilización de la correspondiente matriz de covarianzas en el procedimiento de Markowitz.
En el contexto de este documento, el algoritmo descrito en McAssey (2013) procede como sigue:
Se estiman los parámetros de la distribución de probabilidad multivariada GH para el conjunto de rendimientos de la muestra aleatoria.
a). Luego se simula una muestra aleatoria u1, u2, ..., uN de tamaño 10000 bajo la distribución GH estimada. Los procedimientos de simulación corresponden a los algoritmos descritos en Dagpunar (1989) y Kinderman (1977), bajo la especificación de que X|W ∼ Nn(μ + wγ, wΣ) con W∼GIG(λ,χ,ψ).
b). Mediante la muestra aleatoria simulada se calculan las distancias de Mahalanobis
b).
b).
siendo que
b).
b).
que estima la probabilidad acumulada hasta el punto t s
de las distancias de Mahalanobis
c).
Se elige una partición {p0,p1,...,pT} en el intervalo
[0,1] con p0 = 0, pT = 1, y se calcula mediante
las estimaciones del inciso b) los valores q0=0,
qj=mín{ts∈ℝ|
d).
Finalmente se encuentra Ej=N(pj−pj−1) y se cuentan las observaciones
d).
Para encontrar evidencia a favor o en contra de la hipótesis nula que afirma como correcta la distribución de probabilidad propuesta, se estima el valor de probabilidad usual mediante la repetición de todos los pasos anteriores. Es decir, se construye una muestra aleatoria AT1,AT2,..,ATM de tamaño M de tal manera que se pueda estimar el valor p asociado al estadístico AT (McAssey, 2013).
En este trabajo se encuentra evidencia estadística para no rechazar la hipótesis nula de McAssey (2013). De esta manera se puede afirmar bajo un nivel de significación razonable que la distribución GH se ajusta adecuadamente a la muestra de rendimientos.
Portafolio de Markowitz
El trabajo presentado por Markowitz en los años cincuenta del siglo XX puede verse como el origen de la teoría moderna de portafolios. Markowitz asume un inversionista adverso al riesgo que dispone de un capital inicial y que desea invertir en un conjunto de activos financieros con rendimientos futuros. En ese sentido, busca determinar la proporción de su ingreso a invertir en cada uno de estos activos para maximizar el rendimiento esperado del portafolio y minimizar el riesgo del mismo. El portafolio será eficiente siempre que el rendimiento esperado del mismo sea máximo comparado con otros portafolios posibles dado un nivel de riesgo. En la optimización de portafolios, la desviación estándar fue propuesta por Markowitz como una medida de riesgo (Markowitz, 1959).
Si se supone que rit denota el rendimiento en el periodo t del activo i, entonces
representa la media y varianza del rendimiento del activo i, en tanto que
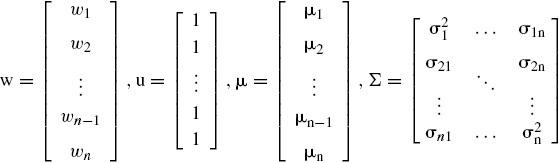
es la covarianza muestral entre los rendimientos de los activos i, j. Si se denota a wi como la proporción de riqueza invertida en cada activo i, entonces bajo términos matriciales se tiene que
En este caso, w es el vector de pesos del portafolio, u es un vector cuyos elementos son el número 1, Σ es la matriz de varianza-covarianza de los rendimientos y μ es un vector de valores esperados para los diferentes rendimientos (Markowitz, 1959).
El problema que se requiere resolver para encontrar el portafolio de mínima varianza sujeto a un rendimiento μ0 es
donde las restricciones reflejan que los pesos correspondientes suman la unidad, los pesos buscados son mayores e iguales a cero y que el rendimiento esperado que se busca es igual a μ0. Este problema de optimización puede resolverse mediante programación cuadrática (Alaitz, Miera y Zubia (2002)).
Adicionalmente, la frontera eficiente (EF) sería el conjunto formado por las parejas
es un subconjunto del plano cartesiano que se obtiene al resolver el problema de optimización señalado arriba para cada nivel diferente de μ0. En este documento se estima el conjunto EF mediante la matriz de covarianzas Σ que se obtiene del ajuste de la distribución GH y se compara con la frontera eficiente que se obtendría bajo los pesos obtenidos al utilizar la matriz de covarianzas muestral.
Este marco de comparación es válido porque se implementa una prueba de hipótesis (McAssey, 2013), para verificar que la distribución GH se ajusta adecuadamente a la muestra de rendimientos, y por ende, representa una mejor aproximación a la matriz de covarianzas poblacional que la matriz usual de covarianzas muestral.
Datos, estimaciones y resultados
El conjunto de datos que se emplea son los precios de cierre de las acciones que componen el índice OMX Stockholm 30 (OMX-30), la frecuencia es diaria y se considera el periodo que va de enero del año 2010 al mes de abril de 2014. OMX-30 es el principal índice bursátil de la Bolsa de Estocolmo, en Suecia, y está conformado por los 30 valores con el mayor volumen de negociación en la región (véase el anexo 1). Se han elegido estos valores para contar con una muestra relativamente pequeña de variables y evitar dificultades en la calibración de los parámetros de la distribución GH (Mata, 2013). Se estudia el periodo completo de la muestra para contemplar el mayor posible contenido de información posterior a la crisis financiera internacional 2008-2009.
Las estimaciones numéricas y resultados estadísticos toman como punto de partida las rutinas del paquete R que presentan Breymann y Lüthi (2013) y Wertz y Setz (2014).
Por otra parte, debe señalarse que los rendimientos diarios se han calculado bajo un enfoque continuo
donde i = 1, ..., n y t denota la variable tiempo que abarca los días durante los años 2010-2014. Bajo esta notación se tiene que
pi,t = precio diario reportado de la acción i en el tiempo t,
ri,t = rendimiento diario de la acción i en el tiempo t.
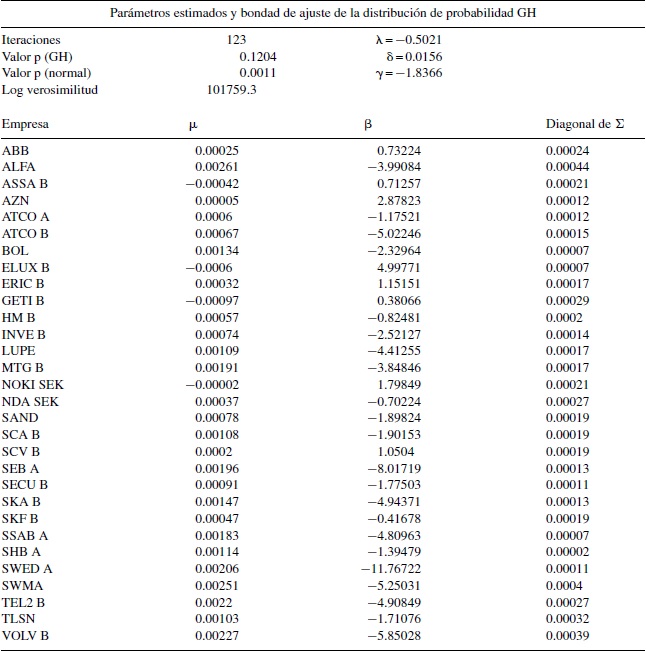
La tabla 1 muestra las estimaciones de la distribución multivariada GH para la muestra aleatoria OMX-30. Los cálculos requeridos se realizan mediante las rutinas del programa estadístico R (Breymann y Lüthi, 2013). El algoritmo presentado en este trabajo se modifica para que el parámetro λ de la función de Bessel no se encuentre fijo.
Los parámetros encontrados así como la diagonal de la matriz de covarianzas se muestran en la tabla 1. Es oportuno señalar que no se presenta la matriz de covarianzas ajustada de tamaño 30 × 30 por motivos de espacio en el documento. El parámetro λ es aproximadamente igual al valor de −1/2, lo cual señala que la forma de la distribución multivariada es muy similar a la distribución multivariada normal inversa gaussiana.
En el anexo 2 se comparan las desviaciones estándar muestrales con las desviaciones estándar que se obtienen de la distribución ajustada GH; se puede apreciar que en algunos casos se subestima la varianza del rendimiento, aunque no se encuentra un patrón específico para todos los casos que permita emitir una conclusión para todo el conjunto de rendimientos.
Asimismo, se puede observar en la tabla 1 que bajo la prueba de hipótesis de McAssey (2013) no se rechaza la hipótesis nula a un nivel de significación del 10%, lo cual nos dice que la distribución de probabilidad multivariada GH es factible para ajustarse al conjunto de información OMX-30. En contraste, si se realiza la prueba de hipótesis de McAssey (2013) bajo la hipótesis nula de normalidad se encuentra un valor p igual a 0.0011, en cuyo caso se rechaza la hipótesis de normalidad multivariada. Este resultado respalda el uso de la matriz de covarianzas estimada bajo la familia GH como insumo en el procedimiento de Markowitz.
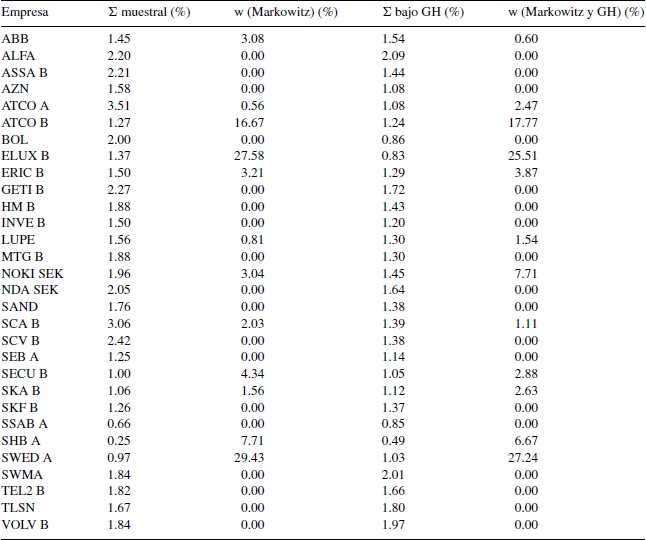
En la tabla 2 se presentan 2 ejercicios de estimación, tanto con la matriz de covarianzas muestral como con la matriz de covarianzas GH. En cada caso se obtiene un portafolio de inversión de mínima varianza, donde la media y la varianza resultantes son distintas para cada portafolio. En ese caso, no es posible comparar directamente ambos portafolios en media y varianza. Por ello se comparan ambos portafolios bajo el coeficiente de variación, donde se puede apreciar que bajo la distribución GH se encuentra un valor más pequeño. En otras palabras, existe evidencia para afirmar que la utilización de la distribución de probabilidad multivariada GH al interior del procedimiento de Markowitz permite valorar poblacionalmente la dispersión de los rendimientos, y por tanto complementar el método de Markowitz.
Tabla 2 Portafolio de mínima varianza
| Estadísticos del portafolio | ||
|---|---|---|
| Markowitz | Markowitz/GH | |
| Rendimiento | 0.00022 | 0.00024 |
| Varianza | 0.00008 | 0.00009 |
| Desviación estándar | 0.00894 | 0.00949 |
| Coeficiente de variación | 40.6558 | 39.5285 |
Fuente: elaboración propia con datos de Bloomberg.
Esta diferencia entre ambos portafolios se atribuye a la bondad de ajuste que presenta la distribución multivariada GH sobre el conjunto de rendimientos. La matriz de covarianzas estimada bajo la distribución multivariada refleja en mayor medida el comportamiento de los rendimientos que la matriz de covarianzas tradicional.
Más aún, como existe evidencia mediante la prueba de McAssey sobre el ajuste razonable de la distribución de probabilidad multivariada GH a la muestra de información, entonces se sabe que la frontera eficiente que se traza bajo la distribución GH se encuentra más próxima a la curva poblacional que aquella obtenida bajo la matriz de covarianza muestral.
La varianza del portafolio GH es mayor a la varianza del portafolio de Markowitz, lo que implica que bajo la matriz de covarianza muestral se estaba subestimando el riesgo medido por la desviación estándar en el portafolio estimado. No obstante, bajo el coeficiente de variación la distribución de probabilidad GH arroja menor dispersión del portafolio resultante, alrededor de la media poblacional.
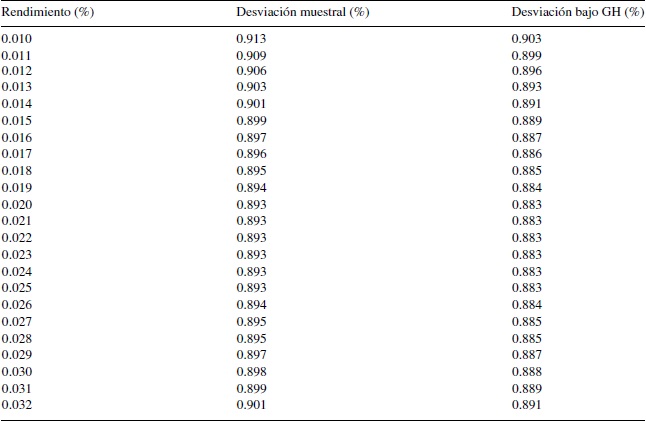
En el anexo 3 se presentan las desviaciones estándar de diferentes portafolios eficientes obtenidas dado un rendimiento fijo para ambas matrices de covarianzas. Para cada nivel de rendimiento se estima un portafolio bajo la distribución de probabilidad GH y se compara con la varianza estimada con el uso de la matriz de covarianza muestral para el procedimiento de Markowitz. Se puede observar que para cada nivel de rendimiento de los portafolios, la desviación estándar es mayor cuando se considera la matriz de covarianza muestral.
En la figura 1 se presentan los gráficos correspondientes de las curvas de los portafolios eficientes para este ejercicio, y se puede visualizar cómo la distribución de probabilidad GH complementa la construcción de portafolios de Markowitz.

Fuente: elaboración propia con datos de Bloomberg.
Figura 1 Comparación entre las curvas de portafolios eficientes.
El gráfico de la figura 1 se ha elaborado modificando algunas partes de la rutina que se presenta en el software R para elaboración de portafolios (Wertz y Setz, 2014). Las modificaciones tienen que ver con la implementación de la distribución GH, según la librería de Breymann y Lüthi (2013).
Conclusiones
En este artículo se confirma la relevancia que tiene la matriz de varianzas-covarianzas empírica en el estudio de los rendimientos de un conjunto de activos. De hecho, cuando se estima la matriz de covarianzas mediante la distribución de probabilidad multivariada GH se observa que esta matriz refleja en mayor medida las asociaciones poblacionales entre los diferentes rendimientos, y que permite complementar el procedimiento clásico de Markowitz.
Esta afirmación resulta confiable dado que se pudo verificar mediante la prueba de McAssey (2013) que la distribución de probabilidad GH se ajusta razonablemente al conjunto de información con un nivel de significación relevante, y que por ejemplo, la distribución normal multivariada no refleja el comportamiento de los rendimientos de la muestra utilizada.
El portafolio obtenido bajo el estimador de la matriz de covarianzas GH registra un coeficiente de variación menor que el que se encuentra con el procedimiento tradicional de Markowitz, donde se emplea el estimador usual de la matriz de covarianzas. Este hallazgo sugiere que la utilización de la distribución de probabilidad multivariada subyacente al conjunto de rendimientos mejora la construcción de los portafolios de inversión, siempre y cuando se tenga evidencia estadística de que la distribución de probabilidad propuesta se aproxima adecuadamente a la distribución de probabilidad conjunta de donde procede la muestra de rendimientos.
Por otra parte, queda abierta la agenda de investigación para realizar una comparación entre los resultados obtenidos mediante la distribución de probabilidad GH y los que se obtendrían mediante matrices GARCH, exponencialmente suavizadas, cópulas, matrices aleatorias o métodos bayesianos, aunque debe recalcarse que el algoritmo comentado en este trabajo emplea la distribución de probabilidad multivariada que mejor se adapta al conjunto de información.











 text new page (beta)
text new page (beta)