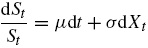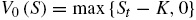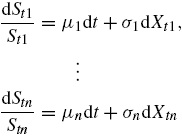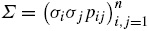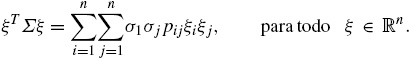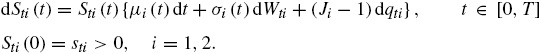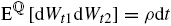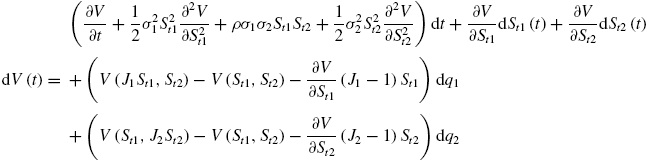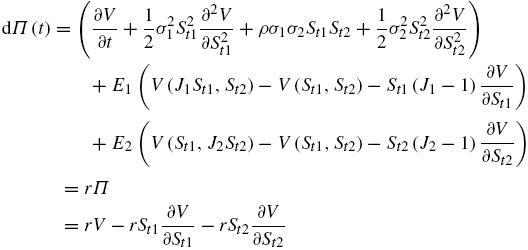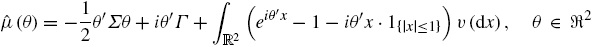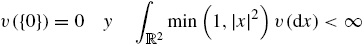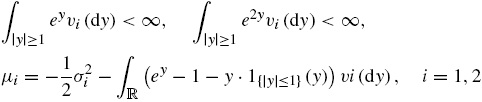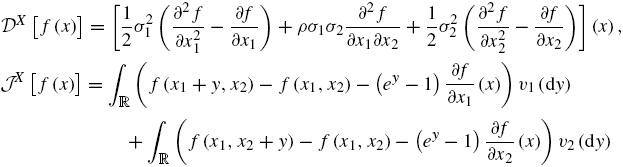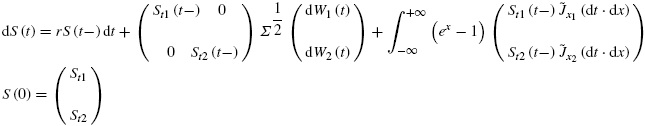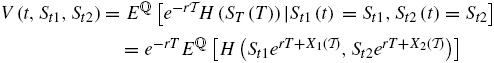Códigos JEL: C15, C53, C63
Introducción
Una opción es un producto financiero derivado que involucra el derecho pero no la obligación de negociar (comprar o vender) un activo riesgoso, como por ejemplo acciones, materias primas o divisas, a un precio fijo predefinido en una fecha predeterminada (opción de tipo europeo). En los mercados financieros se desarrollan instrumentos cada vez más sofisticados y complejos que necesitan ser valuados con nuevas técnicas que involucran métodos matemáticos más sofisticados pero más robustos. Dentro de esta variedad de productos derivados se encuentran las opciones que se valúan en canastas de activos subyacentes y reciben el nombre de opciones sobre canastas; este tipo de opciones han sido de gran interés tanto para operadores como para académicos.
Las opciones arcoíris se han negociado desde hace mucho tiempo en los mercados de derivados. Dentro de esta clase de contratos, las opciones sobre el máximo o el mínimo rendimiento de varios activos riesgosos son muy populares. En su forma estándar, una opción de compra de estilo europeo en el máximo de los rendimientos de n activos ofrece al inversionista, al expirar la opción, si es positiva, la diferencia entre el más alto de los rendimientos de los n activos y el rendimiento del ejercicio. Del mismo modo, una opción de venta en el mínimo (el peor) de los rendimientos de n activos proporciona la diferencia, si es positiva, entre el rendimiento del ejercicio y el más bajo de los rendimientos de los activos subyacentes. En ocasiones se encuentran contratos de opciones arcoíris que consideran, en lugar de diferencias de rendimientos, diferencias de precios de los activos cuando los precios no difieren mucho entre sí. No es difícil entonces ver por qué estos productos resultan de gran interés para los inversionistas. De hecho, les proporcionan estrategias de gran alcance en la diversificación. Por lo tanto, permiten tanto reducir su exposición al riesgo como ampliar las oportunidades de sus inversiones.
La importancia que el presente trabajo tiene para el análisis financiero es que proporciona un esquema consistente para la valuación analítica de opciones europeas sobre el máximo o el mínimo de los rendimientos (o precios) de varios activos riesgosos cuando estos presentan saltos repentinos en sus precios. Esto, sin duda, mejora sustancialmente el estado actual de la literatura especializada en el tema de opciones arcoíris, pues hasta ahora las fórmulas cerradas han sido muy escasas. Asimismo, este trabajo pretende destacar las bondades de estos instrumentos para que se utilicen como instrumentos de inversión y/o cobertura, con lo cual se espera que este trabajo conlleve un mejor conocimiento sobre ellos y, por ende, un incremento en la negociación de este tipo de derivados en el mercado sobre mostrador en México. Por último, con fines ilustrativos, se valúan diferentes tipos de opciones arcoíris con la metodología propuesta, destacando las ventajas en su uso, pero también sus limitaciones.
Como se mencionó antes, infortunadamente, las fórmulas cerradas de este tipo de opciones son muy escasas. Una y solo una fórmula completamente explícita ha sido publicada, la que figura en el documento seminal de Stulz (1982). Anteriormente, Margrabe (1978) valuó el precio de una opción que a su vencimiento permitiera intercambiar un activo por otro. Otra referencia comúnmente citada es el trabajo de Johnson (1987), pero las fórmulas dadas en su documento no son completamente explícitas y no se discute su implementación numérica. Otras contribuciones se han dedicado a la generación de algoritmos de aproximación numérica, como Boyle (1989) y Boyle y Tse (1990). En particular, Boyle (1989) se aproxima al valor de una opción call en el peor de n activos con precio de ejercicio cero planteando el algoritmo de Clark para aproximar los 4 primeros momentos del máximo (o mínimo) de n variables aleatorias distribuidas conjuntamente normales (Clark, 1961). Sus supuestos son bastante restrictivos, ya que todos los rendimientos de los activos deben tener la misma varianza y las correlaciones entre cada par de retornos deben ser iguales. Boyle y Tse (1990) relajan estos supuestos y diseñan un algoritmo de aproximación numérica para el rendimiento general de activos y valores de correlación; su precisión es satisfactoria para las opciones con 3 activos. Más recientemente, la cuestión de la estimación de parámetros ha sido discutida en Fengler y Schwendner (2004). Asimismo, los contratos de opciones americanas han sido estudiados por Detemple, Feng y Tian (2003), quienes proporcionaron los límites inferior y superior de una opción de compra americana en el mínimo de los rendimientos de 2 activos.
El presente trabajo se centra en la valuación analítica de opciones europeas en el máximo o el mínimo de los rendimientos (o precios) de varios activos riesgosos. Existen muchas razones por las que se desea mejorar el estado actual de la investigación publicada en esta área. En primer lugar, la fórmula de Stulz (1982) se limita a 2 activos. Esto limita seriamente el alcance de la diversificación y no permite aprovechar todo el potencial de este tipo de contratos. Una razón fundamental para esta restricción es técnica, es decir, la complejidad en los cálculos matemáticos de una distribución multivariada y, más grave aún, la falta de expresiones analíticas para densidades multivariadas cuando se tienen más allá de 3 activos hace de la valuación de opciones arcoíris una tarea realmente compleja. El problema de la dimensión implica, en muchas ocasiones, recurrir a la simulación Monte Carlo, tan pronto como el número de activos es mayor que 2.
Una segunda limitación en la fórmula de Stulz (1982) es que no se ajusta a las disposiciones de flexibilidad que resultan muy atractivas para los inversionistas, como son las opciones tipo knock-in o knock-out 1 o la implementación de algún tipo de barrera. Una vez más, la razón principal por la que estas características no se incorporan en las fórmulas tradicionales es porque este tipo de instrumentos no son analíticamente tratables en un entorno de varios activos subyacentes.
Una tercera limitación en la fórmula Stulz (1982) es que, al igual que las fórmulas de valuación de opciones de forma cerrada, se basa en los supuestos de la fórmula de Black y Scholes (1973), que está notoriamente en desacuerdo con algunas de las características más destacadas de las observaciones del mercado, tales como el hecho de que los precios de los activos pueden presentar "saltos". Este es precisamente el tema que abarcará la presente investigación.
Los procesos estocásticos con saltos se han convertido en herramientas cada vez más populares en el modelado de las fluctuaciones del mercado debido, en gran parte, a las siguientes razones: a) los procesos con saltos son herramientas más apropiadas para modelar los eventos catastróficos en el mercado; b) los datos de alta frecuencia indican que la trayectoria de precios de los activos no es continua en pequeñas escalas de tiempo; c) los modelos que utilizan procesos de salto son capaces de producir estructuras más ricas en la distribución de los rendimientos de los activos y las superficies de volatilidad implícita de opciones (Cont y Voltchkova, 2005), y d) la evidencia estadística indica la existencia de "saltos" junto con el componente de difusión en la dinámica de precios de los activos (Aït-Sahalia y Jacod, 2009).
En esta investigación, el activo subyacente será modelado para permitir cambios repentinos que generan un número finito de saltos de magnitud aleatoria y que se producen al azar de una distribución conocida, como por ejemplo la distribución de Poisson u otras distribuciones de procesos de Lévy. Cuando el activo subyacente evoluciona por tales saltos, el valor de la opción se puede caracterizar como la solución de una ecuación parcial integro-diferencial (EPID).
El presente trabajo se encuentra organizado de la siguiente manera: en la sección siguiente se desarrolla, brevemente y como referencia, el modelo clásico para la valuación de opciones, es decir, el modelo de Black-Scholes, y posteriormente se amplían los resultados para las opciones arcoíris, para lo cual se introducen las correspondientes funciones de pago y se desarrollan varias aplicaciones; en la tercera sección se extienden las fórmulas clásicas de valuación de opciones arcoíris al incluir la posibilidad de que los activos presenten saltos durante la vida de la opción; en este caso, el precio de una opción arcoíris con saltos en el subyacente se caracteriza como la solución de una ecuación parcial integro-diferencial que involucra procesos de Lévy; en la última sección se presentan las conclusiones y sugerencias para trabajos futuros.
La ecuación Black-Scholes para opciones con varios activos
En 1973, Fischer Black y Myron Scholes publicaron un trabajo que ha sido seminal en la valuación de opciones: "The Pricing of options and Corporate Liabilities" . Robert C. Merton de manera simultánea participó en el desarrollo y en las mejoras en los supuestos de este modelo. El principal mérito del modelo Black-Scholes-Merton es el hecho de que, por primera vez en la teoría de valuación de opciones, el precio de una opción podría determinarse únicamente a partir de cantidades observables y ser independiente de las expectativas de los inversionistas sobre el desarrollo futuro del precio del activo subyacente. El concepto básico para su desarrollo es el principio fundamental de no arbitraje. Este modelo se basa en una serie de supuestos correspondientes a las "condiciones ideales" del mercado: a) la tasa de interés libre de riesgo r es constante durante toda la vida de la opción, y b) el precio de las acciones sigue una caminata aleatoria con una tasa instantánea de cambio que satisface la ecuación diferencial estocástica:
donde S t es el precio de la acción, t es el tiempo, μ es la tasa instantánea de retorno (rendimiento), σ > 0 es la desviación estándar instantánea de la tasa de retorno (también llamada volatilidad instantánea del precio de la acción) y es un proceso de Wiener (o movimiento browniano), es decir, es un proceso estocástico de tiempo continuo que comienza en cero y tiene incrementos independientes que se distribuyen según una distribución normal con media cero y varianza dt . Se supone que μ y σ son conocidas y constantes a través del tiempo. Bajo los supuestos anteriores, Black-Scholes-Merton muestran que el valor, VSt,t, de la opción es solución de la siguiente ecuación diferencial parcial, denominada ecuación de Black y Scholes (1973) y Merton (1973):
Aquí, S t denota el precio del activo subyacente, t es el tiempo (medido como proporción de un año), σ es la volatilidad del activo subyacente, r es la tasa de interés libre de riesgo (de incuplimiento) y T la fecha de vencimiento de la opción. La ecuación parcial diferencial tiene que ser complementada con una condición terminal:
La función de pago V 0 depende del tipo de opción. Si se considera, por ejemplo, una opción de compra europea y K es el precio de ejercicio, entonces:
Por consideraciones análogas, la función de amortización de una opción de venta europea está dada por:
Generalización de la ecuación de Black-Scholes a opciones arcoíris
Un tipo más general de opciones no depende solo de uno, sino de un conjunto de activos subyacentes n . Tales opciones son llamadas opciones de activos múltiples, o bien, a partir de Stulz, opciones arcoíris.
Para la valuación de opciones arcoíris se pueden utilizar los mismos principios que en el caso de las opciones con un solo activo subyacente. Todos los supuestos del modelo Black-Scholes se aplican en este tipo de opciones, excepto que ahora se supone que los precios de los n activos subyacentes S t1 , ..., S tn siguen un movimiento browniano geométrico n -dimensional, es decir, las tasas de rendimiento satisfacen las ecuaciones diferenciales estocásticas:
con tendencias constantes μ 1 , ..., μ n y volatilidades σ 1 , ..., σ n , respectivamente. Los procesos dX 1 , ..., dX n son de Wiener y están correlacionados con coeficientes de correlación constantes ρ ij para cada par dX i y dX j . La matriz de varianzas-covarianzas correspondiente está dada por:
Se requiere que sea definida positiva, es decir:
Si se denota Sn=(St1,...,Stn) y se considera el precio Vn(Sn,t) en el tiempo t de una opción europea tipo arcoíris con fecha de vencimiento T , una derivación análoga al caso de una opción sobre un activo subyacente, basado en el principio de no arbitraje, con la versión n -dimensional de la fórmula de Itô, muestra que V n es solución de la ecuación diferencial parcial (Karatzas y Shreve, 1991):
La cual se conoce como la ecuación parcial diferencial n -dimensional de Black-Scholes, sujeta a la condición terminal:
donde
Las opciones arcoíris más importantes pueden clasificarse en:
Opciones Exchange. El comprador al vencimiento recibirá, si su expectativa fue correcta, la diferencia de lo rendimientos o precios de 2 activos. Este tipo de opción fue introducido por Margrabe (1978).
Opciones sobre el mejor o peor de 2 activos. Son opciones que a su vencimiento entregan el activo que mayor o menor rendimiento o valor haya alcanzado a la fecha de expiración comparado con el precio de ejercicio. Este tipo de opciones fueron introducidas por Stulz (1982) considerando solo 2 activos subyacentes, y posteriormente Johnson (1987) extiende los resultados a n activos.
Para ejemplificar las diferentes modalidades de opciones arcoíris y obtener su respectivo precio se utilizarán los parámetros que se muestran en la tabla 1.
Tabla 1 Parámetros para la valuación de opciones arcoíris
| Parámetros | Valores |
|---|---|
| Precio del activo subyacente (St1,St2) | 100, 95 |
| Volatilidad (σ1,σ2) | 20%, 25% |
| Rendimiento del activo (γ1,γ2) | 5%, 2.5% |
| Correlación (ρ) | 0.40 |
| Precio de ejercicio (K) | 90 |
| Tasa libre de riesgo (r) | 8% |
| Tiempo | 1 año |
Fuente: elaboración propia.
En la tabla 2 se resumen las funciones de pago de las principales opciones arcoíris.
Tabla 2 Función de pago de las principales opciones arcoíris
| Tipo de opción | Función de pago de la opción
|
Precio de la opción |
|---|---|---|
| Opción exchange | max(St1,St20) | 10.6253 |
| Call sobre el mejor de 2 activos | max{max(St1,St2)−K,0} | 21.447 |
| Put sobre el mejor de 2 activos | max{K−max(St1,St2),0} | 14.346 |
| Call sobre el peor de 2 activos | max{min(St1,St2)−K,0} | 7.5712 |
| Put sobre el peor de 2 activos | max{K−min(St1,St2),0} | 6.944 |
Fuente: elaboración propia con base en los datos de la tabla 1.
Modelo de valuación de opciones arcoíris con difusión y saltos
Uno de los principales problemas con el modelo Black-Scholes es que en la realidad los rendimientos del subyacente no se distribuyen normalmente como lo requieren los supuestos del modelo. Es decir, resulta ser que en realidad los datos son asimétricos y tienen una kurtosis mayor que la de la distribución normal. Por lo tanto, con el fin de modelar el comportamiento a través del tiempo se requiere un proceso estocástico más flexible, que generalice el movimiento browniano. Para definir un proceso estocástico con incrementos independientes y estacionarios, la distribución tiene que ser infinitamente divisible. Estos procesos se denominan procesos de Lévy, en honor de Paul Lévy, el pionero de la teoría.
Activos con saltos
El objetivo de esta subsección es obtener la ecuación parcial integro-diferencial (EPID) que satisface el precio de una opción arcoíris. Por medio del generador infinitesimal del proceso de Lévy en 2 dimensiones se obtiene la ecuación de determinación de primas. Al mismo tiempo se muestra que el valor de la opción es la solución de la EPID a través de métodos martingala.
Cuando el comprador intercambia activos, por ejemplo acciones, con el vendedor, puede provocar saltos en el precio de las acciones, sobre todo si el vendedor se quiere deshacer de un volumen grande de poco en poco. Black-Scholes supone que todos los movimientos de precios son pequeños, por lo menos en el día a día. Pero los precios a veces saltan. Por ejemplo, los anuncios de adquisición presentan un salto hacia arriba o hacia abajo, como sucedió durante la crisis subprime a partir de 2007. Un salto incrementa la volatilidad en un tiempo corto de tiempo. La posibilidad de un salto tiene más efecto en opciones a corto plazo que en opciones a largo plazo, y más cuando el precio de las acciones está lejos del precio de ejercicio que cuando se encuentra cerca.
Las desviaciones del paradigma Black-Scholes se observan ubicuamente en subyacentes de renta variable, renta fija, divisas, mercados de crédito y de materias primas, y dan lugar a estructuras de volatilidad dependientes. Varios modelos han sido propuestos para explicar este fenómeno. Si bien muchos de estos modelos incorporan la característica estática y/o estocástica de la dinámica de volatilidad, muy pocos de ellos toman en cuenta los saltos en el subyacente o, más generalmente, muy pocos utilizan los procesos de Lévy en lugar de los procesos estocásticos de Wiener como conductores del precios de los activos.
Los modelos de difusión con saltos, sin duda, captan una realidad que no aparece en el modelo Black-Scholes, y los saltos son cada vez más utilizados en la teoría. Sin embargo, todavía hay varios problemas con los modelos de saltos: la dificultad en la estimación de parámetros, su solución, y la imposibilidad de cobertura perfecta.
Modelo de Merton sobre subyacentes con difusión y saltos para valuar una opción arcoíris
Robert C. Merton (1976) fue el primero en establecer, bajo ciertos supuestos, el precio de una opción europea en subyacentes conducidos por difusiones con saltos, es decir, combinando una distribución lognormal con saltos Poisson. Kou y Wang (2004) complementan este trabajo y estudian el caso de saltos distribuidos de acuerdo con el logaritmo de la doble exponencial. El modelo de Merton ha sido extendido por varios autores que han calculado precios de las opciones europeas con subyacentes dirigido por el proceso de Lévy.
Si se sigue el postulado de no-arbitraje en la derivación del modelo de Black-Scholes-Merton, y se considera una opción arcoíris con procesos de difusión con saltos, se tiene (Andersen y Andreasen, 2000):
donde μi(t)>0 es la tendencia, σi(t) es la volatilidad y (Wt1,Wt2) es un movimiento browniano bidimensional correlacionado con ρ ij :
donde ℚ es una medida neutral al riesgo y el proceso de Poisson dq i está definido por:
El parámetro λ i es la media del tiempo entre llegadas del proceso de Poisson. El tamaño del salto J i sigue una distribución normal con media m i y desviación estándar Γ i . Aquí se supone que los tamaños de los saltos no están correlacionados.
A continuación se toma el caso particular de n = 2. Se supone que los activos se pueden comprar y vender sin restricción. Se desea determinar el valor de V2(t) en el tiempo t de una opción europea que garantiza un pago en el tiempo T . Se usa la notación V2(t), que indica lo que sucede con V2(St1,St2,t) a lo largo de la superficie (S1(t),S2(t),t) a medida que avanza el tiempo. Para hacer esto se construye un portafolio Π compuesto por una unidad de V y una cierta cantidad (−Δ1−Δ2) de los activos subyacentes. En lo que sigue, por simplicidad V(t) se denotará mediante V2(t). Así:
En cada punto en el tiempo se va a ajustar el valor de Δ i , y el objetivo será reducir la incertidumbre (riesgo) en el portafolio Π . Considerando la ecuación diferencial estocástica satisfecha para Π(t):
Como t cambia, también lo hace (S1(t), S2(t), t), por
lo que hay 3 fuentes de cambio en V , uno desde los cambios en
t que contribuirán al término
Así:
Si se elige:
Se tiene que:
El argumento de no arbitraje establece que:
Por lo tanto,
Donde:
Así, se tiene la siguiente ecuación:
Donde;
Esta es la ecuación parcial integro-diferencial (EPID). Se nota que la clásica ecuación diferencial parcial de Black-Scholes para la fijación de precios de una opción arcoíris es un caso especial cuando λ 1 = 0 y λ 2 = 0.
Ecuación parcial integro-diferencial para establecer el precio de una opción arcoíris
Aunque la valuación de opciones con modelos exponenciales de Lévy se discute ampliamente en Andersen y Andreasen (2000) y Geman (2002), estos autores están principalmente centrados en la metodología de valuación de opciones vainilla con un solo activo subyacente. En realidad, este enfoque no puede satisfacer las necesidades de un mercado financiero altamente desarrollado y diversificado. En virtud del argumento de no arbitraje, para determinar el valor de opciones arcoíris en modelos exponenciales de Lévy se requiere el uso de ecuaciones parciales integro-diferenciales (EPID) en 2 dimensiones que se propusieron por primera vez por Fujiwar y Kunita (1989). Por su parte, Amin (1993) propuso un método numérico explícito basado en árboles multinomiales, y Zhang (1997) presentó un esquema de diferencias finitas para PIDE en el modelo de difusión con saltos de Merton. Sin embargo, estos métodos solo tienen precisión de primer orden.
En los mercados de Lévy, los rendimientos logarítmicos de los activos de riesgo se modelan como un proceso de Lévy bajo un espacio de probabilidad Ω,ℱ,ℚ equipado con una filtración ℱ t .Puesto que no existe una medida martingala equivalente a ℚ por la hipótesis de no arbitraje, se puede suponer sin pérdida de generalidad que ℚ es ya una medida martingala. Si {St1(t),St2(t)}t [ ∈0,T ] es el precio spot de los subyacentes involucrados en una opción arcoíris, cuyo vencimiento es el tiempo T , entonces la dinámica subyacente de los 2 activos riesgosos Si(t),i=1,2 satisface:
donde r es la tasa de interés libre de riesgo, X(t)=(X1(t), X2(t))′ es un proceso de Lévy en ℝ2 con características (Σ, Γ, ν) y Si(0)=si, Xi(0)=0, i=1,2. A partir del teorema de representación de Lévy-Khinchine para X(t) ∈ ℝ2 se cumple que:
Donde:
Aquí,
es una matriz simétrica positiva semidefinida en M 2×2 , y
Asimismo v es una medida en ℝ2 que satisface:
En la literatura de valuación de opciones, Σ y Γ representan la matriz de covarianza y el exceso de rendimiento de los activos de S t1 y S t2 , respectivamente, y v(dx) es una medida de Lévy que muestra la actividad de saltos de los activos. El proceso de Lévy X t es también un proceso de Markov; entonces, a partir de la representación de Lévy-Khinchine se obtiene el generador infinitesimal:
Por la hipótesis de ausencia de arbitraje, se supone que los precios reducidos de Ŝ(t)= (Ŝt1(t), Ŝt2(t))′=e−rt. (St1(t), St2(t))′ son martingalas cuadradas integrables bajo ℚ. Esto es equivalente a la siguiente propiedad con Σ,Γ,v:
Si se supone que las condiciones anteriores son válidas para Σ,Γ,v, entonces el generador
infinitesimal
Donde:
y v1(dy), v2(dy) son las medidas de Lévy para describir la actividad de saltos de tamaño y de S t1 y S t2 , respectivamente. Puesto que se supone que los componentes de salto de S t1 y S t2 son independientes, se tiene que v(dy1×dy2)=v1(dy1)×v2(dy)2. De lo anterior, la dinámica del riesgo neutral de los activos
satisface
donde
Como se sabe, el valor de una opción arcoíris en el tiempo t con precio de ejercicio K y fecha de vencimiento T se define como una expectativa condicional de su pago final H(ST1(T), (ST2(T)) bajo la medida martingala ℚ, es decir:
donde H(ST1, ST2) es el pago de unas opciones arcoíris, como se describieron en la tabla 2. A partir de la hipótesis del mercado eficiente, el valor de la opción solo depende del precio actual de los activos St1(t) y St2(t). Por lo tanto, el valor de la opción arcoíris en el tiempo t es:
donde T≙T−t. Para ilustrar la valuación de opciones arcoíris con difusión y saltos, se va a considera la opción canasta o cesta. Una opción canasta (basket option) de venta es similar a una opción vainilla, excepto que el subyacente se sustituye por la suma ponderada de los activos que componen la cesta. La función de pago de este tipo de opciones con pesos positivos w1,w2,...,wn y precio de ejercicio K está dada por:
Con el fin de facilitar la comparación con simples opciones vainilla, es conveniente descomponer el precio de ejercicio K como una función de los pesos wi, los precios iniciales de los activos subyacentes y un vector de parámetros k i que pueden ser interpretados como indicadores de monetización de una opción vainilla sobre los activos subyacentes:
Si todos los parámetros k i son iguales a 1, es decir, si las opciones vainilla individuales están at the money 2, el pago de la cesta de la opción de venta puede ser reescrito como:
lo que lleva a la conclusión de que una opción cesta de venta será siempre más barata que un portafolio de opciones vainilla (con pesos wi) escrito sobre los mismos subyacentes. Y la función de pago para este tipo de opción será:
Para ilustrar la valuación de opciones arcoíris con difusión y saltos se presentan 3 casos: una opción cesta de venta, una opción put sobre el máximo de 2 activos y una opción put sobre el mínimo de 2 activos, para diferentes volatilidades del activo subyacente 2: (0.1, 0.1), (0.1, 0.2), (0.1, 0.3), (0.2, 0.2), (0.2, 0.3), (0.3, 0.3), en 2 diferentes tiempos de vencimiento diferentes 0.1 y 0.9 y con una correlación positiva de 0.3. Es necesario recordar que las opciones son at the money , es decir, que el precio de ejercicio es igual al precio del subyacente, dichos precios están en miles de pesos y que para la opción cesta el peso de los activos w1 y w2 satisfacen w1+w2=1, como se muestra en la tabla 3.
Tabla 3 Parámetros para la valuación de opciones arcoíris con difusión y saltos
| Parámetros | Valores |
|---|---|
| Media del tamaño del salto (v1,v2) | −0.9, −0.9 |
| Media de la volatilidad del salto (γ1,γ2) | 0.45, 0.45 |
| Intensidad del salto (λ1,λ2) | 0.1, 0.1 |
| Correlación (ρ) | 0.3 |
| Precio del activo subyacente (S1t,S2t) | 40, 40 |
| Peso de los activos (w1,w2) | 0.5, 0.5 |
| Precio de ejercicio (K) | 40 |
| Tasa de interés (r) | 0.05 |
Fuente: elaboración propia.
Los parámetros presentados en la tabla 3 se han introducido mediante el programa MATLAB para la obtención del precio de las opciones a distintas volatilidades, y los resultados se muestran en la tabla 4. A partir de este cuadro se puede concluir que:
lo que implica que, en cualquier momento, el precio de la opción cesta de venta es mayor que un put sobre el máximo de 2 activos pero menor que una opción de venta en el mínimo de 2 activos. También se puede percibir que mientras las volatilidades sean más altas y el tiempo de vencimiento sea mayor, el precio de la opción se irá incrementando.
Tabla 4 Resultado de opciones arcoíris con difusión y saltos
| T | σ 1 | σ 2 | Opción cesta | Put sobre el mejor de 2 activos | Put sobre el peor de 2 activos |
|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.1 | 1.8015 | 1.7997 | 1.8038 |
| 0.1 | 0.1 | 0.2 | 1.8342 | 1.8329 | 1.8389 |
| 0.1 | 0.1 | 0.3 | 1.9127 | 1.9096 | 1.9161 |
| 0.1 | 0.2 | 0.2 | 1.8857 | 1.8806 | 1.8901 |
| 0.1 | 0.2 | 0.3 | 1.9834 | 1.9794 | 1.9873 |
| 0.1 | 0.3 | 0.3 | 2.0723 | 2.0702 | 2.0782 |
| 0.9 | 0.1 | 0.1 | 0.6059 | 0.6012 | 0.7002 |
| 0.9 | 0.1 | 0.2 | 1.2413 | 1.2392 | 1.2485 |
| 0.9 | 0.1 | 0.3 | 1.9280 | 1.9231 | 1.9317 |
| 0.9 | 0.2 | 0.2 | 1.7769 | 1.7700 | 1.7810 |
| 0.9 | 0.2 | 0.3 | 2.4397 | 2.4352 | 2.4427 |
| 0.9 | 0.3 | 0.3 | 3.0011 | 2.9923 | 3.0123 |
Fuente: elaboración propia en base a los parámetros de la tabla 3.
Por último, las soluciones gráficas para la opción cesta de venta, y las opciones put sobre el máximo y el mínimo de 2 activos bajo el modelo de difusión con saltos, se muestran en las figuras 1-3, respectivamente.

Fuente: elaboración propia en base a los resultados de la tabla 4.
Figura 1 Opción cesta de venta bajo difusión con saltos.

Fuente: elaboración propia en base a los resultados de la tabla 4.
Figura 2 Opción put en el máximo de 2 activos bajo difusión con saltos.
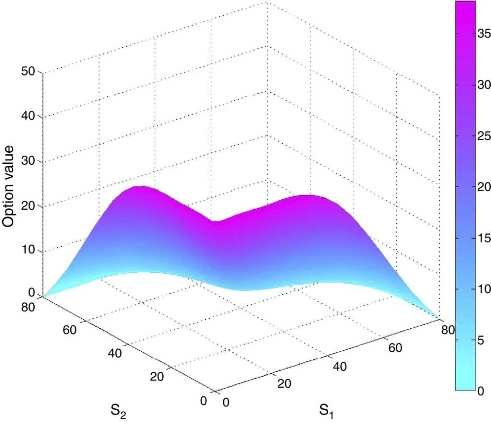
Fuente: elaboración propia en base a los resultados de la tabla 4.
Figura 3 Opción put en el mínimo de 2 activos bajo difusión con saltos.
Conclusiones
En este trabajo, el clásico modelo de Black-Scholes se extendió para la valuación de opciones que tienen 2 o más activos subyacentes, conocidas como opciones arcoíris, y sus respectivas funciones de pago que se pueden adoptar. Posteriormente se presentó un modelo de difusión con saltos para valuar el precio de una opción bajo 2 activos subyacentes, el cual a diferencia de Black-Scholes; la solución se encuentra a través de una ecuación parcial integro-diferencial proveniente de procesos de Lévy. Al realizar la evidencia empírica del modelo mediante 3 tipos de opciones arcoíris en su modalidad de opciones de venta (tipo cesta, y en el máximo y mínimo de 2 activos) se puede notar que conforme aumenta la volatilidad de los activos y el tiempo de vencimiento de la opción es más largo, la prima se incrementa; también se puede deducir que la presencia de saltos en el precio de los activos ocasiona que se incremente la prima de la opción. Por último, se concluye que el precio de una opción cesta de venta siempre será mayor al precio de una opción put en el mínimo de 2 activos pero menor al precio de una opción put en el máximo de 2 activos.
Este trabajo se puede extender en varias direcciones. Primeramente aquí se analizó el comportamiento de opciones de venta, y entonces el siguiente enfoque sería considerar las opciones de compra. Asimismo se estudiaron únicamente opciones estilo europeo, por lo cual resultaría interesante conocer los resultados para opciones americanas (aunque esto dificultaría la obtención de la ecuación parcial integro-diferencial). Finalmente se podría realizar el mismo análisis que en este presente trabajo extendiendo los resultados para el caso en que se tengan 3 o más activos subyacentes, y en el caso en que la tasa de interés, en vez de ser constante, sea estocástica.
El hecho es que la presencia de saltos en la valuación de opciones y específicamente en las opciones arcoíris hace que los resultados sean más realistas, puesto que consideran los posibles acontecimientos en el mercado, es decir, actos que ocasionan que el precio de los activos suban o bajen durante la duración de la opción, y deja de lado el supuesto de que los precios permanecen constantes.











 nova página do texto(beta)
nova página do texto(beta)