Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Contaduría y administración
versão impressa ISSN 0186-1042
Contad. Adm vol.57 no.2 Ciudad de México Abr./Jun. 2012
Procesos estocásticos en la valuación de proyectos de inversión, opciones reales, árboles binomiales, simulación bootstrap y simulación Monte Carlo: flexibilidad en la toma de decisiones
Stochastic processes in the valuation of investment projects, real options, binomial trees, bootstrap simulation and Monte Carlo simulation: flexibility in decision making
Fernando Cruz Aranda
Universidad Panamericana fcruz@up.edu.mx
Fecha de recepción: 18.03.2011
Fecha de aceptación: 30.06.2011
Resumen
En este trabajo se incorporan procesos estocásticos en la valuación de proyectos de inversión utilizando opciones reales, lo que está vinculado al valor de la flexibilidad administrativa; es decir, utilizar la opción con el objeto de tomar decisiones estratégicas acordes con el entorno económico de la empresa. Se valúa un proyecto tomando en cuenta la opción real según la cual se tiene la flexibilidad de abandonar el proyecto si el entorno de ésta lo requiere. En la valoración del proyecto se consideran los flujos de efectivo de la empresa y las simulaciones bootstrap, histórica y Monte Carlo que se llevan a cabo en ellos. Asimismo, se analizan y calculan los flujos de efectivo considerando árboles binomiales para, finalmente, determinar el valor de la opción real y la viabilidad del proyecto de inversión de la empresa.
Palabras clave: proceso estocástico, simulación histórica, simulación Monte Carlo, proyectos de inversión, árboles binomiales y opciones reales.
Abstract
This research incorporates stochastic processes in the valuation of investment projects using real options, which is linked to the value of managerial flexibility, that is, to use the option in order to make strategic decisions in line with the company's economic environment. A project is valued taking into account the real option under which the company has the flexibility to abandon the project if the environment requires it. In the valuation of the project are considered cash fows of the company and bootstrap simulation, historical simulation and Monte Carlo simulation are carried out on them. We analyze and estimate cash fows considering binomial trees to finally determine the real option value and viability of the investment project of the company.
Keywords: Stochastic process, historical simulation, Monte Carlo simulation, investment projects, binomial trees and real options.
Introducción
El término opción real está vinculado al valor de la flexibilidad administrativa, es decir, la opción para tomar nuevas decisiones o para modificar decisiones previas. Una opción real otorga el derecho, pero no la obligación, para tomar una acción o decisión a un costo determinado y por un periodo de tiempo, también predeterminado, denominado la vida de la opción.
En Venegas-Martínez y Fundia Aizenstat (2006) las opciones reales son una herramienta fundamental para el consejo de administración de una empresa cuando se toman decisiones sobre los cálculos financieros de los proyectos o estrategias de negocio si existe la flexibilidad de expandir, diferir, abandonar un proyecto o estrategia de inversión. En Brach Marion (2003) se considera una opción de venta real que permita tener la flexibilidad de abandonar el proyecto y vender los activos de la empresa en caso de que el proyecto no sea lo esperado. En Brennan y Schwartz (1985) se estudia la valuación de proyectos donde la empresa tiene la opción de parar la producción.
Por su parte, Myers (1987, 1990), Kester (1984), Mason y Merton (1985), Trigeorgis y Merton (1987), entre otros; sugieren el uso de técnicas para valuar la flexibilidad gerencial implícita en oportunidades de inversión. Mientras que la flexibilidad gerencial proveniente de la aplicación de un conjunto de opciones reales es estudiado por Trigeorgis (1993,1998).
La teoría de valuación de opciones financieras —desarrollada en el trabajo seminal de Black y Scholes (1973) y Merton (1973), en el cual la dinámica del activo subyacente es guiado por una ecuación diferencial estocástica, y de la cual un sinnúmero de documentos de investigación han sido publicados alrededor de dicho trabajo— se ha intensificado de manera más reciente y ha realizado la valuación de opciones sobre activos de tipo real, es decir, técnicas de valuación de opciones en las finanzas corporativas.
En este trabajo se valúa la opción de abandonar un proyecto de inversión si la capacidad de la empresa no genera los flujos de efectivo sufcientes para concluir el proyecto. Para ello, se considera una base de datos histórica de los flujos de efectivo de la empresa Comercial Mexicana,† denotada de aquí en adelante como CM; en ésta se realiza una simulación de los flujos de efectivo en la que se incorpora la probabilidad de pasar de un cierto nivel de flujos de efectivo a otro nivel a futuro y se incorpora la volatilidad histórica de dichos flujos. Asimismo, se valúa la opción real de abandonar el proyecto si el entorno económico de la empresa lo requiere y así dar un conjunto de recomendaciones para el proyecto de inversión.
Para los fines del presente trabajo, el documento se organiza de la siguiente forma. En la siguiente sección se describe un comparativo entre opciones financieras y opciones reales. Después, se describe la dinámica de la ecuación diferencial estocástica del activo subyacente de una opción financiera y una opción real, además de describir el modelo de árboles binomiales de Cox, Ross y Rubinstein para valuar una opción de abandono del proyecto de tipo americano, es decir, en cualquier instante del tiempo considerado. Asimismo, se desarrollan los métodos de simulación Monte Carlo, simulación histórica y simulación bootstrap, lo cual es una extensión de un trabajo previo publicado en el libro Avances recientes en valuación de activos y administración de riesgos, considerando otra empresa. En la sección siguiente, se aplican las metodologías para valuar un posible proyecto de inversión de la empresa CM con datos históricos de flujos de efectivo de la empresa, considerando o suponiendo que los flujos del proyecto se verán reflejados en los flujos históricos de ésta. Finalmente, se escriben una serie de conclusiones y recomendaciones del modelo de valuación de proyectos de inversión que incorporan opciones reales.
Opciones financieras y la valuación de opciones reales aplicado en proyectos de inversión
Las opciones de activos financieros son negociados en casas de bolsa, como la Bolsa Mexicana de Valores, la Casa de Bolsa en Chicago (Chicago Board Options), la Casa de Bolsa Americana, entre otras. Mientras que los activos reales no se negocian en las casas de bolsa y pueden ser la propiedad intelectual, así como los proyectos. Las opciones reales, en cambio, son la aplicación de las técnicas de valuación de opciones a las finanzas corporativas, en particular al presupuesto de capital y a las decisiones estratégicas de inversión de la empresa.
Cuando un proyecto está en marcha, los administradores pueden observar la precisión de sus pronósticos, las características del mercado y las reacciones de sus competidores en cualquier instante del tiempo. En la práctica, si se requiere, los administradores cambian su estrategia; en otras palabras, ejercen una "opción real" para minimizar las pérdidas o bien para maximizar las ganancias de la empresa de manera óptima.
El criterio del valor presente neto tradicional no toma en cuenta el valor de esa flexibilidad gerencial y, en consecuencia, puede conducir a decisiones erróneas de inversión. El valor presente neto (VPN) es una herramienta estática de "hacer o no hacer"; no obstante, los proyectos son dinámicos, por lo que es necesario contar con una técnica que permita valorar la flexibilidad administrativa y pueda adaptarse a los cambios dados en el entorno económico del negocio.
A continuación se presenta un comparativo entre opciones reales y opciones financieras que hoy en día resultan de gran interés en proyectos de inversión.
En 1973, Fischer Black y Myron Scholes publicaron su artículo "The Pricing of Options and Corporate Liabilities", en el Journal of Political Economy. Desde el supuesto de equilibrio general, dichos autores desarrollaron un modelo para valuar una opción europea sobre una acción que no paga dividendos, cuyo precio es conducido por un movimiento geométrico browniano. En este modelo de valuación se supone que el precio de una acción al tiempo t, S t , es conducido por el movimiento geométrico browniano

En este caso, el parámetro de tendencia, µ ∈ ℜ, es el rendimiento medio esperado del activo subyacente y su volatilidad instantánea σ>0 por unidad de tiempo. Si f = f (St , t) = In St , es decir, si es un modelo de un solo factor, entonces del lema de Itˆo (para mayor profundidad consulte Meyer Michael, 2001; Karatzas Ioannis y Shreve Steven, 1991 y F.Venegas, 2006), conduce a

Así, el precio del activo subyacente al tiempo T es
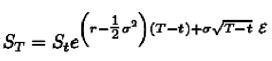
en la que se supone ε~N(0,1) y su función de densidad de tipo normal dada por

Sea h(ε) : = ST, entonces
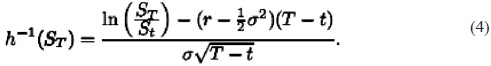
De esta manera, la función de densidad de ST, dado el precio del activo subyacente al tiempo t, St, está dada por
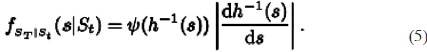
Entonces, se puede calcular el valor esperado del valor intrínseco de una opción europea de compra. Es decir, el valor esperado del máximo de la diferencia del activo subyacente y el precio de ejercicio, y cero traído a valor presente a la tasa de interés libre de riesgo, r, dada la información del mercado al tiempo t, está dada por
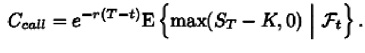
Entonces,
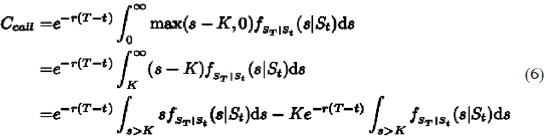
donde la diferencial satisface:
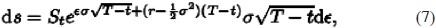
la cual se puede escribir como

Ahora, al considerar que ε~N(0,1) y con el cambio de variable 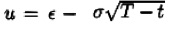 se tiene que el precio de la opción europea de compra es
se tiene que el precio de la opción europea de compra es
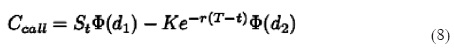
es decir, es una opción que se puede ejercer sólo a la fecha de vencimiento y donde la función Φ(d) es la función de distribución acumulada de ε~N(0,1)

y
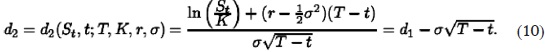
De manera equivalente, al precio de la opción de compra, se tiene que el precio de una opción de venta del tipo europeo, Pput = Pput (ST, t; T, K, r, σ) , está dado por
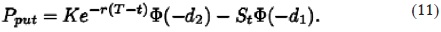
Opciones reales y el modelo de Merton sobre activos
Para la valuación de opciones reales, como una aproximación de valuación, se puede utilizar el modelo de Merton; sin embargo, se debe considerar, por ejemplo, que el activo que se está valuando es un activo real y no un activo financiero, como en la sección anterior. Entonces renombramos a las variables y parámetros, es decir, Ccall es precio real de la opción de compra, FEt el flujo de efectivo o fondos esperados al tiempo t, K el valor de los costos de la inversión, r la tasa de interés libre de riesgo, T fecha de vencimiento de la opción, σ volatilidad de los flujos de fondos esperados, y δ ingresos perdidos durante la vida de la opción. Ahora se supone que el flujo de efectivo de la empresa generados por el proyecto al tiempo t, FEt , es guiado por medio de una ecuación diferencial estocástica, es decir, por un movimiento geométrico browniano, de la forma

Así, el flujo de efectivo al tiempo T es
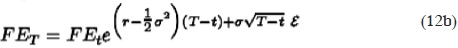
y en el que el precio real de la opción de compra europea que incorpora ingresos perdidos es
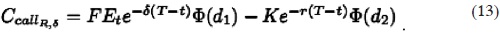
Mientras que para calcular el valor de la opción europea de venta, Put, sobre el flujo de efectivo o fondos esperados al tiempo t con ingresos perdidos está dada por

donde δ son los ingresos perdidos durante la vida de la opción. Sin embargo, sería una opción que sólo se podría ejercer en la fecha de vencimiento, por lo que se requiere de una opción que permita ser ejercida en cualquier instante del tiempo, es decir, de tipo americano y además que brinde la posibilidad de obtener un valor de rescate del proyecto el cual ya se ha iniciado, entonces se podría utilizar la ecuación diferencial estocástica (12) para determinar los flujos simulados del proyecto de inversión y combinarlo con árboles binomiales para determinar la opción de abandono del proyecto. Este último proceso se aplica en la siguiente sección.
Árboles binomiales en la valuación de opciones reales y proyectos de inversión
El modelo de Cox, Ross y Rubinstein (1979), publicado en el Journal of Financial Economics, con árboles binomiales se puede utilizar para valuar una opción de tipo americano para expandir un proyecto, opción para contraer un proyecto, opción de abandono temporal de un proyecto, entre otros. Este modelo permitiría identificar, entender, valuar, priorizar, seleccionar, puntualizar, optimizar y administrar estrategias de negocio y tomar decisiones estratégicas del presupuesto de capital de la empresa cuyos flujos de efectivo futuros son determinados por simulación y estimación. Este tipo de metodologías de valuación permite al consejo de administración de la empresa determinar los posibles valores que toman los flujos esperados del proyecto subyacente y los correspondientes valores de la opción, es decir, descrito por los árboles binomiales en cada periodo.
El modelo binomial de n periodos en la valuación de proyectos de inversión que incorpora opciones reales con valor de recuperación al tiempo t
A continuación se presenta el modelo binomial de Cox, Ross y Rubinstein (1979) aplicado a una opción de tipo real. Para ello, sea FEt el valor presente de los flujos de efectivo esperados en t y descontados a una tasa ajustada por riesgo de mercado y en la que se incorpora una volatilidad σ, ya sea histórica del logaritmo de los rendimientos de los flujos de efectivo o bien calculada por simulación histórica, simulación bootstrap o simulación Monte Carlo. Suponga que FEt puede tomar dos posibles valores uFEt y dFEt (0 < d < 1 < u) con probabilidades neutrales al riesgo p y (1 - p), respectivamente. Se supone que u y d no se modifican en cada periodo de tiempo. Con base en los parámetros anteriores, se sigue la dinámica de FEt e iniciando al tiempo t = 0.
El modelo binomial de n periodos, cada uno de longitud δt = (T - t)/n se retoma para ser considerado en el árbol binomial. De esta forma se puede determinar el valor de una opción real en t = 0. Se supone que el valor esperado de los flujos de efectivo al tiempo t está dado por el valor de los flujos de efectivo futuros y es tal que la magnitud de los flujos de efectivo pueden aumentar o disminuir al tiempo t, es decir,  . Entonces, la probabilidad de que el flujo de efectivo en el siguiente periodo sea mayor está dado por
. Entonces, la probabilidad de que el flujo de efectivo en el siguiente periodo sea mayor está dado por 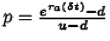 y de que sea menor es 1 - p;
y de que sea menor es 1 - p;  .
.
Para el cálculo de los nodos, en el que se considera una opción de venta americana de abandono de n periodos, el valor del put P, y con valor de rescate Vres del proyecto, se calcula en el n -ésimo periodo como
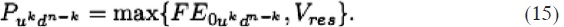
Enseguida, se calculan los valores de la opción de venta en forma recursiva y "hacia atrás" para cada uno de los nodos del árbol binomial con la probabilidad correspondiente. Esto es,
para el periodo n - 1 con k = n, n - 1, n - 2, . . . , 0 en la que k - 1 ≥ 0 y n -k + 1 ≥ 0. Así, se determina el árbol binomial de n periodos.
El valor de la opción real es el valor  al tiempo t = 0 menos el valor de los flujos de efectivo FEt al tiempo t = 0. En la siguiente sección se aplica está metodología para una empresa en la que se supone la construcción de una nueva tienda y que en el proceso se podría abandonar el proyecto si el entorno económico lo amerita. Para este tipo de enfoque puede ver Brach Marion (2003).
al tiempo t = 0 menos el valor de los flujos de efectivo FEt al tiempo t = 0. En la siguiente sección se aplica está metodología para una empresa en la que se supone la construcción de una nueva tienda y que en el proceso se podría abandonar el proyecto si el entorno económico lo amerita. Para este tipo de enfoque puede ver Brach Marion (2003).
Simulación Monte Carlo, simulación histórica y bootstrap de flujos de efectivo
En esta sección se presentan distintas metodologías para determinar los flujos de efectivo de un proyecto de inversión de una empresa.
Simulación Monte Carlo de flujos de efectivo cuya dinámica es guiada por una ecuación diferencial estocástica
En esta sección se presenta la simulación de los flujos de efectivo cuya dinámica es guiada por una ecuación diferencial estocástica, en particular un geométrico browniano. Para determinar los flujos de efectivo futuros de un proyecto de inversión, se puede utilizar simulación Monte Carlo, en la que se requiere de la estimación de los parámetros que aparecen en la dinámica que seguirán dichos flujos; por tanto, se utilizan datos históricos de los flujos de efectivo para ser incorporados en el cálculo de flujos de efectivo futuros simulados.
Las técnicas utilizadas del método de Monte Carlo dependen de algún proceso para generar números aleatorios que imiten precisamente la aleatoriedad de la mejor manera posible. Por ello, se han desarrollado un sinnúmero de investigaciones teóricas con este propósito. Jhon von Neumann (1951) escribió lo que se conoce como el pecado original de la generación de números aleatorios, la cual dice que: "alguien quien considere métodos aritméticos para la producción de dígitos aleatorios está, por supuesto, en un estado de pecado".
Los métodos de generación de variables aleatorias que se distribuyen normalmente son los de Box-Muller, Polar y el de 12 distribuciones uniformes; para un estudio de mayor profundidad en el tema consulte Ross (1999). En este caso, el algoritmo de simulación para determinar los flujos de efectivo futuros cuya dinámica es guiada por una ecuación diferencial estocástica es la siguiente:
i) Simular el comportamiento de los flujos de efectivo; para ello se generan números aleatorios que siguen una determinada distribución, en particular una distribución de tipo normal. La distribución normal se puede generar a partir del método Box-Muller, es decir

o bien
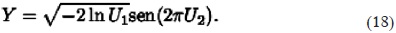
Se considera la dinámica de los flujos de efectivo, en este caso un geométrico browniano. Se utiliza el valor del flujo de efectivo último de los datos históricos, es decir al tiempo t0, FE0, y se continua hasta la fecha o periodo de valuación del proyecto de inversión. Esto da una realización de una trayectoria del flujo de efectivo del proyecto de inversión para el plazo especificado.
ii) Para cada realización o trayectoria de los flujos de efectivo se determinan los valores de dichos flujos en los tiempos ti con i = 1, 2, . . . , n que se desean conocer y se calcula el promedio de los flujos de efectivo de acuerdo con el número de trayectorias realizadas.
iii) Se repiten n veces las realizaciones sobre el mismo periodo de tiempo y se calculan dichos flujos.
iv) Los valores obtenidos por la simulación de los flujos de efectivo del proyecto, FEi, con i = 1, ..., n, serán utilizados para determinar la valuación del proyecto o bien determinar el valor de la prima de la opción de tipo real y que conducirán a una serie de recomendaciones sobre dicho proyecto.
Mientras mayor sea el número de simulaciones o de realizaciones, mejor será la precisión del resultado. Si se aumenta en cien veces las simulaciones, entonces aumenta una décima de corrección.
Se considera que para que exista convergencia sobre los valores de los flujos de efectivo, se deberán realizar al menos 10,000 simulaciones. Cabe señalar que la precisión también depende de la calidad de los números aleatorios propuestos por las diferentes técnicas, por lo que es recomendable hacer pruebas de aleatoriedad.
Simulación bootstrap de flujos de efectivo en el modelo binomial de n periodos para la valuación de proyectos de inversión con opciones reales y un valor de recuperación
Para determinar los flujos de efectivo futuros de un proyecto de inversión se puede utilizar simulación bootstrap (Mun, 2010), que es un método no paramétrico; es decir, para realizar la simulación no hay distribución por considerar y, por lo tanto, no se requiere de la estimación de parámetros; sin embargo, se requieren datos históricos de los flujos de efectivo para ser incorporados en el cálculo de flujos de efectivo futuros.
Asimismo, en el proceso se requiere de la asignación de una medida de probabilidad de los flujos de efectivo futuros. Para ello se determinan las probabilidades de dichos flujos de efectivo. En una muestra pequeña se puede utilizar una distribución t de Student y con los datos históricos se determinan intervalos de clase en la que puede caer alguno de los datos históricos y generar el histograma y la función de distribución acumulada con lo que podrían ser generados dichos flujos. Se busca el máximo y mínimo de los flujos de efectivo históricos; es decir, se establece una banda en la que al utilizar la función de distribución uniforme como generadora de números aleatorios y relacionada con la función de distribución acumulada se determinan los flujos de efectivo futuros. La ley de los grandes números establece que se presentara convergencia a un cierto valor, en este caso a medida que se incremente el número de simulaciones y se considera el valor promedio. El teorema de límite central de Glivenko-Candelli (1933) proporciona información sobre la magnitud del error probable en la estimación con respecto al número de simulaciones realizadas. Se recomienda realizar al menos 10,000 simulaciones por bootstrap para obtener convergencia en los flujos de efectivo simulados.
Con los flujos de efectivo futuros determinados se utilizan árboles binomiales; a partir de las ecuaciones (15) y (16) se determina el valor de la opción de venta tipo americana y se dan recomendaciones sobre el proyecto de inversión.
Simulación histórica en proyectos de inversión
Una parte sustancial en la valuación de proyectos de inversión son los flujos de efectivo futuros del proyecto. Por ello, se pueden utilizar, en el mejor de los casos, una base de datos de los flujos de efectivo trimestrales históricos de la empresa por considerar; así, con los datos de los flujos de efectivo de la empresa, se determinan los escenarios de lo que podrían ser los próximo flujos de efectivo de la empresa y tener la flexibilidad de tomar una decisión. Entonces, en la simulación histórica se considera que
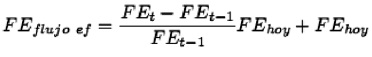
donde FEhoy representa el último flujo registrado. Asimismo, los flujos simulados podrían tener mayor o menor magnitud, por lo que se puede incorporar la volatilidad de los flujos de efectivo históricos.
Valor presente neto de los flujos de efectivo y simulación Monte Carlo en proyectos de inversión
El valor presente neto del proyecto de inversión con los flujos de efectivo esperados; se descuentan del costo del capital ponderado (WACC, por sus siglas en inglés) y se le resta la inversión inicial, es decir
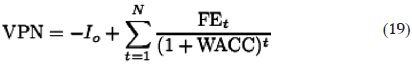
donde Io es la inversión inicial, FEt son los flujos de efectivo en el periodo t. El valor presente neto, VPN, puede ser positivo o negativo, en caso de ser negativo indicaría no invertir. Sin embargo, existe la opción de invertir si se considera una opción real. También se calcula el valor presente neto esperado de los flujos de efectivo que incorpora la inversión del proyecto, E[V PN], como se describe a continuación:
El valor presente neto esperado de los flujos de efectivo que incorpora la inversión del proyecto, E[V PN], donde se considera que los flujos de efectivo simulados pasan de un cierto nivel a otro, implica determinar la probabilidad de dicha situación. De esta manera se tiene:
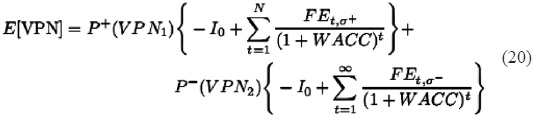
donde N es el horizonte temporal del proyecto, el WACC la tasa de descuento (el costo de oportunidad del capital) apropiada al riesgo del proyecto, FEt,σ+ y FEt,σ- y los flujos de efectivos simulados a partir de una base de datos histórica de la empresa instalada y en la que se incorpora la volatilidad de los flujos, y las probabilidades correspondientes P+( V P N1 ), P-( V P N2), de esta forma se calcula el valor presente neto esperado. Por otro lado, se puede calcular el valor de una opción que permita tener flexibilidad gerencial sobre la toma de decisión del proyecto, como se describe en la siguiente sección.
Valuación de un proyecto de inversión que incorpora opciones reales y simulación
A continuación se determina la valuación de un proyecto de inversión en la que se supone la construcción de una nueva tienda, colocada estratégicamente, y en la que se tiene la opción de abandonar el proyecto de inversión si el entorno económico de la empresa no le es favorable. Se consideran distintos métodos de simulación, en particular una cuya dinámica es guiada por una ecuación diferencial estocástica.
Valuación de un proyecto de inversión que incorpora opciones reales y simulación Monte Carlo: los flujos de efectivo siguen una dinámica estocástica
A partir de la información obtenida de la base de datos † y de los flujos de efectivo trimestrales históricos de la empresa Comercial Mexicana (CM), para el periodo del 31 de marzo de 2007 al 31 de marzo de 2010, se calculan por simulación Monte Carlo los flujos de efectivo futuros para el periodo del 30 de junio de 2010 al 31 de marzo de 2011 con el fin de evaluar la opción real, así como con el objeto de tomar una decisión estratégica sobre el proyecto de inversión; es decir, se considerarán que dichos flujos son los que podría generar el proyecto o bien seguir dicho comportamiento que ha venido generándose en la empresa.
A continuación se presenta una gráfica en la que se muestran algunas trayectorias simuladas de flujos de efectivo futuro y los flujos promedio totales de la simulación. Cabe señalar que para que se presente convergencia se realizan 10,000 simulaciones Monte Carlo de los flujos de efectivo en la que se ha utilizado la ecuación diferencial estocástica (12) y (12b) donde FE=4058815 en t=0 que corresponde al último dato observado, µ=0.1510, σ = 0.4453 y T-t=360, para el periodo dado. En la figura 1 se representan las 10,000 simulaciones por Monte Carlo utilizando el software MATLAB®, para una mayor descripción del tema consulte Huynh, Lai y Soumaré (2008).
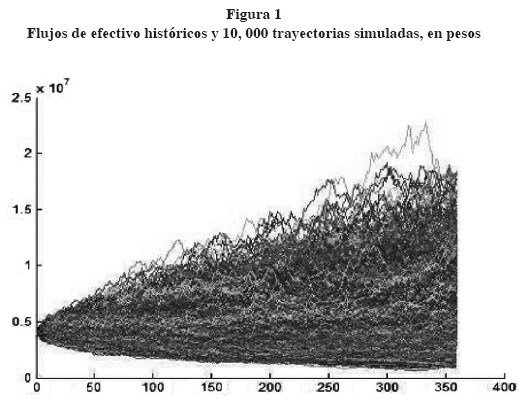
A continuación se presentan en la figura 2 los flujos de efectivo en promedio de las simulaciones realizadas por simulación Monte Carlo y cuyos flujos se utilizarán para determinar el valor de la opción de abandono de un proyecto de inversión.
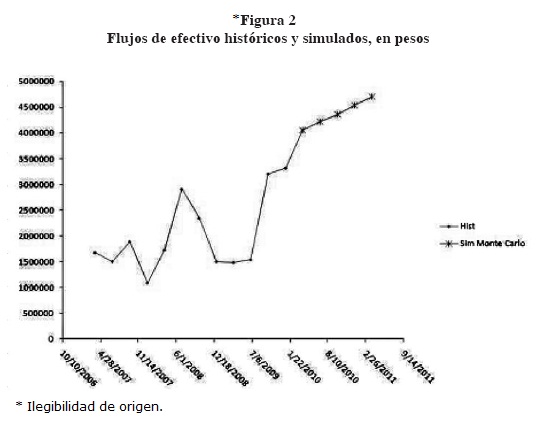
En la siguiente sección se presenta la valuación de la opción real en la que se incorporan árboles binomiales y se resumen los resultados en el cuadro 2.
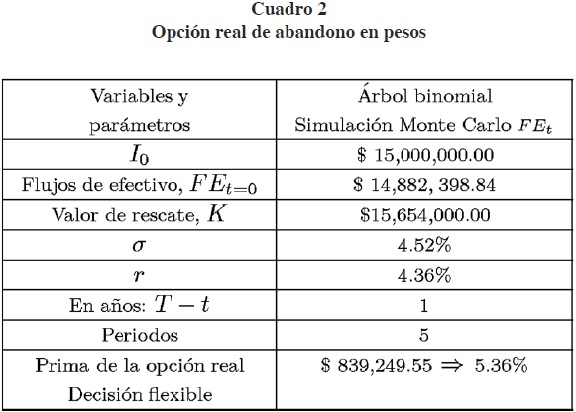
Valuación de un proyecto de inversión que incorpora opciones reales
En el cuadro 4 se presentan un resumen de los cálculos realizados y descritos en los árboles binomiales, figura 3 y figura 4, para los flujos de efectivo y el valor de la opción real que aparecen en la figuras. Es decir, para n = 5 periodos se tiene en n = 5 y k = 5, 4, . . . , 1, 0 con Vres el valor de rescate del proyecto de inversión a un plazo de un año en caso de ser abandonado.

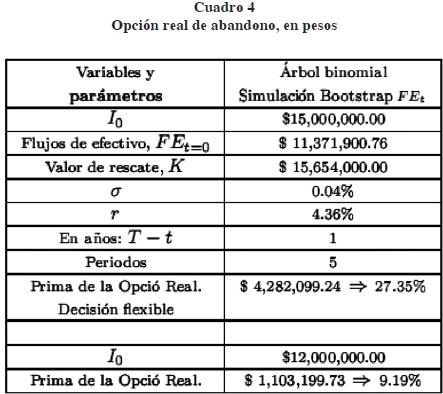

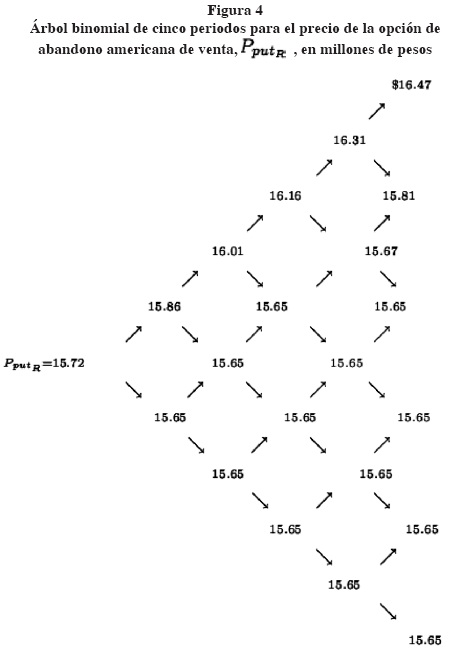
El árbol binomial de la figura 3 describe los flujos de efectivo a lo largo de un año y en el cual el consejo de administración de la empresa podrá ir tomando decisiones relacionadas con su entorno económico real del proyecto; es decir, flexibilidad en la toma de decisiones de la empresa.
Se observa que al final de los 5 periodos (y en este caso un plazo de un año) la empresa tiene la opción de vender y, en consecuencia, abandonar el proyecto con un valor de rescate Vres, o bien continuar con su proyecto. En el momento se tomaría la mejor opción para la empresa; es decir, la mejor estrategia que maximice su benefcio. De la aproximación binomial, el valor de la opción de abandono es el valor de la opción de venta al tiempo t = 0, es decir Pput R menos el valor de los flujos de efectivo al tiempo t = 0. Esto es, Vopc abandono=PputR-FE0 . La prima de la opción real (valor intrínseco de la opción) se describe en el cuadro 2. Dicho valor puede ser comparado con el valor de la opción de venta americana en el que se utilice alguna expresión matemática de valuación en forma cerrada. Si se incrementa el número de periodos la aproximación se mejora y se puede comparar con una valuación obtenida de un modelo de valuación que presenta forma cerrada.
A continuación se presenta un cuadro como resumen de los resultados de los árboles binomiales: (cuadro 2)
Valuación de un proyecto de inversión y opciones reales: flujos de efectivo por simulación histórica
A partir de la información obtenida de una base de datos † de los flujos de efectivo trimestrales de la empresa CM para el periodo del 31 de marzo de 2007 al 31 de marzo de 2010, se calcularán por simulación histórica los flujos de efectivo para el periodo del 30 de junio de 2010 al 31 de marzo de 2011, de manera que se pueda evaluar un proyecto con la flexibilidad que ofrece una opción real. Asimismo, se muestra la gráfica de los flujos de efectivos futuros tanto por simulación histórica y los calculados por simulación Monte Carlo, en la que los flujos de efectivo fueron guiados por una ecuación diferencial estocástica.
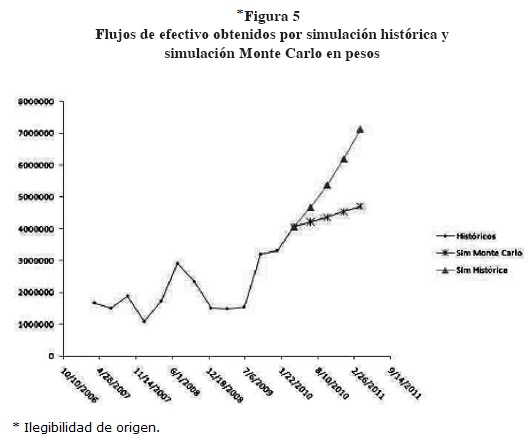
A continuación, se presenta en el cuadro 3 un resumen de los resultados de los árboles binomiales obtenidos:
Valuación de un proyecto de inversión que incorpora opciones reales y simulación bootstrap
A partir de la información obtenida de la base de datos † de los flujos de efectivo trimestrales históricos de la empresa CM para el periodo del 31 de marzo de 2007 al 30 de junio de 2010, se calculan por simulación bootstrap los flujos de efectivo futuros para el periodo del 30 de junio de 2010 al 31 de marzo de 2011 para evaluar la opción real con el objeto de tomar una decisión estratégica sobre el proyecto de inversión; es decir, se considerarán que dichos flujos son los que podría generar el proyecto o bien seguir dicho comportamiento que ha venido generándose en la empresa. Hay un trabajo previo publicado en el libro Avances recientes en valuación de activos y administración de riesgos, aplicado en el análisis de otra empresa. A continuación se presenta la gráfica en la que se muestran algunas trayectorias simuladas de flujos de efectivo futuro y los flujos promedio totales de la simulación. Cabe señalar que para que se presenten convergencias se deben realizar al menos 10,000 simulaciones como en los modelos paramétricos por simulación Monte Carlo.

A continuación se presenta en la gráfica 7 los flujos de efectivo en promedio de las simulaciones realizadas por bootstrap y cuyos flujos se utilizarán para determinar el precio de la opción de abandono de un proyecto de inversión y que podrá ser comparado con las distintas metodologías descritas anteriormente.
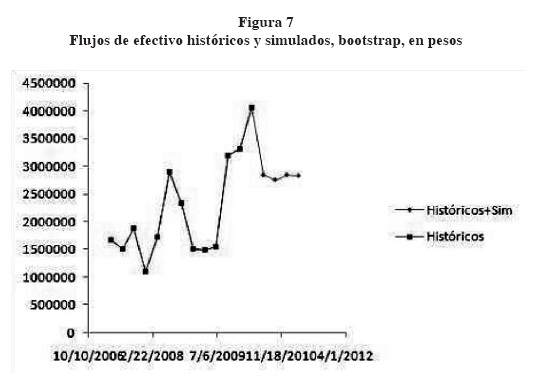
De los resultados obtenidos de la simulación por bootstrap, se tiene que si se considera una inversión con flujos de efectivo total por $11.37 millones de pesos se tendría una prima muy cara; es decir, del 27.35% debido a que se desearía una inversión inicial de $15.00 millones de pesos con un valor de rescate del proyecto por $15.654 millones. Esto se debe a que en la técnica bootstrap, los flujos de efectivo futuros estarían atrapados entre el mínimo y máximo histórico, lo que implicaría no poder alcanzar flujos de efectivo por arriba del máximo histórico, a diferencia de Simulación Monte Carlo que sigue una tendencia de los flujos de efectivo históricos y tiene incorporada una volatilidad constante en la ecuación diferencial estocástica, por lo que, utilizando bootstrap, se recomendaría una inversión del proyecto más moderada es decir si se consideran $ 12.00 millones de inversión, con un valor de rescate de $ 12.523 millones y una prima de la opción del 9.19%. A continuación se presenta un resumen, cuadro 4:
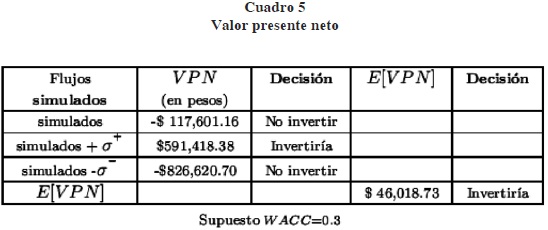
Valuación de un proyecto de inversión y simulación Monte Carlo: V PN y E[V PN]
A partir de la información obtenida de una base de datos † de los flujos de efectivo trimestrales de la empresa CM para el periodo del 31 de marzo de 2007 al 31 de marzo de 2010, se calcularán por simulación Monte Carlo los flujos de efectivo para el periodo del 30 de junio de 2010 al 31 de marzo de 2011, de manera que se pueda evaluar un proyecto con un VPN tradicional con el objeto de tomar una decisión sobre el proyecto de inversión; es decir, se considerarán que dichos flujos son los que podría generar el proyecto o bien seguir dicho comportamiento que ha venido generándose en la empresa. Así, se pueden comparar con la flexibilidad que ofrece una opción real (cuadro 5).
Conclusiones
La valuación de proyectos de inversión utilizando opciones reales le permite al consejo de administración de la empresa tomar decisiones estratégicas y dinámicas; a diferencia de considerar, solamente, la valuación de un proyecto con un valor presente neto tradicional.
Los resultados obtenidos muestran que para los flujos de efectivo obtenidos por simulación Monte Carlo y simulación histórica para valuar el proyecto de acuerdo con el entorno económico de la empresa se tiene una prima que está entre el 5.36% y 6.83% del valor de la inversión del proyecto al utilizar los árboles binomiales.
En este documento se analiza y se obtiene que los flujos de efectivos futuros obtenidos por simulación bootstrap resultan menores que los obtenidos por simulación Monte Carlo y simulación histórica, lo que conduciría a una prima más cara, es decir, del 27.4% del valor de recuperación de $ 15.654 millones. Por tanto, utilizar simulación bootstrap permitiría al consejo de administración presentar una estrategia por una inversión de sólo $12.00 millones de pesos acorde con los flujos futuros calculados y representaría una prima con un valor del 9.19% del valor de recuperación de la inversión en caso de abandonar el proyecto de inversión en cualquier instante (durante la vida de la opción) si el entorno económico de la empresa no le es favorable. Además, en la simulación Monte Carlo, en la que se utiliza una ecuación diferencial estocástica, está incorporada una tendencia de los flujos de efectivo históricos y se considera una volatilidad constante en el modelo, a diferencia de bootstrap que está acotado por el máximo y mínimo histórico de los flujos de efectivo. Es conveniente señalar que en el documento publicado en Ortiz (2011) en relación con proyectos de inversión con opciones reales no se consideró una ecuación diferencial estocástica para los flujos de la empresa, mientras que en este trabajo sí se incorpora una ecuación diferencial estocástica para los flujos de efectivo de la empresa.
Por otra parte, si se toman en cuenta las distintas metodologías, se podría considerar un promedio en el cálculo de la prima de la opción; es decir, una prima con un valor del 13.18% del valor de rescate del proyecto, en la que se han incorporado flujos de efectivo guiados por la ecuación diferencial estocástica ya descrita con anterioridad.
De los resultados, aun con un valor presente neto negativo, se tiene la opción de realizar la inversión si se considera la opción real, ya que ésta da al consejo de administración una flexibilidad estratégica en la toma de decisiones.
En este documento se muestra la factibilidad de extender la aplicación de opciones reales a empresas mexicanas que cuenten con información de flujos históricos y que dan la posibilidad de utilizar metodologías como simulación Monte Carlo de los flujos de efectivo guiados por una ecuación diferencial de tipo estocástico, así como por simulación histórica y simulación bootstrap combinado con árboles binomiales y que brindan al consejo de administración de la empresa la flexibilidad de tomar decisiones estratégicas en el entorno económico financiero en el que se encuentre ésta, y no sólo realizar la valuación de un proyecto con un valor presente neto tradicional y que un valor presente neto negativo implicaría no llevar a cabo el proyecto de inversión.
Esta investigación se puede extender si se considera que la volatilidad de los flujos de efectivo es una función del tiempo. Asimismo, es posible dar una dinámica estocástica sobre los flujos de efectivo que consideren no sólo tendencia y volatilidad, sino además saltos de Poisson que podrían impactar en la toma de decisiones al valuar el proyecto de inversión con la opción de tipo real.
Referencias
Amram, M. y N. Kulatilaka (1999). Real Options Managing Strategic Investment in an Uncertain World, Boston: Harvard Business School Press. [ Links ]
Black, F. y M. Scholes (1973). The Pricing of Options and Corporate Liabilities. Journal of Political Economy LXXXI: 637-654. [ Links ]
Boer, F. P. (2002). The Real Options, Solution. Finding Total Value in a High-Risk World. New York: John Wiley & Sons, Inc. [ Links ]
Brach Marion, A.(2003). Real Options in Practice. New Jersey: John Wiley & Sons. [ Links ]
Brennan, M. J. y E. S. Schwartz (1985). Evaluating Natural Resource Investments. Journal of Business LVIII: 135-157. [ Links ]
Cantelli, F. P. (1933). Sulla determinazione empirica della legge di probabilita. Giorn. Institute. Ital. Attuari (4): 221-424. [ Links ]
Copeland, T. y V. Antikarov (2003). Real Options, A Practitioner's Guide. New York:Thomson Texere. [ Links ]
Cox, J. C., S. A. Ross, y M. Rubinstein (1979). Option Pricing: A Simplified Approach. Journal of Financial Economics (7): 229-263. [ Links ]
Cuthbertson y D. Nitzsche (2001). Financial Engineering, Derivatives and Risk Management. New York:John Wiley & Sons, Inc. [ Links ]
Glivenko, V. (1933). Sulla determinazione empirica della legge di probabilita. Giorn. Institute Ital. Attuari (4): 92-99. [ Links ]
Huynh, Huu Tue, Lai Van Son e Issouf Soumaré (2008). Stochastic Simulation and Applications in Finance with MATLAB® Programs. New York: John Wiley & Sons. [ Links ]
Karatzas, Ioannis y Steven E Shreve (1991). Brownian Motion and Stochastic Calculus. Springer-Verlag. [ Links ]
Kulatilaka, N. (1995). Operating Flexibilities in Capital Budgeting: Substitutability and Complementarity in Real Options. In Real Options in Capital Investments: Models, Strategies, and Applications, L. Trigeorgis (ed.), New York: Praeger. [ Links ]
Malliaris, A. G. (1999). Stochastic Methods in Economics and Finance. North Holland: Elsevier Science 17. [ Links ]
Mascareñas Pérez-Iñigo, J. M. et al. (2004). Opciones Reales y Valoración de Activos, Madrid: Pearson Educación. [ Links ]
Mason, S.P. y R. C. Merton (1985). The Role of Contingent Claims Analysis in Corporate Finance. In Recent Advances in Corporate Finance. E. Altman y M. Subrahmanyam (eds.) Homewood, IL. R. D. Irwin. [ Links ]
McDonald, R. y D. Siegel(1985). Investment and the Valuation of Firms When There is an Option to Shut Down. International Economic Review XXVI: 331-349. [ Links ]
Merton, R. C. (1973). The Theory of Rational Option Pricing. Bell Journal of Economics and Management Science IV: 141-83. [ Links ]
Myers, S. C. (1987). Finance Theory and Financial Strategy. Midland Corporate Finance Journal (5): 6-13. [ Links ]
Myers, S. C. y Majd(1990). Abandonment Value and Proyect Life. Advances in Futures and Options Research (4): 1-21. [ Links ]
Mun, J. (2002). Real Options Analysis, Tools and Techniques for Valuing Strategic Investments and Decisions. New York: John Wiley & Sons. [ Links ]
---------- (2010). Modeling Risk. Applying Monte Carlo Risk Simulation, Strategic Real Options, Stochastic and Portafolio Optimization, 2da Ed., New York:John Wiley & Sons . [ Links ]
Ortiz Arango, F. (2011). Avances recientes en valuación de activos y administración de riesgos, Centros Culturales de México 2: 409-423. [ Links ]
Ross, M. Sheldon (1999). Simulación. México: Prentice Hall. [ Links ]
Schwartz, E. S. y L. Trigeorgis (2001). Real Options and Investment under Uncertainty. London: The Mit Press Cambridge. [ Links ]
Tourinho, O. (1979). The Option Value of Reserves of Natural Resources. Working Paper. Univ. de California at Berkeley. [ Links ]
Triantis, A. J., y J. Hodder (1990). Valuing Flexibility as a Complex Options. Journal of Finance (45): 549-565. [ Links ]
Trigeorgis, L. y S. P. Merton (1987). Valuing Managerial Flexibility. Midland Corporate Finance Journal spring:14-21. [ Links ]
Trigeorgis, L. (1993). The Nature of Options Interactions and the Valuation of Investments with Multiple Real Options. Journal of Financial and Quantitative Analysis (28): 1-20. [ Links ]
Trigeorgis, L. (1998). Real Options, Managerial Flexibility and Strategy in Resource Allocation. Cambridge, The MIT Press, Massachusets Institute of Technology. [ Links ]
Venegas-Martínez, F. y A. Fundia Aizenstat (2006). Opciones reales, valuación financiera de proyectos y estrategias de negocios: aplicaciones al caso mexicano, El Trimestre Económico 73 (2): 363-450. [ Links ]
Venegas-Martínez, F. (2006). Riesgos Financieros y Económicos. Productos derivados y decisiones económicas bajo incertidumbre.México: Thompson. [ Links ]
† Economática














