Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Contaduría y administración
versión impresa ISSN 0186-1042
Contad. Adm vol.57 no.1 Ciudad de México ene./mar. 2012
La restricción externa al crecimiento en México: 1988–2009
The external constraint to growth in Mexico: 1988–2009
Domingo Rodríguez Benavides* y Francisco Venegas–Martínez**
* Universidad Autónoma Metropolitana, Azcapotzalco. domr@economia.unam.mx
** Escuela Superior de Economía, Instituto Politécnico Nacional. fvenegas1111@yahoo.com.mx
Fecha de recepción: 20.09.2010.
Fecha de aceptación: 17.01.2011.
Resumen
Este artículo muestra evidencia empírica acerca del modelo de Thirwall (1979) sobre la restricción de balanza de pagos al crecimiento para México. Thirwall establece que las variables relevantes en la explicación del crecimiento económico son las elasticidades ingreso de las exportaciones e importaciones y el ingreso del resto del mundo. Esta última variable se aproxima, en este trabajo, por el PIB mundial. Los resultados obtenidos, al analizar el periodo 1929–2009, sugieren la existencia de una relación de largo plazo entre el PIB de México y el PIB mundial sólo durante el periodo 1988–2009. La dirección de la causalidad entre el PIB mundial y el de México, como era de esperarse, va del primero al segundo de acuerdo con la dinámica del modelo de corrección del error estimado. No se encontró evidencia de que ambas variables estuvieran relacionadas en un periodo más amplio, lo cual puede atribuirse a que la economía mexicana estaba prácticamente cerrada hasta antes de la década de los ochenta. Esto difiere de lo encontrado en otras investigaciones en donde se utiliza el PIB de Estados Unidos como proxy del PIB del resto del mundo.
Palabras clave: crecimiento económico, balaza de pagos, modelos econométricos.
Clasificación JEL: E12 y C32
Abstract
This article shows empirical evidence about Thirwall' (1979) model on the balance of payments constraint to growth for Mexico. Thirwall states that the relevant variables in the explanation of economic growth are the income elasticities of exports and imports and the income from the rest of the world. The latter variable is approximated, in this work, by the world GDP. The obtained results, by analyzing the period 1929–2003, suggest only the existence of a long–term relationship between Mexico's GDP and global GDP over the period 1988–2009. The direction of causality between global and Mexico's GDP, as expected, goes from the first to the last according to the dynamics of the estimated error correction model. No evidence was found that both variables were related in a longer period, which can be attributed to the fact that the Mexican economy was essentially closed up until the eighties. This differs from other studies in which the US GDP is used as a proxy of the world GDP.
Keywords: economic growth, balance of payments, econometric modeling.
JEL Classification: E12 y C32
Introducción
La teoría poskeynesiana postula que las economías abiertas crecen a ritmos diferentes debido a que la demanda impone restricciones al crecimiento. El crecimiento diferencial observado en la economía mundial se debe, desde esta perspectiva, a que la demanda agregada se expande a tasas diferentes en cada economía: si la expansión de la demanda induce desequilibrios en la balanza de pagos (BP) antes de que la economía haya alcanzado el límite dado por la tasa de crecimiento de corto plazo de la capacidad productiva, entonces el crecimiento se frenará a un nivel que refleja subutilización de la oferta (véase Perrotini, 2002). En consecuencia, se reducirán la inversión y la productividad, pues se detendrá el progreso tecnológico, mientras que el saldo de la balanza comercial empeorará en virtud de que los bienes comerciables pierden competitividad. Además de que no hay razón para esperar que las economías converjan en su crecimiento si las tasas de crecimiento de las exportaciones y la elasticidad ingreso de la demanda de importaciones difiere para cada una de ellas. De esta manera, la brecha de desarrollo observada entre las distintas economías es el resultado de las diferencias en ingresos per cápita resultantes de una expansión heterogénea de la demanda efectiva, lo cual es un hecho estilizado consustancial a la economía mundial moderna, el crecimiento diferencial.
En este trabajo se proporciona evidencia sobre la ley de Thirwall, la cual provee un marco analítico que permite vincular el PIB nacional con la actividad económica del resto del mundo. Es importante destacar que a diferencia de la mayoría de los estudios empíricos para México sobre el tema, los cuales emplean al PIB de los Estados Unidos como proxy del ingreso del resto del mundo, en esta investigación se utiliza el PIB mundial para probar la validez de la ley de Thirwall. De esta manera, se estima lo que se conoce como la restricción externa al crecimiento (un planteamiento de la macrodinámica poskeynesiana), la cual plantea, entre otras cosas, que las variables clave para entender la evolución económica de un país son, básicamente, el ingreso del resto del mundo, las elasticidades ingreso y precio de las exportaciones e importaciones, los términos de intercambio o tipo de cambio real y los flujos netos del capital (véanse, por ejemplo, Davidson, 1990–1991; Guerrero, 2006; Thirwall y Hussein, 1982).
Es importante destacar que esta investigación extiende el trabajo de Guerrero (2006) en varias direcciones: 1) la longitud del periodo de estudio es mayor, 19292003; 2) la variable que se emplea como proxy del ingreso del resto del mundo es el PIB mundial con la finalidad de capturar el impacto que pueda tener el comercio residual con otros países en la estimación de la elasticidad correspondiente; 3) se efectúan pruebas de cambio estructural; 4) se realizan pruebas de causalidad entre las variables en cuestión a través del VECM estimado (Vector Error Correction Model); 5) en cuanto a los resultados, se muestra que el PIB de México no guarda una relación de largo plazo con el PIB mundial para todo el periodo de análisis, sino que sólo mantiene una relación de equilibrio para un periodo reciente, el cual inicia aproximadamente en la fecha en la que la economía mexicana experimentó una notable apertura e integración hacia el exterior.
La presente investigación está organizada como sigue: la próxima sección presenta el marco teórico; posteriormente, se proporciona una breve revisión de la literatura sobre distintos hallazgos empíricos; más adelante, se presentan los resultados empíricos obtenidos mediante un análisis econométrico de series de tiempo; por último, se presentan las conclusiones. Un apéndice contiene detalles técnicos de diversas pruebas econométricas.
Marco teórico
El modelo de Thirwall (1979) puede resumirse mediante un sistema de ecuaciones que representa una economía pequeña y abierta, y con dos bienes (Guerrero, 2006; Moreno–Brid y Peréz, 1999). Se parte de la identidad de la balanza de pagos:

donde Pd es el precio de los bienes y servicios domésticos exportados en pesos, X son las exportaciones, E es el tipo de cambio nominal, Kf son los flujos de capital en dólares, Pf es el precio de las exportaciones en dólares y M son las importaciones.
Si Kf < 0 , entonces en la economía salen más capitales de los que ingresan en un determinado tiempo. La participación de las exportaciones en los ingresos totales se denotan como:

De esta manera, la participación de los flujos netos de capital en los ingresos totales viene dado por:
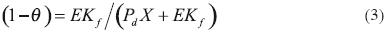
De tal modo que (2) y (3) miden la proporción de la cuenta que resulta de las importaciones financiadas por las exportaciones y los flujos netos de capital, respectivamente. No hay restricciones para el valor de 1—θ, por lo que este puede ser positivo, negativo o cero (véase, por ejemplo, Guerrero, 2006). La forma dinámica de la ecuación (1) está dada por:
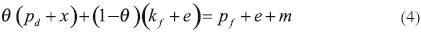
En la expresión anterior, las letras minúsculas representan las tasas de crecimiento de las variables. Por otro lado, la demanda de las exportaciones satisface:

donde η es la elasticidad precio de las exportaciones (η < 0), w es el producto agregado del resto del mundo y π es la elasticidad ingreso de las exportaciones (π < 0). Las importaciones son tales que

en donde 


y
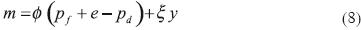
De esta manera, las ecuaciones (7) y (8) son las versiones dinámicas de las ecuaciones (5) y (6), respectivamente. Si se resuelve el sistema de ecuaciones para la tasa de crecimiento económico se obtiene:

A partir de (9) se infiere que la tasa de crecimiento económico del producto doméstico depende de lo siguiente: de la tasa de crecimiento del resto del mundo, w; de la tasa de crecimiento de los flujos netos de capital en pesos constantes, kf + e — pd; de la evolución de los términos de intercambio, pd — pf — e ; y de la elasticidad ingreso de las importaciones. Si en (9) se supone que los términos de intercambio permanecen constantes (pd— pf — e = 0) resulta1 que:
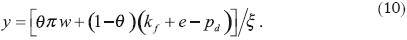
Si se supone además una cuenta corriente equilibrada, de tal forma que θ =1, la ecuación (10) se puede reescribir de la siguiente forma:

Por lo tanto, bajo los supuestos anteriores, la tasa de crecimiento de equilibrio está determinada por tres variables: la elasticidad ingreso de las exportaciones e importaciones y la tasa de crecimiento del resto del mundo (Davidson, 1990–1991). De esta manera, Thirwall sostiene que en el largo plazo la tasa de crecimiento observada (y) es igual a la tasa de crecimiento consistente con el equilibrio de la balanza de pagos (véase, también, Perrotini, 2002). En esencia, ésta es la "ley fundamental del crecimiento" de A. P. Thirwall que establece que en el largo plazo la expansión de una economía se haya restringida por el equilibrio de la cuenta corriente de la balanza de pagos (balance–of–payments constrained, BPC). Las economías alcanzan este punto (y = yb) experimentando grados heterogéneos de utilización de su capacidad productiva. En este marco, las discrepancias macrodinámicas individuales (y ≠ yb) se ajustan tarde o temprano a través de fluctuaciones del empleo y del producto; de ahí la diversidad de tasas de crecimiento del PIB per cápita en la economía mundial, lo cual se identifica como crecimiento diferencial. Del modelo de BPC se desprende que el sector externo es la clave para aumentar la tasa de expansión de largo plazo dado que las exportaciones constituyen el único componente "verdaderamente" autónomo de la demanda agregada, de acuerdo con Thirwall, y dado que hay un límite infranqueable a la capacidad que tiene un país para financiar un déficit en balanza de pagos resultante de la expansión de la demanda. Por último, la formulación con perturbaciones estocásticas, ut, de la ecuación (11) se puede expresar como:

donde α = π / ξ.
Breve revisión de la literatura empírica
La ley de Thirwall se mantiene en debate permanente. Por ejemplo, la crítica neoclásica se inició con el trabajo de Mcgregor y Swales (1985), quienes argumentan que no se trata de una ley general, sino que la ecuación (12) puede ser derivada de un modelo con restricciones de oferta, lo que invalidaría la conclusión fundamental de que la economía está limitada por la demanda efectiva y por el equilibrio de la balanza de pagos. Esta crítica rechaza el supuesto de neutralidad de los precios relativos. Si los precios relativos no son neutrales, pd— pf — e = 0, lo que le permite a Thirwall obtener el resultado de que y = yb, es porque al parecer las ecuaciones (7) y (8) están mal especificadas; de esta forma omiten la importancia de la competencia imperfecta en el comercio internacional.
La respuesta de Thirwall (1986) a esta crítica sostiene que en el largo plazo los precios relativos calculados en una moneda común son constantes debido a tres posibles razones: 1) las variaciones del tipo de cambio inducen alteraciones proporcionales en los precios internos, 2) la estructura del mercado es altamente competitiva y 3) hay competencia oligopólica (McCombie y Thirwall, 1994).
López y Cruz (1999 y 2000) estiman un modelo VAR con variables de diferente orden de integración para algunos países de América Latina en el que, entre otras variables, incluyen al tipo de cambio real, sugiriendo que éste tiene un vínculo directo con el crecimiento del producto. El argumento esgrimido en su trabajo, para proceder de esa forma, es que el tipo de cambio real ha experimentado considerables fluctuaciones en el periodo examinado por ellos. Los autores encuentran que la elasticidad del PIB con respecto del tipo de cambio real es positiva en los casos de Argentina, Colombia y México, y negativa para Brasil, de lo que concluyen que el tipo de cambio real influyó en el ritmo y la estabilidad del crecimiento económico en esos países durante el periodo 1965 –1996.
En el caso de México, Loría (2001a) argumenta que el desequilibrio externo aumenta conforme se expande el nivel de actividad económica debido al patrón de especialización productiva prevaleciente. De acuerdo con sus estimaciones para alcanzar el pleno empleo de la fuerza de trabajo y superar los rezagos asociados al lento crecimiento, la economía mexicana debería crecer al 7%. Según este autor, el modelo exportador adoptado a partir de la liberación comercial, en la década de los ochenta del siglo pasado, ha contribuido a diversificar las exportaciones, pero a la vez ha generado una alta dependencia hacia las importaciones intermedias y de capital, lo cual se traduce en un déficit de carácter estructural. Lo anterior explica el alto valor de K y así México se convierte en una economía con restricción de balanza de pagos.
Asimismo, Loría (2001a) estima que en el caso de México la tasa de crecimiento consistente con yb es igual a 4.3% y que el valor "histórico" de π es aproximadamente de 3.5%; sus resultados también sugieren que aumentar yb a 7% requiere disminuir π a aproximadamente 2.15%. Sin embargo, la brecha no se reduciría con el hecho de incrementar las exportaciones, x, ya que esto requeriría un incremento simultáneo en las importaciones de bienes intermedios y de capital, por lo que la prescripción de Loría (2001a) es la de inducir un cambio estructural que tienda a reducir de manera drástica el valor de π.
Por otro lado, Moreno–Brid (1998, 1999) analiza la economía mexicana desde la perspectiva de la versión alternativa de la hipótesis de la restricción de la balanza de pagos; su procedimiento se basa en lo que él denomina "el procedimiento Mc–Combie"2. Las estimaciones de Moreno–Brid muestran que en México yb ha disminuido considerablemente al pasar de 6.4% a 2.6% entre 1967 y 1999, principalmente a causa de que el valor de π se duplicó en ese periodo (de 1.57% a 3.14%), mientras que los términos de intercambio, no ejercieron influencia significativa en la disminución de la tasa de expansión de largo plazo en México.
Holland et al. (2004) estiman, a través de distintas técnicas econométricas y utilizando la ecuación (11), las elasticidades ingreso de las importaciones en diez países de América Latina (Argentina, Bolivia, Brasil, Chile, Colombia, Ecuador, México, Perú, Uruguay y Venezuela). Las variables incluidas en sus modelos fueron los logaritmos naturales del PIB, de las exportaciones y de las importaciones, todas en términos reales. Ellos encuentran que las tasas medias de crecimiento observadas y estimadas son muy próximas en la muestra considerada de países, principalmente para Argentina, Chile y Uruguay, lo cual es considerado por ellos como un nuevo procedimiento para probar la ley de Thirwall.
Por su parte, Guerrero (2006) analiza empíricamente el crecimiento económico de México durante el periodo 1929–2003 y distintos subperiodos seleccionados, de acuerdo con la perspectiva de la hipótesis de la restricción de la balanza de pagos. De esta manera, Guerrero evalúa el desempeño macroeconómico alcanzado en cada uno de los modelos de desarrollo instrumentados en la historia relativamente reciente de México. Este especialista resalta que el crecimiento económico observado a lo largo del periodo estudiado y de distintos subperiodos es repetidamente menor al crecimiento económico consistente con una cuenta corriente equilibrada, lo cual representa un "hecho estilizado" de la economía mexicana, reflejando debilidades estructurales que se expresan en una mezcla inconveniente de valores de la elasticidad de ingreso y precio de las exportaciones e importaciones. Guerrero estima la ecuación (12) tomando como wt al PIB de los Estados Unidos; los resultados encontrados sugieren que el crecimiento económico de México está ligado básicamente a la dinámica productiva de nuestro vecino del norte y a la evolución de los términos de intercambio.
Por último, Pacheco (2009) muestra evidencia de que la elasticidad ingreso de las importaciones ha aumentado para los países de América Latina en el periodo de liberación comercial, lo cual, de acuerdo con este enfoque, tiende a reducir la tasa de crecimiento consistente con el equilibrio de balanza de pagos para cada país.
Especificación del modelo y resultados empíricos
La restricción en el periodo 1929–2003
A continuación se examina la dinámica del PIB mundial y de México durante 1929–2003. La gráfica 1 muestra la evolución del PIB mundial y de México en el periodo de estudio.
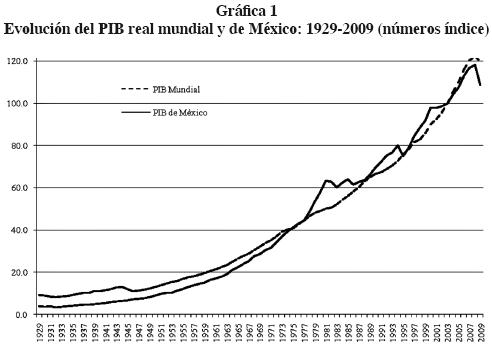
Los datos del PIB mundial provienen de Madison (2007) para el periodo 19502007 y de Capraro (2007) para el periodo 1929–1949. La serie del PIB de México se tomó de Guerrero (2006) para el periodo 1929–2003 y se actualizó con información del Instituto Nacional de Estadística, Geografía e Informática (INEGI). Con el fin de identificar si las series bajo estudio se comportan como caminatas aleatorias, se realizaron pruebas de raíces unitarias. El cuadro 1 presenta los resultados de las pruebas Dickey–Fulle, aumentada para las series del PIB Mundial y de México durante el periodo 1929–2003; en todos los casos la elección del número de rezagos obedece al criterio de Schwarz. (Cuadro 2)
Una vez efectuada las pruebas de raíces unitarias, se puede emplear la técnica propuesta por Johansen (1988) para detectar cointegración entre las series, la cual consiste en pruebas del rango de Γk, la matriz de parámetros asociada al vector de rezagos en los niveles de las variables en el modelo de corrección del error (MCE) de un VAR de m–variables:

donde Γk define la "solución en niveles" de largo plazo en la ecuación (14) (Cuth–bertson, 1992) y k es lo suficientemente grande para asegurar que vt sea un vector de ruido blanco gaussiano, el cual se distribuye idéntica e independientemente con media cero y varianza constante. De esta forma, la técnica prueba el rango de Γk, la matriz de parámetros asociada al vector de rezagos, en los niveles de las variables; mientras que 
Un procedimiento para identificar la posible existencia de rupturas estructurales en la serie es el que sugieren Bai y Perron (1998 y 2003). Tal metodología se puede aplicar a una prueba de raíz unitaria para identificar múltiples cambios estructurales en la serie, así como en un modelo lineal estimado por mínimos cuadrados ordinarios. La especificación del modelo de regresión lineal con "m" rupturas estructurales se define, de acuerdo con Galindo y Cordera (2005), como:
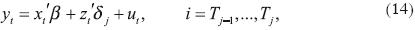
donde yt es la variable observada, xt es el vector de las variables explicativas y zt es una matriz que contiene variables dummy que registran las rupturas estructurales. Los vectores β y δj (j = 1, ..., m + 1) contienen parámetros, ut es el término aleatorio y (T1,...,Tm) son las fechas de posible ruptura estructural, las cuales son desconocidas y se estiman junto con los parámetros con T observaciones disponibles. La ecuación (15) se estima por el método de mínimos cuadrados ordinarios para m particiones de la muestra y el primer punto de cambio se identifica en donde se minimiza la suma de errores al cuadrado, el cual corresponde a una prueba de parámetros constantes. En ese punto, la muestra es dividida nuevamente en dos periodos y en el segundo se sigue un procedimiento similar para estimar un nuevo punto de ruptura estructural. El cuadro 5 presenta el resultado de la prueba de Bai–Perron (1998) de múltiples cambios estructurales.

Del cuadro anterior se puede concluir que el número de rupturas estructurales en la serie del PIB doméstico es de cinco de acuerdo con el criterio bayesiano de información (BIC) correspondientes a los años 1931, 1933, 1980, 1988 y 2007, mientras que la prueba sugiere que el número de rupturas estructurales en el PIB mundial es de cuatro para los años de 1940, 1946, 1972 y 2002.
Debido a que la prueba de Bai–Perron (1998) sugiere diversas fechas de cambio estructural, fue necesario especificar la prueba con diferentes tipos de dummies tanto de de pulso como transitorias. Sin embargo, la incorporación de variables dummy en el procedimiento de Johansen (1988) modifica los valores críticos de las pruebas estadísticas (Johansen, Mosconi y Nielsen, 2000), por lo que se requiere la estimación de los nuevos valores críticos, los cuales se obtienen a través de un proceso de simulación y cuyos resultados se obtuvieron en CATS en RATS versión 2.0.
El cuadro 6 muestra las pruebas de cointegración para las variables PIB mundial y PIB de México con datos anuales para el periodo 1929–2003, en el que se incorporaron distintas variables dummies tanto transitorias como de impulso. Las dummies transitorias que se incorporaron fueron dt3133t y dt4547t La primera (dt3133t) toma los valores de 3, –4 y 8 en los años de 1931, 1932 y 1933, respectivamente, y ceros en los demás años; se incorporó para tener en cuenta la sobre reacción experimentada por el PIB doméstico en los años posteriores a la crisis de 1929. La segunda (dt4547t) toma los valores –5, –3 y 8 en los años de 1945, 1946 y 1947 para tener en cuenta la sobrereacción experimentada por el PIB mundial en los años posteriores al inicio de la Segunda Guerra Mundial. Adicionalmente, se incorporaron seis dummies de impulso correspondientes a los años de 1933, 1940, 1944, 1986, 1995 y 2001, de acuerdo como lo sugiere la prueba de Bai–Perron aplicada a cada una de las series en cuestión. Todas estas variables resultaron estadísticamente significativas en el VECM estimado.

El cuadro 6 muestra las pruebas de cointegración para las variables PIB mundial y PIB de México con datos anuales para el periodo 1929–2003.
Como se aprecia en el cuadro 6, no se puede rechazar la hipótesis nula de no cointegración entre ambas variables, tanto para la prueba con los valores críticos simulados como sin simular, por lo que no se encontró evidencia de que en el periodo 1929–2003 ambas variables contengan una relación de largo plazo. La ausencia de una relación de largo plazo entre las variables PIB doméstico y PIB mundial para el periodo 1929–2003, sugerido por la prueba de la traza de Johansen, se puede atribuir a que la economía mexicana se encontraba prácticamente cerrada en lamayor parte del periodo en cuestión. No fue sino hasta finales de la década de los ochenta cuando se inició un proceso de apertura comercial en México; no obstante, Guerrero (2006) sí encuentra una relación de largo plazo con el PIB de los Estados Unidos para este periodo.
La restricción en el periodo 1988–2009
Dado que no hay evidencia de que el PIB doméstico y el PIB mundial guarden una relación de equilibrio de largo plazo en el periodo 1929–2003, el siguiente paso consiste en averiguar si existe una relación de equilibrio entre ambas variables en la historia reciente de México, dado que se reconoce que a partir de finales de los ochenta la economía mexicana inicio un proceso de apertura comercial. Antes de realizar la prueba de cointegración de Johansen y procediendo de manera análoga al análisis efectuado para el periodo 1929–2003, se realizará nuevamente la prueba de cambios estructurales múltiples para las series de los productos doméstico y mundial en el periodo 1988–2009. Los resultados se presentan en el cuadro 7.

Del cuadro anterior, se puede concluir que el número de rupturas estructurales en la serie del PIB doméstico es de cinco de acuerdo con el criterio bayesiano de información (BIC) correspondientes a los años 1994, 1995, 2000, 2003 y 2008, mientras que la prueba sugiere que el número de rupturas estructurales en el PIB mundial es de cuatro para los años de 1989, 1993, 2002, 2007 y 2008. De esta manera, es necesario especificar el MCE (Modelo de Corrección del Error) con diferentes términos deterministas y realizar la prueba de cointegración de Johansen en presencia de dichos términos. El cuadro 8 presenta los resultados de la prueba de cointegración de Johansen, Mosconi y Nielsen (2000) con dos rezagos aplicada a las series del PIB de México y del PIB mundial para el periodo identificado como de "apertura comercial", que va de 1988 a 2009.

En virtud de que ambas variables cointegran, se estima el siguiente modelo de corrección del error:
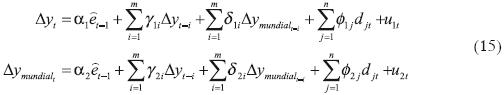
La estimación del MCE con un rezago, para el periodo 1988–2009, se presenta en la siguiente ecuación:

donde dp95t, dp00t y dp0lt son variables dummies de pulso que toman el valor de 1 en los años 1995, 2000 y 2001 y cero en el resto de los años. Esto debido a la crisis severa experimentada en México en 1995, y en 2000 y 2001 por el impacto que tuvo en México el entorno recesivo en el que se vio inmerso Estados Unidos. Por su parte, dt09t toma el valor de –4 en el año 2009 con el fin de tener presente el efecto en ambas variables de la crisis financiera mundial desatada a finales de 2008. El cuadro 9 presenta los parámetros de la ecuación cointegrante estimada.

Como se desprende tanto del VECM estimado (16) como de los resultados presentados en el cuadro 9, el valor del parámetro estimado para este periodo fue 0.723. Ahora bien, si lo multiplicamos por la tasa media de crecimiento del PIB mundial, que resultó ser 3.09%, conduce a 2.23%; este último valor es la tasa de crecimiento consistente con el equilibrio de balanza de pagos y que se aproxima a la tasa de crecimiento media observada del PIB doméstico en este periodo, la cual fue de 2.58%. Los anteriores cálculos se resumen en el cuadro 10.
Como puede observarse en el cuadro 10, la tasa de crecimiento económico compatible con el equilibrio de la cuenta corriente resultó ser menor que la tasa observada del producto para el periodo de estudio; este resultado es consistente con lo encontrado por Holland et al. (2004) para México en el periodo 1958–1999 y por Guerrero (2006) para distintos periodos. Con fines comparativos, el cuadro 11 reproduce los resultados de las estimaciones de OC efectuadas por Guerrero (2006) para México, utilizando el PIB de los Estados Unidos como proxy del PIB del resto del mundo para distintos periodos.
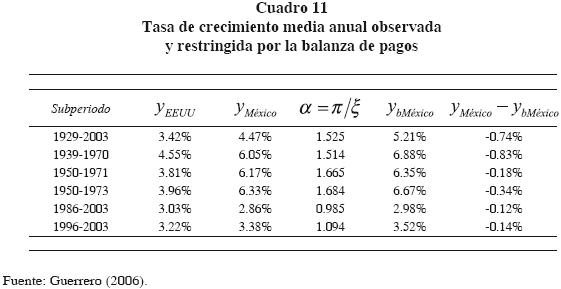
Como se puede ver de los resultados reportados por Guerrero (2006), mostrados en el cuadro 11, la estimación de α, empleando el PIB de los Estados Unidos para el periodo 1986–2003, con datos trimestrales, es mayor al estimado con el PIB mundial para el periodo 1988–2009. De lo anterior se puede deducir que la tasa de crecimiento consistente con el equilibrio de la balanza de pagos es mayor cuando la variable "ingreso del resto del mundo" es aproximada por el PIB de los Estados Unidos.
Adicionalmente, las pruebas de exogeneidad débil del modelo estimado (16) sugieren que la variable exógena débil es el PIB mundial en el MCE y que las variable dummies tanto de pulso como las transitorias, incorporadas en el modelo, resultaron estadísticamente significativas. Este resultado también es consistente con lo encontrado por Ocegueda (2000) para el periodo 1983–1997, quien atribuye lo anterior a un incremento de la elasticidad ingreso de la demanda por importaciones y que supera al registrado en la elasticidad ingreso de la demanda por exportaciones.
Asimismo, Pacheco (2009) argumenta que un proceso similar ha sido experimentado por los países de América Latina, lo cual ha redundado en el crecimiento delproducto de estos países y que ha tenido que ajustarse para mantener el equilibrio de la balanza de pagos.
Lo anterior ha ocurrido de tal forma que el crecimiento del producto ha tenido que ajustarse para mantener el equilibrio en la balanza de pagos. Las pruebas de normalidad para el modelo estimado en la ecuación (16) se presentan en los cuadros 12 y 13.


Como se puede observar en los cuadros 12 y 13, los residuos del MCE estimado se distribuyen normalmente. Los cuadros 14 y 15 muestran las pruebas de autocorrelación y de heterocedasticidad para el modelo en su conjunto y de efectos ARCH de manera individual, respectivamente. Como se puede ver en dichos cuadros, el modelo estimado para el periodo 1988–2009 no presenta problemas de especificación incorrecta, ya que los residuos estimados se distribuyen normalmente; tampoco presentan autocorrelación ni heterocedasticidad, como se deduce de los cuadros 14 y 15, por lo que es posible considerar al modelo reportado en (16) como una buena aproximación al proceso generador de datos (DGP).


Por último, el cuadro 16 muestra los resultados de la prueba de no causalidad en el sentido de Granger en el MCE.

Como se puede ver la prueba permite rechazar la hipótesis nula de que el PIB mundial no causa en el sentido de Granger al PIB de México, revelando de esta manera que la dinámica del PIB mundial determina al PIB doméstico y de que no hay evidencia de que ocurra lo contrario.
Conclusiones
Los resultados anteriores tienden a confirmar la validez de la ley de Thirwall para México en el periodo reciente 1988–2009, ya que se encontró evidencia de la existencia de una relación de largo plazo entre el PIB de México y el PIB mundial. Sin embargo, no se encontró evidencia de que ambas variables también estuvieran relacionadas en un periodo mucho más amplio, lo cual puede atribuirse a que la economía mexicana estaba prácticamente cerrada al exterior hasta antes de la década de los ochenta. Este resultado contrasta en gran medida con lo encontrado por Guerrero (2006), donde el PIB de México está cointegrado con el de Estados Unidos durante el periodo 1929–2003.
Las tasas de crecimiento económico compatible con el equilibrio de la cuenta corriente resultó ser de 2.23%, para el periodo 1988–2009, mientras que la tasa observada para el mismo periodo fue de 2.58%. De lo anterior se infiere que el producto doméstico creció a una tasa mayor que la tasa de crecimiento compatible con el equilibrio de la balanza de pagos en el periodo que se identificó como de apertura comercial. El que un país, o una región, puedan crecer a una tasa superior a la consistente con su equilibrio de balanza de pagos se asocia con un déficit comercial mayor financiado con flujos de capital (Pacheco, 2009), lo cual ciertamente es el caso para México.
De lo anterior, se concluye que cuando se utiliza al PIB mundial como proxy de la variable "ingreso del resto del mundo" en la estimación de la tasa de crecimiento consistente con el equilibrio de la balanza de pagos, el resultado es similar al que se obtiene al utilizar el PIB de los Estados Unidos para este periodo, en tanto que en ambos casos la tasa de crecimiento estimada se aproxima a la observada para el periodo respectivo en el que se realiza la estimación. Un aspecto por considerar es que cuando se emplea el PIB mundial, la tasa de crecimiento consistente con el equilibrio de la balanza de pagos estimada se encuentra por debajo de la tasa observada, mientras que cuando se utiliza el PIB de Estados Unidos la tasa estimada se encuentra por arriba de la observada. No obstante, aún está pendiente la discusión de la pertinencia de emplear el PIB mundial o el de Estados Unidos como variable proxy del ingreso del resto del mundo para esta versión de la prueba de la ley de Thirwall, particularmente para las economías pequeñas y abiertas que poseen un patrón comercial más diversificado como es el caso de muchos países de Latinoamérica, por lo cual se requiere el empleo de otras herramientas estadísticas que sugieran la pertinencia de emplear una u otra variable proxy en la prueba.
La dirección de la causalidad entre el PIB mundial y el de México, como era de esperarse, va del primero a este segundo en la dinámica del modelo de corrección del error estimado. Por último, las estimaciones efectuadas del modelo para el periodo 1988–2009, en la que se tomó como proxy del ingreso del resto del mundo al PIB mundial, sugieren que la restricción externa al crecimiento económico en México se ha incrementado, lo cual pone en duda los beneficios de la política de apertura comercial, o bien la forma en que ésta se llevó a cabo; no obstante, hay que tener presente que en dicho periodo la economía mundial ha mostrado una clara desaceleración, lo cual, sin duda, redunda en condiciones menos favorables para los países que tienen un alto grado de relaciones comerciales con el exterior.
Desde luego, al igual que en la mayoría de los estudios que tienden a validar empíricamente la ley de Thirwall, las recomendaciones en términos de política económica se mantienen: las políticas gubernamentales deben orientarse a superar las restricciones del sector externo a través del incremento de las exportaciones y de la reducción de la elasticidad ingreso de las importaciones.
Referencias
Atesoglu, H. S. (1993). Balance–of–payments–constrained growth. Journal of Post Keyenesian Economics 15 (4): 507–514. [ Links ]
–––––––––– (1994). Balance of payments determined growth in Germany. Applied Economic Letters 1 (6): 89–91. [ Links ]
–––––––––– (1995). An explanation of the slowdown in US economic growth. Applied Economic Letters 2 (4): 91–94. [ Links ]
–––––––––– (1997). Balance–of–payments–constrained growth model and its implications for the United States. Journal of Post Keynesian Economics 19 (3): 327–335. [ Links ]
Bai, J. and P. Perron (1998). Estimating and testing linear models with multiple structural changes. Econométrica 66 (1): 47–78. [ Links ]
–––––––––– (2003). Computation and analysis of multiple structural change models. Journal of Applied Econometrics 18 (1): 1–22. [ Links ]
Capraro, S. (2007). The Thirwall law. A theoretical and empirical approach. The case of Argentina during years 1970–2003. MPRA Paper No. 4868. http://mpra.ub.uni–muenchen.de74868/ [ Links ]
Davidson, P. (1990–1991). A post keynesian positive contribution to theory. Journal of Post Keynesian Economics 13 (2): 298.303. [ Links ]
Dennis, J. G., H. Hansen, S. Johansen and K. Juselius (2005). CATS in RATS, version 2. Illinois: Estima. [ Links ]
Doornik, J. A. y H. Hansen (1994). A practical test of multivariate normality, unpublished paper. Nuffield College. [ Links ]
Galindo L. M. y R. Cordera (2005). Las relaciones de causalidad entre el gasto público y el producto en México: ¿Existe evidencia de cambio estructural? Revista Mexicana de Economía y Finanzas 4 (4): 369–386. [ Links ]
Holland, M, F. V. Vieira, O. Canuto (2004). Economic growth and the balance–of–pay–ments constraint in Latin America, Investigación Económica 63 (247): 45–74 [ Links ]
Ghani, G. M. (2006). Balance of payments constrained growth model: An examination of thirlwall's hypothesis using McCombie's individual country method, Applied Economics Letters 13 (12): 763–768. [ Links ]
Guerrero, C. (2006). Determinantes del crecimiento económico en México, 19292003: Una perspectiva postkeynesiana. Investigación Económica 65 (255): 127–158. [ Links ]
Johansen, S. (1988). Statistical analysis of co–integrating vector. Journal of Economics Dynamics and Control 12 (2–3): 231–254. [ Links ]
–––––––––– and B. Nielsen (2000). Cointegration analysis in the presence of structural breaks in the deterministic trend. Econometrics Journal 3 (2): 216 –249. [ Links ]
Kwiatkowski, D., P. C. B. Phillips, P. Schmidt and Y. Shin (1992). Testing the null hypothesis of stationary against the alternative of a unit root. Journal of Econometrics 54 (1–3): 159–178. [ Links ]
López, J. G. y A. Cruz (1999). Crecimiento económico y tipo de cambio real: un análisis de cointegración para América Latina. Momento Económico, marzo–abril (102): 23–33. [ Links ]
–––––––––– y B. A. Cruz (2000). Thirlwall's law and beyond: The Latin American experience. Journal of Post Keynesian Economics 22 (3): 477–495. [ Links ]
Loría, E. (2001a). El desequilibrio comercial en México, o por qué ahora no podemos crecer a 7%, Momento Económico (113): 16–21. [ Links ]
–––––––––– (2001b). La restricción externa dinámica al crecimiento de México, a través de las propensiones del comercio, 1970–1999. Estudios Económicos 16 (2): 227–251. [ Links ]
–––––––––– (2001c). The mexican economy: balance–of–payments–constrained growth model–the importance of the exchange rate, 1970–1999. Journal of Post Keynesian Economics 25 (4): 659–663. [ Links ]
Lütkepohl, H. y M. Kratzig (2004). Applied time series econometrics. Cambridge: Cambridge University Press. [ Links ]
–––––––––– (1993). Introduction to multiple time series analysis. 2ed. Berlín: Springer–Verlag. [ Links ]
Madison, Angus (2007). The contours of the world economy 1–2030 AD. Essays in Macroeconomic History, Oxford University Press, September. [ Links ]
McCombie, J.S.L. y A.P. Thirwall (1994). Economic growth and the balance of payments constraint. Londres: St. Martin's Press. [ Links ]
McGregor, P. G y J. K. Swales (1985). Thirwall's law" and balance of payments constrained growth. Applied Economics. February (reprinted in McCombie, J. S. L y A. P. Thirwall, 1994). [ Links ]
Moreno–Brid, J. C. (1998). México: crecimiento económico y restricción de la balanza de pagos. Comercio Exterior (6): 478–486. [ Links ]
–––––––––– (1999). Mexico's economic growth and the balance of payments constraint: a cointegration analysis. International Review of Applied Economics 13 (2): 149–159. [ Links ]
–––––––––– y E. Pérez (1999). Balance–of–payments–constrained growth in Central America: 1950–1996. Journal of Post Keynesian Economics 22 (1): 131–147. [ Links ]
Ocegueda, J. M. (2000). La hipótesis de crecimiento restringido por balanza de pagos. Una evaluación de la economía mexicana 1960–1997. Investigación Económica 60 (232): 91–122. [ Links ]
Pacheco, P. (2009). Efectos de la liberación comercial en el crecimiento económico y la balanza de pagos en América Latina. Investigación Económica 68 (267): 13–49. [ Links ]
Perrotini, I. (2002). La ley de Thirwall y el crecimiento en la economía global: Análisis crítico del debate. Revista Venezolana de Análisis de Coyuntura. 8 (2): 117–141. [ Links ]
Thirwall, A. P. (1979). The balance of payments constraint as an explanation of international growth rate differences. Banca Nazionale del Lavoro Quarterly Review (128): 45–53. [ Links ]
–––––––––– y M. N. Hussain (1982). The balance of payments constraint, capital flows and growth rate differences between developing countries. Oxford Economic Papers 34: 498–510. [ Links ]
1 Thirwall (1979) y McCombie y Thirwall (1994) argumentan que existe evidencia considerable de que la razón de precios relativos tiene poco efecto sobre el crecimiento de las importaciones y las exportaciones, lo cual se puede atribuir a las bajas elasticidades precio de la demanda, de tal manera que la condición Marshall–Lerner apenas se cumple; véase, por ejemplo, Holland, Vilela y Canuto (2004).
2 De acuerdo con Perrotini (2002), este método consiste en contrastar el valor de largo plazo de π con su valor de equilibrio hipotético (πH) , el cual se define como el valor crítico al que correspondería la igualdad y = yb. De esta manera, si π = πH , entonces la ley de Thirwall es "empíricamente relevante" (Moreno–Brid, 1999).














