Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Contaduría y administración
Print version ISSN 0186-1042
Contad. Adm n.235 Ciudad de México Sep./Dec. 2011
Artículos de investigación
Cálculo de la relación de margen de contribución en los precios y el surgimiento de la proporción áurea en la estructura de utilidades
Computing the margin contribution percent relationship in price setting and the golden ratio in profits structure
Carlos Hernández Ortega
Escuela Superior de Ingeniería y Arquitectura, IPN y Facultad de Estudios Superiores Acatlán, UNAM. chernandezo@ipn.mx, carloshdez@apolo.acatlan.unam.mx
Fecha de recepción: 06.04.2010
Fecha de aceptación: 19.10.2010
Resumen
El propósito de este trabajo es encontrar un sustento formal al margen de contribución porcentual que debe utilizarse para obtener el precio de un producto ofrecido. Para ello se elaboró una función de ventas cuya dependencia involucró el margen de contribución porcentual y la rentabilidad sobre las ventas, de manera que mediante su manipulación algebraica permitió lograr una relación funcional adimensional. La optimización de la función anterior dio por resultado que el margen de contribución sea una función de la raíz cuadrada de la rentabilidad sobre las ventas. Asimismo, una vez sustituido este resultado en la expresión para las ventas, tenemos que éstas presentan un mínimo para el cual la rentabilidad sobre las ventas es del 25%, el margen de contribución porcentual es del 50%, el costo variable total es igual a las ventas de equilibrio, el apalancamiento operativo es similar a la relación de costos variables totales a costos fijos, etc. De igual forma, se encontró que existe un punto fijo estable en donde la igualdad entre la utilidad y las ventas de equilibrio dan como fruto el cuadrado del inverso de la proporción áurea: 0.381966011... Consecuentemente, y con base en los resultados obtenidos, la determinación de precios no puede ser un proceso subjetivo, sino matemáticamente objetivo y armónico.
Palabras clave: margen de contribución porcentual, rentabilidad sobre las ventas, precios y costos fijos y variables, ventas de equilibrio, proporción áurea.
Abstract
This work aims to find a formal way to show the margin contribution percent that should be used to set the offer price of a certain product. In order to do this, a function that depends on the margin contribution percent and on the sales profit was constructed, and by algebraic manipulation it was possible to generate a non–dimensional relation between the variables. When the aforementioned function was optimized the result obtained was that the margin contribution is a function of the square root of sales profits. Likewise, once this result is substituted in the sales expression, it turns out that the sales have a minimum for which profit is 25%, margin contribution percent is 50%, total variable cost equals the equilibrium sales, operative leverage equals the total variable and fixed costs, etc. Also, a more stable fixed point was found, where the equilibrium between profits and sales is the inverse of the squared golden ratio: 0.381966011...As a consequence, and based on results obtained, the author considers that price setting cannot be a subjective process but a mathematically objective and harmonic one.
Keywords: Margin contribution percent, sales profit, fixed and variable prices and costs, sale equilibrium, golden proportion.
Introducción
Se sabe que el objetivo primordial de todo negocio es la obtención de utilidades y entre mayores sean éstas, menores problemas económicos y financieros se tendrán. No obstante, dichas utilidades no pueden ser arbitrarias y a voluntad de quien o quienes las desean debido a su posible inviabilidad. Por otro lado, también es cierto que aunque una empresa esté obteniendo utilidades no siempre son suficientes para cubrir el costo del capital empleado y, como consecuencia, se encuentre en una etapa en decrecimiento que, incluso, la puedan llevar a la quiebra. Es por ello que entre unas utilidades muy altas deseadas y otras que sean obtenidas insuficientemente existe la opción de conocer aquella utilidad mínima requerida para tomarla como objetivo en la planeación y estructura de las utilidades y, por consiguiente, de todas las demás actividades operativas tales como la generación de los ingresos requeridos y el control de los costos y gastos. Como hipótesis de trabajo supongamos que la utilidad mínima por obtener es una función del costo del capital total empleado, el cual se forma de los intereses generados por el pasivo y de los rendimientos esperados por los accionistas o dueño(s) del negocio.
Así, partiendo de que el costo ponderado del capital total empleado está dado por Cp = rP rP/A P + rC rC/AC, en donde rP representa el rendimiento sobre el pasivo p, rP/A es la razón del pasivo al activo total A , rC es el rendimiento sobre el capital C , y rC/A la proporción que representa el capital respecto al activo total, y además 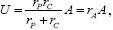 siendo rA, = rprp/A = rCrC/A el rendimiento sobre el activo, entonces se tendrá que la rentabilidad sobre las ventas V es
siendo rA, = rprp/A = rCrC/A el rendimiento sobre el activo, entonces se tendrá que la rentabilidad sobre las ventas V es  , donde ρA es la rotación del activo. Si ahora se considera que del pasivo P = Po + Pi, donde P0 es el pasivo que no genera interés, Pi está impuesto a un interés promedio i, mientras que j es la tasa de rendimiento esperada por los accionistas y tal que cumple que
, donde ρA es la rotación del activo. Si ahora se considera que del pasivo P = Po + Pi, donde P0 es el pasivo que no genera interés, Pi está impuesto a un interés promedio i, mientras que j es la tasa de rendimiento esperada por los accionistas y tal que cumple que 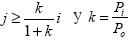 , entonces se pueden obtener los rendimientos rp y rC teniendo en cuenta que
, entonces se pueden obtener los rendimientos rp y rC teniendo en cuenta que 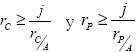 con lo cual se calcularía rA ; lo anterior implica que se puede planear la estructura de utilidades a partir de que la utilidad mínima U ≥ Cp sea no menor que el costo del capital empleado Cp = iPi + jC . Como, en último caso, se hace uso de valores relativos, y no absolutos, lo cual permite cálculos más generalizados e independientes de los valores, entonces en lugar de hablar de utilidad mínima requerida se tendrá que hablar de la rentabilidad sobre las ventas mínimas requeridas. Ahora bien, para calcular los ingresos o ventas necesarios es indispensable asignar un precio a los bienes o productos ofrecidos, de manera que los mismos sean acordes con los desembolsos efectuados en la elaboración y/o adquisición y venta de dichos productos y que, a su vez, permita cubrir los demás costos y gastos de la comercialización, administración y distribución de los mismos, así como la parte correspondiente a la utilidad mínima esperada.
con lo cual se calcularía rA ; lo anterior implica que se puede planear la estructura de utilidades a partir de que la utilidad mínima U ≥ Cp sea no menor que el costo del capital empleado Cp = iPi + jC . Como, en último caso, se hace uso de valores relativos, y no absolutos, lo cual permite cálculos más generalizados e independientes de los valores, entonces en lugar de hablar de utilidad mínima requerida se tendrá que hablar de la rentabilidad sobre las ventas mínimas requeridas. Ahora bien, para calcular los ingresos o ventas necesarios es indispensable asignar un precio a los bienes o productos ofrecidos, de manera que los mismos sean acordes con los desembolsos efectuados en la elaboración y/o adquisición y venta de dichos productos y que, a su vez, permita cubrir los demás costos y gastos de la comercialización, administración y distribución de los mismos, así como la parte correspondiente a la utilidad mínima esperada.
Sin embargo, aunque existen diversas formas de fijar o determinar los precios de un artículo, todas ellas presentan algún grado de subjetividad. Así, por ejemplo, se tienen aquellas formas basadas en cuestiones puramente psicológicas, pasando por las que únicamente siguen los precios de la competencia, y llegando hasta aquellas que usan el costo total como un "piso". Todas estas formas no permiten un análisis matemático que den una pauta adecuada para la toma de decisiones. Por otra parte, hay otras formas alternas basadas en la separación de los costos en fijos y variables que, mediante el sistema del punto de equilibrio, permiten determinar los precios y plantear escenarios para la adecuada toma de decisiones. No obstante, aun este sistema tiene un inconveniente: el margen de contribución porcentual o relación de ingreso marginal usado en todos los cálculos no tiene un fundamento matemático y por lo mismo no es objetivo.
Es por ello que uno de los motivos para la elaboración de este trabajo fue el hecho de encontrar una base matemática para dicha relación de margen de contribución; se logró con creces, ya que surgió en el análisis un resultado inesperado el cual involucra el inverso de la proporción áurea como un punto fijo asintóticamente estable.
Desarrollo
Determinación del precio
Al margen de las cuestiones psicológicas y estimaciones de la demanda que siguen muchas empresas para asignar precios a los bienes con que lucran, en este trabajo se analizan dos procedimientos para la formación de precios; previamente se hace una separación de los costos en variables (CV) y en fijos (CF) , estos últimos periódicos. Respecto a los costos variables, éstos son los relativos a los costos variables unitarios de producción y/o compra (cv) . Así, el costo variable unitario total (cvT) está dado por:

Ahora bien, considerando que r es la relación de aportación o margen de contribución porcentual, que servirá para agregar a los cvT y con ello formar el precio buscado que permita cubrir los costos fijos CF y proporcionar una utilidad U en el periodo bajo análisis, se tendrán los siguientes casos:
• El precio se forma sumando al costo variable unitario total el producto de la relación de aportación por dicho precio de venta; esto es:
pv = cvT = rpv
• la cual al ser combinada con (1) permite obtener:

• El precio se forma sumando al costo variable unitario total el producto de la relación de aportación por el costo variable unitario cv. O sea:
pv = cvT + rcv
cuya combinación con (1) arroja que:
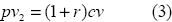
Por otro lado, de las cantidades o variables que entran en las expresiones para el precio, sólo la que corresponde a r es arbitraria, ya que el costo variable unitario es un dato dado. Consecuentemente, los precios se pueden ver como una función de dicha variable r , cuyos dominios son:
• Para pv1 : r
(0,1)
• Para pv2: r
(0, ∞)
En este trabajo se tratarán ambos casos de precios. Para distinguir las ecuaciones correspondientes a cada precio, se manejarán los mismos números sólo diferenciándolos con la asignación de la letra a para el precio dado por (2) , y la letra b para el precio dado por (3) .
Determinación de las ventas
Con el precio dado por (1)
Ahora bien, sea n el número de unidades vendidas al precio pv , cuyo costo variable unitario es cv. Entonces la aportación marginal o margen de contribución M está dado por la diferencia entre las ventas V y los costos variables totales CV . Y como V = npv, y CV = ncv, entonces:
M = n( pv — cv)
o bien,
M = Vr (4α)
donde se ha hecho uso de (2) . Lo anterior indica que el margen de contribución es igual al producto de las ventas por la relación de aportación.
Si ahora se considera que en el periodo que amparan las ventas V se tuviesen costos fijos equivalentes a CF , entonces la utilidad mínima de operación U estará dada por U = M — CF ; o sea
U = Vr — CF
de donde, por álgebra, se tendrá que las ventas V estarán dadas por:
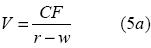
donde w es la rentabilidad sobre las ventas ya definida en la introducción.
Con el precio dado por (2)
Haciendo uso de (3) , se tiene que el correspondiente margen de contribución M será

y puesto que M — CF = U , entonces las ventas estarán dadas por:
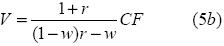
Determinación del punto de equilibrio y otras expresiones importantes
Con el precio dado por (1)
Ahora consideremos el caso especial en el cual U = 0 ; es decir, donde los ingresos son iguales al costo total CT = CV + CF . En este caso, existe cierto número de unidades a vender ne al precio pv , tal que a Ve = nepv se le conoce como ventas o ingresos de equilibrio. En consecuencia, y como U = 0 implica que w = 0 , entonces de (5a) se tiene que:

ahora, de (5a) y (6a) se obtiene que

de donde se consigue una relación muy importante:

Por otra parte, como el apalancamiento operativo g se encuentra definido como  , entonces se puede obtener lo siguiente:
, entonces se puede obtener lo siguiente:
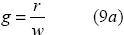
Por otro lado, haciendo uso de (4α) se tendrá que V —CV =Vr . Por lo tanto

mientras que de (5α) :

En consecuencia, la relación de costos variables a costos fijos, 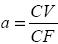 , estará dada por:
, estará dada por:

Con el precio dado por (2)
De (5b), haciendo w = 0 , se tiene
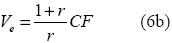
de donde, al combinarla con (5b) , se obtiene que

Sin embargo, a diferencia de (9a), esta expresión no representa el apalancamiento operativo, sino que se puede probar que es igual a la razón de las ventas a los costos fijos; es decir,

Asimismo, de (7b) se comprueba que se sigue cumpliendo (8) . Por otra parte, se tiene que las relaciones correspondientes para este caso, son:

Determinación del valor óptimo para la relación de aportación
Con el precio dado por (1)
Primero se relacionan las ventas con las ventas de equilibrio haciendo uso de (2) y (5a) , con lo cual se obtiene que:
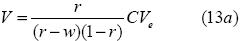
donde CVe = necv representa el costo variable de las ventas de equilibrio. Consecuentemente, definiendo a  como la razón de las ventas por obtener respecto al costo variable de las ventas de equilibrio, entonces:
como la razón de las ventas por obtener respecto al costo variable de las ventas de equilibrio, entonces:
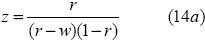
Se observa que si la rentabilidad w es conocida, entonces z es una función de r , cuyo dominio es r  (w, 1) . Ahora bien, debido a que w
(w, 1) . Ahora bien, debido a que w  (0,1), entonces existen diversas combinaciones entre la utilidad U y las ventas por obtener V para lograr dicha rentabilidad. Por lo tanto, para una w dada, la utilidad es directamente proporcional a las ventas. Esto trae por consecuencia que si lo que se desea es obtener la mayor utilidad posible, entonces se debe incrementar el nivel de ventas; sin embargo, el incremento del nivel de ventas sólo puede lograrse mediante dos mecanismos: aumentar el volumen de unidades vendidas o aumentar el precio del producto.
(0,1), entonces existen diversas combinaciones entre la utilidad U y las ventas por obtener V para lograr dicha rentabilidad. Por lo tanto, para una w dada, la utilidad es directamente proporcional a las ventas. Esto trae por consecuencia que si lo que se desea es obtener la mayor utilidad posible, entonces se debe incrementar el nivel de ventas; sin embargo, el incremento del nivel de ventas sólo puede lograrse mediante dos mecanismos: aumentar el volumen de unidades vendidas o aumentar el precio del producto.
Si bien es cierto que el incremento del volumen de unidades vendidas se podría lograr a través de la mercadotecnia, lo cual llevaría a incrementar los gastos, en este sentido se supondrá el caso ideal en el cual tanto volumen como precios están relacionados en forma elástica por la ley de la oferta y la demanda; es decir, se relacionan precio y volumen en forma inversamente proporcional.
Como consecuencia, si se requiere aumentar el volumen por vender, entonces se necesitan reducir los precios. Pero este incremento en el volumen podría rebasar la capacidad de producción, almacenamiento y/o comercialización, con el consiguiente aumento en costos y gastos, así como de espacio, etc. Por otra parte, un incremento de precios puede traer una reducción en el volumen de ventas y consecuentemente una utilidad menor en términos monetarios. No obstante, en ambos casos, se puede estar logrando la rentabilidad impuesta como objetivo.
Con objeto de ver la aplicación de algunas de las fórmulas anteriores, consideremos el siguiente ejemplo sencillo. Supongamos que un pequeño productor de cierto artículo, el cual presenta un costo variable unitario de $60.00, tiene unos costos fijos mensuales de $50,000.00, y ha determinado que la rentabilidad mínima por obtener para cubrir su costo total de capital es del 15% sobre las ventas. Con base en estos datos se ha elaborado la siguiente tabla, en la cual sólo el margen de contribución r se ha dado arbitrariamente, mientras que las otras columnas se han obtenido aplicando las fórmulas (2) y (5a) . Estos elementos calculados son:
1. El precio de venta (pv).
2. Las unidades por vender (n).
3. Las ventas totales por efectuar (V).
4. La utilidad por obtener (U).
5. La rentabilidad sobre las ventas (w)

Las pequeñas diferencias en la rentabilidad se deben, más que nada, a las aproximaciones efectuadas en las unidades por vender. Fuera de esto podemos observar que la rentabilidad es la misma para diferentes combinaciones de utilidad y ventas. Ahora bien, se puede apreciar que conforme se incrementa el margen de contribución porcentual, el precio también aumenta, mientras que el número de unidades por vender disminuye. Asimismo, se confirma que a mayor valor de las ventas, mayor es el valor de la utilidad obtenida, y esta última desciende conforme el valor de las ventas disminuye. Aparentemente no existe indicio alguno que nos permita elegir el renglón mejor posible. Por lo tanto, todo se reduce a encontrar una relación que garantice un precio y un volumen adecuados para lograr la rentabilidad impuesta como objetivo. Por consecuencia, y como lo único que no tiene sustento es la razón de margen de contribución r , empecemos el análisis para darle fundamento a este concepto.
Para ello partamos de (14a), donde se sabe que r  (w,1) . Así que calculando los límites unilaterales en dicho intervalo se observa lo siguiente:
(w,1) . Así que calculando los límites unilaterales en dicho intervalo se observa lo siguiente:
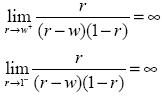
lo cual indica que z es una función convexa que tiene, al menos, un punto crítico. En consecuencia, derivemos z con respecto a r e igualemos a cero para encontrar dicho punto. Así:
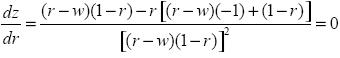
de lo cual se obtiene
–w + r2 = 0
es decir, 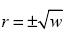 . Ahora bien, como la relación de aportación no puede ser negativa, ya que esto implicaría que los costos variables son superiores a los ingresos por ventas, y además los costos variables fungen como un límite infranqueable o "piso" para la fijación de precios, entonces la solución es la parte positiva; esto es:
. Ahora bien, como la relación de aportación no puede ser negativa, ya que esto implicaría que los costos variables son superiores a los ingresos por ventas, y además los costos variables fungen como un límite infranqueable o "piso" para la fijación de precios, entonces la solución es la parte positiva; esto es:

esto indica que la razón de margen de contribución con el que se deben formar los precios es una función de la raíz cuadrada de la rentabilidad sobre las ventas.
Ahora tenemos que conocer qué tipo de punto crítico representa. Para ello, se toma la segunda derivada de (14a) con respecto de r y luego se evalúa el resultado considerando (15a). Así:

por lo tanto, se puede concluir que en r = √w hay un mínimo, lo cual hace que la función z tenga un valor dado por

Consecuentemente, la relación de aportación que se debe usar para formar los precios de los productos ofrecidos debe ser igual a la raíz cuadrada de la rentabilidad sobre las ventas. Esto garantizará que las ventas por obtener no sean tan altas que requieran un gran volumen de unidades vendidas a precios bajos, ni tan bajas que impliquen un volumen bajo vendidas a precios altos. Así que aplicando este resultado al ejemplo dado anteriormente, donde la rentabilidad impuesta como objetivo es w = 15% , se tiene que la relación de margen de contribución debe ser r = √ 0.15 ≈ 0.38730 . Por lo tanto, el renglón más conveniente por elegir será el quinto.
Con el precio dado por (2)
Considerando todo lo expuesto anteriormente, para el caso del precio dado por (2) , tenemos que la función de ventas es:

de donde la función por optimizar será

Así que derivándola respecto de r se obtiene

donde la única solución estará dada por
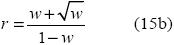
ya que estando w  (0,1), entonces w < √ w. Por otra parte, se puede comprobar que este punto representa un mínimo evaluando la segunda derivada en el punto dado por (156). Así:
(0,1), entonces w < √ w. Por otra parte, se puede comprobar que este punto representa un mínimo evaluando la segunda derivada en el punto dado por (156). Así:

Consecuentemente, si el resultado de (15b) se sustituye en (14b) , se obtendrá nuevamente (16a).
Determinación del valor mínimo para la rentabilidad sobre las ventas
Con el precio dado por (1)
Ahora sustituyendo (15a) en (2) , (4a) , (5a) , (6a), así como de la (9a) hasta la (12a) se obtendrán los siguientes resultados:

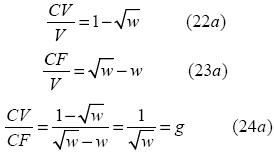
Pero además, de (20a) , (22a) y (23a), se obtendrá que
Ve = CV (25a)
Ahora bien, como anteriormente se expresó, w  (0,1). En consecuencia, se observa el comportamiento de (19a) y (20a) en dicho intervalo. Para ello calculemos los siguientes límites:
(0,1). En consecuencia, se observa el comportamiento de (19a) y (20a) en dicho intervalo. Para ello calculemos los siguientes límites:

Es inmediato darse cuenta que las ventas de equilibrio tienen como asíntota horizontal a los costos fijos, conforme la rentabilidad se aproxima a la unidad. Por otra parte, las ventas por obtener tienen asíntotas verticales en cada uno de los extremos del intervalo. Ello indica que presenta una concavidad hacia arriba (función convexa), por lo cual, para obtener el punto mínimo, se deriva (19a) e iguala a cero. Así:

la que al ser resuelta proporciona que el punto mínimo se da cuando:

lo que implica que el margen de contribución porcentual por emplear será de:

así que sustituyendo estos valores en las expresiones de la (17a) hasta la (24a) , tenemos:
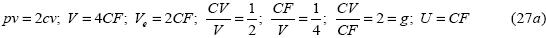
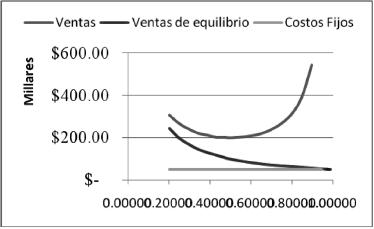
En la siguiente gráfica se puede observar la convexidad de las ventas como una función del margen de contribución porcentual, del punto mínimo que se presenta en  , así como de la tendencia asintótica de las ventas de equilibrio hacia los costos fijos. El valor de estos últimos son los mismos que los del ejemplo anterior. Además, los valores del eje vertical se encuentran en miles de pesos.
, así como de la tendencia asintótica de las ventas de equilibrio hacia los costos fijos. El valor de estos últimos son los mismos que los del ejemplo anterior. Además, los valores del eje vertical se encuentran en miles de pesos.
Con el precio dado por (2)
Sustituyendo (15b) en (3), (4b), (5b), (6b), así como desde la (9b) hasta la (12b) , efectuando las operaciones algebraicas correspondientes, se tendrá que todas las expresiones resultantes de dicha sustitución dan las mismas expresiones dadas desde la (17a) hasta la (25a). Además

el cual coincide con el recíproco de (23a), como se dijo en (9b) . Todo esto indica que las ecuaciones que rigen a los precios, así como a las diversas relaciones que surgen entre las partidas que conforman el Estado de Resultados cuando éstos son analizados a través del sistema del equilibrio, son invariantes ante una adecuada transformación del margen de contribución porcentual como una función de la rentabilidad sobre las ventas.
Asimismo, se puede deducir que se tiene un punto mínimo en  ; sin embargo, el valor del margen de contribución porcentual, para este caso, será de r = 1; además, en este punto, se seguirán cumpliendo todas las relaciones dadas por (27a) .
; sin embargo, el valor del margen de contribución porcentual, para este caso, será de r = 1; además, en este punto, se seguirán cumpliendo todas las relaciones dadas por (27a) .
Acotamiento de los costos fijos
Ahora bien, para que (19a) tenga sentido, se puede demostrar que existe un intervalo tal que el denominador de dicha expresión sea estrictamente positivo. Para ello partamos de (23a) que se obtiene de (19a) ; esto es,  . Recordando que w
. Recordando que w  (0, 1) y que √ w > w en dicho intervalo, entonces √w – w > 0. En consecuencia, definimos una función k(w) = √w – w la cual puede ser optimizada; es decir, existe al menos un punto crítico que puede ser un máximo o un mínimo en el dominio de la función definida.
(0, 1) y que √ w > w en dicho intervalo, entonces √w – w > 0. En consecuencia, definimos una función k(w) = √w – w la cual puede ser optimizada; es decir, existe al menos un punto crítico que puede ser un máximo o un mínimo en el dominio de la función definida.
Derivando e igualando a cero para obtener el o los puntos críticos, se obtiene lo siguiente:

Ahora para saber qué tipo de punto crítico es, se procede a derivar nuevamente, evaluándola en el punto crítico anterior y aplicando el criterio de la segunda derivada. Así:
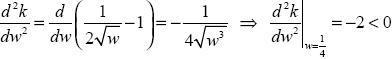
lo cual implica que el punto crítico obtenido es un máximo y el valor de la función es:

de manera que de este último resultado se deduce que los costos fijos tienen como cota superior no sobrepasar el 25% de los ingresos totales. Esto puede verse en la siguiente gráfica:

Surgimiento de la proporción áurea
Ahora bien, debido a que la sustitución de (15a) y (15b) en (2) y (3) , respectivamente, así como en las correspondientes relaciones a cada caso, nos remiten a los mismos resultados, bastará considerar el análisis sin diferenciarlos, excepto para el valor del margen de contribución porcentual, el cual es diferente en cada caso.
Así, se tiene que las ventas dependen, en último de los casos, de la rentabilidad sobre las ventas deseadas, y está dada por (19a), la cual presenta un valor mínimo por ser la función de ventas una función convexa, entonces la misma decrece en el intervalo donde w  (0,
(0, ) obteniendo su valor mínimo cuando w =
) obteniendo su valor mínimo cuando w =  y se vuelve una función creciente cuando w
y se vuelve una función creciente cuando w  (
( ,1) . En todo este intervalo donde w
,1) . En todo este intervalo donde w  (0,1) la utilidad es una función creciente.
(0,1) la utilidad es una función creciente.
Por otra parte, y de acuerdo con (26a) , las ventas de equilibrio se comportan como una función decreciente en dicho intervalo, tendiendo asintóticamente a los costos fijos, los cuales son alcanzados por la utilidad cuando w =  . Por lo tanto, existe un punto de intersección entre las curvas de utilidad y la de las ventas de equilibrio en el intervalo donde w
. Por lo tanto, existe un punto de intersección entre las curvas de utilidad y la de las ventas de equilibrio en el intervalo donde w  (
( , 1) (o bien r
, 1) (o bien r 
 en la siguiente gráfica:
en la siguiente gráfica:
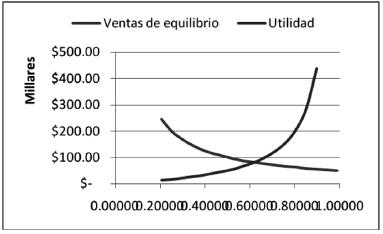
Para calcular dicho punto, hagamos U = Ve y recurramos a (19a) y (20a) . Así:
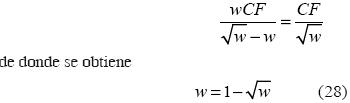
la cual se puede interpretar como una ecuación de punto fijo, f(w) = w , cuya solución da por resultado:

De estos dos puntos fijos, únicamente w1  (0,1) , más aún, w1
(0,1) , más aún, w1  (
( ,1). Si ahora recordamos que la proporción áurea o número de oro está dado por
,1). Si ahora recordamos que la proporción áurea o número de oro está dado por  , entonces la solución a (28) se puede expresar como:
, entonces la solución a (28) se puede expresar como:

lo cual implica que el margen de contribución porcentual a emplear en (15a) tendrá que ser:

Para el margen de contribución porcentual dado por (15b), se tiene que
r1= φ
Ahora sustituyendo (29) y (30) , desde la (17a)hasta la (24a) , se tiene que:
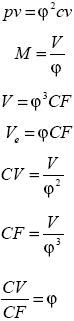
Ahora, se determina el tipo de estabilidad que presenta la función ƒ(w) = 1 – √w, la cual es continuamente diferenciable en el punto fijo encontrado w1. Para ello, derivemos dicha función y evaluémosla en w1 . Así:
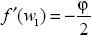
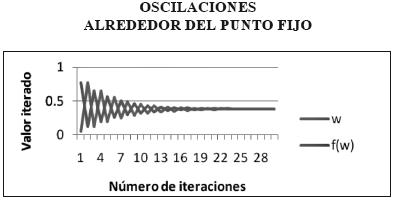
luego entonces, de acuerdo con un criterio de estabilidad local, se tiene que

lo cual implica que el valor dado por (30) es un punto hiperbólico asintóticamente estable. Esto puede observarse en la siguiente gráfica.
Comentarios finales
En la elaboración de este trabajo se logró encontrar una base matemática para calcular la relación de aportación que debe incorporarse al costo variable unitario para formar el precio de venta de un artículo, el cual se calculó de dos diferentes maneras.
Este margen de contribución porcentual, expresado como una función de la rentabilidad sobre las ventas, y diferente en cada uno de los dos casos analizados, cuando es sustituido en las expresiones correspondientes a los mismos, se obtiene de ecuaciones y relaciones idénticas.
En otras palabras, de los cálculos que he efectuado con las formas generales de los precios dados por (2) y (3) , donde en esta última también se obtiene una relación entre la rentabilidad y la relación de aportación, ambas muy diferentes en forma, pero convergiendo a los mismos resultados en cuanto a qué, para productos con el mismo costo variable unitario y considerando los mismos costos fijos, obtenemos idénticas expresiones para la fijación de precios, ventas por obtener, ventas de equilibrio, etc., no es más que un indicativo de la existencia de una invariancia (simetría) ante el uso de una función optimizada que involucre la relación entre el margen de contribución porcentual y la rentabilidad sobre las ventas deseadas.
Como consecuencia, cuando se utiliza esta función en todas las relaciones que involucran al margen de contribución porcentual, se obtienen los siguientes resultados:
1. La función de ventas, dependiente de la rentabilidad, es una función convexa. Por lo tanto, presenta un mínimo.
2. El apalancamiento operativo es igual al recíproco de la raíz cuadrada de la rentabilidad sobre las ventas.
3. La razón del costo variable total a los costos fijos es igual al apalancamiento operativo.
4. El costo variable total es igual al punto de equilibrio.
5. Los costos fijos tienen impuesta una cota superior: no deben sobrepasar el 25% de los ingresos totales.
6. Existe un punto de intersección entre el costo variable total y la utilidad de operación esperada, el cual da por resultado, invariablemente, un punto fijo asintóticamente estable igual al recíproco del cuadrado de la proporción áurea, y que representará la máxima rentabilidad sobre ventas por obtener.
Más aún, el surgimiento de la media áurea como un punto de estabilidad parece apoyar la existencia de un atractor que impide que el margen de contribución porcentual, y por ende los precios y demás partidas en las cuales entra en juego, sea arbitrario y hasta caótico cuando la ambición del hombre se desborda. Asimismo, y en último caso, le confiere una propiedad estética o armónica al sistema de equilibrio.
Por último, y para reforzar lo anterior, consideré los casos más completos en donde los costos variables unitarios los separo en aquellos que dependen de la producción o compra directa (cv) , de aquellos que dependen del precio o volumen, y que son representados como un porcentaje de los mismos (t) , tal como pueden ser las comisiones sobre ventas. Las expresiones para los precios dados por (2) y (3) , en su forma más general, son, respectivamente:

y cuyos respectivos márgenes de contribución porcentuales, son:

Nuevamente, cuando son sustituidos, se obtienen relaciones y resultados análogos a los ya analizados en el presente trabajo, teniendo como punto fijo asintóticamente estable al recíproco del cuadrado de la proporción áurea.
Referencias
Tucker, Spencer A. (1975). El sistema del equilibrio, instrumento para la planificación de utilidades. 4ª. ed. México: Herrero Hermanos Sucs. [ Links ]
Weston, J. Fred y Thomas E. Copeland (1990). Finanzas en administración. 3a. ed., México: McGraw–Hill. [ Links ]
Elaydi, Saber N. (2000). Discrete Chaos. EE.UU.: Chapman & Hall/CRC. [ Links ]
Livio, Mario (2007). La proporción áurea, la historia de PHI, el número más sorprendente del mundo. Madrid: Ariel. [ Links ]














