Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Contaduría y administración
versión impresa ISSN 0186-1042
Contad. Adm no.232 Ciudad de México sep./dic. 2010
Artículos de investigación
Efectos del tipo de cambio sobre el déficit público: modelos de simulación Monte Carlo
Exchange rate effects on public budget: Monte Carlo simulation models
Abigail Rodríguez Nava* y Francisco Venegas Martínez**
* Universidad Autónoma Metropolitana, Xochimilco abigail.rn@prodigy.net.mx
** Escuela Superior de Economía, Instituto Politécnico Nacional fvenegas1111@yahoo.com.mx
Fecha de recepción: 08.04.2008
Fecha de aceptación: 10.08.2009
Resumen
En este documento se estudian los efectos de las variaciones del tipo de cambio sobre el déficit público. Para ello, se extienden los modelos deterministas del balance público, incorporando como supuestos que la variación del tipo de cambio puede describirse mediante un proceso estocástico, y que sus movimientos extremos y repentinos siguen un proceso Poisson; las ecuaciones que describen la dinámica de las fluctuaciones del tipo de cambio se construyen en analogía con los procesos Ornstein–Uhlenbeck y de raíz cuadrada. Con estos supuestos, y mediante simulación Monte Carlo, se estima la variación del tipo de cambio peso–dólar estadounidense y el déficit público asociado para la economía mexicana entre 1990 y 2008. Los resultados obtenidos son consistentes con la evidencia empírica real de esos años, esto indica que la metodología sugerida puede ser útil como herramienta ex ante para la determinación del presupuesto público.
Palabras clave: tipo de cambio, déficit público, procesos estocásticos, simulación Monte Carlo.
JEL: E47, E62, E65
Abstract
This paper is aimed at studying the effects of the exchange–rate variations on the budget deficit. To do this, the available deterministic models of budget deficit are extended by assuming that the movements of the exchange rate are driven by stochastic processes, and that the extreme and sudden changes are governed by a Poisson process. The equation that describes the exchange–rate dynamics is building by using an analogy with both the Ornstein–Uhlenbeck and the square root processes. Under the above assumptions and by using Monte Carlo simulations the variations of the peso–dollar exchange rate and the public deficit are estimated for the Mexican economy, between 1990 and 2008. The obtained results are consistent with the empirical evidence found on such a period; this indicates that the suggested methodology can be useful as an ex–ante tool to establish the budget public.
Key words: Exchange rate, budget deficit, stochastic processes, Monte Carlo simulation.
JEL: E47, E62, E65
Introducción
Generalmente se asume, por lo general, que las variaciones del tipo de cambio guardan una relación directa con el déficit público, en el sentido de que un incremento en el tipo de cambio invariablemente conduce al crecimiento del déficit. Este criterio ignora la participación conjunta de otras variables relevantes como la inflación y las tasas de interés nacional y externa. Asimismo, los estudios del balance presupuestal son, por lo común, miradas retrospectivas de los hechos acontecidos, que aunque son muy valiosos para entender la evolución de las finanzas públicas en conjunto con otros indicadores macroeconómicos, dejan de lado la modelización de escenarios posibles. Derivado de este hecho, casi siempre se considera que los factores que inciden en el déficit público son variables deterministas, es decir, variables cuyas magnitudes son totalmente conocidas.
El propósito principal de este documento es determinar los efectos de las variaciones del tipo de cambio sobre el balance público, atendiendo su relación con otros precios y en los casos determinista y estocástico. Para ello, a partir de las ecuaciones tradicionales empleadas para medir el déficit público, se propone un conjunto de ecuaciones estocásticas del balance público; éstas toman como supuestos principales que es posible modelar las variaciones del tipo de cambio de manera similar a la formalización de la dinámica de la tasa corta de interés, según un proceso Ornstein–Uhlenbeck; y que las variaciones extremas y repentinas del tipo de cambio se asocian con procesos Poisson. Con esto, se pretende contribuir a la definición de la dinámica del tipo de cambio —debido a que comúnmente se supone la acción estática de esta variable— y a sus efectos en el balance público.
La propuesta teórica se complementa con ejercicios de simulación Monte Carlo con los que se modelan las fluctuaciones del tipo de cambio peso mexicano–dólar estadounidense, y por extensión se generan los resultados correspondientes al balance público. A través de este desarrollo empírico se evalúa si la propuesta teórica es coherente con los resultados deterministas del balance público calculados para la economía mexicana entre enero de 1992 y diciembre de 2008.
Con la propuesta teórica y la metodología empírica sugerida se realizan dos contribuciones importantes: 1. Se extiende el escenario tradicional determinista que sólo evalúa los resultados del déficit público considerando como base las magnitudes observadas y conocidas de variables relevantes; en la investigación se muestra la posibilidad de elaborar estudios sobre la dinámica que siguen los principales precios (en este caso, las variaciones del tipo de cambio) y sus efectos sobre el déficit público, justamente cuando la magnitud de algunos precios no se conoce con certeza. 2. El principal beneficio de modelar las fluctuaciones del tipo de cambio y examinar sus efectos sobre el déficit público se halla en la posibilidad de realizar este tipo de estimaciones de forma ex ante a la determinación del presupuesto público anual; así, se tendría un mejor conocimiento de la dinámica de las variables que inciden en el déficit, se reducirían las constantes adecuaciones al presupuesto público programado que se efectúan en el transcurso del año, y con ello se evitaría lesionar a los programas sociales (los principales afectados de los recortes presupuestales) bajo la meta de cuidar el balance presupuestal.
Este trabajo se encuentra organizado de la siguiente manera: en la sección dos se exponen las principales contribuciones teóricas y empíricas que intentan explicar la dinámica del tipo de cambio —o de sus fluctuaciones—, así como su influencia en la magnitud del balance público; en la sección tres se presenta el modelo tradicional para calcular el déficit público, además, se propone la formalización de las variaciones del tipo de cambio a partir de procesos estocásticos específicos y se establecen las ecuaciones estocásticas correspondientes del balance público; en la sección cuatro se estudia la evolución del tipo de cambio peso–dólar estadounidense y del déficit público en la economía mexicana entre los años 1992 y 2008; en la sección cinco se desarrollan los ejercicios de simulación Monte Carlo y se comparan los resultados con los obtenidos previamente en el caso determinista.
Antecedentes teóricos
En la literatura vinculada con el estudio del déficit público son relevantes las siguientes líneas de investigación: 1. examen de la sostenibilidad del déficit público; 2. evaluación de los impactos de la política fiscal en el crecimiento y desarrollo; 3. alternativas para el financiamiento del déficit público; 4. factores determinantes del déficit público o de la deuda pública. A continuación se presenta una revisión de la literatura teórica y empírica relevante asociada con la última línea de investigación, en particular, los casos en que se asocia el comportamiento del tipo de cambio al balance público, y las alternativas sugeridas para representar la dinámica de las fluctuaciones del tipo de cambio.
Aunque es amplia la literatura que examina los determinantes del déficit público o de la deuda pública, son menos los estudios que puntualmente analizan su vinculación con el tipo de cambio. Entre estas contribuciones se encuentra la de Penati (1983), su objetivo es examinar si la política fiscal expansiva altera al tipo de cambio; en su propuesta asume que éste se determina de acuerdo con la hipótesis de expectativas estáticas, es decir, el tipo de cambio esperado en un periodo futuro t + 1, es justamente el tipo de cambio observado en el periodo t. La tasa de interés nominal doméstica se supone que depende de la tasa externa y de la expectativa del tipo de cambio. Penati sugiere que la magnitud y el signo de la relación entre la política fiscal expansiva y el tipo de cambio dependen, entre otros elementos, de los efectos sobre el producto real y los precios, de las expectativas sobre la deuda externa y de las posibilidades de sustitución entre activos, denominados en diferentes monedas.
Hnatkovska, Lahiri y Vegh (2008) mediante un modelo de optimización para una economía pequeña y abierta examinan la vinculación entre las tasas de interés y el tipo de cambio, así como sus efectos sobre algunas variables macroeconómicas. Deducen que el incremento de las tasas de interés ocasiona el incremento de depósitos y de la base monetaria, la reducción en el producto, el incremento de la carga fiscal para el gobierno y expectativas de creciente inflación entre el público. Estos resultados se comprueban en el caso estadounidense utilizando funciones impulso–respuesta de modelos de vectores autorregresivos.
Una de las aportaciones más recientes es la de Martin (2009) quien, con base en un modelo de optimización para hogares y gobierno, examina los efectos de variaciones aleatorias del gasto sobre la deuda pública y su vinculación con las motivaciones para controlar la inflación. Este autor sostiene que lejos de los planteamientos tradicionales que representan a la deuda y a los ingresos impositivos como procesos autorregresivos, la evidencia empírica muestra que ambos (la deuda pública y los ingresos) exhiben reversión a la media, lo que sugiere un comportamiento tendencial de largo plazo.
Otras investigaciones centran su interés en examinar la vinculación entre la tasa de interés y el déficit público, por ejemplo, Ono y Shibata (2001) investigan los impactos de la expansión fiscal sobre la tasa de interés mediante un modelo de crecimiento de dos sectores. Encuentran que si la expansión fiscal afecta a los bienes de consumo, la trayectoria de la tasa de interés de largo plazo difiere considerablemente de la de corto plazo; y si la acción fiscal afecta a los bienes que pueden emplearse en consumo e inversión, entonces, las trayectorias de las tasas para ambos plazos son similares. En su trabajo, Kiani (2009) estudia los efectos del déficit público sobre la tasa de interés de corto plazo y la de largo plazo. Muestra que la política monetaria incide en las tasas de corto plazo; pero el déficit público, las expectativas de inflación y las expectativas de rendimiento sobre los costos de capital influyen en mayor grado sobre las tasas de interés de largo plazo.
En otros casos se examina la relación existente entre tasas de interés, tipo de cambio e inflación; por ejemplo, Sutherland (2006) estudia los efectos de las fluctuaciones del tipo de cambio sobre la estructura de plazos de la tasa de interés. En particular, es relevante su formulación de la dinámica del tipo de cambio, como un movimiento browniano de la forma: 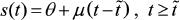 , donde s(t) define al tipo de cambio, θ expresa el tamaño de una devaluación, μ es la tasa esperada de depreciación del tipo de cambio, y
, donde s(t) define al tipo de cambio, θ expresa el tamaño de una devaluación, μ es la tasa esperada de depreciación del tipo de cambio, y  es una fecha específica en que ocurre una crisis (devaluación).
es una fecha específica en que ocurre una crisis (devaluación).
Con respecto al estudio de las variaciones del tipo de cambio, existen las siguientes propuestas para su representación. Entre las pioneras, se encuentra la de Domowitz y Hakkio (1985) quienes investigan la existencia del premio al riesgo en el mercado de tipo de cambio. En su estudio, ellos suponen a partir de la definición convencional de tipo de cambio —número de unidades de moneda doméstica por unidades de moneda extranjera— que la oferta de cada moneda se describe según un proceso estocástico autorregresivo de orden 1.
Hakkio y Leiderman (1986) proponen modelar el tipo de cambio forward como:
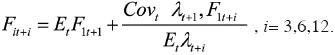
Donde Fit+1 es el tipo de cambio futuro, EtF1t+1 corresponde a la esperanza matemática del tipo de cambio siguiente (o de corto plazo), el segundo término de lado derecho de la ecuación expresa el premio al riesgo que depende de la covarianza condicional en el periodo t, Covt , entre la utilidad marginal λt+l y la tasa forward.
Bazdresch y Werner (2002) buscan explicar el comportamiento de volatilidad del tipo de cambio peso mexicano – dólar estadounidense entre 1995 y 2001. Los autores comparan tres posibilidades de estimación predictiva del tipo de cambio: el valor forward del tipo de cambio, procesos autorregresivos, y un modelo propio en el eme sugieren expresar la dinámica del tipo de cambio mediante la ecuación  donde pi denota la probabilidad de transición entre dos estados posibles.
donde pi denota la probabilidad de transición entre dos estados posibles.
En la literatura financiera existen varios estudios que muestran la conveniencia de representar la dinámica del precio de los activos mediante un proceso browniano y un proceso Poisson. Entre las primeras investigaciones que buscan explicar el comportamiento del tipo de cambio se encuentran la de Ball y Torous (1985); Akgiray y Booth (1986); Khoury y Ghosh (1987); y Akgiray y Booth (1988); en estos casos, los autores demuestran los beneficios de representar la evolución del tipo de cambio combinando un proceso con distribución normal que refleje un comportamiento estable y la distribución Poisson para representar los saltos repentinos que se observan, se asume, la independencia de ambos procesos. Esta caracterización del tipo de cambio ha sido extendida por otros autores con propósitos diferentes; por ejemplo, Chang (2003) busca mayor fidelidad en la representación y utiliza una función bivariada con saltos de Poisson; Venegas (2006), a través de un modelo teórico, demuestra la conveniencia de modelar las variaciones del tipo de cambio como un movimiento browniano con saltos de Poisson porque esto permite examinar los efectos sobre la riqueza y el consumo y el diseño de políticas de estabilización económica ante escenarios inflacionarios. Recientemente, Wang y Tong (2008) extienden esta representación del tipo de cambio para incorporar volatilidad estocástica.
En mayor medida, el proceso de difusión browniano con saltos de Poisson se ha aplicado a la caracterización de la tasa de interés y de instrumentos derivados asociados. Así, por ejemplo, Amin (1993) desarrolla un modelo para valuar opciones financieras extendiendo la propuesta de Cox–Ross–Rubinstein, de modo que el subyacente sigue un proceso browniano con saltos de Poisson (ambos independientes); Arai (2004) utiliza este proceso para encontrar una medida martingala que se asocie a la estrategia de inversión de mínimo riesgo local; en Chernov et al. (1999) el proceso descrito se extiende para permitir que la intensidad del salto sea función del tamaño de los saltos previos y de un factor de volatilidad estocástica; para Chang y Maheu (2002) la representación básica se extiende para modelar la intensidad del salto como un proceso ARMA; Das Sanjiv (1999) extiende la propuesta conocida Heath–Jarrow–Morton para incorporar saltos de Poisson; más tarde este mismo autor (2002) demuestra la viabilidad de explicar la dinámica de las tasas de interés de títulos federales, mediante la combinación independiente de los procesos Gaussiano y Poisson; Kou (2002) utiliza este proceso de difusión combinado para generalizar el precio de las opciones financieras; Stoica (2002) generaliza la formalización básica para demostrar su viabilidad en mercados completos y en presencia de discontinuidades en los coeficientes que definen a los procesos Browniano y Poisson.
Las demostraciones formales que prueban la posibilidad de modelar la dinámica estocástica de activos mediante procesos con distribuciones normal y Poisson no correlacionadas se encuentran en: Duffie y Kan (1996); Duffie (2001); Schönbucher (2003); Duffie y Singleton (2003); Johannes (2004) y en Duffie (2005). En Ahn y Thompson (1988) y en Bouzione (2008) se demuestra además en qué casos es posible combinar un proceso de difusión de raíz cuadrada con un proceso Poisson, manteniendo su independencia.
Balance presupuestal nominal y real
En esta sección se presentan las bases teóricas para determinar el balance público en el caso determinista plenamente conocido y en la extensión estocástica que se propone.
Ecuaciones deterministas del balance público
La medición tradicional para evaluar el balance público es el déficit presupuestal nominal:
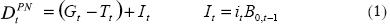
Donde  el déficit presupuestal nominal, Gt corresponde al gasto total público, Tt define el ingreso total público, It expresa el volumen de intereses pagados, it es la tasa efectiva de interés (nominal), y B0,t–1 representa el valor de mercado de la deuda pública total desde el periodo 0 hasta el periodo t–1 (o precio de mercado de la deuda). En la expresión (1) el término entre paréntesis es el déficit primario, en éste el gasto público no incluye el pago de intereses por la deuda contraída. El volumen de intereses está calculado para cada periodo específico t, no se trata del volumen acumulado de intereses desde la fecha inicial 0 hasta la fecha t.
el déficit presupuestal nominal, Gt corresponde al gasto total público, Tt define el ingreso total público, It expresa el volumen de intereses pagados, it es la tasa efectiva de interés (nominal), y B0,t–1 representa el valor de mercado de la deuda pública total desde el periodo 0 hasta el periodo t–1 (o precio de mercado de la deuda). En la expresión (1) el término entre paréntesis es el déficit primario, en éste el gasto público no incluye el pago de intereses por la deuda contraída. El volumen de intereses está calculado para cada periodo específico t, no se trata del volumen acumulado de intereses desde la fecha inicial 0 hasta la fecha t.
Cuando se considera la existencia de deuda externa, y se supone que el volumen de intereses se calcula a partir de una tasa de interés efectiva en capitalización simple, se reescribe (1) como:

Donde 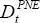 es el déficit presupuestal nominal con sector externo, B0,t–1 es el valor de mercado de la deuda pública interna desde el periodo 0 hasta el periodo t–1,
es el déficit presupuestal nominal con sector externo, B0,t–1 es el valor de mercado de la deuda pública interna desde el periodo 0 hasta el periodo t–1,  es el valor de mercado de la deuda pública externa desde el periodo 0 hasta el periodo t–1, it es la tasa efectiva de interés nacional,
es el valor de mercado de la deuda pública externa desde el periodo 0 hasta el periodo t–1, it es la tasa efectiva de interés nacional,  es la tasa efectiva de interés extranjera, y gt es el tipo de cambio nominal (unidades de moneda nacional por unidades de moneda extranjera).
es la tasa efectiva de interés extranjera, y gt es el tipo de cambio nominal (unidades de moneda nacional por unidades de moneda extranjera).
Por otro lado, el déficit presupuestal real, sin considerar deuda externa se define como:

Donde  es el déficit presupuestal real, Ρt representa el nivel general de precios, Dt equivale a la deuda total monetaria y no monetaria, B0,t–1 expresa la deuda no monetaria, M0,t–1 denota la deuda monetaria y πt es la tasa de inflación. La ecuación (3) establece que el déficit presupuestal real es igual al balance primario real más el pago por intereses de la deuda no monetaria (utilizando una tasa de interés nominal), menos el componente inflacionario de la deuda no monetaria, menos el impuesto inflacionario o componente inflacionario de la deuda monetaria. El tercer término es relevante porque indica que en presencia de inflación, parte del costo financiero o de los intereses que se pagan por la deuda, son en realidad pagos de amortización. Si se utiliza la relación entre las tasas de interés real xt y nominal it :
es el déficit presupuestal real, Ρt representa el nivel general de precios, Dt equivale a la deuda total monetaria y no monetaria, B0,t–1 expresa la deuda no monetaria, M0,t–1 denota la deuda monetaria y πt es la tasa de inflación. La ecuación (3) establece que el déficit presupuestal real es igual al balance primario real más el pago por intereses de la deuda no monetaria (utilizando una tasa de interés nominal), menos el componente inflacionario de la deuda no monetaria, menos el impuesto inflacionario o componente inflacionario de la deuda monetaria. El tercer término es relevante porque indica que en presencia de inflación, parte del costo financiero o de los intereses que se pagan por la deuda, son en realidad pagos de amortización. Si se utiliza la relación entre las tasas de interés real xt y nominal it :
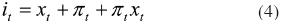
Entonces, podemos reescribir (3) en términos de la tasa real como:

Si en el total de la deuda, se distingue entre la interna y la externa, entonces, el déficit real es:

Considerando ahora que B0,t–1 representa la deuda no monetaria interna y  la deuda externa. Si se define la variación del tipo de cambio como:
la deuda externa. Si se define la variación del tipo de cambio como:
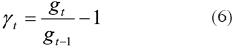
Y la de tasa de inflación como:
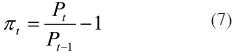
Entonces, el déficit real con sector externo es:
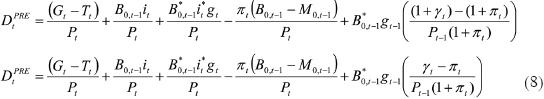
Al observar las ecuaciones (2) y (8), referentes al balance presupuestal nominal y real a partir de la tasa de interés nominal externa, inmediatamente se aprecia que un incremento del tipo de cambio gt , o una variación positiva del tipo de cambio γ , tomando como dadas todas las demás variables, siempre conduce al incremento del déficit público. Esto se deduce formalmente si de las ecuaciones señaladas se observan los signos de las derivadas parciales siguientes:


Comportamiento estocástico del tipo de cambio y de sus variaciones
Como es conocido, en el texto "Racional Theory of Warrant Prices" Samuelson (1965) propuso que la dinámica del precio de un activo puede caracterizarse a través de la ecuación diferencial estocástica del movimiento geométrico browniano:
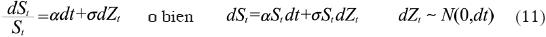
Donde St es el precio del activo, α es el rendimiento esperado instantáneo, σ es la varianza del rendimiento y Zt es un proceso Browniano. Alternativamente, Vasicek en el artículo "An Equilibrium Characterization of the Term Structure" (1977) representa a la tasa de interés como un proceso estocástico con reversión a la media, tal que:

Es decir, la tasa de interés fluctúa en torno a su nivel promedio de largo plazo b, si ocurre que rt > b la tasa de interés tiende a disminuir, y si rt < b la tasa de interés tiende a aumentar; la velocidad de ajuste está determinada por a.
En la propuesta de Cox, Ingersoll y Ross (1985), conocida como modelo CIR:
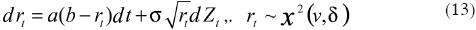
Aquí la tasa de interés se distribuye como una variable aleatoria χ2 con v grados de libertad y parámetro de no centralidad δ. El proceso descrito en (13) se caracteriza porque la tasa de interés exhibe un proceso de reversión a la media (similar al modelo de Vasicek), sus valores son siempre positivos, y la varianza es proporcional a las fluctuaciones de la tasa de interés.
Como se indicó anteriormente, uno de los propósitos es modelar la dinámica de las variaciones del tipo de cambio peso mexicano – dólar estadounidense, es decir, interesa modelar γt; no se modela el tipo de cambio per se, gt. Esto es importante porque, evidentemente, la dinámica de los precios (como es el tipo de cambio) se representa con mayor fidelidad a través de un proceso estocástico de raíz cuadrada pues ello impide obtener valores negativos en la variable subyacente estimada. Sin embargo, cuando se representa la variación del subyacente, en lugar de su magnitud, es perfectamente posible que esta fluctuación sea positiva o negativa y, en consecuencia, puede emplearse para su representación un proceso Ornstein–Uhlenbeck.
En la sección dos de este trabajo se hizo referencia a estudios recientes que han evaluado la conveniencia de modelar las variaciones en precios a través de la combinación de un proceso Browniano y uno Poisson. Con base en estos estudios, en esta investigación se representa la variación del tipo de cambio a partir del Proceso Ornstein–Uhlenbeck con saltos de Poisson como:

Esta ecuación indica que la variación del tipo de cambio fluctúa en torno a su nivel promedio de largo plazo b, con una velocidad de ajuste a, si γt > b la variación del tipo de cambio tiende a disminuir, si γt < b la variación tiende a aumentar. Zt es un proceso Wiener estandarizado (Zt muestra incrementos normales independientes, esperanza matemática cero y varianza dt), dNt es un proceso Poisson homogéneo (su intensidad es independiente del tiempo), λ equivale a la intensidad de un salto de Poisson y η representa el tamaño medio esperado del salto. Los procesos esto–cásticos incluidos en (14) no están correlacionados. Alternativamente, si se utiliza un proceso de raíz cuadrada con saltos de Poisson:

La variación del tipo de cambio se distribuye como una variable aleatoria χ2 con v grados de libertad y parámetro de no centralidad δ. A diferencia de la ecuación (14), aquí la varianza es proporcional a las variaciones del tipo de cambio.
Ecuaciones estocásticas del balance público
Con el fin de estudiar los efectos de las fluctuaciones del tipo de cambio en escenarios no deterministas, se incorporan los procesos Ornstein–Uhlenbeck y de raíz cuadrada, ambos con saltos de Poisson (14) y (15) en las ecuaciones del balance presupuestal cuando se considera la presencia de deuda externa. Para ello, se usa en principio la relación de paridad entre una tasa de interés nacional y una extranjera, esta ecuación establece que:

Entonces, a partir de (2):
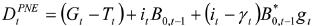
Cuando la variación del tipo de cambio se comporta según el proceso Ornstein–Uhlenbeck con saltos de Poisson, el déficit presupuestal nominal evoluciona como:
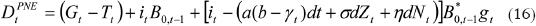
Y si la variación del tipo de cambio sigue un proceso de raíz cuadrada con saltos de Poisson:

Similarmente, para el déficit presupuestal real, si la variación del tipo de cambio se representa como el proceso Ornstein–Uhlenbeck con saltos de Poisson:

Y si la variación del tipo de cambio se representa mediante un proceso de raíz cuadrada con saltos de Poisson, el déficit presupuestal real es:

En la sección cinco se determinan los efectos de las variaciones del tipo de cambio en el déficit público cuando ambos se modelan de forma estocástica, de acuerdo con las ecuaciones (16) a (19).
Déficit público y tipo de cambio en México
Entre las mediciones oficiales del balance público en México destaca la del balance económico, que corresponde a la definición teórica de balance presupuestal nominal.1 En esta investigación se calcula el balance económico primero, sin distinguir entre deuda externa e interna, y después se consideran cada una de ellas; es decir, se calculan las ecuaciones deterministas (1) y (2).
El concepto oficial en el que sí se reconoce la influencia del tipo de cambio y de la inflación es el balance operacional ajustado; sin embargo este concepto es poco útil en la práctica porque no se dispone de series estadísticas para todos sus componentes y, en otros casos, hay diferencias en los periodos de registro. Por ello, en su lugar primero se calcula el balance real, sin distinguir la deuda externa de la interna, y luego atendiendo tal diferencia.2
Los cálculos de los cuatro balances se efectuaron de forma mensual y anual, para la economía mexicana entre 1992 y 2008. Se utilizaron las siguientes series:
a) Gasto total presupuestario del sector público. Se desglosa en gasto programable y no programable. El gasto programable incluye al Gobierno Federal y a los organismos y empresas de control presupuestario directo: Petróleos Mexicanos (PEMEX), Comisión Federal de Electricidad (CFE), Luz y Fuerza del Centro (LFC), Instituto Mexicano del Seguro Social (IMSS) y del Instituto de Seguridad y Servicios Sociales de los Trabajadores del Estado (ISSSTE). En el gasto no programable se incluyen las participaciones a entidades federativas, los Adeudos de Ejercicios Fiscales Anteriores (Adefas) y el costo financiero por la deuda pública (o pago de intereses).3
b) Ingreso total presupuestal. Incluye ingresos tributarios y no tributarios del Gobierno Federal, y los ingresos de organismos y empresas públicos incluso Petróleos Mexicanos (PEMEX), excluye Lotería Nacional (Lotenal) y Caminos y Puentes Federales (Capufe).
c) Deuda económica amplia. Agregado de la deuda externa e interna, del Gobierno Federal, del sector paraestatal y de los intermediarios financieros reconocidos.
d) Valores públicos. Se refiere a la deuda no monetaria, resultante de la emisión de títulos por el Banco de México, el Instituto para la Protección al Ahorro Bancario (IPAB), y el Gobierno Federal. La serie se desglosa en valores en poder de residentes y en poder de no residentes.
e) Base monetaria. Agregados monetarios M1 (billetes y monedas en circulación) y M2 (depósitos de corto plazo).
f) Tasa de inflación nacional. Variación mensual del Índice Nacional de Precios al Consumidor.
g) Tipo de cambio nominal pesos por dólar estadounidense. Tipo de cambio para solventar obligaciones en moneda extranjera (valor de acuerdo con la fecha de determinación).
Los resultados del balance público se presentan en el cuadro 1 con respecto al déficit económico, en general (excepto en los años 2000, 2001 y 2005), la medición que incluye al sector externo es más favorable que en el caso en que no se considera, en el sentido de que los superávit son mayores o los déficit menores. El resultado del balance económico con sector externo es mejor (el déficit es menor y el superávit es mayor) porque al distinguir entre deuda interna y externa se agrega al déficit primario los términos 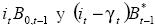 cuya suma es considerablemente menor que si se considerara la deuda en su conjunto multiplicada por la tasa de interés. En los casos atípicos de los años 2000, 2001 y 2005, en los cuales el déficit es mucho mayor al considerar el sector externo, la variación del tipo de cambio fue negativa, es decir, en promedio hubo apreciación en esos años. Esto puede comprobarse con los datos del cuadro 2.
cuya suma es considerablemente menor que si se considerara la deuda en su conjunto multiplicada por la tasa de interés. En los casos atípicos de los años 2000, 2001 y 2005, en los cuales el déficit es mucho mayor al considerar el sector externo, la variación del tipo de cambio fue negativa, es decir, en promedio hubo apreciación en esos años. Esto puede comprobarse con los datos del cuadro 2.
Otro elemento relevante es que la mayor diferencia entre los resultados del balance económico con sector externo y sin él, se encuentra en los años en que es mayor la proporción de la deuda externa en la deuda total. Los saldos del balance real son casi semejantes cuando se ignora la deuda externa y cuando sí se le considera. Es relevante que en los años donde el balance real con deuda externa supera al balance en que se desconoce, la variación del tipo de cambio es mayor que la tasa de interés de ese mismo periodo (excluyendo 1992 y los tres años en que se aprecia el tipo de cambio).
También debe tomarse en cuenta que gran parte del superávit de los años 1991 a 1994 se debe a la inclusión en el ingreso presupuestal de los recursos obtenidos por la privatización de la empresa Teléfonos de México (Telmex), y de las instituciones de banca múltiple. Asimismo, los saldos favorables del balance real de 1994 a 1998 reflejan el hecho de que la tasa de inflación fue superior a la tasa de interés nominal.
Simulación Monte Carlo del tipo de cambio y del gasto público
Para efectuar los ejercicios de simulación, en primer lugar, con base en la serie diaria del tipo de cambio (pesos mexicanos por dólar estadounidense) para solventar obligaciones en moneda extranjera, se calcularon sus variaciones, lo cual permitió identificar dos periodos de distinto comportamiento de las fluctuaciones del tipo de cambio. En el primero, de enero de 1992 a diciembre de 1999, la desviación estándar de las variaciones fue de 0.0100; en el segundo periodo, de enero de 2000 a diciembre de 2008, la desviación estándar fue de 0.0047; claramente, la volatilidad del tipo de cambio en este segundo periodo es menor, a pesar de que en el último año se observó mayor inestabilidad.
En el primer periodo se consideró que el número de saltos de Poisson dNt es el número de observaciones que superan cuatro desviaciones estándar (por encima o por debajo de la media); para el segundo periodo se consideraron tres desviaciones estándar; el número de saltos por unidad de tiempo Nt siempre es uno. La intensidad del salto λ, se calculó como el número de saltos totales por unidad de tiempo entre el total de observaciones n; es decir: λ= dNt t/n. El tamaño medio esperado del salto η, se calculó como la varianza del proceso Poisson por unidad de tiempo entre el número de saltos totales, es decir: η= λt /dNt .
Una vez calculadas las variables asociadas al proceso Poisson, se determinaron los otros parámetros (presentados en el Cuadro 3) de los procesos estocásticos que representan la variación del tipo de cambio, es decir de las ecuaciones (14) y (15); esto se realiza mediante modelos de regresión lineal por mínimos cuadrados ordinarios. La ecuación correspondiente al proceso Ornstein – Uhlenbeck sin saltos de Poisson, escrita en términos discretos es:

Donde β0 — ab , β1 = (1 — a) , β0 y β1 son estimadores de mínimos cuadrados ordinarios, los parámetros deseados son:  El proceso de raíz cuadrada, sin saltos de Poisson, se escribe en forma alternativa como:
El proceso de raíz cuadrada, sin saltos de Poisson, se escribe en forma alternativa como:
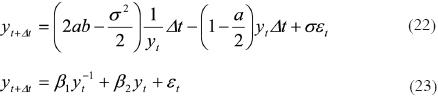
Donde, se utilizó el cambio de variable yt =  aquí
aquí  entonces,
entonces,

Con base en los parámetros estimados, se efectúa la simulación Monte Cario del déficit público. El propósito es simular las trayectorias de evolución de las mediciones representativas del balance público en México, y comparar los resultados con las cifras reales ya calculadas. Específicamente se simulan las ecuaciones (14) a (15) correspondientes a las variaciones del tipo de cambio, y luego las ecuaciones (16) a (19) del balance público. En la simulación se sigue este procedimiento:
a) Se generan n series, cada una de 10 000 números aleatorios con distribución uniforme; luego, se hallan los números aleatorios con distribución normal mediante el método Box – Muller:

b) Se simula la variación del tipo de cambio en cada momento del tiempo recursivamente, usando los parámetros obtenidos. Se utilizan para el proceso Ornstein – Uhlenbeck y el de raíz cuadrada:
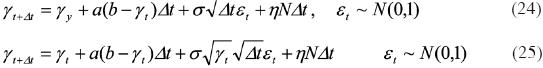
c) Para cada trayectoria se calcula el promedio de las variaciones del tipo de cambio.
d) Se calcula el déficit público utilizando las variaciones promedio del tipo de cambio, de acuerdo con las ecuaciones (16) a (19) se usan los valores promedio como proporción del PIB de Gt , It ,Bt ,
y el valor promedio de πt , y de it , ésta se dedujo como la tasa implícita en el costo financiero.
e) Se calcula el promedio de las n trayectorias del déficit público, este promedio representa la estimación del balance público respectivo para el periodo t.
f) Se repiten los pasos d y e, para cada uno de los t periodos.
En la gráfica 3 se presenta un ejemplo de la simulación Monte Carlo de las variaciones del tipo de cambio, cuando siguen un proceso estocástico tipo Ornstein–Uhlenbeck, con saltos de Poisson. En el cuadro 4 se muestran los resultados para el déficit público simulado, como proporción del PIB, en los casos en que la variación del tipo de cambio se representa mediante el proceso Ornstein–Uhlenbeck y cuando se representa mediante el proceso de raíz cuadrada. En el cuadro 5 se presentan las diferencias entre los resultados observados y los simulados, solamente cuando las mediciones del balance público sí hacen explícita la deuda externa.
Al comparar los resultados de las simulaciones con los obtenidos a partir de datos verídicos encontramos en primer lugar que aunque ambos son consistentes, la estimación del déficit económico difiere del cálculo real entre 1% y 7% (excepto en 1995 cuando la simulación difiere considerablemente de los resultados observados), mientras que la estimación del déficit real sólo difiere del dato efectivamente observado en 0.5% como máximo. Esto indica que la simulación es más efectiva en aquellos casos donde las variables son ajustadas por la tasa de inflación.
En casi todos los periodos la variación simulada del tipo de cambio es menor en casi todos los periodos, que la observada, excepto entre los años 2006 y 2008. También se encontró que para el primer periodo (enero de 1992 a diciembre de 1999), cuando se observa mayor volatilidad en las fluctuaciones del tipo de cambio, la simulación mediante el proceso Ornstein–Uhlenbeck subestima en mayor grado estas variaciones que el proceso de raíz cuadrada (0.3% menos respecto con el promedio de las variaciones y 0.1%, respectivamente). En cambio, en el segundo periodo de baja volatilidad (enero de 2000 a diciembre de 2008), la simulación mediante el proceso Ornstein–Uhlenbeck sobrestima la variación del tipo de cambio, mientras que el proceso de raíz cuadrada la subestima (en 0.3% y 0.2%, respectivamente).
Al comparar los resultados observados con los simulados para el cálculo del balance público se encuentra que en el caso del déficit económico, el modelo de raíz cuadrada con saltos de Poisson es más próximo a los datos reales en el periodo de mayor variación del tipo de cambio. El modelo Ornstein–Uhlenbeck genera las mejores aproximaciones en los años de menor fluctuación del tipo de cambio. En el caso del déficit real, ambos modelos proporcionan resultados semejantes en los dos periodos.
Conclusiones
En este documento se presentaron las ecuaciones tradicionales más representativas para el cálculo del balance presupuestal, las mediciones comunes determinan los resultados del balance público de forma determinista, es decir, una vez conocidas las magnitudes de todas las variables macroeconómicas relevantes. En la investigación, se recuperaron los procesos estocásticos más utilizados para modelar los precios; en la moderna literatura económica y financiera es común que los precios de los activos, fundamentalmente de la tasa de interés, se representen por procesos de difusión en los que se combine un proceso Browniano y uno de saltos de Poisson.
Con estas bases, la investigación se concentró en modelar las variaciones del tipo de cambio (no su magnitud) pesos mexicanos por dólar estadounidense, mediante los procesos estocásticos Ornstein–Uhlenbeck y de raíz cuadrada, ambos con saltos de Poisson. Al estimar las variaciones del tipo de cambio fue posible entonces construir ecuaciones estocásticas del balance público en las que justamente se desconoce con precisión la variación del tipo de cambio y en su lugar sólo se conoce la ecuación que representa su dinámica. Una vez determinados los procesos estocásticos, se diseñó un procedimiento específico para la simulación del déficit económico y del déficit real, recuperando los métodos de simulación Monte Carlo.
Los resultados de las simulaciones del déficit público se contrastaron con los obtenidos a partir de los datos verídicos. Principalmente, se observó que la simulación más precisa es la del déficit real. Asimismo, se encontró que la representación más cercana a la realidad de las variaciones del tipo de cambio es el proceso Ornstein–Uhlenbeck con saltos de Poisson en los años de mayor fluctuación del tipo de cambio; y durante la mayor estabilidad, la mejor simulación corresponde al proceso de raíz cuadrada con saltos de Poisson.
La investigación realizada es una propuesta encaminada a incentivar la realización de estudios de simulación del déficit público de manera ex ante a la determinación del presupuesto público. Si se conocen estimaciones de las posibles variaciones en las variables relevantes que inciden en el balance público, sería posible aminorar las alteraciones repentinas en el programa presupuestal, que afectan generalmente a los proyectos sociales.
Referencias
Ahn, C. M. y Thompson, H. (1988). "Jump Diffusion Processes and the Term Structure of Interest Rates", Journal of Finance, No. 43, pp. 155–174. [ Links ]
Ahn, C. M. y Thompson, H. (1992). "The impact of jump risks on nominal interest rates and foreign exchange rates", Review of Quantitative Finance and Accounting, No. 2, pp. 17–31. [ Links ]
Akgiray, V. y Booth, G. (1986). "Stock price processes with discontinuous time paths: An empirical examination", The Financial Review, No. 21, pp. 163–184. [ Links ]
–––––––––– (1988). "Mixed – diffusion jump process modeling of exchange rate movements", The Review of Economics and Statistics, Vol. 70, No. 4, pp. 631–637. [ Links ]
Amin, K. I. (1993). "Jump diffusion option valuation in discrete time", The Journal of Finance, Vol. 48, No. 5, pp. 1833–1863. [ Links ]
Arai, T. (2004). "Minimal Martingale Measures for Jump Diffusion Processes", Journal of Applied Probability, Vol. 41, No. 1, pp. 263–270. [ Links ]
Ball, C. A. y Torous, W. N. (1985). "On jumps in stock prices and their impact on call pricing", Journal of Finance, No. 40, pp. 337 – 351. [ Links ]
Bazdresch, S. y Werner, A. (2002). "El comportamiento del tipo de cambio en México y el Régimen de libre flotación: 1996 – 2001", Documento de Investigación 2002–09, Banco de México. [ Links ]
Blejer, M. I. y Cheasty, A. (1991). "The Measurement of Fiscal Deficits: Analytical and Methodological Issues", Journal of Economic Literature, Vol. 29, No. 4, pp. 1644–1678. [ Links ]
Bouzione, M. (2008). Pricing Interest Rates Derivatives, Serie: Lecture Notes in Economics and Mathematical Systems, Springer – Verlag, Alemania. [ Links ]
Chang, W. H. (2003). "A correlated bivariate Poisson jump model for foreign exchange", Empirical Economics, No. 28, pp. 669 – 685. [ Links ]
–––––––––– y Maheu, J. M. (2002). "Condicional jump dynamics in stock market returns", Journal of Business and Economic Statistics, No. 20, pp. 377–389. [ Links ]
Chernov, M.; Gallant, A. R.; Ghysels, E. y Tauchen, G. (1999). "A new class of stochastic volatility models with jumps: theory and estimation", Working Paper, CIRANO. [ Links ]
Cox, J. C.; Ingersoll, J. E. y Ross, S. A. (1985). "A Theory of the Term Structure of Interest Rates", Econometrica, Vol. 53, No. 2, pp. 385–407. [ Links ]
Das Sanjiv, R. (1999). "A direct discrete time approach to Poisson – Gaussian bond option pricing in the Heath – Jarrow – Morton model", Journal of Economics Dynamics and Control, No. 23, pp. 333–369. [ Links ]
Das Sanjiv, R. (2002). "The surprise element: jumps in interest rates", Journal of Econometrics, No. 106, pp. 27–65. [ Links ]
Domowitz, I. y Hakkio, C. S. (1985) "Conditional Variance and the Risk Premium in the Foreign Exchange Market", Journal of International Economics, No. 19, pp. 47–66. [ Links ]
Duffie, D. (2001). Dynamic Asset Pricing Theory, Princenton University Press, USA. [ Links ]
–––––––––– (2005). "Credit risk modeling with affine processes", Journal of Banking and Finance, No. 29, pp. 2751–2802. [ Links ]
–––––––––– y Kan, R. (1996). "A yield factor model of interest rates", Mathematical Finance, No. 6, pp. 379 – 406. [ Links ]
–––––––––– y Singleton, K. (2003). Credit Risk. Pricing, Measurement, and Management, Princenton University Press, USA. [ Links ]
Hakkio, C. S. y Leiderman, L. (1986). "Intertemporal asset pricing and the term structures of Exchange rates and interest rates", European Economic Review, No. 30, pp. 325–344. [ Links ]
Hnatkovska, V.; Lahiri, A. y Vegh, C. (2008). "Interest Rates and Exchange Rates: A Non Monotonic Tale", Working Paper, No. 13925, NBER, 43 pp. [ Links ]
Johannes, M. (2004). "The statistical and economic role of jumps in continuous time interest rate models", The Journal of Finance, Vol. LIX, No. 1, pp. 227 – 260. [ Links ]
Kiani, K. M. (2009). "Federal budget deficits and long term interest rates in USA", The Quaterly Review of Economics and Finance, 49, pp. 74–84. [ Links ]
Khoury, S. J. y Ghosh, A. (1987). Recent developments in international banking and finance, Heath & Company, Lexington. [ Links ]
Kou, S. G. (2002). "A jump diffusion model for option pricing", Management Science, Vol. 48, No. 8, pp. 1086 – 1101. [ Links ]
Lasa, A. J. (1997). Deuda, inflación y déficit. Una perspectiva macroeconómica de la política fiscal, UAM – I, México. [ Links ]
Martin, F. M. (2009). "A positive theory of government debt", Review of Economic Dynamics (en prensa). [ Links ]
Merton, R. C. (1973). "Theory of Rational Option Pricing", The Bell Journal of Economics and Management Science, Vol. 4, No. 1, pp. 141–183. [ Links ]
Nielsen, L. T. y Saá–Requejo J. (1993). "Exchange rate and term structure dynamics and the pricing of derivative securities", Working Paper, INSEAD. [ Links ]
Núñez, J. A. y Lorenzo, A. (2006). "Empirical analysis of jumps in a continuous time interest rate in Mexico from 1998 to 2006", Colombian Accounting Journal, Vol. 1, No. 1. [ Links ]
–––––––––– (2008). "Times and sizes of jumps in the Mexican Interest Rate", Análisis Económico, Vol. XXIII, No. 53, pp. 35–45. [ Links ]
Ono, Y. y Shibata A. (2001). "Government spending, interest rates and capital accumulation in a two – sector model", Canadian Journal of Economics, Vol. 34, No. 4, pp. 903–920. [ Links ]
Penati, A. (1983). "Expansionary Fiscal Policy and the Exchange Rate: A Review", Staff Papers – International Monetary Fund, Vol. 30, No. 3, pp. 542–569. [ Links ]
Samuelson, P. (1965). "Racional Theory of Warrant Prices", Industrial Management Review, Vol.6, No. 2, pp. 13–39. [ Links ]
Schönbucher, P. J. (2003). Credit derivatives pricing models, Wiley Finance, Inglaterra. [ Links ]
Stoica, G. (2002). "Sufficient Poisson Jump Diffusion Market Models Revisited", Proceedings of the American Mathematical Society, Vol. 130, No. 3, pp. 819–824. [ Links ]
Sutherland, A. (2006). "Currency crises and the Term Structure of Interest Rates", Open Economies Review, No.17, pp. 17–51. [ Links ]
Tanzi, V. (1980). "Inflationary Expectations, Economic Activity, Taxes, and Interest Rates", The American Economic Review, Vol. 70, No. 1, pp. 12–21. [ Links ]
Uhlenbeck, G. E. y Ornstein, L. S. (1930). "On the Theory of Brownian Motion", Physical Review, Vol. 36, pp. 823–841. [ Links ]
Vasicek, O. (1977). "An Equilibrium Characterization of the Term Structure", Journal of Financial Economics, No. 5, pp. 177–188. [ Links ]
Venegas, F. (2006). "Stochastic temporary stabilization: Undiversifiable devaluation and income risks", Economic Modelling, No. 23, pp. 157–173. [ Links ]
–––––––––– (2008). Riesgos financieros y económicos, 2ª. edición, Cengage Learning, México. [ Links ]
Wang, Y. y Tong, H. (2008). "Modeling and estimating the jump risk of exchange rates: Applications to RMB", Physica A, No. 387, pp. 6575–6583. [ Links ]
1 El concepto de balance económico no debe confundirse con el de balance económico de caja; este último se refiere a la suma del balance presupuestal y del balance extrapresupuestal.
2 En México el déficit operacional ajustado se define como el déficit económico consolidado del sector público menos el componente inflacionario de los intereses sobre la deuda consolidada denominada en moneda nacional, menos el efecto de la inflación sobre la recaudación tributaria del Gobierno Federal, menos el efecto del rezago recaudatorio sobre los intereses reales del Gobierno Federal, menos el efecto de la inflación sobre los subsidios financieros, más la ganancia inflacionaria sobre la deuda monetaria denominada en moneda nacional, más la ganancia inflacionaria sobre la deuda no monetaria denominada en moneda nacional, más el efecto de la inflación sobre la composición de la deuda pública, más el efecto del tipo de cambio real sobre el déficit público consolidado.
3 Las series oficiales del gasto total presupuestario excluyen las aportaciones al ISSSTE.














