Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista mexicana de análisis de la conducta
versión impresa ISSN 0185-4534
Rev. mex. anál. conducta vol.36 no.3 México ene. 2010
https://doi.org/10.5514/rmac.v36.i3.04
10.5514/rmac.v36.i3.04
Artículos empíricos
The Operant Conditioning of Letter String Problem Solving
El condicionamiento operante de la solución de problemas de secuencias de letras
Marco A. Pulido, Cindy Hernández, Lilian M. Peña, Nora M. Ponce and Montserrat Rebolledo
Laboratorio de Condicionamiento Operante Universidad Intercontinental, México. For further information regarding the present study, the first author may be contacted at: mpulido@uic.edu.mx.
Recibido: Junio 11, 2010
Revisado: Septiembre 9, 2010
Aceptado: Octubre 14, 2010
Abstract
The major purpose of the present study was to assess the effects of practice and reinforcement on letter string problem solving. College students were exposed to printed letter string problems. In the first experiment correct answers could be reinforced, punished, ignored, randomly reinforced or presented without a previous example. Data showed punishment significantly decreased the number of correct answers produced by the subjects; additionally practice significantly increased the number of correct answers in one reinforced condition and lowered the number of correct answers in the punishment group. A second experiment assessed behavioral momentum theory in the solution of letter string problems. Subjects were reinforced for producing a determined answer during 12 consecutive problems; subsequently the answer selected for reinforcement changed. Results showed the probability of producing a correct answer significantly decreased when reinforcement contingencies changed. Data from both experiments suggest that approaching letter string problem solving from an operant, rather than cognitive perspective, could allow a better understanding and control of the phenomenon.
Key words: Letter string problem solving, reinforcement, practice, behavioral momentum, college students.
Resumen
El principal objetivo del presente estudio fue el de evaluar los efectos de la práctica y el reforzamiento en la solución de problemas de letras. Estudiantes universitarios recibieron problemas impresos de secuencias de letras. En el primer experimento, las respuestas correctas a los mismos podían ser reforzadas, castigadas, ignoradas, reforzadas aleatoriamente o presentadas sin un ejemplo precedente. Los resultados mostraron que el castigo disminuyó significativamente las respuestas correctas de los sujetos; adicionalmente, la práctica incrementó significativamente el número de respuestas correctas en una condición de reforzamiento, y disminuyó la cantidad de respuestas correctas en el grupo de castigo. En un segundo experimento se evaluó la teoría de momentum conductual en la solución de problemas de secuencias de letras. Se reforzó a los sujetos por producir una respuesta particular en 12 problemas consecutivos; posteriormente, la respuesta seleccionada para reforzamiento cambió. Los resultados mostraron que la probabilidad de producir una respuesta correcta disminuyó cuando se modificó la respuesta seleccionada para reforzamiento. Los resultados obtenidos de los experimentos sugieren que abordar el fenómeno de solución de problemas de secuencias de letras desde una perspectiva operante, en lugar de cognitiva, permite una mejor comprensión y control del mismo.
Palabras clave: Problemas de secuencias de letras, reforzamiento, práctica, momentum conductual, estudiantes universitarios.
When an individual uses a previously learned procedure to solve a problem in a context that differs from the original learning situation, cognitive scientists suggest that analogical transfer may have occurred. The concept is considered fundamentally different from stimulus generalization, concept that is only considered valid to describe basic and primitive "mental" operations (Gick & Holyoak, 1980; Gentner & Holyoak, 1997). Analogical transfer is considered an important issue within the cognitive sciences because it is conceptualized as one of the key components of intelligent behavior and scientific discovery (Spearman, 1927; Raven, 1938; Oppenheimer, 1956; Gentner & Markman, 1997). Regardless of the cognitive relevance that some scientists have attributed to this phenomenon, attempts to reproduce it under laboratory conditions have produced principally negative results (see Pulido, Almaraz, García & Martínez, 2010 for a review).
The negative findings produced so far have been relatively "shocking" to cognitive scientists because most of them have occurred in college students, and the experimental procedures have been relatively simple. Thus the paradoxical nature of the phenomenon, it is assumed as general and fundamental for human adaptive behavior, yet it remains basically irreproducible under basic laboratory conditions.
For instance, in a seminal study conducted by Reed, Dempster & Ettinger (1985) two groups of college students received an algebra problem within a particular solution context (determine distance, mixture or work problems). Previously, the experimental group had received a problem that required the application of the same procedure as the test problem but within a different context. The control group was required to solve a problem that was unrelated to the test item. Reed Dempster & Ettinger found no significant differences between the groups; no differences between the groups appeared even when the students were allowed to use the practice problem when solving the test item; negative results were also found when the practice problem was accompanied by explanatory diagrams. In a final effort to produce evidence of analogical transfer, these scientists used a hierarchical taxonomy developed to classify algebra problems based on their difficulty. College students were exposed to the easiest problems of the aforementioned taxonomy but analogical transfer effects remained elusive.
Equally discouraging effects were found by Gick & Holyoak (1980). These scientists used as test problem Duncker's radiation problem (see Duncker, 1945). Gick & Holyoack designed a family of problems, similar to the target item and presented them to the experimental group. As in the Reed, Dempster & Ettinger study, Gick & Holyoack found no statistical differences between the control and experimental groups. The authors manipulated several aspects of the procedure, designed to favor analogical transfer, however analogical transfer effects could not be evidenced.
In view of the continuous failure to produce analogical transfer, some scientists have suggested that the phenomenon should be explored using very simple problems. For instance, Burns (1996), studied analogical transfer using letter string problems. In this type of problems, a particular sequence of letters is changed in a deliberate way (for instance ABC is changed to ABD) subsequently, the experimental subject is asked to change a new sequence using the previously presented model (for instance: how would you change EFG in the same way). Using letter string problems, Burns found clear evidence of analogical transfer; given his success, other scientists have used this procedure to explore the phenomenon.
For example, Pulido (2002) attempted to replicate Burns's findings in Mexican college students. In general Pulido's findings agreed with those produced by Burns, however Pulido's results also showed that slight procedural variations (for instance changing the model letter sequence), "vaporized" all evidence of analogical transfer. The finding that the particular type of letter sequence used as practice problem disrupts evidence of analogical transfer in letter string problems was once more confirmed by a more extensive replication (a larger number of letter string problems were assessed) conducted by Pulido, de la Garma & Pérez, (2010).
Other studies have assessed the effects of superficial similarities (similarities between problems that are not essential for the solution of a problem) on letter string problem solving by analogical transfer. For instance, Pulido, Olmos & Lanzagorta (2005) compared solutions from groups of subjects that received a practice model that could either be superficially similar (or dissimilar) to the test problem. Results showed analogical transfer was considerably hindered in the group where the practice problem was superficially different from the test problem (thus confirming the findings of many other scientists, see for example: Novick, 1988a; Heydenbluth & Hesse, 1996; Ross & Kilbane, 1997).
In conclusion, contemporary research on analogical transfer suggests that the phenomenon is difficult to produce in the laboratory; additionally, results suggest that the independent variables the module it have not yet been accounted for; results also suggest that analogical transfer is rarely based on the structural characteristics of the problem, (instead, it appears that superficial similarities play an important role for the establishment of analogies between problems).
Given the current status of the literature on the subject, one is prone to ask if there may not be something fundamentally wrong with the way analogical transfer has been conceptualized and studied. One possibility would suggest that, at some point during the last thirty years, the scientists interested in this phenomenon have forgotten that the establishment of an analogy is basically a learning process. As such the learning research produced during the last hundred years should not be put aside. If Thorndike (1911) and Skinner (1938) have taught us anything is that learning is established, fundamentally, by its consequences, and by the repetition of the response–consequence association; thus the effects of both reinforcement and practice appear like an unpardonable omission in the study of analogical transfer. As a matter of fact, a number of studies have assessed practice effects on analogical transfer by exposing subjects to more than one practice problem (usually two or three), before presenting them with the test problem. In agreement with a practice hypothesis, subjects that received multiple practice problems, produced more correct responses in the test item than a control group (see for instance Gick & Holyoak, 1983; Spencer & Weisberg, 1986; Burns, 1994). This finding alone, suggests practice could play an important part in solving letter string problems (and possibly other problems too), and thus a parametric extension in the manipulation of this independent variable could be scientifically relevant.
Experiment 1
Due to the fact that practice and reinforcement effects have not been systematically assessed in the study of analogical transfer, and considering that some studies have showed that practice may enhance analogical learning, the purpose of Experiment 1 was to evaluate the effects of these independent variables on letter string problem solving. It was hypothesized that both practice and reinforcement should considerably enhance letter string problem solving.
Method
Participants:
A total of 79 undergraduate students from a university from Mexico City participated in the study; both male and female students were recruited. Students from all schools and semesters were invited to participate. Previous studies have shown that college students do not differ by sex, age or college major in their ability to produce analogical transfer (Pulido, 2002; Pulido Olmos & Lanzagorta 2005), thus these demographic variables were not registered. Additionally, these same studies have shown that presenting (or not) the complete alphabet to the students, previous to their solutions of letter string problems, has no statistical effects on their ability to solve them; thus no attempt was made to measure alphabetical abilities in the students, previous to their participation in the experiment.
Materials:
Subjects received the letter string problems in printed white booklets. Two different booklets were designed. The first booklet consisted of twelve different letter string problems. The problems presented the following solution model and problem "If ABC is changed to ABD: how would you change KJI in the same way? (For further references in this text ABC:ABD–KJI?). Only the first experimental group received the first booklet, all other experimental and control groups received a second booklet that contained 15 different problems of the following type (ABC:ABD–IJK). The purpose of the problems contained in the first booklet was to assess the solution of an inverted letter string, in the solution test; different studies have suggested that when inverted letter strings are presented in the test phase "correct" responses rarely occur. In the second booklet the model letter string was always presented in alphabetical order and test problems could be in either in alphabetical or inverse order (for example ABC:ABD–KJI? Or ABC:ABD–IJK?) . The purpose of the development of the second booklet was to assess the effects of the independent variables on different types of problems, (and thus assess their effects in a more general fashion). The number of problems in the second booklet was increased from 12 to 15 to better assess practice effects.
The experiment was conceived as a between groups design with 2 experimental groups and 4 control conditions. In the experimental conditions subjects were presented by the experimenter with an example of how letter string problems are solved. The example problem was different from those presented in the booklet, and was only used to develop a general idea of the solution requirement. Once the example problem was presented, the subjects received the test problems, one at a time. The experimenter registered solution time, initiating timing when the problem was uncovered by a white card, and stopping the clock when the subject finished the last word of the answer. If the subject gave the "correct" response to the problem, the experimenter said "very good, your strategy is correct;" if the answer was "incorrect," the experimenter said "your answer is incorrect, please use a different strategy." As soon as the subject was ready, the experimenter presented a new problem. In the first experimental group subjects received the first booklet; in the second experimental group (and in all control conditions, subjects received the second booklet).
The first control condition was identical to the second experimental group, with the exception that subjects received random reinforcement. In order to guarantee that the subjects would receive random reinforcement, previous to the application of the booklet, a coin was tossed fifteen times. The particular obtained sequence of heads and tails determined when the experimenter was going to reinforce or punish the subject's response (heads = reinforcement; tails = punishment).
The second control condition was identical to the second experimental condition with the exception that the subjects received inverse reinforcement. This means that "correct" answers were punished and "incorrect" answers were reinforced.
The third control condition was identical to the second experimental condition with the exception that the subjects received no feedback for their responses. This means that independently of producing a "correct" or an "incorrect" answer the experimenter remained silent.
The last control condition was identical to the second experimental condition with the exception that the subjects did not receive the letter string problem example before answering the booklet. Table 1 synthesizes the experimental procedure.
Procedure:
Subjects were recruited at the library, gardens and cafeteria of the university. They were identified as students by means of their "student identity card." All possible candidates received the following invitation "If you are not busy right now we would very much appreciate if you could participate in a study, designed to assess logical reasoning. The experiment will not take more than twenty minutes of your time and the results will be helpful for the development of theories regarding logical reasoning." If the subject accepted de invitation he (she) was conducted to the laboratory where the experiment took place; in case the invitation was turned down the subject was thanked and left alone. Subjects that agreed to participate were randomly assigned to one of the groups and the application proceeded as was previously described. Subjects also solved the problems in different order. Some subjects were randomly assigned to a condition where they initiated with problem 1 and ended with problem fifteen; other subjects received the problems in inverted order.
Results
Figure 1, shows cumulative success as a function of solving consecutive problems. The figure shows the experimental conditions on the left side, and the control conditions on the right. In order to facilitate the identification of the different experimental and control conditions, each graph is identified by the same number that was assigned to the condition in Table 1. Each graph shows in the "y" axis the number of correct answers; the "x" axis shows consecutive problems.

In general, experimental groups produced a more homogenous performance than control conditions (the exception was group five, the "no reinforcement" control condition that shows homogeneous performance by most subjects). With the exception of two subjects from the first group, all other participants in the experimental conditions increased the number of "correct" answers in a linear fashion, (as exposure to the problems and reinforcement increased). Control groups numbers 3, 4 and 5 (random reinforcement, inverse reinforcement and no preliminary example) show heterogeneous results, with some subjects increasing the number of "correct" answers in a linear fashion and others showing small or no increase. The number of "correct" responses is particularly low in the inverse reinforcement condition (group 4).
Figure 2 shows the average effects of practice, on both solution time and "correct" answers. The figure was designed by averaging the solution times and "correct" answers for all subjects in each condition during the first 5 problems; the second group of 5 problems and the third group of 5 problems (in the first experimental group with only twelve problems, three groups of 4 problems each were formed). The columns in the left side of the Figure show the average number of seconds for the solution of the problems; the columns in the right side of the Figure show the average number of "correct" answers.
The Figure shows that response times decreased in both experimental and control conditions. In some groups times decreased in a steep way (see for instance group 5); in other groups times decreased gradually (see for instance group 6). In contrast with the consistently decreasing effects observed with solution times, the average number of "correct" responses varied across groups. Correct responses increased consistently in both experimental groups (more abruptly for the first experimental group than for the second); "correct" answers decreased in the random and inverse reinforcement groups (more abruptly for the inverse reinforcement group than for the random reinforcement group), and have nil or small effects in the no reinforcement and no example control groups.In order to further assess the effects of the reinforcement contingencies a one way Analysis of Variance was conducted to compare the means of the six groups. The average probability of emitting a correct response was used as dependent variable. The analysis attained statistical significance (F(5/73)=3.202, p.=.011), as did a Games Howell post hoc analysis. The post hoc analyses showed that experimental groups, as well as the no reinforcement and no example groups differed from the inverse reinforcement condition (condition that presented the lowest overall mean). The random reinforcement group did not differ from any experimental or control condition. Reinforcement contingencies did not produce significant effects on response time (F(5/73)=1.858, p.=.112).
In order to assess the effects of practice on the dependent variables, regression equations relating practice (as independent variable) and "correct" answers (as dependent variable) were calculated for each one of the six different groups. Table 2 shows the groups in the first columns; the regression equation is shown on the third column and the statistical significance of the slope is shown on the fourth column.
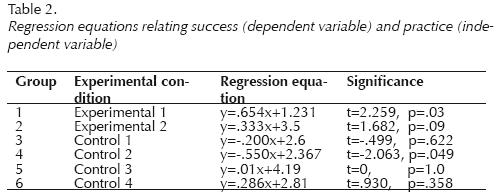
Table 2 shows that two regression slopes attained statistical significance, those corresponding to experimental group 1 and control group 2 (corresponding to the inverse reinforcement control group). These results suggest that practice significantly increases the number of "correct" answers in at least one experimental group (the regression equation presents a positive slope); the results also suggests that practice decreases the number of "correct" answers when those answers are labeled as "incorrect" by the experimenter (the regression equation presents a negative slope).
Table 3 shows regression equations relating practice (as independent variable) and solution times (as dependent variable) calculated for each one of the six different groups. Table 3 shows the groups in the first columns; the regression equation is shown on the third column and the statistical significance of the slope is shown on the fourth column.

Table 3 shows that four regression slopes attained statistical significance (groups 1, 2, 3 and 4); groups 5 and 6 (no reinforcement and no preliminary example control groups did not produce significant regression slopes). All regression equations in Table 3 show negative slopes.
Discussion
In general, the results of the present study suggest that reinforcement contingencies had limited effects on the production of correct responses. Only the inverse reinforcement contingency significantly affected the number of correct responses produced by the experimental subjects (inverse reinforcement significantly decreased the probability of producing a correct answer). Practice had important effects in the first experimental group, where subjects significantly increased the probability of producing a correct answer as they progressed through the problems. Practice also produced important effects in the inverse reinforcement condition, where subjects significantly decreased their probability of producing a correct response as they progressed through the problems. Thus the hypotheses formulated in the present study can be considered only partially confirmed. Reinforcement contingencies may decrease the probability of producing a correct response when they differentially punish their emission; however positive reinforcement produced no discernible effects. In a similar vein, practice had important effects on the first control group and in the inverse reinforcement group but did produce significant effects on any other group. Regarding the effects of the independent variables on solution times, reinforcement contingencies did not produce significant effects, however practice significantly decreased response times in most groups (and in those groups where no significant effects were found, a decreasing function is always found).
Independently of the modest effects of reinforcement contingencies and practice on the probability of producing a correct answer, the most surprising findings of the present study appear when the results are compared with those produced by the experimental literature on the subject. In the experimental groups, with the exception of two subjects in the first group, all participants increased consistently in the number of correct responses; by the end of the fifteen trials (group 2) or twelve trials (group 1) most subjects are invariably producing "correct" answers. Strikingly, by the time the participants reached the last problem, ten out of thirteen subjects had the "correct answer in the first experimental group; seventeen out of eighteen subjects had the "correct" answer in the second experimental group (success rates of 77% and 94%, respectively). Reed et al (1985) reported success rates that ranged from 18% to 56%; Burns (1996) reported success rates that ranged from 21% to 58% ; Pulido (1999) reported success rates that ranged from 5% to 21%; Pulido (2002) reported success rates that ranged from 7% to 28%. Thus, the data produced in the present study represent a substantial increase in the percentage of correct responses produced so far. The data produced by the present study, also suggest that operant conditioning plays an important role on letter string problem solving and on those behavioral effects frequently classified as analogical transfer.
Experiment 2
The first study, suggests that the experimental procedures employed in the first study may considerably enhance the successful solution of letter string problems; additionally, the results suggest that the punishment of "correct" answers considerably hinders the solution of these same problems. Thus the results produced so far suggest that operant conditioning may be an important feature in letter string problem solving. However, the evidence for an operant conditioning account of letters string problem solving, would be more compelling if other well documented effects of instrumental learning, could be reproduced during the solution of these problems. Perhaps, one of the most common effects of operant conditioning is its ability to sustain responding during extinction (after the experimental subject has been exposed to a prolonged history of reinforcement). This effect was initially described by Skinner (1938) and termed "reflex reserve;" subsequent studies have repeatedly shown that once a particular response has been reinforced, it persists for a time in the absence of reinforcement, and even in spite of punishment (see for instance Nevin, 1974; 1979; 1984; 1988; 1992; 1995). Nevin named the effect "behavioral momentum." The purpose of the second experiment was to attempt to reproduce this effect in subjects exposed to letter string problems. Specifically, subjects were reinforced to produce a particular answer during 12 consecutive problems; when presented with the thirteenth problem, subjects were reinforced for producing a different answer. It was hypothesized that, should behavioral momentum occur, subjects would persist in the production of the obsolete answer.
Method
Participants:
A total of 57 undergraduate students from an university from Mexico City participated in the study; both male and female students were recruited. Students from all schools and semesters were invited to participate.
Materials:
Booklets, similar to those used in the first experiment, were used in the second one. A total of four different booklets were designed. In the first booklet subjects received 24 different letter string problems of a successor–successor type; both the model and the test problems were presented in an alphabetical order, for instance: If ABC is changed for ABD, how would you change IJK in the same way? The second booklet also presented 24 different successor–successor problems, however, the model was presented in alphabetical order and the test problem was presented in inversed order, for instance: If ABC is changed for ABD, how would you change KJI in the same way? In the third booklet, subjects were presented with 12 successor–successor problems with both model and problem in direct alphabetical order; when the subjects reached the thirteenth problem, the model remained in alphabetical order but the test problem was presented in inverse order (that is the first twelve problems corresponded to booklet one and the final twelve problems corresponded to booklet two). The fourth and last booklet presented twelve problems from booklet two and subsequently twelve problems from booklet one. Subjects were randomly assigned to each experimental condition. A total of 15 participants solved booklet one; booklet two was also solved by 15 participants; booklet three was solved by eleven participants and the last booklet was solved by 16 participants.
Procedure:
The procedure used in the second experiment was very similar to that employed in both experimental groups in experiment one. Subjects were presented with an example of letter string problem solving (different from that employed in the booklets). Once the example was presented, the participant received one of the booklets and was asked to solve the problems one by one. If the subject produced a "correct" answer he/she was told: "very good, your strategy is correct;" if the subject produced an incorrect answer, he/she was told: "your answer is incorrect, please use a different strategy." With participants in booklets one and two, the correct solving strategy did not change in any of the 24 different problems; however for those subjects that received booklets three and four, one solution strategy was used during the first twelve problems, and a different solution strategy was used during the last twelve problems.
Results
Figure three shows cumulative success for each subject in each experimental condition. The first graph shows the data produced by the first booklet (direct/direct condition); the second graph shows the data produced by the second booklet (inverse/inverse condition); the third graph presents the data produced by the third booklet (direct/inverse condition) and the fourth graph shows the data produced by the fourth booklet (inverse/direct condition). In all graphs, the "X" axis shows consecutive problems; the "Y" axis shows cumulative success.
Figure three shows that those experimental conditions where reinforcement contingencies remained stable produced homogeneous and continuous improvement in letter string problem solving. This effect is more apparent in the Direct/Direct condition and comparably less so for 5 subjects in the Inverse/Inverse condition. The more or less homogeneous improvement observed in the direct/direct and inverse/inverse conditions, disappears in the last two experimental conditions, where most subjects that show improvement suddenly fail to improve after reaching the twelfth problem. Also, only two subjects reached 20 correct answers in the last experimental groups; most subjects in the first experimental conditions had 20 (or more) correct answers.
Figure 4 shows the average number of correct responses of all experimental subjects for each problem and each experimental condition. The graphs are presented in the same order as that used in figure 3. The "X" axis shows consecutive problems; the "Y" axis shows the average number of correct responses for each problem.
Figure 4 shows that the average number of successful responses remains high and stable in the first experimental condition (nearing an average of 15 correct responses throughout the study). The average number of successful responses in the second experimental condition, initiates at relatively low values, but gradually climbs to an average of just above 8 correct responses. The average number of correct responses in the direct/inverse condition, starts at relatively stable values, nearing 7 and 8 correct answers, however, after the twelfth problem, correct answers sharply decline, and never rise above 2 correct answers for the rest of the study. In the inverse/direct condition, the average number of correct responses fluctuates throughout the study, reaching its highest point at the fourth problem, and its lowest points at the second and thirteenth problems.
Figure 5 shows the average probability of producing a correct answer in the last twelve problems for all subjects and experimental conditions. The graph in the left, shows those conditions that ended with the "direct" problems (direct/direct and inverse/direct); the graph in the right, shows those conditions that ended with the "inverse" problems (inverse/inverse and direct/inverse problems). In both graphs, the "Y" axis shows the average probability of emitting a correct answers; the "X" axis shows the experimental conditions.
In general, Figure 5 shows that the probability of producing a correct answer in the last twelve problems was higher in the "direct" conditions than in the inverse conditions. Additionally, figure 5 shows that performance in the last twelve problems is significantly impaired when the answer selected for reinforcement changes after the twelfth problem. The effect attains statistical significance when comparing the direct/direct and inverse/direct conditions (t(22)=18.79, p.=.000); and when comparing the inverse/inverse and direct/inverse conditions (t(22)=17.57, p.=.000).
Discussion
In general, the second experiment shows that "correct" answers, to letter string problems, significantly decreases after subjects have been reinforced for producing different correct answers. The effect is consistent and significant independently of the type of problem assessed (direct or inverse). However, the data also show that subjects "recover" faster from an inverse/direct reinforcement change than from direct/inverse contingencies. Thus, the data produced by the second study are in general agreement with a Behavioral Momentum account of letter string problem solving; however the data also suggest that the effects of previous reinforcement on response persistence may be mediated by the type of problem presented to the subject. The fact that subjects exposed exclusively to "direct" problems, produced substantially higher numbers of correct responses than those subjects exposed exclusively to "inverse" problems, suggests that transitions from "easy" to "hard" problems are associated with higher persistence effects than transitions from "hard" to "easy" problems. This effect may be understood in terms of reinforcement frequency; that is, the data produced by the study suggest that direct problems produce a higher reinforcement frequency than inverse problems, thus subjects exposed to direct/inverse transitions come from richer reinforcement histories to the transition phase than subjects that received an inverse/direct experimental condition. This additional finding is in general agreement with behavioral momentum studies, where a frequently reinforced response shows greater persistence than a response that has only been infrequently reinforced (Bouzas, 1978; Nevin, 1988). The present authors acknowledge that characterizing direct problems as "easy," an inverse problems as "hard," is sustainable only by the execution observed in the direct/direct and inverse/inverse conditions. Subjects in direct/inverse, and inverse /direct conditions began the experiment at relatively similar reinforcement rates (although a small learning curve may be observed in the inverse/direct condition, that is lacking in the direct/inverse condition). However the present authors back the hypothesis that inverse problems are "hard," and direct problems are "easy," based not only in the observations of the present study, but also on ten years of research regarding letter string problem solving (see Pulido, Almaraz, García & Martínez, 2010 for a review).
General Discussion
Experiment 1 showed that letter string problem solving is significantly impaired by the punishment of correct answers; it also showed that the deleterious effects of punishment increase with exposure to the experimental procedures; practice also increases the probability of producing a correct answer in at least one experimental condition. Experiment one also showed that the experimental procedures employed in the study, eventually produce percentages of correct answers that have no precedent in the experimental literature on letter string problem solving.
Although the operant effects documented in the first experiment are quite modest, experiment two shows unambiguously that the reinforcement of a particular answer hinders the acquisition of a new one, in the fashion described by Nevin in the behavioral momentum model. That is, the previously reinforced response persists in the face of punishment, and this persistence is a direct function of previous reinforcement frequency (persistence is higher in those subjects that received the richest reinforcement history).
Thus, in general the idea that the so called analogical transfer effects, in letter string problems solving, may be modulated by the fundamental variables of operant conditioning (reinforcement and practice), appears to have empirical support. However the results obtained in the first experiment suggest that reinforcement contingencies interact with other variables to produce the subject's answers. One possible explanation for the relatively modest effects reported in the first experiment appears when the mean probability of producing a correct answer, of both experimental conditions, are compared. Results show that the average probability of producing a correct answer in the first experimental group was considerably lower than that of the second one (.646<.753). Due to the fact that all other control groups used the same problems developed for the second experimental group, it is possible that the problems selected for the experiment where relatively "easy" problems, and thus the learning process was to brief to be captured by the dependent variables. As was mentioned in the introduction of the first experiment, the problems selected for the first experimental group, had previously been identified as "hard" problems, and thus they produced a more pronounced learning curve that was statistically detected by the regression analysis. Perhaps this possibility could be assessed in a new study where the manipulations used in the first experiment are replicated using the problems in the first experimental condition. Perhaps the effects of reinforcement and practice could also be enhanced using more potent reinforcers, such as money or curricular credits.
An operant conditioning account of letter string problem solving could also be more compelling if other well documented effects of instrumental learning could be replicated using the procedure. One possibility could be to attempt to replicate the results reported by Herrnstein (1961) regarding response allocation in concurrent schedules. In general, Herrnstein's seminal studies (and many others after it) showed that response allocation to different alternatives depends on the obtained reinforcement frequency of each one. Perhaps in a future study different response strategies to letter string problems could be associated with different reinforcement densities. The matching of response strategy frequency to obtained reinforcement frequency would make a strong case for an operant conditioning account of letter string problem solving.
Another research possibility would be to try to replicate the delay gradient effect on letter string problem solving. Reviews by Renner (1964), Tarpy & Sawabini (1974) and Lattal (1987) suggest that delay of reinforcement diminishes reinforcement capability for sustaining operant behavior; thus, if instrumental conditioning is fundamental for letter string problem solving, delayed reinforcement should be less efficient for the acquisition and maintenance of correct answer production, than immediate reinforcement.
But why bother to study the operant conditioning of letter string problem solving in the first place. The experimental literature on letter string problem solving based on a cognitive approach has produced mainly negative findings; additionally results have shown poor or nonexistent external validity (see Pulido et al 2010 for a review). When a particular research field produces this type of results, it is possible that the conceptual framework that produced them is basically incorrect.(Khun, 1962; Kantor, 1971) and a new approach to the problem is needed. The present study conceptualized letter string problem solving as operant behavior, and immediately produced results that have no parallel in the traditional literature on the subject. The probability of producing a correct answer, at the end of the experimental procedures, significantly increased, relative to the data produced by more than ten years of research regarding this phenomenon. Thus, the results of the first study suggest that an operant, rather than cognitive, conceptual framework could be used to further control and understand this particular behavior. This assertion is further supported by the results of the second experiment that showed that a typical operant phenomenon, produced with rodents, and a lever pressing response occurs in human subjects producing letter string problem answers. Lastly, the present results suggest that operant variables could be fundamental for "analogical reasoning," thus; claiming that concepts such as stimulus generalization are not applicable to this phenomenon does not appear to be empirically sustainable. Future studies may help develop this issue.
References
Bouzas, A. (1978). The relative law of effect: Effects of shock intensity on response strength in multiple schedules. Journal of the Experimental Analysis of Behavior, 30, 307–314; available via: http://dx.doi.org/10.1901%2Fjeab.1978.30–307 [ Links ]
Burns, B.D. (1996). Meta–analogical transfer: Transfer between episodes of analogical reasoning. Journal of Experimental Psychology: Learning, Memory and Cognition, 22, 1032–1048; available via: http://dx.doi.org/10.1037%2F%2F0278–7393.22.4.1032 [ Links ]
Duncker, K. (1945). On problem solving. Psychological Monographs, 58, (all No. 270) [ Links ]
Gentner, D., & Holyoak, K.J.. (1997) Reasoning and learning by analogy. American Psychologist 22, 32–34; available via: http://dx.doi.org/10.1037%2F%2F0003–066X.52.1.32 [ Links ]
Gentner, D., & Markman, A.B. (1997) Structure mapping in analogy and similarity. American Psychologist 22, 45–56; available via: http://dx.doi.org/10.1037%2F%2F0003–066X.52.1.45 [ Links ]
Gick, M.L., & Holyoak, K.J. (1980). Analogical problem solving, Cognitive Psychology,12, 305–355; available via: http://dx.doi.org/10.1016%2F0010–0285%2880%2990013–4 [ Links ]
Gick, M. L., & Holyoak, K. J. (1983). Schema induction and analogical transfer. Cognitive Psychology, 15, 1–38; available via: http://dx.doi.org/10.1016%2F0010–0285%2883%2990002–6 [ Links ]
Herrnstein, R.J. (1961) Relative and absolute strength of response as a function of frequency of reinforcement. Journal of the Experimental Analysis of Behavior, 4, 267–272; available via: http://dx.doi.org/10.1901%2Fjeab.1961.4–267 [ Links ]
Heydenbluth, C., & Hesse, F. (1996). Impact of superficial similarity in the application phase of analogical problem solving. American Journal of Psychology, 109, 37–57; available via: http://dx.doi.org/10.2307%2F1422926 [ Links ]
Kantor, J.R. (1971). The aim and progress of psychology and other sciences. Chicago, Principia Press. [ Links ]
Khun, T. (1962). The structure of scientific revolutions. Chicago, University of Chicago Press. [ Links ]
Lattal, K.A. (1987). The effect of delay and of intervening events on reinforcement value. En M.L. Commons, J.E. Mazur, J.A. Nevin y H. Rachlin (eds.), Quantitative Analysis of Behavior (vol 5). New Jersey: Lawrence, Erlbaum Associates Publisher. [ Links ]
Nevin, J.A. (1974). Response strength in multiple schedules. Journal of the Experimental Analysis of Behavior, 21, 389–408. [ Links ]
Nevin, J.A. (1979). Reinforcement schedules and response strength. In M.D. Zeiler & P. Harzem (eds.) Reinforcement and the organization of behavior, London, Wiley. [ Links ]
Nevin, J.A. (1984). Quantitative analysis. Journal of the Experimental Analysis of Behavior, 42, 421–434. [ Links ]
Nevin, J.A. (1988). Behavioral momentum and the partial reinforcement effect. Psychological Bulletin, 103, 44–56; available via: http://dx.doi.org/10.1037%2F%2F0033–2909.103.1.44 [ Links ]
Nevin, J.A. (1992). An integrative model for the study of behavioral momentum. Journal of the Experimental Analysis of Behavior, 57, 301–316; available via: http://dx.doi.org/10.1901%2Fjeab.1992.57–301 [ Links ]
Nevin, J.A. (1995). Behavioral economics and behavioral momentum. Journal of the Experimental Anlayisis of Behavior, 64, 385–395; available via: http://dx.doi.org/10.1901%2Fjeab.1995.64–385 [ Links ]
Novick, L.R. (1988a). Analogical transfer, problem similarity and expertise. Journal of Experimental Psychology: Learning, Memory and Cognition, 14, 510–520; available via: http://dx.doi.org/10.1037%2F%2F0278–7393.14.3.510 [ Links ]
Oppenheimer, J.R. (1956). Analogy in science. American Psychologist, 11, 127–135; available via: http://dx.doi.org/10.1037%2Fh0046760 [ Links ]
Pulido, M.A. (1999). Transferencia meta–analógica: Evidencias empíricas. Unpublished. Masters dissertation, UNAM, México. [ Links ]
Pulido, M.A. (2002) "Transferencia analógica en la solución de problemas de cuatro términos con un diseño de ensayo múltiple." Revista de la Sociedad Mexicana de Psicología, 19, 23–24. [ Links ]
Pulido, M.A., Olmos, E., & Lanzagorta, N. (2005). "La solución de problemas de cuatro términos por transferencia analógica: El efecto de las similitudes superficiales y del tipo de problema." Revista de la Sociedad Mexicana de Psicología. 22, 433–440. [ Links ]
Pulido, M.A., Almaraz, D, García, D., & Martínez, L. (2010). Ten years of research on letter string problem solving by analogical transfer. Journal of Behavior Health and Social Issues, 2, 83–89. [ Links ]
Pulido, M.A., De la Garma, M., & Pérez, C. (2010). Solución de problemas por transferencia analógica: Efectos de la disponibilidad del modelo. Revista Intercontinental de Psicología y Educación. 12, 157–170. [ Links ]
Raven, J.C. (1938). Progressive matrices: A perceptual test of intelligence. London, Lewis. [ Links ]
Reed, S.K., Dempster, A., & Ettinger, M. (1985). Usefulness of analogous solutions for solving algebra word problems. Journal of Experimental Psychology: Learning Memory and Cognition, 11, 106–125; available via: http://dx.doi.org/10.1037%2F%2F0278–7393.11.1.106 [ Links ]
Renner, K.E. (1964). Delay of reinforcement: A historical review, Psychological Bulletin, 61, 341–361; available via: http://dx.doi.org/10.1037%2Fh0048335 [ Links ]
Ross, B.H., & Kilbane, M.C. (1997). Effects of principle explanation and superficial similarity on analogical mapping in problem solving. Journal of Experimental Psychology: Learning, Memory and Cognition, 23, 427–440; available via: http://dx.doi.org/10.1037%2F%2F0278–7393.23.2.427 [ Links ]
Skinner, B.F. (1938). The behavior of organisms. New York, Appleton Century Crofts. [ Links ]
Spearman, C. (1927). The abilities of man. New York: Mc. Millan. [ Links ]
Spencer, R.M., & Weisberg, R.W. (1986). Context–dependent effects on analogical transfer. Memory and Cognition, 14, 442–449. [ Links ]
Tarpy, R.W., & Sawabini, F.L. (1974) Reinforcement delay: A selective review of the last decade. Psychological Bulletin, 81, 984–997; available via: http://dx.doi.org/10.1037%2Fh0037428 [ Links ]
Thorndike, E.L. (1911) Animal intelligence. Experimental studies. New York, McMillan [ Links ]
Note
The authors wish to thank the Facultad de Psicología and the IPIEC of the Universidad Intercontinental for their support in the conduction of the present study. The authors would also like to thank the anonymous reviewers for their helpful comments. All authors contributed equally to this research.














