Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Ciencias marinas
versão impressa ISSN 0185-3880
Cienc. mar vol.40 no.2 Ensenada Jun. 2014
https://doi.org/10.7773/cm.v40i2.2403
Artículos
Análisis del crecimiento del oleaje limitado por el fetch usando radares de alta frecuencia en el golfo de Tehuantepec
Analysis of fetch-limited wave growth using high-frequency radars in the Gulf of Tehuantepec
Vladimir G Toro1,*, Francisco J Ocampo-Torres1, Pedro Osuna1, Héctor García-Nava2, Xavier Flores-Vidal2, Reginaldo Durazo3
1 Departamento de Oceanografía Física, CICESE, Carretera Ensenada-Tijuana No. 3918, Zona Playitas, CP 22860, Ensenada, Baja California, México.
2 Instituto de Investigaciones Oceanológicas, Universidad Autónoma de Baja California (UABC), Km. 103 Carretera Tijuana-Ensenada, CP 22860, Ensenada, Baja California, México.
3 Facultad de Ciencias Marinas, Universidad Autónoma de Baja California, Km. 103 Carretera Tijuana-Ensenada, CP 22860, Ensenada, Baja California, México.
* Corresponding author.
Email: vtoro@cicese.edu.mx, vgtoro@gmail.com
Received February 2014
Accepted May 2014.
RESUMEN
Se analizó el crecimiento del oleaje limitado por el fetch utilizando mediciones de alta resolución espaciotemporal obtenidas con radares de alta frecuencia (HF). Para calcular el espectro del oleaje, el eco de segundo orden (S2N) fue extraído del espectro Doppler y mapeado al dominio de las frecuencias del oleaje. La conversión de S2N al espectro del oleaje se realizó mediante un modelo paramétrico lineal que depende de la velocidad del viento. El crecimiento del oleaje local, representado por la energía y la frecuencia asociada al pico espectral adimensional en función del fetch adimensional, se determinó a partir de los espectros del oleaje calculados para 25 nodos (~400 km2) alrededor del sitio de anclaje de una boya Air-Sea Interaction Spar. Los datos de la boya se utilizaron como referencia y para proveer la información del viento necesaria para el análisis del crecimiento del oleaje. Los datos simultáneos de la boya y los radares HF presentaron una concordancia adecuada con las curvas de crecimiento del oleaje. El análisis en el dominio de los 25 nodos mostró una correlación significativa y cierta dispersión alrededor de las curvas de crecimiento. Las causas probables de esta dispersión están asociadas con errores en el cálculo del espectro del oleaje y del fetch, y a la suposición de condiciones de viento homogéneo. No fue posible determinar la influencia del swell en el crecimiento del oleaje con el set limitado de datos utilizado; sin embargo, es posible que un análisis con mayor variación de la altura del swell podría proveer esta evidencia. No obstante, los resultados sugieren que, con el modelo paramétrico lineal, es posible reproducir el crecimiento del oleaje limitado por el fetch. Este trabajo representa el primer esfuerzo enfocado al análisis del crecimiento del oleaje utilizando mediciones de radares HF.
Palabras clave: crecimiento del oleaje, radares de alta frecuencia, boya ASIS, golfo de Tehuantepec, swell.
ABSTRACT
Fetch-limited wave growth was analyzed using high spatial and temporal resolution measurements obtained with high-frequency (HF) radars. To calculate the wave spectrum, the second-order echo (S2N) was extracted from the Doppler spectrum and mapped to the wave frequency domain. The conversion of S2N to the wave frequency spectrum was carried out using a linear parametric model dependent on wind speed. Wave growth, represented by the dimensionless energy and peak frequency as a function of dimensionless fetch, was determined from the spectra calculated for 25 cells (~400 km2) in the vicinity of a moored Air-Sea Interaction Spar buoy. The buoy data were used as reference and to provide the wind information required for the wave growth analysis. The simultaneous data from the buoy and HF radars showed a suitable agreement with the wave growth curves. The analysis of the 25 cells showed an adequate agreement and certain dispersion around the growth curves. Possible causes of this dispersion are related to errors in the estimation of the frequency spectrum and fetch, and the assumption of homogeneous wind conditions. From the limited data set used, it was not possible to prove any impact of swell on wave growth; however, it is possible that analysis over a wider range of swell heights may provide this evidence. Nevertheless, the results suggest that the linear parametric model is able to reproduce fetch-limited wave growth. This work represents the first effort focused on fetch-limited wave growth using HF radars.
Key words: fetch-limited wave growth, high-frequency radars, ASIS buoy, Gulf of Tehuantepec, swell.
INTRODUCCIÓN
Entender los procesos de generación, crecimiento y evolución del oleaje es necesario para predecir sus efectos en la dinámica oceánica y costera. De estos tres aspectos, el crecimiento del oleaje puede proveer información valiosa en la física compleja de la evolución del oleaje (Young y Verhagen 1996). El oleaje se genera y crece por la acción que el viento ejerce sobre la superficie del mar. Los vientos fuertes asociados a tormentas en el océano abierto generan olas que se pueden desplazar miles de kilómetros. La existencia espaciotemporal de estas tormentas es normalmente aleatoria; por lo tanto, es difícil ubicar suficientes instrumentos en las zonas de generación que permitan medir el crecimiento del oleaje porque no se sabe dónde o cuándo puedan ocurrir las tormentas. El oleaje generado dentro de la zona de fuertes vientos y que comienza a crecer es comúnmente llamado oleaje local. Por otro lado, el crecimiento del oleaje puede estar influenciado por mecanismos físicos tales como la estabilidad atmosférica, el oleaje generado por tormentas lejanas (swell), la variabilidad del viento (Hwang et al. 2011), las interacciones ola-corriente (Kahma y Calkoen 1992) y la distancia sobre la cual se lleva a cabo el crecimiento del oleaje, también llamada fetch (Ardhuin et al. 2007).
Para el análisis del crecimiento del oleaje bajo condiciones controladas, se requiere que el viento sea homogéneo y el fetch sea definido mediante la dirección del viento ortogonal a la línea de costa. Las mediciones in situ raramente cumplen con estos requisitos ya que los campos de viento normalmente no son homogéneos (Hwang et al. 2011) y la orientación de la costa respecto a la dirección del viento solamente es perpendicular bajo ciertas condiciones de viento (Ardhuin et al. 2007, Bottema y van Vledder 2008). El crecimiento del oleaje se ha analizado a partir de mediciones in situ (Hasselmann et al. 1973, Kahma 1981, Young y Verhagen 1996, Bottema y van Vledder 2009), combinando mediciones in situ y simulaciones numéricas (Ardhuin et al. 2007), usando información de modelos numéricos (Tuomi et al. 2012) y utilizando mediciones con altímetros (Ebuchi 1999).
En el golfo de Tehuantepec (México, fig. 1a), se han llevado a cabo campañas de medición para estudiar el crecimiento del oleaje limitado por el fetch bajo condiciones de vientos fuertes. Estos vientos, llamados tehuanos, se presentan en esta región principalmente en invierno, y soplan de tierra a mar durante uno a varios días con velocidades de viento mayores que 20 m s-1 (García-Nava et al. 2009). Los tehuanos, al llegar al océano Pacífico, modifican los patrones de circulación del golfo de Tehuantepec generando remolinos (Flores-Vidal et al. 2011, Velázquez-Muñoz et al. 2014), que se intensifican debido a la presencia de corrientes costeras (Velázquez-Muñoz et al. 2011, Pantoja et al. 2012). Además, en el golfo, los tehuanos crean una zona de generación y crecimiento del oleaje cerca de la costa que se extiende hacia el suroeste. Romero y Melville (2010) realizaron mediciones del oleaje desde un avión en el golfo utilizando dos instrumentos con tecnología laser; con estas mediciones, estos autores obtuvieron información del oleaje con alta resolución espacial a lo largo de un fetch de hasta 500 km en intervalos de hasta 2 h. Ocampo-Torres et al. (2011) realizaron mediciones simultáneas de viento y oleaje utilizando una boya Air-Sea Interaction Spar (ASIS) durante el experimento Interacción Océano-Atmósfera (INTOA). Durante este experimento, también se obtuvieron espectros Doppler con un sistema de radares de alta frecuencia (HF, por sus siglas en inglés) coincidentes en espacio y tiempo con las mediciones de la boya ASIS.
El radar HF ha sido considerado desde hace varias décadas como una tecnología promisoria para el cálculo del espectro del oleaje y las corrientes oceánicas (Crombie 1955). Estos radares se han utilizado como sistemas complementarios en campañas de medición de variables oceánicas (Wyatt et al. 2003), trabajos de simulaciones numéricas con asimilación de datos de corrientes (Breivik y Saetra 2001) y en trabajos de energía renovable para estimar la energía potencial del oleaje (Wyatt 2012). El radar HF es un sistema de emisión y recepción de radiofrecuencias que se instala en la costa. Un radar HF irradia ondas electromagnéticas que viajan cerca de la superficie del mar. Las ondas electromagnéticas son reflejadas hacia el radar por olas que tienen una longitud de onda igual a la mitad de la longitud de onda emitida por el radar (condición Bragg), y la señal es registrada en unidades de potencia o voltaje (Barrick et al. 1974). La frecuencia de la señal reflejada se modifica debido a la rapidez de las olas superficiales y a las corrientes oceánicas, y el cambio respecto a la frecuencia emitida es llamado frecuencia Doppler. La potencia de la señal recibida se puede representar en función de la frecuencia Doppler y de la distancia desde el radar, o bien en función de la frecuencia Doppler (llamado espectro Doppler, fig. 2). Un espectro Doppler está compuesto por dos señales prominentes, conocidas como picos de primer orden, rodeados por un eco continuo de menor potencia, conocido como eco de segundo orden. Los picos de primer orden aparecen en el espectro Doppler debido a la presencia de olas que cumplen la condición Bragg y que se acercan o se alejan del radar. La diferencia (Δω) entre la frecuencia asociada a estos picos de primer orden y la frecuencia Bragg teórica se utiliza para calcular las componentes de la velocidad de las corrientes superficiales (fig. 2).
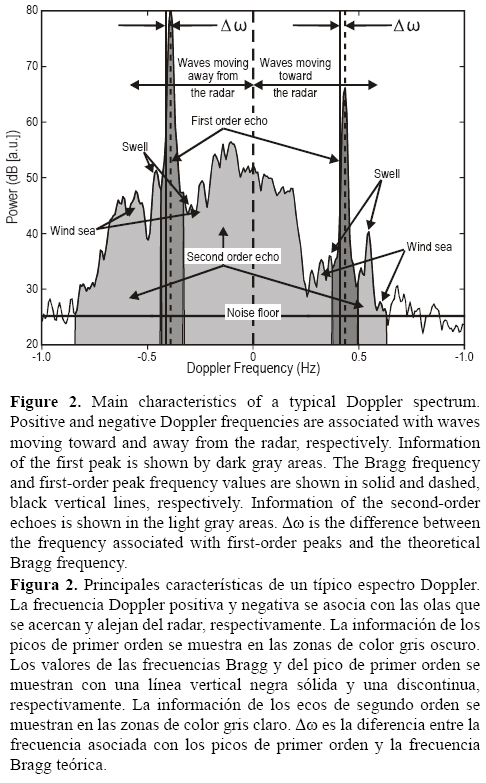
Los ecos de segundo orden se generan por una combinación de procesos hidrodinámicos y electromagnéticos. La información de estos ecos es utilizada para estimar el espectro del oleaje, ya sea a través de una ecuación integral (Barrick 1972, Wyatt 1990, Hisaki 1996, Hashimoto y Tokuda 1999) o por medio de una relación lineal entre el espectro del oleaje y el eco de segundo orden (Hasselmann 1971, Gurgel et al. 2006, Toro 2014). Algunos autores han sugerido que los picos asociados al swell y al oleaje local pueden ser localizados visualmente en los ecos de segundo orden (Lipa et al. 1981, fig. 2). La aproximación lineal a la ecuación integral propuesta por Hasselmann (1971) supone que las áreas de los ecos de segundo orden son proporcionales al espectro en frecuencia del oleaje a través de la razón T1/T2 y que el mapeo de las frecuencias Doppler al dominio de las frecuencias del oleaje es lineal. T1 es una función de la potencia reflejada por el oleaje y la potencia emitida por el radar. T2 es una función de transferencia definida por un coeficiente de acoplamiento entre dos olas que incluye interacciones hidrodinámicas y electromagnéticas. Gurgel et al. (2006) y Toro (2014) aproximan la razón T1/T2 usando un parámetro empírico (αF = T1/T2). Gurgel et al. (2006) calcularon αF como los coeficientes de regresión obtenidos al comparar los ecos de segundo orden normalizados y los espectros del oleaje medidos con una boya durante dos meses de mediciones. Toro (2014) utilizó datos medidos por un radar HF y una boya durante 15 días para calcular el valor medio de αF en función de la razón entre la energía asociada al swell (ESWELL) y la energía asociada al oleaje local (ESEA) o en función de los valores de la velocidad del viento (U10). Con base en el modelo lineal propuesto por Hasselmann (1971), la información del eco de segundo orden y el parámetro αF, Gurgel et al. (2006) y Toro (2014) obtuvieron espectros en frecuencia del oleaje a partir de mediciones con radares HF. Las comparaciones de los espectros en frecuencia, la altura significante (HS) y la frecuencia asociada al pico espectral del oleaje local (FSEA) obtenidos a partir de mediciones in situ y de información obtenida con radares HF en el golfo de Tehuantepec mostraron que el parámetro αF propuesto por Toro (2014) es adecuado para obtener información del oleaje. Las mediciones utilizadas por Toro (2014) se obtuvieron durante el experimento INTOA; parte de los valores medidos in situ fueron usados para calibrar los valores del parámetro αF y otra parte para validar la información del oleaje calculada con el método propuesto. El objetivo de este trabajo es determinar el crecimiento del oleaje limitado por el fetch usando espectros en frecuencia del oleaje calculados con un modelo paramétrico lineal que utiliza información obtenida de radares HF.
MATERIALES Y MÉTODOS
Los datos utilizados en este trabajo corresponden a las mediciones realizadas durante el experimento INTOA (Ocampo-Torres et al. 2011). Este experimento se llevó a cabo de febrero a abril de 2005 en el golfo de Tehuantepec, ubicado al sur de México en el océano Pacífico (fig. 1a). Esta región se distingue porque recibe casi todo el año swell que se produce en el océano Antártico y por la ocurrencia de eventos tehuanos. Durante el periodo del experimento sucedieron varios eventos tehuanos. Las mediciones directas del oleaje y de la rapidez y dirección del viento se realizaron con una boya ASIS ubicada a los 16 °N y 95 °W sobre una profundidad de 60 m. Las componentes del viento fueron medidas por un anemómetro sónico ubicado a 6.5 m por encima del nivel del mar y transformados a una altura de 10 m (U10). La información del oleaje fue medida por un arreglo de alambres capacitores (García-Nava et al. 2009) y fue utilizada para calcular el espectro del oleaje. El espectro direccional solamente se midió durante los 10 primeros días, pero los registros del espectro en frecuencia están disponibles para el periodo completo de observaciones.
Durante el experimento INTOA, se instaló un sistema de radar HF compuesto por dos estaciones, cada una con un arreglo de 16 antenas receptoras. Las estaciones fueron playa Cangrejo (CAN; 16°04'14" N, 95°21'45" W) y Santa María del Mar (STM; 16°12'56" N, 94°01'59" W). Cada estación midió la señal electromagnética continua reflejada de manera difusa por el oleaje en intervalos de 10 min. La frecuencia de operación de los radares fue de 16.3 MHz, y esto permitió realizar mediciones con un alcance de entre 80 y 120 km.
Espectros en frecuencia del oleaje a partir de mediciones con radares HF
El espectro direccional del oleaje (S) puede ser calculado con la información del eco de segundo orden del espectro Doppler (σ2) realizando la inversión de la ecuación integral propuesta por Hasselmann (1971) y Barrick (1972):

donde ωd es la frecuencia Doppler, Γ es un coeficiente de acoplamiento que incluye los efectos no lineales hidrodinámicos (ΓH) y electromagnéticos (ΓEM), c1 y c2 representan un cambio de signo (±), δ es la función delta de Dirac, y k1 y k2 son vectores número de onda (con magnitudes k1 y k2, respectivamente) asociados al oleaje. El número de onda espacial p está definido a lo largo del eje de medición del radar, y q es perpendicular a p. De acuerdo con el trabajo de Hasselmann (1971), de la ecuación (1) se puede obtener una expresión lineal en la cual se relaciona el espectro en frecuencia del oleaje (SF) con la razón entre la potencia del eco de segundo orden y la potencia integrada del eco de primer orden a través de T1/T2:

donde ωb es la frecuencia de Bragg, σ1 es la información asociada al eco de primer orden y S2N es el eco de segundo orden normalizado definido como la razón σ2/σ1. Gurgel et al. (2006) suponen que SF es proporcional a la suma de las señales en las bandas de frecuencia del eco de segundo orden por medio del parámetro αF:

donde ωF es la frecuencia del oleaje, los índices i y j se refieren a la parte positiva y negativa del eco de segundo orden. Combinando las ecuaciones (2) y (3), es posible deducir que αF es proporcional a la razón T1/T2. Los valores de αF se obtienen calculando la razón SF/S2N y, por lo tanto, son función de la frecuencia del oleaje. En este trabajo, se utilizó el parámetro αF en función de U10 tal como lo propone Toro (2014), en el cual el dominio de U10 se describió mediante cuatro escalas: 4 < U10 ≤ 8, 8 < U10 ≤ 12, 12 < U10 ≤ 16 y U10 >16ms-1. A continuación se presentan una serie de pasos que permiten obtener los valores de S2N.
Los espectros Doppler de cada estación fueron mapeados a una malla rectangular de 40 x 50 nodos con una resolución de 4 x 4 km (fig. 1b). El periodo de mediciones utilizado en este trabajo fue del 22 de febrero al 10 de marzo de 2005. Se seleccionaron los 25 nodos más cercanos a la posición de la boya ASIS (~400 km2) y, de esta manera, se aumentó el número total de datos a procesar. Los espectros Doppler utilizados en los cálculos del oleaje fueron seleccionados de acuerdo con el nivel base de ruido de cada espectro. El nivel base de ruido se puede asociar de manera inversa al valor de la razón señal/ruido (SNR, por sus siglas en inglés). Para el cálculo del nivel base de ruido, se utilizó el método de ordenamiento por categorías de la energía espectral propuesto por Heron y Heron (2001). La selección se realizó teniendo en cuenta el nivel base de ruido de cada espectro y un nivel base de ruido promedio. El nivel base de ruido promedio, correspondiente a un ciclo diurno, se definió utilizando la información de los espectros Doppler en el nodo de la boya ASIS durante el periodo completo del experimento INTOA. Para la selección de los espectros con suficiente SNR, se supuso que el nivel base de ruido en los 25 nodos de interés era similar. Por lo tanto, es posible utilizar los valores del ciclo diurno del nivel base de ruido en el nodo de la boya ASIS como un umbral por debajo del cual los valores del nivel base de ruido y sus espectros Doppler asociados se consideran que tienen suficiente SNR. Sólo los espectros que cumplieron estos requisitos fueron utilizados para la extracción del eco de segundo orden. Los espectros de la estación Santa María del Mar mostraron valores bajos de SNR y, por lo tanto, la información de esta estación no se consideró en los análisis posteriores. Las frecuencias Doppler de los espectros seleccionados fueron corregidas debido al efecto de las corrientes oceánicas. Esta corrección se realizó utilizando información de la frecuencia asociada a los picos de primer orden y de la frecuencia Bragg (ωb= [2 g kt]0.5, donde g es la aceleración debida a la gravedad y kt es la longitud de la onda electromagnética emitida).
Para la extracción del eco de segundo orden, primero se cálculo la razón entre la potencia del espectro Doppler y la función de peso propuesta por Barrick (1977). Esta función de peso permitió modificar la potencia del espectro Doppler en bandas de frecuencia particularmente sensibles a la dirección del oleaje. Posteriormente, se definieron cuatro bandas de frecuencia de ecos de segundo orden. Se seleccionaron en primer lugar cuatro frecuencias asociadas a mínimos locales ubicados alrededor de los picos de primer orden. Los mínimos locales se encontraron suponiendo que los picos de primer orden pueden aproximarse cada uno mediante dos líneas rectas. Se definió un mínimo local cuando la diferencia entre la frecuencia del espectro Doppler y la frecuencia asociada a las líneas rectas era mayor que la resolución en frecuencia del espectro Doppler (0.0075 Hz). Las cuatro frecuencias restantes asociadas con cada mínimo local, que permiten definir las bandas de frecuencia de los ecos de segundo orden, se calcularon de acuerdo con el valor del nivel base de ruido del espectro Doppler. Estas bandas fueron definidas por los valores mínimos locales antes mencionados y por las frecuencias donde la potencia del espectro Doppler es menor o igual que el nivel base de ruido. Las frecuencias de cada una de las cuatro bandas fueron mapeadas a frecuencias del oleaje mediante una aproximación lineal que es función de U10 (Toro 2014), y luego se sumaron las potencias de las cuatro bandas (S2N) de acuerdo con la ecuación (3). Finalmente, se obtuvieron los espectros en frecuencia del oleaje mediante el producto de S2N y la función paramétrica αF.
Cálculo de valores de energía del oleaje local y swell a partir del espectro en frecuencia
Comúnmente, los espectros de oleaje incluyen información del swell y del oleaje local. Para estudiar el crecimiento del oleaje, se requiere separar ESWELL y ESEA de la energía total (ETOT). Para identificar ESWELLy ESEA a partir del espectro en frecuencia (SF), se calculó una frecuencia de separación (ƒs) según Hwang et al. (2012):
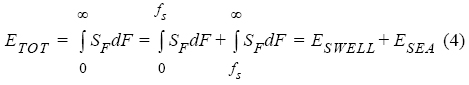
Con los valores de ESEA, ESWELL y ETOT, se calculó HS, la altura significante del oleaje local (HSEA) y la altura significante del swell (HSWELL), suponiendo que el oleaje tiene una distribución tipo Rayleigh y la superficie libre tiene una distribución gaussiana:
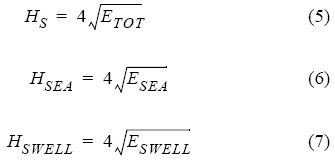
La fracción de la energía correspondiente al oleaje local (wind-sea fraction, wsƒ) se calculó como la razón entre ESEA y ETOT. Los valores de wsƒ entre 0.5 y 1.0 se pueden asociar a niveles altos de energía del oleaje local y aquellos entre 0 y 0.5 a niveles altos de energía del swell. En los análisis de crecimiento del oleaje también se utiliza el valor de la frecuencia asociada al pico espectral del oleaje local (FSEA). Con información del espectro SF asociado al oleaje local (integral entre FS y ∞, ec. (4)), se definió el valor de FSEA como la frecuencia asociada al valor máximo de energía espectral.
Para los análisis posteriores, del periodo completo de mediciones, se seleccionó una parte de la información obtenida a partir de mediciones de radar HF y medida por la boya ASIS correspondiente a los espectros en frecuencia y sus valores asociados de ESEA, ESWELL, ETOT y FSEA. La información seleccionada correspondió a periodos de eventos tehuanos, cuando la rapidez y la dirección del viento fueron, respectivamente, U10 ≥ 8 m s-1 y θ = 180° ± 10° (convención náutica, 0° hacia el Norte, 90° hacia el Este), aproximadamente perpendicular a la línea de costa. Para determinar la correlación entre los valores medidos y calculados, se utilizó la estimación de tres errores estadísticos: error cuadrático medio (RMSE), sesgo y coeficiente de correlación (R2). Con los valores de ESEA y FSEA, se calcularon las variables que permiten describir el crecimiento del oleaje.
Expresiones para el crecimiento del oleaje
El crecimiento del oleaje se analizó mediante la evolución de la energía adimensional (ESEA) y la frecuencia adimensional asociada al pico espectral (FSEA) del oleaje local, en función del fetch adimensional (X). El análisis se realizó con información de ESEA, FSEA, del fetch (X) y de la rapidez del viento U10. El crecimiento del oleaje se puede expresar de acuerdo con las siguientes expresiones (Kitaigorodskii 1962):

Utilizando estas expresiones y la información de múltiples bases de datos de mediciones in situ, Kahma y Calkoen (1992) y Hwang et al. (2011) definieron curvas empíricas para describir el crecimiento de la energía del oleaje local bajo condiciones atmosféricas estables. En el presente trabajo, se utilizaron estas curvas empíricas como referencia para calcular los valores de ESEA y FSEA en función de X.
Los valores de X utilizados para las ecuaciones (8-10) se calcularon trazando una línea recta entre el punto de estudio en el océano y la línea de costa de acuerdo con la dirección del viento. Para el cálculo de ESEA, FSEA y X en los 25 nodos alrededor de la boya ASIS (~400 km2), se supuso que el campo de viento era homogéneo y tenía las mismas condiciones de dirección y rapidez del viento medidas por la boya ASIS. Por lo tanto, usando los valores calculados de ESEA, FSEA y X y siguiendo la suposición de homogeneidad del viento en los 25 nodos, se calcularon los valores de ESEA, FSEA y X de acuerdo con las ecuaciones (8-10).
Los valores de ESEA y FSEA en función de X se analizaron inicialmente con los valores obtenidos con las mediciones de la boya y los obtenidos con los datos del radar HF en el nodo de la boya. A los valores de ESEA y FSEA obtenidos con los datos del radar HF, se les realizó un ajuste lineal en función de X. Por otro lado, se analizaron los valores de ESEA y FSEA en función de X correspondientes a los 25 nodos ubicados alrededor de la boya ASIS. En este análisis se incluyó el cálculo de los valores medios y las desviaciones estándar de ESEA y FSEA, agrupados con respecto al dominio de X en una escala de 102. Además, se utilizaron los valores discretos de HSWELL y wsƒ para estudiar la posible influencia del swell en el crecimiento del oleaje. Se usaron valores de HSWELLagrupados en intervalos de 0.15 m entre 0.5 y 1.1 m, y valores de wsƒ agrupados en intervalos de 0.1 entre 0.35 y 0.85.
RESULTADOS
Los valores de U10 medidos por la boya ASIS oscilaron entre 0 y 20 m s-1 (fig. 3a). La dirección del viento (θ) fue principalmente alrededor de 0° (vientos del sur) y 180° (vientos del norte, tehuanos; fig. 3b). Durante los eventos tehuanos, los valores de U10 fueron de hasta 20 m s-1, mientras que θ se mantuvo aproximadamente constante (180°).
Los parámetros integrales del oleaje obtenidos de las mediciones de la boya y los calculados con información de radar HF, en general, presentaron una alta correlación (fig. 3c-f). Los valores de HS y HSEA (fig. 3c, d) se incrementaron durante los eventos tehuanos, siendo notorio este incremento en los eventos del 4 y 9 de marzo de 2005. Los valores de HSWELL (fig. 3e) presentaron valores aproximadamente constantes, entre 0.5 y 1.1 m. Los valores de FSEA (fig. 3f) se incrementaron principalmente durante los eventos tehuanos. Se observaron algunos valores bajos de FSEA, con frecuencias cercanas a 0.1 Hz.
Los espectros en frecuencia medidos y los calculados en el nodo de la boya ASIS asociados a eventos tehuanos mostraron una alta correlación en los niveles de energía (fig. 4a, b). Los valores de ƒS (asteriscos) fueron similares en los dos grupos de espectros. Las comparaciones de los valores de energía de los espectros medidos y calculados en función de la frecuencia mostraron una concordancia adecuada de los valores FSEA, con diferencias en los valores de energía poco significativas (datos no presentados).
En general, se presentó una correlación adecuada (R2 > 0.5) entre los valores de HS, HSEA, HSWELL y FSEA asociados a los espectros en frecuencia medidos y calculados (fig. 5). Se observó una subestimación de los valores HS calculados con información de radar HF (fig. 5a), asociados a un RMSE de 0.39 m y un sesgo positivo de 0.19 m. Lo mismo se observó para los valores de HSEA (fig. 5b), con un RMSE de 0.36 m y un sesgo positivo de 0.1 m. Los valores de HSWELL (fig. 5c) mostraron una mejor correlación, con un RMSE de 0.24 m y un sesgo positivo de 0.15 m, aunque se mantuvo ligeramente la tendencia a subestimar los valores calculados con información de radar HF. Se observó una correlación significativa entre los valores medidos y calculados de FSEA (fig. 5d), con valores de los errores estadísticos que sugieren una ligera tendencia a sobreestimar los valores calculados con información de radar HF.
Se observó una concordancia adecuada entre los valores de ESEA y FSEA, calculados a partir de los valores obtenidos con las mediciones de la boya ASIS y los obtenidos con los datos de radar HF en el nodo de la boya (fig. 6), con respecto a las curvas empíricas de Kahma y Calkoen (1992) y Hwang et al. (2011). En general, los valores de ESEA y FSEA determinados con la información medida y calculada no presentaron los mismos valores. En el caso de ESEA, la dispersión de los datos con relación a las curvas empíricas fue alta (fig. 6a); sin embargo, el ajuste lineal de los valores de ESEA calculados con información de radar HF presentó una correlación significativa con las curvas empíricas. En el caso de FSEA, la dispersión de los datos con relación a las curvas empíricas fue baja y el ajuste lineal mostró una ligera tendencia a subestimar los valores cuando X > 2 x 103 (fig. 6b).
En los 25 nodos alrededor de la boya ASIS (~400 km2), se observó una alta dispersión de los valores de ESEA y una baja dispersión de los valores FSEA con relación a las curvas empíricas de Kahma y Calkoen (1992) y Hwang et al. (2011) (fig. 7). Los valores de ESEA son los mismos en la figura 7(a, b) y los valores de FSEA son los mismos en la figura 7(c, d); sin embargo, la escala de colores de los puntos corresponde a valores discretos de HSWELL y wsƒ. Los valores medios de ESEA están cercanos a las curvas de Kahma y Calkoen (1992) y Hwang et al. (2011), y están por debajo de las curvas empíricas sólo cuando X > 2.5 x 103. En general, las desviaciones estándar (barras de error) asociadas a los valores medios de ESEA fueron similares para todo el intervalo de valores de X. En el caso de FSEA, los valores medios presentaron valores cercanos a las curvas empíricas, con barras de error similares para todo el intervalo de valores de X y menores respecto a ESEA.
La distribución de los valores de HSWELL alrededor de las curvas empíricas fue aleatorio (fig. 7a, c), mientras que los valores de wsƒ presentaron una distribución en función de X (fig. 7b, d). En el caso de HSWELL, para un intervalo de 60 cm, los valores de ESEA de ~0.6m se ubicaron principalmente por debajo de las curvas empíricas, mientras que los demás valores del intervalo se encontraron dispersos alrededor de las curvas. Los valores de wsƒ entre 0.5 y 0.85 (valores altos de ESEA respecto a ETOT) estuvieron asociados principalmente a los valores de X< 103, mientras que los valores de wsƒ ≤ 0.5 (valores bajos de ESEA respecto a ETOT) estuvieron asociados a los valores de X ≥ 103.
DISCUSIÓN
En un espectro del oleaje es común encontrar información de la energía asociada al swell y al oleaje local. La identificación de ESWELL y ESEA se realiza por medio del análisis del espectro direccional, calculando el área del espectro modificada por el viento y asociada con ESEA (Hanson y Phillips 2001, Tracy et al. 2007). A partir del espectro en frecuencia (SF), Hwang et al. (2012) definieron una frecuencia (ƒS) que permite separar ESWELL y ESEA; para calcular ƒS, estos autores hacen una generalización de la función pendiente de la ola usada operacionalmente por la National Data Buoy Center de la NOAA. Esta función calcula la pendiente de la ola como el producto de HS y su número de onda asociado en función de los momentos del espectro. Hwang et al. (2012) proponen una función de integración espectral (I1) modificando la función pendiente de la ola, donde SF se reemplaza por la razón entre SF y el vector de frecuencias; ƒS se calcula como la frecuencia asociada al valor máximo de la función I1. Otros métodos contemplan análisis espectrales que permiten identificar los valores de energía asociados a las bajas (ESWELL) y altas (ESEA) frecuencias por medio de la descomposición de la señal del espectro (e.g., transformada de Hilbert-Huang). En este trabajo, se utilizó el método de Hwang et al. (2012) porque está basado en conceptos físicos del comportamiento del oleaje y es un método ampliamente usado.
Comparación de los valores de HS, HSEA, HSWELL y FSEA
Las diferencias encontradas en la comparación de valores medidos y calculados de HS, HSEA, HSWELL y FSEA se pueden asociar a errores en el cálculo del espectro en frecuencia obtenido por medio de información de radar HF usando el modelo paramétrico lineal. Toro (2014) sugiere como fuente potencial de error la dependencia del parámetro αF a otras variables no consideradas en su cálculo (e.g., la dirección del oleaje). Gurgel et al. (2006) y Toro (2014) proponen que los errores en el cálculo de la información del oleaje se deben al uso de una sola estación de radar HF. Wyatt (1989) sugiere que la principal razón de los errores es la dirección de propagación del oleaje perpendicular a la dirección de medición del radar. Las características del set de datos del experimento INTOA utilizado en este trabajo coinciden con las condiciones propuestas por Wyatt (1989), Gurgel et al. (2006) y Toro (2014). Estas características del set de datos podrían incrementar los errores en los cálculos de información del oleaje.
Las valores de HSWELL variaron entre 0.5 y 1.1 m y están en concordancia con los valores registrados por García-Nava et al. (2009); sin embargo, el valor bajo de R2 (0.6) sugiere que el modelo paramétrico lineal utilizado en este trabajo no resuelve de manera adecuada la dispersión del swell. Esta dispersión se observa, en la evolución temporal del espectro, como un corrimiento del pico espectral de bajas a altas frecuencias (ver fig. 4 en Ocampo-Torres et al. 2011). Por el contrario, los espectros calculados con información de radar HF mantuvieron, la mayoría de las veces, un valor similar de la frecuencia asociada al pico del espectro del swell. No obstante, la forma y el nivel energético de los picos en los espectros medidos se lograron reproducir en los espectros calculados con los radares HF. Los valores de FSEA cercanos a 0.1Hz se pueden relacionar con eventos no tehuanos. En estos casos, debido a que la energía del espectro en el intervalo de frecuencias de ESEA es baja, el valor de FSEA encontrado es cercano al valor de ƒS calculado con el método de Hwang et al. (2011).
A pesar de las diferencias encontradas entre los valores medidos y los calculados, la concordancia adecuada de las series de tiempo y los valores bajos de los errores estadísticos sugieren que el modelo paramétrico lineal y, particularmente, el parámetro αF, que es función de U10, pueden utilizarse para obtener el espectro en frecuencia del oleaje por medio de información obtenida con radares HF.
Crecimiento del oleaje observado en el nodo de la boya ASIS y en los nodos cercanos
Las comparaciones de los valores de ESEA y FSEA calculados en función de X se realizaron con base en las curvas empíricas de Kahma y Calkoen (1992) y Hwang et al. (2011). Estas curvas son, en la actualidad, el referente principal en el cálculo de estos valores y son fundamentales para los modelos numéricos de oleaje ya que son usadas para validar el crecimiento del oleaje limitado por el fetch (Bottema y van Vledder 2009). En este trabajo, los valores asociados al crecimiento del oleaje estuvieron, en general, cercanos a las curvas empíricas. Los valores analizados en este estudio cubren un intervalo de 350 < X < 2500, que coincide con la mayoría de los trabajos estudiados.
La dispersión de los valores de ESEA y FSEA calculados con información de radar HF respecto a las curvas empíricas podría asociarse a las fuentes potenciales de error relacionadas con el cálculo del espectro en frecuencia. Sin embargo, los valores de ESEA y FSEA calculados con los datos de la boya ASIS también presentaron cierto grado de dispersión. Kahma y Calkoen (1992), Ebuchi (1999) y Bottema y van Vledder (2008) sugieren que parte de la dispersión se debe a que el análisis del crecimiento del oleaje realizado con datos in situ no cumple estrictamente con condiciones controladas de viento y fetch. De igual manera, Young y Verhagen (1996) sugieren que la dispersión es propia del análisis de datos in situ y que se debe a causas tales como la variabilidad estadística del muestreo y la precisión instrumental. Ardhuin et al. (2007) asocian la dispersión de los valores del crecimiento del oleaje respecto a las curvas empíricas con la variabilidad del viento, el desarrollo de la capa límite atmosférica y la presencia de corrientes fuertes de marea. Walsh et al. (1989) y Ardhuin et al. (2007) atribuyen parte de la dispersión de los datos a la existencia de un fetch oblicuo (slanting fetch). Romero y Melville (2010) y Hwang et al. (2011) muestran que la dispersión de los datos del experimento INTOA es similar a la obtenida con otras bases de datos, como la de Kahma y Calkoen (1992) para olas generadas bajo condiciones estables.
En este trabajo se analizó el crecimiento del oleaje estimado a partir de datos medidos in situ. Una de las suposiciones era que el viento en el área de estudio (~400 km2) era homogéneo. Hwang et al. (2011) analizaron los datos de INTOA y demostraron que las posibles causas de la dispersión de los datos respecto a las curvas empíricas eran los campos de viento no homogéneos producidos durante los eventos tehuanos y la presencia del swell que se propaga en contra del oleaje local. Los tehuanos son eventos claramente diferenciables (Hwang et al. 2011) porque se pueden caracterizar mediante valores aproximadamente constantes de la dirección del viento (θ, del norte) y valores altos de U10 (≥8 m s-1). De acuerdo con lo sugerido por diversos autores y tomando en cuenta las condiciones del experimento INTOA, las posibles causas de la dispersión de los datos respecto a las curvas empíricas son las siguientes: los errores en el cálculo del espectro en frecuencia del oleaje mediante información obtenida de radar HF, el cálculo del fetch definido mediante una aproximación lineal utilizando la dirección del viento, las suposiciones del campo de viento homogéneo y la presencia del swell.
La posible influencia del swell en los valores de ESEA y FSEA se analizó utilizando valores asociados de HSWELL y wsƒ. Las variables HSWELL y wsƒ podrían considerarse similares; sin embargo, nótese que los valores de HSWELL son independientes del oleaje local y del viento, mientras que wsƒ cuantifica de manera indirecta los valores de HSWELL. Los resultados obtenidos con estas dos variables mostraron claras diferencias entre sí. La distribución casi aleatoria de los valores de HSWELL respecto a las curvas empíricas sugiere que son los valores de ESEA los que varían significativamente. La presencia de valores de HSWELL de ~0.6 m por debajo de las curvas empíricas podría estar relacionada con los errores en el cálculo del espectro en frecuencia. Por otro lado, el factor wsƒ representa la variación de ESEA respecto a ETOT y, en este trabajo, los valores de wsƒ mostraron una clara relación con X. Debido a que los valores de X varían en menor proporción que U102 y ya que X es inversamente proporcional a U102, los valores de de wsƒ entre 0.5 y 0.85 asociados a X <103 muestran una clara influencia de valores altos de viento. De la misma manera, valores de wsƒ ≤ 0.5 asociados a X≥ 103 están relacionados con valores bajos de viento. El comportamiento de los valores de HSWELL y wsƒ utilizados en este trabajo respecto a las curvas empíricas no presentó una evidencia clara que permita definir la influencia del swell en el crecimiento del oleaje.
La posible influencia del swell en el crecimiento del oleaje también se puede analizar a partir del comportamiento de los ajustes lineales y los valores medios calculados. En el primer caso, se observó una correlación significativa de los ajustes lineales de los valores de ESEA y FSEA con los datos de radar HF y las curvas empíricas de Kahma y Calkoen (1992) y Hwang et al. (2011); por lo tanto, los ajustes lineales no permiten sugerir alguna influencia del swell en el crecimiento del oleaje. Los valores medios de ESEA y FSEA calculados con información de los 25 nodos cercanos a la boya ASIS también se encontraron cercanos a las curvas empíricas. Solamente en el caso de ESEA, cuando X> 2.5 x 103, se observaron valores por debajo de las curvas empíricas, lo cual podría representar una ligera evidencia de la influencia del swell en el crecimiento del oleaje.
Numerosos autores han estudiado la influencia del swell en el crecimiento del oleaje. Los experimentos de laboratorio (Mitsuyasu 1966, Donelan 1987) han mostrado que la presencia de ondas largas reduce drásticamente el crecimiento del oleaje. Kahma y Calkoen (1992) supusieron que ESWELL fue la causa de la dispersión de datos en el análisis del crecimiento del oleaje; sin embargo, aunque sus resultados no mostraron cambios significativos en ESEA debido a HSWELL, sugieren que el swell con pendientes pronunciadas podría influir en el crecimiento del oleaje. Por el contrario, Ardhuin et al. (2007), mediante análisis de datos in situ y modelación numérica, encontraron que los valores moderados de ESWELL opuestos al oleaje local no tienen un impacto significativo en el crecimiento del oleaje limitado por el fetch. García-Nava et al. (2012) sugieren que el swell atenúa las olas cortas pero consideran que su efecto sobre el crecimiento del oleaje es en general despreciable. Los análisis realizados en este trabajo no presentaron evidencias claras de una posible influencia del swell en el crecimiento del oleaje.
En el presente trabajo se obtuvieron valores de ESEA y FSEA en función de X asociados al crecimiento del oleaje cercanos a las curvas empíricas de Kahma y Calkoen (1992) y Hwang et al. (2011). Los valores de crecimiento presentaron una dispersión poco significativa alrededor de las curvas mencionadas. Este trabajo es uno de los primeros esfuerzos enfocados al análisis de crecimiento del oleaje utilizando mediciones de radar HF. El espectro del oleaje calculado por medio de información de radar HF presentó una correlación significativa con los valores obtenidos de mediciones in situ. Estos resultados sugieren que se puede obtener información adecuada del oleaje mediante el método novedoso utilizado para procesar las mediciones de alta resolución espacio-temporal obtenidas con radares HF y el uso de un modelo paramétrico lineal en función de la velocidad del viento.
AGRADECIMIENTOS
Este trabajo fue financiado por el Consejo Nacional de Ciencia y Tecnología (CONACYT, proyectos INGOTEPA 85108 y RugDisMar 155793), SEP-CONACYT (CB-2011-01-168173) y ANUIES-ECOS (M09-U01). RD agradece el apoyo económico de la UABC y CONACYT a través de una beca para una estancia sabática. VGT recibió apoyo de CONACYT y POGO para una beca de doctorado y una beca para una estancia de investigación, respectivamente. Agradecimientos especiales a Mónica Sánchez, Julieta Castro, Carmen Labastida e Ivonne Best por su apoyo logístico y administrativo. Una mención especial a los revisores y editores quienes, con sus comentarios, permitieron un mejoramiento sustancial en la calidad de este trabajo.
REFERENCIAS
Ardhuin F, Herbers THC, van Vledder GP, Watts KP, Jensen R, Graber HC. 2007. Swell and slanting-fetch effects on wind wave growth. J. Phys. Oceanogr. 37: 908-931. [ Links ]
Barrick DE. 1972. First-order theory and analysis of MF/HF/VHF scatter from the sea. IEEE Transactions on Antennas and Propagation 20: 2-9. [ Links ]
Barrick DE. 1977. The ocean wave height non-directional spectrum from inversion of HF sea-echo Doppler spectrum. Remote Sens. Environ. 6: 201-227. [ Links ]
Barrick DE, Headrick JM, Bogle RW, Crombie DD. 1974. Sea backscatter at HF: Interpretation and utilization of the echo. Proc. IEEE 62: 673-680. [ Links ]
Bottema M, van Vledder GP. 2008. Effective fetch and non-linear four-wave interactions during wave growth in slanting fetch conditions. Coast. Eng. 55: 261-275. [ Links ]
Bottema M, van Vledder GP. 2009. A ten-year data set for fetch- and depth-limited wave growth. Coast. Eng. 56: 703-725. [ Links ]
Breivik O, Saetra O. 2001. Real time assimilation of HF radar currents into a coastal ocean model. J. Mar. Syst. 28: 161-182. [ Links ]
Crombie DD. 1955. Doppler spectrum of sea echo at 13.56 Mc/s. Nature 175: 681-682. [ Links ]
Donelan MA. 1987. The effect of swell on the growth of windwaves. Johns Hopkins APL Tech. Dig. 8: 18-23. [ Links ]
Ebuchi N. 1999. Growth of wind waves with fetch in the Sea of Japan under winter monsoon investigated using data from satellite altimeters and scatterometer. J. Oceanogr. 55: 575-584. [ Links ]
Flores-Vidal X, Durazo R, Chavanne C, Flament P. 2011. Coastal circulation in the absence of wind in the Gulf of Tehuantepec, Mexico: High-frequency radar observations. Cienc. Mar. 37: 493-512. [ Links ]
García-Nava H, Ocampo-Torres FJ, Osuna P, Donelan MA. 2009. Wind stress in the presence of swell under moderate to strong wind conditions. J. Geophys. Res. 114: 1-12. [ Links ]
García-Nava H, Ocampo-Torres FJ, Hwang PA, Osuna P. 2012. Reduction of wind stress due to swell at high wind conditions. J. Geophys. Res. 117: C00J11. http://dx.doi.org/10.1029/2011JC007833. [ Links ]
Gurgel K-W, Essen H-H, Schlick T. 2006. An empirical method to derive ocean waves from second-order Bragg scattering: Prospects and limitations. IEEE J. Ocean. Eng. 31: 804-811. [ Links ]
Hanson JL, Phillips OM. 2001. Automated analysis of ocean surface directional wave spectra. J. Atmos. Ocean. Technol. 18: 277-293. [ Links ]
Hashimoto N, Tokuda MA. 1999. A Bayesian approach for estimating directional spectra with HF radar. Coast. Eng. 41: 137-149. [ Links ]
Hasselmann K. 1971. Determination of ocean wave spectra from Doppler radio return from the sea surface. Nature 229: 16-17. [ Links ]
Hasselmann K, Barnett TP, Bouws E, Carlson H, Cartwright DE, Enke K, Ewing JA, Gienapp H, Hasselmann DE, Kruseman P, Meerburg A, Müller P, Olbers DJ, Richter K, Sell W, Walden H. 1973. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Deutsche Hydrogr. Z. Suppl. A(8) 12: 95 pp. [ Links ]
Heron ML, Heron SF. 2001. Cumulative probability noise analysis in geophysical spectral records. Int. J. Remote Sens. 22: 2537-2544. [ Links ]
Hisaki Y. 1996. Nonlinear inversion of the integral equation to estimate ocean wave spectra from HF radar. Radio Sci. 31: 25-39. [ Links ]
Hwang PA, García-Nava H, Ocampo-Torres FJ. 2011. Observations of wind wave development in mixed seas and unsteady wind forcing. J. Phys. Oceanogr. 41: 2343-2362. [ Links ]
Hwang PA, Ocampo-Torres FJ, García-Nava H. 2012. Wind sea and swell separation of 1D wave spectrum by a spectrum integration method. J. Atmos. Ocean. Technol. 29: 116-128. [ Links ]
Kahma KK. 1981. A study of the growth of the wave spectrum with fetch. J. Phys. Oceanogr. 11: 1503-1515. [ Links ]
Kahma KK, Calkoen CJ. 1992. Reconciling discrepancies in the observed growth of wind-generated waves. J. Phys. Oceanogr. 22: 1389-1405. [ Links ]
Kitaigorodskii SA. 1962. Applications of the theory of similarity to the analysis of wind-generated wave motion as a stochastic process. Izv. Akad. Nauk SSSR Geophys. Ser. 1: 105-117. [ Links ]
Lipa BJ, Barrick DE, Maresca Jr JW. 1981. HF radar measurements of long ocean waves. J. Geophys. Res. 86(C5): 4089-4102. [ Links ]
Mitsuyasu H. 1966. Interactions between water waves and wind. Rep. Inst. Appl. Mech. 14: 67-88. [ Links ]
Ocampo-Torres FJ, García-Nava H, Durazo R, Osuna P, Díaz-Méndez GM, Graber HC. 2011. The INTOA Experiment: A study of ocean-atmosphere interactions under moderate to strong offshore winds and opposing swell conditions in the Gulf of Tehuantepec, Mexico. Bound-Lay Meteorol. 138: 433-451. [ Links ]
Pantoja DA, Marinone SG, Parés-Sierra A, Gómez-Valdivia F. 2012. Numerical modeling of seasonal and mesoscale hydrography and circulation in the Mexican Central Pacific. Cienc. Mar. 38: 363-379. [ Links ]
Romero L, Melville WK. 2010. Airborne observations of fetch-limited waves in the Gulf of Tehuantepec. J. Phys. Oceanogr. 40: 441-465. http://dx.doi.org/10.1175/2009JPO4127.1. [ Links ]
Toro VG. 2014. Estudio sobre el crecimiento del oleaje limitado por el fetch en presencia de swell utilizando radares de alta frecuencia. PhD Thesis, Centro de Investigación Científica y de Educación Superior de Ensenada, Ensenada, Baja California, México. 145 pp. [ Links ]
Tracy B, Devaliere E-M, Hanson J, Nicolini T, Tolman H. 2007. Wind sea and swell delineation for numerical wave modeling. 10th International Workshop on Wave Hindcasting and Forecasting and Coastal Hazard Symposium. Oahu, Hawaii, pp. 11-16. [ Links ]
Tuomi L, Kahma KK, Fortelius C. 2012. Modelling fetch-limited wave growth from an irregular shoreline. J. Mar. Syst. 105-108: 96-105. [ Links ]
Velázquez-Muñoz FA, Martínez JA, Chavanne C, Durazo R, Flament P. 2011. Wind-driven coastal circulation in the Gulf of Tehuantepec, Mexico. Cienc. Mar. 37: 443-456. [ Links ]
Velázquez-Muñoz FA, Martínez JA, Durazo R. 2014. Numerical simulation of ocean response by offshore wind stress events. In: Klapp et al. (eds.), Experimental and Computational Fluid Mechanics. Springer-Verlag, pp. 93-110. [ Links ]
Walsh EJ, Hancock DW, Hines DE, Swift RN, Scott JF. 1989. An observation of the directional wave spectrum evolution from shoreline to fully developed. J. Phys. Oceanogr. 19: 670-690. [ Links ]
Wyatt LR. 1989. Measuring the ocean wave directional spectrum with HF radar: The inversion problem. In: Brooks S (ed.), Mathematics in Remote Sensing. Clarendon Press, Oxford, pp. 279-291. [ Links ]
Wyatt LR. 1990. A relaxation method for integral inversion applied to HF radar measurement of the ocean wave directional spectra. Int. J. Remote Sens. 11: 1481-1494. [ Links ]
Wyatt LR. 2012. Use of HF radar for marine renewable applications. Proc. Oceans 2012, Yeosu, Korea, 5 pp. [ Links ]
Wyatt LR, Green JJ, Gurgel K-W, Nieto Borge JC, Reichert K, Hessner K, Günther H, Rosenthal W, Saetra O, Reistad M. 2003. Validation and intercomparisons of wave measurements and models during the EuroROSE experiments. Coast. Eng. 48: 1-28. [ Links ]
Young IR, Verhagen LA. 1996. The growth of fetch limited waves in water of finite depth. Part 1. Total energy and peak frequency. Coast. Eng. 29: 47-78. http://dx.doi.org/10.1016/S0378-3839(96)00006-3. [ Links ]














