Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Ciencias marinas
versão impressa ISSN 0185-3880
Cienc. mar vol.29 no.2 Ensenada Jun. 2003
Artículos
Barotropic background currents in the Gulf of California
Corrientes básicas barotrópicas en el Golfo de California
Vyacheslav Makarov* and Ángel Jiménez-Illescas
Centro Interdisciplinario de Ciencias Marinas Instituto Politécnico Nacional de México Av. Instituto Politécnico Nacional s/n Col. Palo de Santa Rita Apartado postal 592 La Paz, CP 23096, Baja California Sur, México. *E-mail: smakarov@ipn.mx
Recibido en junio de 2002;
aceptado en diciembre de 2002.
Abstract
A field of barotropic background currents (BC) in the Gulf of California is constructed numerically. The definition of BC used here is based on suppositions about (i) the horizontal homogenization of potential vorticity in large-scale gyres, and (ii) the tendency of a current structure to evolve to a state with a minimum of system mechanical energy. In the barotropic case here, the numerical algorithm is reduced to the solution of the Dirichlet boundary problems for planetary, topographic and flowing integral streamfunction components separately. The results obtained are compared to observations and the results of other numerical models. The calculated barotropic BC realistically describe the main features of the circulation in the southern part of the Gulf of California, including its mouth. Cyclonic movement in the deep-water and anticyclonic movement near the coasts are observed. The numerical results for the central and northern parts of the gulf, where seasonal climatological differences are pronounced, coincide with observations in the upper layer only during the winter season; i.e., the circulation here is anticyclonic. Thus, there are reasons to suggest that mainly planetary-topographic forcing, especially in the southern part, forms the circulation in the lower layer. The seasonal variability of currents in the upper layer caused by non-stationary effects such as wind, heat flux and baroclinicity, is apparently in phase with these mechanisms during winter, and in antiphase during summer, particularly for the central and northern gulf.
Key words: Gulf of California, background currents, potential vorticity, barotropic model, planetary-topographic forcing.
Resumen
Un campo de corrientes básicas (CB) barotrópicas en el Golfo de California se construyó numéricamente. La definición de CB utilizada aquí se basa en las suposiciones sobre (i) la homogeneización horizontal de vorticidad potencial en los giros de macroescala y (ii) la tendencia de la estructura de las corrientes a evolucionar hacia un estado con un mínimo de energía mecánica del sistema. En un caso barotrópico el algoritmo numérico se reduce a la solución, separadamente, de los problemas de frontera de Dirichlet para las componentes topográfica, planetaria y de flujo de la función integral de corriente. Los resultados obtenidos se compararon con las observaciones y con los resultados de otros modelos numéricos. Las CB barotrópicas calculadas describen, de una manera realista, las características principales de la circulación en la parte sur del Golfo de California, incluyendo su boca. Se ha observado aquí un movimiento ciclónico en agua profunda y un movimiento anticiclónico cerca de ambas costas. Los resultados numéricos para las partes central y norte del golfo, donde las diferencias climatológicas estacionales son pronunciadas, coinciden con las observaciones en la capa superior solamente durante la estación de invierno; i.e., la circulación aquí es anticiclónica. Por tanto, hay razones para sugerir que principalmente el forzamiento topográfico-planetario, especialmente en la parte sur, forma la circulación en la capa inferior. La variabilidad estacional de las corrientes en la capa superior, causada por efectos no estacionarios tales como el viento, el flujo de calor y la baroclinicidad, aparentemente está en fase con estos mecanismos durante el invierno y está en antifase durante el verano, particularmente para la parte central y norte del golfo.
Palabras clave: Golfo de California, corrientes básicas, vorticidad potencial, modelo barotrópico, forzamiento planetario-topográfico.
Introduction
The hydrographic investigations in the Gulf of California have more than one century of history. Descriptions of the area and the results of oceanographic surveys in the gulf can be found, for example, in the review papers of Roden (1958, 1964), Álvarez-Borrego (1983), Cano-Pérez (1991), and Bray and Robles (1991). Later reviews (Lavín et al., 1997a; Marinone and Lavín, 1997) also include the outcomes of numerical modeling.
This semi-enclosed sea is a large evaporation basin that has its own warm, highly saline water mass of several types (Bray, 1988b), but there is no record of any permanently existing current here. Pronounced seasonal variability of many oceanographic parameters is a characteristic feature of the dynamic and thermohaline structure in the gulf (Baumgartner and Christensen, 1985; Robles and Marinone, 1987; Ripa, 1997). An exception is a vorticity field, which does not show a seasonal cycle, at least in the central gulf (Ripa and Marinone, 1989). Another generally accepted fact is the monsoon-type wind: stronger down-gulf (i.e., northwesterly) during most of the year and weaker up-gulf (southeasterly) in the subtropical summer (Badan-Dangon et al., 1991). Other causes of seasonal variability in the upper layer are different thermohaline structure-forming conditions (e.g., Bray, 1988b) and the influence of the Pacific Ocean through the mouth, for example in the form of a Kelvin wave (Beier, 1997; Ripa, 1997).
The entrance to the gulf is wide and very deep, and thus has its own complicated dynamics, which until now has not been fully studied. Water transport estimates vary from 0.9 Sv (Bray, 1988a, for the central part) to 12 Sv (Roden, 1972). Furthermore, there is no unified opinion regarding the circulation direction. It is traditionally considered that in summer, outflow of gulf water occurs along the coast of the Baja California peninsula and ocean water penetrates along the coast of the mainland, and that in winter, the situation is reversed (e.g., Bray, 1988a; Beier, 1997). Castro et al. (2000) reported that the water exchange at the mouth occurs via cyclonic circulation in spring, fall and winter.
The intricate bottom relief complicates the dynamics even further. The bathymetry of the Gulf of California consists of a system of semi-local basins arranged lengthwise along the gulf that deepen approaching the entrance. The northern gulf is rather shallow, while the continental shelf in the center and south has only a narrow zone, predominantly near the mainland coast. Such a structure should promote the generation of differently scaled eddies and dynamical fronts, which are evident in satellite infrared imagery (Badan-Dangon et al., 1985; Paden et al., 1991; Santamaría-del-Ángel and Álvarez-Borrego, 1994; Lavín et al., 1997b). These effects were also detected by means of the analysis of geostrophic currents from temperature and salinity observations (Álvarez-Sánchez et al., 1978; Marinone and Ripa, 1988; Fernández-Barajas et al., 1994; Collins et al., 1997), and identified on the basis of direct current measurements (Collins et al., 1997; Emilsson and Alatorre, 1997; Lavín et al., 1997b). In addition, the gulf's gaunt configuration causes strong tidal effects, especially in the north, with amplitudes of more than 10 m and velocities of 2-3 m s-1. Such complicated interactions of dynamic phenomena hamper detection of the relative roles of mechanisms and the definition of the hierarchy of these processes on the basis of only oceanographic observations. For this, it is necessary to use numerical simulation.
Various models have been used for the numerical simulation of circulation in the Gulf of California. Dressler (1981) modeled wind-driven vertically integrated currents; Carbajal (1993) applied a three-dimensional homogeneous model. A two-layer linear baroclinic model was used by Beier (1997) for the study of a seasonal cycle in the gulf. Mesoscale circulation induced by atmospheric effects was studied by Martínez (2002). The numerical simulation of the main (somehow background) circulation in the Gulf of California is carried out, as a rule, with the aid of different models of tide- and/or wind-induced residual currents (e.g., Argote et al., 1998). The influences of the most important tidal constituents (Marinone, 1997) and the topographic stress parameterization effects (Marinone, 1998) on circulation were studied. An interesting approach was used by Velasco-Fuentes and Marinone (1999), who investigated advective transport in the field of the flows, computed by a non-linear two-dimensional barotropic model with tide and wind. Most numerical models reproduce the following surface circulation characteristics: generally cyclonic in summer and anticyclonic in winter, with an expressed gyre in the northern part of the gulf and alongshore flows in the southern part. Due to insufficient hydrographic observations for the entire gulf, the baroclinic factors were taken into account on the assumption of a two-layer ocean only (Beier, 1997).
In this study, we attempt to simulate background or main currents forced by only basic stationary mechanisms, reflecting the properties of the region without the influence of external non-steady factors such as wind stress, heat flux and tides. The results of calculations for the Gulf of California with a simple but sufficiently meaningful barotropic model are presented. The results obtained were compared with the existing concepts about the peculiarities of the circulation in this region.
Methodology
The notion of background currents, usually defined as a circulation averaged in some way, is widely used in dynamic oceanology. Here, we used a constructive definition of this notion that was offered by Kozlov (1995). This approach is based on the assumption of conservation of potential vorticity (hereafter PV) n, which is one of the basic characteristics of quasi two-dimensional geophysical currents. It combines contributions of relative vorticity, planetary-topographic interactions and stratification in a general case. The PV in the case of infinitesimally small viscosity is a Lagrangian invariant, i.e., it satisfies the equation (Pedlosky, 1979):

where (u, v) is the vector of horizontal velocity. Due to its invariance, the field of PV is a more suitable characteristic for the determination of the current structure than relative vorticity, so the currents with horizontally homogeneous distribution of PV satisfying (1) can be reasonably accepted as background currents (hereafter BC). The so-called Rhines-Young theorem (Rhines and Young, 1982), often applied both for the construction of different models and for the interpretation of observations, can be used to substantiate the homogenization of PV. It is clear that the structure of the currents depends on the magnitude of PV. The unique solution may be selected on the criterion that the total mechanical energy (sum of kinetic and sensible potential energies) of the system should be minimal. This allows finding a unique value of PV and calculating the relative vorticity field corresponding to it. In general, the background relative vorticity is a function of bottom relief, planetary vorticity and stratification. Some results of the modeling and analysis of BC for the Japan and Okhotsk seas were obtained by Kozlov and Makarov (1996a, b) using this approach.
The model
As is known (see Von Schwind, 1980) for a barotropic ocean, PV has the form

where ƒ(x, y) is the Coriolis parameter associated with planetary vorticity, o = vx - uy is the relative vorticity, and H(x, y) is the depth of the sea. Under the condition of a "rigid lid" at the surface, o is defined by means of the integral streamfunction V using the well-known relation

Substitution of (3) into (2) leads to the subsequent equation for the integral streamfunction

For the nearly closed area D, the boundary condition can be written as

where l is the coordinate along ∂D and Ψ(b) is the given water transport, for example, through the straits. For constant PV, the conservation law is identically valid, and the derivative Φ = ∂Ψ/∂Π according to (1) and (2) is the solution of the boundary problem

The kinetic energy E = (1/2) • ∫D(1/H) • (∇Ψ)2dD is a square function of the parameter Π, where ∇ is a two-dimensional nabla operator. The derivation by this parameter leads to the expression

Since the integral of first term in the square brackets vanishes, the condition of minimum energy reduces to ∫D Φ • (Π • H - f )dD = 0. Now the minimal value Π- = 〈f〉/〈H〉 of PV can be easily found by means of the weighted mean value definition for an arbitrary function F
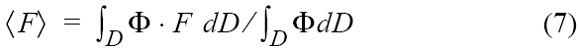
where Fmin ≤ 〈F〉 ≤ Fmax due to Φ ≤ 0. Consequently, equation (4) may be rewritten as

where

represent the topographic and planetary relative background vorticity, respectively.
Thus, we come to a constructive definition of BC as the solution of the boundary problem (8), (5). Obviously, it is first necessary to find the distribution of the auxiliary function O as the solution of the boundary problem (6), and then to calculate the vorticity fields (9) using the definition (7).
According to the structure of the right-hand side of the linear problem (8), (5), the total BC in the field of integral streamfunction are the sum of three components: planetary BC Ψ(f)and topographic BC Ψ(H) with closed boundaries, and irrota-tional flow Ψ(q) caused by the water transport through the boundary ∂D. The parameter 〈ƒ〉 defines the critical latitude, dividing areas of opposite vorticity in the planetary BC field: cyclonic (anticyclonic) in the southern (northern) parts of the sea, which gives a dipole character to the vorticity. The parameter 〈H〉 defines the critical isobath in a similar way, dividing the "shallow-" and "deep-watef parts of the sea, where the relative vorticity of the topographic BC has opposite signs: cyclonic when H > 〈H〉 and anticyclonic when H < 〈H〉. So, the structure of the current depends significantly on the character of the bottom topography that could lead to a division into separate gyres. However, we can always confirm the cyclonic character of circulation in deep-water basins, and anticyclonic velocity shear on the shelf. The total BC field is determined by the values of relative contributions of all three components.
Numerical results
The calculations for the Gulf of California were carried out using spherical coordinates (λ, φ) on a five-minute regular grid. The Coriolis parameter was, as usual, ƒ = 2Ω • sin φ, and the vorticity operator had the form LΨ = [(Ψφ cos φ/H)φ + (Ψλ/H)λ/cos φ]/(R2 cos φ), where R and Ω are the average radius and the angular velocity of the Earth. The ETOPO5 bottom topography archive from the NOAA Oceanographic Data Center (www.nodc.noaa.gov) was used for grid construction and bottom relief approximation (fig. 1). To conserve the simply connected property of the area, a few islands were artificially submerged to a depth of 1 m. Also, the narrow (in relation to grid step) channel between Tiburón Island and the mainland was neglected on the computational grid. The boundary problems (6) for auxiliary function O and (8), (5) for integral streamfunction Ψ were approximated by a monotonic scheme of the second order of accuracy.

Boundary conditions
We considered a line across the entrance to the gulf as the single liquid boundary, neglecting river discharge. To use the boundary condition in form (5) it is necessary to know the values of the integral streamfunction across the mouth, but until now, this area has not been adequately investigated, at least concerning the direction and value of water transport. A reasonable alternative (or supplementation) to (5) is the application of the so-called "free water passage" condition on the "liquid"
part ∂Dl of the total boundary, usually formulated by way of ∂Ψ/∂n|∂Dl = 0, where n is the normal vector to ∂Dl.
The boundary problem (6) for the auxiliary function then becomes

where ∂Ds is the "solid" part of the boundary, and therefore, the parameters 〈ƒ〉 and 〈H〉 obtain other values. In calculations of BC we used both versions of the boundary condition, but mainly the second in this work.
Planetary BC
The boundary problem for this component is

In the case of (10), the calculated parameter 〈ƒ〉 gives the value 25°19' for the critical latitude, above which the motion is anticyclonic and below which it is cyclonic. In the case of (6), i.e., the fully closed boundary (hereafter FCB), this value increases until 25°34.5'. The planetary BC in the field of the integral streamfunction Ψ(ƒ) with amplitude A(ƒ)= Ψ(ƒ)max - Ψ(ƒ)min ≈ 22.07 Sv is shown in figure 2a. There are two gyres of anticyclonic rotation in the central and northern parts of the gulf, and a cyclonic gyre with amplitude of 14.25 Sv in the southern deep part. The central and northern gyres have amplitudes of less than 50% and about 20%, respectively, of the amplitude of the southern ring. The total amplitude for the FCB case is 17.34 Sv, but the intensities of the anticyclonic gyres remain nearly the same. The main difference is that the streamlines in the FCB case are closed in the mouth region.
Topographic BC
The topographic component of BC (fig. 2b) is a solution of the boundary problem


The calculated critical depth is 1722.5 m (1659.7 m for the FCB case), and thus the area of relative topographic cyclonic vorticity according to (9) is located over the deep southern basin of the gulf, and consists of two nuclei over the Pescadero and Farallón basins. The region of opposite rotation in the central part of the gulf includes a few anticyclonic eddies according to features of the bottom topography. In the northern gulf, only one anticyclonic gyre is present. The southern cyclonic gyre is the most intense, with amplitude of 70 Sv, while the total amplitude is 88.6 Sv (79.9 for the FCB case). Anticyclonic transport constitutes 17% and 21% of this value for the northern and central parts of the gulf, respectively. Topographic transport exceeds the planetary transport more than four times. In addition, these effects are in phase for the Gulf of California: the positions of the identically rotating gyres practically coincide for both components.
Effective BC
The total integral streamfunction for the barotropic BC is a sum of planetary and topographic streamfunctions, due to the linearity of equation (8). For the general case, there is a third component, a non-vortex flow Ψ(q), caused by the water transport through ∂D. The model gives the value 106.8 Sv (94.3 for the FCB case) for the total transport A = Ψmax -Ψmin, which exceeds the values observed in the upper layer by approximately one order of magnitude. A similar problem also appeared during the modeling of BC in the Japan and Okhotsk seas (Kozlov and Makarov, 1996a, b). This is a shortcoming of this barotropic model, which leaves out the known effect of damping to a surface of topographic fluctuations owing to vertical stratification. For an assessment of the surface circulation, we used a technique of Kozlov and Makarov (1996a), which consists essentially of some quantitative calibration, founded on estimation of real or supposed water transport across the liquid boundaries. We supposed that the effective BC in the upper layer could be obtained from the barotropic component with the use of the reduction or efficiency constant coefficient, i.e., Ψ(e) = α • (Ψ(H) + Ψ(ƒ)), without taking Ψ(q) into consideration. To determine α for the Gulf of California, we used approximate evaluations of the water transport in the entrance area, which were obtained by Collins et al. (1997) on the basis of direct observations. The intensity of circulation at the mouth was about 5.8 Sv with the value of 0.07 obtained for the efficiency parameter α. The maximum amplitude of the integral streamfunction Ψ(e) in the northern part of the gulf was near 1.2 Sv, and in the central gulf near 1.6 Sv.
Due to predominance of the topographic component, the effective BC for α = 0.07 presented in figure 2c is not considerably different from the scheme in figure 2b. The vector field of mean horizontal velocities may by easily constructed using the relations u = -Ψy(e)/H and v = Ψx(e)/H. The result is shown in figure 3a. The maximal velocities (more then 0.5 m s-1) are observed over the shelf and in the vicinity of the archipelago in the northern part of the gulf. Lower speeds occur in the deep central region. In both areas the direction of movement is anti-cyclonic. The southern gulf has a more complicated velocity field, because of the strong cyclonic circulation in the middle and anticyclonic circulation near the coasts.

A qualitative analysis of the vertical velocities is possible using the expression

for the horizontal divergence, where J is the Jacobian. It is evident that (11) gives only direction of vertical movement, but not magnitudes. The calculated upwelling zones are shown in figure 3b, where darkened areas indicate greater intensity. The spatial distribution of the horizontal divergence has a spotted appearance, correlated with a complicated bottom relief.
Discussion and conclusions
We now compare the calculated effective BC pattern (fig. 3 a) in the Gulf of California with prevalent concepts about the character of circulation in this region. An anticyclonic movement of considerable speeds occupies the northern part of the gulf. The presence of this permanent gyre, which in a longer winter has anticyclonic rotation, is confirmed by the analysis of hydrological observations and direct measurements (e.g., Lavín et al., 1997b). Most numerical models reproduce this gyre. In a shorter summer, however, the direction of currents (as well as wind) reverses due to seasonal variability in the basic geophysical parameters of this generally shallow region (e.g., Carrillo et al., 2002).
In our scheme, a well-organized southward flow with speeds of about 0.2 m s-1 occurs in the main gulf, along practically all the mainland coast. The existence of such a stream in the winter season is confirmed by both observations and numerical results (Beier, 1997; Argote et al., 1998; Marinone, 1998; Velasco-Fuentes and Marinone, 1999). An opposite northward flow along the coast of the peninsula is also present, but this is not so well organized either in summer or in winter, as figure 3a demonstrates. Over the deep part of the central gulf above 26°N, the movement is anticyclonic with low speeds. There is a point of view (Álvarez-Sánchez et al., 1978; Bray, 1988a; Beier, 1997) that the surface circulation patterns there and in the entrance zone also have strong seasonal features. However, Marinone and Ripa (1988) did not find a significant seasonal signal either for surface circulation or, notably, for deep-water circulation for the Guaymas region, for example. Neither did they find a seasonal signal for the relative vorticity field (Ripa and Marinone, 1989). Nevertheless, changes in wind and surface heat flux directions in summer lead to reconstruction of the thermohaline structure; at least wind and baroclinicity in the gulf are in phase (Beier, 1997). These effects, and probably a transformation of the Kelvin wave that penetrates from the Pacific (e.g., Ripa, 1997), evidently dominate in the upper layer and have an effect against the planetary-topographic mechanisms in summer. Therefore, at least on the surface, the directions of currents can reverse, including the alongshore flows, which may have a baroclinic origin.
The circulation in the southern part of the gulf, especially in the mouth region, is very intricate. As shown in figure 3a, a powerful cyclonic gyre exists over the entire deep-water area. Its intensity consists of almost 80% of the total intensity for the entire gulf circulation. The gyre has two cores: one located above the Pescadero basin, in the mouth of the gulf, and the other one above the Farallón basin. At the same time, circulation in the vicinity of La Paz Bay and near the Sinaloa coast, where the continental slope is rather flat, remains anticyclonic. The heavy line in figure 3a indicates the boundary between cyclonic and anticyclonic regions; essentially it is a dynamic front. According to the scheme proposed here, the main inflow of ocean water occurs through the central part of the mouth, closer to the mainland, and the outflow from the gulf is carried along both coasts. Velasco-Fuentes and Marinone (1999) obtained a similar result for winter with a nonlinear, vertically integrated, barotropic model on the f-plane. The analysis of the geostrophic flows, calculated with a dynamic method on the basis of observations from November to December 1969 (Roden, 1972) and February 1992 (Fernández-Barajas et al., 1994), also lead to similar patterns. In August 1992, the inflow was deepened and occurred below 100 m (Fernández-Barajas et al., 1994). The detailed examinations of this region, which were carried out in April, May and December 1992 (Collins et al. , 1997), and the observations from eight oceanographic cruises between 1992 and 1998 (Castro et al., 2000), indicated that the exchange of water between the gulf and the Pacific Ocean, in the southern part of Pescadero Basin, occurred via cyclonic circulation throughout most of the year. No evidence of the outflow from the gulf along the Sinaloa coast exists in these data, however. The cyclonic vortex in the region of the Farallón Basin, first detected through direct measurement by Emilsson and Alatorre (1997) in August 1978, was also present in a field of geostrophic flows for February and August 1992 (Fernández-Barajas et al., 1994). Amador-Buenrostro et al. (2003) reported that the cyclonic structure was almost permanently present in this region on the satellite images. They gave results of direct measurements for the end of November 1997 that demonstrate the existence of this structure. The northward flow near La Paz Bay was also detected in these observations. Such a situation may lead to anticyclonic eddy generation in the vicinity of the EBES seamount. González-Armas et al. (2002) came to similar conclusions based on analyses of copepod and macrozooplankton distributions around the EBES seamount that indicated an upwelling in addition to the probable presence of the eddy. Upwelling also has a place here in our horizontal divergence distribution (fig. 3b). This scheme demonstrates the presence of rather intensive upwelling, mainly on both coasts of the gulf, in the archipelago and in the upper half of the northern gulf. The existence of upwelling in these regions is confirmed by both observations and analysis of satellite images (Badan-Dangon et al., 1985; Álvarez-Borrego and Lara-Lara, 1991; Santamaría-del-Ángel and Álvarez-Borrego, 1994; Santamaría-del-Ángel et al., 1999). It should be noted that coastal upwelling in the gulf is usually connected to the effects of wind stress: the winter upwelling occurs predominately at the mainland, and the summer upwelling, usually weak, occurs near the coast of the peninsula.
Thus, the calculated barotropic BC realistically describe the main features of actual circulation in the southern part of the Gulf of California, including the region of the entrance. The good agreement with the observations suggests that largely planetary-topographical effects support the main circulation in this region. It should be noted that the topography plays a noticeable role in forming the baroclinic structure. The seasonal variability in the southern gulf is apparently not so strongly expressed, except for a surface layer. The background circulation in the central and northern parts of the gulf, where there are drastic seasonal climatological changes, coincides with observations in the upper layer for only the longer winter season. It is clear that the calculated BC are affected chiefly by the contribution of the lower layer. Thus, the predominantly surface seasonal variability is apparently in phase with barotropic planetary-topographic mechanisms during winter and in antiphase during summer.
The authors do not want to overestimate the importance of the barotropic model used here, which can exaggerate the topographical circulation component, while failing to consider other significant factors. Within the framework of the definition of BC utilized here, the construction of more complicated quasi-geostrophic models for the two-layer and continuously stratified ocean is possible (Kozlov, 1995). This approach dampens topographic fluctuations, and in the immediate future, we propose using the model of baroclinic ocean for this area. The model can also be applied to the creation of a stationary mean flow field as background for the examination of non-stationary effects, including chaotic advection (Kozlov and Koshel', 1999). In any case, even this elementary barotro-pic model of BC has allowed us to construct a realistic background circulation for the Gulf of California as reference.
Acknowledgements
This research was supported by funding from the Mexican National Polytechnical Institute (No. 20010321). We thank the anonymous reviewers for their suggestions and comments, which improved the text, and William P. Black for editing the English-language text.
References
Álvarez-Borrego, S. (1983). Gulf of California. In: B.H. Ketchum (ed.), Estuaries and Enclosed Seas. Elsevier, Amsterdam, pp. 427-448. [ Links ]
Álvarez-Borrego, S. and Lara-Lara, J.R. (1991). The physical environment and primary productivity of the Gulf of California. In: J.P. Dauphin and B.R. Simoneit (eds.), The Gulf and Peninsular Province of the Californias. Am. Assoc. Pet. Geol., Mem., 47: 555-567. [ Links ]
Álvarez-Sánchez, L.G., Wyatt, B. y Stevenson, M.R. (1978). Corrientes en la región de la boca del Golfo de California en la primavera de 1970. Ciencias Marinas, 5(1): 105-118. [ Links ]
Amador-Buenrostro, A., Trasviña-Castro, A., Muhlia-Melo, A. and Argote-Espinoza, M.L. (2003). Structure of the flow on the EBES seamount and the Farallón basin in the Gulf of California, November 1997. Geofísica Internacional (in press).
Argote, M.L., Lavín, M.F. and Amador, A. (1998). Barotropic eulerian residual circulation in the Gulf of California due to the M2 tide and wind stress. Atmósfera, 11: 173-197. [ Links ]
Badan-Dangon, A., Koblinsky, C.J. and Baumgartner, T. (1985). Spring and summer in the Gulf of California: Observations of surface thermal patterns. Oceanol. Acta, 8(1): 13-22. [ Links ]
Badan-Dangon, A., Dorman, C.E., Merrifield, M.A. and Winant, C.D. (1991). The lower atmosphere over the Gulf of California. J. Geophys. Res., 96(C9): 16877-16896. [ Links ]
Baumgartner, T.R. and Christensen, Jr. N. (1985). Coupling of the Gulf of California to large-scale interannual climatic variability. J. Mar. Res., 43: 825-848. [ Links ]
Beier, E. (1997). A numerical investigation of the annual variability in the Gulf of California. J. Phys. Oceanogr., 27: 615-632. [ Links ]
Bray, N.A. (1988a). Thermohaline circulation in the Gulf of California. J. Geophys. Res., 93(C5): 4993-5020. [ Links ]
Bray, N.A. (1988b). Water mass formation in the Gulf of California. J. Geophys. Res., 93(C8): 9223-9240. [ Links ]
Bray, N.A. and Robles, J.M. (1991). Physical Oceanography of the Gulf of California. In: J.P. Dauphin and B.R. Simoneit (eds.), The Gulf and Peninsular Province of the Californias. Am. Assoc. Pet. Geol., Mem., 47: 511-553. [ Links ]
Cano-Pérez, F.A. (1991). Golfo de California: Oceanografía física. En: G. Lanza-Espino (ed.), Oceanografía de Mares Mexicanos. AGT Editor, México, D.F., pp. 453-514. [ Links ]
Carbajal, N. (1993). Modeling of the circulation in the Gulf of California. Ph.D. thesis, Institute fur Meerskunde, Hamburg, 186 pp. [ Links ]
Carrillo, L., Lavín, M.F. and Palacios-Hernández, E. (2002). Seasonal evolution of the geostrophic circulation in the northern Gulf of California. Estuar. Coast. Shelf Sci., 54(2): 157-173. [ Links ]
Castro, R., Mascarenhas, A.S., Durazo R. y Collins, C.A. (2000). Variación estacional de la temperatura y salinidad en la entrada del Golfo de California, México. Cien. Mar., 26(4): 561-583. [ Links ]
Collins, C.A., Garfield, N., Mascarenhas Jr. A.S. and Sperman, M.G. (1997). Ocean current across the entrance to the Gulf of California. J. Geophys. Res., 102(C9): 20927-20936. [ Links ]
Dressler, R. (1981). Investigación sobre mareas y efectos de viento en el Golfo de California, mediante un modelo H-N. Sammlung von Publikationen Dressler. Nr. 2. Unpublished manuscript, 26 pp. [ Links ]
Emilsson, I. y Alatorre, M.A. (1997). Evidencias de un remolino ciclónico de mesoescala en la parte sur del Golfo de California. En: M.F. Lavín (ed.), Contribuciones a la Oceanografía Física en México. Monografía No. 3, Unión Geofísica Mexicana, México, pp. 173-182. [ Links ]
Fernández-Barajas, M.E., Monreal-Gómez, M.A. y Molina-Cruz, A. (1994). Estructura termohalina y flujo geostrófico, en el Golfo de California, durante 1992. Cien. Mar., 20(2): 267-286. [ Links ]
González-Armas, R., Palomares-García, R. and Silvia-Dávila, R. (2002). Copepod and macrozooplankton distribution associated to El Bajo Espíritu Santo seamount. In: M.E. Hendrickx (ed.), Contribution to the Study of East Pacific Crustaceans. Instituto de Ciencias del Mar y Limnología, UNAM, México, pp. 183-193. [ Links ]
Kozlov, V.F. (1995). Background currents in geophysical hydrodynamics. Izv. Atmos. Ocean. Phys., 31(2): 229-234. [ Links ]
Kozlov, V.F. and Makarov, V.G. (1996a). Background currents in the Sea of Japan (a barotropic model). Oceanology, 35(3): 601-604. [ Links ]
Kozlov, V.F. and Makarov, V.G. (1996b). Background currents in the Sea of Okhotsk. Russ. Meteorol. Hydrol., 9: 39-44. [ Links ]
Kozlov, V.F. and Koshel', K.V. (1999). Barotropic model of chaotic advection in background flows. Izv. Atmos. Ocean. Phys., 35(1): 123-130. [ Links ]
Lavín, M.F., Beier, E. y Badan, A. (1997a). Estructura hidrográfica y circulación del Golfo de California: Escalas estacional e interanual. En: M.F. Lavín (ed.), Contribuciones a la Oceanografía Física en México. Monografía No. 3, Unión Geofísica Mexicana, México, pp.141-171. [ Links ]
Lavín, M.F., Durazo, R., Palacios, E., Argote, M.L. and Carillo, L. (1997b). Lagrangian observations of the circulation in the northern Gulf of California. J. Phys. Oceanogr., 27(10): 2298-2305. [ Links ]
Marinone, S.G. (1997). Tidal residual currents in the Gulf of California: Is the M2 tidal constituent sufficient to induce them? J. Geophys. Res., 102(C4): 8611-8623. [ Links ]
Marinone, S.G. (1998). Effect of the topographic stress on the tide-and wind-induced residual currents in the Gulf of California. J. Geophys. Res., 103(C9): 18437-18446. [ Links ]
Marinone, S.G. and Ripa, P. (1988). Geostrophic flow in the Guaymas Basin, central Gulf of California. Cont. Shelf Res., 8(2): 159-166. [ Links ]
Marinone, S.G. and Lavín, M.F. (1997). Mareas y corrientes residuales en el Golfo de California. En: M.F. Lavín (ed.), Contribuciones a la Oceanografía Física en México. Monografía No. 3, Unión Geofísica Mexicana, México, pp.111-131. [ Links ]
Martínez, A. (2002). Modeling studies of mesoscale circulation in the Gulf of California. Ph.D. thesis, Oregon State University. [ Links ]
Paden, C.A., Abbott, M.R. and Winant, C.D. (1991). Tidal and atmospheric forcing of the upper ocean in the Gulf of California. 1. Sea surface temperature variability. J. Geophys. Res., 96(C10): 18337-18359. [ Links ]
Pedlosky, J. (1979). Geophysical Fluid Dynamics. Springer-Verlag, New York, 624 pp. [ Links ]
Rhines, P.B. and Young, W.R. (1982). Homogenization of potential vorticity in planetary gyres. J. Fluid Mech., 122: 347-357. [ Links ]
Ripa, P. (1997). Towards a physical explanation of the seasonal dynamics and thermodynamics of the Gulf of California. J. Phys. Oceanogr., 27: 597-614. [ Links ]
Ripa, P. and Marinone, S.G. (1989). Seasonal variability of temperature, salinity, velocity, vorticity and sea level in the central Gulf of California, as inferred from historical data. Q. J. R. Meteorol. Soc., 115: 887-913. [ Links ]
Robles, J.M. and Marinone, S.G. (1987). Seasonal and interannual thermohaline variability in the Guaymas Basin of the Gulf of California. Cont. Shelf Res., 7(7): 715-733. [ Links ]
Roden, G.I. (1958). Oceanographic and meteorological aspects of the Gulf of California. Pacific Sci., 12(1): 21-45. [ Links ]
Roden, G.I. (1964). Oceanographic aspect of the Gulf of California. In: Tj.H. van Andel and G.G. Shor Jr. (eds.), Marine Geology of the Gulf of California: A Simposium. Am. Assoc. Pet. Geol., Mem., 3: 30-58. [ Links ]
Roden, G.I. (1972). Thermohaline structure and baroclinic flow across the Gulf of California entrance and in the Revillagigedo Islands region. J. Phys. Oceanogr., 2: 177-183. [ Links ]
Santamaría-del-Ángel, E. and Álvarez-Borrego, S. (1994). Gulf of California biogeographic regions based on coastal zone color scanner imagery. J. Geophys. Res., 99(C4): 7411-7423. [ Links ]
Santamaría-del-Ángel, E., Álvarez-Borrego, S., Millán-Núñez, R. y Muller-Karger, F.E. (1999). Sobre el efecto débil de las surgencias de verano en la biomasa fitoplanctónica del Golfo de California. Rev. Soc. Mex. Hist. Nat., 49: 207-212. [ Links ]
Velasco-Fuentes, O.U. and Marinone, S.G. (1999). A numerical study of the Lagrangian circulation in the Gulf of California. J. Mar. Syst., 22: 1-12. [ Links ]
Von Schwind, J.J. (1980). Geophysical Fluid Dynamics for Oceanographers. Prentice-Hall, Englewood Cliffs, New York, 307 pp. [ Links ]














