Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Salud mental
versão impressa ISSN 0185-3325
Salud Ment vol.35 no.1 México Jan./Fev. 2012
Artículo original
Aplicación del análisis estadístico de datos censurados para el manejo de respuestas incompletas en la escala CES–D
Application of censored–data analysis for managing CES–D incomplete responses
Ietza Rocío Bojorquez–Chapela,1 Belem Trejo Valdivia,2 V. Nelly Salgado de Snyder2
1 El Colegio de la Frontera Norte.
2 Centro de Investigación en Evaluación y Encuestas. Instituto Nacional de Salud Pública.
Correspondencia:
V. Nelly Salgado de Snyder.
Centro de Investigación en Sistemas de Salud,
Instituto Nacional de Salud Pública,
México. Av. Universidad 655, Col. Santa María Ahuacatitlán,
Cuernavaca, Mor., México.
E–mail: nelly.salgado@insp.mx
SUMMARY
Purpose
To provide an example of censored data analysis in the management of CED–S missing data, using a data set of a study conducted with Mexican rural women.
Material and Methods
Data used for this exercise were collected in a cross–sectional study with 416 women in the Mexican region known as the Mixteca Baja. Using a Survival Analysis (SA) focus we present a general description of the scores, along with the estimation of association patterns between those scores and the independent variables departing from Cox's proportional risk model. A comparison is made of these results and those obtained through a regression analysis.
Results
Using only the information from observations with complete data, the average CES–D score was 11.0 and the prevalence of symptoms above the cut–off point (16) was 23.2%. Twenty–six percent of the women did not respond to at least one item. When conducting the SA, the estimated mean score of the scale was 14.0. Survival above the cut–off point corresponded to an estimated prevalence of 21%.
Conclusions
SA is useful in the management of data sets with missing data in scales such as the CES–D. In this example, the increased percentage of observations with missing data produced a loss of precision in the estimators. The differences in mean item scores between observation with complete and incomplete data suggested a non–random, no–response pattern, if this is not taken into consideration it could bias the estimation in the scale mean and its association with other variables. Conducting SA we were able to use the information of most women participating in the study, including those who did not respond to all items in the scale.
Key words: Analysis of censored data, survival analysis, CES–D.
RESUMEN
Objetivo
Ejemplificar el uso del análisis de datos censurados en el manejo de datos incompletos de la CES–D utilizando una base de datos de un estudio con mujeres rurales de México.
Material y Método
Los datos analizados se recogieron en un estudio transversal con 416 mujeres de la Mixteca Baja, al sur de México. Con un enfoque de Análisis de Supervivencia (AS), se presenta una descripción general del comportamiento de las puntuaciones de la CES–D junto con la estimación de patrones de asociación entre esos puntajes y variables independientes a partir del modelo de riesgos proporcionales de Cox, y se hace una comparación entre estos resultados y los obtenidos de un modelo de regresión lineal.
Resultados
Utilizando sólo la información de las observaciones con datos completos, la puntuación promedio de la CES–D fue de 11.0 y la preva–lencia de síntomas por arriba del punto de corte (16) fue de 23.2%. El 25.2% de las mujeres no contestó al menos un reactivo. Al hacer el AS, el promedio estimado de la puntuación fue de 14.8. La supervivencia por encima del punto de corte corresponde a una prevalencia estimada del 21%.
Conclusiones
El AS es útil en el manejo de bases que presentan datos faltantes por ejemplo en escalas como CES–D. En nuestro ejemplo, el elevado porcentaje de observaciones con respuestas faltantes ocasionó una pérdida de precisión en los estimadores. Las diferencias de puntuaciones promedio por reactivo entre observaciones con datos perdidos y completos sugieren un patrón de no–respuesta que no es aleatorio, y que de no tomarse en cuenta podría sesgar la estimación, tanto del promedio de la escala como de su asociación con otras variables. El AS utilizó la información de casi la totalidad de las participantes en el estudio incluyendo aquellas que no respondieron todos los reactivos de la escala.
Palabras clave: Análisis de datos censurados, análisis de supervivencia, CES–D.
INTRODUCCIÓN
De acuerdo con estimaciones de la Organización Mundial de la Salud (OMS), para el año 2020 la depresión ocupará el segundo lugar en el rango de los padecimientos que contribuyen con un mayor peso a la carga global de la enfermedad.1 En México, la prevalencia de depresión a nivel nacional es de 4.5%, con una prevalencia más alta (5.8%) para las mujeres.2 El reto principal para la atención de este tipo de problemas es la dificultad para identificar síntomas y acudir a solicitar ayuda profesional. En general los problemas de salud mental pasan desapercibidos, tanto para quienes los padecen como para sus familiares y la comunidad en general, ya que frecuentemente los síntomas no son inhabilitantes y no producen dolor físico ni molestias de salud física.3
La detección de posibles casos de depresión, por medio de la evaluación de los síntomas, en investigaciones con población abierta, no institucionalizada, es importante porque al hacer la traducción de los resultados permite hacer recomendaciones puntuales a los sistemas de salud para la confirmación oportuna del diagnóstico clínico en las unidades de primer nivel de atención y su referencia a especialistas para el tratamiento adecuado.
Existe una gran cantidad de instrumentos que se han desarrollado con el propósito de identificar posibles casos de depresión e incluso de diagnosticarlos por la aplicación de entrevistas administradas por personas especialmente capacitadas, como el Composite International Diagnostic Interview (CIDI), avalado por la OMS.4 Sin embargo, en encuestas poblacionales los más utilizados son instrumentos breves, con reactivos generalmente de respuesta cerrada que miden los síntomas más comunes de la depresión, por ejemplo la Escala de Depresión del Centro de Estudios Epidemiológicos (CES–D)5 y las escalas de Hamilton,6 Zung7 y Beck.8
La CES–D es un instrumento que tiene una serie de características que lo han convertido posiblemente en el instrumento de tamizaje más utilizado en la investigación con población abierta para identificar la presencia de malestar psicológico generalizado o sintomatología depresiva.
Su utilidad como un instrumento de tamizaje para la investigación poblacional se ha mantenido a través de los años. Si bien la CES–D no permite hacer el diagnóstico de un trastorno psiquiátrico, es un indicador válido de la presencia e intensidad del malestar emocional.9–11
Un problema con el uso de escalas en salud mental es la falta de respuesta a uno o más de los reactivos que las componen.12,13 Este problema es más frecuente cuando las escalas se administran a población abierta en entornos social y económicamente marginados, debido a la posible falta de compresión de algunos reactivos y/o a la confusión en la interpretación de la pregunta. La no respuesta a uno o más reactivos de una escala ocasiona una disminución en el número efectivo de participantes y puede afectar al poder para detectar asociaciones estadísticamente significativas y disminuir la precisión de los estimadores. Además, la no respuesta a algunos reactivos podría deberse a características de los individuos. En esta situación, que se da por ejemplo en el caso de no respuesta diferencial por sexo, nivel educativo, o dependiente de la verdadera puntuación en la característica que está siendo evaluada (en este caso la puntuación total, no observada, en la escala), se presentan sesgos en las estimaciones, resultando en conclusiones erróneas y recomendaciones poco sólidas.14
Se han propuesto diversas soluciones para el manejo de respuestas faltantes a los reactivos.12–14 La más sencilla consiste en excluir de los análisis que requieran la puntuación de la escala a los participantes con datos incompletos (<<análisis de casos completos>>). Si la no respuesta a los reactivos ocurre completamente al azar, ésta es una estrategia razonable. En cambio, si la no respuesta se asocia con características del participante, excluirlos podría causar resultados sesgados. Otras maneras de manejar las situaciones con datos incompletos se basan en la imputación de valores. En los métodos de imputación se adjudica un valor a los reactivos que quedaron sin responder y se obtiene la suma total en la escala a partir de los valores imputados, más los valores realmente observados. Para la adjudicación de valores una de las técnicas más frecuentes en la investigación en salud mental es la imputación por la media, en la que se obtiene el promedio de puntuación de los reactivos que sí contestó el individuo y se adjudica este valor a los reactivos que no se respondieron. Mediante este procedimiento se soluciona el problema de la pérdida de poder, pero tiene la debilidad de estar basado en el supuesto de que las respuestas a todos los reactivos son similares. Este supuesto puede no ser cierto, por ejemplo, cuando los reactivos perdidos representan dimensiones de la escala diferentes a las dimensiones representadas por los reactivos que sí se respondieron. Otros métodos de imputación explican la puntuación en los reactivos como resultado de otras variables y adjudican los valores predichos a los reactivos que quedaron sin responder, o adjudican los valores de la observación más parecida en sus características generales a aquella con datos perdidos.15 El supuesto común en estas técnicas es que las variables utilizadas como predictores son adecuadas, lo cual, nuevamente, podría no ser cierto.
Una solución novedosa al problema de la no respuesta a reactivos individuales de una escala la constituye el uso de análisis de datos censurados, en donde una de las áreas más populares es el análisis de supervivencia (AS).16 El uso más conocido del AS es en el modelamiento del tiempo entre la ocurrencia de dos eventos, a través de la función de supervivencia o de la función de riesgo. Una de las ventajas del análisis de supervivencia es la posibilidad de utilizar información de todas las observaciones, no sólo de aquellas en las que el seguimiento fue completo sino también de aquellas que se censuraron, para la construcción de estas funciones.16,17
Al aplicar el AS al manejo de datos incompletos en una escala, se establece una analogía en la que el proceso de ir respondiendo a los reactivos de la escala simula el proceso de seguimiento, por lo que un individuo con <<seguimiento>> completo sería aquel que respondió a todos los reactivos, y los individuos con valores faltantes en una o más respuestas se consideran pérdidas en el seguimiento o censuradas. Con este enfoque para el manejo de la información es posible utilizar tanto las observaciones con <<seguimiento completo>> (aquellas con respuestas a todos los reactivos de la escala), como la información de las <<censuras>> (observaciones con respuestas faltantes en uno o más reactivos) en el análisis general de la escala y en el análisis de los patrones de asociación entre la puntuación total en ésta y otras variables de interés. El análisis de supervivencia tiene la ventaja de aprovechar la información de todos los individuos en la muestra, de no hacer imputaciones sobre los datos censurados y de no requerir supuestos distribucionales sobre el proceso de censura.
El objetivo de este artículo es proponer una aproximación novedosa al manejo de los datos incompletos en la CES–D, utilizando información de un estudio en mujeres de una zona rural mexicana. Para ello, se describe en primer lugar el patrón de datos incompletos en las respuestas a los reactivos de la escala, siguiendo las recomendaciones de Schlomer et al.13 Con el enfoque de Análisis de Supervivencia se presenta una descripción general del comportamiento de las puntuaciones de la CES–D en la muestra, junto con la estimación de patrones de asociación entre la puntuación en la CES–D y una serie de variables independientes de interés a partir del modelo de Cox de riesgos proporcionales; finalmente se hace una comparación entre estos resultados y los obtenidos a partir de un modelo de regresión lineal. Mediante este ejercicio, las autoras hacen una aportación al conocimiento de una herramienta poco explotada para el análisis de información de escalas en salud mental, en situaciones con gran número de datos faltantes.
MATERIAL Y MÉTODO
Muestra
Los datos que aquí se analizan se recogieron como parte de un estudio transversal sobre las asociaciones entre migración y salud.* La investigación se llevó a cabo en 2005, en tres municipios rurales de los Estados de Guerrero, Oaxaca y Puebla, que forman parte de la región denominada La Mixteca Baja. El proyecto fue aprobado por la Comisión de Ética del Instituto Nacional de Salud Pública.
El muestreo siguió un diseño estratificado por municipios, al interior de cada municipio se seleccionaron localidades por muestreo proporcional a la población de las mismas y se seleccionaron hogares dentro de las localidades mediante muestreo sistemático. En cada hogar se entrevistó a una mujer en edad reproductiva. Pueden consultarse mayores detalles acerca de los métodos del estudio en el trabajo de Bojorquez, Salgado y Cacique.18 La muestra estuvo compuesta por 468 mujeres de entre 15 y 49 años de edad. Para el análisis que se presenta se utilizaron únicamente los datos de aquellas que al momento de la encuesta se encontraban casadas o en unión libre (n=416), ya que uno de los aspectos explorados fue la relación entre migración internacional del cónyuge y síntomas depresivos (SD) en la mujer.
Instrumento
Las participantes respondieron un cuestionario que incluía información demográfica (edad, estado de unión, etc.), así como preguntas acerca de la situación de migración del cónyuge y diversos temas de salud.
Se utilizó la CES–D para evaluar la presencia e intensidad de la sintomatología depresiva en la semana previa a la entrevista.5 La CES–D es un instrumento diseñado para el estudio de síntomas de depresión en encuestas comunitarias que ha mostrado ser sensible a la mejoría en pacientes deprimidos, ser confiable de acuerdo al criterio de test–retest y tener buena validez de criterio en comparación con una entrevista psiquiátrica estandarizada.9,10,19,20 La CES–D está compuesta por 20 reactivos, que representan seis áreas componentes de la depresión, tanto anímicas como somáticas: ánimo deprimido, culpa/minusvalía, desesperanza, retardo psicomotor, pérdida del apetito y alteraciones del sueño. Las respuestas, en escala tipo Likert, corresponden a la frecuencia de estos síntomas en la última semana. El rango teórico de la escala va de 0 a 60, con una mayor puntuación indicando mayor número y frecuencia de SD. Se ha sugerido que una puntuación por encima de 16 puede considerarse clínicamente significativa.19
La escala fue previamente probada en México con mujeres en una zona rural, mostrando buena validez y confiabilidad.11 En la muestra que aquí se reporta, utilizando sólo las observaciones con datos completos, los reactivos que componen la escala tuvieron un valor de a de Cronbach = 0.84.21
Análisis estadístico
En el Proyecto Mixteca, algunas mujeres no respondieron a la totalidad de los reactivos de la CES–D, por lo que las respuestas en la muestra constituyen un conjunto de datos con información incompleta. El Análisis de Supervivencia (AS) puede utilizarse en el análisis de datos incompletos, abordándolos como censuras, esto es, observaciones en que sólo se cuenta con una parte de la información.16 En el AS, cuando el tiempo hasta la falla es igual o mayor al tiempo durante el cual se siguió al individuo, se dice que se trata de una censura por la derecha.17 Las respuestas faltantes a los reactivos de la CES–D constituyen censuras por la derecha, ya que sabemos que la verdadera puntuación es al menos tan alta como la observada, y por tanto que, de haberse tenido respuesta a todos los reactivos, la puntuación hubiera sido igual o mayor a ésta. Así, como variable indicadora de la censura en este análisis se utilizó el tener o no datos completos en la CES–D, donde el valor 1 correspondió a una observación con datos completos (falla) y el valor 0 a una observación con datos incompletos (censura). Dicho de otra manera, el tiempo de supervivencia (puntuación total en la CES–D) es conocido para las mujeres que respondieron a todos los reactivos del instrumento, y es desconocido para aquellas que dejaron uno o más reactivos sin responder, por lo que estas últimas se consideran como censuras y las primeras como fallas. El AS toma en cuenta la información de las observaciones censuradas y modela la función de supervivencia, que representa la probabilidad de que un individuo alcance al menos cierto valor.22 En nuestro caso, la probabilidad de que una participante obtuviera un puntaje mayor o igual a cierto valor de la escala equivaldría a la función de supervivencia.
Para el análisis, dado que el rango de puntuación en la CES–D inicia en 0, lo que no corresponde estrictamente a una puntuación nula sino a la más baja posible, con fines de cómputo se utilizó un valor de 0.01 como puntuación total obtenida en el caso de que ésta fuera de 0. El análisis exploratorio de la información se enfocó en el comportamiento de la tabla de vida, el estimador Kaplan–Meier de la función de supervivencia, y de aquí se calcularon el tiempo mediano (puntaje mediano) y la media restringida (puntaje promedio).
Uno de los temas de interés en el Proyecto Mixteca fue la asociación entre la migración internacional del cónyuge y la presencia de SD en las mujeres que permanecían en las localidades de origen. Para ejemplificar las ventajas del uso de AS en situaciones de datos faltantes, se muestran sus resultados para esta asociación. Para mostrar un ejemplo más realista de análisis incluyendo covariables, se utilizó una regresión de Cox para riesgos proporcionales, en la que se incluyeron como variables de ajuste, además de la migración del cónyuge (1= migrante, 0= no migrante), la edad de la mujer (años) y su condición laboral (tiene trabajo remunerado= 1, no lo tiene= 0). Se verificaron los supuestos del modelo mediante análisis de residuos generalizados. El modelo de riesgos proporcionales de Cox permite estimar la razón de riesgos de presentar la falla en un momento dado, entre individuos con diferentes valores de las variables independientes de interés. En este caso, los resultados deben interpretarse como la razón de riesgos de terminar de contestar la CES–D (falla) con una cierta puntuación, comparando entre mujeres con y sin cónyuge migrante, con y sin trabajo remunerado, y con un año más de edad. Esto es, un incremento en el riesgo debe interpretarse como una mayor probabilidad de tener puntuaciones más bajas. Los resultados con el modelo de Cox se comparan con los de una regresión lineal que incluyó a las mismas variables, pero que no tomó en cuenta la información de las mujeres con cuestionarios incompletos.
RESULTADOS
Se incluyeron en el análisis 416 mujeres, casadas o en unión libre al momento de la entrevista. El rango de edad fue de 15 a 49 años (promedio 34.8 años, d. e. 8.3 años). El 34.1% de las participantes reportó que su esposo era migrante a los Estados Unidos y el 22.7% dijo tener trabajo remunerado.
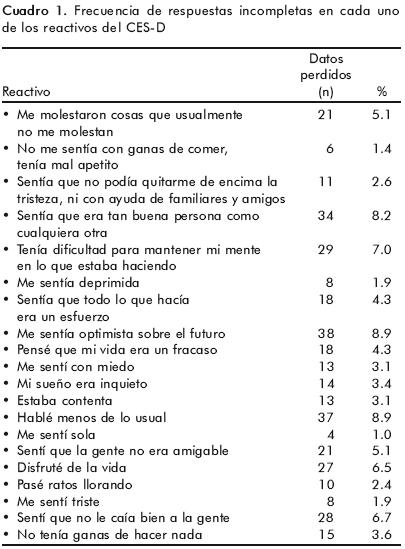
Al utilizar sólo la información de las observaciones con datos completos, el promedio de puntuación en la CES–D fue de 11.0 (d.e. 8.9, rango 0–51), y la prevalencia de síntomas por encima del punto de corte de 16 fue de 23.2%. El 25.2% (105) de las mujeres dejó de contestar al menos uno de los reactivos del CES–D.
El cuadro 1 muestra el porcentaje de datos faltantes para cada uno de los reactivos, el cual varía desde 1.0% para <<me sentí sola>>, hasta 8.9% para <<me sentía optimista sobre el futuro>> y <<hablé menos de lo usual>>. Las mujeres con datos faltantes en al menos uno de los reactivos no fueron diferentes a quienes tuvieron respuestas completas en términos de edad (t=0.9912, p=.322), ni del porcentaje con cónyuge migrante (35.6% vs 33.6%, chi2=.1427, p=.706), pero un porcentaje significativamente mayor de ellas (31.4%) tenía empleo remunerado, en comparación con quienes tuvieron respuestas completas (19.7%) (chi2=6.1820, p=.013). El promedio de puntuación en los reactivos individuales fue de 0.6 (d.e.= 0.5) para las mujeres con datos incompletos, y de 0.5 (d.e. = 0.4) para las mujeres con datos completos.
La figura 1 presenta la probabilidad de que una mujer obtenga un puntaje igual o mayor que un valor dado (equivalente a la curva de supervivencia de Kaplan–Meier). Se observa que esta probabilidad disminuye rápidamente, lo que en este caso debe interpretarse como que es muy poco probable que se observen puntuaciones muy altas en la CES–D en este grupo poblacional. A partir de esta misma curva se identifica el tiempo mediano igual a 12 (IC 95% 11, 13); esto es, de manera global cada mujer tiene un 50.0% de probabilidades de obtener un puntaje mayor o igual que 12; adicionalmente, el área bajo esta curva es una estimación del puntaje promedio y en este caso corresponde a un valor de 14.8 (IC 95% 13.6,16.1). Este último resultado muestra que el promedio calculado sólo con base en las observaciones con datos completos (11.0) es una subestimación del verdadero valor.

Por otro lado, la probabilidad de que una mujer alcance un puntaje por encima del valor de 16 en la CES–D fue de 0.21, lo que equivaldría a tener una estimación de prevalencia de 21.0% para la puntuación por encima del punto de corte de este instrumento.
El ajuste de un modelo de riesgos proporcionales permite identificar una asociación significativa entre tener un cónyuge migrante y el tener un empleo remunerado, con el puntaje de SD en la mujer, mientras que la edad no se asocia con SD (cuadro 2).
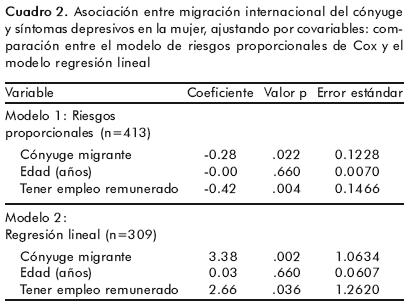
El coeficiente negativo asociado con tener un cónyuge migrante indica que aquellas mujeres con cónyuge migrante tendían a tener puntuaciones más altas en la CES–D que aquéllas cuyo cónyuge no era migrante. Lo mismo ocurre para el efecto de tener un empleo remunerado. Por otro lado, el modelo de regresión lineal ajustado para los datos completos en la CES–D mostró un resultado en la misma dirección (mayores puntuaciones entre las mujeres con cónyuge migrante y empleo remunerado) (cuadro 2). Sin embargo, las estimaciones de los efectos anteriores tienen una mayor precisión dentro del modelo de Cox ya que utiliza información de 413 mujeres (la totalidad de la muestra, menos dos mujeres sin información de situación de migración del cónyuge, y una sin información de empleo remunerado), mientras que el modelo de regresión lineal emplea solamente los datos de 309 mujeres, al excluir a aquellas con datos incompletos en el CES–D.
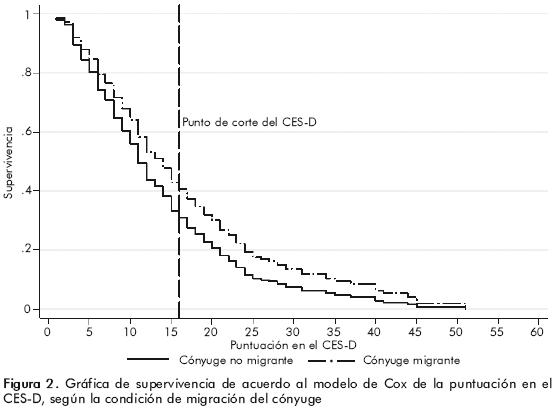
En la figura 2 se comparan las probabilidades de obtener puntuaciones iguales o mayores que cada valor entre las mujeres con y sin cónyuge migrante, obtenidas a partir del modelo de riesgos proporcionales de Cox. En ella se observa que la probabilidad de tener puntuaciones elevadas en la CES–D es constantemente mayor para las mujeres cuyo cónyuge había migrado. De acuerdo con esta estimación, la probabilidad de que una mujer en este último grupo tuviera una puntación mayor al punto de corte del instrumento, fue casi 25% mayor a la de las mujeres cuyo cónyuge no había migrado.
DISCUSIÓN
En las situaciones en que no se cuenta con respuestas a todos los reactivos de una escala, los abordajes más frecuentes son la exclusión del análisis de aquellos casos con datos incompletos, y los diversos métodos de imputación de valores.12,14 Como se mencionó en la introducción, el análisis de casos completos tiene dos desventajas importantes: la pérdida de eficiencia y la posibilidad de que los individuos con datos completos tengan puntuaciones no representativas de las de la muestra original. En cuanto a la imputación de valores, uno de los métodos más utilizados en salud mental, el de la imputación de la media, se basa en la teoría psicométrica convencional que asume que los reactivos de una escala son indicadores de un sólo constructo subyacente. Sin embargo, en una escala multidimensional como la CES–D esto no necesariamente se cumple. Además, este método conduce a una subestimación de la varianza ya que la dispersión de los reactivos alrededor de la media se disminuye artificialmente.13,14 Una de las soluciones para estos problemas es el uso de pesos diferenciados a los reactivos en la predicción de los valores perdidos.23 De acuerdo con un estudio de simulación, los métodos de imputación múltiple o mediante máxima verosimilitud permiten en general obtener mejores resultados en comparación con la imputación de la media, aunque esto depende en parte del tipo de estimación de interés.13,15 Sin embargo, todos estos métodos implican hacer uso de valores no observados para estimar las asociaciones de interés en el estudio.
En este artículo mostramos cómo el Análisis de Supervivencia (AS) puede contribuir en el manejo de situaciones en que escalas como la CES–D presentan una gran cantidad de datos faltantes. En nuestro ejemplo, el elevado porcentaje de observaciones con respuestas perdidas en la escala ocasionó una pérdida de precisión en los estimadores. Además, la diferencia en las puntuaciones promedio en los reactivos, que fueron más elevadas para las mujeres con datos faltantes, sugieren un patrón de no respuesta no aleatorio, que si no se toma en cuenta podría ocasionar un sesgo en la estimación, tanto del promedio en la escala como de la asociación entre ésta y otras variables de interés. El uso del AS permitió utilizar la información de casi la totalidad de las mujeres participantes en el estudio original, algo que no se hubiera conseguido de haberse eliminado del análisis a aquellas que no respondieron a la totalidad de los reactivos de la escala.
Al comparar los resultados con los obtenidos en el análisis tradicional observamos dos diferencias que deben resaltarse: primero, que la media de puntuación estimada fue menor en este último, lo que podría representar una subestimación, debida a que las personas con más SD tuvieron más probabilidad de no contestar la totalidad del cuestionario. La segunda diferencia consiste en la mayor precisión obtenida en los estimadores.
Hasta donde sabemos, no se han reportado otras experiencias con el uso del Análisis de Supervivencia para el manejo de datos incompletos en escalas para la medición en salud mental. Se trata de un campo en el que aún es necesario investigar, para definir por ejemplo en qué clase de datos resulta más conveniente este tipo de análisis y su desempeño en comparación con métodos de imputación. Como una primera aproximación, este trabajo constituye una propuesta para el análisis de información de escalas en salud mental, cuando interesa hacer este análisis aprovechando toda la información disponible.
REFERENCIAS
1. Murray CJL, Lopez AD (eds). The global burden of disease: A comprehensive assessment of mortality and disability from disease, injuries and risk factors in 1990 and projected in 2020. 1st Ed. Boston: Harvard School of Public Health; 1996. [ Links ]
2. Belló M, Puentes–Rosas E, Medina–Mora ME, Lozano R. Prevalencia y diagnóstico de depresión en población adulta en México. Salud Pública Mex 2005;47(1):S4–S11. [ Links ]
3. Organización Mundial de la Salud (OMS). Mental health and development. Ginebra: Ediciones de la OMS; 2010. [ Links ]
4. Kessler RC, Andrews G, Mroczek D, Ustun TB et al. The World Health Organization Composite International Diagnostic Interview Short Form (CIDI–SF). Int J Method Psych 1998;7(4):171–185. [ Links ]
5. Radloff LS. The CES–D Scale: A self–report depression scale for research in the general population. Appl Psych Meas 1977;1:385–401. [ Links ]
6. Hamilton M. Development of a rating scale for primary depressive illness. Br J Soc Clin Psychol 1967;6(4):278–296. [ Links ]
7. Zung WWK. A self–rating depression scale. Arch Gen Psychiat 1965;12:63–70. [ Links ]
8. Beck AT, Ward CH, Mendelson M, Mock J et al. An inventory for measuring depression. Arch Gen Psychiat 1961;4:561–571. [ Links ]
9. Haringsma R, Engels GI, Beekman AT, Spinhoven P. The criterion validity of the Center for Epidemiological Studies Depression Scale (CES–D) in a sample of self–referred elders with depressive symptomatology. Int J Geriatr Psychiatry 2004;19(6):558–563. [ Links ]
10. Caracciolo B, Giaquinto S. Criterion validity of the center for epidemiologic studies depression (CES–D) scale in a sample of rehabilitation inpatients. J Rehabil Med 2002; 34(5): 221–225. [ Links ]
11. Salgado de Snyder VN, Maldonado M. Respuestas de enfrentamiento e indicadores de salud mental en esposas de emigrantes a los Estados Unidos. Salud Mental 1992;15(4):28–35. [ Links ]
12. Dunn G. Statistics in psychiatry. Londres: Arnold; 2000. [ Links ]
13. Schlomer GL, Bauman S, Card NA. Best practices for missing data management in counseling psychology. J Couns Psychol 2010;57(1):1–10. [ Links ]
14. Fayers PM, Curran D, Machin D. Incomplete quality of life data in randomized trials: missing items. Stat Med 1998;17(5–7):679–696. [ Links ]
15. Peyre H, Lepelège A, Coste J. Missing data methods for dealing with missing items in quality of life questionnaires. A comparison by simulation of personal mean score, full information maximum likelihood, multiple imputation, and hot deck techniques applied to the SF–36 in the French 2003 decennial health survey. Qual Life Res 2011;20(2):287–300. [ Links ]
16. Klein JP, Moeschberger ML. Survival analysis: Techniques for censored and truncated data. Nueva York: Springer; 2003. [ Links ]
17. Kleinbaum DG, Klein, M. Survival analysis: A self–learning text. Nueva York: Springer; 1996. [ Links ]
18. Bojorquez I, Salgado N, Casique I. International migration of partner, autonomy and depressive symptoms among women from a Mexican rural area. Int J Soc Psychiatr 2009;55(4):306–321. [ Links ]
19. Weissman MM, Sholonskas D, Pottenger M, Prusoff BA et al. Assessing depressive symptoms in five psychiatric populations: A validation study. Am J Epidemiol 1997;106:203–214. [ Links ]
20. Bowling A. Measuring disease: A review of disease–specific quality of life measurement scales. Buckingham: Open University Press; 1995. [ Links ]
21. Bojorquez I, Salgado de Snyder N. Características psicométricas de la Escala Center for Epidemiological Studies–depression (CES–D), versiones de 20 y 10 reactivos, en mujeres de una zona rural mexicana. Salud Mental 2009;32:299–307. [ Links ]
22. Collett D. Modelling survival data in medical research. 2da Ed. Boca Ratón: Chapman & Hall/CRC; 2003. [ Links ]
23. Gale T, Hawley C. A model for handling missing items on two depression rating scales. Int Clin Psychopharmacol 2001;16(4):205–214. [ Links ]
* Proyecto <<Migration, health and mental health in the context of globalization>>, financiado por The Wellcome Trust, grant GR074006MA.














