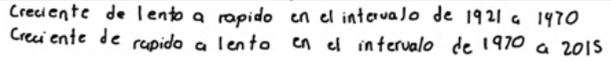Introducción1
A partir del cambio en el modelo educativo de México en el año 2017, los autores de este artículo hemos tenido la oportunidad de ser parte de un grupo de profesionales conformado por docentes e investigadores (en formación o consolidados) de matemática educativa para colaborar en el acompañamiento de docentes de matemática en el nivel de preparatoria (formación de estudiantes entre 15 a 18 años). El modelo educativo centra su atención en los aprendizajes esperados que corresponden a descriptores del proceso de aprendizaje e indicadores del desempeño que deben lograr los estudiantes para cada uno de los contenidos específicos (SEP, 2017).
El acompañamiento docente está muy relacionado con la literatura referida al “coaching” como modelo para la asesoría en la educación. Si bien su traducción es “entrenamiento” o “capacitación” (traducción que no calza con nuestra visión de acompañamiento), muchos trabajos en esta línea muestran su interés en la reflexión alrededor de la práctica docente más allá de pensar en posibles deficiencias o en la enseñanza de contenido (Neuberger, 2012; Piper y Zuilkowski, 2015; Silva-Peña et al., 2013).
Para la construcción de lo que significa acompañamiento docente se reflexiona alrededor de los trabajos de Robertson (Robertson, 2009; Robertson y Miller, 2007; Robertson y Webber, 2000), pues consideramos que es un modelo de trabajo donde se crea una relación especial y recíproca entre las personas que trabajan juntas para lograr un determinado objetivo profesional, en este caso, en la educación matemática. Este modelo está centrado en la reflexión generada por la interacción del colectivo y las implicaciones que conlleva en el escenario escolar y el saber matemático.
El equipo de colaboración trabajó en la confección de materiales (videos, audios, actividades para el aula y su rediseño), así como en diversas reflexiones para cada uno de los aspectos de los aprendizajes esperados que se presentan en los seis ejes del modelo educativo, y otros relacionados con los ambientes propicios de aprendizaje (como son género, interculturalidad, gestión y recursos, entre otros), con el objetivo de acompañar al docente en la comprensión y gestión del cambio curricular. Se elaboraron más de 380 materiales junto con el apoyo en foros que involucran reflexiones con el docente inscrito en la página web2 creada para este fin.
Este trabajo muestra el proceso que se vivió para la confección de cuatro materiales relacionados con el aprendizaje esperado sobre localizar máximos, mínimos e inflexiones en gráficas de funciones. Se busca ayudar a la reflexión del docente sobre el saber escolar en juego, pero que además resulte de utilidad en un escenario real de la escuela.
Dentro del escenario escolar prevalece el manejo procedimental rígido, fuertemente orientado o restringido al uso del álgebra o propiedades analíticas para el estudio de los máximos, mínimos y puntos de inflexión de una función (Castañeda, 2002). Esto muestra la forma en la que se enseñan la concavidad y el punto de inflexión y cómo son abordados como prácticas en el aula, ya que prevalecen los procedimientos y reglas con derivadas, que se aplican algunas veces de forma mnemotécnica. Ésta es una de las razones por las cuales se desea investigar sobre este contenido matemático, con el fin de ofrecer al docente una nueva perspectiva que enriquezca el aprendizaje matemático de dicho contenido, centrado en su significado desde el uso en contextos situacionales reales.
En este sentido, Jones (2019) muestra varios significados de la concavidad en una función y se apoya en ejemplos en contextos reales para aportar al significado del punto de inflexión. Este autor considera al mundo real para referirse a cualquier contexto perteneciente al mundo físico en el que vivimos, ya sea de la física, la química, la biología, la economía, la geografía o la cosmología.
Para el diseño de los materiales se tomó en cuenta la temporización con variables discretas para la comprensión de los datos recolectados del comportamiento de un fenómeno y el estudio de su cambio, lo que nos brinda significados de los máximos, mínimos y puntos de inflexión. De acuerdo con Cantoral et al. (2018: 83) la temporización consiste en “discretizar el fenómeno reconociendo las etapas intermedias en su desarrollo”.
Este estudio tiene un carácter de investigación y acción social. El problema que abordamos es ¿cómo contribuye la consideración de un contexto real de un fenómeno que se presenta con datos discretos en la comprensión y significado de los máximos, mínimos y puntos de inflexión en las gráficas de funciones?, y ¿cómo esto contribuye en la comprensión y significado de los máximos, mínimos y puntos de inflexión en las gráficas de funciones? Con el objetivo de acompañar y brindar una propuesta a docentes para la significación de los puntos de inflexión, mínimos y máximos en las gráficas de funciones partimos de la hipótesis de que el estudio local de estos datos da un carácter predictivo a la gráfica de una función, apoyados desde el estudio del cambio en un contexto situacional real.
Encuadre teórico
Este trabajo se desarrolla desde el enfoque de la teoría socioepistemológica de la matemática educativa, específicamente desde la línea del pensamiento y lenguaje variacional (Cantoral y Farfán, 1998), cuyo propósito es permitir la articulación entre la investigación y las prácticas que dan vida a la matemática de la variación y el cambio en los sistemas didácticos. El pensamiento y lenguaje variacional forma parte del pensamiento humano que estudia los cambios e invariantes que pueden surgir al realizar un proceso que lleve a la transición de un estado E i a un estado E j y viceversa.
De acuerdo con Cantoral et al. (2018) la variación comprende una cuantificación del cambio en las variables de un fenómeno; no puede ser cualquier variable, sino aquéllas que están relacionadas causalmente. Por otro lado, el primer orden de variación consiste en la medición del incremento en el valor de la variable de estudio; el segundo, en la medición del incremento del primer orden de variación, y así sucesivamente para órdenes de variación superiores.
Sobre esto y su relación con la derivada tenemos que este concepto se construye a través de la síntesis que resulta del estudio de cada orden de derivada, donde se han identificado características y relaciones entre cada orden, así como la información que proporcionan; al coordinar toda esa información surgen elementos que posibilitan expresar el concepto de derivada como tal (Castañeda, 2002).
Castañeda (2002) problematiza en torno al punto de inflexión al analizar las obras de los matemáticos Guillaume de L’Hôpital y María Gaetana Agnesi. Menciona que la característica de tales obras es su carácter geométrico presente en las argumentaciones y explicaciones: “algunas caracterizaciones de los conceptos del cálculo tienen fundamento geométrico, por lo cual no se requiere disponer de mayores argumentos que algunas nociones de la geometría” (Castañeda, 2002: 39).
Para este estudio se profundiza sobre el trabajo realizado por Agnesi (1748) titulado Instituzioni analitiche ad uso della gioventù italiana, por tres motivos: i) es una obra creada para el aprendizaje de los principios del álgebra, geometría cartesiana y cálculo basado en el método didáctico propuesto por la autora para la juventud italiana que inicia estudios de la matemática (Mazzotti, 2001); ii) la autora explica que “el uso de la geometría dentro de su obra proporcionaba sencillez al estudio de las nociones del cálculo” (Castañeda, 2002: 39); y iii) por la reflexión que comparten Farfán y Simón-Ramos (2018) sobre considerar aspectos de género en las problematizaciones del saber matemático que se enmarcan en la socioepistemología y, para nuestro caso, por mostrar el rol de la mujer en las obras matemáticas que la humanidad se encargó de opacar.
María Gaetana Agnesi, además de filósofa, al estudiar las matemáticas enfrentó el problema más difícil de su época: el cálculo infinitesimal, que había sido introducido de forma independiente por Leibniz en 1684 y Newton en 1687, y que evolucionó en dos líneas diferentes, en medio de un acalorado debate (Sesti, 2020). Su trabajo recibió elogios en toda Europa, especialmente por la precisión del lenguaje y la claridad de la exposición (Betti y De Tullio, 2018). Con respecto a la noción de diferencial, ella expresa lo siguiente:3
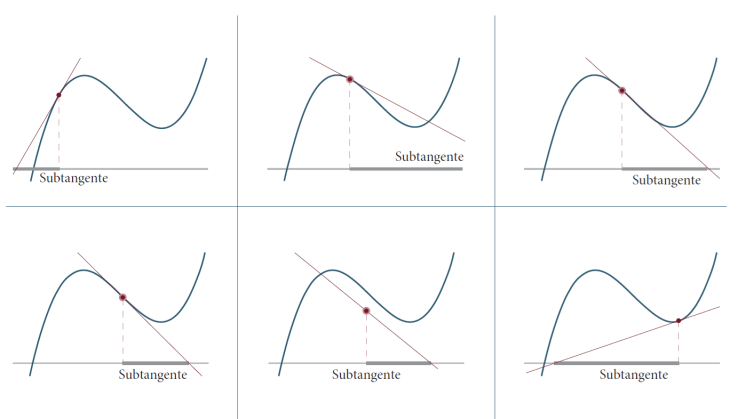
En la obra de Agnesi, específicamente en el libro II, capítulo IV, Castañeda (2002) reconoce dos caracterizaciones del punto de inflexión: desde una propiedad infinitesimal; o referente a la subtangente. La subtangente es el segmento formado por la proyección sobre el eje horizontal (en este caso) creada por el segmento de la tangente en un punto de una curva y que está comprendido entre el punto de tangencia a la curva y el punto donde la tangente corta al eje considerado. En la Fig. 2 se puede observar el cambio de la subtangente en diferentes puntos de la curva.
Con respecto a la propiedad infinitesimal considera dos casos: mínimas diferencias y máximas diferencias. Estas caracterizaciones se explican en la Tabla 1:
Tabla 1 El punto de inflexión caracterizado desde la propiedad infinitesimal
Fuente: las imágenes son producción propia basadas en las originales de Agnesi (1748: 554-555), tomo II, figuras 64 y 65 (Castañeda, 2002: 38).
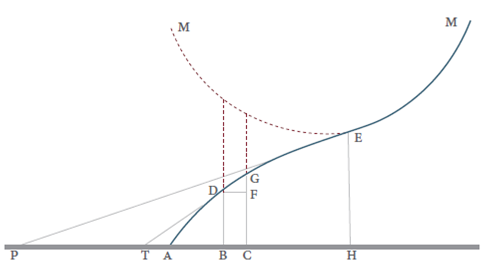
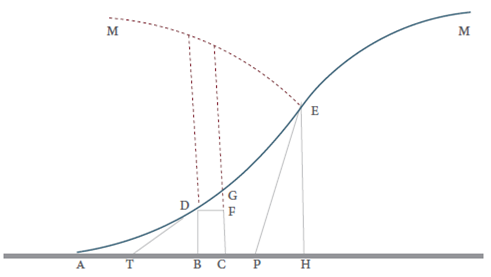
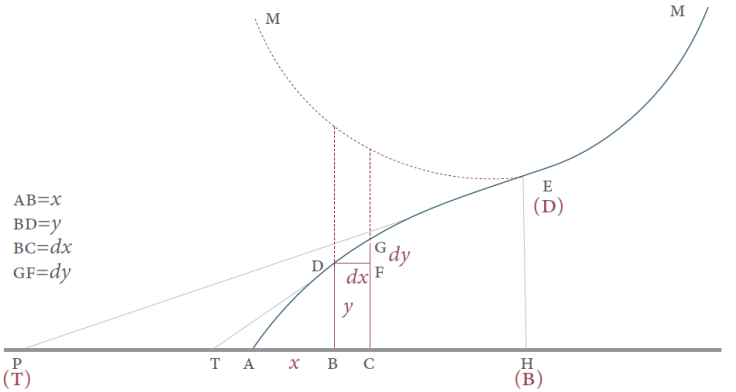
Además, Agnesi brinda otra caracterización del punto de inflexión a partir de matematizar el estudio del cambio de la subtangente. Agnesi, para su época, toda una experta en la geometría dinámica, usando tinta y papel, estudia el cambio de la subtangente y lo cuantifica para probar que en el punto de inflexión la subtangente tiene su menor cambio, es decir, cero. En la Tabla 2 se estudia el comportamiento de la subtangente desde el análisis infinitesimal y apoyo en la gráfica.
Tabla 2 El punto de inflexión caracterizado desde el comportamiento de la subtangente
Fuente: la imagen es producción propia basada en las originales de Agnesi (1748: 555-556), tomo II, figura 64 (Castañeda, 2002: 39).
Esta producción realizada por Agnesi con fines de difusión para la comprensión del punto de inflexión emplea un lenguaje variacional con usos del análisis infinitesimal apoyados en diferentes puntos de la gráfica de una curva (uso dinámico de la gráfica). De este estudio se rescatan dos características para desarrollar en el diseño de situaciones de aprendizaje y su análisis en la implementación, relacionadas con la interpretación del segundo orden de variación para el significado del punto de inflexión:
Desde la propiedad infinitesimal, se muestra la verbalización del cambio al explicar la comparación de las diferencias en las alturas (imágenes de una función) antes y después del punto de inflexión.
En la Tabla 2 se realiza un estudio comparativo del cambio en la subtangente estimando los posibles comportamientos de la recta tangente y, en consecuencia, de la subtangente, alrededor del punto de inflexión.
Esto da pauta para propiciar que la población estudiantil utilice argumentos como “crece o decrece” para hacer referencia al primer orden de variación (cómo cambia). Además de explicaciones verbales como: “crece o decrece cada vez más”, “crece o decrece cada vez menos” y “crece o decrece de forma constante” para referirse a interpretaciones del segundo orden de variación (cómo cambia el cambio). Este estudio cualitativo del cambio se apoya con la representación gráfica de funciones, como se presenta en la Fig. 3.
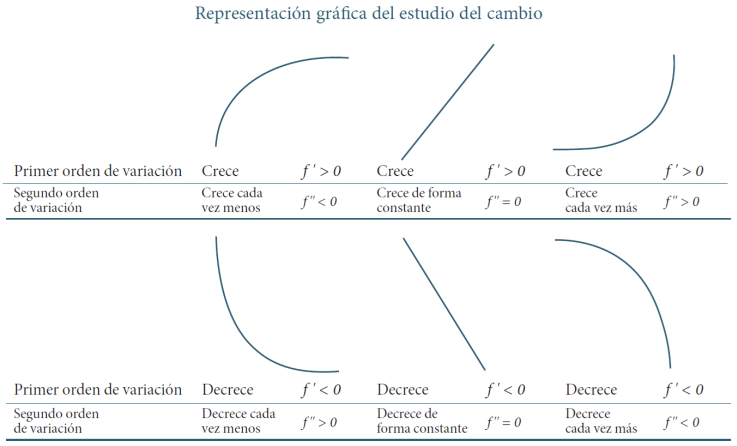
Fuente: elaboración propia.
Figura 3 Interpretación de los órdenes de variación desde diferentes curvas
El uso de la gráfica en el cálculo y el análisis es una gran herramienta para visualizar el cambio y dar significado a objetos matemáticos relacionados con la derivada (Aydın y Ubuz, 2015; Furinghetti et al., 2011; Hoffkamp, 2011; Hong y Thomas, 2015; Jones, 2019; Sánchez-Matamoros et al., 2015). Particularmente Furinghetti et al. (2011: 230) reportan que la dialéctica “visual vs. simbólico” tiene alguna relación con la diálectica “informal vs. formal”, donde formal para los estudiantes significa uso de fórmulas, definiciones y teorema.
En este estudio consideramos igual de importante el uso de la gráfica, pero apoyados en un contexto situacional real y un estudio cualitativo del cambio para construir argumentos variacionales como las explicaciones mencionadas por Agnesi. Por argumentos variacionales entendemos aquellas justificaciones que expresan las personas para una cualificación (¿cómo cambia?, ¿qué cambia?) y cuantificación del cambio (¿cuánto cambia?).
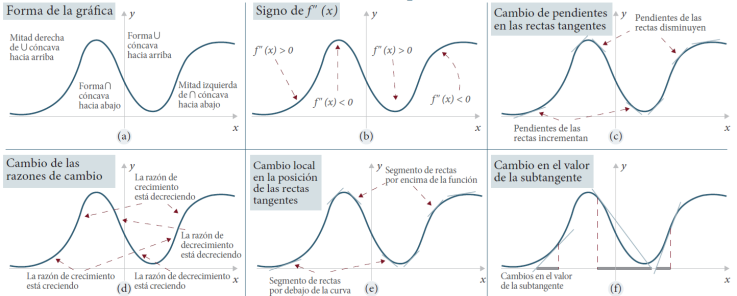
Jones (2019) nos presenta cuatro formas de interpretar la concavidad relacionadas con el concepto de punto de inflexión. Como se observa en la Fig. 4, la concavidad se relaciona con: a) la forma de la gráfica; b) el signo de la segunda derivada; c) el cambio de pendientes de las rectas tangentes; y d) el cambio en las razones de cambio.
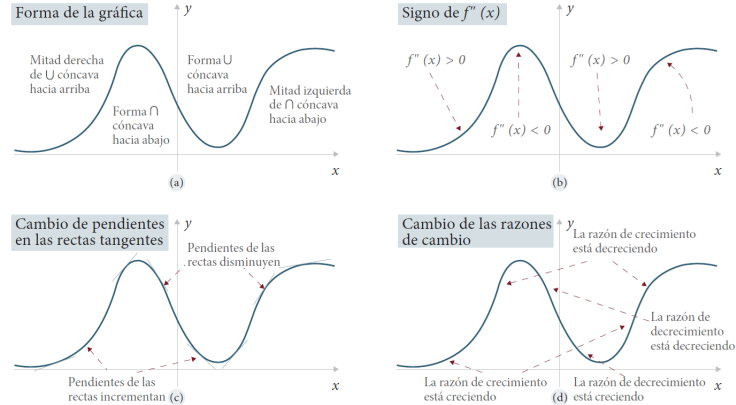
Fuente: traducción realizada del original (Jones, 2019).
Figura 4 Cuatro formas de interpretar la concavidad
Además de visualizar el cambio en el comportamiento de fenómenos, centraremos la atención en prácticas reportadas por Caballero‑Pérez y Cantoral (2013) gracias a un análisis documental de trabajos inscritos en el pensamiento y lenguaje variacional para el estudio del cambio y la construcción de objetos matemáticos relacionados. Partimos de estas prácticas como referente para la construcción de conocimiento en el estudio del cambio:
Comparación. Asociada a la acción de establecer diferencias entre estados, lo que permite identificar si hubo un cambio y poder analizarlo con base en las características de esos cambios y su variación. Esta práctica hace notar el uso de un punto de referencia para argumentar y realizar la comparación.
Seriación. Se relaciona con la comparación, ya que está asociada con la acción de analizar estados sucesivos y establecer relaciones entre ellos. La diferencia es que con la seriación se analizan varios estados y no únicamente dos, con el objetivo de encontrar una relación o propiedad entre ellos, como hallar una relación funcional dada una tabla, encontrar un patrón en el comportamiento de una gráfica o relaciones entre variables.
Predicción. Asociada a la acción de anticipar un comportamiento, estado o valor, luego de realizar un análisis del cambio en estados previos. La predicción no busca encontrar en sí una relación, sino que postula un nuevo estado del sistema o comportamiento del fenómeno dado al análisis del cambio.
Estimación. Conociendo el comportamiento de un fenómeno en estados previos, se proponen nuevos estados del sistema sin tanta exactitud como la predicción. Por ejemplo, se usa en el análisis del crecimiento de poblaciones para saber si crecerá o disminuirá, en tanto que la predicción puede servir para decir hasta qué punto crecerá, o para establecer la cantidad de población dentro de un tiempo específico.
Con estos aportes teóricos nos acercamos al objetivo del trabajo con la intención de que una situación de aprendizaje sea la vía para significar a los máximos, mínimos y puntos de inflexión en la gráfica de una función. Una situación de aprendizaje es un conjunto de momentos en un escenario real o hipotético donde se cuestiona y construye conocimiento ante una problemática para motivar a que la persona razone, argumente, conjeture, haga uso de representaciones y las interprete. Busca inhibir el uso exclusivo de recursos mnemotécnicos. Lo que se observará durante su implementación es un conocimiento puesto en uso, y lo que se obtiene es la construcción de nuevo conocimiento, por lo que se observa una organización de prácticas que transforman una evolución conceptual. En cuanto construcción de nuevo conocimiento, éste podría obtener nuevos significados a lo construido previamente por la escuela. En efecto, “se considera que todo conocimiento es una respuesta, una adaptación que la humanidad ha logrado ante situaciones que ha enfrentado ante problemas que se ha planteado” (Cantoral, 2013: 86).
Método
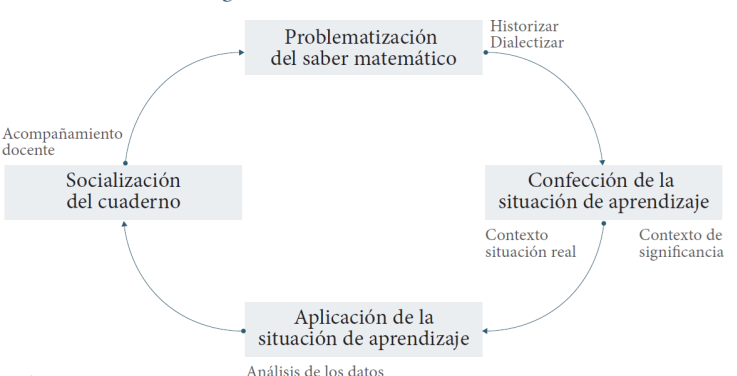
Metodológicamente, este estudio se divide en cuatro fases: problematización del saber matemático; creación de la situación de aprendizaje; aplicación de la situación de aprendizaje; y socialización del cuaderno (que incluye la situación, reflexiones de la aplicación y profundizaciones sobre el saber matemático) con los profesores (Fig. 5). Cada fase se vivió en equipo, de manera cooperativa y dinámica, y se describe en los siguientes apartados de esta sección.
Problematización del saber matemático
Un método utilizado por las investigaciones de corte socioepistemológico que ayuda para abrir una relación con el saber desde las prácticas es la problematización del saber matemático. Además de relacionarse con la construcción de un problema de investigación, consiste en estudiar un conocimiento matemático en uso desde uno o varios escenarios de un saber técnico, popular o científico, situado contextual y temporalmente, que ayuda a confrontar los conocimientos institucionalizados en la matemática escolar.
Dos mecanismos que caracterizan a este método son historizar y dialectizar. Historizar es reconocer el valor histórico (pasado, presente o futuro) del objeto de estudio descrito en la problemática, a partir de conectar con una epistemología situada y una historia social del objeto. Una vez que se reconoce este valor histórico se inicia una confrontación del conocimiento matemático escolar construido y su significado, esto es, se dialectiza, mecanismo que invita a identificar contradicciones para vivir un proceso de análisis crítico ante el conocimiento matemático. Estos mecanismos ofrecen elementos que ayudan a la reflexión del saber matemático en las dimensiones didáctica, cognitiva, epistemológica y social; donde esta última permea, modifica, integra y sistematiza las demás dimensiones.
Específicamente en este trabajo se inicia la problematización del saber a partir del diálogo entre las y los integrantes del equipo, comenzando con la recomendación de buscar y leer artículos relacionados con el punto de inflexión, la matemática del cambio y los resultados de investigaciones desde el pensamiento y lenguaje variacional. Además, se propone que se apoyen en las experiencias y sugerencias de los docentes participantes en el equipo.
La discusión de los artículos y la confrontación con las experiencias de los docentes permitió reconocer una epistemología tanto en el uso y construcción del punto de inflexión y la concavidad en un contexto del cálculo infinitesimal (aportaciones de Agnesi), como en las investigaciones enmarcadas en la didáctica del estudio del cambio y del cálculo. Se reconoció el peso de los métodos algebraicos para determinar el valor de los máximos, mínimos y puntos de inflexión, algunos significados y su relación con el registro gráfico y el esfuerzo por crear propuestas que ayuden a la comprensión conceptual del objeto matemático.
La experiencia del docente aportó en gran medida a las dimensiones didáctica -en reconocer el estudio del tema en los libros de texto y estrategias para su enseñanza- y cognitiva -dificultades y estrategias que realizan los estudiantes- además de una interpretación de lo curricular. Y, sobre todo, la dimensión social que permea la visión entre las dimensiones del saber, al centrar la propuesta en las prácticas reportadas por los trabajos en la línea del pensamiento y lenguaje variacional.
Una síntesis de esta problematización nos mostró la necesidad de considerar los siguientes aspectos para la construcción de situaciones de aprendizaje y reflexión con el docente: los argumentos variacionales utilizados por Agnesi y la visualización en la matemática (a partir del estudio del gráfico de una función con dinamismo y funcionalidad); el significado desde un contexto situacional real; las prácticas asociadas al estudio del cambio que aportan a la construcción de estos objetos (comparar, seriar, estimar, predecir); y el estudio cualitativo de los órdenes de variación y las cuatro formas de interpretar la concavidad.
Situación de aprendizaje
Una situación de aprendizaje es un conjunto de momentos en los que se plantea la imposibilidad de resolverlos solamente mediante estrategias memorísticas, y en los que se propone el desarrollo del pensamiento matemático del individuo y de cada uno de los que integra el colectivo. Además, la construcción de una respuesta o explicación favorece el uso de un razonamiento abductivo (creando hipótesis y validándolas).
Para aportar a este constructo se consideró el ejemplo de Cantoral (2013), que presenta la gráfica de una función real (sin su expresión analítica) y se pregunta por la región donde f > 0, f ’ > 0, f ’’ > 0 y f ’’’ > 0. Tanto profesores como estudiantes pueden identificar en la gráfica los intervalos en donde la función cumpla con f > 0, f ’ > 0 y f ’’ > 0. Sin embargo, para determinar de manera visual el intervalo donde se cumple que f ’’’ > 0 se requiere de otras estrategias y no sólo de técnicas memorísticas.
Esta pregunta suele plantear un reto especial, tanto a los estudiantes como a los profesores, pues, aunque entienden efectivamente el enunciado del problema, no pueden construir una respuesta que les parezca convincente. Esta dificultad se agudiza si en la pregunta elevamos el orden de la derivada involucrada, dado que se carece de elementos cognitivos y didácticos que les permitan construir una respuesta adecuada, “consideramos que es hasta este momento en que ellos se encuentran en situación de aprendizaje, ya que la serie de tareas anteriores les permite, aunque sea sólo con recursos mnemotécnicos, dar una respuesta a las preguntas planteadas” (Cantoral, 2013: 201).
Reyes-Gasperini (2017) señala que desde la propuesta socioepistemológica se debe considerar al contexto situacional real cuando se estudia un fenómeno real (con un escenario real o hipotético) y, a partir de su estudio, generar un ambiente de aprendizaje en el individuo, así como el contexto de significancia, que se refiere a la manera de contextualizar la construcción del conocimiento matemático basada en una evolución pragmática (prácticas). El contexto situacional real acepta la existencia de un saber popular, técnico y científico, bajo el argumento de que podría vivir en la matemática misma y en otros escenarios; si este contexto se elimina de la situación de aprendizaje, la matemática ya no tendría sentido.
Relacionada con la situación de aprendizaje está la buena pregunta, que se centra en una problemática real en la cual es necesario experimentar un estado de confrontación o desequilibrio. Esta pregunta no se puede responder de forma inmediata; invita a la duda, a la indagación, al diálogo en colectivo y a una serie de momentos organizados en la situación de aprendizaje para obtener conclusiones alrededor de la pregunta y no necesariamente una respuesta con solución. Con respecto a la estructura, esta pregunta puede ser colocada en el mismo título de la situación de aprendizaje para llamar la atención del estudiante o en alguna parte de dicha situación, de manera que poco a poco se irá respondiendo.
Otros elementos que considera el diseño de una situación de aprendizaje son las variables de control. Éstas pueden ser de carácter didáctico o epistemológico, con el objetivo de viabilizar el aprendizaje a los involucrados. Las variables de control didácticas están relacionadas con lo mencionado por Artigue (2020) y sirven para construir indicaciones para las interacciones entre estudiantes, profesores y saber, en tanto que establecen indicaciones respecto al medio y el contexto. Las variables de control epistemológicas están muy relacionadas con la forma como queremos que se relacione el estudiante con el saber, en la medida en que se tenga control sobre los significados o sobre la misma naturaleza del saber y se propicien momentos de confrontación (que le permitan entrar en situación de aprendizaje); por ejemplo, que vivencie una dificultad u obstáculo reportado por la literatura o por las mismas experiencias.
La Fig. 6 expone los elementos que se requieren para el diseño de una situación de aprendizaje desde la postura socioepistemológica; incluye, además, las ideas que se usaron para la confección del diseño en este estudio.
El contexto de la situación de aprendizaje
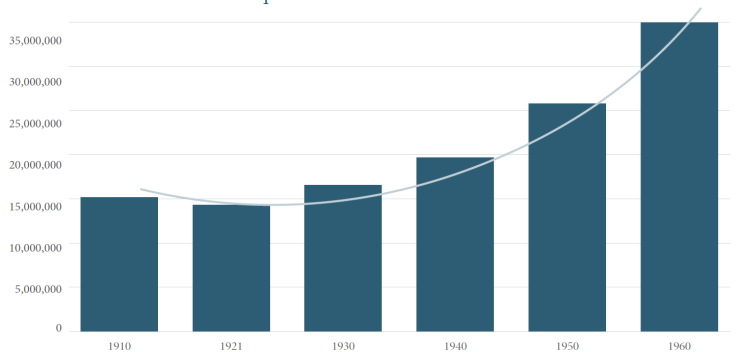
Ante la problematización del saber matemático y de la síntesis de lo estudiado es posible obtener elementos para reconocer la naturaleza de este saber en el estudio del cambio y la variación, así como las prácticas de comparar, seriar, estimar y predecir, que son parte del contexto de significancia. El objetivo del diseño es contribuir a la conceptualización de los máximos, mínimos y puntos de inflexión en una función. Se procede a la búsqueda de un contexto situacional real que involucre datos reales de un fenómeno que muestre cambios en el segundo orden de variación. Para ello usamos la información que nos muestra el INEGI (2015) sobre el crecimiento poblacional de México (Fig. 7).
En esta gráfica se observa una disminución del año 1910 a 1921 como resultado de la fuerte incidencia de enfermedades infecciosas, la presencia de enfermedades trópico endémicas, paludismo, numerosos brotes epidémicos de viruela, tifo, peste, cólera, fiebre amarilla y gripe española; todo en un contexto de crisis económica, inestabilidad política, migración y guerras devastadoras (Zavala, 1992). Con respecto al cambio del crecimiento que se observa cerca de la década de los setenta, el Consejo Nacional de Población estableció una política con objetivos y metas para obtener un crecimiento más lento de la población (Ordorica, 2008) con apoyo de la comunicación educativa en pro de la planificación familiar.
La buena pregunta que guía al diseño de los momentos en la situación de aprendizaje es: ¿cuál es el rol de los acontecimientos históricos, sociales y culturales en el comportamiento de la población mexicana con respecto a los años en estudio? Esta pregunta tiene un carácter predictivo para darle sentido a la forma del comportamiento de los datos.
La variable de control epistemológica consistió en formular preguntas relacionadas con el estudio del cambio y su visualización guiadas por las prácticas (epistemología de prácticas que propicia el enfoque teórico). Las variables de control didácticas se relacionan con el estudio de los datos obtenidos del crecimiento poblacional, uso de gráfica de una función (sin la expresión analítica) y registros numéricos para el estudio cualitativo del cambio de la recta tangente. Con esto, la situación se separa en tres momentos:
Estudio cualitativo del crecimiento poblacional. Se propicia la comparación de los datos y se describe la forma en la que cambia la población. Luego se da la seriación de los datos, determinando de forma visual los tipos de crecimiento y, por último, se da una explicación desde la historia del punto mínimo y de inflexión con carácter predictivo.
Conjeturación. Se estudia la validez de proposiciones y se construyen supuestos que ayudan a confrontar la relación entre el estudio del cambio y los puntos máximos, mínimos y de inflexión. En esta confrontación los estudiantes se colocan en situación de aprendizaje.
Si el comportamiento de un fenómeno pasa de crecer a decrecer, entonces ¿debería existir un máximo?
Si un fenómeno decrece de lento a rápido y luego pasa a decrecer de rápido a lento, entonces ¿debería existir un punto de inflexión?
¿La diferencia de estados sucesivos determina si un fenómeno crece o decrece?
Particularmente en un comportamiento de crecimiento, éste puede tener dos formas de crecer; el punto de inflexión, ¿marca la diferencia entre ambas formas de crecimiento?
Visualización del cambio en el comportamiento de la recta tangente. Se utilizan gráficas de funciones y tablas numéricas (con el valor de las pendientes) para visualizar el comportamiento de la recta tangente en diferentes puntos. Las últimas preguntas buscan estudiar una relación entre el máximo, el mínimo y los puntos de inflexión de una función y lo que representan en ésta.
Aplicación de la situación de aprendizaje
Previo a la implementación, los materiales fueron presentados al equipo que diseña. A partir de ese momento se realizaron reflexiones y sugerencias para la mejora de las preguntas que se habían propuesto. La situación de aprendizaje se llevó a cabo con seis estudiantes mujeres de segundo año de preparatoria (16 a 17 años) en el Centro de Bachillerato Tecnológico No. 3, Zumpango, Estado de México, que estaban aprendiendo elementos del cálculo diferencial. Se contó con el apoyo del profesor Alejandro García, quien también formó parte del equipo de trabajo. El instrumento utilizado para analizar las respuestas de las estudiantes considera dos categorías de análisis con su respectivo indicador y dato.
Tabla 3 Categorías de análisis
| Categoría de análisis | Indicadores | Dato |
|---|---|---|
| Desarrollo de prácticas (comprender el hacer de la estudiante) |
|
Prácticas y significado del objeto |
| Noción de variación |
|
Primer orden de variación |
| Segundo orden de variación e interpretación de la concavidad |
Fuente: elaboración propia.
Socialización de los materiales
Por último, con el sistema de gestión de contenidos WordPress se compartió este material en la plataforma, específicamente en la cápsula 13 (“Entre puntos finos de la historia”). El material se organiza en cuatro documentos: i) para comenzar (inicia con una breve reflexión sobre el estudio del cambio en la población mexicana); ii) para hacer (estudio cualitativo del crecimiento poblacional); iii) para reflexionar (estudio del comportamiento de la recta tangente en la gráfica de una función); y iv) para profundizar, en el que se comparten algunas respuestas de las estudiantes y conclusiones. Este material se acompaña, además, de un muro virtual -donde los docentes pueden colocar comentarios- y un foro para seguir reflexionando sobre el estudio del cambio.
Resultados
La situación de aprendizaje provocó que las estudiantes realizaran una breve indagación sobre los hechos históricos de México que afectaron al crecimiento de la población; parte de su explicación para referirse a la población mínima que refieren los datos tiene que ver con la revolución mexicana. Además, notaron el cambio de crecimiento en la década de los setenta, pero no lo asociaron con algún hecho histórico que explicara ese comportamiento, quizá por estar relacionado con medidas de carácter social; sin embargo, el docente sí comentó el motivo de este cambio.
Las estudiantes compararon los datos cualitativamente de una década a otra para tener una estimación del comportamiento de la población. Ellas supusieron que los datos que no aparecían entre cada década tenían un comportamiento estimado con los datos que sí se muestran. Así lo muestra Cíhuatl4 en la Fig. 8.
Fuente: elaboración propia.
Figura 8 Estimación que realiza Cíhuatl sobre el comportamiento de los datos que no se muestran entre cada década
Algunas estudiantes no mostraron este trazo, pero lo expresaron gestualmente con la mano o implícitamente para luego referirse a un patrón de comportamiento en el crecimiento de la población (seriación) dicho desde el estudio cualitativo del cambio. Con respecto a este patrón de comportamiento se obtuvieron varias caracterizaciones del punto de inflexión y del estudio del segundo orden de variación (Tabla 4).
Tabla 4 Argumentos sobre el punto de inflexión y el segundo orden de variación
Fuente: elaboración propia.
En el episodio de Amellali, ella observa que la población está en aumento, pero nota que existe un punto donde se marca un cambio en el aumento; de lento a rápido y luego de rápido a lento. El episodio de Cíhuatl es muy similar al de Amellali, pero se refiere al crecimiento. Estas argumentaciones variacionales se acercan a lo que plasmaba Agnesi para el estudio del punto de inflexión referente a la propiedad infinitesimal sobre la verbalización del cambio al explicar la comparación de las diferencias en las alturas antes y después del punto de inflexión.
Un argumento similar al de Agnesi sobre la propiedad infinitesimal es el que presenta Zyania en el caso B, cuando explica cómo se obtiene el mayor valor para dy. Ella observa que el crecimiento más grande se obtiene en datos cercanos a la década de los setenta.
Por otro lado, en la parte de la visualización del cambio en el comportamiento de la recta tangente las estudiantes notan que en el punto de inflexión las rectas tangentes pasan a estar “por encima de la gráfica” a estar “por debajo de la gráfica”, como lo muestra Yaocíhuatl en la Fig. 9. Esto aporta a otra forma de estudio de la concavidad diferente a las mencionadas por Jones (2019).

Fuente: elaboración propia.
Figura 9 Visualización del cambio de posición de la recta tangente con respecto a la función, realizado por Yaocíhuatl (episodio 1)
Este argumento es válido para vecindarios de los puntos de tangencia. A esta estrategia la hemos llamado cambio local en la posición de las rectas tangentes, comprendido como segmentos de las rectas tangentes que están por debajo o por arriba de la función.
Una de las dificultades que se reportaron es que algunas de las estudiantes no reconocen al máximo global como un máximo. Esto podría ser resultado de la relación que tienen los máximos y mínimos con la algebrización de estudiar los valores para los cuales la primera derivada es cero.
Tabla 5 Identificación del mínimo, máximo y punto de inflexión del crecimiento poblacional por parte de Yaocíhuatl (episodio 2)
Fuente: elaboración propia.
En la última pregunta de la situación se les dio una gráfica de una función f ’ respecto de la cual se les solicitaba determinar los valores de para los cuales la gráfica de la función f presenta máximos, mínimos o puntos de inflexión. Si bien las estudiantes dieron las respuestas, en éstas se determinan los máximos, mínimos y puntos de inflexión de la función f ’. Los motivos de estas respuestas pueden ser diferentes, desde el cansancio hasta la comprensión y relación de la gráfica de f ’ con respecto a f .
Por último, retomando las cuatro formas de estudiar a la concavidad reportadas por Jones (2019), este estudio permitió agregar dos nuevas formas: a partir del cambio local en la posición de las rectas tangentes reportado por las estudiantes; y como resultado de estudiar el cambio en la subtangente, tal como lo demuestra Agnes, presentado en la Tabla 2 de este artículo. En la Fig. 10 se muestran estas seis formas de estudiar la concavidad.
Conclusiones
En este estudio, particularmente en el crecimiento poblacional, se utilizaron datos discretos y esto no fue impedimento para la comprensión conceptual del punto de inflexión y del mínimo local en funciones de variable real; es más, aportó al estudio cualitativo del cambio que apoya a los argumentos variacionales para el estudio de las gráficas de funciones continuas de variable real. Además, la forma en como es presentada la gráfica en el crecimiento poblacional contribuyó a que las estudiantes hicieran comparaciones cualitativas de los datos (sin conocer el número) y dar estimaciones del comportamiento local entre cada década.
Esta situación es sólo un diseño (de muchos más que pueden existir) para la comprensión y significado del máximo, mínimo y punto de inflexión (concavidad). Se prueba la hipótesis de este estudio, al mostrar que el significado de estos puntos finos estuvo asociado a hechos históricos, sociales o culturales que hicieron que el crecimiento poblacional se comportara de esa forma, lo cual aporta un carácter predictivo a la concavidad de la función. El mínimo fue comprendido como una consecuencia de la Revolución mexicana, movimiento social que marcaría el futuro del país y que afectaría al crecimiento poblacional; y el punto de inflexión como los años en que existieron políticas sociales de planificación familiar para el control natal.
Por otro lado, Agnesi desde el análisis infinitesimal, y las estudiantes desde el cálculo escolar, no obstante provenir de contextos diferentes, reportan semejanzas en los argumentos utilizados para explicar el problema que abordan. Lo que no varió fue el uso de argumentos variacionales sobre el segundo orden de variación en frases como “crece de rápido a lento”, “crece de lento a rápido” y su interpretación visual de la recta tangente que se reportó en los resultados. Esto robustece al estudio y la interpretación de la concavidad de una función ofrecida por Jones (2019).
La situación de aprendizaje descrita trabajó con la interacción de dos contextos situacionales reales que se complementaron entre sí: en el primer escenario se trabajó con los datos y la interpretación del crecimiento poblacional, y se hizo un estudio cualitativo del cambio; el segundo escenario correspondió al estudio del cambio y uso de la gráfica en matemática. Esto permitió que se reconocieran interpretaciones sobre la concavidad y que se agregara, desde la teoría socioepistemológica, la articulación de contextos situacionales reales para la resignificación de los objetos matemáticos como parte de la situación de aprendizaje.
Es claro que la visualización jugó un papel importante en este estudio, ya que no se trata simplemente de ver o acompañar con registros gráficos lo que se realiza algebraicamente (centración en los procesos algebraicos); la visualización consiste en centrar los estudios en las interpretaciones gráficas (uso de gráficos con dinamismo) y obtener significados y hasta conjeturas que ayudan indudablemente al estudio algebraico que se quiera realizar. Agnesi nos demuestra esto al hablar del cambio a partir de la gráfica, lo cual le da cierta simulación a lo que demuestra de forma analítica. Esta práctica ayuda a representar, informar, argumentar, transformar, comunicar, trasmitir y explicar información que se construye con imágenes mentales, aquéllas que nacen entre la interacción del exterior y el interior de la persona.
Sobre el acompañamiento, los docentes han mencionado el valor que tiene el estudio del cambio que invita a relacionar a la matemática con otras disciplinas. Con las buenas preguntas reconocen que no necesariamente se debe tener algo matemático como producto final, sino que considerar una problemática desde un escenario cercano al estudiante permite ir obteniendo en el camino diversos productos para el aprendizaje y desarrollo del pensamiento matemático. Como profesores o investigadores es una buena ruta empezar a observar problemáticas distintas al objetivo matemático. El diálogo en colectivo con otros docentes y otras disciplinas es el mejor acompañamiento y contribuye a nuevas ideas para que los estudiantes experimenten situaciones de aprendizaje. Esta investigación permitió reflexionar, con el colectivo docente en matemática, que una ruta para desarrollar situaciones descentradas del objeto matemático que permitan la construcción de la derivada es estudiar cualitativa y cuantitativamente el cambio en fenómenos donde se perciba movimiento.











 nova página do texto(beta)
nova página do texto(beta)