Introducción
La matemática es de gran importancia en la formación de un ingeniero, ya que constituye el lenguaje de modelación, el soporte simbólico con el cual expresan las leyes que rigen el objeto de su trabajo; está vinculada a las actividades de modelar, interpretar y comunicar en lenguaje preciso (Brito et al., 2011). La matemática es la herramienta más poderosa del ingeniero y su dominio le permitirá el progreso a lo largo de su formación profesional; adicionalmente, ayuda al desarrollo del razonamiento abstracto, el cual es fundamental en la formación del ingeniero (Ruiz et al., 2016).
Dentro de esta gran área, el objetivo del cálculo es proporcionar conocimientos en los estudiantes que les permitan interpretar, plantear y resolver problemas de ingeniería (Zúñiga, 2007), ya que la formación de ingenieros demanda aprendizajes matemáticos que contribuyan a resolver problemas específicos de corte tecnológico, pero sobre todo práctico (Ruiz et al., 2016). El propósito general de un curso de cálculo diferencial en una carrera de ingeniería es que los estudiantes apliquen los conceptos y procedimientos del cálculo en la diferenciación de funciones, mediante el uso de límites y teoremas de derivación, para resolver problemas cotidianos de ciencia e ingeniería. Particularmente en las ingenierías, la asignatura de cálculo diferencial es precedente de cursos como cálculo integral, ecuaciones diferenciales, cálculo multivariable, transferencia de calor y masa, estática, dinámica, electricidad y magnetismo, circuitos eléctricos, entre otras.
Hay gran cantidad de estudios dedicados a conocer la importancia del cálculo diferencial desde un punto de vista teórico (Cantoral y Farfán, 2004; Trigueros, 2005; Mateus, 2011; Jiménez et al., 2018; Artigue, 2018), y del desarrollo del pensamiento matemático (Cantoral et al., 2005; Acosta et al., 2009; Pérez y Ocaña, 2013; Vergel et al., 2015); también los hay sobre modalidades de aprendizaje (Sanabria, 2019) en un área en particular (Medina et al., 2017), en la formación de docentes (Fonseca y Alfaro, 2018), en el proceso de enseñanza y/o aprendizaje (García et al., 2006; Iglesias, 2019), en los materiales y herramientas de apoyo (Villalobos et al., 2018; Gutiérrez, 2019; Rosales-Mata y Chavira, 2019), en forma de propuestas para mejorar la calidad de la enseñanza (Duarte y Castro, 2015; Martínez-Reyes, 2019) y sobre la evaluación del mismo conocimiento en profesores (Moreno y Cuevas, 2004), sin embargo, son pocos los que muestran y validan confiablemente los temas donde el estudiante encuentra una mayor dificultad para así abordarlos de una forma pertinente y significativa.
En las últimas décadas ha crecido el interés respecto del estudio de la problemática de reprobación, rezago y abandono de los estudiantes de primer año de licenciatura en ingeniería (Muñoz y Arce, 2001; Montalto et al., 2002; Zavaleta y Flores, 2009; Correa et al., 2009; Arraiz y Valecillos, 2010), así como por la evaluación del aprendizaje a gran escala, ya que permiten un mejor conocimiento y caracterización del logro educativo de los estudiantes.
Las evaluaciones permiten detectar las habilidades generadas en los estudiantes a partir de la enseñanza, lo cual posibilita la creación de estrategias y programas de atención para remediar el bajo aprovechamiento de los estudiantes. Este factor es una preocupación generalizada en las universidades (Posso, 2005).
Con el propósito de contribuir a estos aspectos, se realizó una investigación en una universidad pública de México con los siguientes objetivos: 1) presentar el examen colegiado de cálculo diferencial (ECCD) de opción múltiple, criterial, alineado con el currículo y de alto impacto (Popham, 1990; Nitko, 1994; Contreras, 1998; 2000) que evalúa los conocimientos que los estudiantes universitarios adquieren en un curso de cálculo diferencial; 2) demostrar que el ECCD es un instrumento de evaluación válido, confiable y con poder de discriminación aceptable (Carmines y Zeller, 1987; Backhoff et al., 2000; Contreras y Backhoff, 2004; Ding et al., 2006; Engelhardt, 2009) ; 3) realizar un análisis de los resultados obtenidos por los estudiantes en el ECCD en cuanto a conceptos, procedimientos (Sfard, 1991; Contreras y Backhoff, 2004; Hähkiöniemi, 2006; Harel et al., 2006) y desde la perspectiva de las diferentes actividades cognitivas y registros de representación (Duval, 1993; 2000; 2006a; 2006b; 2006c); y 4) formular recomendaciones a partir de los resultados expuestos en cuanto a la posibilidad de mejora del ECCD y al diseño instruccional.
Lineamientos teóricos
Dado que los jóvenes que asisten a las escuelas están destinados a adquirir principalmente conocimientos teóricos y prácticos, resulta conveniente analizar si los contenidos sobre cuyo dominio son evaluados se refieren a conceptos o a procedimientos. Para Sfard (1991) la visión estructural o conceptual se caracteriza por un ente que posee rasgos propios, es estática, instantánea e integradora. Para Contreras y Backhoff (2004) se refiere a las características, atributos ontológicos y definición del propio concepto; se distingue también por la apropiación de una regularidad. Harel et al. (2006) consideran que es abstracta y que implica una creencia implícita sobre la naturaleza de las entidades matemáticas que se describen mediante definiciones formales.
En cuanto a la visión operacional o procedimental, Sfard (1991) menciona que se matiza por acciones y algoritmos, que es dinámica y procedimental o secuencial. Contreras y Backhoff (2004) la refieren al dominio de las fases que implica la secuencia de operaciones involucradas, la utilización de algoritmos y el cómo, cuándo y dónde se usan.
Desde la perspectiva de la teoría de representaciones semióticas de Raymond Duval (1993; 2000; 2006a; 2006b; 2006c), los objetos matemáticos no son directamente accesibles a la percepción, de manera que para su estudio y tratamiento se requiere contar con sus representaciones. Las representaciones externas a las que hacemos alusión pueden ser de carácter geométrico, algebraico y numérico del objeto. Como lo señala el mismo Duval (2000), el uso de sistemas de representaciones semióticas para el pensamiento matemático es esencial debido a que, a diferencia de campos de conocimiento como la biología, la geología o la física, no existen otras maneras de lograr el acceso a los objetos matemáticos más que al producir algunas representaciones. En este sentido, las representaciones permiten el acceso, el estudio y el tratamiento del objeto matemático.
En la teoría de las representaciones de Duval (2006a) , la actividad cognitiva de representación constituye una marca o conjunto de marcas perceptibles e identificables respecto de un objeto matemático; el tratamiento es la transformación de la representación dentro del mismo registro de representación y depende, de alguna manera, de las convenciones o reglas matemáticas de ejecución; y la conversión es la transformación de la representación en otra representación de un registro diferente al original, pero que conserva su esencia. A través de estos procesos de representación, tratamiento y conversión se pueden exteriorizar las representaciones mentales de los individuos, así como motivar la retroalimentación y mejorarla.
Presentación del ECCD
El ECCD objeto de esta investigación se aplicó de manera formal en una universidad pública de México a todos los estudiantes que cursaban la asignatura de cálculo diferencial (más de 3 mil 500 alumnos por año distribuidos en los diferentes campus de ingeniería). Los resultados de este examen forman parte de su evaluación ordinaria y proporciona 30 por ciento de la calificación final del curso de cálculo diferencial, mientras que el otro 70 por ciento lo otorga el docente que imparte la asignatura. El ECCD se aplica desde el año 2005, está integrado actualmente por 60 reactivos y cuenta con las siguientes características: es criterial, toda vez que tiene el propósito de evaluar el aprendizaje al informar qué puede hacer o no el examinado; está alineado con el currículo, ya que se desprende de una actividad para identificar lo esencial de éste y evaluarlo; es de opción múltiple, pues se pide al estudiante elegir la respuesta correcta de entre cuatro que se ofrecen; y es de gran escala, ya que su aplicación corresponde a miles de estudiantes.
En la construcción del ECCD se adoptó el modelo de Nitko (1994) para desarrollar exámenes orientados por el currículo. Dicho modelo fue complementado por la metodología para la construcción de test criteriales de Popham (1990) y con aportaciones metodológicas y operativas de Contreras (1998; 2000). El diseño y construcción del ECCD implicó un proceso compartido por un amplio equipo de profesores de la universidad, quienes recolectaron información y formularon juicios de valor de forma consensuada (Corral, 2009) para la toma de decisiones en la construcción del examen. Lo anterior permitió que la información obtenida fuese válida en cuanto a su contenido. Este tipo de instrumento de medición motiva la objetividad y la estandarización del conocimiento.
El ECCD explora cuatro unidades básicas de conocimiento del curso de cálculo diferencial, los reactivos que componen cada unidad y su competencia específica (Tabla 1).
Tabla 1 Competencia y reactivos del examen de cálculo diferencial
| Unidad | Nombre | Competencia | Reactivos |
|---|---|---|---|
| 1 | Funciones de una variable | Identificar y distinguir los diversos tipos de funciones mediante sus diferentes representaciones, gráfica, numérica y analítica, para su uso en los procesos de derivación | 1 - 23 |
| 2 | Límites y continuidad | Determinar los límites y continuidad de funciones en sus representaciones gráfica, numérica y analítica mediante la utilización de los teoremas y criterios gráficos correspondientes para su aplicación en diferenciación de funciones | 24 - 37 |
| 3 | La derivada | Determinar las derivadas de funciones en sus representaciones gráfica, numérica y analítica mediante la utilización de los teoremas y criterios gráficos correspondientes para su aplicación en problemas de optimización | 38 - 51 |
| 4 | Aplicaciones de la derivada | Aplicar la derivada de una función empleando los criterios de la primera y segunda derivada para resolver problemas de optimización | 52 - 60 |
Fuente: elaboración propia.
Para el diseño de cada uno de los reactivos se elaboró previamente una especificación técnica con base en dos componentes: el punto de vista del contenido de cálculo diferencial y el psicométrico.
Las especificaciones técnicas de los reactivos tienen el propósito principal de proporcionar a los diseñadores el contenido específico que debe ser evaluado y los detalles técnicos necesarios para que ellos puedan generar reactivos efectivos. Sin embargo, otro propósito asociado es comunicar a los usuarios del examen (profesores y estudiantes) qué es lo que mide cada reactivo, así como la cobertura y alcance de las competencias evaluadas.
La especificación consta de una sección de datos de identificación del contenido a evaluar, una interpretación de su sentido, las características de los estímulos que el reactivo presentará al examinado (instrucciones para responder, base del reactivo, distractores, respuesta correcta, tablas o figuras de apoyo, etc.), así como un reactivo muestra que ilustra la aplicación de dichas normas de diseño del reactivo (Fig. 1).
Método
Los datos empleados en esta investigación corresponden a los resultados del ECCD aplicado durante los ciclos escolares 2018-2 y 2019-1. El examen se aplicó a un total de 3 mil 751 estudiantes de primer semestre de las carreras de ingeniería. La administración del ECCD se realizó en los laboratorios de cómputo de la misma universidad y tuvo una duración máxima de dos horas. Las respuestas fueron registradas y procesadas en la plataforma de datos QuestionMark.
Se realizó un análisis de confiabilidad mediante el coeficiente de Kuder-Richarson (KR-20), el cual permite obtener la confiabilidad de un instrumento a partir de los datos obtenidos en una sola aplicación (Corral, 2009); si el coeficiente es mayor que 0.80 es aceptable (Kehoe, 1995; Contreras y Backhoff, 2004; Muñoz y Mato, 2008; Ding et al., 2006). De manera adicional se calculó el coeficiente delta de Ferguson, que mide el poder de discriminación de una prueba completa; el rango de dicho coeficiente es [0, 1] y es satisfactorio cuando es mayor que 0.90 (Ding et al., 2006).
El índice de dificultad (ID) está relacionado con la proporción de estudiantes que resuelven correctamente un reactivo, y se calcula de acuerdo a Crocker y Algina (1986). Existen parámetros para la aceptación de un reactivo de acuerdo con su nivel de dificultad; el establecido por Contreras y Backhoff (2004) dice que debe ser mayor que 0.05 y menor que 0.95. Para Engelhardt (2009) el promedio de este índice en la prueba debe ser 0.5 para maximizar la discriminación. De acuerdo con Backhoff et al. (2000), el nivel medio de dificultad del instrumento debe oscilar entre 0.5 y 0.6; los valores del índice de dificultad deben distribuirse de la manera siguiente: 5 por ciento de reactivos altamente fáciles (0.87< ID<1), 20 por ciento medianamente fáciles (0.74<ID<0.86), 50 por ciento con una dificultad media (0.53<ID<0.73), 20 por ciento medianamente difíciles (0.33<ID<0.52) y 5 por ciento altamente difíciles (ID<0.32).
El índice de discriminación (IDC) del reactivo permite diferenciar (discriminar) entre aquellos estudiantes que obtuvieron buenas calificaciones en la prueba y quienes obtuvieron bajo puntaje. Está relacionado con una alta posibilidad de que los estudiantes con un desempeño general sobresaliente en la prueba respondan correctamente el reactivo, situación opuesta para el caso de los estudiantes con un desempeño deficiente; en este análisis se considera el 54 por ciento de la población muestral, toda vez que se incluye 27 por ciento de los estudiantes con alto rendimiento e igual porcentaje de estudiantes con el más bajo rendimiento por cada reactivo que se revisa. Para Contreras y Backhoff (2004) el valor discriminativo del reactivo se considera apropiado si es mayor que 0.2. De acuerdo con Backhoff et al. (2000), la escala del IDC es: malo (IDC<0.20); regular (0.20<IDC<0.30); bueno (0.30<IDC<0.40); y excelente (IDC>0.40).
También se calculó el coeficiente de correlación del punto biserial (rpbis). Para algunos investigadores (Henrysson, 1971; Molina et al. 2015), este coeficiente es un indicador de validez predictiva, ya que se relaciona la respuesta a un reactivo por un estudiante y el resultado que obtuvo de la prueba; este indicador psicométrico se calcula de acuerdo al modelo de Backhoff et al. (2000) y la escala de valores de este indicador es: discrimina pobremente (rpbis<0.14), regularmente (0.15<rpbis<0.25), buen poder discriminativo (0.26<rpbis<0.35) y excelente nivel de discriminación (rpbis>0.35). Para Ding et al. (2006) el rpbis debe ser mayor a 0.2, aunque sólo unos cuantos reactivos de la prueba podrían no cumplir con esta condición.
La base de datos de la plataforma QuestionMark contiene la respuesta a cada reactivo por cada estudiante. Los resultados de los reactivos se valoran como respuesta correcta (1) o incorrecta (0). Estos resultados fueron analizados a través del programa IBM SPSS Statistics y Microsoft® Office Excel. El tratamiento de la información permite obtener los índices de dificultad y discriminación, y el coeficiente de correlación del punto biserial, además de la confiabilidad de la prueba por el método de Kuder Richardson (KR-20) y delta de Ferguson.
Para cumplir con el tercer objetivo expuesto en párrafos anteriores, el reactivo muestra de cada especificación fue clasificado en cuanto a su registro de representación inicial, final (lenguaje natural, numérico, algebraico y gráfico) y la actividad cognitiva (representación, tratamiento o conversión) requerida para la resolución del reactivo, así como también el carácter conceptual o procedimental del reactivo.
Se realizaron análisis de varianza mediante la prueba post-hoc de Tukey con la finalidad de encontrar diferencias significativas entre grupos y dentro de los mismos.
Resultados y discusión
Esta sección se ha dividido en dos partes: la primera se refiere al análisis de calidad del ECCD, y la segunda alude al análisis de los resultados que obtuvieron los estudiantes en el ECCD.
Análisis de la calidad del ECCD
La documentación física existente (contenido y retícula de la materia, justificación de los contenidos, tabla de especificaciones y especificaciones de los reactivos) sobre el diseño y construcción del ECCD evidencia la selección de indicadores adecuados, relacionados con los procesos matemáticos y el contraste de la validez de los reactivos a través del juicio de expertos (Alsina y Coronata, 2014). La validez de contenido se garantizó con la participación de jueces expertos (profesores de cálculo diferencial con experiencia docente mínima de 5 años) y método de consenso grupal (Corral, 2009), en los temas objeto de la validación. Estos jueces analizaron la coherencia de los reactivos con los que se desea evaluar, la complejidad de los reactivos y la habilidad cognitiva a evaluar (Barraza, 2007), así como la suficiencia y pertinencia de los reactivos, considerando los aspectos del constructo que son relevantes, incluidos en las competencias y los indicadores (Cisneros et al. 2012).
Participaron en el examen 3 mil 751 estudiantes: 2 mil 098 para el ciclo 2018-2 y 1 mil 653 para el ciclo 2019-1.
La confiabilidad fue calculada mediante KR-20, donde r=0.88 para Contreras y Backhoff (2004) y para Muñoz y Mato (2008) es considerado como apropiado cuando es mayor o igual que 0.85 en el caso de instrumentos estandarizados y de gran escala, mientras que para Ding et al. (2006) es satisfactorio cuando se utiliza el método KR-20 y se obtiene una confiabilidad r>0.80, así como para Kehoe (1995) en el caso de exámenes con más de 50 reactivos.
La distribución de los puntajes totales se calculó mediante la prueba delta de Ferguson y se obtuvo 0.99, lo que satisface ampliamente el criterio establecido (Ding et al., 2006; Engelhardt, 2009).
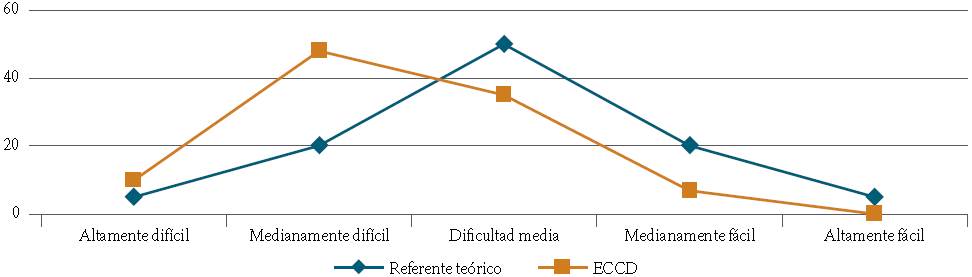
El promedio del índice de dificultad es de 0.50 ± 0.14 (media ± desviación estándar), por lo que resulta un nivel medio de dificultad y adecuado (Backhoff et al., 2000; Ding et al., 2006; Engelhardt, 2009). La distribución porcentual resultante del ID está constituido por: reactivos altamente fáciles (0 reactivos, 0 por ciento); medianamente fáciles (4 reactivos, 7 por ciento); dificultad media (21 reactivos, 35 por ciento); medianamente difíciles (29 reactivos, 48 por ciento); y altamente difíciles (6 reactivos, 10 por ciento). Claramente se observa en la Gráfica 1 un desfasamiento a la izquierda respecto de la distribución de la dificultad del referente teórico, lo cual indica que el ECCD es difícil de acreditar; sin embargo, 29 por ciento obtuvo una calificación igual o superior a 60, con la que acreditaron el ECCD.
Fuente: elaboración propia.
Gráfica 1 Comparativo entre la dificultad del referente teórico y el ECCD
A continuación (Tabla 2) se describen las características del reactivo más difícil y el más fácil, de acuerdo al ID. Ambos quedan dentro del criterio de dificultad expuesto por Contreras y Backhoff (2004) y la teoría clásica de los test.
Tabla 2 Características de los reactivos
| Reactivo | Unidad | Indicador de logro | ID |
|---|---|---|---|
| 50 | 3 | Resolver enunciados de problemas de tasas de variación relacionadas que tienen una función implícita como modelo matemático | 0.23 |
| 7 | 1 | Representar gráficamente una función de variable real | 0.81 |
Fuente: elaboración propia.
El promedio del IDC es 0.44 ± 0.12 (media ± desviación estándar), el cual cae dentro de una calificación considerada como excelente (Backhoff et al., 2000), y cumple también con el criterio declarado por Ding et al. (2006), en el cual el IDC promedio es mayor a 0.3. Se cuenta con que el 72 por ciento (43) de los reactivos tienen discriminación excelente, 15 por ciento (9) buena, 6.5 por ciento (4) regular, mientras que 6.5 por ciento (4) tiene discriminación mala.
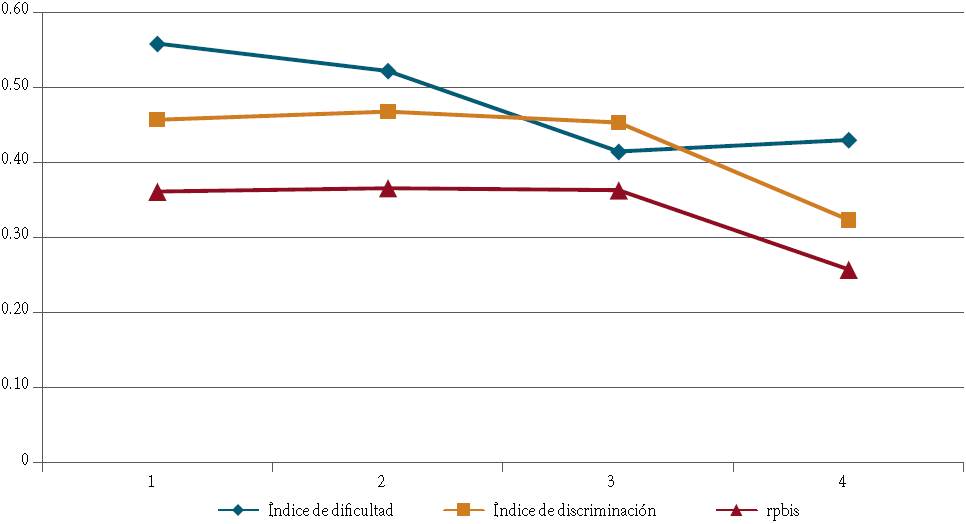
Una prueba post-hoc de Tukey entre las unidades de reactivos y el IDC mostró diferencias significativas (p=0.035), específicamente entre la unidad 4: Aplicaciones de la derivada, y el resto de las unidades que conforman la prueba. Los promedios del IDC para las cuatro unidades consideradas son: 0.46 para la unidad 1 (funciones de una variable); para la unidad 2 (límites y continuidad) es 0.47; la unidad 3 (la derivada) tiene un IDC promedio de 0.45; y 0.32 para la unidad 4 (aplicaciones de la derivada). Se identifica el mayor poder de discriminación para los reactivos correspondientes a las unidades 1, 2 y 3 (Gráfica 2); en contraste se determinó que el menor poder de discriminación es para los reactivos de la unidad 4, referidos a las aplicaciones de la derivada. Los reactivos en esta unidad se asocian con un alto grado de dificultad para su resolución.
Fuente: elaboración propia.
Gráfica 2 Gráfica de puntos unidad contra índice de dificultad, discriminación y correlación biserial
Se identificaron cuatro reactivos con un IDC menor a 0.20, mismos que se describen en la Tabla 3 y que, de acuerdo con los criterios psicométricos, son reactivos que se sugiere sean revisados en cuanto a una posible discriminación errónea, un error de edición, de redacción o, en su caso, debido a su complejidad cognitiva, ya que los cuatro reactivos son alta o medianamente difíciles.
Tabla 3 Reactivos con IDC menor a 0.20
| Reactivo | Unidad | Indicador de logro | IDC | ID |
|---|---|---|---|---|
| 21 | 1 | Representar gráficamente una función trigonométrica inversa a partir de su expresión algebraica | 0.13 | 0.32 |
| 50 | 3 | Resolver enunciados de problemas de tasas de variación relacionadas que tienen una función implícita como modelo matemático | 0.17 | 0.23 |
| 58 | 4 | Probar las hipótesis del teorema del valor medio para una función en un intervalo | 0.18 | 0.33 |
| 59 | 4 | Plantear y resolver problemas de ingeniería que requieran acciones de optimización para su solución | 0.15 | 0.39 |
Fuente: elaboración propia.
El promedio de los coeficientes de correlación biserial de la prueba es 0.35 ± 0.09 (media ± desviación estándar). El coeficiente cumple con la recomendación de los especialistas (Ding et al., 2006; Engelhardt, 2009) en cuanto a que el promedio del rpbis sea superior a 0.2. Se cuenta con que 55 por ciento (33) de los reactivos tienen discriminación excelente, 31.7 por ciento (19) buena discriminación, 10 por ciento (6) discriminación regular y 3.3 por ciento (2) discrimina pobremente.
Los resultados de las pruebas realizadas exhiben que el ECCD es una prueba confiable y con poder de discriminación satisfactorio.
Análisis de los resultados que obtuvieron los estudiantes en el ECCD
El promedio de las respuestas correctas en el ECCD es 29.83 de 60 puntos posibles; el promedio expresado en porcentaje respecto del total de puntos es 50 por ciento, el cual corresponde al ID promedio de 0.50.
La distribución del número de reactivos correctos fue significativamente no normal (Kolmogorov-Smirnov, D(3751) = 0.071, p<0.01; Shapiro-Wilk, W (3751)=0.983, p<0.01). La asimetría de la distribución del número de reactivos correctos es 0.336 (desviación=0.040). Dichos valores indican una asimetría positiva. La curtosis de la distribución es -0.494 (desviación=0.080). Por el tipo de distribución se adicionan las medidas de tendencia central y de dispersión; la mediana es 29, la moda es 25, el cuartil 1 es 22, el cuartil 2 es 29 y el cuartil 3 es 37. Los estudiantes tuvieron dificultad con 31 reactivos (calificados como alta y medianamente difíciles) y la asimetría positiva evidencia la dificultad del ECCD: sólo 29 por ciento obtuvo una calificación igual o superior a 60 (en la escala de 0 a 100) con la que acreditan el ECCD, es decir, de los 3 mil 751 estudiantes que aplicaron el ECCD, sólo 1 mil 088 lo aprobaron.
Una prueba post-hoc de Tukey entre las unidades de reactivos y el ID mostró diferencias significativas, específicamente entre la unidad 1: funciones de una variable (ID=0.56), con las unidades 3: la derivada (ID=0.42) y 4: aplicaciones de la derivada (ID=0.42). En la unidad 3 se presenta una cantidad importante de teoremas y reglas de derivación que se requieren para obtener la derivada de una función, sobre todo si es compuesta. Para Daza y Garza (2018) el lenguaje simbólico y el alto nivel de abstracción en el tratamiento de la derivada suelen representar una dificultad trascendente para el estudiante de ingeniería. En la unidad 4 se le demanda al estudiante, además de la aplicación de conceptos matemáticos (variación, máximo, mínimo, creciente, decreciente, concavidad e inflexión) intuición, argumentación, así como también la ejecución de secuencias para resolver enunciados de problemas de variación u optimización. En Malaspina (2007) se perciben en los estudiantes deficiencias en el uso de proposiciones, procedimientos y argumentos al resolver los problemas de optimización. Para la unidad 2, referida a límites y continuidad, el ID promedio es 0.52; en donde la actividad cognitiva necesaria para la resolución de los reactivos es el tratamiento, en esta unidad se utilizan teoremas y técnicas para el cálculo de los límites como la factorización, racionalización, tabulación y la observación.
Con los resultados obtenidos se observa que las unidades 3 y 4 son prácticamente las más difíciles para los estudiantes. Los reactivos clasificados como altamente difíciles, y algunos calificados como medianamente difíciles son, sin duda, una amenaza para el éxito de los estudiantes en la asignatura (Tabla 4).
Tabla 4 Los 10 reactivos más difíciles en el ECCD
| Reactivo | Unidad | Indicador de logro | ID |
|---|---|---|---|
| 50 | 3 | Resolver enunciados de problemas de tasas de variación relacionadas que tienen una función implícita como modelo matemático | 0.23 |
| 51 | 3 | Plantear y resolver enunciados de problemas de tasas de variación relacionadas que tienen una función implícita como modelo matemático | 0.24 |
| 37 | 2 | Calcular la razón de cambio instantánea en un punto a partir de la gráfica de una función y su recta tangente | 0.29 |
| 39 | 3 | Representar gráficamente la función derivada a partir de la gráfica de la función | 0.30 |
| 57 | 4 | Probar las hipótesis del teorema de Rolle para una función | 0.32 |
| 21 | 1 | Representar gráficamente una función trigonométrica inversa a partir de su expresión algebraica | 0.32 |
| 46 | 3 | Calcular la derivada de una función trigonométrica inversa | 0.33 |
| 52 | 4 | Determinar los valores absolutos (máximos, mínimos o ambos) de una función en un intervalo | 0.33 |
| 58 | 4 | Probar las hipótesis del teorema del valor medio para una función en un intervalo | 0.33 |
| 48 | 3 | Calcular la derivada de una función logarítmica | 0.36 |
Fuente: elaboración propia.
El planteamiento y la resolución de problemas de variación resultan de mayor dificultad para los estudiantes (reactivos 50 y 51). Estos problemas de la vida real deben ser traducidos a una función que les permita obtener la variación en un momento determinado; sin embargo, esta traducción está identificada como una dificultad importante en los estudiantes de cálculo, además de la falta de asociación entre el concepto de la derivada y los problemas de aplicación de variación y optimización (Areaya y Sidelil, 2012). Sánchez et al. (2008) identificaron en los estudiantes dificultades y errores sobre los conceptos de velocidad instantánea de un movimiento variado y la tasa de variación instantánea de una función que impiden la resolución de problemas de variación.
Calcular la derivada de una función logarítmica y de una función trigonométrica inversa (reactivos 46 y 48) también son motivo de dificultad para los estudiantes en el ECCD. De manera adicional, aunque no se encuentran dentro de los primeros 10 más difíciles, los reactivos 45 (calcular la derivada de una función trigonométrica mediante la regla de la cadena, ID=0.37) y 47 (calcular la derivada de una función exponencial, ID=0.39) comparten la problemática expuesta, en el sentido de que el estudiante debe identificar la estructura de la función para aplicar adecuadamente la regla de derivación, en ocasiones más de una (producto, cociente y cadena). Lo anterior concuerda con Maharaj y Ntuli (2018), quienes observaron que los estudiantes tienen serias dificultades para derivar ciertos tipos de funciones algebraicas en las que se requiere aplicar múltiples reglas de derivación en forma simbólica.
La dificultad para representar gráficamente una función trigonométrica inversa a partir de su expresión algebraica (reactivo 21) puede deberse a lo señalado por Buendía y Ordóñez (2009) en el sentido que, en el discurso matemático escolar, la relación entre una función y sus derivadas para las funciones periódicas resulta poco significativa, debido a que se privilegia a los aspectos analíticos asociados y descontextualizados, al igual que los teoremas de Rolle y valor medio (reactivos 57 y 58). Sólo 29 por ciento de los estudiantes logra determinar la pendiente de la recta tangente en un punto (reactivo 37) a partir de su gráfica y la recta tangente trazada en un punto; confusiones comunes son el signo de la recta tangente, la intersección de la recta tangente con el eje horizontal y la ordenada en el origen de la recta tangente (Sánchez et al., 2008).
En el reactivo 52 (ID=0.33) se solicita a los estudiantes determinar los valores absolutos (mínimo, máximo o ambos) en un intervalo dado a partir de una función polinomial de segundo o tercer grado. La dificultad detectada estriba en que los estudiantes asocian directamente el límite inferior del intervalo como la abscisa del mínimo absoluto, y el límite superior del intervalo como el máximo absoluto; no indagan lo que sucede dentro del intervalo y no recurren a la producción de un gráfico para apoyar sus resultados.
El reactivo 39 causa una mayor dificultad a los estudiantes; en él se solicita obtener la gráfica de la función derivada a partir de la gráfica de la función. Ya que para la resolución de este reactivo no hay una regla de derivación o fórmula directa, se presume, al igual que en el experimento de Borji, Alamolhodaei y Radmehr (2018), que el estudiante no logra asociar o no sabe la relación entre el valor de la recta tangente con el valor de la derivada. En este reactivo se demanda una actividad mental en un ambiente meramente gráfico, en el cual se requiere que se realicen varias asociaciones además de la mencionada; los signos de la recta tangente de la función f con la situación de función creciente o decreciente de f’, puntos críticos de f con los ceros de f’ son ejemplo de tales asociaciones. En una investigación reciente Borji, Font, Alamolhodaei y Sánchez (2018) encontraron problemas importantes para que los estudiantes determinaran los puntos críticos y la variación de las rectas tangentes en una representación gráfica. Para algunos investigadores (Orhun, 2012; Park, 2012) los estudiantes adoptan el concepto de derivada como una operación derivada llevada a cabo mediante teoremas en un ambiente algebraico; esto se debe al método de enseñanza tradicional, en el cual los estudiantes no tienen éxito en hacer conexiones entre la gráfica de la función derivada y la función original. En sus investigaciones, Berry y Nyman (2003) observaron que el estudiante requiere de un esfuerzo cognitivo muy importante para asociar una gráfica de la derivada con la función original; para los estudiosos del cálculo (Baker et al., 2000; Sahin et al., 2015) en general los estudiantes no alcanzan una comprensión conceptual correcta de la representación gráfica de la derivada.
Se calcularon también los promedios del coeficiente de correlación biserial por unidad y se ordenaron, de mayor a menor: límites y continuidad (unidad 2, rpbis=0.37), la derivada (unidad 3, rpbis=0.36), funciones de una variable (unidad 1, rpbis=0.36) y aplicaciones de la derivada (unidad 4, rpbis=0.26).
Una prueba post-hoc de Tukey entre las unidades de reactivos y el rpbis mostró diferencias significativas (p=0.016), específicamente entre la unidad 4: Aplicaciones de la derivada, y el resto de las unidades que conforman la prueba. En esta unidad hay un descenso importante -aunque no significativo- en los indicadores psicométricos: se tienen los índices más bajos de discriminación y rpbis; sólo un reactivo de esta unidad es de dificultad media y ninguno está calificado como medianamente fácil o altamente fácil. De manera más específica, en la Tabla 5 se exhiben los 10 reactivos con mayor rpbis; se incluyen también el ID e IDC con el objeto de evidenciar que dichos reactivos que son predictores del éxito de un estudiante en el ECCD a su vez son de dificultad media y discriminan de manera excelente de acuerdo a Backhoff et al. (2000).
Tabla 5 Reactivos predictores del éxito de los estudiantes en el ECCD
| Reactivo | Unidad | Indicador de logro | rpbis | ID | IDC |
|---|---|---|---|---|---|
| 43 | 3 | Calcular las derivadas de orden superior de una función algebraica | 0.509 | 0.62 | 0.66 |
| 41 | 3 | Calcular la derivada de una función mediante la regla del producto | 0.503 | 0.62 | 0.64 |
| 14 | 1 | Representar gráficamente una función polinomial a partir de su expresión algebraica | 0.482 | 0.64 | 0.62 |
| 3 | 1 | Representar algebraicamente una función de valor absoluto a partir de su gráfica | 0.464 | 0.61 | 0.61 |
| 8 | 1 | Representar algebraicamente una función a partir de una tabla numérica | 0.459 | 0.69 | 0.58 |
| 15 | 1 | Representar gráficamente una función racional a partir de su expresión algebraica | 0.459 | 0.54 | 0.60 |
| 12 | 1 | Representar gráficamente una función lineal a partir de su expresión algebraica | 0.449 | 0.67 | 0.56 |
| 42 | 3 | Calcular la derivada de una función mediante la regla del cociente | 0.440 | 0.42 | 0.57 |
| 28 | 2 | Determinar límites unilaterales a partir una representación gráfica | 0.437 | 0.54 | 0.59 |
| 9 | 1 | Representar algebraicamente una función cúbica a partir de su gráfica | 0.433 | 0.55 | 0.56 |
Fuente: elaboración propia.
Los estudiantes consiguen buenas notas cuando tienen habilidades para obtener la primera y segunda derivada de funciones algebraicas en reactivos donde se requiere utilizar las reglas de derivación (41, 42 y 43), particularmente la de una constante, potencia, producto y cociente. Se predice también el éxito de los estudiantes cuando representan algebraicamente las funciones a partir de su gráfica, y viceversa; para ello tienen que relacionar semióticamente las características visuales y las unidades simbólicas significativas de los registros gráfico y algebraico de las funciones polinomiales, de valor absoluto y racionales. En estos reactivos (14, 3, 8, 15, 12 y 9) se requiere de la actividad cognitiva de conversión, en la que no hay reglas ni asociaciones básicas (Duval, 2006c).
En cuanto a la actividad cognitiva, 11.66 por ciento (7) de los reactivos son de representación, 35 por ciento (21) pertenecen a la actividad de tratamiento y 53.33 por ciento (32) son reactivos que requieren de la conversión para su resolución. Los promedios del ID son: 0.63 ± 0.14, 0.46 ± 0.10 y 0.49 ± 0.14 (media ± desviación estándar) respectivamente. Una prueba post-hoc de Tukey entre las actividades cognitivas y el ID mostró diferencias significativas (p=0.013) entre la actividad cognitiva de representación y las actividades de tratamiento y conversión; resultó ser la actividad de representación de menor dificultad (calificada como dificultad media) para los estudiantes en contraste con la actividad de tratamiento y conversión, cuya dificultad se califica como medianamente difícil.
El 15 por ciento (9) de los reactivos cuenta con lenguaje natural como registro inicial; 5 por ciento (3) numérico; 58 por ciento (35) tienen registro inicial algebraico y 22 por ciento (13) registro gráfico. Los promedios del ID para los registros iniciales son: 0.48 ± 0.19, 0.60 ±0.12, 0.49 ± 0.12 y 0.52 ± 0.14 (media ± desviación estándar) respectivamente. Una prueba post-hoc de Tukey entre los registros iniciales de los reactivos y el ID no mostró diferencias significativas. Los reactivos de mayor dificultad tienen como registro inicial el lenguaje natural y el algebraico, mientras que los más fáciles son aquéllos con registro inicial numérico.
El 10 por ciento (6) de los reactivos cuenta con lenguaje natural como registro final; 32 por ciento (19) numérico; 48 por ciento (28) tienen registro final algebraico y 12 por ciento (7) registro gráfico. Los promedios del ID para los registros finales son: 0.58 ± 0.19, 0.47 ± 0.13, 0.48 ± 0.11 y 0.56 ± 0.19 (media ± desviación estándar) respectivamente. Una prueba post-hoc de Tukey entre los registros finales de los reactivos y el ID no mostró diferencias significativas. Los reactivos de mayor dificultad tienen como registro final el numérico o el algebraico, mientras que los más fáciles son aquéllos cuyo registro final es el lenguaje natural o el gráfico. En la literatura no se encontraron documentos que identificaran cuál registro inicial o final causa mayor dificultad a los estudiantes cuando resuelven un examen de alto impacto como el que se describe en esta investigación; sin embargo, en sus estudios Borji y Sánchez (2019) encontraron que en el examen de admisión a la universidad que se aplica en España e Irán la mayoría de las preguntas relacionadas con el cálculo diferencial e integral son de corte algebraico, y un porcentaje muy pequeño están referidas a otros registros y a las relaciones entre ellos.
En el ECCD se cuenta con que 33 por ciento (20) de los reactivos son del tipo conceptual y 67 por ciento (40) son procedimentales. Los promedios del ID son: 0.59 ± 0.13 y 0.45 ± 0.11 (media ± desviación estándar) respectivamente. Una prueba T de muestras independientes (p<0.001) permite declarar que hay diferencia significativa en los ID promedio para los reactivos de tipo conceptual y procedimental. Los reactivos de corte procedimental son los de mayor dificultad y caen en la categoría de medianamente difíciles, mientras que los conceptuales quedan en la categoría de dificultad media. De los 10 reactivos más difíciles, 80 por ciento son de corte procedimental, mientras que 20 por ciento son conceptuales. Esta distribución con una carga superior a reactivos de corte procedimental presume que el trabajo en el aula conserva una carga similar. Algunos especialistas (Areaya y Sidelil, 2012) identificaron que los conocimientos previos al cálculo por parte de los estudiantes son aparentemente más procedimentales que conceptuales; además, los resultados de sus investigaciones evidencian que el proceso de enseñanza y aprendizaje del cálculo en las aulas, así como la propia evaluación es predominantemente procesal. Habre y Abboud (2006) encontraron que los estudiantes de cálculo diferencial privilegian el enfoque procedimental simbólico, ya que se les dificulta interpretar las gráficas de las funciones y sus derivadas; para Abbey (2008)) el desequilibrio entre el conocimiento operacional y el conceptual es un factor trascendente que contribuye a la debilidad del estudiante para graficar funciones y obtener información sobre la derivada.
La composición del ECCD en cuanto a los registros inicial y final utilizados en los reactivos es reflejo, de alguna manera, del tipo de enseñanza en el aula por parte de los profesores y diseñadores del ECCD; se presume que existe un desequilibrio en el manejo de los registros de representación y una carga predominante con el registro algebraico. Para De la Barrera (2010) no es útil privilegiar el registro simbólico que se le da al estudio de la variación como introducción de la noción de derivada; en este mismo sentido, los esquemas algebraicos de los estudiantes son muy dominantes porque les han reportado resultados exitosos en sus estudios de matemáticas previos (Berry y Nyman, 2003; Abbey, 2008). Para Borji y Sánchez (2019), en los exámenes de alto impacto -como los de admisión a las universidades- no se debería obligar a los estudiantes a concentrarse en exceso en las representaciones algebraicas de conceptos.
Conclusiones
Se revisó la calidad del ECCD que se aplica a gran escala en una universidad pública de México y cuyas características principales son: criterial, alineado al currículo, de opción múltiple y de alto impacto; data del año 2005, con una actualización en 2012, y consta de 60 reactivos. Se determinó que el ECCD es válido, confiable y con poder de discriminación satisfactorio. Se calculó la confiabilidad mediante el método KR-20 y se obtuvo un coeficiente r=0.88; también se determinó el coeficiente delta de Ferguson, cuyo valor resultante es 0.99. Ambos son considerados por los especialistas como satisfactorios.
La asimetría de la distribución del número de reactivos correctos evidenció la dificultad del ECCD con un promedio en el ID=0.50, mismo que se encuentra en el límite inferior del rango establecido por Backhoff et al. (2000). No se identificó ningún reactivo con ID menor a 0.2 ni mayor a 0.85, sin embargo, se detectaron tres reactivos (21, 50 y 58) altamente difíciles y un reactivo (59) medianamente difícil con discriminación deficiente, mismos que se sugiere sean revisados a profundidad, toda vez que reducen la probabilidad que tienen de responder correctamente aquellos estudiantes con un desempeño general sobresaliente en la prueba. Las unidades 1, 2 y 3 contienen reactivos que en promedio discriminan de manera excelente.
El análisis de calidad de la prueba permitió establecer que los reactivos predictores del éxito de un estudiante en el ECCD están asociados a la dificultad media y a una discriminación excelente. Se encontró que el éxito de los estudiantes en el ECCD se debe al desempeño favorable que tuvieron al utilizar las reglas de derivación, particularmente la de una constante, potencia, producto y cociente, así como también cuando representan algebraicamente las funciones (polinomiales, de valor absoluto y racionales) a partir de su gráfica y viceversa.
Los resultados de la prueba muestran que las unidades 3 (la derivada) y 4 (aplicaciones de la derivada), que abarcan 38 por ciento del ECCD, son las de mayor dificultad para los estudiantes. Los reactivos de estas unidades se caracterizan por la necesidad de ejecutar varias secuencias de operaciones algebraicas para su resolución: el uso de más de un teorema o regla de derivación, abundante abstracción, la transformación del lenguaje natural al lenguaje algebraico, el uso de la intuición y la exploración e indagación. De manera particular, exhibimos los 10 reactivos con mayor dificultad cuyas demandas cognitivas son: plantear y resolver enunciados de problemas de tasas de variación, calcular la razón de cambio instantáneo en un punto a partir de su gráfica, probar las hipótesis de los teoremas de Rolle y valor medio, calcular máximos y mínimos, representar gráficamente la función derivada a partir de su gráfica, representar gráficamente una función trigonométrica inversa a partir de su expresión algebraica, calcular la derivada de una función logaritmo y de una función trigonométrica inversa. En estas unidades y en estos reactivos se demandan conceptos previos sobre funciones y límites, abunda el lenguaje simbólico y se tiene alto grado de abstracción; las actividades cognitivas predominantes son el tratamiento en un contexto algebraico y la conversión, mismas que cuentan con la mayor dificultad para los estudiantes, en contraste con la actividad cognitiva de representación.
Desde la perspectiva de las representaciones semióticas, estos 10 reactivos cuyas demandas cognitivas se describen, dan cuenta de su dificultad de resolución a partir de la necesidad, de parte del estudiante, de manipular efectivamente el lenguaje algebraico y transitar de un registro de representación a otro. Aunque el dominio total o parcial de la manipulación algebraica les ha permitido avanzar en los niveles educativos previos a la licenciatura, aquí también se evidencia que esto no es suficiente cuando se trata de resolver ciertos problemas asociados a la derivada que son conceptuales o procedimentales y que implican la ejecución de múltiples secuencias ordenadas o contienen un alto nivel de abstracción.
La dificultad para los estudiantes de acreditar el ECCD (29 por ciento obtuvo una calificación igual o superior a 60, con la que se aprueba) puede explicarse a partir del predominio de las actividades cognitivas de tratamiento y conversión (88 por ciento de los reactivos), en la resolución de los reactivos que son procedimentales y requieren, en algunos casos, simplificaciones algebraicas importantes para determinar el resultado.
El ECCD muestra, a través de los registros de representación inicial y final, un abundante lenguaje algebraico que para los estudiantes es una de las causas del bajo rendimiento. A partir de los resultados obtenidos se hacen las siguientes recomendaciones:
Modificar el ECCD con una estructura equilibrada entre los registros de representación, las actividades cognitivas y las perspectivas estructural y procedimental.
Revisar las concepciones de los profesores en cuanto a su preferencia por los procedimientos algebraicos para abordar los conceptos de cálculo diferencial y la manera en que piensan que sus alumnos aprenden.
Liberar a los estudiantes del predominio del aprendizaje de manera operacional con una orientación más conceptual en la enseñanza del cálculo.
Incluir en el diseño instruccional el análisis e interpretación de la información gráfica, así como la vinculación de las representaciones y la verbalización de las mismas.
Promover en el curso de cálculo diferencial el equilibrio en el uso de los distintos registros de representación, de manera que se fortalezcan las actividades cognitivas de tratamiento y conversión.
Enfatizar en la representación gráfica de la derivada e incluir la exploración y demostración para reforzar la perspectiva conceptual con aplicaciones reales.
Motivar la incorporación de aplicaciones reales en el diseño instruccional para mejorar la transformación del lenguaje natural al lenguaje matemático y viceversa.
Promover en los estudiantes las habilidades de indagación, experimentación, exploración, demostración y argumentación que favorecen el enriquecimiento de la apropiación conceptual, sobre todo en el campo del cálculo diferencial.
Promover el uso de aplicaciones o programas de cómputo con el fin de observar o visualizar conceptos en sus distintos registros de representación semiótica.
Los resultados de esta investigación aportan a investigadores y docentes elementos para la creación o modificación de materiales didácticos que ayuden a mejorar el entendimiento de los estudiantes en los temas de mayor dificultad.
Como trabajo futuro se pretende analizar la enseñanza del cálculo diferencial directamente en las aulas, particularmente en lo que se refiere a problemas de tasas de variación relacionadas y problemas de optimización, ya que representan una dificultad importante al estudiante. Por otra parte, analizar las técnicas y herramientas docentes al utilizar las diferentes representaciones semióticas para abordar los conceptos del cálculo diferencial.











 nueva página del texto (beta)
nueva página del texto (beta)



