Antecedentes
Indagar las ideas de los niños acerca de las relaciones entre área y perímetro (en adelante relaciones A-P) se justifica por ser un tema poco trabajado por los investigadores de la educación matemática. Continuar su indagación es pertinente, además, por ser un contenido inserto en el currículo de educación básica de muchos países y, sobre todo, por constituir un tema donde la medición y la geometría plantean retos interesantes que pueden favorecer la visualización, la elaboración y prueba de hipótesis, así como la argumentación, aspectos de la educación matemática reconocidos como fundamentales en el nivel internacional.
Fueron Piaget y sus colaboradores quienes iniciaron el estudio de estas relaciones (Vinh Bang, 1965a, 1965b; Piaget et al, 1971; Piaget et al., 1973; Piaget e Inhelder, 1997). Posteriormente, las francesas R. Douady y M.J. PerrinGlorian (1983) continuaron la indagación sobre el tema. Estas investigadoras estudiaron la variación del área y el perímetro cuando una superficie es sometida a ciertas transformaciones y constataron que, para los niños, existe una íntima relación entre estas magnitudes. Es decir, que predomina en ellos la siguiente idea: “si el perímetro de una superficie aumenta, su área también (y recíprocamente), y si dos superficies tienen el mismo perímetro, tienen la misma área (y recíprocamente)” (Douady y Perrin-Glorian, 1983; Perrin-Glorian y Douady, 1988). Con base en tal constatación, estas investigadoras plantearon una secuencia didáctica cuyo objetivo fue favorecer que los alumnos lograran independizar: a) el área de la forma (dos superficies de formas diferentes pueden tener áreas iguales); y b) el área del perímetro (dos superficies pueden tener la misma área y perímetros diferentes) (Douday y Perrin-Glorian, 1983).
Algunas conclusiones obtenidas por los niños participantes en esta indagación -según reporte de las autoras- fueron las siguientes:
para la misma área, entre más retorcida esté la forma, más grande es el perímetro;
dos superficies con la misma área, no tienen necesariamente el mismo perímetro;
para comparar las áreas de dos superficies, no sirve de nada comparar los perímetros (Douady y Perrin-Glorian, 1983: 49).
Posteriormente, Corberán (1996) obtuvo conclusiones sobre el mismo problema al solicitar a estudiantes de niveles educativos diversos, que trataran de transformar un rectángulo y un rombo dibujados en una hoja de papel, de manera que, al conservar o agrandar el perímetro, el área de las figuras fuera menor. Al respecto, la investigadora anota: “fueron muchos los estudiantes de todos los niveles los que no supieron modificar un rombo para transformarlo en otra superficie de menor área y mayor perímetro, o manifestaron que lo que se solicitaba era imposible” (Corberán, 1996: 130). El experimento se replicó con un polígono cóncavo y se constató que los alumnos actuaron de la misma manera que con el rombo: muchos de los participantes en la investigación manifestaron que figuras de igual perímetro no pueden tener diferente área. Una reflexión que Corberán (1996) deriva de su trabajo es que los alumnos no podrán enfrentarse exitosamente a situaciones como las que se les plantearon mientras no acepten la independencia entre el área y el perímetro de una superficie.

Fuente: Douady y Perrin-Glorian, 1983.
Figura 1 Figura elaborada por niños participantes en el trabajo de Douady y Perrin-Glorian.
Un trabajo más reciente, dedicado también a analizar las relaciones A-P, es el de D’amore y Fandiño (2007). Estos autores recuperan los estudios de Stavy y Tirosh (1996), quienes mostraron que existe una fuerte relación de dependencia entre el área y el perímetro, del tipo
Si A y B son dos figuras planas, entonces: si el perímetro de A es mayor que el perímetro de B, el área de A es mayor que el área de B (lo mismo sucede con menor e igual), por lo cual dos figuras iso-perimétricas son necesariamente equi-extensas; y viceversa (D’Amore y Fandiño, 2007: 44).
Sobre la base de tales ideas, estos autores buscaron responder a las siguientes cuestiones: “¿surge espontáneamente la idea de que, al aumentar el perímetro de una figura plana aumenta también el área?, ¿se necesita recurrir a construcciones cognitivas anteriores y a la propia experiencia, para convencerse que las cosas no son así?” (D’Amore y Fandiño, 2007: 47-48).
Una vez identificadas las “convicciones iniciales” respecto de la relación A-P, D’Amore y Fandiño analizaron el cambio que se opera en ellas mediante la discusión con el investigador, y concluyeron que, después de haber trabajado las actividades propuestas, las ideas erróneas ligadas a la intuición mayor A, mayor P y sus variantes casi desaparecieron.
Marco conceptual
La intuición más A, más B
Stavy y Tirosh (1996) plantearon una idea que resultó muy sugerente para muchos estudiosos de la educación matemática. Estas investigadoras afirman que, tanto en física como en matemáticas, los estudiantes reaccionan de forma similar ante una gran diversidad de tareas no relacionadas entre sí, debido a que sus respuestas parecen descansar en las mismas ideas intuitivas. Una de estas ideas se expresa en la regla “más de A, más de B”, la cual se refleja en las respuestas de los estudiantes ante tareas diferentes, incluidas las clásicas piagetianas de conservación del número, la materia, el peso o el volumen.
Otros investigadores realizaron estudios tratando de confirmar la existencia de la regla identificada por Stavy y Tirosh o alguna de sus variantes: “igual A, igual B”, o “menos A, menos B” (Tsamir y Mandel, 2000; Stephanou y Pitta-Pantazi, 2006). En todos los casos, las ideas de Stavy y Tirosh recibieron apoyo empírico. Nosotras consideramos que, además de confirmar la probable existencia de dicha intuición, desde el punto de vista cognitivo y educacional tendría un importante interés explicar el proceso por el cual es posible abandonarla. Por esta razón, el foco de nuestro estudio es indagar la probable existencia de la intuición “más A, más B”, y tratar de caracterizar y entender el proceso por el cual sería posible abandonarla en el caso de las relaciones A-P.
Con el fin de lograr tal entendimiento, tomamos el marco construido por Jean Piaget y sus colaboradores, especialmente el trabajo de Vinh Bang (1965a; 1965b). Nuestro objetivo es doble: en primer término, identificar la existencia (o no) de la intuición “más A, más B”; y, de ser constatada ésta, documentar el proceso mediante el cual 12 niños de alto desempeño escolar en matemáticas abandonan esta intuición y transitan hacia la deducción operatoria, en el contexto de las relaciones entre el área y el perímetro de figuras planas.
La intuición geométrica y la deducción operatoria según Piaget
Piaget y sus colaboradores abordaron el problema de las relaciones A-P en términos de intuición geométrica y deducción operatoria. En esta perspectiva, la imagen visual tiene un papel esencial (Piaget, 1971; Piaget e Inhelder, 1997). En el nivel preoperatorio del pensamiento del niño, la imagen visual permanece estática y es incapaz de representar las transformaciones más elementales. Es hacia los 7 u 8 años -cuando las operaciones intelectuales comienzan a constituirse- que la imagen adquiere una cierta movilidad por la influencia de aportes exteriores, proporcionados fundamentalmente por las operaciones intelectuales que desarrolla el propio sujeto (Piaget, 1971).
Cuando el niño no llega aún por vía deductiva a las conservaciones elementales de superficie, necesita de la experiencia directa con las superficies involucradas, como podría ser la superposición de elementos para comprobar, por ejemplo, que un rectángulo compuesto por seis cuadrados agrupados en la forma 2 x 3 abarcará la misma superficie que el rectángulo formado por la alineación de esos cuadrados, o sea, 6 x 1 (Piaget, 1971).
Según Piaget, la abstracción reflexiva y constructiva es el mecanismo que permite imaginar el resultado de las transformaciones sobre las imágenes sin necesidad de recurrir a la experiencia física. La abstracción, dice, es: reflexiva, porque hay “reflexión”, en el sentido de una proyección de las acciones sobre el plano de las representaciones; constructiva (por reflexión mental), en el sentido en que una deducción sustituye a la comprobación experimental, siendo aquélla más rica que ésta por el hecho de poseer más movilidad y tener un campo mucho más amplio (Piaget, 1971) al sobrepasar libremente las configuraciones y anticipar las transformaciones.
En esta perspectiva, hay que distinguir, entonces, las imágenes de simple reproducción y las imágenes anticipatorias. Cuando la acción intelectual del niño ya no se apoya en las imágenes ni en la experiencia física para obtener alguna conclusión que resultaría de alguna transformación, se ha logrado una deducción operatoria en geometría.
Vinh Bang y las relaciones área-perímetro desde la postura piagetiana
Vinh Bang estudió las relaciones entre superficie y perímetro bajo la siguiente perspectiva:
Se puede suponer que las primeras formas de vinculación con la representación visual se apoyan únicamente sobre esta representación, mientras que las operaciones espaciales rebasarán, en un momento dado, el contenido sensible para devenir deducción operatoria. En la deducción operatoria la imagen ya no es estática, anticipa las transformaciones, y rebasa las simples constataciones (1965a: 1).
El principal problema estudiado por Bang (1965a; 1965b), para el interés de nuestra investigación, es la conservación de un contorno o perímetro y la variación de la superficie contenida en ese contorno o perímetro; y, paralelamente, la conservación de una superficie y la variación del contorno que la contiene.
Superficie y perímetro, dice Bang, están materialmente vinculados pero cada uno goza de propiedades geométricas diferentes. ¿Cómo logra el niño diferenciar las relaciones A-P y dominar las primeras formas de vinculación intuitivas para deducir las propiedades geométricas subyacentes? Concretamente, Bang intenta captar cómo los niños diferencian lo variante y lo invariante a través de las transformaciones geométricas que se les pide efectuar. Señala que los niños, sobre todo en las primeras etapas, generalizan fácilmente que “a perímetro constante, superficie constante”. Sólo mediante las constataciones perceptivas donde la transformación sobre la figura es muy evidente aceptan la independencia entre la variación de una magnitud y la otra. Pero la explicación de Bang va más allá y define niveles en la comprensión de las relaciones A-P (Bang, 1965a).
En la etapa inicial (5-6 años), la figura geométrica se toma como un objeto físico estático. Las transformaciones sólo se entienden como desplazamientos de las figuras. También en esta etapa, de la conservación del perímetro los niños infieren la conservación de la superficie, puesto que el criterio de estimación es de orden perceptivo. Los niños creen que cuando se empujan un poco las varillas de un cuadrado o un rombo que se deforman no cambia nada; es sólo cuando se empuja mucho -y que la transformación es muy notable- que la superficie se hace más pequeña.
Después de haber realizado físicamente las transformaciones, niños de 7 u 8 años dan respuestas que reflejan cierta evolución. Las transformaciones ya son entendidas como deformaciones: toda transformación implica variaciones y deformaciones de las dimensiones de las figuras. Pero en este periodo no existe la idea de compensación; la disminución de la altura de un rombo no implica un aumento en su largo, por lo que las figuras, en la perspectiva del niño, sufren una disminución en sus dos dimensiones.
Hacia los 8-10 años predominan las “falsas conservaciones”, aplicadas indistintamente a las transformaciones de superficie o de perímetro. La conservación de uno entraña la conservación de la otra y recíprocamente. El niño persiste en su creencia de que, a pesar de las transformaciones, todas las superficies (áreas) permanecen iguales, porque todas tienen el mismo perímetro (p. ej., “la superficie es del mismo tamaño [que en la otra figura], porque aún tenemos el mismo hilo [perímetro]”) (Bang, 1965a: 18). En esta etapa, es sólo hasta la transformación límite (superficie nula) que se reconoce el cambio en el área.
Hacia los 10-12 años aparecen dudas en el juicio perceptivo: “No se puede saber, tal vez sea más grande, tal vez sea igual”. También a esta edad, pero en un momento que Bang considera más avanzado, las conductas de los niños se caracterizan por un progreso hacia la deducción: se pueden anticipar las transformaciones de las figuras, así como diferenciar la variación del área de la del perímetro. Las constataciones empíricas a partir de la manipulación de materiales siguen siendo útiles: sirven para verificar las hipótesis elaboradas por el niño pues, aunque en esta etapa se ha rebasado el límite de la imagen física, la representación visual apoya de manera importante el progreso hacia la deducción geométrica.
Es hasta los 11-12 años cuando las relaciones entre superficie y perímetro se diferencian con claridad. En esta etapa se observan dos tipos de respuestas: a) las que siguen apegadas a las transformaciones materialmente realizables; b) las que se orientan hacia la generalización.
En suma: Piaget y sus colaboradores consideran que la intuición geométrica propia de las etapas iniciales corresponde a un pensamiento estático, dependiente de las imágenes concretas, incapaz de anticipar transformaciones y que se fía de falsas conservaciones. En cambio, la deducción operatoria entraña flexibilidad de pensamiento, capacidad de anticipar, de transformar sin recurrir a la acción concreta, de reconocer las consecuencias de las transformaciones y, en el caso del área y el perímetro, de independizar la variación de estas dos magnitudes. Es decir que la deducción operatoria en geometría implica la capacidad de transformar operatoriamente las imágenes y desprenderse de ellas, al rebasar el pensamiento los límites de la imagen física. El tema de nuestro trabajo es si los niños participantes en nuestra indagación siguen este proceso en su comprensión de las relaciones entre A y P de figuras planas.
Objetivos y preguntas de la investigación
Con base en el marco recién presentado planteamos una investigación con los objetivos y preguntas que se exponen a continuación.
Conocer si los niños participantes en la investigación:
al resolver problemas que implican relaciones entre área y perímetro, inicialmente lo hacen poniendo en acto la regla intuitiva “más A, más B”, sugerida por Stavy y Tirosh, es decir, si aceptan espontáneamente, y como relación obligada, que “a mayor perímetro, mayor área”.
De ser este el caso, conocer si, al proponerles una serie de problemas que implican diversas relaciones área-perímetro:
¿Los niños abandonan la intuición inicial expresada en la regla “mayor perímetro, mayor área” durante el proceso de resolución de los problemas?
De ser positiva la repuesta a la pregunta anterior, ¿cuál es el proceso mediante el cual ocurre el abandono de dicha intuición?
Específicamente:
¿Qué papel juegan las imágenes en este proceso?
¿Qué papel juegan la anticipación y la prueba de hipótesis?
¿En qué momento y ante qué situaciones se rebasan los límites de la imagen concreta y se actúa con base en la deducción operatoria?
¿Qué situaciones problemáticas se muestran útiles para promover que la intuición se supere y se favorezca el desarrollo de la deducción operatoria?
Metodología
Para recoger la información que permitiera responder las preguntas planteadas, trabajamos con 12 niños que cursaban cuarto, quinto y sexto grado de educación primaria (cuatro de ellos en cada grado) y cuyas edades oscilaban entre los 9 y los 12 años en el momento de la indagación. La decisión de trabajar con niños de estas edades se debió a dos razones: la primera es que, conforme a los datos aportados por Vinh Bang (1965a; 1965b), su desarrollo cognitivo les haría accesibles en distintos niveles los problemas que plantearíamos; la segunda razón es que, conforme a los programas oficiales de educación primaria vigentes, los niños tendrían conocimientos escolares que les permitirían calcular tanto el perímetro de figuras planas de lados rectos, como el área del cuadrado y el rectángulo, conocimientos necesarios para abordar las situaciones elaboradas para esta investigación. Es por esto último que, como primera actividad, planteamos situaciones y preguntas que permitieran constatar que efectivamente tenían los conocimientos mencionados.
Once de los niños participantes asistían a una escuela pública con prestigio académico importante, y que estaba catalogada, por sus logros, sobre el primer cuartil de las escuelas de la Ciudad de México, según los resultados de exámenes nacionales aplicados en los últimos años (esta información fue proporcionada por la directora y los profesores del plantel). También incluimos las respuestas de un niño de quinto grado que asistía a otra escuela que participó cuando exploramos la viabilidad de las tareas propuestas. Al ser útiles e interesantes sus respuestas -y puesto que este niño asistía a una escuela de características similares que aquella en la que realizamos el estudio principal- decidimos incorporarlas en el análisis.
Aunque no era la intención inicial, debido a que los profesores de los grupos escogieron a los participantes (decisión que no pudimos refutar), los niños seleccionados tenían un desempeño escolar destacado en matemáticas. Esto lo constatamos cuando, al iniciar la actividad, todos comentaban que sus calificaciones en matemáticas iban del 9 al 10, que son las más altas que se otorgan en la educación primaria mexicana. Posteriormente, la directora de la escuela corroboró el desempeño destacado de los seleccionados.
Lo anterior debe tomarse en consideración al leer los resultados, pues se trata de niños que se encuentran por encima del promedio de sus pares mexicanos en cuanto a desempeño escolar en matemáticas. Aunque en esta investigación no buscamos evaluar ningún desempeño escolar, sino las ideas en torno a las relaciones entre área y perímetro, es probable que exista alguna relación entre ambos.
En el Cuadro 1 se anotan los datos generales de los niños. Las referencias posteriores a cada uno de ellos se harán con la inicial de su nombre ficticio, el grado que cursa y su edad. Por ejemplo, D6-11 refiere a Diana, de sexto grado y 11 años.
Cuadro 1 Datos generales de los niños participantes en la investigación
| Nombre | Sexo | Edad | Grado que cursa | Calificación y observaciones sobre el desempeño escolar en matemáticas |
| Diana | F | 11 años | 6° | 9 y 10 |
| Zaida | F | 10 años | 10 | |
| Federico | M | 11 años | 10. Obtuvo el primer lugar en su escuela y segundo en su zona escolar | |
| Emiliano | M | 12 años | 10 | |
| Karina | F | 11 años | 5° | 9 y 10 |
| Virgilio | M | 10 años | 9 y 10 | |
| Javier | M | 11 años | 9 y 10 | |
| Martín | M | 11 años | 10 | |
| Arely | F | 10 años | 4° | 10 |
| Carola | F | 9 años | 10. Ha participado en cursos para “niños talento” | |
| Noemí | F | 10 años | 10 | |
| Gabriel | M | 9 años | 10 |
Fuente: elaboración propia.
Para realizar la indagación elaboramos seis problemas que fueron planteados oralmente, a cada niño por separado. En el artículo se analizan sólo tres por razones de espacio. El problema “las dos plazas” (ver adelante) se planteó dos veces: al iniciar la actividad y al finalizarla, y constituye un instrumento de diagnóstico y de evaluación de los avances logrados durante el proceso de resolución de los problemas.
Se pusieron a disposición de los participantes materiales que eventualmente podrían utilizar: lápiz, tijeras, calculadora, hojas blancas y cuadriculadas, regla graduada, listones y “cuadrados-unidad”, así como las figuras correspondientes al planteamiento de algunos de los problemas, recortadas en cartón. Se trabajó en la biblioteca escolar cuando ésta no estaba en uso. La actividad, dependiendo de la habilidad de cada uno de los niños para resolver los problemas, duró entre 45 minutos y una hora. El proceso fue audio grabado, y se tomaron fotografías de las soluciones porque no se autorizó a video-grabar.
Al finalizar la resolución de cada problema se interrogaba al niño para que nos explicara el porqué de cada solución. También pedimos comprobar la validez de las respuestas y, cuando lo consideramos pertinente, incorporamos una contra-argumentación, en voz de niños supuestos, para obtener más elementos de interpretación de las soluciones y las ideas subyacentes a las mismas. Es decir que la base de la entrevista eran los problemas planteados y su solución y, a partir de ello, recurrimos al interrogatorio crítico (Piaget et al., 1973) para dilucidar mejor el razonamiento de los niños acerca de las relaciones A-P.
Ahora bien, aunque en los estudios de tipo cualitativo y basados en el interrogatorio crítico, lo común es que el número de participantes sea reducido, dándose el caso de estudios basados en las respuestas de dos, tres o cinco niños, conviene mencionar que el total de 12 participantes en esta investigación fue decidido en función de lo que en ciencias sociales se denomina “saturación de la información”. Ésta refiere al punto en que, una vez realizado un cierto número de cuestionamientos o entrevistas, nuevos interrogatorios dejan de proporcionar datos diferentes a los ya recogidos. Así, cuando los interrogatorios comenzaron a arrojar datos similares a los ya colectados e identificamos ciertos patrones en las respuestas, cerramos la etapa de recolección de datos.
Para interpretar los datos utilizamos el enfoque inductivo general (GIA) de Thomas (2006) para organizar y analizar datos cualitativos. Este enfoque se concreta en cuatro etapas que en conjunto permiten reducir y analizar los datos, así como elaborar categorías con ellos:
lectura cuidadosa y repetida de los datos crudos para identificar temas de interés conforme a los objetivos de la investigación;
limpieza y condensación de los datos en un formato reducido;
creación de categorías con base en el marco conceptual adoptado; y
revisión continua de los datos y refinamiento del sistema de categorías resultante.
Resultados
Primer acercamiento a las relaciones A-P: el problema “las dos plazas”
Una vez constatado el conocimiento de los niños respecto del área y el perímetro de las figuras a las que se haría referencia durante la investigación, se plantearon los problemas previstos. En primer lugar, propusimos el que llamamos “las dos plazas”, tomado y adaptado de D’Amore y Fandiño (2006). Con este problema identificamos las ideas espontáneas respecto de las relaciones A-P. Se planteó oralmente de la siguiente manera:
En un pueblo hay dos plazas, una plaza se llama Benito Juárez y la otra se llama Madero. El perímetro de la plaza Benito Juárez es mayor que el de la plaza Madero, ¿cuál de las dos plazas tiene un área mayor?
Cuadro 2 Tipos y frecuencia de respuestas al planteamiento inicial sobre la relación área-perímetro
| Grado que cursa | Con base en la intuición “a mayor perímetromayor área” | Con base en la intuición “a mayor perímetromayor área”, que luego se busca justificar | Respuestas que abandonan la aceptación inmediata (se problematiza la situación, se anticipan posibilidades y se busca evidencia: rectángulos de distintas medidas) | |
| 6° | 2 | 0 | 2 | |
| 5° | 2 | 1 | 1 | |
| 4° | 3 | 1 | 0 | |
| Total | 7 | 2 | 3 | 12 |
Fuente: elaboración propia.
Respuestas
Todos los niños sostuvieron inicialmente la idea de que la plaza Benito Juárez (con mayor perímetro), tiene un área mayor. No obstante, hallamos una diferencia respecto de los resultados reportados por Stavy y Tirosh (1996), pues no siempre la respuesta “a mayor P, mayor A” fue dada con base en la simple intuición. Varias de las respuestas muestran que la aceptación no es inmediata, y otras parecen “intermedias” entre la intuición y su abandono. Así, recogimos: a) respuestas sustentadas en la simple intuición; b) respuestas sustentadas en la intuición, que luego se tratan de justificar; c) respuestas que abandonan la aceptación inmediata. Veamos en seguida cada una de ellas.
a) Respuestas sustentadas en la simple intuición. Se trata de una aceptación espontánea e inmediata basada en la intuición “más A, más B”. No se requiere evidencia para responder, porque el problema y su respuesta son evidentes en sí mismos. En este momento inicial, los argumentos vertidos para justificar la respuesta “a mayor perímetro, mayor área” fueron expresados con certeza por la mayoría de los niños; tal relación parecía obvia, obligada. Ejemplos de esto son las siguientes respuestas:
Porque el mismo problema te está diciendo que la plaza Benito Juárez es mayor (D6-11).
Para que tenga cierta superficie, debe tener cierto perímetro, y si la Benito Juárez tiene más perímetro, significa que tiene más espacio (J5-11).
b) Respuestas sustentadas en la intuición, que luego se tratan de justificar. Están basadas en la intuición “mayor P-mayor A” y se acompañan de evidencias para “probarlas”. Las respuestas clasificadas aquí se dieron con inmediatez, y son similares a las clasificadas en a). Por ejemplo: “porque la figura es grande, tiene números mayores y te da medidas [áreas] mayores” (K5-11). Empero, las diferenciamos de aquéllas porque, aunque la situación se considera evidente en sí misma, a petición, quienes las dan no responden de manera tautológica, argumentando “la obviedad de la situación”, sino que esgrimen argumentos que -se supone- muestran la validez de “mayor P, mayor A”:
Porque la Benito Juárez es más grande del perímetro, y si multiplicas base por altura -yo me la imaginé rectángulo- sería mayor el resultado, y el otro si el perímetro es de 9 por 4, daría 36, y el otro es de 10 x 4, daría 40 (A4-10).
c) Respuestas que abandonan la aceptación inmediata. Las respuestas clasificadas aquí también incorporan evidencia producida por los resolutores, pero ésta tiene un papel distinto que el que orienta a probar la intuición “más A, más B”. Se sustentan en la problematización de la situación y exploran posibles soluciones mediante producción de evidencias. Quienes dieron una respuesta de este tipo son alumnos de quinto y sexto grados y ninguno de ellos acepta inmediatamente (por simple intuición) que “a mayor P, mayor A”.
En los tres casos clasificados aquí se considera que la situación planteada es problemática, que la respuesta no es obvia, y que debe producirse y recogerse evidencia para poder responder. Para colectar la evidencia se recurrió siempre al trazo de rectángulos y al cálculo de su área. Un ejemplo de respuesta es el siguiente:
E6-12: [dice pensativo]: “depende”, luego dibuja rectángulos con medidas diferentes y calcula el área y el perímetro de cada uno. Al hacerlo, intenta obtener evidencia para explorar alguna posible solución (Fig. 2).

Fuente: dibujo elaborado por E6-12.
Figura 2 Estrategia de E6-12 para explorar la validez de su hipótesis sobre la relación que plantea el problema “las dos plazas”
Sin embargo, los casos que considera E6-12 no lo llevan a una conclusión clara sobre la relación posible entre área y perímetro, veamos por qué (Cuadro 3). Como se ve al comparar las figuras A y B dibujadas por este estudiante, el perímetro se conserva, pero en una de ellas el área es mayor; al comparar la figura C con la A y la B, el perímetro disminuye y el área también. En la figura D, el perímetro es menor que en las figuras A y B, e igual que en la C, el área es menor que en el resto de las figuras. No le es posible, entonces, concluir sobre la relación que analiza con base en casos cuyos resultados no conducen a mostrar que es posible que un perímetro menor pueda determinar un área igual o mayor. Las exploraciones de los otros dos niños ubicados en esta categoría son similares.
Cuadro 3 Síntesis de las estrategias utilizadas por E6-12 en su primer acercamiento al problema “las dos plazas”
| Figuras propuestas por E6-12 | Perímetro | Área | Observaciones |
| A | 30+30+10+10 = 80 u | 300 u2 | |
| B | 20 x 4 = 80 u | 400 u2 | Igual perímetro y mayor área que A |
| C | 25 + 25 + 10 + 10 = 70 u | 250 u2 | Menor perímetro y área que A y B |
| D | 5 + 5 + 30 + 30 = 70 u | 150 u2 | Menor perímetro y área que A y B. Igual perímetro y menor área que C |
Fuente: elaboración propia.
Ahora bien, utilizar rectángulos donde se hacen variar las medidas como camino para recoger evidencias es un método pertinente, sin embargo, “el espacio de prueba” generado tiene limitaciones: además de no ser sistemático se restringe a un cierto tipo y número de casos.
La conclusión que obtenemos de las respuestas iniciales al problema “las dos plazas”
Los tres corrales están cercados con alambre de púas, para que no se salgan los animales. ¿Tú crees que en todos se gastó la misma cantidad de alambre para cercarlo, o en cada uno se gastó distinta cantidad? es que, si bien algunos niños abandonan la aceptación inmediata y problematizan la situación, finalmente todos aceptan que “a mayor perímetro, necesariamente mayor área”. A ello contribuye que, quienes problematizan y exploran soluciones, generan pruebas que no los conducen a mostrar que la relación mayor P, mayor A, no es obligada. Es decir, que no es la intuición la que sustenta la respuesta, sino la calidad de la evidencia recogida.
El poder heurístico de las imágenes. Frente al problema “los tres corrales”
Una vez planteado el problema de “las dos plazas”, se plantearon otros cinco. Analizaremos tres de ellos, ya que es lo que el espacio nos permite. Comenzamos con “los tres corrales” (Fig. 3) que parece ser un punto de inflexión en el razonamiento de los niños.
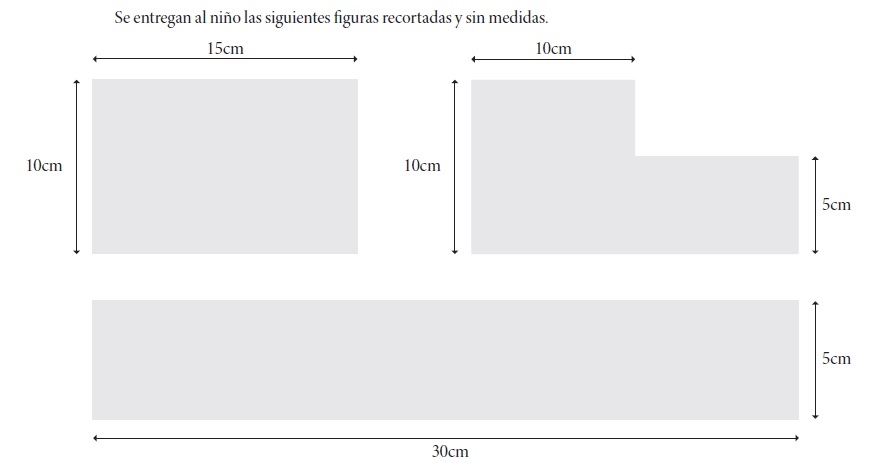
Se plantea el problema: estas figuras representan corrales. Fíjate en ellas y luego contesta las preguntas que te haré:
a) ¿Crees que hay alguno en el que quepan más animales que en los otros, o no?
b) ¿Cómo lo sabes?
c) Los tres corrales están cercados con alambre de púas, para que no se salgan los animales. ¿Tú crees que en todos se gastó la misma cantidad de alambre para cercarlo, o en cada uno se gastó distinta cantidad?
d) ¿Cómo lo sabes?
Fuente: elaboración propia.
Figura 3 Problema “los tres corrales”
Este problema tiene diferencias importantes con “las dos plazas”:
En “las dos plazas” era necesario imaginar la forma de las plazas. En “los tres corrales” se proporcionaron representaciones físicas de los corrales, por lo que su forma es perceptible, además de que dichas representaciones pueden manipularse y medirse.
En el problema “las dos plazas” se exploró la relación perímetro-área, y en “los tres corrales” se explora la relación áreaperímetro (específicamente la aceptación de la idea “igual A, diferente P”).
En “los tres corrales” las palabras área y perímetro no se mencionan. Se exploró si los niños relacionan estas nociones con la cantidad de animales que les cabe a los corrales y el alambre necesario para cercarlos.
En el Cuadro 4 se anotan los tres tipos de respuesta dados al problema.
Cuadro 4 Tipos de respuesta al problema “los tres corrales”
| Sostiene dependencia entre A y P | Declara la independencia entre A y P, con base en evidencia empírica (visualización o medición) | Declara independencia entre A y P por deducción operatoria | |
| A4-10, D6-11, Z6-10 | V5-10, J5-11, N4-10, C4-9 | E6-12, F6-11, M5-11, K5-11, G4-9 | |
| 3 | 4 | 5 | Total: 12 |
Fuente: elaboración propia.
a) Respuestas que sostienen dependencia entre área y perímetro. Aquí, el problema y su solución son evidentes en sí mismos. Por ejemplo, ante la pregunta c), una vez que se comprueba la igualdad de áreas, las respuestas respecto del perímetro son del tipo:
Yo digo que en todos [se gastó] lo mismo [de alambre], porque tienen la misma área [“¿Tú piensas eso?”, pregunta la investigadora].
Sí, yo digo [con certeza, como confirmando que esa es su opinión] (D6-11).
b) Respuestas que declaran independencia A-P, basadas en evidencia empírica. Estas respuestas se caracterizan porque no se anticipan hipótesis; se hace necesario medir (recoger evidencia) para llegar a una conclusión. Un ejemplo de esto, habiéndose establecido la igualdad de las áreas, y también ante la pregunta
c), es el siguiente:
Depende del perímetro [decide medir antes de ofrecer su respuesta; concluye]: éste necesita menos alambre [señala el rectángulo largo, por error de medición] (J5-11).
Al margen del error cometido, las respuestas clasificadas en este rubro reflejan que quienes las dan aceptan una posible independencia entre área y perímetro, pues si bien ya habían señalado que al rectángulo largo y al hexágono les cabía la misma cantidad de animales, no consideraron contradictorio que el corral representado por el rectángulo largo necesitara una diferente cantidad de alambre, pues ésta “depende del perímetro” y no del área.
d) Respuestas que declaran independencia entre área y perímetro, por anticipación deductiva. A diferencia de lo que sucedió con el problema “las dos plazas”, en “los tres corrales” seis niños notaron, desde un principio, la independencia entre área y perímetro. Habiendo establecido la igualdad entre las áreas de las tres figuras, afirmaron que los perímetros eran distintos. Los argumentos fueron anticipatorios y se recurrió a elementos obtenidos por visualización como medio de argumentación de las respuestas, pero las variables de la situación que llevaron a esa deducción fueron distintas:
La mayor longitud (notablemente evidente) de dos de los lados de la figura en forma de rectángulo (3 veces).
El número de ángulos o de lados (3 veces).
La forma más próxima al cuadrado (una vez).
Una respuesta que ejemplifica el caso 2 es la siguiente:
Yo digo que puede cambiar… [el perímetro] tal vez en éstos sea igual [señala los dos rectángulos], pero éste [el hexágono] tiene aquí otro espacio sobrante, que ocuparía más cerca, porque éstos [el rectángulo ancho y el rectángulo largo] tienen cuatro lados, pero en este caso [el hexágono], tiene seis lados, es mayor perímetro, porque [el alambre] tendría que ocupar este espacio [señala los lados de la concavidad] (E6-12).
La siguiente respuesta integra argumentos del tipo 1 y 2. En este caso, el hexágono se sustituyó involuntariamente por el octágono (la herradura) del problema “dos corrales” (ver adelante). A pesar de esto, la insertamos por la claridad de los argumentos esgrimidos:
M5-11: yo digo que en estos dos gastaron más [señala el rectángulo largo y la “herradura”], ya que tienen un perímetro mayor estos dos.
Inv: ¿tienen un perímetro mayor?
M5-11: me imagino que sí tienen un perímetro mayor, éste simplemente por estar mil veces más largo que éste; y éste, por el hecho de tener que rodear así [señala la concavidad en la herradura], por lo tanto, en el que menos han de haber gastado ha de haber sido en éste [señala el rectángulo ancho].
Los dos corrales: aun frente a representaciones físicas de las figuras
Casi todos los niños a los que se planteó este problema (9 de los 12) establecieron la desigualdad de las áreas y notaron la independencia A-P. Cinco de ellos respondieron inmediatamente, sin recurrir a la medición, fijando la atención en la concavidad de uno de los corrales (G4-9, N4-10, M5-11, E6-12, Z6-10). Ejemplos de los argumentos vertidos en este caso, son:
Pues es lo mismo que en el problema anterior. Es que tiene “como entradas” (G4-9).
Si aquí le quisiéramos poner más alambre, le tendríamos que poner… esta parte se añade [señala los lados de 5 cm paralelos a los de 10 cm], porque acá [señala el lado de 15 cm del rectángulo] nada más está recto, y aquí esto se añade [señala de nuevo los lados de 5 cm paralelos a los de 10 cm] (Z6-10).
El resto de los niños (4) decidió medir antes de dar su respuesta.

Pregunta: estas dos guras representan corrales.
a) ¿A cuál de estos corrales les cabrán más [animales]?
b) ¿En cuál se gastará menos cantidad de alambre de púas para cercarlo?
Fuente: elaboración propia.
Figura 4 Problema “los dos corrales”
Con base en las respuestas a este problema, observamos que la concavidad fue esencial para confirmar la independencia A-P, pues ayudó a percatarse de que hay figuras con mayor área, pero menor perímetro que otras; específicamente, se hizo evidente que (en este caso) el rectángulo tiene mayor área y que -en lo que parecería una paradoja- la concavidad aumentó el perímetro a la vez que disminuyó el área.
Dos corrales (imaginados) con perímetros iguales: ligero retroceso ante la falta de evidencia física Imaginar dos corrales para establecer relación entre su área y su perímetro
Los problemas donde se eliminaron las representaciones físicas para pensar la relación A-P constituyeron un punto crítico en el proceso hacia la deducción operatoria. Ilustramos este hecho con el siguiente problema:
Como se ve en el Cuadro 5, la mitad de las respuestas reflejan un retorno a la intuición “mayor P, mayor A”, que atribuimos a la ausencia de evidencia física.
Cuadro 5 Problema cinco: los dos corrales de igual perímetro
| Retorna a la dependencia entre A y P (igual P, igual A) | Retorna a la dependencia A-P, pero el interrogatorio ayuda a recuperar la idea de independencia P-A | Declara independencia entre P y A, por deducción operatoria | ||
| La respuesta al problema de nuevo es evidente en sí misma | Busca justificar | |||
| G4-9, V5-10, D6-11 | N4-10 | K5-11 | A4-10, C4-9, J5-11, E6-12, F6, Z6-10, M5-11 | |
| 3 | 1 | 1 | 6 | Total: 12 |
Fuente: elaboración propia.
Las respuestas recabadas son, hasta cierto punto, reiterativas de las dadas en otros problemas, lo que parece constatar la validez de nuestra categorización. Veamos:
respuestas que retornan a la dependencia A-P, en este caso “igual P-igual A”;
respuestas con base en la dependencia A-P, que se tratan de justificar;
respuestas en las que el interrogatorio ayuda a restablecer la independencia P-A;
respuestas que declaran independencia A-P, producidas por deducción operatoria.
Veamos primero un ejemplo de respuesta tipo a) y uno de tipo b) ante el problema “dos corrales (imaginados) de igual perímetro”:
[Los dos corrales tendrán] la misma área, el mismo tamaño, porque como las dos figuras que hagas son del mismo perímetro, van a tener la misma área (V5-10).
Porque si hay un perímetro igual, también tiene que medir la misma área [trata de justificar utilizando dos listones de igual longitud para hacer un círculo y un triángulo isoperimétricos, pero después de unos momentos de reflexión no continúa porque no tiene elementos para medir sus áreas] (N4-10).
A continuación, insertamos algunas respuestas ubicadas en d), así como los razonamientos que las sustentan.
Respuestas que declaran independencia P-A por deducción operatoria. En este caso, los argumentos se basan en una anticipación (deductiva) de las transformaciones. Identificamos dos tipos de argumentos:
Las concavidades, o número de vértices o lados, provocan una variación en el área (3 niños).
A una variación en las medidas de rectángulos isoperimétricos corresponde una variación en el área; los rectángulos más próximos al cuadrado tienen mayor área (3 niños).
Los siguientes son ejemplos de 1).
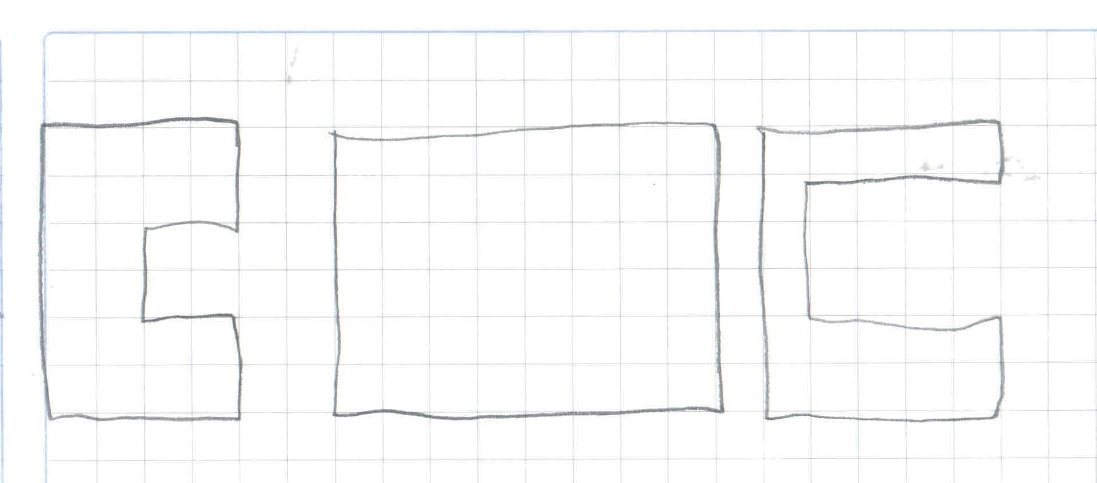
Se señalan como prueba las figuras cóncavas elaboradas en problemas anteriores (A410), como se ve en la Fig. 6:
Fuente: elaboración propia.
Figura 6 Figuras que muestran que las concavidades provocan una variación en el área
Con más esquinas quedaría el espacio reducido; [“dibuja” en el aire una figura en zigzag y luego dibuja una figura con muchas entrantes en el papel] (C4-9).
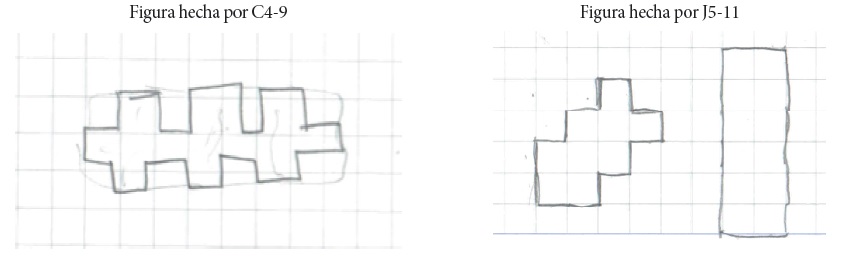
Hice dos figuras diferentes, y con esas dos figuras pude hacer mismo perímetro pero que en el área cupieran menos animales (J5-11).
Fuente: elaboración propia.
Figura 7 Figuras elaboradas para mostrar que las concavidades pueden disminuir el área y mantener el perímetro constante
Ejemplos de respuestas tipo 2) son:
E6-12 y F6-11 usaron como argumento implícito de su respuesta que, entre un cuadrado y un rectángulo no cuadrado isoperimétricos, el cuadrado tiene un área mayor. Uno pensó en un rectángulo con medidas 30 x 10 y un cuadrado de lado 20; el otro, en un rectángulo de dimensiones 15 x 5 y un cuadrado de lado 10. Ambos mostraron que el perímetro es el mismo, pero las áreas son diferentes.
Z6-10 utilizó los argumentos mencionados en 1) y 2) para explicar su respuesta y luego extrajo la siguiente conclusión:
Pues saco [por conclusión] que no depende del perímetro cómo sea el área, y no depende del área cómo sea el perímetro, como en estos dos ejemplos… Porque haz de cuenta que aquí tienen el mismo área, pero no tienen el mismo perímetro, y aquí tienen el mismo perímetro, pero no tienen el mismo área [va señalando las figuras del problema “tres corrales” y luego las que hizo con los listones disponibles para resolver el problema] (Z6-10).
Al final del proceso: abandono diferenciado de la intuición “mayor P, mayor A”
Como se mencionó al inicio del escrito, para finalizar la actividad se planteó de nuevo el problema “las dos plazas”. En el Cuadro 6 se aprecian los cuatro tipos de respuesta que se obtuvieron, y que muestran distinto nivel de progreso en la deducción operatoria ante la relación A-P; los describimos a continuación.
Cuadro 6 Respuestas al segundo planteamiento del problema “las dos plazas”
| Abandono de la intuición “mayor P, mayor A”, ante la evidencia física y retorno ante su ausencia | Otras respuestas (respuestas locales, dadas en función del contexto) | Son posibles distintas relaciones A, P, pero sólo hay certeza si se conocen las figuras y las medidas | Abandono franco de la intuición y aceptación de la independencia entre área y perímetro mediante deducción operatoria | |
| V5-10, G4-9, D6-11 | C4-9 | N4-10, K5-11 | F6-11, E6-12, Z6-0, J5-11, M5-11, AK4 | |
| 3 | 1 | 2 | 6 | Total: 12 |
Fuente: elaboración propia.
Retorno a la intuición “mayor P, mayor A”
Se ubican aquí las respuestas de niños que habían aceptado la independencia A-P ante la evidencia física, pero que regresaron a la intuición “mayor P, mayor A” ante la ausencia de tal evidencia. Es así que a este segundo planteamiento se responde: “la plaza Benito Juárez tiene más área porque tiene más perímetro”. El siguiente es uno de estos casos:
La plaza de más perímetro tiene más área… porque si tiene más perímetro tiene más área adentro, y si tiene menos perímetro tiene menos área adentro (G4-9).
La posibilidad de variación depende del contexto
Sólo en un caso (C4-9) se exponen ideas que se modifican según el contexto del problema. Se pueden hacer polígonos cóncavos para disminuir el área y mantener o aumentar el perímetro en el caso del alambre para los corrales, pero no se pueden modificar las plazas, porque “ahí es como más fijo”. De este modo, si se trata de corrales y de cercas de alambre para que no se salgan los animales, las respuestas pueden sustentarse en la independencia entre área y perímetro, pero se basan en una idea estática del área, y responden a la intuición inicial “mayor P, mayor A”, si el referente físico es difícilmente modificable (C4-9).
Son posibles distintas relaciones áreaperímetro, pero sólo hay certeza si se conocen las figuras y las medidas
Estas respuestas se diferencian de las anteriores porque, aunque parecen aceptar -en principio- las distintas relaciones A-P, hacen explícita la necesidad de referirse a figuras específicas para determinar dicha relación con certeza:
K5-11 había dicho: “[para que quepan más animales en un corral] deberá tener la forma de un rectángulo, pero más parecido al cuadrado […] Porque aquí [en un rectángulo cercano al cuadrado] está más junto todo lo de adentro, entonces sería menos cerca de alambre y en el más alargado usarías más”.
En cambio, cuando se le preguntó por las dos plazas contestó: “no podemos saber, porque si no te dan las medidas, no puede saberse” (K5-11).
Respuestas que reconocen abiertamente la independencia área-perímetro
Este tipo de respuestas fueron las más numerosas. En quienes responden de este modo prevalecen algunas formas de razonamiento: la perspectiva sobre el área se ha vuelto totalmente dinámica, es decir que es posible anticipar transformaciones y elaborar respuestas a partir de estas anticipaciones. Una idea importante que aparece en quienes responden de esta manera es que hay transformaciones en el perímetro que afectan el área:
El área, depende de cómo esté organizado el perímetro (M5 -11).
Puede [ser] que la plaza que tiene menor perímetro tenga más área, por como se pueden acomodar las plazas (J5-11).
Otra idea poderosa que predomina entre quienes responden por deducción operatoria es la construcción de rectángulos isoperimétricos (o no isoperimétricos, según sea el caso), para tratar de explorar la relación entre las medidas de los lados y el área. Surgen aquí dos ideas-fuerza en los niños que podemos considerar como en un nivel más alto de comprensión de las relaciones área-perímetro: a) “el cuadrado tiene más área que un rectángulo” no cuadrado (F6-11); b) dados dos perímetros iguales, “un rectángulo ultra-largo y ultra-angosto” te asegura que el área sea más pequeña (M5-11).
Algunas ocasiones (cuatro) apareció la idea de elaborar polígonos con entrantes para disminuir el área, manteniendo el perímetro; es otra estrategia que permitió a los niños concluir: “[el área] depende de cómo esté acomodada la figura”, o “si [el perímetro] tiene más ‘vueltas’, puede disminuir [el área]” (A4-10).

Figura 8 Figura elaborada por J5-11 para mostrar cómo el área de la plaza depende de “cómo esté acomodada”

Fuente: elaboración propia.
Figura 9 Rectángulo elaborado por M5-11 para mostrar la validez de su idea acerca de cómo un rectángulo “ultra-largo” y “ultra-angosto” tiene menos área que otro isoperimétrico con forma más cercana al cuadrado
En general, entre quienes han reconocido independencia entre el área y el perímetro, hay un desprendimiento de los casos específicos, aunque se basan en ellos para obtener conclusiones del tipo: “la forma cambia el área” (F6-11), refiriéndose a que el área depende de las dimensiones de los rectángulos isoperimétricos, “saco [por conclusión] que no depende del perímetro cómo sea el área, y no depende del área cómo sea el perímetro, como en estos dos ejemplos (Z6-10)”. El dinamismo de las imágenes alcanzado por estos niños se ve también en expresiones como: “contesté mal [el problema la primera vez] porque no había pensado en la forma de las plazas” (E6-12), o “¡pues ya ni sé, porque resulta que a veces una figura tiene un perímetro grande y un área bien chiquita! Pueden ser las dos” (M5-11 se refiere a que puede cumplirse tanto la afirmación “mayor P, mayor A”, como “mayor P, menor A”).
Conclusiones
Esta investigación tuvo como primer objetivo conocer si un grupo de niños de entre 9 y 12 años acepta espontáneamente la regla “mayor perímetro, mayor área”. Una vez comprobado que éste era el caso, la intención fue evaluar si al proponer a los participantes una serie de problemas que implican diversas relaciones área-perímetro: a) abandonan la intuición expresada en esta regla durante el proceso de resolución de dichos problemas; y b) cuál es el proceso mediante el cual ocurre este abandono.
La indagación se realizó con 12 niños de alto desempeño escolar en matemáticas que cursaban cuarto, quinto y sexto grado de educación primaria. No obstante que los participantes estaban por encima del promedio en su desempeño matemático escolar, en su mayoría no habían reflexionado sobre las relaciones entre el área y el perímetro de figuras planas, o al menos no dieron muestra de ello. Todos sostuvieron inicialmente que “a mayor perímetro, mayor área” y, en su mayoría, mostraron una perspectiva estática del área, así como una convicción de que la relación enunciada entre área y perímetro es necesaria. No obstante, de manera distinta a como se ha afirmado en investigaciones como la de Stavy y Tirosh (1996), identificamos tres niños que desde su primer acercamiento problematizaron la situación y trataron de obtener evidencias que sustentaran su respuesta dibujando rectángulos de dimensiones variadas y calculando y comparando sus áreas. Es debido a la falta de sistematicidad en las pruebas generadas por ellos mismos para explorar las relaciones A-P, que en su primer encuentro con estas relaciones concluyeron en el sentido que dicta la intuición.
No obstante, los datos muestran que con el diálogo derivado de la resolución de los problemas planteados -y habiendo mediado el apoyo de representaciones físicas de las figuras y su manipulación libre- la mayoría comprendió que las relaciones A-P no son obligadas. Es decir, aceptaron la independencia entre el área y el perímetro, aunque con distintos niveles de claridad y certeza. El proceso que antecedió a tal aceptación se describe en seguida, conforme a nuestras preguntas y objetivos de investigación.
El papel heurístico de las imágenes. Piaget sostuvo hace décadas que el papel heurístico de las imágenes es fundamental en el desarrollo de la deducción operatoria en geometría. En esta investigación constatamos dicho valor. Proporcionar a los alumnos representaciones físicas de las figuras referidas en algunos problemas fue un factor esencial para el abandono de la intuición “a mayor perímetro-mayor área” y sus variantes, incluso entre quienes desde el inicio problematizaron la relación. En efecto, el hecho de visualizar y manipular figuras donde se puso en evidencia la independencia A-P (problema “los tres corrales”) pareció favorecer la ruptura con la intuición “más A, más P”. En esta situación, la manipulación y la reflexión sobre ella dio a cuatro niños la posibilidad de identificar la independencia en el caso “igual área, distinto perímetro”. Mientras que, para otros cinco, proporcionó un medio para comprobarla.
Las figuras incluidas en el problema “los dos corrales” tuvieron un papel similar al anterior. En este caso, la concavidad en una de ellas jugó un rol fundamental para reconocer (o confirmar, en el caso de quienes desde el inicio desconfiaron de la intuición) que es posible la relación “mayor perímetro-menor área”. Lo anterior al hacerse evidente que es posible lo que parece una paradoja: la concavidad aumenta el perímetro a la vez que disminuye el área.
La anticipación y la prueba de hipótesis. Bang (1965a; 1965b) afirma que las constataciones empíricas a través de manipulación de materiales sirven para verificar hipótesis elaboradas por los niños. En su opinión, la representación visual apoya de manera importante en el progreso hacia la deducción geométrica. En este estudio, como ya lo mencionamos, las representaciones físicas y su manipulación efectivamente favorecieron, tanto la reflexión sobre las relaciones implicadas, como la capacidad de elaborar hipótesis. Esto porque, como señalan Piaget (1971) y Piaget e Inhelder (1997), el resultado de la acción se proyecta hacia el plano de las representaciones (mentales), y con ello favorece la capacidad de anticipar los resultados de posibles transformaciones, tanto sobre las figuras presentes, como sobre figuras imaginadas.
Estas hipótesis anticipatorias se observaron progresivamente en las tareas de resolución de los problemas y mostraron su funcionalidad en el progreso hacia la deducción operatoria en el caso específico de las relaciones A-P, puesto que constituyeron un instrumento que, como vimos, permite manipular y transformar las figuras y establecer relaciones A-P en el pensamiento sin que las figuras estén físicamente presentes, o sin que las transformaciones se realicen físicamente. Tal fue el caso de la producción de figuras con muchas entrantes para disminuir el área y aumentar el perímetro.
Conviene, empero, enfatizar que esta capacidad de generar hipótesis y anticipar resultados no es lineal. Ante los problemas en los que -ya avanzada la actividad- no se proporcionaron representaciones físicas de las figuras (por ejemplo, en el problema “corrales [imaginados] de perímetro igual”), cinco niños regresaron a la primera intuición, al perder de vista las distintas posibilidades en las relaciones A-P, cuestión que habían ganado con la manipulación física de las figuras.
A pesar de esta “recaída” observada en algunos niños, al finalizar la resolución de los problemas y haber establecido un diálogo reflexivo sobre las soluciones, la mayoría modificó su perspectiva inicial sobre las relaciones A-P.
Así, ante el segundo planteamiento del problema “las dos plazas”, actividad con la cual se cerró la secuencia que permitió identificar el proceso hacia la deducción operatoria, la mitad de los participantes mostró haber abandonado de manera franca la idea inicial para dar paso a otra más flexible y dinámica: las relaciones entre área y perímetro no son obligadas.
El valor de la anticipación y generación de hipótesis se constató, por ejemplo, en los acercamientos producidos para resolver el problema “las dos plazas” y otros similares:
Imaginar diversos rectángulos y calcular sus áreas y perímetros, donde las medidas obtenidas (áreas) se convierten en la evidencia que permite extraer conclusiones con un cierto espacio de validez.
Organizar el perímetro de manera tal que determine una figura con suficientes concavidades para que, a la vez que el perímetro se conserve, el área decrezca.
La potencia de la anticipación y producción de hipótesis, y su impacto en el pensamiento, se observa especialmente en las respuestas de algunos niños: en el hecho de “hacer rectángulos ‘ultra largos’ y ‘ultra angos- tos’ para producir figuras ‘con mucho perímetro’ y área ‘bien chiquita’”, y en hacer figuras con múltiples entrantes para aumentar el perímetro y disminuir el área, o en sugerir plazas y parques con perímetros notablemente sinuosos.
¿En qué momento y ante qué situaciones se rebasan los límites de la imagen concreta y se actúa con base en la deducción operatoria? Al iniciar la investigación nos planteamos esta pregunta. Al finalizarla, nos damos cuenta que la respuesta, ni es fácil, ni es única. Algunos niños, nos parece, iniciaron la actividad con una reflexión importante sobre las figuras concretas; de ahí que no hayan respondido intuitivamente ni siquiera al problema de las dos plazas. Otros, en cambio, no habían hecho ninguna reflexión al respecto.
No obstante la dificultad mencionada, hay aspectos que es posible destacar. En el punto final de la secuencia, quienes reconocieron la independencia en la variación área-perímetro utilizaron la deducción operatoria, que en geometría se caracteriza por la capacidad de transformar las figuras en el pensamiento, de anticipar las transformaciones y sus consecuencias, de apartarse de las imágenes concretas e ir más allá de ellas para obtener conclusiones. Algunos niños, en cambio, sostuvieron sus ideas iniciales y otros titubearon, o señalaron la necesidad de contar con medidas precisas para poder establecer la relación con certeza. Pero aún este último tipo de respuestas nos parece un avance en el abandono de la intuición “mayor P, mayor A”, y en el camino hacia la deducción operatoria en geometría, porque las respuestas ya no reflejan el automatismo inicial, ni una concepción estática del área, sino una cierta reflexión que lleva a considerar necesario medir para poder responder.
Ahora bien, en muchos de los niños se observa la capacidad de resolver (con base en la deducción operatoria) los problemas donde los corrales ya no están presentes físicamente, mientras que, para otros, las manipulaciones físicas se mostraron como condición obligada para mantenerse alejados de la intuición y, por ello, fallaron en estos problemas.
En otras palabras, por ahora no es posible dar una única respuesta a nuestra pregunta. Los distintos niveles de progreso en la capacidad deductiva con que cada niño inició la secuencia parecen intervenir en ello. No obstante, reiteramos que la visualización y manipulación de figuras, en general, fueron fundamentales para hacer progresar hacia la deducción operatoria, sin importar el nivel que ésta hubiera alcanzado al momento de resolver los problemas.
Por último, un dato destacable es que la edad parece contar en alguna medida en el desarrollo de la deducción operatoria, pues es fácil observar que, a excepción de una niña de cuarto grado, los niños de 11 o 12 años son los que reflejan en sus respuestas un abandono franco de la intuición y la aceptación de la independencia A-P mediante deducción operatoria.
Reflexiones adicionales sobre las situaciones planteadas
En los programas de matemáticas para la educación primaria vigentes en México se incluyen las relaciones A-P y su tratamiento se basa en un enfoque en el que figuras de lados rectos dibujadas sobre cuadrículas prevalecen como recurso de enseñanza; con tal acercamiento se espera lograr el entendimiento de que la relación entre estas dos magnitudes no es obligada. En los hechos, se trata de un enfoque aritmético en el que la actividad que se promueve es básicamente el conteo de cuadritos, o “lados de cuadritos”, y donde se observa que a un cierto perímetro pueden corresponder dos o más figuras de área distinta. O viceversa: a figuras con la misma área (mismo número de cuadritos) puede corresponder un perímetro distinto.
La investigación aquí reportada tuvo por objetivo conocer el proceso por el cual se abandona la intuición “a mayor área, mayor perímetro”, y se avanza hacia la deducción operatoria para pensar las relaciones entre tales magnitudes. Sin embargo, las situaciones planteadas para conocer dicho proceso ameritan algunas reflexiones potencialmente útiles para la enseñanza. En este trabajo, nos valimos de un acercamiento de tipo geométrico en el que se situó a los niños frente a problemas que obligan a la anticipación de soluciones y la prueba de hipótesis mediante manipulación física o mental de ciertas figuras.
Trabajar las relaciones A-P desde esta perspectiva geométrica se muestra como un recurso poderoso que lleva a reflexionar en torno a relaciones que, como dijeron varios de los participantes, nunca habían pensado. Al respecto cabe destacar que la manipulación libre de figuras como apoyo para resolver un problema, así como la anticipación de soluciones a los problemas que permitieron un acercamiento desde el campo geométrico, contribuyeron de manera esencial al abandono de la intuición que considera necesaria la relación “mayor A, mayor P”, y que algunos autores han considerado incluso como un obstáculo epistemológico.
En tal sentido, esta investigación también proporcionó evidencias de que las propuestas basadas exclusivamente en acercamientos predominantemente aritméticos (como el dibujo de figuras sobre cuadrículas y el conteo de unidades cuadradas) tienen limitaciones que es importante rebasar para que las relaciones entre área y perímetro de figuras planas proporcionen a los estudiantes un espacio auténtico de exploración y reflexión matemática.











 nueva página del texto (beta)
nueva página del texto (beta)



