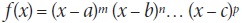Introducción
Uno de los objetivos mayores de la enseñanza de las matemáticas radica en alcanzar la meta, si bien ambiciosa, de dominar los procesos y conceptos matemáticos para tratar críticamente con la vida del alumnado, es decir, desarrollar entre el estudiantado una manera matemática de pensar que permita interpretar al mundo y sus relaciones. En este sentido, más que reducir la enseñanza a la repetición de algoritmos, procesos y conceptos, se debe buscar significarles mediante el uso en situaciones realistas para quien está en proceso de aprender.
La noción matemática de función se encuentra en el centro mismo de esta misión, pues es con ellas, y a través de ellas, que representamos una gran cantidad de relaciones causales entre variables asociadas con fenómenos.
Es posible interpretar el desempeño cardiovascular mediante el análisis e interpretación de un electrocardiograma, y desde ahí, tomar decisiones sobre el estado de salud de un paciente. Dicho electrocardiograma puede obtenerse a partir de una colección articulada de gráficas de funciones elementales (Gómez, 2008), y como lo ha estudiado Moreno-Durazo en diversas de sus publicaciones, en su interpretación se involucran las prácticas de comparación, seriación y estimación como base para el estudio de los cambios entre estas gráficas (Moreno-Durazo y Cantoral, 2015, 2016; Moreno-Durazo, 2016).

Fuente: Marriott's practical electrocardiography, Wagner y Strauss, 2014: 16 (trad. propia).
Figura 1 Ondas en el ciclo cardiaco completoFuente
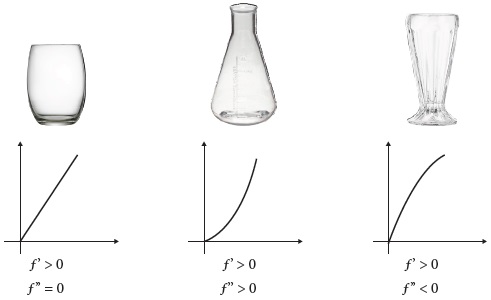
Del mismo modo, es posible analizar el comportamiento visual de una curva mediante diversas acciones relativas al estudio de la variación, como se señala en los estudios de Caballero (Caballero-Pérez, 2013, 2016; Caballero-Pérez y Cantoral, 2016), lo que permite establecer relaciones funcionales en fenómenos como el llenado de recipientes mediante una correspondencia entre el concepto de derivada y el comportamiento gráfico del fenómeno. La forma de una gráfica está determinada por la naturaleza del fenómeno de estudio. Ambos enfoques permiten tratar a las formas gráficas de una manera novedosa, misma que se puso de manifiesto en este diseño de intervención para el desarrollo profesional docente entre profesores de enseñanza secundaria.
Estos dos elementos, conjuntamente con la investigación realizada con anterioridad (Farfán 2013; Montiel, 2013), permitieron realizar un diseño de intervención didáctica con fines de predicción, donde las gráficas adquirieron un significado novedoso que amplió el discurso del aula de matemáticas. La visualización y la argumentación correspondiente nos permitieron alcanzar éxitos notables, como veremos a continuación.
De manera tradicional, la temática principal de las matemáticas previas al cálculo se enfoca en el estudio de las relaciones funcionales mediante su definición, clasificación y propiedades; esto lo podemos observar en libros clásicos de precálculo (Stewart et al., 2001). La educación secundaria incluye parte de este estudio en el eje “manejo de la información”, donde se propone el tratamiento de relaciones de proporcionalidad, lineales y cuadráticas; en particular, se promueve el manejo de sus representaciones algebraica, gráfica y numérica, además de su aplicación en contextos diversos como la física, la química y la biología, entre otros (SEP, 2013).
Los procesos de enseñanza escolares usualmente tratan el tránsito de la representación algebraica a la gráfica a través de la representación numérica (método de tabulación); esto es, dada la expresión analítica de una función, se evalúan algunos valores, se localizan en un plano cartesiano y, finalmente, se unen los puntos mediante trazos curvos o rectos. La implementación de estos esquemas de graficación impide el desarrollo de procesos de visualización y estimación de comportamientos de la función, pues reduce el tratamiento sobre la gráfica a un procedimiento algorítmico, sin profundización; más aún, la tabulación como recurso único ante la graficación impide la significación de la función (Cantoral, 2013).
Ahora bien, planteamos en el seminario con los profesores de la MEMES un escenario que permitiera la profundización tanto de la matemática escolar de la secundaria (nivel educativo del que son profesores), como de la matemática avanzada. Para ello, tomamos como referente principal la propuesta de Cantoral y (Montiel, 2014), que propone el estudio de funciones reales de variable real desde un enfoque gráfico y visual con el fin de favorecer el desarrollo del pensamiento matemático; específicamente, sobre el desarrollo de la visualización y estimación de formas gráficas de funciones. De esta manera, el análisis gráfico que se promueve no se limita a la manipulación algebraica, sino que a partir de él se generen argumentos visuales que propicien la significación sobre la expresión analítica.
En particular, en el seminario se propició el desarrollo de argumentos que permitieran la estimación de formas gráficas de funciones polinomiales del tipo
y funciones racionales del tipo
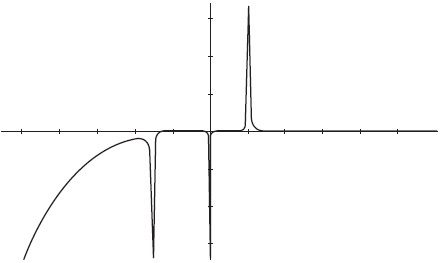
Nos interesaba la construcción de argumentos que justificaran, por ejemplo, por qué la gráfica de la Fig. 3 no puede representar una función racional.
Fundamento teórico del Seminario de précalculo desde un enfoque visual
El pensamiento y lenguaje variacional (PyLVar) es una línea de investigación desarrollada a la luz de la teoría socioepistemológica de la matemática educativa, cuyo objetivo es el estudio de las formas culturales de apropiación del cambio con fines predictivos. Este objetivo exige de una estructuración de las prácticas que acompañan a los objetos matemáticos, relativas al estudio del cambio y la variación. Diversas investigaciones reportan que el desarrollo del pensamiento y lenguaje variacional requiere tanto de la noción de predicción como del manejo amplio y rico en significados sobre un universo de formas gráficas (Cantoral y Farfán 1998; Cantoral et al., 2005).
Derivado de los proyectos desarrollados bajo el PyLVar, se han podido caracterizar estrategias y argumentos variacionales indispensables para la predicción. En consecuencia, se han desarrollado una serie de situaciones de aprendizaje para la mejora educativa, tanto en el aula y la escuela, como en la vida misma. Por ejemplo, (Farfán, 2013) plantea, para el establecimiento de un isomorfismo entre el lenguaje algebraico y el gráfico, la posibilidad de operar gráficas en analogía con los números; para ello, propone el análisis gráfico a partir de las transformaciones de reflexión, traslación, contracción y dilatación.
Ahora bien, en las situaciones de aprendizaje propuestas para el seminario con los profesores oaxaqueños, se planteó el estudio de funciones algebraicas tomando a la función prototípica y=x como base para la construcción de estas funciones. Es decir, el hecho de concebir a la gráfica como un ente matemático susceptible de ser operado permitió partir del entendimiento de gráficas de funciones prototípicas a la generación de universo gráfico (Cantoral y Montiel, 2014).
Estructura del seminario
Las primeras sesiones del seminario se enfocaron en la construcción de argumentos sobre la articulación entre el lenguaje gráfico y el algebraico para funciones lineales, cuadráticas y cúbicas; todas éstas, excepto la cúbica, son tratadas en el nivel de secundaria. Se parte de la expresión y = x para construir, a través de la movilización del cuerpo, los giros y traslaciones de la recta, de manera que, en la expresión y = mx + b se significa al parámetro m como aquello que gira o modifica la pendiente de la recta, y el parámetro b como aquello que la traslada sobre el eje y.
La profundización en la función lineal se realiza mediante la suma de funciones, lo que conceptualmente refiere a la operación numérica entre puntos específicos de las gráficas. Esto es, el método de sumar dos gráficas no implica sumar punto a punto todo el dominio de la función, sino que la atención se centra en puntos particulares de las gráficas que presentan una relación particular con los valores de la suma, lo que los autores denominan análisis local de los puntos. Por ejemplo, para la suma gráfica de dos rectas se determina la raíz de cada recta, y al sumarse las ordenadas en esos puntos es necesario considerar solamente una de ellas (Fig. 4).
Las funciones cuadráticas y cúbicas se construyen a partir de la multiplicación de rectas. Para realizar el bosquejo de esta multiplicación se identifican las regiones en el plano por las que la nueva función debe cruzar. Por ejemplo, en la Fig. 5 se muestra el producto de las rectas f(x) y g(x); primeramente, las regiones en las que se “partirá” el plano cartesiano se identifican a partir de la raíz de cada función y se determina, con base en el signo de las ordenadas de las funciones en cada región, la zona por la que debe cruzar la función resultante; por ejemplo, en la región 2, los puntos de f(x) tienen valores de ordenada positivos, y los puntos de g(x) tienen valores de ordenada negativos, por tanto, h(x) tendrá valores de ordenada negativos. A este método se le agregan consideraciones como el hecho de que la función producto conserva las raíces de las funciones que se multiplican.
Una vez construidas las funciones polinomiales de grado 2 y 3, se tratan problemas de reversibilidad para profundizar en ellas, mediante problemas como: “dada la gráfica de una función cuadrática determinar el par de rectas que se deben multiplicar para generarla”. Además, se recurre de nuevo a la movilización corporal para describir los efectos como “alargamiento”, “abrir o cerrar la parábola”, “aplanar” y “trasladar”, que se provocan en la gráfica de las funciones en la movilización de los parámetros sobre las expresiones algebraicas de funciones cuadráticas (y = ax 2 + bx + c, y = A(x - B)2 + C y funciones cúbicas (y = A(x - B)3 + C).
Es importante enfatizar que el interés principal no se reduce al tratamiento de las expresiones algebraicas y la significación de sus parámetros, como se hace en muchos trabajos educativos, sino que éstas son resultado de los argumentos gráficos generados ante cuestiones como ¿cualquier función cúbica se puede generar al modificar los parámetros de y = (x - a)3 + c ? Lo anterior es atendido por los profesores con argumentos como “ni la traslación horizontal o vertical, ni el ‘estiramiento’ de la gráfica y = x 3 generan una función cúbica con raíz real de multiplicidad dos, por lo tanto, no es posible generar cualquier función cúbica mediante el modelo y = (x - a)3 + c”.
Hasta este momento, los argumentos y las significaciones construidas se relacionan con la matemática del nivel educativo en el que laboran los profesores y, además, son estos argumentos la base para el análisis gráfico de las funciones racionales y la generalización sobre las polinomiales. Previo al tratamiento de estas funciones, se requiere de una generalización sobre el comportamiento gráfico de las funciones del tipo y = xn ; para n par, la forma de la gráfica se parecerá a la parábola f (x) = x 2, con la diferencia de que entre mayor sea el valor de n, la gráfica tenderá a pegarse más al eje horizontal, y para el caso de n impar, para valores grandes tenemos que la forma de la función se asemeja al de la función f (x) = x 3, con la diferencia de que la zona central, cerca del punto de inflexión, tiende a pegarse cada vez más al eje horizontal.
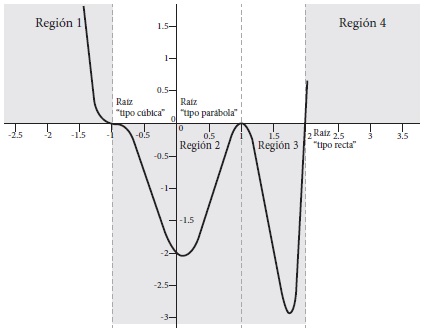
La visualización y la estimación de formas gráficas para funciones polinomiales toman como base las gráficas “tipo parábola” y “tipo cúbica”, junto con la forma recta de las funciones lineales. Por ejemplo, en la Fig. 6 se muestra la gráfica de la función f (x) = (x - 2)(x - 1)2(x + 2)3, la cual es de grado par y, por tanto, el comportamiento global de la gráfica será de “tipo parábola”. Además, la forma de corte en las raíces depende del grado del monomio del que surja: en el caso de la raíz x = 2 la forma de corte será de “tipo lineal”; en x = 1 el factor tiene un exponente de grado par, por lo que el corte con el eje horizontal es de “tipo parábola”; y finalmente, en x = -2 el factor correspondiente es de grado impar mayor a 1, por lo que el corte con el eje horizontal es de “tipo cúbica”.
En la visualización y estimación de formas gráficas de funciones racionales se conjunta todo lo mencionado anteriormente; además, se deben considerar casos en los que el grado del polinomio del denominador sea mayor al grado del polinomio del numerador. Para ello, analizamos el comportamiento de funciones del tipo
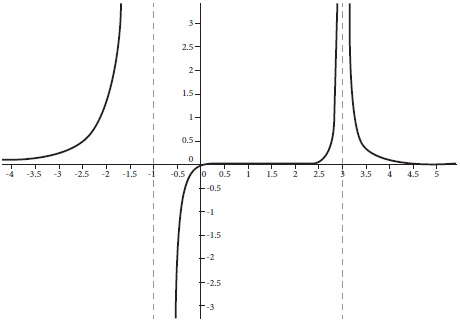
De manera que, si consideramos la función
En x = -1 el factor correspondiente en el denominador es impar, por lo que la gráfica se orientará en direcciones opuestas de la asíntota, en x = 0 la raíz tiene un factor de grado 1, por lo que el corte en el eje x será de “tipo recta”, en x = 2 será de “tipo parábola” por tener un factor de grado 2 en el numerador, y en x = 3 la asíntota tiene un factor de grado par, por lo que la gráfica en esa zona se orientará hacia la misma dirección. Finalmente, una vez determinado el comportamiento que tendrá la gráfica en las raíces y asíntotas, se analizan las regiones para saber dónde se ubican los puntos de la gráfica.
La profundización en esta segunda parte del seminario (análisis del comportamiento gráfico de funciones racionales y generalización de las polinomiales), se lleva a cabo con problemas de reversibilidad. Por ejemplo, dada la gráfica de una función algebraica, proporcionar la expresión algebraica, o dada la expresión proporcionar la gráfica de la función; esto mediante análisis sobre el comportamiento de las funciones de manera global y local.
Resultados de la experiencia
Hablamos de los resultados del seminario con relación a las respuestas de los profesores en actividades de análisis y construcción de gráficas de funciones presentes en el texto de (Cantoral y Montiel, 2014), donde se puede observar el tipo de argumentos construidos. En particular, centramos la atención en actividades que precisan el análisis de funciones racionales del tipo
Bosquejo de la gráfica con base en las características de la función
Una de las actividades que se plantearon en la parte final del seminario fue bosquejar la gráfica de una función una vez conocidas algunas de sus características, por ejemplo, el número de raíces y su multiplicidad, las asíntotas verticales y el “tipo de asintoticidad” (conservan la forma global de la función
Responder esta actividad requería del análisis local de los puntos dados, aspecto que los profesores retoman satisfactoriamente al relacionar la multiplicidad de las raíces con el tipo de comportamiento de la gráfica; por ejemplo, ellos mencionan que en las de multiplicidad 2 la función se comporta como parábola, mientras que en las de multiplicidad 3 se comporta como cúbica; en cuanto a las asíntotas, determinan que en la raíz de multiplicidad impar se comporta como la función
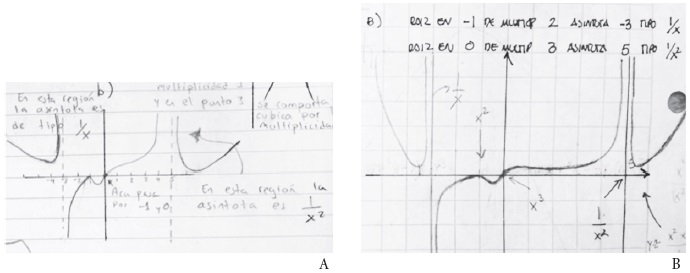
Fuente: extracto de la tarea entregada por los profesores.
Figura 8 Bosquejo de profesores dadas las condiciones sobre la función
Ahora bien, además del análisis local se precisa el análisis global con base en el grado de la función, con el fin de determinar el comportamiento de la función en los extremos, cuando la variable independiente tiende a +∞ o -∞. Si bien el bosquejo de los profesores presentado en la Fig. 8 es correcto, el análisis global no es explícito en su procedimiento; esto no significa que no realicen dicho análisis, pues como veremos en los demás ejemplos, para otras actividades sí lo explicitan. Consideramos que esto puede deberse, o bien a la forma de presentar la información de las funciones, o al hecho de que ellos mismos ya no requieren hacerlo explícito, dado que ésta fue una actividad al final del seminario.
Proponer la expresión analítica dada la gráfica de una función
Otra actividad que se trabajó fue construir la expresión analítica a partir de la gráfica de una función racional. Por ejemplo, observamos en la Fig. 9 que el profesor analiza cada uno de los puntos característicos de la gráfica (raíces y asíntotas) para determinar el tipo de comportamiento en cada uno. Con base en ese análisis establece la expresión analítica de la función, apoyándose en una relación del tipo de comportamiento en los puntos característicos con la multiplicidad que tendría el factor correspondiente.

Fuente: extracto de la tarea entregada por los profesores.
Figura 9 Análisis de los comportamientos locales de una función racional
Cabe señalar que, formalmente, esa multiplicidad que señalan puede ser de cualquier grado en el caso de n > 1, pero los profesores limitan estos valores entre 1 y 3. Más que a un descuido o a una falta de comprensión, esto se debe a que en el curso se hizo énfasis en caracterizar los comportamientos a partir de formas gráficas básicas, más que en determinar con precisión los exponentes. En ese sentido, la propuesta del profesor se considera correcta, ya que su modelo expresa el tipo de comportamiento gráfico.
Asimismo, el análisis local de las raíces y asíntotas que permiten al profesor establecer la expresión analítica se complementa con el análisis global. El profesor establece que dados los exponentes que él propone, la expresión analítica corresponde a un comportamiento global “de tipo cubico”, dado que el exponente global es impar, y señala, además, que debe ser positivo, lo que se verifica al ver la forma de la gráfica en los extremos (Fig. 10).

Fuente: extracto de la tarea entregada por los profesores
Figura 10 Análisis del comportamiento global de una función racional
Otros profesores mostraron un análisis similar al determinar la expresión analítica de la función, con la diferencia de que se asignaron exponentes diferentes a los factores correspondientes a las raíces en x = 0 y x = 4. En el procedimiento anterior, el profesor asumió que, en una vecindad a ambas raíces, la gráfica se comportaba como cúbica, pero en el procedimiento del profesor de la Fig. 11A, se considera que en x = 0 la gráfica se comporta como recta; en tanto que el profesor de la Fig. 11B, asocia a x = 4 el corte de tipo recta.

Fuente: extracto de la tarea entregada por los profesores.
Figura 11 Propuesta de expresiones algebraicas para funciones racionales
Esta discrepancia en los exponentes de los factores correspondientes a las raíces x = 0 y x = 4 se debe, desde nuestro punto de vista, a que la gráfica en cuestión fue reproducida por los profesores a mano en sus libretas, lo que ocasionó algunas diferencias de forma según cada dibujo. No obstante, resaltamos en estos procedimientos que los profesores reconocen un tipo de comportamiento con base en la forma gráfica que perciben, y esto, a su vez, lo asocian con la multiplicidad de la raíz. En ese sentido, se generaron argumentos funcionales para la interpretación de las gráficas.
Bosquejar la gráfica con base en la expresión analítica
Como hemos mencionado anteriormente, el análisis sobre los comportamientos locales de la función racional es una estrategia para su graficación, tanto el comportamiento seguido por sus raíces como el de sus asíntotas. En la Fig. 12 observamos cómo un profesor identifica primeramente los puntos que son raíces y asíntotas, y sin explicitarlo, identifica también el tipo de comportamiento que la gráfica seguirá en esos puntos. Además, para proponer el bosquejo requiere del análisis global de la gráfica; lo que él menciona como “a lo lejos se espera ver como si fuese la gráfica de y=x” (refiriéndose a la gráfica).

Fuente: extracto de la tarea entregada por los profesores.
Figura 12 Bosquejo de la gráfica dada la expresión algebraica
Por último, consideramos relevante incluir evidencia de cómo el lenguaje verbal, de manera transversal, tuvo una participación importante para el desarrollo de argumentos sobre la visualización de funciones. Por ejemplo, los profesores no sólo articularon el lenguaje gráfico y el algebraico, sino que esto les permitió reconocer procedimientos para la estimación de formas gráficas, tal como se puede observar en la Fig. 13.
Conclusiones
En este artículo se mostró la estructura de un seminario especializado cuya intención fue la de favorecer el desarrollo argumental respecto de la visualización de funciones algebraicas. En todo momento seguimos la guía teórica de la socioepistemología al poner en uso el conocimiento escolar habitual. Esto es, los argumentos que las y los profesores construyeron sobre el comportamiento de funciones lineales, cuadráticas y cúbicas resultaban elementos de naturaleza transversal que permitían el tratamiento de funciones no consideradas por el currículo del nivel educativo en el que laboran: las funciones racionales y las polinomiales de grado mayor a 2, en general de grado n.
Para la socioepistemología, la significación de los objetos matemáticos se da en relación al desarrollo de las prácticas que le dieron origen al conocimiento. En este sentido, las prácticas de comparar comportamientos globales y locales en una función algebraica a partir de los comportamientos de funciones prototipo, argumentar los comportamientos de la función y bosquejarla, desde el desarrollo de la estimación gráfica y la visualización, son elementos esenciales para el desarrollo del pensamiento matemático. En particular, resultan relevantes para el manejo y significación de un universo de formas gráficas más amplio que, conjuntamente con las acciones de reversibilidad del pensamiento, son requisitos para el desarrollo del pensamiento y lenguaje variacional.
Con esto, lo que señalamos es que las matemáticas, profundizadas en el tratamiento didáctico en el seminario, no son ajenas a la mirada transversal de las y los profesores, puesto que centramos las discusiones sobre los elementos transversales y funcionales del análisis gráfico. De hecho, en las investigaciones que desarrollamos dentro de la línea de investigación del PyLVar encontramos que la comparación y la estimación son estrategias utilizadas en el estudio del cambio y la variación ante la predicción de fenómenos dinámicos. Por ejemplo, en situaciones de llenado de recipientes (Caballero-Pérez y Cantoral, 2016) o la predicción en fenómenos no escolares, como la interpretación que hacen los médicos de un electrocardiograma (Moreno-Durazo y Cantoral, 2016).
Para finalizar, ofrecemos un reconocimiento público al profesorado de la Maestría en la Enseñanza de las Matemáticas en la Educación Secundaria (MEMES) de la ENSFO, por su gran dedicación, arduo trabajo y trato especial en el desarrollo del Seminario de precálculo descrito anteriormente, a pesar de que en muchas situaciones tienen, por así decirlo, la adversidad al frente. Consideramos que los excelentes resultados obtenidos darán evidencia de su empeño y compromiso con el desarrollo profesional docente, donde algunos profesores incluso mostraron interés por la investigación de temáticas cercanas a las discusiones realizadas en el seminario. Hoy día las están llevando a sus aulas escolares.











 nueva página del texto (beta)
nueva página del texto (beta)