Introducción

Diversas investigaciones actuales abordan la problemática de la enseñanza y el aprendizaje del álgebra (^{Butto y Rojano, 2004}; ^{Filloy et al., 2008}; ^{González, 2012}; ^{Filloy y Kieran, 1989}; ^{Malisani, 1999}; ^{Mejía y Barrios, 2008}; ^{Palarea, 1999}; ^{Ruiz et al., 2015}; ^{Ursini y Trigueros 2006}; Usiskin, 1999), trabajos que, si bien son adecuados para localizar los obstáculos didácticos, epistemológicos y cognitivos, no han sido suficientes, ya que aún persiste la problemática. Esta situación, aunada a evidencias empíricas del trabajo en el aula, tales como el alto índice de reprobación, dio pie a la presente investigación. En este sentido, resulta innegable reconocer las limitaciones de nuestra perspectiva inicial, centrada en los objetos matemáticos, en la “aprobación”, en el cómo enseñar, sin problematizar el conocimiento, es decir, soslayando aspectos cognitivos, epistemológicos y socioculturales.

El trabajo desarrollado en los seminarios de la Maestría en la Enseñanza de las Matemáticas en la Educación Secundaria (MEMES) con investigadores del Área Superior del Departamento de Matemática Educativa del Centro de Investigación y Estudios Avanzados (CINVESTAV-IPN), dio lugar a un cambio en nuestra relación con el conocimiento matemático, lo que permitió una visión más amplia de la problemática. Esto nos llevó a una revisión del estado del arte del objeto de estudio, donde identificamos, entre otros aspectos: 1) que la enseñanza y aprendizaje del lenguaje algebraico requiere de otros lenguajes, como el natural o el geométrico (^{Butto y Rojano, 2004}; ^{Malisani, 1999}; ^{Palarea, 1999}; ^{González, 2012}; ^{Filloy y Kieran, 1989}); 2) reconocimos que las dos rutas que se desarrollan en los libros de texto del sistema educativo mexicano para abordar el lenguaje algebraico: el planteamiento de “problemas tipo” y “la medida desconocida”, lo presentan como un conocimiento acabado, preexistente, atomizado, en contextos ficticios, donde se excluye al alumno de la construcción del conocimiento. En términos de (^{Soto y Cantoral, 2014}), esta situación se reconoce como consecuencia del discurso matemático escolar (dME), entendido éste como un sistema de razón que produce violencia simbólica, y que norma la dirección del aprendizaje y la enseñanza de las matemáticas hacia la imposición de un solo tipo de argumentación, de significados y de procedimientos asociados al saber matemático escolar. Esto excluye a los actores del sistema didáctico de la construcción del conocimiento matemático, ya que sólo se “entrega” el producto final.

Así mismo, la falta de marcos de referencia influye en la significación y resignificación del conocimiento (^{Cordero, 2001}; ^{Montiel, 2005}; ^{Soto, 2010}); en el aula, por acción del dME olvidamos que la matemática responde a otras asignaturas, y que es ahí donde se encuentra la base de significados naturales del conocimiento matemático; esto nos ha llevado a la enseñanza de una “matemática sin sentido”, desconectada de la realidad del aprendiz, indiferente a los saberes previos y a los procesos cognitivos del alumno, desvinculada de las otras asignaturas del currículo escolar. Así, el estudiante se encuentra con una matemática escolar con significados artificiales que le resulta ajena.

De forma cotidiana en el aula, el docente normado por el dME comunica verdades preexistentes, carentes de significado o con significados artificiales, ajenos a la naturaleza intrínseca de la Matemática; y esto porque, desde nuestra visión, ésta toma sentido y significado a partir de prácticas que no se limitan a la disciplina misma, sino que pertenecen a un universo sociocultural mayor. Es decir, asumimos que “la matemática escolar está al servicio de otros dominios científicos y otras prácticas de referencia en donde la Matemática adquiere sentido y significación” (^{Buendía, 2004: 5}).

Por lo anterior, las rutas del lenguaje algebraico plasmadas en los libros de texto plantean una mirada parcial de la estructura del saber, ya que ignoran el contexto sociocultural de los alumnos, así como la epistemología del lenguaje algebraico; dado su carácter hegemónico, imponen situaciones que no permiten que el alumno sea partícipe de la construcción del aprendizaje.

Según (^{Cervantes, 2015}), las dos rutas mencionadas anteriormente (“problemas tipo” y “la medida desconocida”) se consideran trayectos que giran en torno a los objetos matemáticos; a partir de éstas, el lenguaje algebraico se muestra ante los alumnos como “un conjunto de reglas”, como “un conocimiento terminado y lineal” que impone objetos preexistentes, que excluye al aprendiz, lo limita, coarta la posibilidad de nuevas hipótesis y, por lo tanto, le niega la oportunidad de hacer predicciones, de inferir, de ser partícipe de la construcción del conocimiento matemático, y de transformar las situaciones que hacen emerger los significados naturales del saber en cuestión. Ambas rutas tienen una visión de carácter utilitario del conocimiento; no conciben la matemática como resultado de la actividad humana; se la exhibe desde una perspectiva simplista, como “una regla útil para resolver determinados problemas” en el aula, esto es, centra la atención en objetos y procesos matemáticos, y en el tipo de problemas que resuelve. De aquí que el conocimiento no tome un carácter funcional, y que aparezca excluido de la visión de la construcción social del conocimiento matemático (^{Soto y Cantoral, 2014}).

El objetivo principal de nuestra investigación es encontrar una ruta en el plano de nuestra realidad que permita la construcción de un lenguaje simbólico cercano a la noción de lenguaje algebraico. Una ruta donde, de forma natural, se ponga en uso dicho conocimiento. Asumimos que, antes de ser partícipes del simbolismo del lenguaje algebraico propio del dME, la noción de lenguaje algebraico es puesta en juego, a través de sus significados, en alguna práctica socialmente compartida asociada a la naturaleza intrínseca de este saber. En este sentido, nos interesamos en el estudio de la albañilería, asumiéndola como una práctica socialmente compartida; buscamos analizar las dinámicas del saber, la forma en la que se aprende y se construyen tanto edificaciones como conocimiento en uso, a partir de la trasmisión por vía oral: de maestro albañil a peón (que también, de acuerdo a su avance o aprendizaje, se le llama peón o “media cuchara”). Estos conocimientos van desde la forma de sujetar una herramienta y la proporción de materiales para preparar la mezcla, hasta la elaboración de presupuestos.

Desde nuestra óptica, enmarcada en la teoría socioepistemológica, consideramos a las prácticas sociales como fuentes del saber, que dotan de razón y sentido al conocimiento. Por lo anterior, en nuestra investigación nos planteamos lo siguiente:

Marco teórico

La teoría socioepistemológica de la matemática educativa establece un método de acercamiento a las problemáticas que surgen dentro y alrededor de los fenómenos concernientes a la construcción social del conocimiento matemático y su difusión institucional. Postula la necesidad de un examen minucioso del saber, amplio y sistémico, que considere las múltiples relaciones del triángulo didáctico, así como las restricciones institucionales pedagógicas. Atiende las múltiples dimensiones del saber y considera, también, las restricciones específicas del saber matemático.

Desde la teoría socioepistemológica (^{Cantoral, 2013}) hemos problematizado el lenguaje algebraico a través de una unidad de análisis socioepistémica (UASE) concebida como una estructura teórica con base en el análisis sistémico de las dimensiones didáctica, epistemológica, cognitiva y social del saber matemático en cuestión (^{Reyes-Gasperini, 2011}; ^{Reyes-Gasperini y Cantoral, en prensa}; ^{Reyes-Gasperini y Cantoral, 2014}).

La dimensión social permite estudiar a los saberes matemáticos identificando la dimensión funcional, situacional e histórica, basada en la praxis, que está al nivel de la actividad y es soslayada y desdibujada en la práctica por el discurso matemático escolar (dME). La dimensión social, aunada a la dimensión epistemológica, que estudia la naturaleza del saber, reconoce a la matemática como parte de una cultura producto de la actividad humana.

Asimismo, bajo la mirada socioepistemológica se concibe que los conocimientos se dotan de significados a través de su uso y su funcionalidad; por tanto, se plantea la necesidad de que docentes y estudiantes, aunque inmersos en un sistema educativo, se relacionen con el conocimiento matemático de una manera más activa, con la intención de que construyan ideas fundamentales sobre dicho conocimiento, que vayan más allá de las abstracciones, procedimientos y el aprendizaje propios de su aplicación; es decir, que comiencen a relacionarse con el saber matemático concibiéndolo como un conocimiento puesto en uso. Esto es, la significación que se construirá a partir de la actividad de relacionarse con el saber matemático, permitirá entender en profundidad aquellas nociones que las miradas pla tónicas consideran como “la matemática escolar”.

Para poder hacer este análisis, la dimensión didáctica del saber juega un papel importante, pues será a través del estudio de libros de texto, programas de estudio, notas e investigaciones, entre otros, que se investigará cómo se presenta el conocimiento matemático estudiado en el sistema didáctico. Conjuntamente con estos análisis, es a través del estudio de la dimensión cognitiva que se exploran los procesos de apropiación del saber matemático basado en el reconocimiento de que el paso del conocimiento al saber responde a procesos propios del desarrollo del pensamiento matemático.

Este enfoque se ubica al nivel de las prácticas, privilegia la práctica social como normativa de la actividad humana, busca entender “¿quées lo que nos hace hacer lo hacemos?”. Se caracterizan fenómenos didácticos en un sentido amplio; para ello se utilizan diversos métodos que dependen del escenario contextual, como: el aula, comunidades profesionales, comunidades artesanas, albañiles, etc.

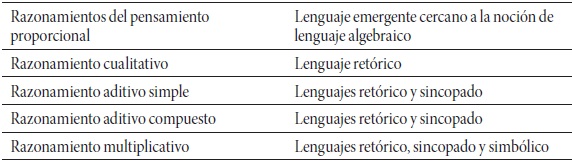
Por otra parte, de acuerdo con (^{Malisani, 1999}), en la historia del álgebra tiene importancia tanto la historia de los conceptos como el sistema de símbolos utilizados; esta mirada de nuestro objeto de estudio, aunque parcial, no riñe con nuestra perspectiva teórica. Respecto a la historia de los conceptos, (Nesselman, cit. por ^{Malisani, 1999: 4}) distingue tres fases en el desarrollo del lenguaje algebraico:

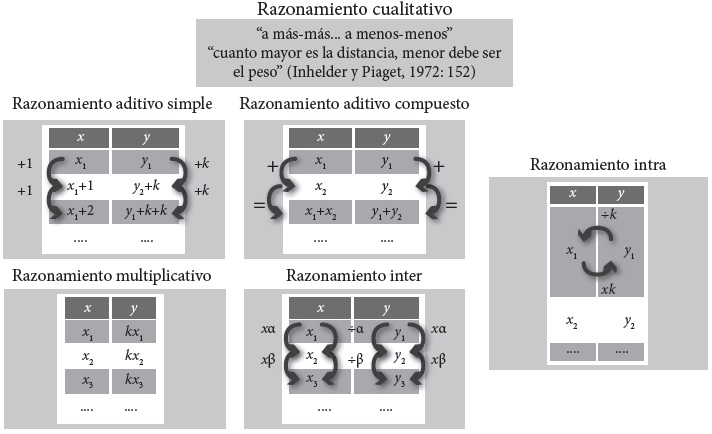
Por otro lado, retomaremos el esquema construido respecto a los razonamientos proporcionales para el desarrollo del pensamiento proporcional: estos razonamientos son el cualitativo, aditivo simple, aditivo compuesto, multiplicativo, inter e intra (^{Reyes-Gasperini y Cantoral, 2014}).

De acuerdo con los autores, el razonamiento cualitativo precede a los modelos cuantitativos de pensamiento proporcional (que caracterizaremos más adelante) ya que el primero se refiere a una relación descriptiva entre dos magnitudes, mientras que los segundos refieren a relaciones métricas. En este sentido, Piaget e Inhelder afirman que el niño alcanza el modelo cualitativo cuando se reconoce un elemento de compensación para mantener el “equilibrio”, donde “un incremento en una variable independiente da el mismo resultado que un decremento en la variable dependiente” (^{Piaget e Inhelder, 1977: 144}), equilibrio que podemos enunciar como “a más-más… a menos-menos”.

Fuente: elaboración propia.

Figura 1 Razonamientos del pensamiento proporciona 

Razonamiento intra

La razón entre el elemento del dominio y el elemento del codominio es siempre constante.

● Ejemplo: si pagué 80 pesos por 8 kilos de pan, entonces, el precio del kilo de pan es de 10 pesos (80 ÷ 8 = 10).

En este caso aparece una cantidad a partir de una unidad de medida llamada precio, que es un concepto en sí mismo.

Debe entenderse que la confección del pensamiento proporcional hasta el momento tiene sustentos cognitivos desde una perspectiva que podríamos denominar tradicional o clásica. Sin embargo, para la teoría socioepistemológica, “lo cognitivo” no sólo se reduce a un proceso del pensamiento a través de sus representaciones, sino que también estaremos hablando de las prácticas que tengan la capacidad de “hacer emerger” el significado y que podrán relacionarse con los razonamientos puramente cognitivos. Por tanto, la que para visiones tradicionales se centra en la evolución cognitiva y sus diferentes representaciones, para la socioepistemología será la evolución de los procesos de significancia constructivos mediante la práctica, su evolución pragmática: la significación mediante el uso. Entonces, dado que ya hemos caracterizado a nivel cognitivo tradicional el “modelo del pensamiento proporcional”, ahora nos proponemos la búsqueda de las prácticas que permitan hacer emerger esa significación. Para ello, será necesario estudiar la construcción social del conocimiento matemático, y de este modo, hablaremos de lo social.

Retomamos los resultados expuestos anteriormente y los reorientamos hacia la búsqueda de un lenguaje simbólico cercano a la noción de lenguaje algebraico, bajo la siguiente hipótesis: en cada razonamiento de manera intrínseca emerge en uso un lenguaje pleno de significados, lenguaje que hace posible expresar la relación planteada en cada razonamiento:

Tabla 1 Lenguajes posibles que emergen en los diferentes modelos 

Fuente: ^{Cervantes, 2015}.

Lo anterior, bajo la consideración de que la proporcionalidad es un contenido transversal de la educación básica, en donde la transversalidad del conocimiento es usada como herramienta vital de la construcción integral del conocimiento matemático.

El marco teórico presentado nos brindará las herramientas para realizar el análisis correspondiente a la hora de buscar las prácticas asociadas al conocimiento matemático. Analizaremos la razón de ser “del porquéhacen lo que hacen los albañiles” (¿por qué accionan o trabajan de esa manera?), para, en el ejercicio de las mismas prácticas, reconocer el conocimiento en uso, el saber emergente. Particularmente, hablamos de un saber popular que es válido porque es el resultado de años de prácticas de un cierto grupo social, además de ser funcional. Saber que en un momento fueron nociones, procedimientos, propiedades que fueron evolucionando hasta formas de saber socialmente establecidas.

Por último, una característica de este enfoque, en el marco de la dimensión social, es que se pretende intervenir en el sistema didáctico: no es contemplativo, porque, de acuerdo con (^{Cantoral, 2013}), debido a la naturaleza de los conceptos matemáticos, éstos no sólo viven en el aula, sino que trascienden más allá del uso escolar.

Metodología

El estudio está enmarcado en la línea cualitativa-interpretativa, cuyo método de investigación es el estudio de caso; al ser transparadigmático y transdisciplinario, este método puede ser utilizado desde cualquier paradigma de investigación (^{Durán, 2012}).

En nuestro estudio nos apoyamos en la propuesta de (^{Reyes y Hernández, 2008}):

Estudiaremos nuestro fenómeno: la construcción social del lenguaje algebraico desde las prácticas, a partir del análisis de las interacciones y el quehacer de un albañil de la comunidad mixteca en el estado de Oaxaca, a quien, por motivos de confiabilidad, sólo le llamaremos Rosendo.

Análisis

El álgebra, como todo lenguaje, emergió con ambigüedad y riqueza de significados, y al formalizarse quedó desprovista de ellos (^{Malisani, 1999}), o con significados artificiales, ajenos a la naturaleza del saber y a nuestra realidad: un simbolismo carente de sentido y significado (^{Filloy y Kieran, 1989}). Su aprendizaje requiere un cambio de pensamiento que permita ser consciente de sus procesos de significación; en este viraje deberán considerarse las limitaciones semánticas del lenguaje algebraico, la complejidad de su enseñanza y aprendizaje, así como de la necesidad de recurrir a otros lenguajes como el natural y el geométrico (^{Butto y Rojano, 2004}; ^{Filloy y Kieran, 1989}; ^{González, 2012}; ^{Malisani, 1999}; ^{Palarea, 1999}).

A fin de favorecer el análisis de la información, ordenamos las interacciones en tres episodios que resultan ser bastante extensos, motivo por el cual seleccionaremos sólo algunos fragmentos, donde a criterio del investigador se muestra lo que se pretende evidenciar: la construcción del pensamiento proporcional y, al menos, una de las fases de desarrollo del lenguaje algebraico (^{Malisani, 1999}).

1. Interacciones (episodio 2, Rosendo, 11 de agosto de 2014).

[95.] R: por botes de arena se guía uno más, porque en veces eh, eh… en botes de arena, porque ya sabes que le vas a poner un bulto de cal, esa es la medida se puede tomar ¿no?; eh, seis botes de arena y el de cal, ya en el cemento puede variar... Puede variar porque en una construcción vas a prevenir la humedad de... entonces en una parte le puedes poner ya revuelta tu mezcla. Puedes echar un poco más de cemento a una parte más baja por prevención de la humedad, pero la base, la base es el bulto de cal y los seis botes de arena, y el medio de cemento. Ya después como digo ¿no?, dependiendo del lugar que sea puede variar.

Es su práctica la que orienta el actuar de Rosendo cuando calcula el presupuesto de una obra: material y mano de obra; ya sea de manera formal o informal, en este último caso cuando se pretende dar una idea general de la obra sin que esto implique un acuerdo; sólo para que se tome como una referencia. En los presupuestos, proceso que Rosendo realiza casi de forma ritual (necesaria, mas no algorítmica) antes de hacer un trabajo, su conocimiento va más allá de operaciones aritméticas: estima, aproxima, realiza cálculo de áreas, volúmenes, conversiones de unidades, situaciones de conteo y un fuerte manejo de la noción del pensamiento proporcional en el que más adelante se abundará. La albañilería, en sus prácticas, encierra saberes milenarios que, con el uso reiterado en la comunidad de trabajadores de la construcción, instituyen actividades, procesos y relaciones; por ejemplo, determinan la cantidad de bultos a considerar por metro cúbico o el número de anillos por metro lineal en el armado de una trabe o castillo; sin desatender el uso, la disposición o las condiciones climáticas. Aquí se comienza a develar la albañilería como una potencial práctica de referencia.

Es importante señalar que las prácticas del albañil, a pesar de institucionalizarse, no dejan de estar sujetas a la funcionalidad o pertinencia, lo que determina, a su vez, su permanencia o cambio, en una suerte de readaptación de prácticas. Por ejemplo, la salida al mercado de una cal más cocida llevó a los albañiles a cambiar su práctica en el revoque pulido: dejaron de pudrir la cal con arena y agua para ahora quemar más la cal con su llana (herramienta parecida a la cuchara), como en el caso del pulido de una pared (acabado parecido al y eso pero con mayor resistencia, dado que utilizan cemento, cal y arena).

2. Interacciones (episodio 3, Rosendo, 26 de agosto de 2014).

[102.] R: ¡ya, no!; ahorita es, si no es afinado es yeso, casi ya no, afinado otros; pero, así hacían. Ahorita te estoy hablando todavía de eso, de que se... en México fue en el 67; 67, 68 allá en México todavía lo hacían. Aquí con don Boni, en San Marcos también se hacía; pero, surgieron estas cales como la ésta que te digo, la Calusa.

[103.] E: ¿y así más rápido?

[104.] R: así más rápido; pero, por eso; de que cuando es un pulido se truena, aunque lo que... tienes que quemar mucho la cal. Quemar es de que le pasamos una pasada con llana y luego al rato ya que fraguóun poco, le pasamos y tiene que quedar brilloso el pulido, es eso.

Se reconoce una función normativa en la práctica. De acuerdo con Sierra, “…debido a un proceso de transferencia generacional del conocimiento. Asociado al proceso permanencia-cambio y al proceso de conservación institucional del conocimiento es como se considera un conocimiento institucionalizado y como se comprueba el estatus normativo de la práctica social” (^{Sierra, 2008: 71}). En las interacciones, Rosendo hace referencia a los procesos de permanencia-cambio relacionados con el uso de la cal, en donde, sin que hubiese un acuerdo por escrito ante la nueva cal, los albañiles cambiaron sus prácticas, dejaron de pudrir la cal para trabajarla de forma inmediata; en el caso del pulido los obligó también a cambiar la forma de trabajar la cal, de tal forma que su práctica fuera funcional. Lo anterior contribuye al entendimiento de la consecución de saberes: al hacer un ajuste a sus prácticas, se las trasmite a su peón, a sus hijos o a otros albañiles. Un conocimiento en uso que pasa de una generación a otra, que se trasmite después de una readaptación o ajuste que le permite seguir siendo funcional. En este sentido reconocemos la naturaleza social del conocimiento a través de la reiteración intencional y compartida de prácticas, como resultado de una práctica de referencia: “la albañilería”.

De acuerdo con Cantoral, “la práctica social no se filma, se infiere”. Esta inferencia la entendemos como resultado de un estudio o investigación; en este sentido, buscamos entender “por qué hace lo que hace Rosendo”; “las causas del por qué lo hace, describir las circunstancias de cómo y cuándo lo hace, ¿en dónde?, y ¿por qué lo hace? ¿Y cómo se autoconcibe haciéndolo? Esto da lugar a las funciones de la práctica social” (^{Cantoral, 2013: 180-181}). A partir de lo que se puede inferir de las prácticas socialmente compartidas que viven los albañiles, conjeturamos que existe una práctica social que norma dichas prácticas. Prueba de ello es la caracterización que haremos de las funciones normativa, identitaria, reflexiva y pragmática, aunque por cuestiones de espacio sólo retomaremos brevemente esta última.

El carácter activo de la práctica social se manifiesta a través de la función pragmática, la cual “permite orientar las acciones en la actividad humana, al adquirir la capacidad de producir intencionalidad e iteración de la actvidad con la práctica hasta alcanzar la expertez o experiencia” (^{Cantoral, 2013: 181}). Rosendo comenzó de peón y poco a poco fue mejorando, adquiriendo más saberes y perfeccionando los anteriores, proceso que resulta evidente a lo largo de los tres episodios:

3. Interacciones (episodio 2, Rosendo, 11 de agosto de 2014).

[361.] E: y eso ¿cómo se aprende? ¿Se lo dijeron o...?

[362.] R: en la práctica, en el camino del trabajo ¡se aprende!, porque empe zamos, en veces no tuvimos la oportunidad deee... de que nos dijera alguien, y este, o alguien nos dice; pero si no, uno mismo; ya sabes que de hecho ¡yaa desde peón!, ya vienes escuchando del maistro que dice “le di...”, táuno de peón y le dice el maistro, el albañil al colador o que a su peón: ¿cómo está la grava?, o lo ve el albañil “¡no, está delgada; échale más de grava porque está delgada, se parte!”

Durante el estudio, Rosendo señaló, una y otra vez, la importancia de la práctica como la forma de aprender y alcanzar la expertez.

Este estudio nos permitió reconocer la albañilería como una práctica de referencia que, a su vez, encierra diferentes prácticas socialmente compartidas, como el revoque de paredes, el pegado de tabique, el colado de lozas, la construcción de escaleras, etcétera. Éstas encierran, en forma anidada, diversas acciones, actividades y prácticas, normadas por una práctica social, es decir, identificamos un sistema anidado de prácticas, normado por aquello “que le hace hacer lo que hace” a Rosendo; aquello, que le hace buscar una especie de equilibrio funcional en su práctica.

Una vez caracterizada y evidenciada la práctica de referencia, es que nos proponemos estudiar cómo se construye conocimiento matemático en ella. En particular, buscamos la construcción de la noción de proporcionalidad en el oficio de la albañilería para luego comenzar la construcción de un lenguaje simbólico orientado a la noción del lenguaje algebraico. Sin embargo, al analizar las evidencias encontramos que la albañilería cumple el rol de práctica de referencia y, en este contexto, identificamos el lenguaje algebraico en su fase retórica puesto en uso, el cual se caracteriza por el uso del lenguaje natural como soporte de expresión para plantear, analizar y resolver diferentes problemas propios de su práctica (^{Malisani, 1999}); es decir, no utiliza símbolos, como se muestra:

4. Interacciones (episodio 2, Rosendo, 26 de agosto de 2014).

[131.] R: ah, mira; un metro eh, mira ahorita vas a ver… un metro cúbico de concreto de la proporción de cuatro, de cuatro bultos.

[132.] E: cuatro por cuatro.

[133.] R: cuatro por cuatro a un cúbico; se tiene ya, como base ya calculado, que se lleva nueve botes, nueve bultos por metro cúbico de un concreto de losa.

En esta explicación Rosendo no recurre al uso de símbolos; los planteamientos y resoluciones los realiza en lenguaje natural, es decir, se sitúa en la fase retórica del lenguaje algebraico. Al analizar la interacción 3 identificamos dos relaciones proporcionales: “un metro cúbico de concreto de la proporción de cuatro, de cuatro bultos” y “nueve bultos por metro cúbico de un concreto de losa”. La expresión “cuatro por cuatro” se refiere a la cantidad de botes de arena y grava por bulto de cemento, que tiene un significado específico en la práctica para Rosendo: la resistencia del concreto. Matemáticamente podemos reconocerla como una relación entre dos magnitudes, esto es, una razón proporcional, que a su vez se representa como: 4 : 4 o 4/4. De manera semejante, se identifica la segunda expresión como una razón proporcional, donde se relaciona la cantidad de bultos de cemento por metro cúbico, es decir que 9 bultos de cemento rinden un metro cúbico, que se representa como: 1 : 9, 9 : 1, 1/9 o 9/1. Desde la perspectiva socioepistemológica, importa resaltar que las relaciones que se simbolizan como 4 : 4 y 9 : 1 tienen sentido y significado para Rosendo, aun siendo sólo retórica, porque le son funcionales en su práctica, en su contexto.

Por otra parte, en el lenguaje algebraico en uso por parte de Rosendo, a través de expresiones de su propia práctica identificamos uno a uno los diferentes razonamientos del pensamiento proporcional (^{Reyes-Gasperini y Cantoral, 2014}).

5. Interacciones (episodio 2, Rosendo, 26 de agosto de 2014).

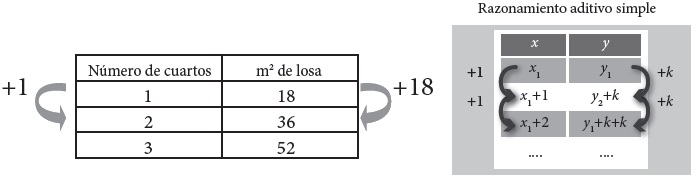
[189.] E: digamos un tamaño normal, si ese es, si es un cuarto; ¿y si fueran dos cuartos?

[190.] R: dos cuartos; son 18 ¡si llega ves, si llega!, son dos cuartos: 18, 36… ¿con su baño?... 45 metros… ¡45 metros! Eso es lo que vas a ver…

[191.] E: ¿y si fueran tre…?; ahí, digamos ya van considerando conforme va creciendo, no sólo son los cuartos… sino que, ya planeado es de qué va a llevar…

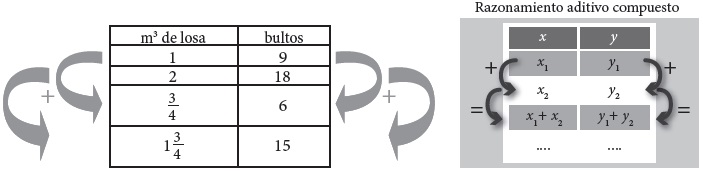
El análisis nos lleva a identificar el razonamiento aditivo simple, para lo cual realizamos el siguiente esquema:

En la Fig. 2 se evidencia, a través de la modelación, el pensamiento desarrollado por Rosendo, quien recurre a estrategias aditivas: incrementa de 18 en 18 (+k) para calcular los metros cuadrados de losa, y de uno en uno el número de cuartos. Cabe señalar que dichos cálculos están sujetos a un cierto margen de error, en virtud de que son realizados mentalmente. Este hecho da muestra de la evolución de lo proporcional, como relación adecuada, sobre la proporcionalidad como cálculo exacto, en las prácticas donde el saber popular está puesto en juego (Reyes-Gasperini, 2016).

Fuente: elaboración propia.

Figura 2 Análisis y contraste del razonamiento aditivo simple 

De la misma forma, identificamos los razonamientos aditivo compuesto e inter de pensamiento proporcional en la siguiente interacción.

6. Interacciones (episodio 2, Rosendo, 26 de agosto de 2014).

[275.] E: y ¿18 metros cuadrados, que casi está cerca de 20?

[276.] R: igualmente, porque estaba yo sacando cuentas: es un metro cúbico, uno… con… ochenta centímetros algo así…

[284.] R: le vas a hacer… no, ya no serían este… son, si fueran dos metros serían 18; pero no, ahí se va llevar este… 15 bultos…

[295.] E: ¿por qué dice usted?

[296.] R: porque estoy sumando el, eh… estoy sumando los dos metros cúbicos.

[297.] E: ajá.

[298.] R: así, mentalmente… porque dije nueve, nueve bultos de ese… del metro cúbico ese; pero, como del otro son prácticamente son tres cuartos, pero ya no; entonces ya le quitamos a… los dos bultos a… ya le quito al, en lugar de que sea metro cúbico entero el otro, pues yo saco primero que fuera, como si fueran los dos…

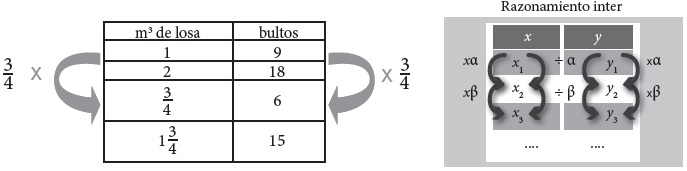
Modelamos la situación anterior a través de la Fig. 3, a fin de estructurar la intervención y hacer el análisis:

Fuente: elaboración propia.

Figura 3 Análisis del razonamiento inter 

En un primer momento se aprecia el cálculo que hace Rosendo para encontrar el número de bultos que corresponde a 3/4 de un m ³; donde asume que a 3/4m ³ de losa le corresponden 3/4 de los 9 bultos, es decir, 3/4 es el escalar β por el que multiplica ambas variables. Además, realiza un ajuste de los 6.75 bultos a seis, por dos razones: primera, en las tiendas de materiales no venden 0.75 bultos y, segunda, en repetidas ocasiones durante las interacciones Rosendo señala que de cada m3 le sobra medio bulto aproximadamente. De acuerdo con (^{Carretero, 1989: 86}) en esta situación se exploran “dos tipos de ‘estructuras multiplicativas’ en situaciones problemas que implican una o varias operaciones de multiplicación y/o división”.

Al mismo tiempo, en esta situación reconocimos el razonamiento aditivo compuesto. Rosendo plantea una relación de proporcionalidad directa al tener dos razones identificadas, y calcula una tercera mediante la suma. Apoyándonos en los funcionales de Cauchy (^{Roa, 2010}) esto puede expresarse como f(x + y) = f(x) + f(y), o bien, la imagen de la suma es igual a la suma de las imágenes, como se muestra a continuación:

Fuente: elaboración propia.

Figura 4 Análisis del razonamiento aditivo compuesto 

En la siguiente interacción se reconoce, asimismo, el razonamiento multiplicativo:

7. Interacciones (episodio 2, Rosendo, 26 de agosto de 2014).

[258.] R: ¿sí?, no, no este… hasta el final; son nueve bultos: cada metro, cada metro cúbico de ahí de los nueve, te va a sobrar como medio bulto… de cemento; y eso ya por experiencia me ha tocado, ya lo he hecho. Porque he pedido los nueve, porque era más fácil sacar, eh… como son 50 metros se rían 5 metros cúbicos; por eso saqué de los 45…

[259.] E: ¿cinco metros cúbicos?

[260.] R: ajá, cinco metros cúbicos ¿por nueve?, ¿serían que… los 45?

[261.] E: 45.

[262.] R: 45, pero no se lleva los 45; se lleva un poquito menos, porque cada…

Realizamos el siguiente esquema para el análisis:

Fuente: elaboración propia.

Figura 5 Análisis del razonamiento multiplicativo 

De lo expresado se puede sintetizar la relación de la forma n→9n, n ⋲ Z, que corresponde al razonamiento multiplicativo. Por último, de acuerdo a los diferentes razonamientos, sólo falta el razonamiento intra, identificado en la siguiente interacción:

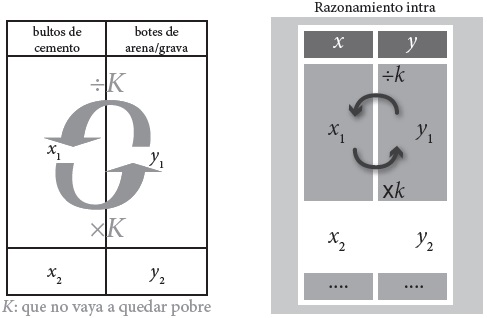
8. Interacciones (episodio 2, Rosendo, 26 de agosto de 2014).

[430.] R: si ya tiene que… si, ya se da cuenta él; ya más o menos. La recomendación que dices tú, que te estoy dando ehh… ya lo platicamos, él ya lo sabe; porque ya lo vio con nosotros, lo único que le vas a decir ¡que no vaya a quedar muy pobre!, si le dices ya así: sin, sin números “¡no vaya a quedar muy pobre, ehhh!”, “o sea, ¡regular!”; entonces dice, si él ya acostumbraba a echarle cinco o seis, no pus… ahí entonces ya se va a calcular cuántos bultos; porque va a colar este cuarto o va a colar un bañito, ya va a hacer como decimos ¿no? ¡Que no quede muy pobre!, o ves la revoltura ya que, ya la hizo; “¿cuántos bultos hiciste?”, “pus, ¡tres!”. “Oye, ¿no está muy pobre?”. “Maistro, es que le eché… tanto”. “Pues, échale… ¿son, cuántos botes? Échale otros dos botes, ¿o qué?”. Pero ya a cuenta de lo que él te dijo cuanto que le echó; así es…

Fuente: elaboración propia

Figura 6 Análisis del razonamiento intra 

Es precisamente la expresión “¡no vaya a quedar muy pobre, ehhh!”, donde se establece una relación entre magnitudes heterogéneas (bultos de cemento y botes de arena/grava); esta expresión corresponde a la estructura del razonamiento multiplicativo funcional, señalado así por (^{Carretero, 1989}), al que referiremos, de manera semejante a (^{Lamon, 1993}), como razonamiento intra. Cabe señalar que, para Rosendo, esta razón va más allá de una relación aritmética, porque en ésta él considera diversos factores, como las características de los materiales, las condiciones físicas o la disposición de la obra. Es decir, aunque no se llega a la simbolización, la relación queda explícita en la textura de la mezcla, a pesar de su complejidad y medio de expresión, donde atiende factores específicos.

Reflexiones y conclusiones

Como resultado de la investigación identificamos la albañilería como una práctica de referencia que orienta las actividades del albañil en su cotidiano. Cuando Rosendo determina las cantidades de material a utilizar en la mezcla, proceso donde considera distintos factores como el propósito de la mezcla (para qué la va a utilizar, ya sea para revocar o para pegar tabique), las características de los materiales (grosor de la grava o de la arena o el estado del cemento) y el contexto (atendiendo las consideraciones del clima o la disposición del lugar donde se empleará la mezcla: amplio, reducido, con humedad o seco, de carga o normal, volado o no, etcétera), se evidencia el proceso de construcción del conocimiento y de su uso, es decir, su tránsito al saber, como el caso del pensamiento proporcional mostrado en el análisis.

En el marco de la práctica de referencia de la albañilería, como resultado de la investigación postulamos que la noción de proporcionalidad a través de los modelos identificados en uso, en una suerte de simbiosis con el lenguaje algebraico en su fase retórica, conforman una ruta alternativa a las dos rutas planteadas en los libros de texto. Las evidencias encontradas muestran que aun antes del simbolismo es posible que emerja el lenguaje algebraico con sentido y significados en un contexto determinado por una práctica de referencia específica.

Aunado a lo anterior, cabe señalar el paralelismo entre el desarrollo del lenguaje algebraico en la historia de la matemática y el lenguaje encontrado en la práctica de referencia de la albañilería de la mano del pensamiento proporcional (dos conocimientos puestos en uso), que serán el punto de partida para continuar el desarrollo del lenguaje algebraico. Nótese que encontramos una ruta ya trazada, un camino funcional hacia el lenguaje algebraico simbólico inmerso en una práctica de referencia. No planteamos una nueva ruta, sino que la ruta ya está trazada, y responde a la naturaleza del saber. Sólo falta continuar o seguir la ruta identificada en la albañilería, una ruta natural que continuaremos bajo la consideración de que si las fases de desarrollo del lenguaje algebraico se sucedieron en la historia de la humanidad, es posible plantearlo bajo el mismo esquema en el individuo.

En comparación con el denominado programa funcionalista (centrado en la estructura sintáctica del lenguaje algebraico, que si bien resulta adecuado para localizar los obstáculos didácticos que se han documentado en el aprendizaje del lenguaje algebraico, no ha resuelto plenamente el problema del aprendizaje del álgebra, como muestran las evaluaciones internacionales), el aporte central de esta investigación es la propuesta de una estrategia centrada en las prácticas situadas. Prácticas socialmente compartidas que atraviesan la realidad de quien aprende, donde se asume el saber como un conocimiento en uso, y se toma por base en los modelos de pensamiento proporcional y desarrollo del lenguaje algebraico. A diferencia del programa funcionalista, consideramos la sintaxis algebraica en un segundo término porque, como evidenciamos en la investigación, aun antes de los símbolos existen significados; además, el lenguaje algebraico está “presente” en el propio uso. Nuestro programa pretende influir directamente en el sistema educativo a través de propuestas de intervención didácticas, proceso en el que seguimos trabajando. Por último, sostenemos la hipótesis de que esta vía favorece la construcción de otras nociones o conocimientos, como la noción de función, o más ampliamente, la noción de linealidad; pero, esto es motivo de otra investigación.