Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Diánoia
versión impresa ISSN 0185-2450
Diánoia vol.54 no.63 Ciudad de México nov. 2009
Artículos
De la matemática clásica a la matemática moderna: Hilbert y el esquematismo kantiano
From Classical to Modern Mathematics: Hilbert's Formalis and Kant's Schematism
Carlos Torres Alcaraz
Departamento de Matemáticas, Facultad de Ciencias, UNAM. carlos.torres.0505@gmail.com
Recibido el 15 de enero de 2008
Aceptado el 16 de junio de 2009
Resumen
En este artículo se examina la manera en que Hilbert elabora su primer formalismo al investigar los fundamentos de la geometría. El interés se centra en la forma en que elabora una nueva concepción de las teorías matemáticas. Se contrasta la postura de Hilbert con el constructivismo de Kant, el cual perduró en la filosofía de las matemáticas durante mucho tiempo. Para ello, en la primera parte se examina la manera en que Kant explica la demostración geométrica y se muestra el vínculo entre su explicación y la teoría de esquemas que él mismo sostiene. También se expone la concepción subyacente a los Grundlagen der Geometrie de Hilbert, y se busca reconstruir el camino que siguió hasta alcanzar esa concepción. En particular se examina el lugar que ocupan la geometría proyectiva y el principio de dualidad en sus reflexiones. Por último, se apunta a la idea de que el primer formalismo de Hilbert constituye una generalización necesaria de la filosofía matemática de Kant.
Palabras clave: dualidad, fundamentos de la geometría, elementos ideales, método axiomático.
Abstract
This essay examines the manner in which Hilbert worked out his first formalism in his investigations on the foundations of geometry. To elucidate these views, Hilbert's position is compared with that of Kant, who set forth a constructive notion of "geometrical objects" which endured in the Philosophy of mathematics for a long time. In the first part, the author explores the way in which Kant explains the notion of proof in classical geometry and clarifies how his account relates to his theory of schematism. Next, the conception underlying Hilbert's Grundlagen der Geometrie is presented and an attempt is made to recreate the path he followed until he reached his point of view. In particular this article explores the role that projective geometry and the principle of duality played in his reflections. Finally, Kant's ideas are contrasted with those of Hilbert in his first formalism, pointing toward the view that the latter constitutes a necessary generalization of Kant's mathematical philosophy.
Key words: duality, foundations of geometry, ideal elements, axiomatic method.
Cuando se habla de la concepción formalista de David Hilbert suele pasarse por alto que ésta se desarrolló básicamente en dos etapas. En la primera de ellas —o etapa geométrica—, Hilbert se enfocó en los fundamentos de la geometría adoptando la siguiente postura: en su forma axiomática, las teorías matemáticas no expresan un conjunto de verdades acerca de un dominio específico de objetos; más bien, constituyen una red o entramado de relaciones lógicas entre conceptos definidos implícitamente por los axiomas. Tales entramados pueden ser compartidos por sistemas de objetos de muy diversa índole. En particular, la geometría es un sistema hipotético deductivo, el cual sólo depende de relaciones entre objetos espaciales determinadas por los axiomas.1
En una segunda etapa, que aquí llamaremos aritmética, Hilbert fue más allá del punto de vista anterior hasta llegar a la siguiente conclusión: toda teoría axiomática se puede refinar al punto de ya ni siquiera proponer un entramado de relaciones lógicas entre conceptos, sino simples esquemas de relación entre símbolos. Esta idea, concebida en la década de 1920 como una extensión de su punto de vista inicial, exige la estricta formalización (mecanización) de los métodos deductivos de las matemáticas, al punto en que los aspectos semánticos ceden su lugar a una mera sintaxis que convierte la inferencia lógica en un juego combinatorio de fórmulas sujeto a reglas precisas.
Trataremos básicamente con la primera de estas dos etapas. El texto se inicia con una exposición de las principales ideas de Kant acerca de la geometría, brindando especial atención a su teoría de esquemas. A continuación se examina la manera en que esta teoría entró en conflicto con el desarrollo de las matemáticas en el siglo XIX y la manera en que Hilbert reelaboró la noción de objeto matemático en general.
Si alguna utilidad ha de tener este estudio, espero que sea, por una parte, ofrecer una valoración distinta de la escuela de Hilbert mostrando que sus preocupaciones fueron más allá de la inquietud por la certeza matemática;2 y por la otra, destacar la importancia de la teoría kantiana de esquemas para la filosofía de las matemáticas, la cual, creo, no ha sido debidamente valorada.
1. El punto de vista de Kant
Comenzaremos con algunas ideas de Kant acerca de la geometría, las cuales subyacían en casi todos los debates en torno a esta disciplina durante el siglo XIX y principios del XX.
En la Crítica de la razón pura, Kant establece una filosofía constructiva de las matemáticas en la que ofrece un fundamento epistemológico para el conocimiento matemático en general. Su teoría tiene dos puntos de apoyo: por una parte, la idea de que tanto la aritmética como la geometría tienen como base las formas puras de la intuición, siendo ésta una de las razones por las que califica sus juicios de sintéticos a priori; por la otra, una noción constructiva de los objetos matemáticos basada en su teoría de esquemas para los conceptos del entendimiento. En particular, con estas herramientas Kant pretende justificar y dar fundamento al tipo de razonamiento que encontramos en los Elementos de geometría de Euclides, paradigma de la demostración matemática hasta el siglo XIX.
Veamos a través de un ejemplo cómo entiende Kant la demostración euclidiana (y, por ende, la demostración geométrica en general), y cómo articula su teoría de esquemas con dicha interpretación. Se trata de la proposición 32 del libro I de los Elementos de Euclides, a la que Kant hace abierta referencia en la Crítica de la razón pura (v.gr., en B 743–45):
Proposición I.32. Si en un triángulo se prolonga uno de los lados, el ángulo externo es igual a los dos internos y opuestos, y los tres ángulos internos del triángulo son iguales a dos ángulos rectos.

Sea ABC el triángulo y prolónguese el lado BC hasta D.
Digo que el ángulo externo ACD es igual a los dos internos y opuestos CAB y ABC y que los tres ángulos internos del triángulo ABC, BCA y CAB son iguales a dos rectos.
Demostración. Por el punto C trácese la recta CE paralela a la AB. [I.31]
Puesto que AB es paralela a CE, y AC es incidente con las dos, los ángulos alternos internos BAC y ACE son iguales entre sí. [I.29]
Por otra parte, puesto que AB es paralela a CE, y BC es incidente con las dos, el ángulo externo ECD es igual al interno y opuesto ABC. [I.29]
Mas se demostró que el ángulo ACE es igual al ángulo BAC.
Luego el ángulo entero ACD es igual a los internos y opuestos BAC y ABC.
Añádase el ángulo común ACB.
Según esto serán los ángulos ABC, BCA y CAB iguales a los ángulos ACD y ACB.
Más los ángulos ACD y ACB son iguales a dos rectos. [I.13]
Luego los ángulos ABC, BCA y CAB son iguales a dos rectos.
Por lo tanto: en todo triángulo, si se prolonga uno de los lados, el ángulo externo es igual a los dos internos y opuestos, y los tres ángulos internos del triángulo son iguales a dos rectos. Q.E.D.3
Como se ve, Euclides utiliza un diagrama en torno al cual organiza el argumento. Esto no es algo circunstancial, sino una práctica usual entre los geómetras que Kant quiere explicar. La figura o diagrama en el ejemplo anterior corresponde a lo que Kant denomina "construcción de conceptos", un rasgo distintivo de las ciencias matemáticas. Dice Kant: "El conocimiento filosófico es un conocimiento racional derivado de conceptos; el conocimiento matemático es un conocimiento obtenido por la construcción de los conceptos" (B 741), y añade: "el conocimiento filosófico sólo considera lo particular en lo universal; las matemáticas, lo universal en lo particular, e incluso en lo singular, pero sólo a priori y por medio de la razón" (B 742).
El diagrama de la proposición I.32 es, en el sentido recién indicado, una construcción de los conceptos de triángulo, línea recta, etc., conforme a cierto diseño que Euclides adopta por conveniencia.4 Y sobre la figura así construida desarrolla el razonamiento ulterior, el cual ya no es general: nos habla del ángulo ABC, de la recta CD, etc., en vez de "cualquier ángulo interior de cualquier triángulo" o de "cualquier extensión de cualquiera de los lados de ese triángulo cualquiera". Considera, pues, lo universal en lo singular.5
La importancia del diagrama se manifiesta desde la formulación de la proposición, donde Euclides habla de ángulos internos y ángulos externos sin que haya en los Elementos una definición de estas nociones. De hecho, el significado de tales términos sólo se entiende con la figura (digamos que "interior" y "exterior" son nociones definidas implícitamente a través de ella). Así, el diagrama expone ciertos objetos en consonancia con los conceptos aludidos en la proposición, un triángulo ABC y una extensión CD de uno de sus lados, pero en él se muestran muchas cosas más; por ejemplo, la interioridad o la exterioridad de los ángulos. Todavía más, en el texto Euclides nos pide trazar una recta CE paralela a AB sin indicar el sentido en que se debe dibujar. Esto sólo se aclara recurriendo al diagrama, donde dicha línea aparece hacia arriba, dividiendo el ángulo ACD en dos ángulos ACE y ECD, un hecho esencial para el argumento posterior. Esta propiedad de la línea CE sólo se puede reconocer en el diagrama, el cual se convierte de esta manera en una parte importante de la demostración.6
Podemos decir, siguiendo a Lisa Shabel (2003), que en los Elementos muchos pasos cruciales en la demostración se dan en virtud de observaciones hechas en el diagrama; por eso, a este tipo de razonamientos se les suele llamar diagramáticos.
Lejos de ver un defecto en lo anterior, Kant lo considera un rasgo esencial de la demostración matemática, un recurso sin el cual no sería posible el conocimiento matemático en general. Para destacar su papel e importancia nos pide imaginar qué pasaría si, por ejemplo, preguntáramos a un filósofo la misma cuestión (¿a qué son iguales los ángulos internos de un triángulo?) y lo dejáramos hallar la respuesta a su manera. El punto es que nunca daría con algo parecido a la proposición I.32: sólo contaría con los conceptos de recta, ángulo, etc., y por mucho que reflexionara sobre éstos no alcanzaría ninguna conclusión nueva. El filósofo no podría seguir el camino de Euclides, pues sólo conoce por conceptos, no por construcción de conceptos. Trazar un triángulo sería considerar lo universal en lo particular, pero él "sólo considera lo particular en lo universal". Él podría analizar y clarificar tales conceptos, pero nunca llegaría a propiedades no contenidas en ellos. En el otro extremo tenemos al geómetra, quien lo primero que hace es representar los conceptos mediante una o más construcciones, para después razonar sobre los diagramas resultantes; al hacerlo, descubre propiedades de los objetos que no están contenidas en los conceptos mismos (es decir, que no se pueden extraer de los conceptos considerados de manera aislada y al margen de toda intuición).7 Podemos decir, entonces, que el diagrama no es una mera ilustración de la proposición I.32, sino un elemento central de la prueba que orienta nuestros razonamientos. En las propias palabras de Kant: "A través de una cadena de inferencias y guiado siempre por la intuición, el geómetra consigue así una solución evidente y, a la vez, universal del problema" (B 745) (las cursivas son mías). Tal uso de los conceptos in concreto es, para Kant, un rasgo distintivo del método matemático y en él apoya la idea de que los juicios de la matemática son sintéticos a priori.
Éste es el argumento de Kant: la geometría es sintética porque sus resultados se obtienen realizando construcciones.8 La geometría es a priori porque de los objetos construidos sólo considera aquello que se sigue de las condiciones universales de la construcción; es por ello que el geómetra puede afirmar la validez del resultado para todas las intuiciones correspondientes al concepto (al respecto, véase B 44). Como veremos, estas afirmaciones tienen hoy en día un valor limitado.
2. La teoría kantiana de esquemas
Una prueba como la de la proposición I.32 es realizable cuando se tiene la posibilidad de producir objetos de la intuición que sean imagen de los conceptos implicados. Según Kant, esto se logra mediante la aplicación de esquemas, es decir, por razón de ciertos procedimientos o reglas que indican en general cómo construir tales objetos.9
Refiramos esto al ejemplo anterior. Veamos, por ejemplo, la definición de triángulo que se halla en los Elementos: triángulo es cualquier figura rectilínea comprendida por tres rectas. El cometido de esta definición, como el de tantas otras, es delimitar el concepto correspondiente, es decir, señalar las condiciones que una figura ha de cumplir para ser un triángulo. Para poderla aplicar (i.e., para poder decir "¡esto es un triángulo!") debemos tener un objeto, cuya producción no resulta de la definición misma. Al respecto, la definición es inerte, pues nada dice acerca de la producción o el manejo de los triángulos. Lo mismo puede decirse de otras definiciones, como la de círculo. Por lo tanto, sin la posibilidad de construir triángulos, el concepto resulta inoperante. Y es precisamente esta posibilidad lo que, según Kant, separa al geómetra del filósofo: el primero cuenta con un esquema que le permite producir triángulos. Actúa, por decirlo de alguna manera, sirviéndose de un procedimiento que los trae a la representación, ya sea mediante imágenes mentales, ya sea mediante construcciones sensibles.
La prueba de la proposición I.32 se apoya decididamente en la posibilidad anterior. En ella, Euclides traza un triángulo ABC, prolonga el lado BC hasta D, etc., preparando de este modo el escenario para la demostración. Estas construcciones las realiza con base en ciertos esquemas, que en este caso corresponden al uso, real o imaginario, de la regla y el compás; v.gr., la figura ABC es un "triángulo" porque su elaboración se puede llevar a cabo con tales instrumentos. Tales usos de la regla y el compás están sugeridos en los tres primeros postulados, a los que dan vida:
Postulado I. Trazar una línea desde un punto cualquiera a otro punto cualquiera;
Postulado II. Prolongar por continuidad en línea recta una recta delimitada;
Postulado III. Para cada centro y radio describir su círculo.
El uso de la regla y el compás está claramente presupuesto en lo anterior. De hecho, estos instrumentos han sido parte del bagaje del geómetra desde la antigua Grecia hasta nuestros días, al punto de colmar la geometría elemental con estas figuras. Esto es particularmente cierto de los Elementos, donde con base en ellos se construyen todos los diagramas. Dice Kant:
lo que en matemáticas se llama postulado es una proposición práctica que no contiene más que la síntesis a través de la cual nos damos un objeto y producimos su concepto. Por ejemplo, describir un círculo con una línea dada, partiendo de un punto dado, en un plano. Semejante proposición no puede demostrarse, ya que el procedimiento que exige es precisamente el procedimiento a través del cual producimos el concepto de esa figura. (B 287)
Veamos la pertinencia de lo anterior con relación al tercer postulado de Euclides; éste: (i) sintetiza los conceptos de punto y línea; (ii) para cada punto y línea dados, determina un objeto: el círculo con centro en el punto dado y radio la línea dada; y (iii) alude a un procedimiento (a un esquema fundamental) que se halla en la base del concepto de círculo.
En resumen: según Kant, es con base en ciertos esquemas como el geómetra realiza la construcción de conceptos; y es examinando los objetos construidos como descubre sus propiedades. Los esquemas conectan de manera confiable los conceptos con sus representaciones, y como en la indagación el geómetra no se sirve de nada empírico, sino sólo de lo que es común a todas las figuras del género propuesto, la conclusión alcanzada la puede afirmar para todas ellas. De ahí el salto de lo singular a lo general. Por ello, la última línea de la proposición I.32: "Por lo tanto: en todo triángulo, si se prolonga uno de los lados, el ángulo externo es igual a los dos internos y opuestos, y los tres ángulos internos del triángulo son iguales a dos rectos."
Finalizaré esta sección con un breve comentario acerca del problema que significó el uso de diagramas en el siglo XIX. Esto tenderá un puente hacia las discusiones venideras.
Al tratar de probar el teorema de que toda magnitud que crece continuamente, pero no más allá de toda medida, se aproxima a un valor límite, Dedekind se vio obligado a recurrir a evidencias geométricas. Su respuesta fue buscar un riguroso fundamento, puramente aritmético, para los principios del análisis infinitesimal. El resultado al que llegó (1872) es bien conocido: se trata del concepto de número real definido a través de las llamadas cortaduras, las cuales son centrales en la construcción genética de los números reales. Un problema con las cortaduras es que no son esquematizables. En la sección 9 volveremos a este punto.
Poco tiempo antes, en 1861, Weierstrass había presentado un ejemplo de función continua que no es diferenciable en ningún punto, es decir, una "curva" que, siendo continua, no tiene tangente en ninguna parte. Esto contradijo la idea intuitiva de que toda función continua es diferenciable excepto en puntos especiales, algo claramente sugerido por los diagramas.10 Surgieron muchas preguntas: ¿cómo tratar con esta clase de "curvas", para las que no se tienen esquemas de producción?, ¿en qué sentido se puede decir que estas entidades son objetos matemáticos?11
Los anteriores no fueron casos aislados, sino parte del acontecer matemático durante la segunda mitad del siglo XIX, cuando hubo una fuerte oposición al uso de diagramas en las pruebas matemáticas. Por ejemplo, en 1882, Pasch estableció como norma apoyar los argumentos matemáticos exclusivamente en los axiomas y en la lógica. Dice al respecto:
Si la geometría ha de ser realmente deductiva, entonces la deducción ha de liberarse por completo de cualquier referencia al significado de los conceptos geométricos, al igual que de las figuras. Así, sólo reconocemos aquellas pruebas en las que cada paso se apoya en las proposiciones precedentes y las definiciones.12
Al examinar con espíritu rigorista los argumentos de Euclides, el mismo Pasch descubrió algunas suposiciones que nadie había notado con anterioridad; por ejemplo, las relacionadas con el orden de los puntos en una línea. Todos pueden trazar un diagrama y notar que si en una línea recta un punto B está entre un punto A y un punto C, entonces ni C está entre A y B, ni A está entre B y C. No obstante, nadie antes de Pasch había sentado las bases para tratar lógicamente con esta clase de observaciones, quizá porque se las consideraba demasiado obvias. La consecuencia de tal desatención fue, precisamente, la necesidad de recurrir a la intuición, de manera que la forma lógica de lo que se hacía era poco clara. A diferencia de Kant, Pasch vio en el método deductivo el método de las matemáticas y no sólo una parte de él, lo cual exigió acentuar el rigor.
3. Algunas cuestiones relacionadas con el apriorismo en la matemática después de Kant
En el siglo XIX, los matemáticos no sólo cuestionaron la legitimidad del razonamiento diagramático en las demostraciones: también expresaron sus dudas respecto de la validez del punto de vista de Kant acerca de la naturaleza a priori de las matemáticas. Por ejemplo, en 1817, en una carta dirigida a Olbers, Gauss expresa abiertamente su recelo respecto del carácter necesario de la geometría con las siguientes palabras:
Cada vez me convenzo más de que la necesidad de nuestra geometría no se puede probar, al menos no mediante la comprensión humana ni para la comprensión humana [Gauss se refiere a los intentos por probar el quinto postulado de Euclides]. Quizá en otra vida alcanzaremos otros puntos de vista acerca de la naturaleza del espacio que por ahora nos son inasequibles. Hasta entonces, no se deberá poner a la geometría en el mismo rango que la aritmética, que se yergue a priori, sino en la misma situación que, digamos, la mecánica.13
Así, donde Kant establece una similitud epistemológica entre la geometría y la aritmética, Gauss vislumbra una asimetría. Tiempo después, la llegada de las geometrías no euclidianas y las pruebas de su respectiva posibilidad alimentaron esta sospecha: la aritmética y la geometría parecían no compartir una misma naturaleza epistemológica. Dilucidar esta cuestión se convirtió en un tema central de la filosofía de las matemáticas y orientó en gran medida el estudio de sus fundamentos. Es más, fue esta cuestión, y no la preocupación por asegurar un fundamento, la causa primordial de las investigaciones de Frege, Dedekind, Poincaré, Hilbert, Bernays, Brouwer y Weyl, entre otros.
A grandes rasgos, hubo tres formas de resolver el problema, según el modo de disponer del a priori. Estas formas guardan un estrecho vínculo con las escuelas clásicas conocidas hoy en día como logicismo, intuicionismo y formalismo. Por ejemplo, Brouwer y Weyl, en conformidad con Gauss, optaron por retener la concepción kantiana de la aritmética (esto es, basada en la intuición a priori del tiempo), adoptando a la vez una concepción no kantiana de la geometría (es decir, viendo en ella algo cuya fuente no es una forma a priori de la intuición). La de Frege fue la contraria: retuvo la concepción kantiana del espacio (como algo basado en una intuición a priori), y desechó la concepción kantiana de la aritmética. La de Hilbert fue un poco más compleja: mantuvo cierto apriorismo en ambos casos, aunque en forma limitada.
4. El formalismo de Hilbert en los Grundlagen der Geometrie
En los Grundlagen der Geometrie de 1899, Hilbert exhibe el formalismo de su primera etapa. El tratamiento que da a la geometría en esta obra difiere radicalmente del que le otorga Euclides en los Elementos. En particular, evita en todo momento hacer referencia a la intuición espacial, no sólo en las pruebas, sino en los axiomas y las definiciones. Ésta es una cuestión esencial. Una consecuencia de lo anterior es que la demostración se ve forzada a marchar dentro de los cánones de la lógica, sin recurrir al señalado razonamiento diagramático.
En cuanto a Kant, una diferencia es que Hilbert desdeña la exigencia de que los axiomas sean proposiciones prácticas que contengan la síntesis a través de la cual nos damos un objeto y producimos su concepto.14 En los Grundlagen los axiomas no presuponen ni se sustentan en ninguna clase de hechos preestablecidos, aunque tales hechos se hayan tenido en mente al elaborarlos. Esto lo expresa en una carta dirigida a Frege en 1899 con las siguientes palabras:
No quiero asumir nada como algo conocido por anticipado; considero mi explicación de la sección 1 [de los Grundlagen] como una definición de los conceptos punto, línea, plano —si se añaden nuevamente todos los axiomas de los grupos I al V como marcas características. Si se buscan otras definiciones de "punto", v.gr., mediante paráfrasis en términos de inextensión, etc., entonces me debo oponer a tales intentos en forma decisiva; se busca algo que nunca se encontrará porque no hay nada allí. (Frege 1980, p. 39)
Aquí se hace presente la teoría de las definiciones implícitas de Hilbert. Ahora bien, lo que de momento nos interesa es aclarar el espíritu con el cual Hilbert elabora los Grundlagen der Geometrie y recorrer parcialmente el camino que lo llevó a adoptar este punto de vista.
Para Hilbert, la axiomatización es un modo de ordenar los hechos que conforman una esfera del conocimiento. En sus propias palabras, esto se logra
recurriendo a una trama de conceptos relacionados entre sí, de tal manera que a cada objeto y a cada hecho del campo del conocimiento de que se trata le corresponda, respectivamente, un concepto de esa trama y una relación lógica entre conceptos del mismo. La trama de conceptos no es otra cosa que la teoría de esa esfera del saber. (Hilbert 1993, p. 23)
En el caso de la geometría, la esfera en cuestión es la de los hechos geométricos; los conceptos son los de punto, línea, triángulo, etc.; los hechos relevantes son los de incidencia, congruencia, paralelismo, etc., entre puntos, líneas y otras figuras. Para referirnos a tales hechos utilizamos expresiones como "A está en a", "A está entre B y C", "a y b son paralelas", "AB es congruente con CD", etc., las cuales corresponden en el orden lógico a relaciones entre conceptos, como lo señala Hilbert.15
En una conferencia pronunciada en 1930,16 Hilbert expone con cierto detenimiento su punto de vista con relación al conocimiento geométrico. Sostiene que, además de la experiencia y la deducción lógica, disponemos de cierto discernimiento a priori necesario para la construcción de un marco teórico para la realidad. Tal discernimiento subyace en la génesis de nuestro conocimiento. No obstante, traza la frontera de este a priori de manera diferente de como lo hace Kant, tanto para la aritmética como para la geometría. En su opinión, Kant sobreestimó el papel y el alcance del a priori en ambos casos. Dice al respecto:
En los días de Kant se podía pensar que las representaciones [Vorstellungen] que uno tenía del espacio y del tiempo eran aplicables de un modo tan inmediato y general a la realidad como, por ejemplo, nuestras representaciones de número, sucesión y cantidad, las cuales se utilizan constantemente en la manera que nos es familiar en la teoría matemática y física. Pero, entonces, la teoría del espacio y el tiempo (y en particular la geometría) precedería, como la aritmética, nuestro conocimiento de la naturaleza. No obstante, el punto de vista de Kant fue abandonado por Riemann y Helmholtz incluso antes de que la teoría física obligara a hacerlo, y con toda razón, pues la geometría no es otra cosa que esa parte del marco de los conceptos físicos que modela las posibles relaciones de posición entre los cuerpos rígidos en el mundo de las cosas reales.17
Es así como Hilbert despoja a la geometría elemental del poder de determinar las propiedades del espacio sintéticamente y a priori. Lejos de lo anterior, ve en ella una ciencia cuyo cometido es describir la forma externa de las cosas que se nos manifiestan al observar la naturaleza. Esta postura la subraya con las siguientes palabras: "hay principios que Kant considera a priori y que nosotros asignamos a la experiencia; por ejemplo, la totalidad de los hechos fundamentales de la geometría, así como las propiedades elementales del espacio y la materia" (Hilbert 1993, p. 124). De lo anterior se sigue la imposibilidad de establecer las propiedades del espacio por pura reflexión, ya que es en la contemplación intuitiva de los hechos geométricos donde nace la geometría. El punto de partida es doble: por un lado, la experiencia u observación; por el otro, nuestra percepción de las relaciones espaciales (es decir, la manera como percibimos tales relaciones).
En el caso de la geometría, la observación de las configuraciones espaciales se da en el marco de lo que Hilbert refiere en alemán con el vocablo Anschauung, que podemos explicar como "intuición o contemplación intuitiva con una fuerte carga de evidencia". Ésta es la fuente de muchos axiomas; es también la fuente de muchos teoremas como, por ejemplo, el relativo a la igualdad entre los ángulos de la base de un triángulo isósceles. La aceptación inmediata de tales hechos geométricos resulta de la consideración intuitiva de las figuras y es lo más cercano que tenemos al apriorismo en geometría.
Al respecto, Hilbert parece admitir que la forma en que percibimos las relaciones espaciales es la descrita por la geometría euclidiana. Esto no obliga a nada con relación a los fenómenos, pues nuestra percepción es inexacta. Al axiomatizar, idealizamos tales observaciones dándoles un carácter de absoluta exactitud y generalidad. Así, aunque partimos de observaciones que son válidas dentro de ciertos límites de exactitud, en los axiomas sustituimos los resultados de ellas por aseveraciones de total precisión y universalidad. Pero, entonces, la teoría axiomática es acerca de relaciones ideales entre objetos ideales. En otras palabras, la validación intuitiva de los axiomas deja de ser un fundamento para la teoría; es más, tal validación escapa a las matemáticas.18 Al mismo tiempo, el matemático queda en libertad de interpretar los términos geométricos y sus relaciones como le plazca. Así, frente a la idea de una teoría que trata con un fuerte núcleo de "realidad geométrica" o "intuición intersubjetiva", Hilbert coloca, independientemente de su origen, una teoría abstracta que trata con términos susceptibles de distintas interpretaciones. Ergo, el significado intuitivo que tales términos pudieran tener no debe intervenir en las demostraciones, donde ya no hay lugar para los razonamientos diagramáticos. Ésta es la postura que da sustento a los Grundlagen der Geometrie de 1899.
Llegar a estas ideas no fue cosa de un día, sino el resultado de largas reflexiones en las que Hilbert hubo de ponderar el carácter de la nueva matemática. En particular, las geometrías no euclidianas y la geometría proyectiva aportaron suficientes elementos como para poner en tela de juicio la visión tradicional. Un hecho particularmente notable fue la aparición del principio de dualidad en la geometría proyectiva, el cual hizo ostensible cómo ciertos teoremas geométricos siguen siendo válidos cuando sus términos se reemplazan por otros con un significado distinto. Esto permitió ver que el modo en que los conceptos se entrelazan en la teoría puede muy bien corresponder a otros órdenes de objetos; es decir, que nuestra descripción teórica puede convenir por igual a otros sistemas. Esto apremió al método axiomático a que diera cuenta de su condición.
5. El principio de dualidad en la geometría proyectiva
En la matemática actual, el término "dualidad" tiene varios significados, los cuales se relacionan entre sí por una sola idea: la de una conversión de conceptos, teoremas y estructuras matemáticas en otros conceptos, teoremas o estructuras mediante una transformación específica. El caso más conocido (y el primero en la historia) es el llamado principio de dualidad de la geometría proyectiva:
PRINCIPIO DE DUALIDAD. Dado cualquier teorema de la geometría proyectiva plana, al intercambiar en él los términos "punto" y "línea" (intercambiando, de ser necesario, las frases "estar en" y "pasar por"), lo que resulta es otro teorema igualmente válido.
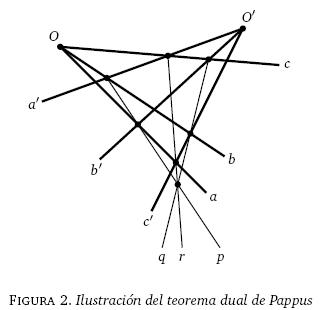
Veamos, a través de un ejemplo, cómo trabaja la dualidad, para después ver de qué manera su surgimiento afectó la visión clásica de las teorías geométricas. Consideremos el teorema de Pappus, un importante resultado de la geometría proyectiva.
TEOREMA DEL HEXÁGONO DE PAPPUS Si los puntos A, B y C están en una recta, y los puntos A′, B′ y C′ están en otra recta, entonces los puntos de intersección P = AB′
A′B,Q = BC′
B′C y R = CA′
C′ A están alineados. (En otras palabras: Si los vértices de un hexágono se hallan alternados en dos rectas, entonces los puntos de intersección de los lados opuestos están alineados).
El dual de este teorema es el siguiente.
DUAL DEL TEOREMA DE PAPPUS. Si las rectas a, b y c concurren en un punto, y las rectas a′, b′ y c′ concurren en otro punto, entonces las líneas p, q y r definidas por las parejas de intersecciones (a
b′, a′
b), (b
c′, b′
c) y (c
a′, c′
a) son concurrentes.19
Aquí la dualidad se presenta con un par de teoremas, cada uno de los cuales se puede obtener del otro mediante un esquema simple y uniforme de sustitución de términos: punto  línea, puntos alineados
línea, puntos alineados  líneas concurrentes, punto de intersección de líneas
líneas concurrentes, punto de intersección de líneas  línea por los puntos.
línea por los puntos.
El valor de la dualidad es que con ella disponemos de un procedimiento que duplica nuestra capacidad para demostrar teoremas, pues nos ofrece dos resultados por el costo de uno, una ganancia del cien por ciento.20 Esta cuestión, sumamente valorada por Hilbert, sería motivo de un amplio comentario a no ser porque nuestro interés es otro por el momento: dilucidar la lectura que hiciera Hilbert del principio de dualidad. Para ello, conviene contrastar su punto de vista con el de Pasch.
Pasch fue un matemático que trabajó laboriosamente en los fundamentos de la geometría proyectiva durante el siglo XIX; en particular, fue uno de los primeros en ofrecer una presentación axiomática de esta teoría en la que el principio de dualidad se halla presente. Al respecto, Pasch no sólo vio en este principio una herramienta de gran utilidad, sino algo contrario a nuestra comprensión intuitiva de las nociones de punto y línea, pues no consideraba creíble que estos términos se pudieran intercambiar.21 Esta simple observación muestra que, para él, como para otros geómetras del siglo XIX, la geometría seguía siendo una ciencia con una clara semántica para sus términos.
En contraste, hay una segunda lectura del principio de dualidad que toca la esencia del primer formalismo de Hilbert: no sólo se trata de algo contrapuesto a nuestras ideas acerca de lo que son los puntos y las líneas, sino de una señal. En efecto, la posibilidad de intercambiar los términos "punto" y "línea" se debe a que, en el interior de la teoría, estas nociones son simétricas. Por lo tanto, podemos permutar su interpretación sin caer en incorrecciones; es decir, sin que los enunciados de la teoría dejen de ser una descripción objetiva de ciertos hechos geométricos.
Aclaremos lo dicho en el párrafo anterior. Si proporcionáramos los axiomas de la geometría proyectiva a dos individuos que ignoraran el significado intuitivo que les damos a las palabras "punto" y "línea", y les pidiéramos que ilustraran el teorema de Pappus con un diagrama, bien podría suceder que el primero de ellos diera como respuesta la figura 1 y el segundo la figura 2 anteriores: uno llamaría punto a lo que el otro denomina recta, y viceversa. Simplemente, cada uno de ellos habría escogido una interpretación diferente para estos términos, ambas válidas.22

Esta posibilidad amplió considerablemente el horizonte: los teoremas geométricos se podían interpretar de manera distinta de como en un principio se tenía en mente. Por tanto, no encajaba concebir la teoría como representación unívoca de un sistema de objetos; más bien, ésta asomaba como un montaje de relaciones entre términos cuyo significado podía variar.23 En otras palabras (y dicho en tiempo presente): lo único que logra la teoría es delimitar los objetos que le dan origen como parte de un sistema (o estructura), reflejando sus propiedades y mutuas relaciones.
Hilbert tenía en claro todo lo anterior al momento de escribir los Grundlagen der Geometrie. Como testimonio, veamos cómo se expresa en una carta dirigida a Frege en 1899, que este último resumiera en un cuaderno de notas:
es obvio que toda teoría es tan sólo un andamiaje o esquema de conceptos junto con las relaciones necesarias entre ellos, y que los elementos básicos se pueden pensar como uno quiera. Si al hablar de mis puntos pienso en algún sistema de objetos, v.gr., el sistema: amor, ley, deshollinador, [...] y tomo mis axiomas como relaciones entre estas cosas, entonces mis proposiciones, v.gr., el teorema de Pitágoras, son válidas también para estas cosas. En otras palabras: cualquier teoría se puede aplicar a una infinidad de sistemas básicos de elementos. Lo único necesario es aplicar una transformación reversible [...] y establecer que los axiomas serán correspondientemente los mismos para las cosas transformadas. Esta circunstancia se utiliza, por ejemplo, en el principio de dualidad, etc., y yo me he servido de ella en mis pruebas de independencia. [...] Pero la circunstancia que he mencionado no puede ser un defecto de las teorías (representa más bien una enorme ventaja), y es en todo caso inevitable. (Frege 1980, pp. 40–41; las cursivas son mías.)24
La mención que Hilbert hace de la dualidad muestra que, al escribir los Grundlagen, ya tenía en mente la lectura recién expuesta de dicho principio. Es más, hoy en día podemos remitir el origen de estas ideas al periodo 1891–1893.
En el otoño de 1891, Hilbert asistió a la primera reunión anual de la Sociedad Matemática Alemana, celebrada en la ciudad de Berlín. Ahí escuchó una conferencia de Hermann Wiener acerca de los fundamentos y el desarrollo sistemático de la geometría. En su disertación, Wiener abordó complejas cuestiones relacionadas con la geometría proyectiva, entre las que se encuentran: a) la idea de edificar dicha teoría como una ciencia abstracta; b) la tentativa de quitar el ropaje geométrico a los términos de la teoría a fin de poner al descubierto la manera en que se combinan y se opera con ellos; c) la relación entre la continuidad, los teoremas de Desargues para el plano y el espacio, el teorema de Pappus, el orden entre los puntos de la recta y el modo de obtener haces de puntos armónicos sobre la recta; d) la cuestión de la demostración matemática y las hipótesis que servirían como base para el desarrollo de la teoría; y e) la posibilidad de reconstruir la geometría proyectiva a partir de un sistema simple de suposiciones.25
Al parecer, la conferencia de Wiener atrajo a Hilbert hacia tales problemas y avivó su interés por la axiomática. Esto no sólo se puede advertir en los Grundlagen, donde recoge muchas de las cuestiones planteadas por Wiener, sino en el hecho de que entre 1891 y 1898 impartió cuatro cursos en los que discurre en torno a los fundamentos de la geometría.26
Con base en estos y otros elementos podemos ubicar los orígenes del formalismo de Hilbert en esos años. Hasta hace poco tiempo, lo único que teníamos era una anécdota relatada por Otto Blumenthal, quien reporta que Hilbert, al comentar con otros matemáticos la plática de Wiener en la estación de Berlín, habría dicho: "Uno siempre debe poder decir mesa, silla y tarro de cerveza en vez de punto, línea y plano."27 Esta frase se considera representativa del punto de vista que años más tarde Hilbert expondrá en forma sistemática. En apoyo a lo dicho por Blumenthal, hoy en día contamos con una nota escrita por Hilbert alrededor de 1893 en la que habla de "las matemáticas sobre sistemas de mesas, pizarrones, etc. (Tisch, Tafel, etc.)".28 Por lo tanto, podemos señalar el año de 1891 como el momento en que Hilbert transitó hacia una nueva concepción de las matemáticas.
Podemos decir, entonces, que el papel de la geometría proyectiva en la génesis del formalismo de Hilbert fue doble. Primero, le sugirió que, en un sistema axiomático, los términos matemáticos no actúan semánticamente como constantes, sino como variables; es decir, como expresiones cuyo significado puede cambiar. Segundo, le sugirió que ninguna teoría matemática tiene una única lectura como si estuviera referida a un dominio particular de objetos; más bien, las teorías son sólo formas o moldes diseñados para alojar una gran variedad de materias que se van a tratar. Las siguientes son algunas expresiones que se han utilizado para referirse a esta situación: "recipientes vacíos" (Pasch), "teorías hipotético–deductivas desligadas de toda interpretación concreta posible" (Weyl), "sistemas de objetos no interpretados" (Curry).
6. Un nuevo modo de "hacer" matemáticas
Comparemos el punto de vista de Hilbert en su formalismo geométrico con la teoría kantiana del conocimiento matemático, poniendo especial atención en la teoría de esquemas. En la Crítica de la razón pura, Kant sostiene que es imposible pensar los conceptos geométricos sin darles un objeto: "No podemos pensar en una línea sin trazarla en el pensamiento, ni un círculo sin describirlo, como tampoco representar tres dimensiones del espacio sin construir tres líneas perpendiculares a partir del mismo punto" (B 154). Esta simple observación es un signo indicativo de que el peso de los esquemas geométricos en la epistemología matemática de Kant es superior a lo que aquí he dicho. En efecto, en las secciones precedentes me he referido a los esquemas como instancias que permiten construir en la representación objetos en conformidad con los conceptos. Pero lo dicho por Kant en el pasaje anterior les otorga una mayor importancia: sin esquemas es imposible pensar los conceptos geométricos en absoluto, pues esta actividad precisa una representación interna de ellos.
Lo anterior no constituye ningún problema para Kant, pues, para él, los conceptos geométricos nacen ligados a una forma de representación. Pero, desde la perspectiva que abre el principio de dualidad, este maridaje entre esquemas y conceptos se rompe: las "rectas" pueden ser lo que siempre fueron o lo que originalmente eran los "puntos". Ergo, los conceptos definidos por los axiomas son algo más que los esquemas, poseen una mayor generalidad, con lo que la teoría se descubre como algo más abstracto de lo previsto, como algo que ya no está indisolublemente ligado a un sistema fijo de objetos. De hecho, en la geometría de Hilbert, los conceptos se piensan sin esquemas, aunque hay circunstancias en las que esto no es lo más adecuado para el investigador. Esta disociación entre los conceptos y sus representaciones abrió una feraz posibilidad: pensar la teoría per se, es decir, convertirla en un objeto de estudio.
Esto último lo hace Hilbert en los Grundlagen der Geometrie. Lo que ahí investiga no son los objetos que dice Kant (ciertas entidades construibles en la intuición pura), sino la teoría misma. Digamos que la escudriña primariamente: a ella, no a sus interpretaciones.
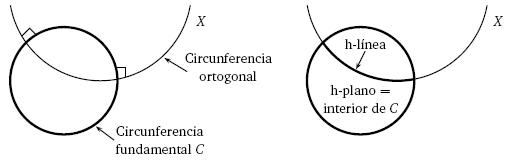
Esta manera de abordar la teoría señala el surgimiento de la teoría de modelos, donde el juego consiste en interpretar los términos y las relaciones fundamentales de distintas maneras.29 En particular, muchos modelos de la teoría geométrica y sus variantes resultan de enlazar sus conceptos con ciertos esquemas. Un notable ejemplo es el modelo de Poincaré para la geometría hiperbólica, en el que al concepto formal de línea se le asocia un esquema euclidiano como sigue. Sea C una circunferencia fija en el plano euclidiano. Si X es una circunferencia que corta ortogonalmente a C, entonces el arco de X que se halla en el interior de C es una h–línea (la "h" con el propósito de diferenciarla de las líneas euclidianas). Aquí, el caso es que contamos con un esquema (euclidiano) para producir circunferencias ortogonales a C, y es a través de este esquema que especificamos las h–líneas del modelo (para una geometría que no es euclidiana).
Este modo de tratar la teoría geométrica significó un desplazamiento en las investigaciones y tuvo importantes consecuencias. Para empezar, permitió una enorme economía de pensamiento: cada proposición demostrada era válida en todos los modelos de la teoría, donde ya no se la tenía que investigar. Y las ganancias no se redujeron a eso. La posibilidad de interpretar la teoría de distintas maneras permitió a Hilbert explorar su conexión con otros dominios de la matemática, con sorprendentes resultados. Por ejemplo, este nuevo tratamiento lo llevó a relacionar los teoremas de Desargues y Pascal con las propiedades de los anillos en el álgebra; v.gr, "Si el teorema de Desargues es válido en un dominio, entonces el álgebra de segmentos es un anillo quizá no conmutativo"; o bien, "El álgebra de segmentos basada en el teorema de Pascal es un anillo conmutativo." Estas investigaciones forman parte de los Grundlagen der Geometrie. Es más, el sentido del trabajo se puede invertir: en vez de ver qué clase de álgebra resulta a partir de un espacio, se pueden "construir" espacios a partir de las álgebras (v.gr., espacios afines a partir de anillos ternarios).
Es evidente que nada de lo anterior habría sido posible si la matemática se hubiera mantenido dentro de los estrechos límites impuestos por el concepto de objeto matemático ofrecido por Kant. Esto lo sabía Hilbert, para quien la investigación axiomática representó un factor de expansión y descubrimiento en esta disciplina.
Podemos decir, entonces, que para Hilbert la axiomática es algo más que un instrumento para ordenar las teorías; más bien, se trata de un medio para la investigación matemática. Esto se advierte claramente en los Grundlagen der Geometrie, donde "jugando" con los axiomas, Hilbert obtiene numerosos resultados: geometrías no arquimedianas, nuevos teoremas acerca de la continuidad, una nueva caracterización topológica del plano, una caracterización de la geometría euclidiana y de la geometría de Bolyai y Lobachevsky mediante grupos de desplazamientos, un análisis del papel de los teoremas de Desargues y de Pascal en la coordenatización del espacio, un estudio comparativo de las distintas geometrías entre sí, y una investigación de los medios requeridos para demostrar ciertos teoremas.
En este sentido, las investigaciones de Hilbert en torno a los fundamentos de la geometría significaron un triunfo para el método axiomático, al punto de que, en su opinión, éste estaba llamado a ocupar un lugar preeminente no sólo en la matemática, sino en la ciencia en general.30
7. Nociones ideales y dualidad
El principio de dualidad de la geometría proyectiva guarda un estrecho vínculo con el llamado "método de los elementos ideales". En su sentido original, este método consiste en introducir en una teoría elementos sin ninguna base intuitiva o constructiva. Su inclusión se justifica aduciendo que ésta es fructífera o tiene un efecto simplificador. En el caso que nos ocupa se trata de la incorporación de los puntos y la recta al infinito en el plano euclidiano, con lo que el espacio geométrico deviene en un espacio proyectivo.
A continuación se expondrán estas ideas con base en algunos conceptos pertenecientes a la teoría de conjuntos.31 Sea II el conjunto de puntos del plano euclidiano y Λ el correspondiente conjunto de rectas. Asociado a cada haz  de líneas paralelas de Λ, incorporamos un punto adicional
de líneas paralelas de Λ, incorporamos un punto adicional  , un "punto al infinito". Ahora extendemos cada línea
, un "punto al infinito". Ahora extendemos cada línea 
 a una "línea"
a una "línea"  como sigue:
como sigue:
Asimismo, introducimos una nueva "línea"  , la "línea al infinito", de la siguiente manera:
, la "línea al infinito", de la siguiente manera:
 es un haz de líneas paralelas de A}
es un haz de líneas paralelas de A}
Por último, extendemos el plano (afín) euclidiano a un plano proyectivo (ΙΙ', Λ') como sigue:
ΙΙ' = ΙΙ U { |
|  es un haz de líneas en Λ}; Λ' =
es un haz de líneas en Λ}; Λ' = 
¿Qué ventajas ofrece esta extensión del plano? Primero, que ya no hay excepciones: cualesquiera dos líneas se intersectan en al menos un punto; cuando éstas son euclidianamente paralelas entre sí, su intersección es el correspondiente punto al infinito  . Segundo, que entre las nociones de punto y línea aparece la simetría ya señalada: el principio de dualidad es válido para esta nueva geometría, pues el plano se ha convertido con esta extensión en un espacio proyectivo.
. Segundo, que entre las nociones de punto y línea aparece la simetría ya señalada: el principio de dualidad es válido para esta nueva geometría, pues el plano se ha convertido con esta extensión en un espacio proyectivo.
Las entidades recién introducidas son un claro ejemplo de lo que en matemáticas se denomina "elementos ideales": por una parte, se trata de objetos que no corresponden a nada en la intuición espacial; por la otra, son objetos cuya incorporación da unidad y simplicidad a la teoría, al evitar la existencia de casos especiales en los que ciertas propiedades no se cumplen.
La adopción del método de los elementos ideales conllevaba, entre otras cosas, sobrepasar los límites del constructivismo kantiano, y eso fue lo que hizo Hilbert con todas sus implicaciones: abandonó la teoría de esquemas. A fin de cuentas, no sólo se trataba de la geometría, sino del análisis matemático y, sobre todo, de la teoría de los números transfinitos de Cantor.
8. Un ejemplo de la utilidad del método
El uso de nociones ideales forma parte del desarrollo de las matemáticas. Hilbert ve en este método un factor de progreso al que no debemos renunciar, pues de su aplicación resultan nuevas matemáticas.32
Al respecto, podemos ilustrar la utilidad del método con un ejemplo. Se trata de la solución de un problema aritmético "simple" (es decir, relativo a números enteros) en el contexto de los números complejos.
Consideremos la sucesión de números enteros 1,1,0, –2, –4, –4,0, 8,16,16, 0, –32,...; la cual se genera a partir de la base doble f(0) = 1, f(1) = 1 con la regla recursiva
f(n + 2) = 2f(n + 1)–2f(n).33
Si bien esta regla indica un procedimiento para calcular cualquier elemento de la sucesión, tiene el inconveniente de que, para computar f(n), es preciso calcular todos los valores anteriores.34 Se trata, claro está, de un procedimiento ineficiente, por lo que nos preguntamos si habrá una fórmula que nos permita calcular directamente el valor de f(n) (esta cuestión forma parte de la teoría de las funciones generatrices, la cual se estudia en los cursos de combinatoria).35
La respuesta a la interrogante anterior (en su forma general, es decir, con relación a cualquier sucesión recursiva) es afirmativa. No obstante, a la fecha no se conoce otra manera de hallar la fórmula que adentrándose en el dominio del análisis complejo. En otras palabras: para resolver un problema relativo a números enteros, no conocemos otro camino que el de acudir a una extensión de la teoría mediante la adición de ciertas nociones ideales, como lo son los números irracionales y la unidad imaginaria i =  . Y si bien aquí no es el lugar para abordar los detalles técnicos de la solución general, al menos podemos traer a colación la fórmula buscada. Se trata de la fórmula
. Y si bien aquí no es el lugar para abordar los detalles técnicos de la solución general, al menos podemos traer a colación la fórmula buscada. Se trata de la fórmula

que explícitamente se sirve de los números complejos. Esto resulta sorprendente si consideramos que en un principio se trataba de una cuestión que sólo concernía a los números enteros. Y si bien la presencia de i se puede obviar en la fórmula anterior escribiendo (mediante ciertas transformaciones trigonométricas)

queda el hecho de que, para obtener esta última fórmula, se ha tenido que realizar una digresión por el dominio de los números complejos. Tenemos, por lo tanto, fuertes razones para justificar la extensión de los números enteros mediante la introducción de estos elementos ideales: la teoría gana en poder y generalidad.
Desde la perspectiva de los números enteros, el carácter ideal de los números complejos es evidente: se generan mediante la introducción de una unidad imaginaria i. ¿Tendrán algún tipo de existencia real tales objetos? Hilbert diría, con justa razón, que para hacer matemáticas no es necesario aclarar esta cuestión. Lo manifiesto es que tales números existen como un eficaz instrumento de la imaginación, y eso es todo lo que necesitamos saber. Su importancia radica en que, con ellos, la teoría aritmética se enriquece y se pueden resolver problemas para lo que quizá de otra manera no podríamos encontrar la solución. Y es por esto que los admitimos. Aquí cabe recordar lo que algún día le dijera Hilbert a Brouwer tras una charla de este último en el Instituto de Matemáticas de Gotinga: "Con sus métodos [constructivos], la mayor parte de los resultados de la matemática moderna tendrían que ser abandonados, y para mí la cosa más importante no es obtener menos resultados, sino más" (Reid 1970, p. 184).
Fue a partir de consideraciones de este tipo como Hilbert formuló un criterio sui generis de existencia matemática: en una teoría se puede admitir como existente todo aquello que no sea contradictorio con los supuestos básicos. Esto debilita la noción de existencia matemática, pues la reduce a la mera relatividad de la no contradicción, una cuestión lógica alejada del constructivismo kantiano. Esta noción se ajusta muy bien a la tendencia abstracta predominante en su momento. Al respecto, Hilbert establece los siguientes criterios como única condición de aceptación de nuevos elementos y nociones en una teoría: (a) que su anexión sea coherente con los contenidos de la teoría subyacente, y (b) que aporten eficiencia y simplicidad en la producción del conocimiento matemático. Con base en estos criterios se les debe juzgar, no por la particularidad de satisfacer ciertas normas constructivas.36
9. Nuevos objetos, nuevas matemáticas
¿En qué sentido es el conjunto de los números naturales un objeto matemático? Ciertamente, no lo es en el sentido de Kant: lo que para este último caracteriza a los objetos matemáticos es la posibilidad de su construcción en la intuición pura, y ninguna totalidad infinita se puede elaborar de esta manera.37 Antes bien, el conjunto de los números naturales es sólo una idea, es decir, un concepto racional del que no puede haber en la experiencia objeto adecuado alguno. Y la matemática del siglo XIX cobijó una multitud de entidades de esta naturaleza. Por ejemplo, el sistema de los números reales, los números transfinitos de Cantor, el conjunto (fractal) de Cantor, o curvas como la de Peano (que cubre un área rectangular) y la de Weierstrass, calificada por Hermite como "un mal deplorable". Frente a la negativa de algunos matemáticos a aceptar entidades de esta naturaleza —v.gr., Kronecker y Poincaré—, Hilbert optó por extender conceptualmente esta ciencia y defender la libertad que tiene el matemático de elegir sus métodos y objetos de estudio. Como ya lo hemos visto, esto lo llevó a sobrepasar el constructivismo kantiano, hasta admitir como objetos ciertas ideas. En otras palabras, Hilbert decidió generalizar el concepto de objeto en las matemáticas. Tal ampliación vino emparejada con lo que podemos denominar cuasi esquemas, es decir, procedimientos infinitos que se admiten como procedimientos idealmente realizables.38
Nada de lo anterior carecía de sustento; más bien, era la expresión filosófica de una creciente tendencia generada en el interior de la matemática.
Consideremos, por ejemplo, las cortaduras de Dedekind, cuya aparición en el siglo XIX significó la primera exposición formal del continuo numérico. Toda cortadura es un conjunto infinito de números racionales que representa a un número real. Estas entidades las podemos sumar y multiplicar, formando de esta manera un campo completo. Obviamente, estas operaciones sólo tienen lugar en el pensamiento, sin la posibilidad de contar en todos los casos con un esquema que permita producir un objeto. Aun así, esta elaboración teórica es la base del análisis matemático moderno, una pieza central en el conocimiento de la naturaleza a la que Hilbert no estaba dispuesto a renunciar. Y frente al rechazo del sistema de los números reales en virtud del carácter no constructivo de sus elementos, Hilbert decidió extender el concepto de "objeto matemático" hasta admitir ciertas ideas (elementos ideales en sus palabras). En conformidad, también decidió acoger y dar soporte a la generalización de la teoría kantiana de esquemas hasta incluir, como ya lo he señalado, procedimientos sólo realizables en un plano ideal, es decir, procedimientos que sólo tienen cabida en el pensamiento, nunca en la representación.
Un claro ejemplo de lo anterior es la prueba que ofrece Cantor de que los puntos de un cuadrado se pueden poner en correspondencia uno a uno con los puntos de uno de sus lados. Quien siga la demostración verá que el procedimiento de intercalación de fracciones continuadas infinitas es tan sólo el apunte de una posibilidad, la generalización de un procedimiento realizable cuando el número de dígitos es finito. Y frente a la imposibilidad real de llevar a cabo el "encaje" propuesto, Cantor simplemente supone consumado el proceso e imagina el resultado: otra fracción continuada.39 Surgen con ello las dudas en torno de la existencia de estos objetos: ¿en qué sentido podemos afirmar su existencia? La respuesta de Hilbert sería la siguiente: en el sentido de que son algo pensado sin incurrir por ello en contradicciones.
Obviamente, nada de lo que se "hace" en dominios como el de los números reales o la teoría cantoriana de conjuntos sería posible sin la correspondiente extensión del concepto de esquema a entidades no construibles.
Sin adentrarnos en esta cuestión, debemos notar que, hacia 1920, Hilbert concibió las nociones ideales como ideas regulativas en el sentido de Kant, y que con base en esta concepción fue que ideó su programa. Baste este comentario indicativo de que la epistemología de Hilbert se nutrió en todo momento con elementos tomados de la filosofía crítica. Y si bien, al referirse al origen de la geometría, adopta una perspectiva empirista, su visión general de las matemáticas se sustenta en muchas ideas tomadas de Kant.40 Esto es evidente en su segundo formalismo, donde preconiza el carácter a priori del conocimiento aritmético y se sirve de principios tomados de la Dialéctica trascendental a fin de dar cabida a la moderna teoría del infinito.41
10. Comentarios finales
En el prefacio del libro Anschauliche Geometrie,42 escrito en colaboración con S. Cohn–Vossen en 1921, Hilbert advierte:
En las matemáticas, como en cualquier otra disciplina científica, se hallan presentes dos tendencias. Por una parte, la tendencia hacia la abstracción, que busca cristalizar las relaciones lógicas inherentes al caudal de resultados estudiados tratando de unificar el material de manera sistemática y ordenada. Por la otra parte, la tendencia a la comprensión intuitiva, que nos alienta a significar de manera inmediata tales relaciones lógicas, subrayando su significado concreto.
En la geometría, la tendencia abstracta ha conducido a las magníficas teorías de la geometría algebraica, la geometría de Riemann y la topología; estas teorías se sirven ampliamente del razonamiento abstracto y del cálculo simbólico en el sentido del álgebra. No obstante, hoy en día sigue siendo tan cierto como siempre que la comprensión intuitiva desempeña un papel principal en este dominio. Tal intuición concreta es de gran valor no sólo para el investigador, sino para todo aquel que desee estudiar y apreciar los resultados de la geometría. (Hilbert 1952, p. iii)
Las palabras anteriores muestran un aspecto muy poco conocido del pensamiento de Hilbert. Para él, la formalización no es un objetivo final, sino una fase en el movimiento propio del pensamiento matemático. Desde su punto de vista, la matemática se desenvuelve en medio de una dialéctica entre lo formal y lo intuitivo, entre la forma y el contenido. El libro de cuyo prefacio he tomado el pasaje anterior es en sí una viva expresión de esta duplicidad, donde el lector podrá descubrir diversos aspectos visuales de la geometría proyectiva y diferencial, de la cinemática y la topología. Y si bien en este ensayo nos hemos concentrado casi en exclusiva en las ideas que tiene Hilbert acerca de las matemáticas puras, sería un error desestimar la perspectiva anterior. Hilbert no es el formalista radical que muchos autores presentan, ni un purista para quien las matemáticas se reducen a un juego formal con vacuos conceptos; más bien, ve en la formalización un instrumento para: i) elaborar un montaje conceptual con relación a una teoría, ii) generalizar las teorías y iii) investigar las teorías mismas y establecer vínculos entre distintas áreas de las matemáticas. En cuanto a la perspectiva general que nos ofrece Hilbert de la matemática pura, espero haber proyectado suficiente luz sobre su pensamiento como para clarificar su imagen: la de un pensador que no sólo nos legó una obra matemática vasta y profunda, sino una manera diferente de entender esta disciplina.43
En cuanto a Kant, espero haber contribuido a esclarecer su teoría del conocimiento matemático al mirarla bajo la luz de la teoría de esquemas. De hecho, la consideración del esquematismo kantiano nos permitió: (i) entender con mayor claridad la epistemología hilbertiana, aunque en este trabajo sólo hayamos hecho un esbozo parcial de la misma; (ii) examinar el pensamiento de Kant desde un ángulo que aclara la noción que sustenta de los objetos matemáticos; (iii) iluminar los cambios ocurridos en la matemática durante el siglo XIX; (iv) entender cómo se relacionan los conceptos y los objetos en la geometría clásica, y (v) entender la noción de objeto matemático que introduce Hilbert en la filosofía de las matemáticas. Al respecto, aquí sólo se consideró el esquematismo kantiano desde la perspectiva de la geometría clásica, sin tocar en absoluto su relación con la aritmética. Esto es así en virtud de que las primeras manifestaciones del formalismo de Hilbert se dieron en torno a los fundamentos de la geometría, tema central de este ensayo. De igual forma, no se consideró en plenitud la explicación que da Hilbert del conocimiento matemático en general, pues esta tarea la acomete justo en la segunda etapa de su formalismo, un tema que escapa a los propósitos de este ensayo. No obstante, con los elementos ofrecidos espero haber puesto en claro que el formalismo de Hilbert, antes que una negación de la epistemología kantiana, constituye una generalización necesaria de ella en adecuación a la matemática moderna.
BIBLIOGRAFÍA
Aspray, W. y P. Kitcher, 1988, History and Philosphy of Modern Mathematics, Minnesota Studies in the Philosophy of Science, University of Minnesota Press, Minneápolis. [ Links ]
Benacerraff, P., y H. Putnam (comps.), 1983, Philosophy of Mathematics, Selected Readings, Cambridge University Press, Cambridge, Mass. [ Links ]
Bennett, M.K., 1995, Affine and Projective Geometry, John Wiley and Sons, Nueva York. [ Links ]
Blumenthal, O., 1935, "Lebensgeschichte", en Hilbert 1935, pp. 388–429. [ Links ]
Brouwer, L.E.J., 1948, "Consciousness, Philosophy, and Mathematics", en Benacerraf y Putnam 1983, pp. 90–96. [ Links ]
Brouwer, L.E.J., 1912, "Intuitionism and Formalism", trad. Arnold Dresden, en Benacerraf y Putnam, 1983, pp. 77–89. [ Links ]
Burris, S., 2003, "Gauss and Non–Euclidean Geometry" [en línea], disponible en <http://www.math.uwaterloo.ca/~snburris/htdocs/noneucl.pdf>. [ Links ]
Corry, L., 2002, "David Hilbert y su filosofía empiricista de la geometría", Boletín de la Asociación Matemática Venezolana, 2002, vol. 9, no. 1, pp. 27– 44; también disponible en línea en: <http://www.emis.de/journals/BAMV/conten/vol9/corry.pdf>. [ Links ]
Dauben, J.W., 1979, Georg Cantor, Harvard University Press, Cambridge, Mass. [ Links ]
Dedekind, R., 1963, Essays on the Theory of Numbers, Dover Publications, New Cork. [ Links ]
Detlefsen, M., 1993, "Hilbert's Work on the Foundations of Geometry in Relation to his Work on the Foundations of Arithmetic", Acta Analytica, vol. 8, no. 11, pp. 27–39. [ Links ]
Dummett, M., 1977, Elements of Intuitionism, Oxford University Press, Londres. [ Links ]
Euclides, 1992, Elementos de geometría, trad. Juan David García Bacca, Universidad Nacional Autónoma de México, México. [ Links ]
Eves, H., 1976, An Introduction to the History of Mathematics, Holt, Rinehart and Winston, Nueva York. [ Links ]
Ewald, W.B. (comp.), 1996, From Kant to Hilbert: A Source Book in the Foundations of Mathematics, 2 vols., Clarendon Press, Oxford. [ Links ]
Frege, G., 1980, Philosophical and Mathematical Correspondence, trad. Hans Kaal, ed. Gottfried Gabriel et al., The University of Chicago Press, Chicago. [ Links ]
––––––––––, 1972, Conceptografía. Los fundamentos de la aritmética y otros estudios filosóficos, trad. Hugo Padilla, Instituto de Investigaciones Filosóficas–UNAM, México. [ Links ]
––––––––––, 1874, "Methods of Calculation Based on an Extension of the Concept of Quantity", Disertación para la Venia Docendi [Habilitationsschrift] en la Escuela de Filosofía de Jena, trad. Hans Kaal, en McGuinness 1984, pp. 56– 92. [ Links ]
Friedman, M., 1992, Kant and the Exact Sciences, Harvard University Press, Cambridge, Mass. [ Links ]
––––––––––, 1985, "Kant's Theory of Geometry", en Posy 1992, pp. 177–220. [ Links ]
Graham, R., D. Knuth y O. Patashkin, 1989, Concrete Mathematics, Addison–Wesley, Reading, Massachusetts. [ Links ]
Hallett, Michael y Ulrich Majer (comps.), 2004, David Hilbert's Lectures on the Foundations of Geometry 1891–1902, Springer, Berlín/Heidelberg. [ Links ]
Harper, W., 1984, "Kant on Space, Empirical Realism, and the Foundations of Geometry", en Posy 1992, pp. 257–292. [ Links ]
Hartshorne, R., 2000, Geometry: Euclid and Beyond, Springer, Nueva York/Berlín/Heidelberg. [ Links ]
Hayashi, S., 2007, David Hilbert's Mathematical Notebooks [en línea], disponible en <http://www.shayashi.jp/HistorySociology/HistoryOfFOM/Hilbert NotebookProjectHomepage/index.html>, modificada por última vez el 8 de febrero de 2007. [ Links ]
Hersh, R., 1979, "Some Proposals for Reviving the Philosophy of Mathematics", Advances in Mathematics, vol. 31, pp. 31–50; reimpreso en Tymoczko 1986, pp. 9–28. [ Links ]
Hilbert, D., 1993, Fundamentos de las matemáticas (recopilación), Facultad de Ciencias–UNAM (Colección MATHEMA). [ Links ]
––––––––––, 1935, Gesammelte Abhandlungen, Vol. III, Julius Springer, Berlín. [ Links ]
––––––––––, 1931, "Die Grundlegung der elementaren Zhalenleher", Mathematische Annalen, vol. 104, 1931, pp. 485–492. [Versión en castellano: "La funda–mentación de la teoría elemental de números", trad. Luis Felipe Segura, en Hilbert 1993, pp. 123–135.] [ Links ]
––––––––––, 1930, "Naturerkennen und Logik", Die Naturwissenschaften, vol. 18, pp. 953–963. [Versión en inglés: "Logic and the Knowledge of Nature", trad. William B. Ewald, en Ewald 1996, pp. 1157–1165.] [ Links ]
––––––––––, 1926, "Über das Unendliche", Mathematische Annalen, vol. 95, 1926, pp. 161–190. [Versión en castellano: "Acerca del infinito", trad. Luis Felipe Segura, en Hilbert 1993, pp. 83–121.] [ Links ]
––––––––––, 1917, "Axiomatisches Denken", en Hilbert 1935, vol. 3, pp. 146–156. [Versión en castellano: "El pensamiento axiomático", trad. Luis Felipe Segura, en Hilbert 1993, pp. 23–35.] [ Links ]
––––––––––, 1900, "Mathematische Probleme. Vortrag, gehalten auf dem internatio–nalen Mathematiker Kongress zu Paris, 1900", Archiv der Mathematik und Physik, 3a. serie, 1, 1901, pp. 44–63 y 213–237. [Versión en inglés: "Mathematical Problems", en Proceedings of Symposia in Pure Mathematics, vol. 28, American Mathematical Society, 1976, pp. 1–34, trad. Mary Winston New–son.] [ Links ]
––––––––––, 1899, Grundlagen der Geometrie, Teubner, Leipzig/Berlín. [Versión en inglés: Foundations of Geometry, trad. E.J. Townsend (con algunas adiciones hechas por Hilbert a la edición francesa de 1899), Open Court, La Salle, Illinois, 1962.] [ Links ]
Hilbert, D. y P. Bernays, 1934, Grundlagen der Mathematik I, Springer, Berlín. [ Links ]
Hilbert, D. y S. Cohn–Vossen, 1952, Geometry and the Imagination, trad. P. Ne–menyi, Chelsea, Nueva York. [ Links ]
Hintikka, J., 1967, "Kant on the Mathematical Method", en Posy 1992, pp. 21– 42. [ Links ]
Jørgensen, K.F., 2005, "Kant's Schematism and the Foundations of Mathematics", tesis doctoral, Universidad de Rosklide, disponible en línea en <http:// akira.ruc.dk/~frovin/construction.pdf>. [ Links ]
Kant, I., 1997, Crítica de la razón pura, trad. Pedro Rivas, Alfaguara, Madrid. [ Links ]
Kitcher, P., 1975, "Kant and the Foundations of Mathematics", en Posy 1992, pp. 109–131. [ Links ]
Kline, M., 1994, El pensamiento matemático de la antigüedad a nuestros días, Alianza, Madrid, 3 vols. (Alianza Universidad, 715, 724 y 729). [ Links ]
Mancosu, P., 1998, From Brouwer to Hilbert, Oxford University Press, Nueva York/Oxford. [ Links ]
Mancosu, P., K. Frovin Jørgensen y S.A. Pedersen (comps.), 2005, Visualization, Explanation and Resoning Styles in Mathematics, Springer Verlag, Dordrecht (Synthese Library, 327). [ Links ]
McGuinness, B., 1984, Collected Papers on Mathematics, Logic and Philosophy, Blackwell, Oxford. [ Links ]
O'Connor, J.J. y E.F. Robertson, "Moritz Pasch", en The MacTutor History of Mathematics Archive [en línea], School of Mathematics and Statistics–University of St. Andrews, Escocia, julio de 2009, disponible en <http://www.history.mcs.st–andrews.ac.uk/Biographies/Pasch.html>. [ Links ]
Parsons, Ch., 1969, "Kant's Philosophy of Arithmetic", en Posy 1992, pp. 43–79. [ Links ]
Poncelet, J.–V., 1995, Traité des propriétés projectives de figures, Editions Jacques Gabay, París. [ Links ]
Posy, C. (comp.), 1992, Kant's Philosophy of Mathematics. Modern Essays, Kluwer Academic Publishers, Dordrecht/Boston/Londres. [ Links ]
Reid, C., 1970, Hilbert, Springer Verlag, Berlín/Heildelberg. [ Links ]
Sestier, A. (comp.), 1981, Documentos históricos de la matemática, Editorial del Valle de México, México. [ Links ]
Shabel, L., 2003, Mathematics in Kant's Critical Philosophy, Routledge, Londres. [ Links ]
Torres, C., 2005, "Kant visto desde las matemáticas", Revista Digital Universitaria, vol. 6, no. 1, 2005, disponible en <http://www.revista.unam.mx/>. [ Links ]
––––––––––, 1999, "Hilbert, Kant y el fundamento de las matemáticas", Theoria, Revista del Colegio de Filosofía (Facultad de Filosofía y Letras–UNAM), nos. 8– 9, diciembre de 1999, pp. 111–129. [ Links ]
––––––––––, 1995, "The Philosophy and the Program of Hilbert", Mexican Studies in the History and Philosophy of Science, vol. 172, pp. 151–172, Kluwer Academic Press, Dordrecht. [ Links ]
Tuller, A., 1967, A Modern Introduction to Geometries, Van Nostrand, Nueva York. [ Links ]
Tymoczko, T. (comp.), 1986, New Directions in the Philosophy of Mathematics, Birkhäuser, Boston/Basel/Stuttgart. [ Links ]
Weyl, H., 1949, "David Hilbert, 1862–1943", Obituary Notices of Fellows of the Royal Society, vol. 4, 1942–1944, Londres. [ Links ]
––––––––––, 1965, Filosofía de las matemáticas y de la ciencia natural, trad. Carlos Ímaz, Universidad Nacional Autónoma de México, México. [ Links ]
Weyl, H., 1944, "David Hilbert and His Mathematical Work", Bulletin of the American Mathematical Society, vol. 50, pp. 612–654. [ Links ]
Young, J.M., 1984, "Construction, Schematism and Imagination", en Posy 1992, pp. 159–175. [ Links ]
Ziwet, A., 1892, "The Annual Meeting of German Mathematicians", Bulletin of the New York Mathematical Society, vol. 1, no. 4, pp. 96–101; disponible en línea en: <http://projecteuclid.org/DPubS?service=UI & version=1.0 & verb =Display & handle=euclid.bams/1183407270>. [ Links ]
1 A esta etapa pertenece la presentación axiomática de la geometría que hace Hilbert en los Grundlagen der Geometrie de 1899, la cual significó un giro en las investigaciones. No todas las axiomatizaciones de la geometría son de esta índole; por ejemplo, la de Euclides no lo es. Hilbert y Bernays califican las teorías axiomáticas como la de Euclides con el adjetivo "inhaltliche" ("material", en el sentido de que poseen un contenido) para indicar que éstas se elaboran considerando las propiedades y relaciones de un sistema de objetos prestablecidos (véase Hilbert y Bernays 1934, p. 2). Como veremos, tal interpretación de los términos de la teoría suele desempeñar un papel en las pruebas. Esto se hace patente no sólo en el uso de diagramas, sino en las definiciones, donde en ocasiones Euclides dirige nuestra atención a ideas que jamás utiliza en las demostraciones; v.gr., "Punto es aquello que ya no tiene partes (D.I.1)".
2 Al respecto, espero aportar suficientes elementos como para desterrar la pobre imagen que algunos autores ofrecen del formalismo de Hilbert, al describirlo como una corriente según la cual la matemática es una colección de sistemas formales en que los términos son meros símbolos y los enunciados son fórmulas que nada significan (véanse, por ejemplo, Eves 1976, p. 481; Kline 1994, pp. 1593–1594, y Hersh 1979, autores éstos que presentan una pálida imagen de esta corriente). Asimismo, quiero combatir la idea que algunos autores como Reuben Hersh, Thomas Tymoczko, William Aspray y Philip Kitcher parecen sostener, según la cual el objetivo central de las investigaciones en torno a los fundamentos de las matemáticas de Hilbert (al igual que las de Frege, Russell y Brouwer) era responder a ciertas interrogantes, como ¿en qué radica la certeza del conocimiento matemático? Así, por ejemplo, el programa de Hilbert se ha interpretado como la búsqueda de una prueba finitista de consistencia para las matemáticas clásicas a través de la formalización (véanse Hersh 1979, y las introducciones de Aspray y Kitcher 1988 y Tymoczko 1986). Por el contrario, yo creo que el interés de Hilbert iba más allá de tales preocupaciones —las cuales sí se hallaban presentes— hasta abarcar la naturaleza misma de las matemáticas y el desarrollo de nuevas herramientas de trabajo e investigación para esta disciplina.
3 Esta prueba aparece ampliamente comentada en Friedman 1992, y un caso similar en Torres 2005.
4 En palabras de Kant, "construir un concepto" consiste en "presentar la intuición a priori que le corresponde [al concepto]". En A 713 y B 741 da claras indicaciones de cómo se debe entender esta caracterización.
5 Kant podría presentar el siguiente argumento como justificación de la validez de la proposición: "Si bien la construcción se realiza en la intuición sensible, en la investigación no se toma en cuenta ningún rasgo empírico del objeto así construido (como, por ejemplo, la longitud de sus lados o la medida de sus ángulos); y si bien el diagrama es empírico (un objeto sensible), en la demostración sólo se considera la acción de construir sus elementos (un triángulo, una recta, etc.) sin hacer uso de ninguna particularidad propia de los objetos específicos que resultan de la construcción. Por tanto, las propiedades establecidas son válidas para todas las figuras que se pueden obtener de esa manera." Como veremos, Euclides suele contravenir sutilmente esta exigencia en muchas demostraciones.
6 En la proposición I.32, cuando Euclides habla de trazar por el punto C la recta CE paralela a la AB, se refiere al trazo de lo que hoy denominamos el segmento CE. Es por esto que Euclides debería indicar en qué sentido se ha de realizar la construcción, pues hay dos sentidos posibles y sólo uno de ellos conduce al fin propuesto. Obviamente, si la recta utilizada fuera de suyo ilimitada en ambas direcciones, nuestra crítica se vendría abajo; no obstante, lo hecho por Euclides no corresponde a lo anterior, pues lo que él hace es trazar una línea de un punto C a otro punto E (los extremos de la línea, según reza la definición DI.3). Aquí, Euclides se conduce con estricto apego al espíritu griego, según el cual lo positivo es el estado de finitud; así, considerar una línea recta infinita y sin extremos sería tanto como considerar un objeto en estado de imperfección.
7 Esta observación de Kant alude a la actividad de un geómetra anterior al siglo XIX, y sólo es aplicable en forma limitada a la matemática contemporánea.
8 Es más, la sinteticidad también se debe a que muchas propiedades de los objetos geométricos resultan de su construcción, donde se tornan evidentes, sin que las mismas resulten de las definiciones, axiomas y postulados. La construcción es, en este sentido, indispensable.
9 Conforme a lo que afirma Kant, entre un concepto y las cosas particulares que se subsumen bajo él se halla una instancia mediadora, un término que hace posible la aplicación del primero a las segundas. Esta instancia tiene un pie de cada lado; por una parte, es una representación pura (libre de todo elemento empírico); por la otra, es intelectual y sensible a la vez (Véase, CRP, A 138/B 177). Kant denomina esquemas trascendentales a tales representaciones. En cada caso se trata de la representación de un procedimiento general por el cual la imaginación ofrece su imagen a un concepto. Kant diría al respecto que, sin esquemas, los conceptos son vacíos, pues no les podemos dar ningún objeto.
10 Históricamente, la curva de Weierstrass es el primer fractal conocido. Lo notable en este caso es que disponemos de una fórmula para ella:
 , donde 0 < a < 1, b es un entero impar y ab >
, donde 0 < a < 1, b es un entero impar y ab >
11 Aquí podemos anticipar la respuesta de Hilbert, quien en una nota escrita hacia 1893 dice lo siguiente: "Cualquier cosa que sea objeto del pensamiento es por lo mismo objeto de las matemáticas. La matemática no es el arte de la computación, sino el arte de la no computación" [Alles was Gegenstand des Denkens ist, ist daher Gegenstand der Mathematik. Die Mathematik ist nicht die Kunst des Rechnens, sondern die Kunst des Nichtrechnens]. Al respecto, véase Hayashi 2007.
12 Citado en "Nineteenth Century Geometry", Stanford Ecyclopedia of Philosophy, disponible en línea en: <http://plato.stanford.edu>.
13 Tomado de Burris 2003, p. 8.
14 Comparemos el axioma 1 del grupo I de Hilbert con el primer postulado de Euclides:
Axioma I.1. Dos puntos distintos A y B siempre determinan por completo una línea recta a. Escribimos AB = a o BA = a.
Este axioma no trata ni con construcciones ni con esquemas de ninguna clase; no dice, como el de Euclides, "Trazar una línea recta desde un punto cualquiera a otro punto cualquiera". Más bien, establece una relación de determinación entre ciertos objetos (la de una "recta" que depende de dos "puntos"), los cuales, por lo demás, permanecen indefinidos.
15 Véase Hilbert 1899, § 1.
16 Hilbert 1930.
17 Hilbert 1930; cita tomada de Ewald 1996, p. 1162. En cuanto a las "relaciones de posición", éstas sólo se plantean como posibilidades, debiendo ser confirmadas o refutadas en la experiencia. V.gr., el que haya cuerpos rígidos móviles y cuáles sean sus relaciones de posición es una cuestión de experiencia, no algo determinado a priori.
18 En efecto, para determinar la corrección o no de la teoría geométrica respecto del espacio físico debemos recurrir a la experiencia, donde se le ha de poner a prueba junto con ciertas convenciones; por ejemplo, que en el espacio físico las "líneas rectas" son las trayectorias de los rayos de luz. Esa cuestión ya no compete a las matemáticas.
19 Obviamente, la noción dual de "puntos en una recta" es la noción de "líneas concurrentes". Es importante notar que cada enunciado geométrico tiene la misma forma lógica que su dual.
20 Otra famosa pareja de teoremas duales es la formada por el teorema del hexágono de Pascal y el teorema de Brianchón:
TEOREMA DEL HEXÁGONO DE PASCAL (1640): Si los vértices de un hexágono se hallan sobre una cónica, entonces los puntos de intersección de los lados opuestos están alineados.
TEOREMA DE BRIANCHÓN (1806): Si los vértices de un hexágono se hallan sobre una cónica, entonces las líneas que pasan por los vértices opuestos son concurrentes.
Un caso de teorema autodual es el siguiente:
TEOREMA DE DESARGUES (1636): Dos triángulos están en perspectiva desde un punto, si y sólo si están en perspectiva desde una línea.
21 Véase al respecto la nota biográfica sobre Moritz Pasch de J.J. O'Connor y E.F. Robertson que aparece en The MacTutor History of Mathematics Archive: <http://www.history.mcs.st–andrews.ac.uk/Biographies/Pasch.html>.
22 Esto no fue lo que hicimos al trazar las figuras 1 y 2. En ambos casos las palabras "punto" y "línea" las utilizamos de la misma manera. Lo diferente eran las proposiciones ilustradas (la primera era el teorema de Pappus, la segunda el teorema dual de Pappus). No obstante, la dualidad se puede entender también como la posibilidad de intercambiar directamente la interpretación de esto términos sin desvirtuar con ello la validez de los teoremas. Por lo tanto, la figura 2 es también una ilustración del teorema de Pappus si aceptamos llamar "línea" a lo que antes llamábamos "punto", y viceversa.
23 Esta manera de entender los enunciados teóricos es el sostén de la teoría de modelos, de la que los Grundlagen der Geometrie son un exponente histórico.
24 Con relación a la geometría proyectiva, la señalada transformación reversible no es otra cosa que el esquema de sustituciones que se ha utilizado en el caso del teorema de Pappus y su dual: punto  línea, puntos alineados
línea, puntos alineados  líneas concurrentes, etcétera.
líneas concurrentes, etcétera.
25 Un reporte de la conferencia de Wiener, quien fuera profesor de la Universidad de Halle, se encuentra en Ziwet 1892, p. 98.
26 En Hallett y Majer 2004 se hallan las notas de dos de estos cursos, uno sobre geometría proyectiva y otro sobre los fundamentos de la geometría, impartidos en 1891 y 1894. En ellos, Hilbert expone muchas piezas de su filosofía como, por ejemplo, la idea de que la teoría no es sino un esquema de conceptos. En cuanto a los Grundlagen, entre las cuestiones planteadas por Wiener y que Hilbert recoje podemos mencionar la relación entre los teoremas de Desargues y Pappus (o Pascal), y la de éstos con la continuidad y otras nociones. Éste es, de hecho, uno de los temas centrales del libro, cuyo desarrollo ocupa los capítulos V y VI. Es más, quien lea el reporte de la conferencia de Wiener se dará cuenta de que muchos resultados de los Grundlagen están inspirados en las interrogantes de Wiener.
27 "Man muβ jederzeit an Stelle von 'Punkte, Geraden, Ebenen' 'Tische, Stühle, Bierseidel' sagen können." Otto Blumenthal fue el primer estudiante de doctorado de Hilbert y uno de los asistentes a la reunión de la Sociedad Matemática Alemana. El lugar donde narra lo anterior es en su "Lebensgeschichte" [Historia de la vida (de Hilbert)], reproducido en Hilbert 1935, pp. 388–429. Al respecto, quiero agradecer a uno de los árbitros anónimos de este trabajo el haberme proporcionado el lugar exacto de la cita.
28 Hayashi 2007, sección 2.1.7. Se trata de un archivo publicado en Internet por Susumu Hayashi y colaboradores en el que dan a conocer algunos fragmentos de los cuadernos de notas de Hilbert, escritos entre 1888 y 1910.
29 Grosso modo, un modelo es una interpretación de los términos primitivos de una teoría que hace verdaderos a los axiomas.
30 Véase, al respecto, Hilbert 1917.
31 Véase, al respecto, Bennett 1995, p. 43.
32 Entre los ejemplos que Hilbert menciona se hallan los siguientes:
1. La introducción de la unidad imaginaria i =  que da lugar al teorema fundamental del álgebra: Todo polinomio de grado n con coeficientes reales tiene n raíces.
que da lugar al teorema fundamental del álgebra: Todo polinomio de grado n con coeficientes reales tiene n raíces.
2. La adición de los puntos y la recta al infinito al plano euclidiano para completar un plano proyectivo.
3. La utilización plena de la lógica clásica en el análisis matemático y la teoría de conjuntos, donde el principio del tercero excluido se presenta como una noción ideal. Este principio sirve como base para las pruebas de existencia por reducción al absurdo que él mismo impulsara.
4. El axioma de elección en la teoría de conjuntos, con el caudal de resultados que se prueban con base en él.
Otros ejemplos que podemos mencionar son la introducción de las cortaduras de Dedekind, la generalización cantoriana del concepto de número mediante la introducción de los números transfinitos, el lema de Zorn, la recursión transfinita y más recientemente, las curvas fractales.
33 El ejemplo más famoso de esta clase de sucesiones recursivas es, sin lugar a dudas, la sucesión de Fibonacci: f(0) = 1,f(1) = 1 y f(n + 2) = f(n + 1) + f(n).
34 Por ejemplo, para computar f(7) es necesario conocer los valores f(6) y f(5), lo cual exige a su vez conocer los valores f(4) y f(3), etc.
35 En Graham, Knuth y Patashkin 1989 hay una clara exposición de esta teoría.
36 Fue en el siglo XX cuando Hilbert emprendió abiertamente la defensa del método de los elementos ideales. A ello corresponde el referido programa de los años veinte y la etapa aritmética de su formalismo, temas de los que me ocuparé en otro trabajo. No obstante, algunas ideas básicas ya las tenía en mente al escribir los Grundlagen der Geometrie, y se hallan presentes en su concepto del método axiomático.
37 Hagamos algunas precisiones con relación a la noción de objeto matemático en la epistemología de Kant. En su opinión, todo objeto matemático ha de satisfacer dos condiciones: primero, ha de ser construible en el espacio y en el tiempo; segundo, se le ha de entender como una unidad, i.e., ha de haber un concepto que una sus partes en una totalidad. Es aquí donde entran en escena los esquemas: los conceptos sólo se puede relacionar con los objetos a través de ellos. Estos criterios están claramente establecidos en la Estética trascendental (v.gr., en A 19/B 33), en la Analítica trascendental (v.gr., en A 137–47/B 176–87) y en la Lógica trascendental (v.gr., en A 92–3/B 125).
38 Repitamos las palabras de Hilbert ya citadas en la nota al pie 11, supra: "Cualquier cosa que sea objeto del pensamiento es por lo mismo objeto de las matemáticas. La matemática no es el arte de la computación, sino el arte de la no computación."
39 Quizá el caso más famoso de desdén al esquematismo kantiano lo constituye el axioma de elección, introducido por Zermelo en 1908.
40 En la sección 4 ya se han citado algunos pasajes en los que Hilbert otorga un origen empírico a la geometría (segunda cita in extenso y párrafo que le sigue). Quizá lo siguiente ayude a aclarar su postura al respecto. Las siguientes citas datan de 1894: "el origen [de los axiomas de la geometría] se halla en la experiencia. Los axiomas son, como Hertz diría, imágenes o símbolos en nuestro espíritu, de manera que las consecuencias de las imágenes nuevamente son imágenes de las consecuencias, es decir, aquello que deducimos lógicamente de las imágenes vuelve a ser cierto en la naturaleza" (Hallett y Majer 2004, p. 74). Un poco antes afirma: "Los axiomas corresponden a observaciones [...]. Estos simples hechos de la experiencia son de tan frecuente observación [...], y por lo tanto tan conocidos, que el físico no necesita comprobarlos en el laboratorio."
41 Este tema será tratado en otro lugar, en el contexto del formalismo aritmético desarrollado por Hilbert en la década 1920–1930 en íntima conexión con el finitismo y el programa.
42 Hilbert y Cohn–Vossen 1952 es una traducción de este libro al inglés.
43 Obviamente, en un espacio tan reducido no es posible abordar múltiples aspectos de suma importancia en el pensamiento de Hilbert. En particular, no se tocó el lugar que le otorga a las matemáticas en el contexto de las otras disciplinas científicas, siendo que para él las matemáticas obedecen también al interés de ser un instrumento esencial en el conocimiento de la naturaleza.














