1. Introduction
Empirical and anecdotal evidence supports the idea that unionization and imperfectly competitive markets go hand in hand. As Booth (1995) recognizes, “it appears to be an empirical regularity that imperfections in the labor market are correlated with imperfections in the product market”. Moreover, the presence of unionized labor markets, the related bargaining institutions, as well as the degree of competition play a vital role in determining the organizational shape of an industry. These subjects are relevant for economists, policymakers and antitrust authorities, in particular for the proper design and implementation of labor, industrial and regulatory policies.
In this framework, the issue of the union(s)-firm(s) bargaining scope is notably relevant. The most commonly detected bargaining models in the real world are, on the one hand, the right-to-manage (RTM) model (e.g.Nickell and Andrews, 1983) in which unionized labor and firms negotiate only wages; and, on the other hand, the efficient bargaining (EB) model (e.g.McDonald and Solow, 1981) in which the firms and unions bargain simultaneously over wages and employment levels.
The analysis of the more profitable bargaining agenda in unionized industries has been first analyzed by Dowrick (1990). As reported in the International Handbook of Trade Unions, that author finds “that profits under the right-to-manage (RTM) model exceed those under efficient bargaining (EB)” (Naylor, 2003, p. 59). Moreover, this result with regard to the RTM agenda is valid irrespective of whether simultaneous or sequential EB (SEB) are considered: “under unionised monopoly, the firm will prefer to keep employment off the bargaining agenda, whatever the degree of union influence over employment. In other words, the right-to-manage outcome generates higher profits than either the efficient or sequential bargains, for a given level of union influence over the wage” (Naylor, 2003, p. 61).
At the current stage, these findings represent the benchmark of the literature on the negotiation agenda between firms and unions at decentralized level.1 However, it should be noted that those results can sharply change once a more robust analysis conducted in terms of a “game-theoretic approach” is applied. For instance, using this “game-theoretic approach”, Fanti and Buccella (2017) have extended the analysis of the Handbook as regards the choice of the agenda introducing the SEB model (Manning, 1987a, 1987b). Nonetheless, those authors have restricted the study 1) to the case of quantity competition and 2) without considering a game on the timing of the negotiations.
The question is not whether RTM or EB are more profitable for firms when exogenously compared between them (as made by most of the established literature) as much as whether the strategic interaction between firms leads to a robust equilibrium in a “game-theoretic” sense. This paper contributes to shed lights on this issue as regards the bargaining agenda, being the first paper to look at the possibility that the timing of the agenda’s moves influences the occurrence (if any) of an equilibrium agenda.
In fact, the received economic literature has not dealt with the natural possibility that, in the presence of the mixed case in which one firm selects EB and the other RTM, the EB arrangement leads also the timing of the negotiations to be a decisional variable at the discretion of firms. More precisely, the EB firm in the mixed case can be either Stackelberg wage follower or Stackelberg output leader. To date, the timing of the game of a EB firm against a rival RTM has been always assumed as exogenously given. If the timing of the game is endogenous, the game passes from a 2x2 (two choice variables for each player) to a 3x3 structure of the payoff matrix (three choice variables for each player). Therefore, making use of this correct game-theoretic approach in the presence of a conjectural variation (CV) model2, the current paper studies how the interaction between alternative bargaining arrangements and the different degrees of market competition affect the firms’ endogenous preferences over the negotiation agenda in a duopoly industry. Thus, the work aims to answer the following research question. If firms can strategically select the bargaining scope3, what is the effect of a not univocal specification of the game rules in the case of EB on the endogenous selection of the agenda?
The change from a 2x2 to a 3x3 structure with the endogenous choice of the timing strongly modifies the solutions of the game. New and, somehow, disquieting results emerge. In fact, a first striking result is that, for a large set of the parameters’ space (union bargaining power and conjectural parameter), no equilibria arise in pure strategies. On the other hand, RTM emerges as the unique equilibrium agenda first in the presence of high competition and lower unions’ bargaining power and then, as the unions’ strength increases, for a wider range of the conjectural parameter. Moreover, multiple, asymmetric equilibria emerge in a small area of the parameters’ space characterized by concurrent collusive firms’ behavior and significantly high bargaining power. Finally, in contrast to the received literature, the EB agenda disappears as sub-game perfect equilibrium. Of course, the presence of a wide area in which no agenda emerges in equilibrium under pure strategies may call for the investigation of mixed strategies. However, given that the focus of this paper is on the existence of a "rational" choice of the agenda in a deterministic context, it is beyond the scope of the present work.
The fact that, in the real-world industries, different agendas and timings are often present without a precise motivation supporting such choices may be coherent with our finding of the non-existence of a "rational" choice in a deterministic context for an ample parametric set. Furthermore, our finding may have a testable implication: for instance, in industries characterized by a competition according to the Cournot conjecture (i.e. in our model, a value of the CV parameter about zero) if unions are relatively “weak” it should be more often detected a multiplicity of agendas, while if unions are relatively “strong” (for instance, it suffices a near-parity in the bargaining power) it should be more often detected the presence of the RTM agenda. Thus, these findings seem to suggest that authorities and policymakers need to intervene in labor market regulations to fix the specification of the timing in negotiations to guarantee the existence of a “common bargaining practice” in the industry.
The paper contributes to a line of research in the literature dealing with the analysis of the bargaining scope and selection of union-oligopoly negotiation agendas, and represented by Dobson (1997), Bughin (1999), Petrakis and Vlassis (2000), Vannini and Bughin (2000), Kraft (2006), Buccella (2011) and, more recently, Fanti (2014, 2015), Buccella and Fanti (2015) and Fanti and Buccella (2018).
The rest of the paper is organized as follows. Section 2 reviews the related literature. Section 3 develops the model and derives the results. Section 4 closes with a brief discussion.
2. Literature review
Petrakis and Vlassis (2000) focus on the possibility of an agreement between firms and unions on the bargaining agenda. The rules of the game are peculiar. At stage 1 each firm/union unit simultaneously decides on the bargaining agenda which can be: 1) EB, if there is a consensus by the firm and its union, or 2) RTM, if the firm poses a veto on the inclusion of employment in the agenda. At stage 2, the EB firm implements its employment level while the RTM firm chooses its employment taking into account the rival’s choices. Given these hypotheses, the main results are that universal (all firms adopting) EB can never arise as the industry bargaining practice in pure strategy equilibrium; on the other hand, either RTM is universally selected only if the unions’ bargaining power is adequately large, or a mixed duopoly equilibrium (one firm selects RTM, the rival EB) if their power is sufficiently low. In the same vein, Kraft (2006) assumes that the EB firm is Stackelberg wage follower. However, in contrast to Petrakis and Vlassis (2000), that author draws the conclusion that EB is the dominant strategy for firms but firms are cast into a “prisoner’s dilemma” situation concerning profits.
Under the assumption that the EB firm in the mixed case is Stackelberg wage follower, Bughin (1999) considers the issue of the strategic selection of the bargaining agenda first in a given duopoly, and then in a monopoly with the threat of entry. Using a CV model, Buccella (2011) revisits Bughin’s (1999) and derives the following sub-game perfect Nash equilibria (SPNE) agendas: No matter the degree of competitiveness of the industry, the RTM model is the SPNE 1) in a given duopoly with committed bargaining; and 2) in a given duopoly with flexible bargaining, also in presence of potential entry. Likewise, Fanti (2014) investigates this subject in a duopoly and remarks that the previous results crucially depend on the hypothesis that, in the mixed case of duopoly, the EB firm is Stackelberg wage follower: in the first stage, the RTM firm and its union negotiate the wage; then, in the second stage, the RTM firm selects employment, and the EB firm simultaneously bargains with its union wage and employment levels.
In a Cournot duopoly framework, Vannini and Bughin (2000) focus on the firms’ decision whether to adopt a cost-raising strategy via the recognition of labor unions. Those authors show that unionization can generate vertical interdependence between the labor and the product markets, that firms can strategically exploit to raise profits. Nonetheless, the firms’ profitability is crucially altered by the institutional features of the bargaining process, e.g. the structure and the scope. In particular, Vannini and Bughin (2000) show that, under precise conditions (low union power, low product differentiation, centralized bargaining, EB firm Stackelberg wage follower), firms can prefer EB rather than RTM negotiations, although they have to pay higher wages.
However, as Buccella (2011) points up, and Fanti (2015), Buccella and Fanti (2015), and Fanti and Buccella (2017) study, it is possible to specify an alternative timing for the game in which the EB is Stackelberg output leader: in the first stage, the EB firm and its union concurrently bargain wage and employment levels while the RTM firm and the respective union negotiate the wage; in the second stage, the RTM firm selects its employment level. This modification is not innocuous because different equilibria arise: the set of cases in which the equilibrium implies the selection of EB considerably increases. Thus, the equilibrium bargaining agenda in the industry is sensitive both to the scope and how negotiations are conducted, i.e. the rules and timeline of the game.
The analysis of the bargaining agenda is currently subject of renewed interest. Recent extensions have been devoted to the selection of the negotiation agenda in network industries (Fanti and Buccella, 2016a), in a context of international trade with strategic trade policy (Bandyopadhyay and Bandyopadhyay, 2001; Fanti and Buccella, 2016b), and in the presence of different union preferences toward wages (Fanti and Buccella, 2018). Nonetheless, all those contributions have abstracted from the game-theoretically founded choice of the timing of the bargaining model.
3. The model and the results
All the works described in the previous section consider 2x2 games in which firms can select RTM vis-à-vis EB, and in the case of mixed duopoly, the EB firm can be either Stackelberg wage follower or Stackelberg output leader. This paper makes a step further: it builds a 3x3 game with a CV model in which firms can negotiate under RTM or EB, and in the case of mixed duopoly, the EB firm can choose to be either Stackelberg wage follower or Stackelberg output leader, therefore making endogenous the choice of the timing.
Consider a duopoly market where firms 1 and 2 compete for homogeneous goods with labor the unique factor of production. A constant returns-to-scale technology characterizes the industry, so that one unit of labor (l) is needed for one unit of output (q). The linear (inverse) market demand is:
where p denotes the price and
for firm 1 and 2, respectively. The model assumes that the firms decide their production levels according to a CV model (see De Fraja, 1993). Thus, define φ
The bargaining structure in the industry is decentralized at the firm level. The bargaining solution is modelled by the following generalized Nash product:
where the parameter
Mixed case 1 (EB1) (Bughin, 1999; Buccella, 2011; Fanti, 2014). Stage 1: Firm j and union j bargain over the wage. Stage 2: Firm j chooses employment and firm i and union i bargain over wage and employment. With this timing, firm i and union i, when bargaining over wage and employment, can observe the wage that resulted from bargaining between firm j and union j. In this case, firm i acts as Stackelberg wage follower: i, j = 1, 2, i ≠ j.
Mixed case 2 (EB2) (Fanti, 2015; Buccella and Fanti, 2015). Stage 1: Firm i and union i bargain over wage and employment while firm j and union j bargain over the wage. Stage 2: Firm j chooses employment. With this timing, firm j when chooses output can observe the wage and employment that resulted from bargaining between firm i and union i. In this case, firm i is Stackelberg output leader: i, j = 1, 2, i ≠ j.
In other words, in the mixed case, when a firm chooses RTM, it means that in the first stage it and its corresponding union bargain over wage and in the second stage they bargain over output/employment. In EB1, the wage and employment bargaining in the EB unit takes place in the second period while, in EB2, the bargaining takes place in the first period.
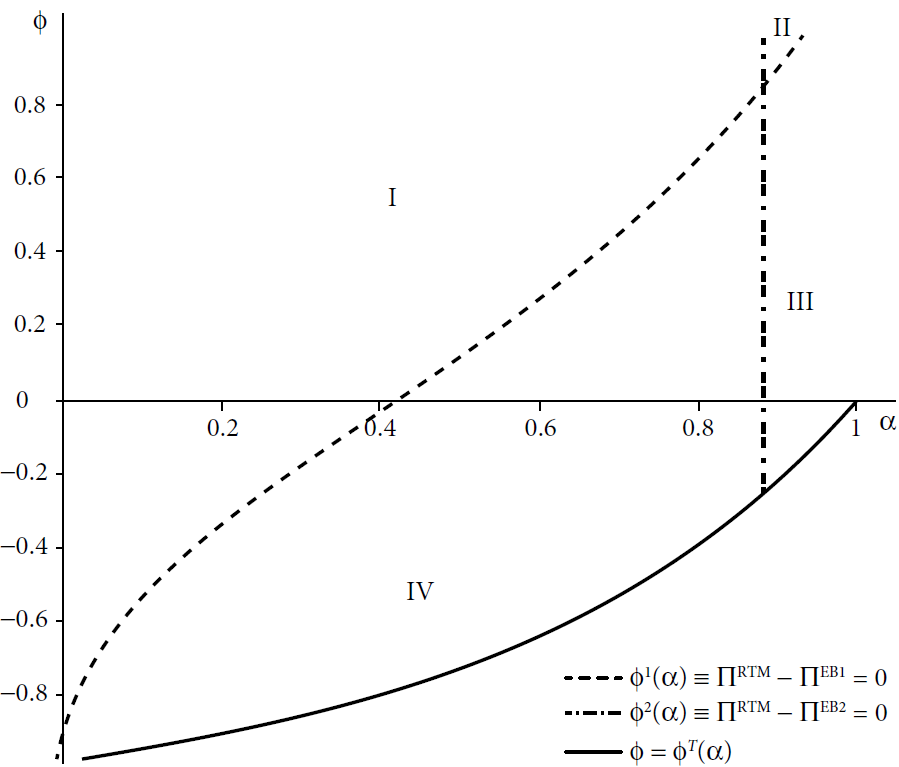
Using Equations [2]-[4] and solving the Nash Product in Equation [5], direct computations (see the Appendix) allow obtaining the expressions in Table 1. With the firms’ payoffs in Table 1, it is possible to construct Figure 1 that defines the regions in which the firms’ profits have different rankings. The non-negativity condition on profits implies that Π i ≥ 0.
Table 1 Unionized duopoly firms’ profits, alternative timing of the game
| Firm 2 → Firm 1↓ | RTM | EB1 | EB2 |
|---|---|---|---|
| RTM |
|
|
|
| EB1 |
|
|
|
| EB2 |
|
|
|
However, it can be verified that under EB2:
While
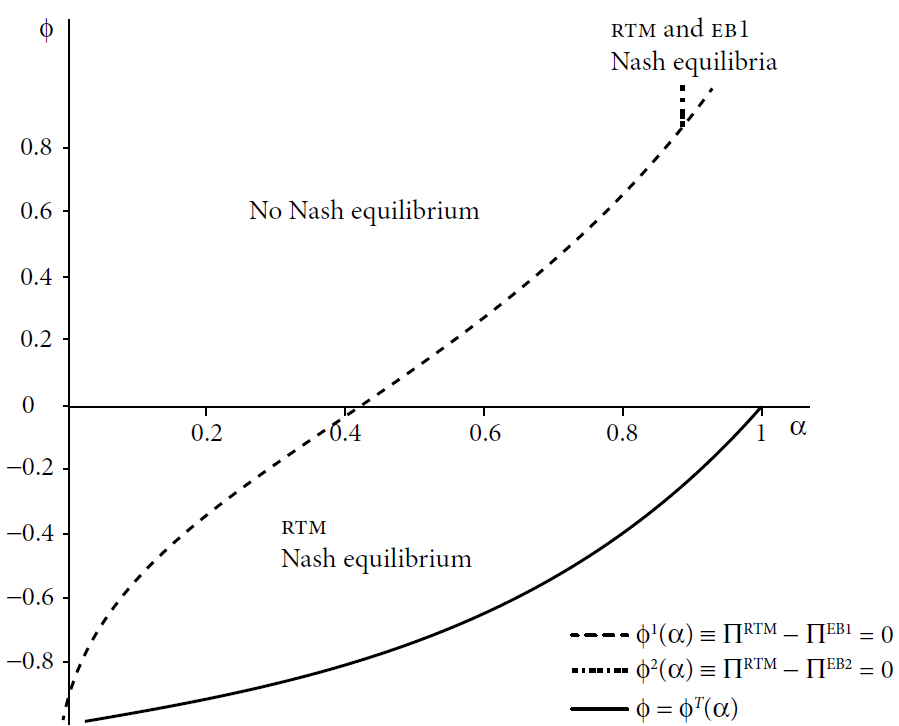
In region I, when firm 1 plays RTM, firm 2 replies EB1. However, when firm 2 plays EB1, in that area the firm 1’s best reply is EB2. As a consequence, in region I no Nash Equilibrium arises. In region II, when firm 1 plays RTM, firm 2 again replies EB1. However, in this area, when firm 2 plays EB1, firm 1’s best reply is RTM. Thus, multiple asymmetric equilibria emerge. In region III, RTM is the best reply for firms whatever is the strategic choice of the rival: RTM is the dominant strategy. In region IV, RTM is a mutual best response for firms; therefore, RTM is the Nash equilibrium. Proposition 1 summarizes these findings.
Proposition 1. Under the CV model, in a 3x3 game in which firms strategically choose the bargaining agenda (RTM, EB1 and EB2): a) in the set (φ
With regard to region I, the interconnections between the unions’ bargaining power, the strategic choice of the negotiations’ timing (and, in particular, the strategic wage undercutting under EB1), and the firms’ more/less collusive behavior in the market, are extremely complex. Each of those elements has an impact on the negotiated wage and output level, and therefore on market price, firms’ total revenues and margins, which affects the selection of the agenda. Whichever the agenda’s choice of a bargaining unit, the rival has a strategic incentive to shift towards a different one; however, given the strategic selection of the rival unit, the other unit has an incentive to move to a different agenda from the initial one. On the other hand, with regard to region II, every union has an incentive to deviate towards the RTM agenda, provided that the rival unit bargains under the EB1, and vice versa. Thus, two asymmetric equilibria arise. The rationale for this finding can be explained as follows. For each bargaining unit it is beneficial to switch to RTM when the union’s power is adequately high and the degree of competition low because, due to the identical market price for the homogeneous products, lower negotiated wages and lower output for the RTM unit (an effect magnified by a higher degree of collusion) lead to margins higher than the EB1 firm.
However, if also the rival unit selects RTM, the effect of an increase in price because of lower production is not sufficiently large to counterbalance the related revenues reduction due to lower output. Therefore, to be profitable the switch towards RTM, the rival bargaining unit has to keep the EB1 negotiation agenda. Thus, EB1 emerges as equilibrium because wages are not concurrently negotiated in the rival units, suggesting that, having knowledge of the wage rate at the RTM rival firm, the EB unit undercuts the negotiated wage to a level which keeps a relative profitability in the mixed case. The non-trivial result of no Nash equilibria in a relevant area of the economy’s feasible set in Proposition 1 is in sharp contrast to the existing literature that considers 2x2 games. In fact, in a 2x2 game characterized by EB1, Buccella (2011) and Fanti (2014, Appendix) show that the RTM model is the dominant strategy for firms. Therefore, if the duopolists have the right to select the negotiation agenda, RTM arises as the unique equilibrium, regardless of the degree of competitiveness of the industry. On the other hand, in a 2x2 game characterized by EB2, Fanti (2015) and Fanti and Buccella (2017) find that in a Cournot duopoly as regards firms, RTM is the unique equilibrium for high values of the union bargaining power; for intermediate values, multiple symmetric equilibria arise in which both firms opt either for RTM or EB while, when the unions are sufficiently weak, the EB becomes the unique equilibrium agenda. Making use of a CV model with EB2, Buccella and Fanti (2015) further extend the results of Fanti (2015). Those authors show that EB is the unique equilibrium for almost all the degree of market competition when the unions are extremely weak. When the unions’ bargaining power increases, both RTM and EB arise as equilibria of the game for large degrees of market competition while EB is the unique equilibrium in the presence of collusive-like behaviours. Finally, if the union is strong, RTM emerges as the unique equilibrium.
Therefore, these findings may provide with a useful insight for authorities and policy makers. Even if the bargaining parties have large degrees of freedom in the conduct of negotiations, a clear intervention in labour regulations is needed to set the rules of the timing to ensure the rise of a “common practice” in the industry, especially in the most observed and realistic cases in which the unions’ power is not too high, and whenever firms tend to restrict market rivalry.
4. Conclusion
As known the issue of the bargaining agenda investigates how firms may strategically choose how to conduct their negotiations opting either for the RTM or the EB institution. However, in the mixed case of duopoly, the specification of the timing of the game leads the firm which selects EB to act either as the Stackelberg wage follower (EB1) or the Stackelberg output leader (EB2). So far the literature has assumed either EB1 or EB2 as exogenously given. Consequently, the conclusions of the literature may appear assumption-dependent. In fact, depending on the exogenous hypotheses with regard to the timing, there are different economic parameters that qualifies either the RTM or the EB equilibrium. However, the timing itself is a decision variable that have to be taken into consideration in a correct game-theoretic approach. This paper shows that using this approach the results are surprising.
It is shown that, in a large area of the parameters’ space, the game presents no equilibria in pure strategies. On the other hand, the RTM institution endogenously emerges as the unique equilibrium agenda with low unions’ bargaining power and a high degree of competition and, as the unions’ strength rises, for larger ranges of the CV parameter. In addition, a restricted area of the parameters’ space, characterized by collusive firms’ behavior and extremely high bargaining power, shows multiple, asymmetric equilibria. Moreover, the EB institution disappears as the industry bargaining institution in equilibrium, in contrast to what has recently established the received literature. Therefore, this result suggests, on the one hand, that the exogenous assumption of a certain bargaining agenda as commonly made by the received literature may be not robust and, on the other hand, that policymakers and antitrust authorities need to intervene in labor market regulations to set the timing in negotiations in order to ensure that a “common bargaining practice” may emerge in the industry.
The present work has been built on precise assumptions. The intensity of competition in the product market, for instance, can be modeled by introducing product differentiation. Price competition à la Bertrand or à laHotelling (1929) represent other extensions of the model. Moreover, with regard to the labor unions, different production technologies (e.g., decreasing returns to scale), and the introduction of a more general utility function to weight the preferences over wages and employment, are all elements requiring further analysis. This is left for future research.











 nueva página del texto (beta)
nueva página del texto (beta)