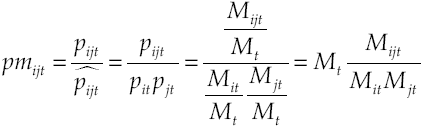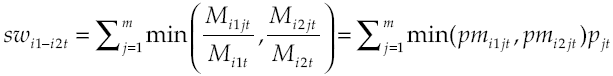Clasificación JEL: J61, J62, J63, J64.
JEL Classification: J61, J62, J63, J64.
Introducción
Una posible estrategia para analizar bases de datos que contienen una gran cantidad de observaciones o elementos consiste en clasificarlos en un número determinado de clusters o grupos, de manera tal que cada agrupación presente, en un escenario ideal, una alta homogeneidad interior y una alta heterogeneidad respecto a otras agrupaciones. Así, más que analizar las características de cada elemento de la muestra por separado, lo que hacemos es analizar las características de los grupos de esos elementos que se han formado1.
Existen multitud de técnicas para agrupar o clasificar datos en clusters; todas ellas han de hacer frente al menos a tres cuestiones metodológicas: generar una medida de proximidad o similitud entre los elementos que se van a agrupar, definir un procedimiento jerarquizado o no de formación de los grupos y proponer una regla de parada o de determinación de grupos en el proceso de clustering.
Álvarez de Toledo, Núñez y Usabiaga (2014) proponen una medida de similitud que tiene como principal característica su aplicabilidad a datos de emparejamiento oferta-demanda; por ejemplo, dos demandantes (o dos grupos reducidos de ellos) ―empresas que demandan trabajadores, familias que buscan vivienda, ahorradores que demandan activos financieros, etc.― serán tanto más parecidos cuanto más similar sea la forma en que se emparejan con el otro lado del mercado. Este análisis se puede aplicar a los dos lados del mercado, agrupando en clusters a oferentes por un lado y a demandantes por otro, siendo posible, además, obtener un bicluster del mercado mediante la combinación de los dos clusters anteriores con base en los intercambios o emparejamientos producidos entre ellos. El presente trabajo aplica esta metodología de bicluster al mercado de trabajo español,2 y más concretamente a la información sobre altas laborales (colocaciones) disponible en la Muestra Continua de Vidas Laborales (MCVL) durante el periodo 2011-2013.3 Dicha metodología permite, a partir de la información disponible para cada colocación, dividir el mercado de trabajo en clusters (o mercados de trabajo específicos) a través del agrupamiento, no de trabajadores o puestos individuales, sino de una serie de pequeñas agrupaciones de ellos definidas según las características del trabajador que se emplea en el momento de su búsqueda (características como el sexo, la edad, el municipio de residencia, el grupo de ocupación y el sector de actividad) y según las características del puesto vacante que se ocupa (municipio del centro de trabajo, grupo de ocupación y sector de actividad de la vacante). Dichas agrupaciones de partida suponen la división del mercado de trabajo en segmentos laborales de trabajador y de puesto; nuestro análisis se centra en dichos segmentos laborales más que en los trabajadores y en los puestos considerados individualmente.
Esta segmentación de partida del mercado de trabajo se ajusta bien a la forma en que describen el intercambio laboral los modelos de emparejamiento con fricciones y búsqueda por los dos lados del mercado ―en esta línea, véanse, por ejemplo, los trabajos de Pissarides (2000, 2011), Petrongolo y Pissarides (2001) y Shimer (2007)―. En estos modelos, la búsqueda de empleo que subyace al desempleo no consiste únicamente en encontrar un puesto con buen salario, sino en hallar un buen emparejamiento en su conjunto. Por otro lado, no sólo es el trabajador el que se preocupa por encontrar un buen puesto, con la empresa simplemente dispuesta a contratar a aquél que acepte su oferta salarial, sino que la empresa también está preocupada por la localización de un buen candidato. La base del modelo de emparejamiento es que cada trabajador tiene características distintas, que le convierte en adecuado o no según el tipo de trabajo. Asimismo, los requisitos de cada puesto de trabajo difieren entre las empresas, y los empleadores no son indiferentes sobre el tipo de trabajador que contratan, dado un nivel salarial. Este enfoque microeconómico de los dos lados del emparejamiento laboral permite incorporar características del mundo real, como las diferencias que existen entre los trabajadores y entre los puestos de trabajo, o las diferencias existentes en la estructura institucional de los mercados de trabajo, que pueden ayudar a la interpretación de los resultados observados; por ejemplo, respecto al comportamiento del desempleo.
Dentro de los modelos microeconómicos que se están desarrollando en este campo, nuestro trabajo puede enlazar al menos con dos tipos de modelos: los que tratan de microfundamentar la función de emparejamiento y los de asignación bilateral (two-sided matching games). Los primeros pretenden hacer explícitas las fricciones y heterogeneidades que subyacen en dicha función de emparejamiento agregada.4 Así, modelos como el de islas, bolas en urnas, taxis, colas, stock-flow o el de desajuste o mismatch, han explorado diferentes tipos de fricciones que permiten microfundamentar a la función de emparejamiento, dividiendo de una forma u otra el mercado de trabajo en diferentes partes o segmentos.5 En cuanto a los segundos (los modelos de two-sided matching games), pueden también constituir un marco teórico adecuado para nuestro trabajo, ya que analizamos datos individuales de colocaciones detectando “quién se empareja con quién” (who matches with whom); colocaciones que se producen, según este enfoque, a partir de una determinada función o tecnología de asignación bilateral basada en las preferencias de los individuos.6
Nuestro trabajo no tiene la intención de ampliar o evaluar los modelos teóricos comentados, más bien intenta proponer unas variables empíricas que pueden tener implicaciones importantes en el marco de esos modelos. Por ejemplo, hay que tener en cuenta que el “mapa” que generamos de propensiones al emparejamiento (entre segmentos de trabajadores y segmentos de puestos), y la posibilidad de identificar segmentos (de trabajadores o de puestos) con una elevada similitud en cuanto a la forma en que participan en el emparejamiento laboral, pueden ser interpretados como procesos que mejoran la información sobre el empleo; mejoras que pueden producir una reducción del mismatch existente en la función de emparejamiento o en la tecnología subyacente a los modelos de asignación bilateral ―pudiendo incluso provocar una revisión de las preferencias de los individuos en dichos “juegos” de asignación―.
Este trabajo, al analizar biclusters o mercados de trabajo específicos reales de la economía española, profundiza y amplía el análisis propuesto por Álvarez de Toledo, Núñez y Usabiaga (2014).7 Este último trabajo plantea la posiblidad de agrupar el mercado laboral en mercados locales o “islas” laborales, pero lo hace usando una medida de similitud común a ambos lados del mercado ―mientras que en este trabajo analizamos las similitudes por separado― y, además, no llega a implementar empíricamente dicha clasificación.8 En suma, este estudio supone un importante paso adelante desde varias perspectivas (metodología, tratamiento de los datos, etc.) y podría ser útil como herramienta para mejorar el emparejamiento y la política laboral, como se ejemplifica para la economía española.
El resto del trabajo se estructura de la siguiente forma. En la sección segunda explicamos la metodología seguida para segmentar una base de datos sobre emparejamientos ―dando lugar a una matriz de emparejamientos entre segmentos de trabajador y segmentos de puesto― y generar las variables empíricas que sinteticen su distribución; variables como la similitud o proximidad entre dos segmentos laborales. En la sección tercera procesamos y agrupamos los datos de colocaciones contenidos en la MCVL con el objetivo de generar la matriz de emparejamientos entre segmentos de trabajador y segmentos de puesto; matriz cuya dimensión y estructura deben ser operativas computacionalmente para poder obtener las variables descritas en la sección anterior y para poder generar, a partir de dichas variables, un “mapa” bicluster. Por su parte, en la sección cuarta se muestra cómo la información sobre el flujo de entrada al empleo se puede sintetizar dando lugar a la generación de una serie de mercados laborales idiosincrásicos (biclusters), cuya estructura puede ser analizada también desde el punto de vista de la duración del empleo (sección quinta). Finalmente, la sección sexta recoge las principales conclusiones de nuestro trabajo.
Metodología
Este trabajo toma como base metodológica el esquema empírico de segmentación propuesto por Álvarez de Toledo, Núñez y Usabiaga (2014). Dicho documento define, a partir de una base de datos de colocaciones, una serie de segmentos laborales según las características del trabajador que se emplea (características correspondientes al periodo de búsqueda del individuo, como el sexo, la edad, el municipio de residencia, la ocupación y el sector de actividad) y según las características del puesto vacante que se ocupa (municipio del centro de trabajo, ocupación y sector de actividad de la vacante). En cada periodo t cada trabajador que busca un empleo es asignado a uno de los n segmentos de trabajador existentes, W
it
(i = 1,2…n); cada vacante es asignada a uno de los m segmentos de puesto, J
jt
(j = 1,2…m), y cada uno de los emparejamientos trabajador-puesto da lugar a un segmento conjunto, S
ijt
, formado por la unión del segmento del trabajador y del puesto. Cada tipo de segmento viene definido por el correspondiente conjunto de características
En cada periodo t dispondremos de una matriz n×m de distribución de frecuencias o colocaciones, donde las filas representan a los segmentos de trabajador y las columnas a los segmentos de puesto. Cada elemento de la matriz M
ijt
representa el número de emparejamientos que se ha producido en el segmento conjunto correspondiente; la matriz completa muestra, por tanto, quién se empareja con quién.10 El número total de colocaciones,
Interpretaremos que el mercado de trabajo está segmentado cuando los trabajadores de un segmento de trabajador específico tienden a emparejarse con las vacantes de un determinado segmento de puesto en mayor o menor medida a como lo harían si la asignación del empleo en el mercado fuera puramente aleatoria. En relación con esta idea de segmentación, proponemos dos medidas empíricas obtenidas a partir de nuestros datos de emparejamiento: la “propensión al emparejamiento” entre un segmento de trabajador y un segmento de puesto y el “grado de similitud” entre dos segmentos de trabajador (o dos segmentos de puesto).
La propensión al emparejamiento entre un segmento de trabajador i y un segmento de puesto j determinados en cada periodo t, pm ijt se obtiene como el cociente entre la probabilidad, de acuerdo con nuestros datos, de observar una colocación en el segmento conjunto que forman y la probabilidad de dicho emparejamiento en el caso de que el proceso de emparejamiento sea puramente aleatorio (colocaciones asignadas por “sorteo”).
Debido a que M ijt es menor o igual que M it y que M jt , el valor de pm ijt oscilará entre cero y M t ―valdrá cero cuando M ijt = 0 y tomará un valor máximo de Mt en el caso particular de que M ijt = M it = M jt = 1―. Por otro lado, una propensión mayor a la unidad indicaría que la “conexión” entre el segmento de trabajador y el segmento de puesto es más fuerte que la que se obtendría en un escenario de asignación aleatoria de las colocaciones, y a la inversa. Según el enfoque two-sided, una propensión alta entre trabajadores de W i y puestos de J j se deberá a la combinación de tres factores: preferencia de los trabajadores tipo i por los puestos tipo j; preferencia de los puestos tipo j (nos referimos a las personas que hacen la selección para esos puestos) por los trabajadores tipo i, y empleo de canales de búsqueda comunes.
En cuanto a la medida de similitud, consideramos a dos segmentos de trabajador, W i1 y W i2 , “similares” cuando sus emparejamientos se distribuyen porcentualmente de forma parecida entre los distintos segmentos de puesto ―esta medida de similitud puede ser expresada en función de la variable pm ij ―:
El valor de la similitud, sw i1-i2t , oscila entre cero y uno. Cuando es cero, W i1 no dirige ninguna colocación a los segmentos de puesto a los que dirige sus colocaciones W i2 . Cuando es uno, las distribuciones de las colocaciones de ambos segmentos de trabajador son idénticas. Análogamente, consideramos a dos segmentos de puesto “similares” cuando sus emparejamientos se distribuyen de forma parecida entre los distintos segmentos de trabajador.
Generación de datos laborales segmentados a partir de la MCVL
Nuestro trabajo aborda la aplicación de una metodología de clusters a la información disponible en la MCVL de 2013 sobre las altas laborales producidas durante el periodo 2011-2013. Por lo tanto, el objetivo es analizar al colectivo de personas que entra a formar parte de la muestra porque ha transitado al empleo en algún momento dentro del periodo, dando lugar al alta laboral correspondiente en la Seguridad Social; y esto con independencia de la situación administrativa de perceptor o no de prestación o subsidio que tenga el trabajador empleado ―además, hay que tener en cuenta que un individuo puede ser al mismo tiempo afiliado en alta y pensionista, entrando así en la población de referencia de la muestra por ambas vías―.
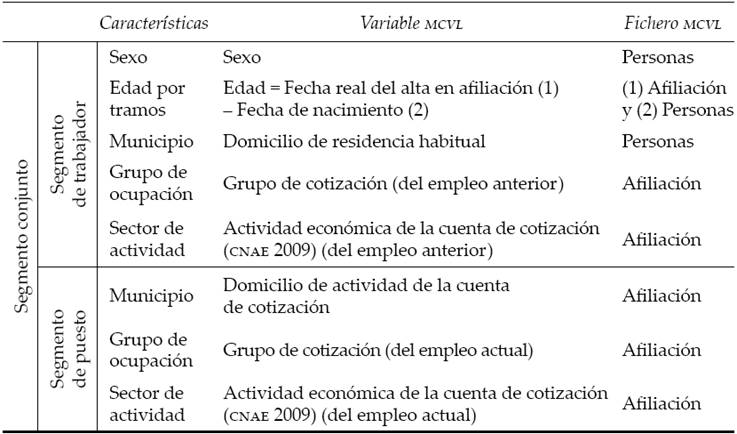
A partir de estos datos de emparejamientos, podemos dividir el mercado de trabajo en segmentos de trabajador y en segmentos de puesto atendiendo a las características o atributos de los trabajadores y de los puestos. En concreto, nos centraremos en cinco características del trabajador (en el momento de su búsqueda) que pueden influir en su emparejamiento: municipio, grupo de ocupación, tramo de edad, sexo y sector de actividad; y en tres características del puesto cubierto: municipio, grupo de ocupación y sector de actividad. Así, cada colocación dará lugar a un segmento conjunto formado por ocho características, las cinco del segmento de trabajador y las tres del segmento del puesto. El siguiente cuadro resume las variables de la MCVL que hemos empleado para obtener cada característica.
La variable edad, que se corresponde con la edad (en años) que tiene el trabajador en el momento en que consigue una colocación, se ha expresado en intervalos para evitar una excesiva segmentación de nuestros datos. De esta forma, los intervalos que hemos considerado han sido: 16 a 29 años; 30 a 44 años; 45 a 54 años, y más de 54 años. En cuanto a los municipios (del trabajador y del puesto), hay que indicar que, lamentablemente, no es posible identificar en la muestra a los municipios con población igual o inferior a 40 000 habitantes, los cuales son agrupados por provincia. Cabe señalar también que nos hemos aproximado al atributo grupo de ocupación a través de la variable grupo de cotización. Finalmente, nuestro análisis supone que el grupo de ocupación del trabajador y su sector de actividad (durante la búsqueda de empleo) son el grupo de ocupación y el sector de actividad del último empleo que ha tenido ―evidentemente, si se trata del primer empleo, estas variables han quedado sin informar―. Pensamos que todos estos supuestos o criterios son plausibles y no distorsionan apenas los resultados obtenidos.
Los datos utilizados representan algo más de dos millones de colocaciones o altas laborales. De todas estas colocaciones, hemos descartado aquellas para las que no se conoce el municipio o la ocupación del trabajador o del puesto, características esenciales a la hora de introducir segmentación en el mercado de trabajo.11 Tras aplicar dicha restricción, quedan algo menos de dos millones de colocaciones (1 967 441),12 las cuales dan lugar a 585 420 segmentos conjuntos no nulos (segmentos donde se ha observado al menos una colocación), 139 504 segmentos de trabajador y 39 981 segmentos de puesto. Por consiguiente, según la estructura de nuestros datos, el mercado laboral español está claramente segmentado, es decir, existe un número reducido de segmentos conjuntos no nulos, que muestran por lo general propensiones al emparejamiento elevadas, y una gran cantidad de segmentos conjuntos que muestran frecuencias conjuntas nulas y, por ende, propensiones al emparejamiento nulas.13 Sin embargo, hay que tener en cuenta que nuestros datos (a pesar de su importante volumen) podrían estar ofreciendo una visión del mercado de trabajo demasiado segmentada. Pensemos que si dispusiéramos de una muestra de colocaciones significativamente más grande que la empleada (MCVL), se podrían observar colocaciones en un mayor número de segmentos conjuntos, existiendo más propensiones al emparejamiento mayores que cero. Este problema de carácter muestral se conoce con el nombre de “problema de las frecuencias nulas”.14 Además, no sólo el problema de las frecuencias nulas puede condicionar nuestros resultados, sino también la existencia de frecuencias demasiado bajas.15 Para corregir estos problemas hemos adoptado dos soluciones que pretenden conseguir, de forma acumulativa, una matriz de emparejamientos con mayores frecuencias. Por un lado, hemos considerado los tres años analizados (2011 a 2013)16 como un periodo único; ello implica que renunciamos a adoptar un enfoque dinámico, que considere cada año por separado, a cambio de poder acumular un mayor número de colocaciones observadas en cada segmento. Por otro lado, hemos optado por unir entre sí a segmentos de trabajador con frecuencias reducidas (inferiores a diez colocaciones) y, a su vez, a éstos con segmentos de mayor frecuencia. Dicho proceso de unión ha tenido un elevado carácter endógeno, ya que se ha basado fundamentalmente en la similitud entre los municipios de cada par de segmentos ―cuanto más se parecen en la forma en que se emparejan con los diferentes segmentos de puesto, más similares son dos municipios de trabajador―, sujeto a la coincidencia del resto de sus características. Todo este proceso de agregación se ha llevado también a cabo con los segmentos de puesto. Tras estos agrupamientos, el número de segmentos de trabajador ha quedado reducido a 9 170 (segmentos que engloban a los 139 504 de partida), y el número de segmentos de puesto ha quedado reducido a 9 208 (segmentos que engloban a los 39 981 de partida).17 Hay que tener en cuenta que las sucesivas agrupaciones de segmentos que llevamos a cabo en este trabajo no suponen pérdida alguna de información, esto es, en cada momento conocemos los segmentos iniciales u originales que hay dentro de cada agrupación y las frecuencias o colocaciones de éstos; de hecho, el análisis descriptivo de cada bicluster laboral se basará en dichos segmentos de partida.
Análisis bicluster del mercado de trabajo español
En esta sección, los algo más de 9 000 segmentos de trabajador y segmentos de puesto obtenidos en la sección anterior serán agrupados en clusters jerárquicos, clusters que serán posteriormente combinados en función de los emparejamientos para generar biclusters18 que permitan obtener una visión panorámica de la segmentación existente en el mercado de trabajo español y realizar otros análisis.
El proceso comienza con la obtención de un cluster jerárquico de segmentos de trabajador. Es decir, vamos a ir agrupando los 9 170 segmentos de trabajador de la etapa anterior en grupos o clusters de segmentos, basándonos en la medida de similitud entre ellos (sw i1-i2 ) recogida en la ecuación [2]. En esencia, consideramos a dos segmentos de trabajador “similares” cuando sus emparejamientos se distribuyen de forma muy parecida entre los distintos segmentos de puesto. A partir de aquí, seguimos un método jerárquico, en el que se van agrupando progresivamente los segmentos menos distantes (más próximos) en clusters, y los clusters entre sí para formar clusters mayores (que contienen cada vez un mayor número de segmentos). Esto es, se comienza considerando cada segmento por separado, después se agrupan los dos segmentos entre los que existe mayor proximidad (menor distancia), y así sucesivamente, pudiendo continuarse el proceso hasta la fusión del total en un único segmento de trabajador.
Hay que tener en cuenta que cada ronda de agrupación requeriría actualizar la matriz de emparejamientos ―al tener que acumularse las frecuencias de los elementos (segmentos o clusters) que se han unido― y volver a calcular las similitudes de todos los elementos existentes de cara a una siguiente ronda de agrupamiento. Sin embargo, existen buenas aproximaciones que pueden evitar este recálculo continuo, como el procedimiento de “enlace promedio” que finalmente hemos empleado, en el que en cada ronda de agrupamiento la distancia entre dos clusters se calcula como la media de todas las distancias de los elementos de uno y otro cluster.
El proceso de agrupamiento se puede detener en un número de clusters determinado previamente o, por ejemplo, tratando de garantizar la existencia de clusters cuyos elementos no superen una determinada distancia. Además, los resultados del proceso pueden mostrarse gráficamente mediante un dendrograma, figura en forma de árbol en la que se observa cómo se van formando clusters cada vez mayores y más distantes entre sí.
A modo de ejemplo, las siguientes figuras muestran los respectivos dendrogramas aplicados a las provincias, a los grupos de ocupación y a los sectores de actividad de los trabajadores, considerando cada variable por separado. Las provincias de trabajador se van agrupando entre sí por lo parecidas que son en la forma en que se emparejan con las diferentes provincias de puesto, y análogamente se realiza para los grupos de ocupación y sectores de actividad. Estas figuras ofrecen una información preliminar de interés.
El dendrograma de las provincias de trabajador (Figura 1) muestra que las dos primeras provincias en formar un cluster son Madrid y Guadalajara. A continuación, dicho cluster se une con Toledo para formar un nuevo cluster, de tres provincias. La siguiente unión de provincias es la que se produce entre Lugo y A Coruña. Se puede apreciar que estas primeras provincias apuntadas son cercanas geográficamente. El proceso de fusiones continuaría hasta que todas las provincias quedasen agrupadas en un único cluster.
Por su parte, el dendrograma por grupos de ocupación (Figura 2) muestra un hecho interesante: los trabajadores cualificados pertenecientes al grupo de “ingenieros, licenciados y alta dirección” no se parecen demasiado en el emparejamiento a los trabajadores, también cualificados, del grupo “ingenieros técnicos y ayudantes titulados”. Se puede observar en la figura que los grupos que se unen primero (más próximos desde la perspectiva del emparejamiento) corresponden a trabajadores de baja cualificación.
Finalmente, el dendrograma por sector de actividad (Figura 3) muestra cómo se van agrupando, de forma progresiva, las actividades relacionadas entre sí. Ciertas actividades, como las sanitarias o las relacionadas con el cuero, la minería o el transporte marítimo, aparecen bastante diferenciadas de las demás, es decir, sus trabajadores se emparejan de una forma específica, que tiene poco que ver con la forma en la que se emparejan los trabajadores de otros sectores de actividad.
Volviendo al conjunto de los 9 170 segmentos de trabajador, lo que proponemos es analizar el dendrograma de clusters de segmentos de trabajador cuando restan 256 clusters, dado que hemos comprobado que para dicho nivel de agrupamiento empiezan a detectarse suficientes clusters con un número aceptable de elementos o segmentos de trabajador.19 El proceso de agrupamiento hasta 256 clusters se ha aplicado también a los 9 208 segmentos de puesto. En este caso, la medida de similitud entre segmentos de puesto se basa en la idea de que dos segmentos de puesto serán tanto más parecidos cuando más se parezca la forma en que sus emparejamientos se distribuyen entre los distintos segmentos de trabajador.
Una vez que tenemos los 256 clusters de segmentos de trabajador y los 256 de segmentos de puesto, podemos proceder a combinarlos entre sí, dando lugar a un bicluster del mercado de trabajo que se puede representar fundamentalmente a través de dos matrices de dimensiones 256×256: la de frecuencias o colocaciones, y la de propensiones al emparejamiento entre clusters. Ambas matrices están formadas por 256 filas, que representan a los clusters de segmentos de trabajador, y 256 columnas, que representan a los clusters de segmentos de puesto. Cada uno de los 65 536 elementos (o biclusters) de la matriz de frecuencias representa la acumulación de las colocaciones de los segmentos conjuntos contenidos en el cruce o bicluster correspondiente, esto es, la acumulación de las colocaciones que se han formado entre los segmentos del correspondiente cluster de trabajador y los segmentos del correspondiente cluster de puesto―. Por su parte, la matriz de propensiones representa la propensión al emparejamiento entre cada cluster de trabajador y cada cluster de puesto correspondiente; calculada dicha propensión a partir de las colocaciones acumuladas en la matriz de frecuencias anteriormente descrita y de acuerdo con la ecuación [1].
Un bicluster con una propensión al emparejamiento nula es un bicluster donde los segmentos del cluster de trabajador no se relacionan con los segmentos del cluster de puesto. Por el contrario, un bicluster que muestre una propensión al emparejamiento relativamente elevada señala que los trabajadores de los segmentos de trabajador del bicluster muestran una elevada propensión a emparejarse con los puestos vacantes de los segmentos de puesto del bicluster, y a la inversa; este segundo escenario puede ser considerado como un yacimiento de empleo o mercado generador de empleo “específico o idiosincrásico”.20
Hay que tener en cuenta que, de los 65 536 elementos de la matriz de propensiones, se han observado valores positivos en 5 072 casos, es decir, hemos identificado 5 072 biclusters o mercados laborales específicos, cuyos principales parámetros se recogen en el siguiente cuadro.
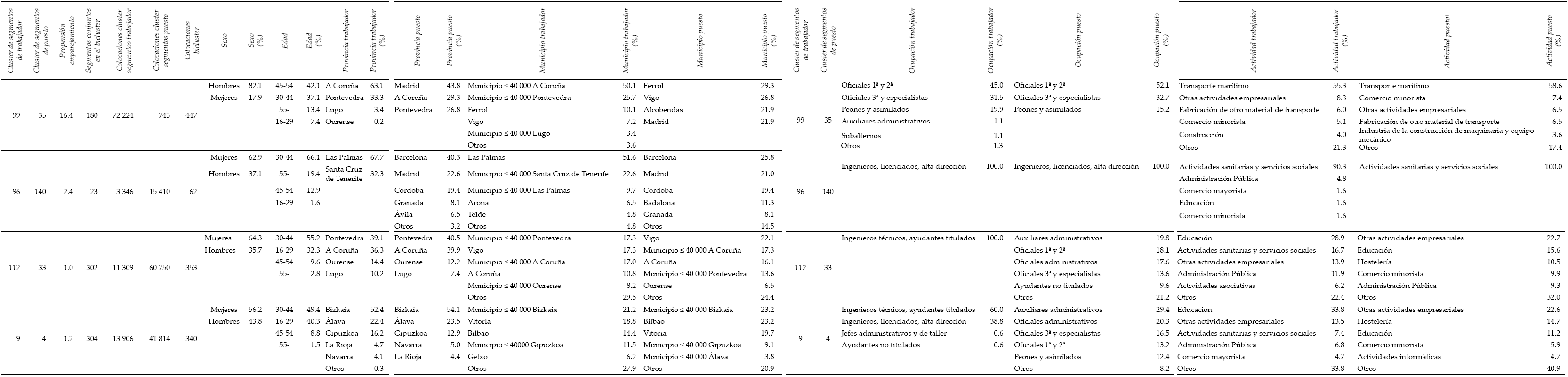
Llegados a este punto, puede resultar ilustrativo realizar un análisis descriptivo de aquellos biclusters que puedan suscitar interés por cumplir ciertas propiedades. En este sentido, el Cuadro 3 muestra la estructura de cinco mercados laborales (biclusters) que se caracterizan por cumplir, cada uno de ellos, un triple criterio: el cluster de trabajador presenta una frecuencia (o cantidad de colocaciones) relativamente elevada; el cluster de puesto muestra una frecuencia relativamente elevada al compararlo con otros clusters de puesto que forman un bicluster con el cluster de trabajador seleccionado; y la propensión al emparejamiento entre ambos clusters es elevada. Tanto por el lado de los trabajadores como por el de los puestos, a cada cluster se le asigna un número identificativo (recogido en las dos primeras columnas del cuadro) que es relevante dentro del proceso de agrupamiento jerárquico, ya que se refiere al orden de los elementos de partida del cluster dentro del dendrograma.
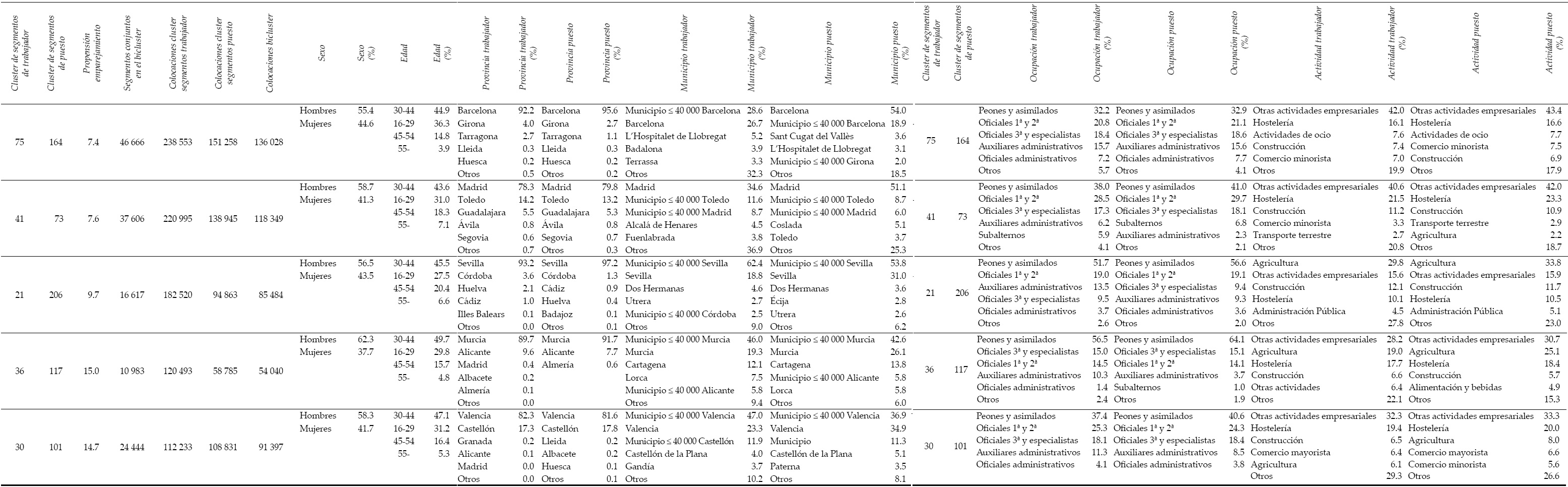
Cuadro 3: Bicluster del mercado laboral español. Elevadas frecuencias de trabajador y de puesto y alta propensión al emparejamiento
Lo primero que podemos destacar del Cuadro 3 es que todos los clusters de trabajador superan las 100 000 colocaciones en el periodo objeto de estudio, mientras que los biclusters y los clusters de puesto superan, todos, las 50 000 colocaciones. Se trata, por tanto, de yacimientos de empleo importantes. Además, la propensión a emparejarse supera el valor 7 en todos los casos ―se trata de propensiones situadas en el cuartil más alto de la distribución de propensiones―.
En cuanto a las características de los trabajadores, observamos mayores porcentajes de hombres que de mujeres, especialmente en el bicluster 36-117, situado fundamentalmente en la provincia de Murcia. El tramo de edad mayoritario es el comprendido entre los 30 y 44 años, seguido de los trabajadores más jóvenes (16 a 29 años).
A nivel espacial, se observa que los trabajadores y los puestos de cada bicluster tienden a concentrarse en áreas geográficas bastante parecidas, destacando también el hecho de que los municipios con una población menor o igual a 40 000 habitantes de una provincia determinada, considerados conjuntamente, pueden llegar a aportar más trabajadores y/o más puestos que las propias capitales de provincia; esto sucede de forma más significativa en el bicluster 21-206, situado fundamentalmente en la provincia de Sevilla. Finalmente, se observa que los diferentes mercados identificados están dominados por trabajadores y puestos de baja o media cualificación, siendo los sectores de actividad predominantes los de otras actividades empresariales:21 hostelería, agricultura y construcción.
Dado que los mercados laborales comentados se construyen básicamente sobre trabajadores de cualificación baja o media, vamos a incluir en nuestro estudio el análisis de una serie de biclusters que se caracterizan por la presencia mayoritaria de trabajadores con estudios superiores ―grupos de cotización 1 y 2― (véase el Cuadro 4), siguiendo un criterio de selección de biclusters similar al utilizado en el caso anterior.
En conjunto, y a diferencia de los mercados anteriormente comentados, el cuadro muestra que las colocaciones observadas en los diferentes biclusters corresponden principalmente a mujeres. En cuanto a la edad del trabajador en el momento de la colocación, predominan los tramos de 30 a 44 años y de 16 a 29 años; en los biclusters situados fundamentalmente en las provincias de Madrid y Barcelona tienen un mayor peso los trabajadores más jóvenes, sobre todo en el caso de Barcelona.
A nivel espacial, la muestra de biclusters de trabajadores cualificados se sitúa en torno a las provincias de Barcelona, Madrid, Valencia, Bizkaia, Sevilla y Pontevedra, lo cual sucede tanto por el lado de los trabajadores como por el de los puestos, es decir, el cluster de trabajador y el de puesto se sitúan en zonas geográficas parecidas. Destaca, además, el hecho, a nivel del análisis de los municipios, de que en los clusters de puesto los municipios que son capital de provincia tienen mayor peso que en los clusters de trabajador, esto es, las capitales ofrecen un volumen relativamente importante de puestos, los cuales son ocupados por trabajadores que proceden de la propia capital o de municipios cercanos.
En cuanto a los grupos de ocupación, dado nuestro criterio adicional de selección, el Cuadro 4 ofrece biclusters donde los trabajadores pertenecen mayoritariamente a los grupos de cotización 1 (“ingenieros, licenciados y alta dirección”) y 2 (“ingenieros técnicos, peritos y ayudantes”). En general, se observa que los clusters de puesto son también dominados por estos grupos. Finalmente, podemos indicar que los sectores de actividad de los trabajadores cualificados, y de los puestos que éstos ocupan, se concentran fundamentalmente en las actividades sanitarias y servicios sociales, educación, Administración Pública y otras actividades empresariales.
A continuación, nuestro análisis muestra algunos ejemplos de biclusters (véase el Cuadro 5) que, aunque no dan lugar a un volumen de colocaciones demasiado elevado, se caracterizan por la existencia de cierto desajuste o mismatch22 en el emparejamiento, ya sea espacial u ocupacional, es decir, los trabajadores (al comienzo de su búsqueda) y los puestos se sitúan, hasta cierto punto, en zonas geográficas o en ocupaciones diferentes, por lo que los trabajadores requieren de una movilidad geográfica u ocupacional. Así, los dos primeros biclusters muestran un desajuste espacial. En el primer bicluster se observa un movimiento de trabajadores desde provincias gallegas hacia puestos situados en Madrid, y en el segundo bicluster la movilidad va desde las provincias de Las Palmas de Gran Canaria y Tenerife hacia provincias como Madrid, Barcelona y Córdoba. Se trata de mercados donde el empleo masculino tiene más peso y donde los trabajadores tienen en su mayoría 30 años o más. El primer bicluster corresponde principalmente a trabajadores de cualificación media, siendo el sector de actividad principal el de transporte marítimo. El segundo bicluster corresponde a trabajadores con estudios superiores que se dedican fundamentalmente a actividades sanitarias y de servicios sociales.
El tercer y el cuarto bicluster constituyen ejemplos de mismatch ocupacional: los trabajadores pertenecen sobre todo a los dos grupos de más elevada cualificación, los cuales no aparecen por el lado de los puestos entre las cinco categorías de mayor representación; este hecho constituye una muestra de “sobrecualificación” en el empleo ―aunque hay que tener en cuenta que la propensión al emparejamiento de los correspondientes clusters de trabajador y de puesto es relativamente reducida―. El tercer bicluster se sitúa principalmente en Galicia, mientras que el cuarto lo hace en el País Vasco. Se trata de mercados donde el empleo femenino tiene un mayor peso y donde los trabajadores tienen en su mayoría entre 30 y 44 años. Los sectores de actividad con mayor representación en estos dos biclusters son educación, otras actividades empresariales, Administración Pública y actividades sanitarias y servicios sociales.
Un análisis de las duraciones del empleo por biclusters
El análisis desarrollado en la sección anterior se puede completar con una descripción de la duración de los episodios de empleo observados en los diferentes biclusters. El Cuadro 6 ofrece información sintetizada de dichas duraciones tanto en los biclusters descritos en los Cuadros anteriores (3, 4 y 5) como en seis nuevos biclusters, de los cuales tres se caracterizan por tener el mayor número de colocaciones de duración igual o superior a dos años, y los otros tres se caracterizan por tener el mayor porcentaje de colocaciones de duración igual o superior a dos años de entre todos aquellos biclusters que han generado durante el periodo considerado más de 1 000 colocaciones ―garantizamos de esta forma el estudio de biclusters que generan un número significativo de colocaciones―. Las duraciones del empleo han sido divididas en seis intervalos: duraciones inferiores a un mes; superiores o similares a un mes e inferiores a tres meses; duraciones entre tres meses y menos de seis meses; entre seis meses y menos de un año; entre un año y menos de dos años; y duraciones iguales o superiores a dos años. Hay que tener en cuenta que la muestra empleada se centra en el flujo de altas laborales producidas desde el 1 de enero de 2011 hasta el 31 de diciembre de 2013, por lo que puede haber episodios de empleo que no han concluido todavía cuando se alcanza dicho momento final, existiendo, por tanto, censura por la derecha en nuestros datos.
La distribución de las colocaciones por duraciones resulta en general decreciente, de manera que la mayor parte de los empleos muestran una duración inferior a un mes ―en concreto, un 59.1% del total de la muestra―. Dicha preponderancia se observa claramente en dos biclusters de trabajadores cualificados, el 112-30, situado en Galicia, y el 90-141, situado mayoritariamente en Valencia, donde las colocaciones de escasa duración superan el 80%; ambos focos de generación de empleo se corresponden con el sector de actividad sanitario.
A pesar de la tendencia descrita respecto a la temporalidad del empleo, existen también ciertos biclusters donde las duraciones iguales o superiores a dos años son relativamente importantes. Esto sucede, por ejemplo, en los biclusters 41-74, 75-164 y 41-73, que pese a estar compuestos mayoritariamente por episodios de empleo de corta duración ―los porcentajes de colocaciones de menos de un mes rondan o superan el 50% en los tres casos―, son los que presentan un mayor número absoluto de colocaciones con duración superior a dos años. El primero y el tercero se sitúan fundamentalmente en la provincia de Madrid, mientras que el segundo lo hace principalmente en Barcelona. El primer bicluster corresponde sobre todo a trabajadores de los grupos de auxiliares administrativos y de oficiales administrativos, mientras que en los otros dos resultan más importantes los grupos de peones y asimilados y de oficiales de 1ª y 2ª. En los tres mercados destacan sectores de actividad como el de otras actividades empresariales, el de las actividades de ocio y el de la hostelería.
Otros biclusters interesantes desde el punto de vista de la estabilidad del empleo son el 75-149, el 9-2 y el 75-162, que se caracterizan por presentar el mayor porcentaje de colocaciones con duración superior o igual a dos años entre los biclusters con más de 1 000 colocaciones ―estos porcentajes son, respectivamente, 42.1, 16.6 y 14.4―. El primero y el tercero se sitúan fundamentalmente en la provincia de Barcelona y se corresponden con trabajadores de cualificación media (jefes administrativos y de taller, auxiliares administrativos y ayudantes no titulados); el primero está vinculado al sector de la intermediación financiera, y el tercero se vincula a los sectores de otras actividades empresariales, comercio mayorista y comercio minorista. Por su parte, el segundo de estos tres biclusters se ubica principalmente en el País Vasco y se corresponde con trabajadores titulados que encuentran empleo en los sectores de otras actividades empresariales y Administración Pública.
Como ya hemos señalado, un aspecto característico de la economía española es el elevado grado de temporalidad del empleo, sobre todo del flujo de generación de nuevos empleos. El fenómeno de la temporalidad guarda una estrecha relación con el hecho de que un número significativo de trabajadores experimentan una dinámica consistente en encadenar un número considerable de relaciones laborales de corta duración, ya sea en la misma o en diferentes empresas ―sobre el fenómeno de la temporalidad y la recurrencia en el empleo en España véanse, por ejemplo, los trabajos de Dolado, García-Serrano y Jimeno (2002), Alba-Ramírez, Arranz y Muñoz-Bullón (2007) y Arranz y García-Serrano (2014)―. Evidentemente, este rasgo idiosincrásico de nuestro mercado de trabajo debe tener su reflejo en el mapa de biclusters obtenido, de manera que aquellos biclusters con mayor temporalidad deberían mostrar un mayor porcentaje relativo de empleo recurrente. Para mostrar esta idea, hemos analizado el número de contratos acumulado por un trabajador (y su duración media) en el total de la muestra y en un par de biclusters que difieren claramente en su grado de temporalidad. En el total de la muestra se observa que el 52.2% de los trabajadores ha tenido sólo uno o dos contratos a lo largo del periodo analizado (contratos cuya duración media es igual a 312.7 días23), mientras que el porcentaje de trabajadores con más de diez contratos es del 8.8% (contratos de duración media igual a 17.2 días). Sin embargo, estos valores son, respectivamente, del 48.7% (duración media 383.2 días) y del 32.3% (duración media 11.5 días) en el bicluster sanitario de elevada temporalidad 112-30, situado en Galicia, es decir, el porcentaje de trabajadores que han experimentado once o más contratos aumenta significativamente, respecto al total de la muestra, en este bicluster. Por su parte, los valores analizados son respectivamente 96.5% (duración media de 566.3 días) y 0.3% (duración media de 59.3 días) en el bicluster de empleo relativamente estable 75-149, situado en Barcelona y dedicado principalmente a la intermediación financiera; en este bicluster, la mayor parte de los trabajadores solamente ha tenido uno o dos contratos entre 2011 y 2013. Como se puede apreciar, existe una notable heterogeneidad a este respecto entre los biclusters.
Los casos que hemos seleccionado y comentado en la sección anterior y en esta sección resultan ilustrativos de la utilidad de nuestra metodología para conocer la estructura de los yacimientos de empleo y orientar el diseño de las políticas activas en este campo. Asimismo, hay que tener en cuenta que todo el análisis desarrollado en este artículo se podría ampliar, al menos, en dos direcciones. Por un lado, se podrían incluir nuevas variables, procedentes de la MCVL, que permitieran conocer mejor la estructura de los segmentos, de los clusters y de los mercados laborales (biclusters) identificados; variables como el tipo de contratación, el tipo de jornada, el nivel salarial promedio, etcétera. Por otro lado, resultaría posible abordar el análisis desde un punto de vista dinámico, ya que la MCVL contiene información fiable de altas laborales desde 2005. Por lo tanto, resultaría posible, por ejemplo, analizar el efecto del ciclo económico en los diferentes segmentos laborales, o en los clusters que éstos forman, e incluso tratar de identificar segmentos o clusters emergentes a partir de la evolución de sus colocaciones, conociendo, además, toda la dinámica de las propensiones al emparejamiento observadas.
Finalmente, nos gustaría destacar la versatilidad de nuestra metodología, ya que podría ser aplicada a mercados laborales de otras economías, o a otras bases de datos laborales, o incluso ser aplicada a bases de datos no laborales pero que estén basadas en emparejamientos ―mercados financieros, inmobiliarios, etc.―.
Conclusiones
El presente trabajo pretende mostrar cómo a partir de bases de datos individuales con millones de colocaciones es posible obtener una visión sintética de “quién se empareja con quién” en el mercado de trabajo, dando lugar a un mapa de biclusters laborales o mercados específicos generadores de empleo. Estos mercados están formados por grupos de segmentos de trabajador y de segmentos de puesto que tienden a emparejarse entre sí en mayor medida de lo que sucedería en un escenario donde los emparejamientos funcionaran de forma puramente aleatoria. La metodología de agrupamiento propuesta, ejemplificada mediante el uso de la MCVL (periodo 2011-2013), permite procesar la ingente cantidad de información existente sobre las colocaciones ya producidas, con el fin último de generar una “hoja de ruta” sobre los diferentes focos de generación de empleo del mercado de trabajo español. Esta forma novedosa de estructurar la información puede redundar en una reducción del mismatch laboral, tal y como es entendido en los modelos de emparejamiento.
Nuestro proceso de síntesis informativa puede estructurarse en tres etapas. En primer lugar, generamos segmentos (pequeños grupos) de trabajadores y de puestos atendiendo a las características de los trabajadores y de los puestos en cada colocación observada; esta segmentación resulta coherente con la forma en que los modelos de búsqueda (por los dos lados del mercado) y emparejamiento entienden el funcionamiento del mercado de trabajo. En concreto, nos centramos en cinco características del trabajador que pueden provocar segmentación en el emparejamiento: municipio, grupo de ocupación, tramo de edad, sexo y sector de actividad; y en tres características del puesto cubierto: municipio, grupo de ocupación y sector de actividad. Cada colocación dará lugar a un segmento conjunto (de ocho características). Interpretamos que el mercado de trabajo está segmentado cuando los trabajadores de un segmento específico tienden a emparejarse de forma más o menos intensa con ciertos segmentos de puesto específicos en comparación con una asignación aleatoria. En relación con esta idea de segmentación, proponemos dos medidas empíricas: la “propensión al emparejamiento” entre un segmento de trabajador y un segmento de puesto, y el “grado de similitud” entre dos segmentos de trabajador (o dos segmentos de puesto). En segundo lugar, hemos procedido a realizar una agrupación de los segmentos de trabajador, por un lado, y de los de puesto por otro, atendiendo fundamentalmente a la “similitud” de sus respectivos municipios; de esta forma pretendemos conseguir una matriz de emparejamientos entre segmentos con un mayor número de colocaciones o frecuencias en cada cruce de segmento de trabajador y de puesto ―tratamos de resolver un problema de excesivas frecuencias muy bajas o nulas―. Aumentando las frecuencias conjuntas observadas, mejoramos nuestro análisis, ya que aumenta la fiabilidad de las medidas de propensión al emparejamiento y de similitud entre segmentos. Finalmente, los 9 170 segmentos de trabajador y los 9 208 segmentos de puesto obtenidos en la agrupación anterior han sido respectivamente agrupados en 256 clusters jerárquicos en función de las similitudes de los diferentes segmentos entre sí, clusters que son posteriormente combinados según sus emparejamientos para generar biclusters (clusters de trabajador con una cierta propensión a emparejarse con clusters de puesto) que permitan obtener una visión sintética de la segmentación existente en el mercado de trabajo. Hay que tener en cuenta que las sucesivas agrupaciones de segmentos que llevamos a cabo en este trabajo no suponen pérdida alguna de información, es decir, conocemos en todo momento los segmentos iniciales u originales que hay dentro de cada agrupación y las frecuencias o colocaciones de éstos; de hecho, el análisis descriptivo de cada cluster laboral se basa en dichos segmentos de partida.
Los resultados obtenidos, aparte de confirmar la elevada segmentación y excesiva temporalidad existente en el mercado de trabajo español, indican que los principales mercados laborales específicos detectados muestran un grado de desajuste o mismatch relativamente reducido tanto a nivel geográfico como ocupacional. Así, los trabajadores y los puestos de aquellos biclusters generadores de empleo, y con una alta propensión al emparejamiento, se sitúan aproximadamente en la misma área geográfica ―si bien los puestos se concentran algo más en las capitales de provincia que los trabajadores, lo que podría apuntar hacia cierto grado de commuting― y en grupos de ocupación similares ―aunque parece haber algún indicio de “sobrecualificación” en el empleo, no parece ser un problema de peso en este tipo de biclusters―. Sin embargo, este escenario de ajuste parece no cumplirse en ciertos mercados donde las propensiones al emparejamiento entre clusters son algo más moderadas; así, en estos biclusters la movilidad geográfica u ocupacional del trabajador podría jugar un papel más relevante.
Nuestra aproximación puede ser muy versátil en su aplicación, ya que se puede orientar hacia el problema específico que se desee estudiar; por ejemplo, permite analizar de forma sintetizada el problema de la falta de estabilidad en el empleo en los diferentes ámbitos laborales. La división, de forma endógena (según los datos manejados, en nuestro caso la MCVL), del mercado de trabajo global en un conjunto de mercados específicos, generadores de empleo, posibilita el diseño de políticas laborales más desagregadas y ajustadas, por ejemplo, de movilidad geográfica y ocupacional; políticas que van a depender de la estructura laboral que encontremos dentro de cada mercado o bicluster. Evidentemente, la calidad del diseño de estas políticas dependerá del grado de información que se tenga sobre cada mercado específico detectado. Nuestro trabajo ha intentado mostrar la metodología propuesta de detección de esos mercados laborales, así como varias aplicaciones representativas.











 nueva página del texto (beta)
nueva página del texto (beta)