Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Investigación económica
versión impresa ISSN 0185-1667
Inv. Econ vol.68 no.270 Ciudad de México oct./dic. 2009
Dinámicas tecnológicas y el mercado internacional de bienes de alta tecnología
Technological dynamics and the international market of high–tech products
Eva Yamila da Silva Catela y Flávio de Oliveira Gonçalves*
Universidad Federal de Santa Catarina, evadasilvacatela@gmail.com
Facultad de Ciencias Económicas de la Universidad Federal de Paraná, f.goncalves@ufpr.br
Manuscrito recibido en junio de 2008
Aceptado en junio de 2009
Resumen
El trabajo analiza la existencia de clubes de exportadores de alta tecnología en la economía mundial a partir del estudio de la distribución de las exportaciones de alta tecnología de 123 países para el periodo 1985–2004. Las conclusiones validan las hipótesis de Quah (1996) al mostrar que existe una pequeña probabilidad de que las economías migren entre grupos, a pesar de la alta probabilidad de mantenimiento del status quo. Entre otras cuestiones, se observa cómo los miembros de los clubes interactúan comercial y tecnológicamente entre sí y con participantes de otros grupos. El estudio toma como base empírica tres clubes tecnológicos cuyas dinámicas demuestran formas de acumulación e irreversibilidad del avance técnico. Este estudio contribuye a la literatura de convergencia en dos líneas. Primero, al encontrar parámetros que definen clubes de convergencia en la economía mundial. Segundo, al describir cómo se interrelacionan los miembros de los clubes, dentro de y entre los grupos, en términos de flujos de comercio y tecnología.
Palabras clave: convergencia tecnológica, mixturas finitas, matriz de Markov, convergencia en clubes.
Clasificación JEL:** C19, F14, O33
Abstract
This paper discusses the existence of high tech export clubs in the world economy by analyzing the distribution of technology–intensive exports in 123 countries during the period 1985–2004. The findings are compatible with the conclusions of the seminal work of Quah (1996), showing that in spite of the high probability of maintenance of the status quo, there exists a small probability of migration between groups. The irreversibility of the technological trajectories is discussed. The paper contributes to the convergence literature in two ways. First it provides estimations of the parameter values leading to club convergence in the world economy. Secondly, it describes how club members interact, within and between groups, in terms of trade and technology flows.
Key words: technological convergence, finite mixtures, Markov chains, club convergence.
Introducción
El avance tecnológico es una de las más importantes fuentes de crecimiento a largo plazo. Las tasas y los patrones de crecimiento varían considerablemente entre países y las diferencias en capacidades tecnológicas tienen un papel fundamental. Las innovaciones en productos expanden las posibilidades de exportación, generando al mismo tiempo mayores niveles de demanda interna, de ingresos y de importaciones. Existe así un fuerte nexo entre tecnología,1 comercio y crecimiento: la innovación tiene un papel fundamental en el desarrollo de nuevos productos, en el aumento del comercio de calidad y en el crecimiento de los países (Hausmann et al. 2005).
El objetivo principal de este trabajo es identificar la existencia de diferentes clubes de exportadores de alta tecnología (AT) en la economía mundial, caracterizarlos y analizar sus dinámicas. Para alcanzar este objetivo, analizaremos la distribución de las exportaciones de alta tecnología de 123 países y su evolución para el periodo 1985–2004. El comportamiento de tal distribución nos puede brindar importantes evidencias sobre la manifestación de clubes de exportadores de alta tecnología en el mundo, su conformación, su evolución o los cambios en su expansión y distribución a lo largo del tiempo.
La importancia de este análisis se hace evidente si consideramos que diferencias en capacidades tecnológicas, asociadas a mayor o menor exportación de alta tecnología, pueden explicar la existencia de polarización y clubes de convergencia de ingreso en la economía mundial (Castellacci y Archibugi 2005). En este sentido, el trabajo seminal de Baumol (1986) señala la existencia de clubes de convergencia (por ejemplo, la Organización para la Cooperación y el Desarrollo Económicos, ocde, economías centralmente planificadas en países en desarrollo) y demuestra que los patrones de convergencia difieren entre estos grupos. A medida que los estudios sobre crecimiento divergente fueron avanzando (Durlauf y Johnson 1995; Quah 1996; Pritchett 1997) los modelos de crecimiento endógeno comenzaron a explorar los posibles factores que podrían explicarlos patrones de persistencia, polarización y formación de clubes en la distribución del ingreso mundial.
Recientemente, varios trabajos formularon la idea de que la existencia de clubes de convergencia relativos a los niveles de ingreso per cápita es resultado de diferencias en capacidades tecnológicas (Nakajima 2003; Howitt y Mayer–Foulkes 2002; Archibugi y Michie 1995). Fagerberg y Verspagen (2007) muestran que, para los países de menor producto en la década de los noventa, superar el atraso o fallar en el intento depende fundamentalmente de su habilidad para desarrollar su sistema de innovación, en contraposición a la estrategia de la década anterior de imitar tecnologías.
El presente artículo pretende comprobar la correspondencia entre grupos de exportadores de alta tecnología y clubes de convergencia de renta, ya caracterizados en los referidos trabajos. Las conclusiones siguen la línea lanzada por el trabajo seminal de Quah (1996), la cual muestra que existe una pequeña probabilidad de que las economías migren entre grupos, a pesar de la alta probabilidad de mantenimiento de status quo. En las estimaciones con ingreso o producto, las transiciones son más frecuentes que en aquellas estimaciones que utilizan variables tecnológicas, influenciadas principalmente por cambios en los precios relativos y consecuentemente en el descenso/ promoción de los países ricos en recursos naturales. Un análisis basado en las exportaciones tecnológicas se muestra, por lo tanto, más robusto al explicar el proceso de desarrollo e inserción en la economía mundial. El trabajo contribuye también a la teoría econométrica al proponer una prueba para cuatro grupos y aumentar el poder del modelo de mixturas finitas.
El trabajo está organizado en siete secciones. Primero se justifica la importancia del estudio. Posteriormente, se proporciona un análisis exploratorio de los datos, así como la descripción del método empleado para la realización del análisis empírico: el modelo de mixturas finitas y el instrumental econométrico usado. Luego se presentan los principales resultados econométricos. Después de determinar el número de componentes en los grupos de exportaciones de alta tecnología, se analiza la evolución y dinámica dentro de la distribución de las exportaciones de alta tecnología, utilizando los datos de media, desviación estándar y probabilidades estimadas en los modelos. Por último, se expone el análisis de cadenas de Markov, para estudiar la dinámica de transición entre los grupos y el equilibrio estocástico de largo plazo considerando la hipótesis de ergodicidad de la distribución.
CONTENIDO TECNOLÓGICO DE LAS EXPORTACIONES, ECONOMÍAS DE ESCALA Y CRECIMIENTO DEL PRODUCTO
El comportamiento de la distribución del producto interno de los países se caracteriza por la existencia de dos o más grupos que definen un mundo polarizado y sugieren la existencia de equilibrios múltiples. Numerosos trabajos, desde los pioneros de Barro (1991), Barro y Sala–i–Martin (1992), Quah (1996) hasta los más recientes de Fagerberg y Verspagen (2002) y Beaudry et al. (2005) discuten el tipo de patrón (convergente o divergente) que gobierna el desarrollo de la producción mundial.
A partir de las evidencias del avance de algunos países en la posguerra, la literatura económica produjo una serie de relatos y pruebas de convergencia en todas las variantes conocidas: convergencia absoluta, convergencia sigma, convergencia condicional y convergencia en clubes. La forma determinística con que se tratan los modelos de crecimiento lleva a una conclusión poco apoyada por los hechos estilizados: la existencia de trampas de pobreza (y de riqueza) donde, aun con presencia de equilibrios múltiples, estos serían equilibrios estables.
Experiencias positivas de recuperación realizadas por los países del Sudeste Asiático, España y más recientemente Irlanda, estarían excluidas del análisis de convergencia tradicional. El caso contrario tampoco se explica dentro del equilibrio determinístico, es decir, países como Argentina y Venezuela que en cierto punto de la historia reciente tenían productos per cápita que los colocaban junto a países ricos y que pasaron por desastres de crecimiento.
A partir de los trabajos de Quah (1993, 1996), Bernard y Durlauf (1996) y Pritchett (1997), se comenzaron a buscar las causas de la divergencia en el crecimiento entre los países. En este sentido, diferentes trabajos (cf. Nakajima 2003; Howitt y Mayer–Foulkes 2002; Castellacci y Archibugi 2005) formalizaron la idea de que la existencia de clubes de convergencia de los niveles del producto per cápita podría ser resultado de diferencias en las capacidades tecnológicas. Estos autores muestran como las diferencias en las capacidades tecnológicas determinan la existencia de tres grupos de países: (i) los países avanzados, conductores de la actividad innovadora; (ii) un grupo de países de producto medio, que consigue imitarlas tecnologías extranjeras, (iii) un cluster de países retardatarios, que no son capaces de innovar ni de imitar. Al mismo tiempo que se reconoció el carácter acumulativo del progreso tecnológico, también llama la atención la capacidad de aprendizaje y, por lo tanto, la posibilidad de transición de un grupo hacia otro.
Desde la perspectiva de la teoría del ciclo del producto, Dosi et al. (1990) enfatizan que la distribución sectorial de las actividades tecnológicas y exportadoras depende de las trayectorias nacionales específicas y acumulativas, las cuales generan ventajas de productividad en ciertos sectores de un país. El proceso de competencia tecnológica implica trayectorias a lo largo de coeficientes fijos e irreversibilidades. Sin embargo, tal como reconoció Vernon (1979), esta situación comienza a cambiar a inicios de la década de los setenta, cuando muchos países en desarrollo aumentan su industrialización y sus producciones comienzan a incluir productos que se encuentran en las primeras etapas de su ciclo de vida. Fabergerg y Verspagen (2007) afirman que en los años noventa existe un cambio en la forma en que la economía global funciona, pasando de un régimen de tasas de crecimiento altas para otro de tasas más bajas. Ese cambio es especialmente pronunciado en los países menos desarrollados y es una consecuencia, según los autores, del agotamiento de la imitación tecnológica como generadora de crecimiento. Durante los años noventa, este factor de crecimiento es sustituido por la necesidad de desarrollar sistemas de innovación propios.
Empíricamente, la evidencia muestra que la varianza en términos de distribución de exportaciones mundiales puede ser explicada por un conjunto de variables tecnológicas que presenta cada país o sector (Amable y Verspagen 1995; Montobbio y Rampa 2005).
El trabajo de Montobbio y Rampa (2005) explora la relación entre actividad tecnológica, cambio estructural de las exportaciones y trayectorias de crecimiento, contraponiendo las experiencias de los países asiáticos y latinoamericanos. Sus resultados concluyen que existen diferentes caminos en los cuales las actividades tecnológicas pueden mejorar o empeorar el comercio de un país. Las economías en desarrollo tienden a concentrar sus esfuerzos de innovación en industrias tecnológicamente estancadas, lo que genera un impacto negativo a través de los patrones de especialización heredados. La dificultad de salir de unas actividades que ofrecen pocas oportunidades tecnológicas impide, a su vez, transitar hacia actividades tecnológicamente dinámicas. Sin embargo, la experiencia de China y Singapur muestra la posibilidad de superar desventajas históricas. El análisis econométrico confirma que las actividades tecnológicas pueden generar ganancias de exportaciones en sectores de alta tecnología si el país expande sus actividades de innovación hacia industrias con niveles crecientes de oportunidades tecnológicas, en industrias de tecnología media (si el país se especializa en sectores de bajas oportunidades) y en tecnología baja (si se especializa en sectores que no presentan ningún tipo de oportunidad tecnológica). O sea, cualquier avance es importante para mejorar la calidad de las exportaciones dependiendo del punto del cual se parte.
Otros trabajos enfatizan la importancia de las economías de escala en el aprendizaje tecnológico, lo cual puede ser determinante de los patrones internacionales de las exportaciones en general y de las exportaciones de alta tecnología en particular. La primera contribución puede ser atribuida a Krugman (1979), que propone un modelo de equilibrio general en el cual sólo el Norte puede innovar y producir nuevos productos, mientras que el Sur imita las tecnologías. Retornos crecientes de escala e innovación de productos generan especialización en el comercio y ventajas de líderes. Sin embargo, en equilibrio, la imitación reduce las brechas tecnológicas entre países y el poder monopólico de los líderes es temporal. En este caso una polarización inicial tiende a desaparecer en el tiempo con una aproximación de los grupos Norte–Sur.
En Grossman y Helpman (1995) el énfasis recae en la experiencia tecnológica acumulada, es decir, los resultados del aprendizaje que resultan de hacer o exportar, donde el capital humano y sus costos determinan la distribución internacional de recursos para investigación y desarrollo (I&D). El modelo tiene un equilibrio caracterizado por la aglomeración geográfica de las actividades innovadoras, con países capaces de convertirse en líderes en sectores tecnológicos a través de altas tasas de innovación. Aquí, las condiciones iniciales de capacidades tecnológicas son cruciales, no permitiendo transiciones entre los grupos.2 La característica principal de este modelo es el efecto de la escala sobre el crecimiento: un cambio permanente en la intensidad investigadora (generada por un aumento de la fuerza de trabajo que se dedica a investigar o por una política pública) lleva a un cambio en las tasas de crecimiento.
Jones (1999) muestra que el modelo de Grossman y Helpman puede resultar en un aumento exponencial de la tasa de crecimiento del producto per cápita, lo que contradice lo que sucedió en el siglo XX. Jones (1999) restablece los fundamentos de la función de producción de nuevas ideas.3 En este caso, los cambios en la intensidad de la actividad de investigación (aumento de la fuerza de trabajo) no afectan la tasa de crecimiento de largo plazo, pero afectan el nivel del producto. Así, la escala es significativa no para garantizar un aumento permanente en la tasa de crecimiento de largo plazo, sino para afectar el nivel de producto. De esa forma, el nivel de actividad de investigación (y no la participación relativa), define el nivel de producto. Otra dimensión a tener en cuenta es la importancia de los encadenamientos productivos para explicar diferencias en la productividad y consecuentemente en la renta de los países.
Bair (2005) revela que estos encadenamientos deben ser analizados en cuatro dimensiones (estructura insumo–producto, alcance geográfico, estructura de gobierno y contexto institucional) para conocer cómo los países más pobres pueden acceder a las habilidades y competencias necesarias para realizar las mejoras que cambien su posición en las cadenas globales de valor.
DATOS UTILIZADOS
El trabajo utiliza la base de datos de comercio internacional de la Oficina de Estadística de las Naciones Unidas (United Nations Commodity Trade Statistics Database, UN–comtrade). Se trata de datos de comercio generados en un punto de la venta/compra entre los participantes de la transacción de comercio internacional.4 Los datos captados de UN–comtrade son valores, medidos en dólares corrientes de Estados Unidos, de las importaciones anuales por tipo y país de origen, tal como lo informan los países importadores, utilizando la Clasificación Uniforme para el Comercio Internacional, Revisión 2 y 3. El número de países informantes utilizados es 73.5 Los países importadores reportan cuáles son los países de origen de sus importaciones. De esta forma, la base UN–comtrade incorpora más de 90% del comercio mundial. Dada la amplia cobertura de la muestra, el problema de datos perdidos puede descartarse.
La clasificación de exportaciones de alta tecnología utilizada sigue dos métodos: ocde (Hatzichronoglou 1997) y Trade Competitive Analysis of Nations (TradeCAN) de la Comisión Económica para América Latina y el Caribe (CEPAL 2006). La clasificación de la ocde fue construida por sector industrial y complementada después por tipo de producto, teniendo en cuenta tanto el nivel de tecnología especifica del sector, como la tecnología incluida en las compras de bienes intermedios y de capital. La clasificación a cinco dígitos tiene como ventaja incluir sólo los productos considerados de alta tecnología, aun cuando estos se encuentren dentro de una cadena productiva de menor intensidad tecnológica, evitando problemas de sobrestimación o subestimación de productos considerados de alta intensidad tecnológica. Existen, de esta forma, dos desventajas para la utilización de esta base: a) muestra sesgada: para el año 1990 disponemos de datos sólo para 48 países y a partir del 2000 tenemos datos para 90 países de diferentes características; b) imposibilidad de comparar los valores medios y desviaciones de la variable considerada, dado que estos valores se ven influenciados a lo largo del tiempo por la incorporación de nuevos países (necesarios a su vez para un análisis no sesgado).
La clasificación de TradeCAN es a tres dígitos que, comparada con la base ocde, en algunos casos sobrestima y en otros subestima los bienes considerados de alta tecnología para los diferentes países. Como ventaja para su uso, se puede señalar una mayor cantidad de países dentro de la muestra a lo largo del periodo contemplado, lo que facilita comparaciones a lo largo del tiempo y evita el problema de la muestra sesgada.
Una comparación de ambas bases nos permite concluir que, aun existiendo diferencias, éstas no son determinantes en la definición de los resultados. La configuración de grupos y la ubicación de los países en cada uno de estos no se modifica si se usa una u otra clasificación.
La muestra abarca 123 países de todos los continentes, industrializados y en desarrollo. No incluye países de la ex Unión Soviética ni de Europa Oriental, así como países para los que faltan datos o que tienen menos de un millón de habitantes.
ESTIMACIÓN DE DENSIDAD DE KERNEL
En el siguiente cuadro se presentan las estadísticas descriptivas de las exportaciones de alta tecnología (AT) durante 1985 y 2004. La primera característica que aparece es el aumento de la media de estas exportaciones y el aumento conjunto del error estándar para el total de países. Podemos inferir que a lo largo de estos años se pudo haber producido algún tipo de movilidad dentro de la distribución a partir de estos cambios tanto en la media como en la dispersión.

Un primer acercamiento de gran utilidad es el análisis exploratorio de los datos, en especial con relación a su distribución a través de estimadores no paramétricos, los cuales ayudan a diagnosticar la situación antes de la estimación propiamente dicha. La observación de las distribuciones es una buena forma de comenzar a analizar los valores de los predictores lineales que vamos a utilizar posteriormente para cada grupo o club en la realización con las pruebas de mixturas finitas.
El estudio de los patrones de la dinámica de la distribución, como por ejemplo la posible evidencia de polaridad, es de extrema importancia si la misma implica una mejora o empeoramiento de la situación del progreso tecnológico y, consecuentemente, del crecimiento económico. En términos teóricos, el estimador de densidad de Kernel introducido por Rosenblatt (1956) generaliza el histograma usando una función alternativa de pesos.6
En la siguiente gráfica se presentan dos funciones de densidad de Kernel para 1985 y 2004, con amplitud media óptima. Cuanto mayor es la amplitud, mayor será la suavidad de la curva. Sin embargo, también es mayor la pérdida de información.

El análisis no paramétrico sugiere que a partir de 1985 las economías antes polarizadas en dos grupos comienzan a agruparse en tres componentes para 2004. Este tipo de análisis, a pesar de ser bastante intuitivo y esclarecedor, no nos informa el grado de confianza de nuestras conclusiones sobre la existencia de clubes y su cantidad, los límites de su alcance, las medias de sus participantes, su composición ni, principalmente, nos muestra los movimientos que ocurren dentro de la distribución a lo largo del tiempo.
La evidencia del análisis no paramétrico va en contra de las conclusiones de Grossman y Helpman (1995) sobre clubes tecnológicos cerrados. Los datos apuntan a una formación de clubes no cerrados con una pequeña probabilidad de transición entre grupos.
En las siguientes secciones consideraremos estas cuestiones a partir de un modelo de mixturas finitas para poder definir el número de grupos, su composición y el análisis de cadenas de Markov para estudiar la dinámica de transición entre los grupos y el equilibrio estocástico de largo plazo sobre la hipótesis de ergodicidad de la distribución.
PRUEBA DEL NÚMERO DE COMPONENTES EN UN MODELO DE MIXTURA FINITA
fx la densidad de distribución de las exportaciones de alta tecnología entre países de un año, y sea fY la densidad de las exportaciones de AT, entonces fY (y) = fx (ey)ey. La multimodalidad surge de fx como una mixtura finita de otras densidades unimodales. Entonces:

Donde los pesos pi > 0, Σpi = 1 y g(x; μ, σ) son una familia de densidades paramétricas, la distribución es log–normal. En este caso, en la distribución de exportaciones de alta tecnología los componentes corresponden a grupos con diferentes niveles de exportaciones de AT.
Las pruebas de modelos paramétricos se efectúan frecuentemente usando la prueba de razón de probabilidades (RP) . Para probar el número de componentes en modelos de mixtura finita, la teoría convencional de la prueba RP no se aplica. Recientemente Chen et al. (2001, 2004) sugieren modificar la prueba RP para resolver este problema.
En primer lugar, se considera la prueba de uno sobre dos componentes en la mixtura. Supongamos que Φ(x; μ, σ) es la distribución normal con media μ, y error estándar σ, y se considera la mixtura de dos componentes:
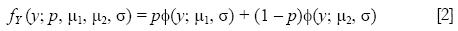
El problema a probar es: H0: fy tiene una distribución normal contra H1: fyes de la forma [2].
La función de verosimilitud es dada por:

Donde C es una constante fija (en este caso C=2). Sean  los parámetros que maximizan In(p, μ1, μ2, σ) y
los parámetros que maximizan In(p, μ1, μ2, σ) y  los que maximizan
los que maximizan  . La hipótesis H1 es rechazada para valores grandes de la prueba RP modificada:
. La hipótesis H1 es rechazada para valores grandes de la prueba RP modificada:

Para valores desconocidos de o la distribución asintótica de Mn se desconoce. Sin embargo Chen etal. (2001) demuestran que la distribución chi–cuadrada es una buena aproximación (en el límite superior).
RESULTADOS DEL ANÁLISIS ECONOMÉTRICO
Definición de los grupos dentro de la distribución
Aplicamos la metodología de los modelos de mixtura finita para el periodo 1985–2004 para todos los países de la muestra. En el cuadro 2 se presentan dos criterios de bondad de ajuste de los modelos, además de la prueba RP. El criterio de información de Akaike (AIC) (Akaike 1973) y el criterio de información bayesiano (BIC) (Schwarz 1978), dados por –2l+2k y –2l+k, donde l es el logaritmo de la probabilidad; k, el número de parámetros; n, el número de observaciones. El AIC siempre aparece en favor del modelo de tres componentes, mientras que el BIC se inclina por el modelo de dos componentes, lo que es de esperarse dado que tiende a seleccionar el modelo de menor número de componentes en el caso de muestras finitas, como es el caso de modelos de mixturas finitas. Debe recordarse que cuanto menor es el tamaño de los criterios AIC y BIC, mejor resulta el ajuste del modelo.
Como ya se mencionó, la prueba rp convencional no es válida en este caso. Chen etal. (2004) sugieren, con base en un estudio de simulación sobre la hipótesis nula de dos grupos, que la estadística calculada se distribuye como una x2 con 2v–2 grados de libertad, siendo v el número de parámetros extras en el modelo de tres grupos. Las hipótesis nula y alternativa son dadas por: H0: fy tiene n componentes7 contra H1: fy tiene n+1 componentes. En primer lugar, se observa que siempre dos grupos son preferibles a un grupo. Cuando comparamos dos y tres grupos, vemos que desde el inicio de la muestra (1985), los valores de la probabilidad van cayendo y, a partir de 1995, la prueba RP rechaza el modelo de dos grupos con un nivel de 5%. En las últimas columnas se comparan los modelos de tres y cuatro grupos dentro de la distribución. Para todos los años la prueba RP y los criterios de información de AIC y bic rechazan la presencia de cuatro grupos.
Resumiendo, nuestro análisis confirma la hipótesis realizada a partir del análisis gráfico, es decir, que al inicio de la distribución (en 1985) se inicia un configuración de tres grupos que sería confirmada en los años siguientes, como se verifica por el aumento de la significancia de la prueba RP sobre la hipótesis nula de tres grupos.
Composición de los grupos y evolución de la distribución
En el cuadro siguiente mostramos la distribución de los grupos para los años analizados, sus medias y sus errores estándar. Este cuadro resume las principales características de la distribución de los modelos de tres componentes desde 1985 hasta 2004. Comparando los resultados del primer y último año de la muestra, encontramos que 25 de los 123 países (20%) cambiaron de grupo en la distribución de exportaciones de alta tecnología (véase el Apéndice A). Esto implica una (relativamente) baja movilidad de países, dado que uno de cada cinco países cambia de situación o de grupo dentro de la distribución en casi dos décadas analizadas. Estudiar el comportamiento de los países según el enfoque de clubes tecnológicos tiene la ventaja de poder obtener parámetros de análisis más confiables dentro de una muestra de economías más homogénea. La existencia de diferentes componentes estocásticos en el proceso de desarrollo de las capacidades tecnológicas, mostrado con las pruebas de mixturas finitas, confirma la necesidad de segregación de estos grupos para el análisis. Estos clubes tienen dinámicas diferentes de convergencia/divergencia dentro y entre grupos.

El paso de 1985 a 2004 permite vislumbrar una polarización de la distribución, siendo el grupo intermedio el que presenta una mayor movilidad, proveyendo miembros para los grupos polares. La probabilidad de pertenecer al componente dos disminuye de 51 a 37 por ciento, aumentando la probabilidad de pertenecer al componente uno (de 29 a 35 por ciento) y al componente tres (de 20 a 28 por ciento).
Siguiendo el análisis de Krugman (1979), el desfase entre los grupos con menor intensidad tecnológica en sus exportaciones parece disminuir, dado que el grupo de menores exportaciones presenta un crecimiento de 1.7%, en tanto que el grupo intermedio presenta un crecimiento medio de 1.4% en sus exportaciones de alta tecnología. La diferencia de éstos con relación al grupo de mayor nivel de exportaciones de at aumenta, evidenciando la existencia de barreras a la imitación (por ejemplo, la disponibilidad de capital humano para I&D o la especificidad de la tecnología desarrollada en los países avanzados). A pesar de todo el cambio estructural observado en el periodo, con la reducción de la importancia relativa de la actividad industrial en los países de mayor nivel de ingreso, las exportaciones de bienes de alto tenor tecnológico tienen una tasa de crecimiento de 1.8% en los países avanzados, lo que aumenta las diferencias con relación a los otros grupos.
Al analizar la dispersión dentro de cada grupo, podemos notar que el de menor nivel de exportaciones presenta un aumento significativo del error estándar asociado a la variable en análisis. Podemos observar también que este aumento de la dispersión se debe principalmente a la inclusión de nuevos miembros ocurrida después de 1990. Este aumento de la dispersión se contrapone al grupo más avanzado que, aun cuando recibe nuevos miembros continuamente en el periodo analizado, presenta un error estándar decreciente entre 1985 y 2000, mientras que en 2004 retorna al nivel de 1985. El grupo intermedio tiene una distribución interna más homogénea hasta 1995 y hacia el 2000 se observa un aumento significativo de la dispersión, cuando 7% de sus miembros migran para otros grupos. La pérdida de estos miembros se consolida en el último año analizado, donde se nota una significativa reducción de la dispersión observada.
Los diferentes comportamientos observados dentro de los grupos muestran evidencias a favor del análisis de Baumol (1986). La configuración de estos grupos es compatible, a su vez, con la que determinan Castellacci y Archibugi (2005) en la conformación de tres clusters de acuerdo con diversos indicadores tecnológicos.8 A continuación se presentan estos grupos según la clasificación de los autores y se introducen los países en cada uno de los grupos a los que pertenecerían.9
Cluster 1: marginados (habilidades bajas, innovación baja, recuperación casi inexistente)
Se trata del mayor grupo de países, agrupaba más de 60% de la población mundial en 1990 y generaba 23% del producto interno bruto (PIB) mundial a inicios de la década del 2000. El núcleo de este cluster lo constituyen los países de África. Los miembros aumentan a lo largo del periodo considerado y sólo un número restringido de economías consigue recuperarse y sumarse al cluster de "seguidores" en la década del 2000 (Albania, Chad, Vietnam).
En el caso de Albania, la entrada al grupo de seguidores (tecnológicamente más avanzados) se da principalmente por la diversificación de sus exportaciones en tres rubros: aparatos eléctricos rotativos y sus partes, máquinas para la elaboración automática de datos y equipo de telecomunicaciones. Estos productos pasaron a representar 0.8, 1.5 y 1.1 por ciento del total de sus exportaciones. Las relativas a AT representaban 0.5% en 1985, para final del periodo pasaron a 4.3%. El avance de Chad se debe únicamente al aumento de un rubro, las aeronaves y equipo conexo, que pasa de 0.15% del total de exportaciones del país a casi 4 por ciento.
Otros países entran en el grupo porque disminuyen las exportaciones de alta tecnología (Bahamas, Barbados, Benin, Congo, Etiopía, Irak) o porque el aumento de éstas es menor que el aumento medio del grupo intermedio (Honduras,10 Jamaica, Zimbawe, Argelia).
Cluster 2: seguidores (habilidades medias– altas, baja innovación, lenta recuperación)
Comparado con el cluster anterior, este grupo muestra una habilidad mayor para crear e imitar conocimientos avanzados. La composición de este cluster se mantiene relativamente estable durante la década de 1990 e inicios de la década del 2000, y su núcleo está constituido por economías del Sudeste Asiático, el sur de Europa, Medio Oriente, América Latina, más el grupo de países que conformaban la ex Unión Soviética.
A inicios de la década del 2000 se producen algunos cambios en este grupo, especialmente la salida de un pequeño conjunto de economías dinámicas de Asia y Europa central (Hungría y Polonia), que se mueven hacia el grupo de países tecnológicamente avanzados. Se observa también la entrada de algunos pocos países de Asia (Vietnam), Medio Oriente (Siria) y América Central que mejoraron rápidamente sus capacidades tecnológicas a lo largo de los años noventa.
Vietnam muestra un aumento muy diversificado de exportaciones de AT, representando sólo 0.10% de las exportaciones totales en 1985. La diversificación hacia las exportaciones de máquinas para elaboración automática de datos y sus partes, equipos para telecomunicaciones, aparatos de electricidad, máquinas y aparatos eléctricos, lámparas, tubos y válvulas electrónicas de cátodo, aparatos eléctricos rotativos y sus partes, lleva a que éstas representen 3.4% en el total de las exportaciones para el 2004.
Cluster 3: avanzados (gran escala de producción de bienes de alta tecnología, habilidades, alta innovación, líderes dinámicos)
Grupo de países más avanzados tecnológicamente, compuesto por un pequeño grupo de economías industrializadas. Los miembros de este cluster se mantienen relativamente estables a lo largo del tiempo, siendo el mayor cambio registrado a inicios del siglo XXI con la entrada de unos pocos países muy dinámicos de Asia (Singapur, Hong Kong y Corea del Sur). Singapur ya tenía, a mediados de los años ochenta, una base exportadora de alta tecnología, dado que 28% de sus exportaciones totales era de rubros de AT. Por entonces consigue migrar al grupo de países que más exportan tecnología, representando esas exportaciones más de 50% del total para el 2004. Dos rubros muestran el mayor dinamismo: máquinas para elaboración automática de datos (al pasar de 1 a 15 por ciento del total exportado) y lámparas, tubos y válvulas electrónicas de cátodo (al pasar de 8 a 20 por ciento del total exportado).
En el mismo periodo, Corea del Sur tiene un crecimiento más explosivo y diversificado de sus exportaciones de AT. Éstas pasan de 14 a 43 por ciento de las exportaciones totales. Este crecimiento se explica especialmente por el aumento de equipo de telecomunicaciones (de 3 a 12.5 por ciento), máquinas para la elaboración automática de datos y sus partes (de 1.5 a 8 por ciento), instrumentos y aparatos de óptica (de 0.10 a 3.4 por ciento) y lámparas, tubos y válvulas electrónicas de cátodo (de 5 a 13.6 por ciento). Tailandia presenta un comportamiento similar (sus exportaciones de AT pasan de menos de 8 a 33 por ciento del total exportado) y los rubros de mayor dinamismo son los mismos que Corea del Sur.
Los países pertenecientes a este último grupo entran en una trayectoria tecnológica irreversible, al no observarse transiciones hacia los grupos inferiores. Se trata de países que logran captar tecnología en sus dos dimensiones: en primer lugar, tienen el conocimiento acerca de cómo crear nuevos productos de alta tecnología y, en segundo lugar, el conocimiento acerca de cómo producirlos. En otras palabras, cuentan con los conocimientos para innovar, tanto en los productos como en los procesos de producción de éstos (Fagerber y Verspagen 2002).
La capacidad tecnológica se muestra de esa forma acumulativa, en el sentido de que las innovaciones ocurren a través de un proceso continuo e irreversible. Países de ingreso medio y bajo con gran mercado (ya sea interno o por una buena inserción en el comercio internacional de bienes de alto contenido tecnológico) son más propicios a alcanzar a sus pares en términos de producto per cápita que aquellos con altos ingresos basados en recursos naturales. En la próxima sección haremos una comparación de las transiciones ocurridas entre los grupos estimados a partir de la estructura productiva o grupos estimados a partir del PIB per cápita.
Otros casos que se encuentran dentro del grupo de países altamente exportadores de bienes de alta tecnología no pueden insertarse dentro de esta clasificación de países avanzados tecnológicamente. Se trata del caso de Tailandia, China, Brasil, India y México. Si bien cada caso particular amerita un estudio que excede los límites de este trabajo, algunas consideraciones pueden ser establecidas. En general se trata de países con una escala importante de exportaciones de alta tecnología que no exhiben encadenamientos productivos fuertes, especializados en ciertas etapas de la cadena productiva que sólo requiere mano de obra barata y que presenta poca o nula innovación.
En el periodo considerado, Brasil e India no consiguen que la gran masa de exportaciones de AT implique un cambio en la estructura exportadora. Las exportaciones de AT pasan de 2 a 5 por ciento del total exportado en la India y ese aumento se debe principalmente al crecimiento de las exportaciones de productos medicinales y farmacéuticos. En el caso de Brasil, las exportaciones de AT representan 8% de las exportaciones totales, partiendo de 3% en 1985. Los rubros que sustentan este aumento son aeronaves, equipos conexos y sus partes y equipos de telecomunicaciones.
Diferente es el caso de China y México, que a lo largo del periodo aprovechan la gran escala de las exportaciones de AT para cambiar la estructura de exportaciones: China pasa de 2.5 a 30 por ciento de exportaciones de AT en el total exportado y México pasa de 9 a 24 por ciento11). El perfil del dinamismo es similar para los dos países, basado en un aumento notable de las exportaciones de máquinas para la elaboración automática de datos y sus partes, equipos de telecomunicaciones, lámparas, tubos y válvulas electrónicas de cátodo, además de receptores de televisión (México) y máquinas y aparatos eléctricos (China).
Reconociendo que estos últimos países están logrando un proceso de avance tecnológico, un estudio más amplio de la cadena productiva específica de cada producto y para cada país en las cuatro dimensiones apuntadas por Bair (2005), revelaría si estos cambios en la producción y exportación se reflejaron en beneficios sectoriales, generales o si en realidad generaron un proceso de exclusión (Gibbon 2001).
CADENA DE MARKOV
Muchos modelos de crecimiento resaltan la importancia de las condiciones iniciales en la determinación de equilibrios múltiples de largo plazo y la consecuente polarización de los niveles de PIB per cápita o capacidades tecnológicas. Nuestra hipótesis es menos restrictiva al asumir que existe una probabilidad positiva de transición entre los clubes en un periodo finito de tiempo. En este sentido, la herramienta adecuada para el análisis de un posible equilibrio de largo plazo es la cadena de Markov. Analizar la cadena de Markov es un elemento fundamental para conocer la evolución de las observaciones entre estados de una distribución. Dado un conjunto de estados, S = {s1, s2, ..., s r}, el proceso de Markov comienza con la distribución de las observaciones entre estos estados y analiza sus transiciones sucesivas de un estado a otro. Si la economía comienza en el estado si, posteriormente se mueve al estado sj con una probabilidad de pij, y esa probabilidad no depende del estado en el cual se encontraba antes.
Las probabilidades pij son llamadas probabilidades de transición. La economía puede, sin embargo, permanecer en el mismo estado, con probabilidad pii. Una distribución de probabilidad inicial, definida sobre S, especifica el estado inicial como un estado particular.
Para nuestro caso de tres grupos, podemos definir la matriz de transición como sigue:

Las entradas de la primera columna de la matriz P representan las probabilidades de que los distintos niveles de exportaciones de alta tecnología (baja, media y alta) ocurran después de que la economía pertenezca al grupo de bajas exportaciones de bienes de alta tecnología. Las entradas de la segunda y tercera columna representan las probabilidades de que los grupos de exportadores pasen al nivel medio y alto de exportaciones de alta tecnología, respectivamente.

No se observó ningún cambio significativo entre las dos matrices para el periodo inicial, intermedio y final de la muestra. Para la matriz de transición 85–95, la línea B indica, en pbb, la probabilidad de que los componentes pertenecientes al grupo de menor cantidad exportada de at en 1985 permanezcan en el mismo grupo en 1995 (85% del total de países permanece en la misma situación); en pmb, la probabilidad de los componentes que, perteneciendo al grupo de baja cantidad de exportaciones de AT en 1985, pasan hacia el grupo de media cantidad de exportaciones de AT (16% de los países) y, en pab, la probabilidad de los componentes que, perteneciendo al grupo de baja cantidad de exportaciones de AT, pasan a altas exportaciones de AT. Existe una transición frecuente entre los dos primeros grupos en los periodos analizados, lo que muestra la fragilidad del proceso de despegue tecnológico. Más raras son las transiciones del grupo intermedio hacia el de gran producción y exportación de bienes de alto contenido tecnológico (0.5% dos países). Sin embargo, esta transición parece haber crecido en el segundo periodo, aunque no llega a 1% de probabilidad, lo que muestra que aun aumentando, no representa una gran cantidad de países.
La matriz presenta una diagonal principal dominante, resaltando la inercia del status quo. Para conocer el comportamiento estocástico de largo plazo de nuestra distribución, procuramos el vector ergódico. Una cadena de Markov es llamada ergódica si es posible cambiar de un estado particular a otro cualquiera. Por otro lado, la cadena será regular si la matriz de transición tiene sólo elementos positivos. En otras palabras, para cualquier n es posible cambiar de cualquier estado a otro en exactamente n pasos.
Para llegar al vector ergódico, partimos del estado inicial de la distribución. Se considera el vector de probabilidades iniciales, que es un vector columna de r componentes cuyas entradas son negativas y suman 1. Si u es el vector de probabilidades que representa el estado inicial del proceso de Markov, entonces el componente i–ésimo de u representa la probabilidad de que el proceso comience en el estado si. Para 1985, el vector de probabilidades de estado inicial es:

Sea P la matriz de transición de un proceso de Markov y sea u el vector de probabilidades que representa la distribución inicial, entonces la probabilidad de que el proceso llegue al estado si después de n pasos es la i–ésima entrada en el vector:
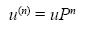
Para nuestro caso, tenemos el siguiente vector de probabilidad de la distribución de largo plazo, después de diecinueve pasos:

La matriz de transición de exportaciones de alta tecnología es regular, pero no puede ser caracterizada como ergódica, dado que tenemos un estado absorbente en la última fila de la matriz. Un estado si de una cadena de Markov es llamado absorbente si es imposible dejar ese estado (pii = 1). Una cadena de Markov es absorbente si tenemos al menos un estado absorbente y si para todo estado es posible convertirse en otro estado que sea absorbente. Una característica de matrices de Markov absorbentes es que no podemos encontrar el vector único fijo de largo plazo que definiría un equilibrio de largo plazo, esto es, una matriz de Markov que converge para un estado en el cual los tres vectores columna de la matriz son iguales.
Un ejercicio útil es comparar la matriz de transición de exportaciones de alta tecnología con otra matriz de PIB per cápita para el mismo periodo. Esta matriz de producto fue construida a partir de los datos de producto per cápita real (ajustado por paridad de poder de compra) de la Penn World Table, mark 6.2 (Heston et al. 2006). Como puede observarse, las matrices son similares con predominio de la diagonal principal, lo que manifiesta que así como los países tienden a mantenerse en la misma situación a lo largo del tiempo respecto a la cantidad exportada de bienes de alta tecnología, la misma situación aparece con los niveles de producto per cápita. Sin embargo, podemos apreciar algunas diferencias. En primer lugar, existe una movilidad mayor en la línea de bajo ingreso que en el caso de las exportaciones. Es verdad que ningún país de la muestra pasa del grupo bajo al alto, pero una cantidad mayor de países migra de la situación de bajo producto hacia producto medio per cápita, que en el caso de migraciones de exportaciones (24% contra 14%). En segundo lugar, la situación contraria sucede en el grupo intermedio: la movilidad es mayor en el caso de las exportaciones de alta tecnología que en el caso del producto.
Podemos observar que las líneas se van diferenciando a medida que crece el nivel de exportaciones de bienes de alta tecnología. Para la primera línea de probabilidades de transición, los dos indicadores son bastante próximos, lo que puede significar que la transición entre los dos primeros grupos puede estar más disociada del proceso de mejora de las capacidades tecnológicas. Las transiciones del grupo intermedio se diferencian más entre los indicadores presentados. Las mayores diferencias se observan en los países de mayores exportaciones de bienes con alto contenido tecnológico y aquellos de mayor producto. Mientras que en la matriz de transición de grupos de PIB per cápita existe una probabilidad positiva de que las economías del grupo de los ricos descienda al grupo intermedio, en la matriz de transición de exportaciones de AT esta probabilidad es nula. Dos ejemplos de transición que se observan en el primer caso son Venezuela e Irán, países en el grupo de los ricos en la década de los setenta que después de cambios en los precios relativos del petróleo vieron reducirse sus niveles de producto per cápita a la media de los países intermedios. El segundo hecho refleja la acumulación del aprendizaje tecnológico en contraposición a la fragilidad relativa de los altos niveles de producto per cápita cuando éstos se basan en recursos naturales.
Una vez que la economía entra en el círculo virtuoso del aprendizaje al exportar bienes de alta tecnología (aprendizaje por la práctica y aprendizaje por exportar) existe una "trampa positiva del conocimiento" que impide que esa economía vuelva a exportar en los niveles de los grupos inferiores. Nuevamente, debe aclararse que esto no significa inequívocamente que se produzca una mejora en el ingreso per cápita del país que realiza tal avance.
CONCLUSIONES
El trabajo tuvo como objetivo principal analizar el número de grupos que pueden estimarse dentro de la distribución de exportaciones de alta tecnología, considerando el periodo 1985–2004. La prueba RP modificada permite concluir que existen tres componentes en todos los casos, aumentando la significancia desde el inicio de la muestra (1985, 9%; 2004, 5%). Las pruebas de AIC y BIC divergen en cuanto al número de grupos elegidos, lo que se esperaba por la definición de estos criterios, concluyendo que el AIC elige tres componentes dentro de la distribución y el BIC, dos componentes. La prueba concluye, por lo tanto, un aumento de la polarización de los niveles de contenido tecnológico de las exportaciones de los países de la muestra.
A lo largo del periodo se percibe una movilidad importante interdistri–bución, partiendo hacia una mayor polarización, como puede analizarse a partir de la disminución de miembros en el segundo componente a favor del primero y del tercer componente. La media de exportaciones de productos de alta tecnología aumenta en todos los grupos; sin embargo, con una mayor dispersión en el primer grupo y mayor concentración en el grupo de países avanzados. El aumento de la media en el conjunto de países atrasados se da principalmente por la llegada al grupo de nuevos miembros provenientes del grupo intermedio, que no logran mantenerse en este grupo y que al pasar al grupo de bajas exportaciones de AT generan un aumento de la media de este grupo.
El análisis de las distribuciones de largo plazo no significa que no hubo un movimiento de cambio del régimen de Markov en el periodo analizado. La polarización del producto estaba "escrita" desde los años iniciales del análisis. A través de la comparación de las matrices de transición de exportaciones y de producto podemos concluir que éstas están fuertemente ligadas con ventajas para el análisis de tecnología. El carácter acumulativo de la tecnología permite una mayor estabilidad de nuestros grupos, principalmente el de alto contenido de tecnología/PIB per cápita porque excluye, en estos casos, países con alto producto basados en productos básicos y, por lo tanto, con gran fragilidad con relación a cambios de precios relativos.
Referencias
Akaike, H., "Information theory and an extension of the maximum likelihood principle", en B.N. Petrov y P. Csaki (eds.), Second International Symposium on Information Theory, Estados Unidos, (IEEE), 1973, pp. 267–281. [ Links ]
Amable, B. y B. Verspagen, "The role of technology in market share dynamics", Applied Economics, vol. 27, núm. 2, 1995, pp. 197–204. [ Links ]
Archibugi, D. y J. Michie, "The globalization of technology: a new taxonomy", Cambridge Journal of Economics, vol. 19, 1995 (número especial sobre tecnología e innovación). [ Links ]
Bair, J., "Global capitalism and commodity chains: looking back, going forward", Competition & Change, vol. 9, núm. 2, 2005, pp. 153–180. [ Links ]
Bair, P. y E. Peters, "Global commodity chains and endogenous growth: export dynamism and development in Mexico and Honduras", World Development, vol. 34, núm. 2, 2006, pp. 203–221. [ Links ]
Barro, R., "Economic growth in a cross section of countries", National Bureau of Economic Research (NBER) Working Papers no.3120,1991. [ Links ]
Barro R. y X. Sala–i–Martin, "Convergence", Journal of Political Economy, vol. 100, núm. 2, 1992, pp. 223–251. [ Links ]
Baumol, W.J., "Productivity growth, convergence and welfare: what the long–run data show", American Economic Review, vol. 76, núm. 5, 1986, pp. 1072–1085. [ Links ]
Beaudry, P.; E Collard y D.A. Green, "Changes in the world distribution of output per worker, 1960–1998: how a standard decomposition tells us an unorthodox story", Review of Economics and Statistics, núm. 87, 2005, pp. 741–753. [ Links ]
Bernard A. y S. Durlauf, "Interpreting test of the convergence hypothesis", Journal of Econometrics, vol. 71, núm. 1, 1996, pp. 161–173. [ Links ]
Castellacci, F. y D. Archibugi, "The technology clubs in the world economy", mimeo, 2005. [ Links ]
Chen, H.; J. Chen y J.D. Kalbfleisch, "A modified likelihood ratio test for homogeneity in finite mixture models", Journal of the Royal Statistical Society: Series B (Statistical Methodology), vol. 63, 2001, pp. 19–29. [ Links ]
––––––––––, "Testing for a finite mixture model with two components", Journal of the Royal Statistical Society: Series B (Statistical Methodology), vol. 66, 2004, pp. 95–115. [ Links ]
Dosi, G.; K. Pavitt y L. Soete, The economics of technical change and international trade, Londres, Harvester–Wheatsheaf, 1990. [ Links ]
Durlauf, S.N. y P.A. Johnson, "Multiple regimes and cross–country growth behavior", Journal of Applied Econometrics, vol. 10, núm. 4, 1995, pp. 365–384. [ Links ]
Fagerberg, J. y B. Verspagen, "Innovation, growth and economic development: have the conditions for catch–up changed?", International Journal of Technological Learning, Innovation and Development, vol. 1, núm. 1, 2007. [ Links ]
––––––––––, "Technology gaps, innovation–diffusion and transformation: an evolutionary interpretation", Research Policy, vol. 31, núms. 8–9, 2002, pp. 1291–1304. [ Links ]
Gibbon, P., "Upgrading primary production: a global commodity chain approach", World Development, vol. 29, núm. 2, 2001, pp. 345–363. [ Links ]
Grossman, G. y E. Helpman, "Technology and trade", en G. Grossman y K. Rogoff (eds.), Handbook of International Economics, Elsevier, vol. 3, 1995. [ Links ]
Hatzichronoglou, T., "Revision of the high–technology sector and product classification", Organization for Economic Co–operation and Development (OECD) Science, Technology and Industry Working Papers no. 1997/2, 1997. [ Links ]
Hausmman, R.; J. Hwang y D. Rodrik, "What you Export Matters", NBER Working Paper Series no.1905, 2005. [ Links ]
Heston, A., R. Summers y B. Aten, Penn World Table Version 6.2, Center for International Comparisons of Production, Income and Prices at the University of Pennsylvania, 2006. [ Links ]
Howitt, P. y D. Mayer–Foulkes, "Implementation and stagnation: a Schumpeterian theory of convergence clubs", NBER Working Papers no. 9104, 2002. [ Links ]
Jones, C., "Growth: with or without scale effects?", American Economic Review Papers and Proceeding, vol. 89, núm. 2, 1999. [ Links ]
Krugman, P., "A model of innovation, technology transfer, and the world distribution of income", Journal of Political Economy, vol. 87, núm. 2, 1979, pp. 253–266. [ Links ]
Montobbio, F. y F. Rampa, "The impact of technology and structural change on export performance in nine developing countries", World Development, vol. 33, núm. 4, 2005, pp. 527–547. [ Links ]
Nakajima, T., "Catch–up in turn in a multi–country international trade model with learning–by–doing and invention". Journal of Development Economics, vol. 72, núm. 1,2003, pp. 117–138. [ Links ]
Pritchett, L., "Divergence, big time", Journal of Economic Perspectives, vol. 11, núm. 3, 1997, pp. 3–17. [ Links ]
Quah, D.T., "Empirical cross–section dynamics in economic growth", European Economic Review, vol. 37, núm. 2–3, 1993, pp. 426–434. [ Links ]
––––––––––, "Twin peaks: growth and convergence in models of distribution dynamics", Economic Journal, vol. 106, núm. 437, 1996, pp.1045–1055. [ Links ]
Rosenblatt, M., "Remarks on some nonparametric estimates of a density function", Annals of Mathematical Statistics, vol. 27, 1956. [ Links ]
Schwarz, G., "Estimating the dimension of a model", Annals of Statistics, núm. 6, 1978. [ Links ]
TradeCAN, Base de datos de comercio de la CEPAL y World Bank, CD–ROM, 2006. [ Links ]
Vernon, R., "The product cycle hypothesis in a new international environment", Oxford Bulletin of Economics and Statistics, núm. 41, 1979, pp. 255–267. [ Links ]
* Los autores agradecen los valiosos comentarios y sugerencias de dos dictaminadores anónimos de la revista, así como de Gabriel Porcile, Antonio Carlos Macedo e Silva y Gustavo Sorá.
** JEL: Journal of Economic Literature–Econlit.
1 La tecnología es el resultado de una actividad humana que puede ser entendida si tenemos en cuenta cuatro aspectos fundamentales apuntados por Archibugi y Michie (1995). En primer lugar, la tecnología no es un bien libre, los productores de nuevos conocimientos cuentan con una variedad de métodos legales y económicos para obtener retornos por sus innovaciones. La imitación tiene un costo y consume tiempo. En segundo lugar, una amplia parte del conocimiento asociado a la tecnología es tácito, específico de agentes económicos como individuos, empresas y naciones. Este conocimiento sólo puede ser adquirido por largos procesos de aprendizaje. En tercer lugar, existen variaciones entre diferentes campos tecnológicos y esas variaciones implican variaciones en la experiencia necesaria para tener acceso a esas tecnologías. Por último, la evolución del conocimiento es influenciado por el conocimiento acumulado por los agentes en el pasado.
2 Llamamos a estos grupos clubes verdaderos con interacción entre sus miembros. La hipótesis probada aquí es más general, es decir, economías con diferentes grados de especialización en bienes de alta tecnología agrupadas por elementos de la distribución de probabilidades comunes, independientemente de su localización geográfica y socios comerciales.
3 En el modelo de Grossman y Helpman (1995) la producción de nuevas ideas crece a una tasa de

donde A son nuevas ideas, L es la fuerza de trabajo. En el caso del modelo de Jones (1999), este crecimiento estará dado por A = δLAAΦ, donde Φ<1. Así, cambios en la actividad investigadora no generan más un crecimiento exponencial.
4 El tipo de datos observados puede ser considerado como datos longitudinales o en panel. Este tipo de datos es obtenido por una selección de una muestra S y la recolección de observaciones por una secuencia de periodos de tiempo, t = 1, ...,T.
5 Quedan excluidas principalmente las importaciones de las economías en transición, y las importaciones de algunos países africanos. El número de países informantes puede variar ligeramente de la versión anterior debido a la disponibilidad de datos, dado que fueron descartados los países sin información por más de tres periodos consecutivos.
6 Esta función está dada por:

donde los parámetros son h y el de suavidad (smoothing parameter) llamado de amplitud. K es el tipo de función de Kernel utilizada (Epanechnikov, uniforme, Gaussiano, Quartic).
7 En el caso de un componente dentro de la distribución se trata de una distribución normal.
8 Incluye medidas de ocho características: patentes, publicaciones científicas, penetración de internet, penetración de telefonía, consumo de electricidad, matrículas en el nivel terciario en ciencias e ingeniería, años medios de estudio y tasa de alfabetización.
9 Debe dejarse claro que este ejercicio, sin embargo, no significa una relación uniquívoca entre exportaciones de alta tecnología–innovación tecnológica.
10 Para un análisis de la relación entre exportaciones y crecimiento de Honduras véase Bair y Peters (2006).
11 El caso de México, además de presentar un aumento de las exportaciones manufactureras aumentando su participación en el comercio mundial, presenta también una caída en la participación mundial del valor agregado manufacturero, lo que estaría mostrando el carácter de país ensamblador.














