Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Investigación económica
versão impressa ISSN 0185-1667
Inv. Econ vol.68 no.269 Ciudad de México Jul./Set. 2009
Integración comercial del sector agrícola y desigualdad económica en los países en vías de desarrollo
Trade integration of the agricultural sector and economic inequality in developing countries
Thierry Baudasse* y Cuauhtémoc Calderón Villarreal**
*Universidad de Orleáns (Francia) <thierry.baudasse@univ–orleans.fr>
**El Colegio de la Frontera Norte, <ccalderon22@hotmail.com>.
Manuscrito recibido en febrero de 2008
Aceptado en mayo de 2009.
Resumen
Este artículo analiza el impacto de las políticas de liberalización en el sector agrícola en los países en vías de desarrollo. Nuestro trabajo pone en evidencia que la liberalización de la agricultura en estos países no reduce automáticamente la desigualdad del ingreso en su territorio. Se utilizó una muestra de 54 países, para los períodos 1980–1990 y 1980–2000 y realizamos estimaciones de sección cruzada para estudiar el efecto Kuznets–Ahluwalia sobre esta muestra. En el artículo se concluye que en los países con una proporción baja de productos alimentarios en el consumo total la liberalización del sector aumenta las desigualdades, mientras que en el caso de los países con una proporción alta de productos alimentarios en su consumo la liberalización disminuye las desigualdades en términos generales.
Palabras clave: desigualdad económica, liberalización del sector agrícola, políticas proteccionistas.
Clasificación JEL: Q17, F15, C21, D33
Abstract
In this paper, we analyse the impact of liberalization policies on agriculture in developing countries. Our work suggests that agricultural liberalization in developing countries is not necessarily generating a decrease in inequality. We use a sample of 54 countries for the periods 1980–1990 and 1980–2000 and apply cross–sectional estimations to study Kuznets–Ahluwalia effects. We have found that for countries where the share of alimentary products in the consumption basket is small, liberalization of agriculture tends to increase inequality as oppose to those where such share is larger, in which case liberalization tends to diminish income inequality.
Key words: economic inequality, agricultural liberalization, protection policies.
INTRODUCCIÓN
En las últimas décadas el sector agrícola de los países en vías desarrollo ha estado sometido a importantes cambios estructurales. Las estrategias de desarrollo económico aplicadas en el período 1960–1970 dieron prioridad a la aplicación de políticas agrícolas cuyo objetivo fue la manipulación de los términos internos del intercambio. Su intención era transferir recursos del sector agrícola al sector industrial y contribuir de este modo al proceso de industrialización de estos países. Esta política agrícola contribuyó a mantener al sector agrícola en el estancamiento, a reducir su productividad y a aislarlo del progreso técnico. Esta política tampoco incitó a los productores agrícolas a modernizar ni a aplicar los frutos del progreso técnico. Además, la presencia de infraestructuras públicas inadecuadas e insuficientes y la falta de acumulación de capital humano contribuyeron a mantener esta tendencia hacia el estancamiento económico y baja o nula productividad.
Entre 1980 y 1990, ante un sector agrícola estancado y con baja productividad, los gobiernos y las agencias internacionales como el Banco Mundial propusieron un nuevo modelo que implicaba la puesta en marcha de un proceso de cambio estructural en este sector. Esta nueva estrategia se proponía liberalizar la producción y la comercialización de los productos agrícolas de los países en vías de desarrollo. Para ello el objetivo prioritario era la desregulación de los mercados agrícolas para permitir la asignación eficaz de los recursos productivos. El Banco Mundial sugirió que la liberalización y la desregulación de estos sectores serían las medidas adecuadas para mejorar la situación económica de los sectores más desfavorecidos de la sociedad como la población rural. Así, de acuerdo con la propuesta del Banco Mundial la presencia de un sector agrícola desregulado y abierto a la competencia lo conduciría a la especialización con base las ventajas comparativas haciendo a la agricultura más eficiente y productiva. Con lo cual se incrementarían los ingresos de los productores agrícolas y se reducirían así las desigualdades de ingreso en los países no desarrollados. De este modo, desde la perspectiva del Banco Mundial la liberalización del sector agrícola conduciría por vía de los automatismos del mercado a la reducción de la desigualdad económica en estos países.
Sin embargo, este razonamiento es cuestionable ya que no se puede reducir al sector agrícola de los países en desarrollo a una agricultura basada en la ventaja comparativa. Dado que, una parte importante de este sector está formado por productores que ofrecen productos alimenticios que compiten con las importaciones agrícolas (cereales, ganadería, entre otros). La apertura del mercado de las agriculturas tradicionales y poco eficientes hace que sus productos entren en competencia con las importaciones provenientes de países con mayores ventajas o con productos subvencionados. Esta situación provoca una reducción del precio nacional de los bienes alimenticios y la disminución de los ingresos agrícolas, cuestión que trae consigo el incremento de los movimientos migratorios internos, el aumento del desempleo y la eclosión del sector informal de la economía. El análisis que presentamos a continuación se sitúa en esta perspectiva teórica.
En la primera sección, presentaremos un modelo teórico que reproduce el conjunto de circunstancias estilizadas de una economía en desarrollo con un sector agrícola tradicional de substitución. Este modelo se utiliza enseguida para realizar una evaluación numérica de los efectos de la baja del precio agrícola interno sobre la distribución de los ingresos. Se identifican dos casos principales en función de la proporción de bienes alimenticios en la canasta de consumo (α): uno de ellos establece una relación negativa entre los precios y las desigualdades del ingreso (α pequeña), el otro presenta una indeterminación de la cual hablamos posteriormente (α grande). Después proponemos una interpretación intuitiva de la importancia de α y algunas simulaciones.
En la segunda sección, realizamos un análisis econométrico donde presentamos los aspectos metodológicos y los resultados de la aplicación de un modelo de corte transversal. En una primera parte se expone la metodología económica aplicada. En el segundo apartado se presentan los resultados econométricos de las regresiones de corte transversal estimadas por mínimos cuadrados ordinarios (MCO). Y por último se presenta la interpretación de los resultados empíricos.
DISMINUCIÓN DE LOS PRECIOS AGRÍCOLAS Y DESIGUALDADES EN LOS INGRESOS: ANÁLISIS Y SIMULACIONES
Modelo
El equilibrio del modelo está determinado por las doce ecuaciones que mencionamos a continuación, en las que las variables endógenas son: Pa, Pu, P, La, Li, Eu, Lu, wa, wi, ra, ru, y q y las variables exógenas son: pa, pu, α, Ka, Ku, N, Qi, wu y h:

Este sistema define un equilibrio al estilo Harris–Todaro–Fields. La idea básica del modelo es que los trabajadores se distribuyen entre las diversas actividades económicas, mediante las migraciones entre sectores hasta que se iguala la esperanza de ingreso de las diferentes actividades. En este caso, la elección se realiza entre el sector agrícola (en el que el salario es perfectamente flexible y por ende la oferta de trabajo es igual a la demanda), el sector urbano formal y el sector informal.
Si pa es el precio del bien agrícola y f(La, Ka) la función de producción del sector,1 el salario nominal agrícola es el valor del producto marginal [Pa · f'L(La, Ka)] y el salario real denominado wa es igual al salario nominal sobre el índice general de precios (P), por ejemplo, el precio de la canasta de consumo. Pa es igual al ratio pa/P según la ecuación [10]. En el sector urbano formal, el salario real (wn) está fijado institucionalmente por encima del salario de equilibrio, lo que genera una oferta excedentaria de trabajo. Si q es la probabilidad de encontrar un empleo formal urbano, cuando esta búsqueda de empleo se realiza a tiempo completo, y si en caso de existir desempleo el ingreso primario es nulo, la esperanza de ingreso correspondiente a una búsqueda de empleo a tiempo completo es q · wu (ecuación [2]).
Una tercera probabilidad es trabajar en el sector informal urbano y seguir buscando al mismo tiempo una actividad formal. Esta hipótesis fue presentada por primera vez por Fields (1975) y consiste en afirmar que los trabajadores agrícolas no pueden, desde el sector rural, buscar un empleo urbano formal. Sin embargo, estos poseen dos estrategias en caso de que deseen pasar al sector urbano. La primera opción consiste en ir a la ciudad y abocarse a la búsqueda de empleo a tiempo completo; a pesar de que esto implique para el trabajador no recibir remuneración durante el tiempo que tarde en encontrar un empleo. La segunda opción es ocupar un empleo informal en la ciudad (se supone que el acceso al sector informal es libre); esperando que esta situación les permita multiplicar las oportunidades de encontrar un empleo formal y al mismo tiempo ejercer una actividad remunerada durante el tiempo de espera. Esta visión del sector informal es evidentemente imperfecta y no da cuenta de la complejidad de las situaciones y de las motivaciones de los trabajadores del sector informal. Sin embargo, adoptaremos esta hipótesis del sector informal como sector de espera a fin de simplificar la representación de nuestra economía.
Evidentemente, la búsqueda de un empleo formal es más difícil al ocupar un empleo en el sector informal. El parámetro h mide esta dificultad: si q es la probabilidad de encontrar un empleo abocándose de tiempo completo a esta tarea, la probabilidad de obtener un empleo formal para un miembro del sector informal es h*q, siendo que h está comprendida entre 0 y 1. La igualdad de la esperanza de ingreso del sector de espera y del sector agrícola está representada en la ecuación [3]. La ecuación [4] expresa el valor del salario real del sector informal: supondremos, para simplificar, que este sector está constituido por pequeños empresarios idénticos, que comparten también un nivel fijo (en términos reales) de actividad (Qi). Por lo tanto, el ingreso real (wi) en el sector informal es una función inversa del número de trabajadores de ese sector (ecuación [4]). La ecuación [5] permite determinar tanto el nivel del empleo2 (Eu) en el sector formal, en función de wu fijado de manera institucional, como el de Pu que es el ratio del precio del bien (pu) producido por ese sector y del nivel general de precios (P). La ecuación [12] da el valor de P = α · pa + (1 – α) · pu3 en el cual aparece el parámetro a que representa el peso de los productos agrícolas en el consumo global. Este parámetro tendrá una importancia particular en los resultados del modelo y conviene destacarla. Eu representa el número de empleos formales urbanos deseados tanto por la fuerza de trabajo formal urbana (Lu) como por la fuerza de trabajo informal urbana (Li). La probabilidad promedio de conseguir un empleo formal es entonces de Eu/(Lu + Li ). Se demuestra gracias a la formula de probabilidades totales, que si q es la probabilidad de conseguir un empleo formal para un elemento de Lu entonces q = Eu/(Lu + Li · h) (ecuación [6]). Las ecuaciones [7] y [8] dan el valor de la remuneración real del capital en la agricultura (ra) y en el sector formal urbano (rn).
Por último, supondremos que cada capitalista del sector agrícola posee una unidad de capital y de esta manera Ka representa a la vez el capital del sector agrícola y al número de capitalistas de dicho sector. Ocurre lo mismo en el sector formal urbano, Ku representa al número de capitalistas urbanos y la cantidad de capital de ese sector. No existe capital en el sector informal. La población total, N, es fija y está compuesta, además de los capitalistas, por N – Ka – Ku trabajadores, que son trabajadores del sector agrícola (La), o trabajadores del sector informal (Li), o trabajadores del sector urbano formal (Eu), o individuos en busca de empleo a tiempo completo (Lu – Eu) (ecuación [9]).
Es conveniente destacar que nuestro punto de partida es la hipótesis de que el salario real del sector formal es superior al salario de equilibrio; esto supone que Lu > Eu. Para reunir esta condición es necesario y suficiente que:

Al sustituir el valor de wa dado por [1] y el valor de Eu dado por [5] en [16] se obtiene una ecuación que determina implícitamente el valor de La, y de wa, lo que permite determinar Li y posteriormente Lu. En consecuencia, las demás variables se determinan fácilmente.
Disminución de pa y evolución de los ingresos primarios4
Evolución del número de desempleados
Un primer enfoque consiste en estudiar la evolución del número de individuos sin empleo, cuyo ingreso primario es nulo. Se demuestra que:

mientras que el segundo término puede ser negativo o positivo. Este término está compuesto a su vez por dos factores. El primero, dwa/dpa puede ser positivo o negativo, según α sea pequeña o grande, mientras que el segundo es necesariamente negativo si se respeta la condición [13]. Por lo tanto, si dwa/dpa es positivo (α pequeña) Lu – Eu aumenta cuando pa disminuye, lo que significa que la disminución de los precios agrícolas aumenta el número de desempleados. Cuando dwa/dpa es negativa la expresión [17] posee en el numerador un término negativo y un término positivo. La expresión [17] puede, en ese caso, ser positiva si el segundo término es un valor absoluto superior al primero. Para explicitar este razonamiento presentaremos un ejemplo más adelante en el que el número de des empleados disminuye cuando pa disminuye.
Evolución de los ingresos del trabajo y del capital
El ingreso real global de los activos puede disminuir o aumentar luego de una disminución de pa, según el signo de dwa/dpa. Efectivamente, el ingreso real global5 es igual a Eu · wu + La · wa + Li · wi. Ahora bien, se puede demostrar que:

lo que significa que el signo de la ecuación [18] es el mismo que el signo de dwa/dpa. Por lo tanto, cuando dwa/dpa es positivo (α pequeña) el ingreso real global de los asalariados disminuye si pa disminuye, mientras que una disminución de pa genera un aumento del ingreso global de los asalariados en caso contrario. Por otra parte, el número de activos que comparten el ingreso global es N–Ka – Ku por hipótesis constante. De esta forma, el ingreso real promedio de los activos evoluciona en forma paralela a wa.
Además, la evolución del ingreso real de los capitalistas varía según el sector de actividad.6 Se demuestra que:

lo que significa que cuando pa disminuye los beneficios del sector rural se reducen, mientras que los beneficios del sector urbano aumentan. El ingreso real total de los capitalistas (ru · Ku + ra · Ka) puede entonces aumentar o disminuir según el signo de:

Por lo tanto, la evolución relativa de los ingresos de los capitalistas y de los trabajadores no es fácil de estudiar a partir del caso general. Es por eso que a continuación nos limitaremos a un estudio más detallado de las desigualdades dentro de la categoría de los trabajadores. Debe destacarse sin embargo que cuando α tiende a cero, dru/dpa tiende también a cero,7 mientras que dra/dpa permanece positivo,8 lo que significa que cuando α tiende hacia cero, el ingreso real total de los capitalistas tiende a caer cuando pa disminuye.
Evolución de las desigualdades entre los trabajadores
La curva de Lorenz que representa las desigualdades entre los trabajadores (incluyendo los trabajadores sin empleo) tiene la siguiente forma:

En este gráfica, el eje horizontal muestra el porcentaje acumulado de trabajadores y el eje vertical el de los ingresos recibidos por los trabajadores. Los trabajadores más pobres son los individuos sin empleo que representan una fracción (Lu – Eu)/(Lu + Li+ La) de la población activa y comparten 0% del ingreso total. La jerarquía de los salarios de los otros trabajadores se establece fácilmente a partir de las ecuaciones [2] y [3]: queda demostrado que necesariamente tenemos wu > wa > wi. Los salarios más bajos son los del sector informal que representan una fracción Li(Lu + Li + La) de la población y comparten una fracción Liwi/(Eu · wu + La · wa + Li· wi) del ingreso total. Le siguen los asalariados agrícolas y por último los asalariados del sector formal urbano. Los movimientos de la curva de Lorenz, cuando pa desciende dependen del movimiento de los puntos A, B y C. Sabemos por otra parte que la pendiente de AB es wi/(Eu · wu + La · wa + Li · wi)/(Lu + Li + La), es decir, el ratio de wi sobre el ingreso promedio de la población activa. La población activa posee por hipótesis un número constante de individuos N – Ka – Ku, por ende la pendiente de AB varía como el ratio wi/(Eu · wu + La · wa + Li · wi) que, a partir de ahora, denominaremos γ. Ahora bien tenemos que:

lo que significa que el signo de dya/dpa es el mismo que el signo de dwa/dpa. Sabemos finalmente que la pendiente de CD es igual al ratio de wu sobre el ingreso promedio de los activos, que varía como sigue: wu/(Eu · wu + La· wa + Li · wi). Teniendo en cuenta que wu es constante y positivo, la derivada de este ratio con respecto a pa es de signo opuesto a dwa/dpa (en virtud de la ecuación [18]). Para estudiar los deslizamientos de la curva de Lorenz es necesario diferenciar el caso en que dwa/dpa es positivo del caso en que es negativo.
Caso 1: dwa/dpa positivo. En este caso, sabemos que si pa disminuye, Lu –Eu aumenta (véase la ecuación [17], la pendiente de AB disminuye y la pendiente de CD aumenta. Por lo tanto, la curva de Lorenz se desliza hacia el exterior: las desigualdades entre activos aumentan cuando pa disminuye.
Caso 2 : dwa/dpa negativo. En este caso es necesario distinguir entre dos sub–casos: uno en el que d(Lu –Eu)/dpa es positivo (el número de desempleados disminuye cuando pa desciende) y otro en el que d(Lu –Eu)/dpa es negativo. En el primer subcaso, nos encontramos en la hipótesis inversa al caso 1: estamos en presencia de un deslizamiento de la curva de Lorenz hacia el interior cuando pa disminuye, entonces las desigualdades disminuyen. El segundo subcaso es más complejo dado que el nuevo punto A se sitúa por debajo de la anterior curva de Lorenz, mientras que la pendiente de CD disminuye, las dos curvas de Lorenz se cruzan. En este último caso, puesto en evidencia por Atkinson (1975) entre otros, es difícil evaluar la evolución de las desigualdades, pues siempre pueden encontrarse dos indicadores de desigualdades que evolucionan en sentido contrario. En el ejemplo de la última parte de esta sección, demostraremos que un índice como el de Gini y otro índice más que utilizamos,9 varían en este contexto en sentido inverso.
Interpretación intuitiva
El modelo que expusimos en las secciones precedentes muestra que la evolución de las desigualdades depende sustancialmente del valor del parámetro α , que representa la parte de los bienes agrícolas en la canasta de consumo. Así en el caso que α sea grande el incremento del empleo formal urbano es lo suficientemente importante para absorber el flujo migratorio que proviene del sector rural; mientras que si tenemos un α pequeño la expansión del sector urbano formal no es lo suficientemente grande para absorberlo. El incremento del empleo formal está ligado a la caída de los precios agrícolas, que permiten disminuir el salario nominal conservando el mismo salario real. Cuando α es grande la caída de los precios agrícolas disminuye fuertemente el nivel general de precios y por tanto es posible reducir sustancialmente el salario nominal en el sector urbano, de donde se da una expansión del empleo en ese sector.
Si α es grande, la caída del precio interno de los insumos agrícolas no reduce mucho el salario real en el sector rural, dado que los trabajadores sólo consumen los bienes agrícolas que producen (en presencia de autoconsumo en el sector rural). En este caso la presión migratoria no proviene del deterioro de la situación rural, sino del mejoramiento del empleo urbano formal. El mejoramiento del empleo urbano formal trae consigo efectos positivos sobre el sector rural y una disminución del empleo informal nacional y extranjero.
En el caso de un α pequeño los trabajadores rurales producen un bien agrícola cuyo precio disminuye y consumen esencialmente bienes manufacturados cuyos precios son constantes. La degradación de los términos del intercambio interno (relación entre los precios agrícolas y los precios de los bienes manufacturados) trae consigo una caída de los salarios reales en el sector rural. Y el sector formal urbano no experimenta una expansión notable. La migración rural–urbana es consecuencia de la degradación de la situación rural. Dado que el empleo urbano formal no crece el empleo informal nacional e internacional aumenta.
Una simulación numérica

con los siguientes valores: pu = 400, N = 111 000, Ka = 10 000, Ku = 1 000, wu = 5/1 000, h = ½, Qi = 20

pa puede tomar diferentes valores: 200, 100, 50, 40.
Diferenciaremos el caso en que a es pequeña (0.2) y por lo tanto dwa/dpa es positivo (caso 1), y el caso en que a es grande (0.7), por lo tanto dwa/dpa es negativo (caso 2).
Caso 1: α es pequeña
Cuando pa es igual a 100, la distribución del ingreso primario de los activos (asalariados y trabajadores sin empleo) está dada como se muestra en el cuadro 1.

Mientras que cuando pa es igual a 200 pasamos a la siguiente distribución:

El desplazamiento de las curvas de Lorenz está resumido en la gráfica 2. Notamos que cuando pa disminuye, las desigualdades aumentan (la curva de Lorenz se desplaza hacia el exterior).

Caso 2: α es grande
En este caso es necesario distinguir dos subcasos: uno en el que la derivada de (Lu –Eu) con respecto a pa es positiva (caso 2.1) y otro en el que esta derivada es negativa (caso 2.2). El primer caso está ilustrado por un cambio de pa = 50 a pa = 40, mientras que el segundo caso está ilustrado por un cambio de pa = 200 a pa = 100.
Caso 2.1: d(Lu – Eu)/dpa es positivo. Consideremos la distribución cuando pa es igual a 50:

y la distribución cuando pa es igual a 40:

La transición de la primera a la segunda repartición está representada en la gráfica siguiente, que muestra el deslizamiento de la curva de Lorenz:

Constatamos aquí que la disminución de pa trae aparejado un deslizamiento de la curva de Lorenz hacia el interior, es decir, una reducción de las desigualdades.
Caso 2.2: d(Lu–Eu)/dpa es negativo. El siguiente cuadro resume la distribución del ingreso primario al equilibrio cuando pa = 100:

Cuando pa = 200 la distribución del ingreso se modifica como sigue a continuación:

El deslizamiento de las curvas de Lorenz está representado en la gráfica 4.

Constatamos que las curvas de Lorenz se cruzan. Es entonces aventurado concluir un aumento o una disminución de la desigualdad cuando pa disminuye. Efectivamente, es posible medir el nivel de desigualdades mediante el índice de Gini.10 De esta manera es posible utilizar como índice de desigualdad la relación entre la porción de ingresos en manos del 20% más rico y la porción de ingreso en manos del 40% más pobre (índice denominado I1); o de manera más simple, el porcentaje del ingreso total en manos del 50% de los individuos más ricos (índice que llamaremos I2). En el ejemplo, los valores de estos índices se muestran en el cuadro 7.

Notamos que cuando pa disminuye, el índice de Gini muestra una disminución de las desigualdades, mientras que los índices I1 y I2 presentan un aumento de las desigualdades.
ANÁLISIS ECONOMÉTRICO
En los párrafos siguientes se presentan los aspectos metodológicos y resultados de un ejercicio econométrico. Estimamos un modelo de corte transversal sobre una muestra de 54 países en vías de desarrollo. El objetivo del estudio es contrastar empíricamente la hipótesis siguiente: existe una relación negativa entre los precios agrícolas y las desigualdades en aquellos países donde la proporción de consumo de bienes alimentarios (α) con respecto al consumo total es relativamente pequeña; mientras que puede existir una relación positiva para aquellos países donde existe una α relativamente grande. Se utiliza el coeficiente de Gini como un indicador de la desigualdad del ingreso.
El tamaño de la muestra estuvo condicionada por la disponibilidad de los datos correspondientes a las variables utilizadas (véase el cuadro 8).

Metodología empírica
La literatura especializada sobre la curva de Kuznets considera que la relación entre el índice de Gini y el ingreso per cápita tiene la forma de una "U" invertida. Por lo que una dificultad en nuestro trabajo consistió en eliminar el efecto de esta relación estructural. Para ello decidimos "controlar" el índice Gini de los efectos estructurales inducidos por el nivel de desarrollo. Procedimos en dos etapas: en la primera, estimamos una relación de tipo Kuznets "condicionada" a partir de la versión propuesta por Ahluwalia (1976) donde además de la forma cuadrática del ingreso (expresada en logaritmos11 LY y L2Y) incorporamos como variable de control la tasa de escolarización secundaria (scol). Las estimaciones se realizaron para tres años 1980, 1990 y 2000. Obtuvimos tres regresiones de base (Gini80, Gini90 Gini00, véanse los cuadros A1 y A3). A partir de estas regresiones de base contrastamos nuestras hipótesis.
En la segunda etapa utilizamos como variable explicada las variaciones de los residuos para cada uno de los períodos de estudio 1980–1990 y 1980–2000 y como variable explicativa las variaciones del precio agrícola (definido como la relación del deflactor del valor agregado agrícola con respecto al deflactor del producto interno bruto, PIB). Es decir:

donde, dresl es la variación de los residuos y dprd es la variación de los precios agrícolas.
El modelo sugiere la existencia de un valor hipotético α* a partir del cual podemos dividir la muestra en dos grupos de países: los países cuyo α es inferior a α*, (α < α*), donde existe una relación precio–desigualdad decreciente; y los países cuyo α es superior a α* (α > α*) donde existe una relación precio–desigualdad creciente. En un primer momento establecimos la hipótesis de que este valor es común a todos los países y calculamos el valor empírico de α* a partir del cual se puede definir la existencia de dos grupos de países. Para ello estimamos la ecuación [21] para la totalidad de la muestra de países (54) y contrastamos la estabilidad de esta ecuación con la ayuda de la prueba de Chow recursiva. Se trata de un proceso iterativo que determina el valor del parámetro α* que maximiza el estadístico de Chow (que es un Fischer). De este modo se busca un punto crítico para el cual la inestabilidad de la regresión es la más fuerte. Los resultados de las pruebas de Chow recursivas, para el período 1980 –1990 y 1980–2000, se encuentran en los cuadros A2 y A4 y en las gráficas A1 y A2.
Finalmente utilizamos un modelo probit para verificar la influencia de la variable α sobre la relación entre precios agrícolas y desigualdades.
Resultados
En los cuadros A1 y A3 del Anexo A se presentan los resultados de las regresiones de sección cruzada estimadas por MCO. En el cuadro A1 se exponen los resultados del período 1980 1990, y se puede destacar que el efecto Kuznets–Ahluwalia es muy significativo en 1980 mientras que la influencia del ingreso sobre el índice de Gini es menos significativa en 1990. En el cuadro A3 se exponen los resultados correspondientes al período 1980 y 2000.
En la muestra de las α pequeñas en ambos períodos la variable dresl tiene una relación negativa pero no significativa con la variable dprd (veánse los cuadros A1 y A3), y en la muestra de las α grandes existe una relación positiva y significativa entre dichas variables.
Para confirmar nuestros resultados sobre la muestra total construimos una variable dummy (propos) que toma el valor de 1 cuando el producto dprd*dresl es positivo, lo que significa que los precios agrícolas y las desigualdades varían en el mismo sentido. El resultado esperado es que cuando α es más grande la probabilidad de que la variable dummy (propos) tome el valor de 1 es mayor.
El modelo probit dio los resultados siguientes para el período 1980–1990:
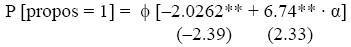
donde Φ es la función integral de la ley normal.
Los resultados del modelo probit para el período 1980–2000 fueron los siguientes:
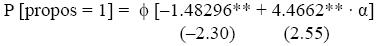
donde Φ es la función integral de la ley normal.
Ambos resultados confirman la validez de las hipótesis del modelo que hemos aplicado.
Interpretación de los resultados empíricos
La falta de significancia de la relación estadística que relaciona a las variables dresl y dprd cuando α es pequeña no es necesariamente consecuencia de la debilidad del modelo teórico utilizado. De acuerdo con el marco teórico existe un valor teórico α* igual a 1/C. En el caso de que el valor efectivo tomado por α sea inferior a α* se daría una relación negativa entre el precio agrícola y las desigualdades. Sin embargo, nada dice que el valor "frontera" α* sea el mismo para todos los países. Por lo que es conveniente distinguir entre cuatro tipos diferentes de datos:
• Los valores efectivos de αi, en cada país que son los datos empíricos utilizados en nuestro estudio econométrico.
• Los valores frontera teóricos α*i, que dependen de las características económicas y técnicas de cada país. Estos valores están dados para el modelo como iguales a 1/C y son específicos para cada país.
• El valor vinf tal que, cualquiera que sea el país i, vinf < α*i. Este es el valor mínimo tomado por α*i.
• El valor vsup tal que, cualquiera que sea el país i, vsup > α*i. Este es el valor máximo tomado par α*i.
Si se tiene un gran número de países para los cuales el valor efectivo de αi es inferior a vinf tendremos para todos estos países una relación negativa y significativa entre los precios agrícolas y las desigualdades, puesto que para todos estos países se tendrá un αi < vinf < α*i. Si existe un gran número de países para los cuales se tiene un valor efectivo αi superior a vsup, tendríamos para todos estos países una relación positiva y significativa entre los precios agrícolas y las desigualdades. Puesto que para el conjunto de estos países se tendrá αi > vsup > α*i, nuestros resultados significan que el valor vsup es aproximadamente 0.45 (si tomamos como medida de α la parte de los productos agrícolas en el consumo total). No determinamos estadísticamente el valor de vinf probablemente porque no existen suficientes países para que αi sea inferior a vinf. Ejemplo:

En este ejemplo el valor vsup = Max (α*i) = 0.39 y el valor vinf = Min (α*i) = 0.2. Tenemos cuatro países de los nueve (B, C, F y I) que tienen valores de α superiores a vsup, y por lo tanto se puede subrayar que para todos los países que tienen un α superior a 0.39 tenemos una relación positiva entre desigualdad y precios agrícolas. Por el contrario, no existen países que tengan un valor de α inferior a vinf mientras que tres de nueve países cumplen con la condición α < α*. Si tomamos 0.39 como valor que separa a nivel global a los países con "una gran α" de los países con "una pequeña α" obtendríamos:

En el grupo de países con "una gran α" se puede destacar fácilmente la existencia de una relación positiva entre precios agrícolas y desigualdad. Sin embargo, en el grupo de países con "una α pequeña" es evidente que la relación entre precios agrícolas y desigualdades es no significativa, puesto que para tres países de este grupo (E, G y H) la relación es negativa, pero en el caso de dos países del grupo (A y D) es positiva.
CONCLUSIONES
La importancia de nuestro trabajo radica en que definimos un criterio científico a partir del cual se pueden estudiar y diferenciar los efectos del proceso de liberalización del sector agrícola sobre la desigualdad económica en los países en vías de desarrollo. Consideramos que estos efectos dependen sustancialmente del valor del parámetro α, que representa la parte de los bienes agrícolas en la canasta de consumo. Si en los países existe un parámetro α pequeño la liberalización del sector agropecuario incrementará la desigualdad; si se da un α grande el efecto será ambiguo (en unos países la liberalización reducirá la desigualdad, mientras que en otros la aumentará). De esta manera, concluimos que las teorías ortodoxas, promovidas en el marco de las políticas del Consenso de Washington, según las cuales la liberalización del sector agrícola trae consigo la reducción automática de las desigualdades económicas no tienen validez general y sólo se cumplen para cierto grupo de países donde existe un α grande. Del grupo de 54 países en vías de desarrollo que estudiamos, encontramos que en aquellos países cuyo parámetro α es pequeño la liberalización del sector agrícola incrementa las desigualdades; mientras que en los países cuyo parámetro α es grande la liberalización tiende a reducir las desigualdades económicas. Dentro del universo de países en vías de desarrollo que estudiamos identificamos dos grupos. El primero está integrado por aquellos con un α pequeño, para los cuales la apertura del sector agrícola empeoró la distribución del ingreso aumentando la desigualdad económica, como es el caso de México, Brasil y la India. Y el Segundo grupo está integrado por los países que cuentan con un α grande, para los que la apertura del sector agrícola mejoró la distribución del ingreso como es el caso de Bangladesh, Egipto e Indonesia (Anexo B). El modelo que utilizamos sugiere que la liberalización de la agricultura en los países en vías de desarrollo no trae consigo la reducción automática de la desigualdad del ingreso. Dado que en aquellas economías cuyo sector rural está protegido y cuyas ventajas comparativas no se explotan el desmantelamiento de la protección propicia movimientos migratorios intensos, causantes de fuertes desequilibrios económicos. El sector moderno urbano puede absorber a la oferta de trabajo suplementaria únicamente si la rentabilidad de la actividad económica urbana aumenta; con salarios reales rígidos la baja del precio relativo de los productos alimenticios puede solucionar el problema a condición de que los productos alimenticios tengan un peso importante dentro de la canasta de consumo (un gran α). Mientras que en el caso contrario (α pequeño) la rentabilidad cae y el sector urbano no es capaz de absorber el exceso de mano de obra. Las reformas Mexicanas son un caso paradigmático y una muestra clara de cómo en un país con un α reducido las reformas aplicadas no sólo fracasaron sino que acentuaron las desigualdades económicas, puesto que posibilitaron el incremento de la migración del sector rural hacia el urbano, así como el aumento en el tamaño del sector informal y la aceleración de la migración de fuerza laboral mexicana hacia Estados Unidos. Conduciendo con ello al incremento de la desigualdad económica entre los mexicanos. En el caso de México las reformas económicas liberalizadoras del sector agropecuario procuraron la constitución de un private–sector–driven rural economy, es decir, un sector rural orientado por la dinámica del mercado, lo que implicó la desaparición de toda forma de propiedad social sobre la tierra (reforma constitucional del 1992) y la minimización de toda forma de propiedad estatal de producción y comercialización. Junto con estas reformas se aplicaron medidas de política social de tipo asistencialista para mitigar los desequilibrios derivados de la transición hacia unaprivate–sector–driven rural economy, como Procampo, Alianza para el Campo y Solidaridad. Aunado a esto el Acuerdo General sobre Aranceles Aduaneros y Comercio (GATT) y el Tratado de Libre Comercio de América del Norte (TLCAN) trajeron consigo la reducción progresiva de los aranceles a la importación de productos agropecuarios provenientes de Estados Unidos. En el marco del TLCAN la liberalización de las partidas agropecuarias (01–24) tuvo varios plazos (0, 5, 10 y 15 años) con un plazo máximo de 15 años, a partir de la entrada en vigor del tratado el 1 de enero de 1994. Cerca de 38% de los rubros se liberalizó inmediatamente después de la firma del TLCAN al reducir sus aranceles a la importación en 0%. En plazos de 5, 10 y 15 años se liberalizaron 11, 38, y 13 por ciento de los rubros (Calderón 2006). Sin embargo, el resultado de estas reformas fue modesto, el sector agropecuario se estancó, la participación del sector agropecuario en el PIB total cayó de 7.5% en 1995 a 4% en 1999, y la pobreza se incrementó en el sector, lo cual aceleró la migración hacia los sectores urbanos y hacia Estados Unidos.
El análisis de las políticas de liberalización del sector agrícola en los países en desarrollo deja en claro que el nivel de tolerancia de la sociedad a las reformas del sector rural constituye un desafío crucial. Las economías que lo liberalizan, sobre una base multilateral o regional, deben prever importantes desequilibrios en el plano económico sectorial y migratorio.
En términos de política económica se deberá poner más atención en las dificultades derivadas de la liberalización del sector agrícola en las economías con un α reducido, como es el caso de los países latinoamericanos, asiáticos y otros países (Anexo B) cuya liberalización trajo consigo el aumento de: la migración internacional, el sector informal urbano, las ciudades y las desigualdades económicas. Por lo tanto, para el caso de estas economías las medidas más adecuadas consistirían en liberalizar tan sólo parcialmente a este sector y de manera gradual de 5 a 15 años. Acompañando este proceso con dos tipos de acciones, las primeras tendientes a reforzar las capacidades productivas y competitivas de la unidades productivas nacionales del sector y las segundas medidas de política social–integral tendientes a corregir los efectos negativos de la liberalización sobre la distribución de la riqueza. El objetivo prioritario sería minimizar la migración internacional y establecer también un acuerdo migratorio temporal con el país receptor del flujo laboral, como por ejemplo Estados Unidos.
Todas estas medidas de política económica procurarían fortalecer la productividad del sector agrícola y la competitividad de las unidades productivas. Además es necesario aplicar la ciencia para el desarrollo de nuevas tecnologías que fortalezcan la productividad. Asimismo, serían necesarias medidas de planeación que acompañen el crecimiento de los polos urbanos de manera ordenada, así como incrementar la capacidad de las actividades económicas para absorber al sector informal y sobre todo poner en marcha una reforma fiscal integral para corregir las desigualdades económicas emanadas de la liberalización.
AGRADECIMIENTOS
Este artículo es parte del Proyecto de Investigación de Ciencia Básica del Consejo Nacional de Ciencia y Tecnología (Conacyt) núm. 60098 "Integración de México en el TLCAN: sus efectos sobre el crecimiento, la reestructuración productiva y la migración", cuyo director es Cuauhtémoc Calderón Villarreal. Los autores agradecen los valiosos comentarios y sugerencias de dos dictaminadores anónimos.
REFERENCIAS
Adelman, I. y N. Fuwa, "Income inequality and development, the 1970's and 1980's compared", Economie Appliquée, tomo 46, núm. 1, 1994, pp. 7–29. [ Links ]
Ahluwalia, M.S., "Inequality, poverty and development", Journal of Development Economics, vol. 3, 1976, pp. 307–342. [ Links ]
Alesina, A. y R. Perotti, "The political economy of growth: a critical survey of the recent literature", The World Bank Economic Review, vol. 8, núm. 3, 1994, pp. 351–371. [ Links ]
Anand, S. y S.M.R. Kanbur, "Inequality and development, a critique", Journal of Development economics, vol. 41, 1993, pp. 19–43. [ Links ]
Atkinson, A.B., The Economics of Inequality, Oxford, Oxford Clarendon Press, 1975. [ Links ]
Batra, R.N. y N. Naqvi, "Urban unemployment and the gains from trade", Economica, vol. 54, 1987, pp. 368–381. [ Links ]
Baudassé, T. y T. Montalieu, "Les Conséquences de l'ALENA sur l'agriculture traditionnelle, le secteur informel et les mouvements migratoires au Mexique", en J. De Melo y P. Guillaumont (eds.), Commerce nord–sud, migration et délocalisation economica, 1997, pp. 343–361, [ Links ].
Bhagwati, J.N. y T.N. Srinivasan, "On reanalyzing the Harris–Todaro model: policy rankings in the case of sector–specific sticky wages", American Economic Review, vol. 64, 1974, pp. 502–508. [ Links ]
Bowman, K.S., "Should the Kuznets effect be relied on to induce equalizing growth: evidence from the post–1950 development", World Development, vol. 25, núm.1, 1997, pp.127–143. [ Links ]
Calderón, C., "Apertura económica, salarios y migración internacional", Análisis Económico, vol. XXI, núm. 46, primer cuatrimestre de 2006, pp. 167–187. [ Links ]
Carter, M.R. y B.L. Barham, "Level playing fields and laissez faire: postliberal development strategy in inegalitarian agrarian economies", World Development, vol. 24, núm. 7, 1996, pp.1133–1149. [ Links ]
Clarke, G., "More evidence on income distribution and growth", Journal of Development Economics, vol. 47, 1995, pp. 403–427. [ Links ]
Cleaver, K.M. y W.G. Donovan, "Agriculture, poverty and policy reform in sub–saharan Africa", World Bank Discussion Papers no. 280, 1995, 49 p. [ Links ]
Corden, W. M y R. Findlay, , "Urban unemployment, intersectoral capital mobility and development policy", Economica, vol. 42, 1975, pp. 59–78. [ Links ]
Datta, C.T., "A theoretical analysis of the informal sector", World Development, vol. 17, 1989, pp. 351–355. [ Links ]
Datta, C.T. y S. Adhikari, "Free trade zones with Harris–Todaro unemployment: a note on Young–Miyagiwa", Journal of Development Economics, vol. 41, 1993, pp. 157–162. [ Links ]
De Janvry, S. y G. Gordillo de Anda, "Nafta and Mexico's Maize Producers", World Development, vol. 23, núm. 8, 1995. [ Links ]
Fields, G.S., "Rural–urban migration, urban unemployment and underemployment and job search activity in LDC's", Journal of Development Economics, vol. 2, 1975, pp. 165–187. [ Links ]
––––––––––, "Changes in poverty and inequality in developing countries", World Bank Research Observer, vol. 4, núm. 2, 1989, pp. 167–185. [ Links ]
Gupta, M.R., "Rural–urban migration, informal sector and development policies", Journal of Development Economics, vol. 41, 1993, pp. 137–151. [ Links ]
––––––––––, "Tax on foreign capital income and wage subsidy to the urban sector in the Harris–Todaro model", Journal of Development Economics, vol. 47, 1995, pp. 469–479. [ Links ]
Harris, J.R. y M.P. Todaro, "Migration, unemployment and development: a two sector analysis", American Economic Review, vol. 60, 1970, pp. 126–142. [ Links ]
Jha, S.K., "The Kuznets curve: a reassessment", World Development, vol. 24, núm. 4, 1996, pp. 773–780. [ Links ]
Josling, T., "Agricultural trade policies in the Andean Group", World Bank Technical Paper, núm. 364, 1997, 35 p. [ Links ]
Khan, M.A., "The Harris–Todaro hypothesis and the H.O.S. trade model", Journal of International Economics, vol. 10, 1980, pp. 527–547. [ Links ]
Kuznets, S., "Economic growth and income inequality", American Economic Review, marzo, 1955. [ Links ]
Levy, S. y S. Van Wijnbergen, "Maize and the Free Trade Agreement between Mexico and the United States", World Bank Economic Review, vol. 6, núm. 3, 1992, pp. 481–502. [ Links ]
––––––––––, "Labor markets, migration and welfare. Agriculture in the North American Free Trade Agreement", Journal of Development Economics, vol. 43, 1994, pp. 263–278 [ Links ]
Marjit, S., "Agro–based industry and rural–urban migration", Journal of Development Economics, vol. 35, 1991, pp. 393–398. [ Links ]
Martin, W. y L.A Winters (eds.), "The Uruguay Round and the developing economies", World Bank Discussion Papers no. 307, 1995, 456 p. [ Links ]
McCool, T., "Wage subsidies and distortionary taxes in a mobile capital Harris–Todaro model", Economica, vol. 49, 1982, pp. 69–79. [ Links ]
McKinley, T. y D. Alarcon, "The prevalence of rural poverty in Mexico", World Development, vol. 23, núm. 9, 1995, pp. 1575–1585. [ Links ]
Neary, J.P., "On the Harris–Todaro model with intersectoral capital mobility", Economica, vol. 48, 1981, pp. 219–234. [ Links ]
Oshima, H.T., "The impact of technological transformation on historical trends in income distribution of Asia and the West", The Developing Economies, vol. XXXI, núm. 3, septiembre de 1994. [ Links ]
Persson, T. y G. Tabellini, "Is inequality harmful to growth?", American Economic Review, vol. 84, núm. 3, 1994, pp. 600–621. [ Links ]
Psacharopoulos, G., S. Morley, A. Fiszbein, H. Lee y WC. Wood, "Poverty and income inequality in Latin America during the 1980's", Review of Income and Wealth, vol. 41, núm. 3, 1995, pp. 245–264. [ Links ]
Rakowski, C.A., "Convergence and divergence in the informal sector debate: a focus on Latin America, 1984–92", World Development, vol. 22, 1994, pp. 501–516. [ Links ]
Ram, R., "Economic development and income inequality: further evidence on the "U" curve hypothesis", World Development, vol. 16, núm. 11, 1988, pp. 1371–1375. [ Links ]
Randolph, S.M. y WF. Lott, "Can Kuznets effect be relied on to induce equalizing growth ?", World Development, vol. 21, núm. 5, 1993, pp. 829–840. [ Links ]
Rauch, J.E., "Modelling the informal sector formally", Journal of Development Economics, vol. 35, 1991, pp. 33–47. [ Links ]
Rodrik, D., "King Kong meets Godzilla: The World Bank and the East Asian miracle", Centre for Economic Policy Research (CEPR) Discussion Paper no. 944, 1994. [ Links ]
Todaro, M.P, "A model of labor migration and urban unemployment in less developed countries", American Economic Review, vol. 59, 1969, pp. 138–148. [ Links ]
Valdés, A., "Surveillance of agricultural price and trade policy in Latin America during major policy reforms", World Bank Discussion Papers no. 349, 1996, 67 p. [ Links ]
Valdés, A. y J. Zietz, "Distorsions in world food market in the wake of GATT: evidence and policy implications", mimeo, World Bank, 1994, 27 p. [ Links ]
Zénou, Y, "Chômage urbain et migration dans les PVD ", Revue d'Economie Politique, vol. 105, 1995, pp. 293–314. [ Links ]
FUENTES DE DATOS
Gini: World Institute for Development Economics Research of the United Nations University (UNU–WIDER), World Income Inequality Database, version 2.0a, junio de 2005. Disponible en la página web: <http://www.wider.unu.edu/wiid/wiid–introduction–2005–1.htm> [ Links ].
α2 (productos alimenticios en el consumo total, datos de 1996): US Department of Agriculture, Economic Research Service. Disponible en la página web: <http://www ers.usda.gov/data/InternationalFoodDemand> [ Links ].
αl (productos alimenticios en el PIB, datos de 1985): Banco Mundial, CD–ROM World Development Indicators, 1994. [ Links ]
Tasa de escolarización secundaria y producto nacional bruto (PNB) por cabeza en dólares corrientes (método del ATLAS): Banco Mundial, CD–ROM World Development Indicators, 2004. [ Links ]
Deflactores del PIB y deflactores del valor agregado agrícola: Banco Mundial, CD–ROM World Development Indicators, 1994 y 2004.
1 La función/(L, K) es homogénea lineal, 
2 La función de producción del sector que denominamos g(Ku, Lu) tiene las mismas propiedades que la función f (cfr. nota anterior).
3 Se supone que el sector informal produce el mismo bien que el sector formal, de precio pu , lo que explica que nuestra economía se compone de tres sectores pero sólo dos bienes: un bien urbano de precio pu y un bien agrícola de precio pa.
4 Las demostraciones de los razonamientos matemáticos de este artículo no se incluyen por restricciones de espacio pero pueden solicitarse a los autores.
5 Asalariados y desempleados.
6 Suponemos que no hay movilidad de capital entre los sectores, lo que implica que Ka y de Ku permanecen constantes.
7 Cuando los bienes agrícolas no forman parte de la canasta de consumo nacional la disminución de los precios agrícolas no tiene consecuencias sobre los beneficios urbanos.
8 La disminución de los precios agrícolas continúa afectando los beneficios agrícolas.
9 Que dan mayor peso a los más pobres.
10 
11 La forma cuadrática del ingreso lineal también fue contrastada y proporciona resultados menos robustos.














