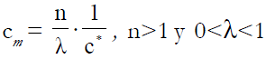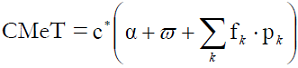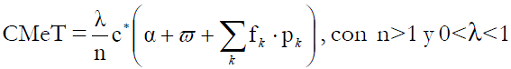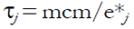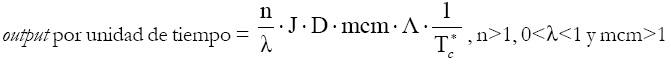Introducción
Nicholas Georgescu-Roegen fue un matemático y economista original y brillante cuya obra, con múltiples aportaciones en los ámbitos de la estadística y la teoría económica, está siendo injustamente olvidada.1 Entre sus muchos trabajos, destaca el modelo de los fondos y los flujos cuyas bases teóricas propuso en los años sesenta y la primera mitad de los setenta del pasado siglo. Se trata de un modelo de equilibrio parcial sobre los procesos productivos diseñado como una alternativa a la función de producción neoclásica. Los autores de este artículo pensamos que este modelo, a pesar de sus limitaciones, debería merecer una mayor atención habida cuenta de su enorme capacidad, como se demuestra en este trabajo, para abordar con éxito aspectos clave de la organización de las actividades productivas.
Aspectos básicos del modelo
De forma muy simplificada, tres son las ópticas para el análisis económico de la producción.
La transformación de unos determinados insumos en productos. Este punto de vista subraya los rasgos técnicos de los elementos implicados en el proceso e intenta una descripción pormenorizada de las operaciones llevadas a cabo en su seno.
Creación de valor. En este caso, el objetivo analítico primordial es desvelar los mecanismos que definen y modifican los precios relativos de los elementos implicados en el proceso.
Un conjunto de decisiones de gestión y control de las tareas productivas.
El modelo de los fondos y flujos pertenece claramente a la primera categoría. En efecto, el modelo se configura como una fotografía detallada de la organización interna del proceso productivo, que deja a un lado la concepción de caja negra empleada por otras propuestas teóricas. Por consiguiente, el modelo contiene una lista exhaustiva de los elementos participantes en él, clasificados en fondos y flujos, a la vez que el tiempo aparece como una dimensión explícita del proceso. En suma, el modelo aborda el proceso de producción como un conjunto de operaciones coordinadas y ejecutadas por elementos complementarios entre sí y cuyas actuaciones están ordenadas en fases, según una clara secuencia temporal.
Los fondos se caracterizan por aportar sus servicios productivos durante un cierto intervalo de tiempo. Por ello, los fondos entran y salen del proceso. Son fondos los trabajadores, la tierra (entendida en tanto que superficie), las instalaciones y equipos de producción y los stocks.
Como es sabido, durante el proceso de producción los trabajadores se fatigan y los fondos fijos se deprecian. Georgescu-Roegen (1969; 1971; 1976) sugiere que las actividades dedicadas a la recuperación, mantenimiento y reparación de los fondos sean consideradas como procesos separados del estudiado, simplificando así el análisis.
Los flujos entran como insumos o abandonan como outputs el proceso. Hay cinco tipos de flujos: el output principal (simple o conjunto), las unidades de output que no cumplen el estándar de calidad establecido, los subproductos y residuos, los recursos naturales (como la radiación solar, el aire, el agua, los minerales, etc.) y, para finalizar, los bienes intermedios procedentes de procesos previos como las materias primas, los productos semielaborados, las partes y componentes, la energía, las semillas, etcétera.
El modelo de los fondos y los flujos se preocupa por la composición temporal del proceso de producción. Así, el modelo lleva a cabo una labor de disección con base en el siguiente esquema:
Las operaciones básicas son todos aquellos gestos, movimientos corporales, etcétera, que toda actividad de transformación requiere. Por otra parte, “una tarea es un operación productiva completa llevada a cabo sin interrupción sobre un objeto particular” (Scazzieri, 1993, p. 84). En este punto, hay que recordar que cada proceso de producción se puede identificar por el programa específico de tareas que contiene (Landesmann y Scazzieri, 1996a, p.198; Landesmann, 1986, p. 289).
Las fases coinciden con las grandes transformaciones que sigue el producto en curso. Por ejemplo, en el caso del automóvil aparecen seis fases claramente separadas: el mecanizado de los bloques de motor y acoplamiento de sus componentes básicos, el troquelado de paneles de chapa con prensas y matrices, el montaje y soldado de carrocerías, la aplicación de la pintura (con diversos tipos y capas), las operaciones de montaje de conjuntos (añadido de motores, ejes y sistemas de transmisión, etc.), el ensamblaje manual de interiores (asientos, salpicadero, etc.) y la revisión final.
Sin duda, el concepto clave es el de proceso elemental: la disposición temporal de actividades de transformación, que permiten obtener una unidad de producto en una determinada planta. La elaboración de esta unidad separable de output, exige la puesta en marcha de un conjunto de materiales, equipos y agentes que constituyen la unidad técnica mínima del proceso (Morroni, 1992, p. 23). Así pues, por una parte, un proceso cuya escala sea menor que un proceso elemental, no está económicamente justificado, aunque pueda ser técnicamente factible y, por la otra, todas las operaciones productivas de un proceso elemental configuran un determinado estado tecnológico.
Finalmente, por proceso de producción se entiende la actividad corriente de las explotaciones agrícolas o de las instalaciones industriales. Esto es, el conjunto de procesos elementales, o volumen de output por unidad de tiempo, que elabora una unidad de producción o planta. Por tanto, el concepto de proceso de producción se refiere al aspecto más directamente observable de la actividad productiva: la sucesión de los procesos elementales según las tres formas de disponer su ejecución: en secuencia, en paralelo o en línea.2
Los rasgos esenciales de cada una de estas modalidades de organizar un proceso productivo son los siguientes:
La disposición secuencial consiste en ejecutar al completo un proceso elemental tras otro. De esta forma, cuando se ha terminado del todo la elaboración de una unidad de output, se inician las operaciones productivas correspondientes a la siguiente. Este método de organizar la producción se asocia con la fabricación artesanal de mercancías.
El despliegue en paralelo es típico de la agricultura. En este caso, la producción reúne una gran cantidad de procesos elementales, todos ellos llevados a cabo al unísono. En efecto, si cada planta o árbol se considera un proceso separado, cualquier campo se puede contemplar como un amplio espacio donde se replica, con la misma cronología y un elevado número de veces, un mismo proceso elemental.
La producción en línea, comúnmente denominada en serie o en masa, corresponde a la forma industrial de elaboración de bienes. Una modalidad cuyas ventajas fueron definitivamente admitidas a principios del siglo XIX, conocida entonces como Factory System (Babbage, 1971; Leijonhufvud, 1989; Landesmann y Scazzieri, 1996b). En este caso, las unidades de output se fabrican de forma tal que, para empezar la siguiente, no se espera a haber terminado completamente la anterior. Por ejemplo, mucho antes de que un automóvil salga de la cadena de montaje ya se ha empezado a ensamblar el siguiente. En realidad, no sólo el siguiente, sino muchos otros siguientes están ya sobre la cinta transportadora. En esta modalidad, los fondos se especializan en tareas, o fases, particulares del proceso. Cabe indicar que, si bien toda la actividad industrial se ajusta a la modalidad de producción en línea, existen diversos subtipos claramente diferenciados, según cual sea el grado de intermitencia del flujo de producción y el grado de similitud entre las unidades de output elaboradas por unidad de tiempo: producción por lotes, línea de ensamblaje, producción de flujo continuo, etcétera (Spencer y Cox, 1995).
Para finalizar con esta somera descripción de las bases del modelo de los fondos y los flujos, resulta instructivo recalcar que el proceso de producción se concibe como una matriz. En efecto, cada elemento de esta tabla denota la tasa (entrante o saliente) de un determinado flujo, o el tiempo de servicio de un cierto fondo, todos ellos dispuestos por filas, para cada una de las etapas del proceso, ubicadas por columnas, en que se ha convenido dividir el proceso.3
Aplicación empírica del modelo
La representación propuesta del proceso de producción se acomoda muy bien a los requerimientos del trabajo empírico. Para ello, basta con hacer algunas pequeñas adaptaciones del modelo teórico para facilitar la recogida y el procesado de datos, así como poner un poco de imaginación para presentar los resultados de forma que sean fácilmente interpretables.
Versiones aplicadas del modelo de los fondos y los flujos han sido desarrolladas para el análisis de la eficiencia de procesos agrarios (Polidori y Romagnoli, 1988; Romagnoli, 1989), de la producción ganadera (di Sandro, 1993) o agroindustriales (Giovannetti, 1991), así como de redes de telecomunicación (Marini y Pannone, 1998 y Pannone, 2001). No obstante, merece dedicar atención especial al programa informático Kronos Production Analyser TM (Morroni, 1992 y 1999; Morroni y Moriggia, 1995) desarrollado para sistematizar los datos relativos a los rasgos técnicos y económicos de los procesos productivos reales y, tras los cálculos pertinentes, presentarlos de forma adecuada.
De entrada, se construyen dos tablas: una puramente técnica (que detalla la totalidad de fondos y flujos del proceso) y otra cuyos elementos son magnitudes económicas, puesto que todos sus componentes han sido multiplicados por sus respectivos precios, sean de mercado o imputados (Morroni, 1992, p. 82). Tales precios son datos exógenos. Estas tablas, no obstante, tienen que ser readaptadas para su uso en la investigación aplicada. Ello implica el desarrollo de una amplia batería de conceptos técnico-económicos relativos tanto a las variables más sobresalientes de todo proceso productivo, como a sus tiempos internos. Para empezar, se define la suma de los costos salariales más el costo de los flujos de inputs como el costo directo. La suma de este último más los costos de mantenimiento y amortización de los equipos, constituye el costo de transformación. Éste, añadido a los costos de almacenaje y los derivados de los inmuebles, deviene el costo industrial. La combinación del precio de salida de fábrica con los costos indicados permite calcular distintos tipos de márgenes. Otro punto a tener en cuenta son los tiempos de operación de los equipos, ya que para el fondo trabajo se toma la jornada laboral efectiva. A continuación, se definen los intervalos temporales del proceso en sí, tal como muestra de forma simplificada la Figura 1 (Morroni y Moriggia, 1995; Morroni, 1992, pp. 72-75):
Tiempo neto (bruto) de procesado (Net -Gross- Process Time): lapso requerido para producir una unidad de output mediante una unidad técnica elemental, excluidas todas las interrupciones por carga y descarga, por puesta en marcha de los equipos, por mantenimiento, etcétera. Se trata, en definitiva, de la suma de los intervalos de transformación física o química del producto en curso. El tiempo bruto incluye el almacenaje técnico de inputs u outputs.
Tiempo de elaboración o de trabajo (Working Time): suma de los periodos anteriores más el almacenaje de productos semielaborados por rupturas de continuidad entre las fases de un proceso (o stocks organizativos).
Duración neta (bruta) del proceso: en términos netos incluye el lapso de elaboración más la duración media de los stocks de inputs y finales del producto acabado. En términos brutos, se incluye además el tiempo de respuesta.
Tiempo de respuesta (Response Time): Se trata del lapso medio transcurrido entre la recepción del pedido y la entrega del producto al cliente.
Duración completa del proceso (Duration): tiempo total transcurrido desde la entrada en el proceso del primer input hasta el producto completamente acabado. Abraza todo tipo de interrupciones, incluso las debidas a la necesidad de reajuste de los equipos por cambios en el output-mix.
Como aspecto adicional, debe de indicarse que, en un proceso real, algunos de los intervalos temporales definidos pueden coincidir.
El programa Kronos Production Analyser TM distingue dos grandes tipos de stocks: los técnicos (el producto en curso exige que sea almacenado para su maduración, decantación, etc.) y los organizativos (divididos en el almacenaje de los diversos inputs flujo, los stocks correspondientes al producto acabado y los debidos a la existencia de cuellos de botella entre las distintas fases del proceso).
Con base en la adaptación conceptual expuesta y los datos recogidos, Kronos Production Analyser TM genera la tabla cuantitativa y temporal del proceso (Morroni, 1992, pp. 86-92) que muestra los requerimientos necesarios de flujos y de fondos para producir una unidad económicamente indivisible de la mercancía considerada. Sus filas muestran las cantidades de los elementos de la producción, mientras que sus columnas detallan las fases que componen el proceso productivo.
Se construye, además, otra tabla que concentra información adicional sobre las características de la mano de obra, del aparato administrativo, etcétera, de la planta estudiada. Se trata del esquema organizativo del proceso (Morroni, 1992, pp. 92-98). Esta tabla se divide en dos bloques. El primero, expone el patrón de utilización de los servicios del trabajo. Para ello se muestra la distribución de los trabajadores por categorías y horarios de trabajo (jornada y turno). También contienen información adicional sobre su composición por edades, sexo y nivel de escolaridad. Finalmente, expone la distribución general de las tareas para cada categoría de trabajadores. El segundo bloque se refiere a la maquinaria utilizada. Ésta se enumera según tipos y, para cada uno de ellos, se describen sus tiempos de preparación, carga, uso, descarga y mantenimiento, así como su velocidad de operación.
Con ambas tablas se obtiene, como era previsible, una muy buena instantánea del proceso productivo. En un caso real estudiado por los autores de este artículo (Mir y González, 2003, pp. 57-64) los resultados obtenidos contrastados con los procedentes de la contabilidad analítica de la empresa eran idénticos. Ello pone de manifiesto la calidad del modelo aplicado. Además, a su precisión técnica y económica hay que añadir la información que aporta sobre los tiempos del proceso.
Kronos Production Analyser también constituye un potente andamiaje conceptual para abordar con detalle las innovaciones del proceso, por dos razones:
Por su capacidad descriptiva. En efecto, el modelo capta perfectamente la organización interna de los procesos y las características técnicas de los elementos implicados.
Porque permite la investigación empírica en el plano de la planta (o establecimiento). Esto es, a nivel del locus donde se implementan las innovaciones.
El uso del programa, pues, puede desplegarse en las dos direcciones siguientes (Loasby, 1995):
Transversalmente: se trata de investigar simultáneamente diferentes unidades productivas dedicadas a un mismo proceso. Esta aplicación tiene indudable interés para el estudio comparativo de la eficiencia de cada planta, el análisis de las economías de escala, la valoración de las ventajas y limitaciones que suponen las indivisibilidades de algunos factores, etcétera.
Longitudinalmente: se estudian las modificaciones producidas en un determinado proceso a lo largo del tiempo. Para ello, esta línea de investigación selecciona una misma planta y la analiza a través de los años.
En ambos casos, si la empresa tiene experiencia en contabilidad de costos, el trabajo de campo no es demasiado complejo.
Escalas y costos de producción
Los conceptos seminales propuestos por Georgescu-Roegen, al margen de sus virtudes teóricas y aplicadas, resultan muy útiles para profundizar en el estudio de las relaciones entre la escala de la producción y los costos. A ello se destinan las próximas páginas.4
Equilibrado y escala de procesos en línea
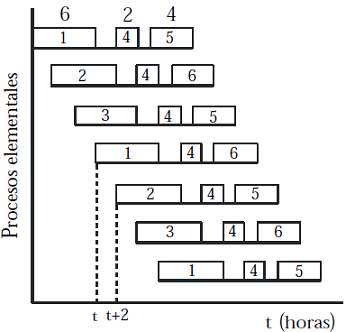
Sea el proceso elemental representado en la Figura 2 que contiene tres fases de seis, dos y cuatro horas.5 Dada la diferente longitud de tales fases, el despliegue en línea sólo resultará posible si existe un determinado retraso en el inicio de los diferentes procesos elementales consecutivos.
Como se indica en la figura, si cada dos horas arranca un nuevo proceso elemental o, dicho de otra forma, se inicia la elaboración de la siguiente unidad de output, desaparecen los posibles lapsos de inactividad. Ahora bien, para sostener esta cadencia continuada de producción, se requiere disponer de varias unidades fondo especializadas. En este ejemplo, tal como indican las cifras de cada rectángulo, se necesitan tres trabajadores especializados en la primera fase, uno en la segunda y dos en la última. En total, seis trabajadores distintos, cada uno con sus propias herramientas y equipos.
Cada fase (d j ) puede expresarse como el producto de dos importantes factores:
donde δ* indica el máximo común divisor de la longitud temporal de las fases que componen el proceso elemental y v j se corresponde con el número de unidades fondo que deberán ser movilizadas para cada fase en concreto. En el ejemplo, δ*=2 horas y v1=3, v2=1 y v3=2. Como el lector puede comprobar, δ* es el intervalo temporal óptimo entre procesos elementales consecutivos y cualquier valor superior provoca graves desajustes en la cadencia del proceso en línea. Obviamente, cada δ* unidades de tiempo, el volumen de producción será de una unidad de output. En el ejemplo propuesto, una unidad cada dos horas.
Para profundizar un poco más en las condiciones del equilibrado de líneas de fabricación, sea el caso ilustrado por la Figura 3.
La figura muestra un proceso elemental con una sola fase dividida en cinco tareas donde operan diferentes fondos.6 Cada fondo aporta sus servicios productivos durante un determinado tiempo de servicio (s i ). Este lapso temporal de actividad se compone de un periodo de transformación (p i ) y de otro de no-transformación (π i ). Este último intervalo de tiempo se consume en desplazar herramientas, en inspeccionar el trabajo realizado, en cargar o descargar máquinas y en transferir entre estaciones el output en curso. Por otra parte, el tiempo de transformación corresponde a la ejecución efectiva de operaciones productivas sobre las unidades de output en curso.
Solamente si coinciden los tiempos de servicio en cada estación de trabajo, el flujo del output en curso circulará de forma regular y continuada. No obstante, ello sólo sucederá por casualidad. Así, como acontece en la estación tercera del ejemplo sugerido, el obrero deberá permanecer en espera, ya que su tiempo de servicio es comparativamente más corto que en otras estaciones. Por consiguiente, el equilibrado de la línea exigirá que algunas estaciones tengan lapsos de ocio o de inactividad.
En definitiva, la duración total de cada tarea, o ciclo de producción (c), viene dada por la expresión,
siendo l i el tiempo perdido o de inactividad por exigencias del equilibrado.
Denominando c* al ciclo óptimo7 y expresándolo en horas, resulta que por cada hora se producirán 1/c* unidades de output. Además, de acuerdo con el ejemplo expuesto en la figura,
donde n w es el número de estaciones de trabajo requeridas por el proceso elemental en cuestión, en este caso, n w =5.
Una vez resuelto el asunto del equilibrado de una línea de fabricación, ya estamos preparados para abordar el tema de la escala de producción, concepto que se define como el volumen de producto por unidad de tiempo. Por simplicidad, supóngase que la técnica de fabricación no cambia y que la demanda absorbe sin problemas la producción adicional. La pregunta entonces es ¿cómo aumentar el output por unidad de tiempo o escala del proceso? La respuesta es conocida por todos: acelerando el ritmo de producción. Indudablemente, un intervalo temporal menor que c*=δ*, esto es c<c*, generará un mayor volumen de producto. Ceteris paribus si la cadencia de la producción es c=c*/n, n>1, el output por hora pasará a ser n/c*, sujeto a la condición de que no existen restricciones técnicas ni roturas en el suministro de insumos.
Este aumento del output por unidad de tiempo, requerirá un mayor número de unidades de fondos. En concreto:
¿Cuál será el número de procesos elementales simultáneamente activos en una planta debido a la reducción de la duración del ciclo de producción?,
¿Cuántas unidades de cada fondo especializado (k j ) serán necesarios en cada estación de trabajo (se supone que cuando c=c*, k j =1)?
Si se denota M p el tamaño del proceso en línea, esto es, el número de procesos elementales en curso en cada momento en la planta, entonces los valores de M p y el número de unidades de un determinado fondo k i vienen dados por las expresiones,
Como era previsible dada la simplicidad del caso expuesto, el tamaño del proceso en línea crece en la misma proporción que c* disminuye. Además, el número de fondos en cada estación de trabajo (k i ) guarda proporcionalidad con el factor de reducción del intervalo temporal. Por ejemplo, si c se reduce la mitad, k i se duplica. En efecto, puesto que cada estación de trabajo sólo ha finalizado la mitad de su tarea cuando la siguiente unidad de output en curso entra en escena, el número de fondos tiene que duplicarse para sostener el mayor ritmo de producción.
Para aumentar la capacidad productiva de una línea de producción existe otra opción: la reducción temporal de los componentes del proceso elemental (T F ). Este objetivo puede alcanzarse de las dos maneras siguientes:
La disminución del lapso de transformación (p i ) por la reorganización de las operaciones básicas llevadas a cabo en las estaciones de trabajo, cosa que puede acarrear cambios en el diseño y manejo de las herramientas, la estandarización de componentes y partes, etcétera.
La reducción del tiempo de no-transformación (π i ), muy especialmente los intervalos de transferencia entre estaciones de trabajo.
Probablemente, la caída de los tiempos de servicio recortará la magnitud absoluta de los lapsos de ocio por equilibrado (l i ) puesto que en el proceso elemental juegan un papel residual. Así pues,
Ceteris paribus, la contracción de T F implica una reducción de c* y, por consiguiente, un mayor output por hora.
En resumen, pues, existen dos formas de aumentar la producción por unidad de tiempo o escala del proceso. La primera, es la aceleración del proceso, cosa que reduce de forma directa c*. La cinta transportadora es el ejemplo clásico. Henry Ford la incluyó para aumentar la escala de producción de sus líneas de montaje. En general, la transferencia automática del output en curso entre estaciones de trabajo, provoca el descenso de π i y obliga a los trabajadores a trabajar según el ritmo de la cinta. La segunda estratagema para aumentar la escala, es acortar la duración de las tareas. Frederick Taylor insistió en el estudio y control de los tiempos y movimientos para aumentar el rendimiento de los operarios, sin que ello implicase necesariamente mayores cambios técnicos. Obviamente, como es muy conocido, ambos métodos se han aplicado y reforzado mutuamente.
Sea la Figura 4 que representa la relación entre el nivel de producción por unidad de tiempo (eje vertical) y el ciclo de producción (eje horizontal).
Como se observa, el nivel inicial de producción (O* en c*) aumenta hasta O m cuando,
Con ello, la productividad del trabajo por unidad de tiempo también habrá crecido n/λ veces.
En la figura, más allá del punto c m no hay curva de output por unidad de tiempo. Con ello se quiere indicar que la reducción del ciclo (sea por el método que sea) choca con límites físicos. Así c m indica el mínimo nivel de output alcanzable si no median cambios técnicos u organizativos mayores. Alteraciones severas de las capacidades de los fondos y los métodos de producción, provocarán el desplazamiento del punto c m .
Los métodos fordistas y tayloristas aumentan la producción por unidad de tiempo de las líneas de producción y, como consecuencia, reducen el costo medio de fabricación, como se ratificará de inmediato con el desarrollo del modelo de los fondos y los flujos.
Escala de producción y costos
El costo medio total (CMeT), o costo unitario, de un proceso de producción es la suma de los costos anuales provocados por el uso de fondos y el consumo de flujos, dividido por el output anual, esto es,8
donde: W es el pago anual por los servicios del trabajo, A es la anualidad pagada en concepto de depreciación,9 y
La cantidad producida (Q) se puede expresar como el flujo de producto por unidad de tiempo, multiplicado por el periodo productivo (H), esto es, Q = H·1/c*. Esta expresión del costo unitario del output incluye el factor tiempo.
La expresión anterior puede ser escrita como:
donde ω es el volumen de salario por hora (ω=W/H) y α la carga por depreciación también por hora (α=A/H).
Dado que el aumento de la escala de producción supone la disminución del ciclo de producción, se llega a la siguiente expresión del costo:
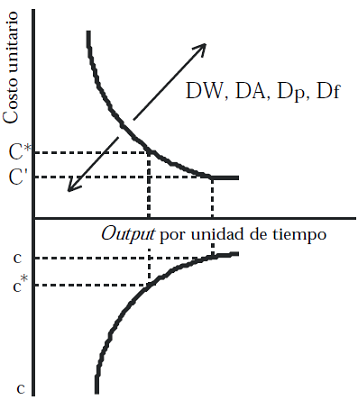
Esta función expresa el costo medio total a medida que crece la escala de producción. La Figura 5 ilustra la relación entre las tres variables clave de la escala o nivel de output por unidad de tiempo, el costo unitario y el intervalo temporal entre procesos elementales consecutivos. Cambios en los parámetros (W, A, H, f k y p k ) provocan desplazamientos de la curva de costos. La posición de esta curva depende de tres tipos de circunstancias: el tiempo, la eficiencia en el uso de materiales y los precios de los fondos y flujos. En cualquier caso, se demuestra que el costo no es ajeno al nivel de producción por unidad de tiempo.11
Por lo que respecta a la eficiencia temporal del proceso, ésta se ve influida por aspectos institucionales como la duración de la jornada de trabajo (J) y el número total de días laborales (D), así como factores relacionados con la organización interna del proceso y las capacidades de los fondos.
Como conclusión, el modelo de costos expuesto, desarrollado a partir de los postulados del modelo de los fondos y los flujos de Georgescu-Roegen, revela la existencia de importantes economías de escala en los procesos dispuestos en línea.
Equilibrio de capacidades de los fondos indivisibles
En esta sección se añaden al modelo los fondos capaces de intervenir, a la vez, sobre varias unidades del output en curso. Ello significa que se disponen en paralelo varios procesos elementales de un mismo tipo. Como se demostrará, el despliegue en línea de procesos paralelos permite ampliar sobremanera la escala de producción, aunque plantea un nuevo problema de equilibrado.
La capacidad de trabajo múltiple es una característica de muchos fondos. Hay máquinas que cortan, manipulan, cuecen, pintan, etcétera, simultáneamente varias unidades de output. En el modelo de los fondos y los flujos, el concepto de indivisibilidad de algunos fondos se interpreta como capacidad de trabajo múltiple. Dado que donde existe indivisibilidad, pueden darse excesos de capacidad, existe una nueva fuente de ineficiencia y costos superiores. Nace, así, el problema de cómo saturar las capacidades de los fondos indivisibles.
Sea el ejemplo de la Figura 6 donde aparece un proceso con una sola fase y cinco tareas. Los rectángulos de diferentes tamaños representan las capacidades de los diversos tipos de fondos. En la figura, para conseguir la plena utilización de todos los fondos empleados, deben disponerse lateralmente seis procesos elementales. Estamos, pues, ante un proceso paralelo activado en línea.
Sea e* j ≥ 1 (j=1, 2, …, J) el número máximo de procesos elementales que una unidad fondo del tipo j puede llevar a cabo simultáneamente. Entonces, el coeficiente de capacidad usada (γ j ) se define como la razón (Petrocchi y Zedde, 1990, p. 67),
donde e j es el número de unidades de output que el fondo maneja realmente en un proceso dado. Si este coeficiente se aproxima a la unidad, el exceso de capacidad en el uso del fondo en cuestión disminuye.
Para evitar capacidad ociosa, el número de unidades empleadas de un determinado fondo (τ j ) tiene que ser igual al mínimo común múltiplo (mcm) de las e* j dividido por la capacidad propia del fondo j, esto es (Petrocchi y Zedde, 1990, p. 70),
Como aparece en el ejemplo, e*1=1, e*2=2, e*3=3 y e*4=6. Por tanto, mcm=6. Esto supone seis unidades del fondo del primer tipo, tres del segundo, dos del tercero y una del último.
El número de procesos elementales simultáneamente activos en cualquier momento en este proceso paralelo activado en línea, es igual a:
Además, la producción por unidad de tiempo es igual a mcm·1/c*
En la Figura 7 se expone cómo, en un proceso elemental múltiple nacido del equilibrado de fondos con diferentes capacidades de producción y activado en línea, el aumento del nivel de producción por unidad de tiempo es, ceteris paribus, igual al valor mcm. Por ello, la curva 1/c se desplaza hacia arriba.
Las escalas de la producción
Tras los argumentos expuestos en los apartados anteriores, se pueden recoger en una única fórmula todos los factores que inciden sobre la escala de producción. La expresión es la siguiente:
donde n/λ representa la reducción del ciclo de producción provocada por los métodos tayloristas y fordistas, J la longitud de la jornada de trabajo, D el número de días laborales durante el año, mcm resulta de la coordinación de las diferentes capacidades de los fondos indivisibles, el escalar Λ indica el número de veces que el proceso elemental múltiple es replicado en la planta de producción y, para terminar, 1/T* c denotaría el nivel básico de producción.
Con respecto al parámetro Λ, hay que señalar que, puesto que un proceso elemental múltiple es una disposición productiva eficiente, cualquier número múltiplo de éste también lo será. Esta afirmación es conocida con el nombre del Factory Principle enunciado hace 170 años por Babbage12 y que, en el lenguaje expuesto en este trabajo, afirma que, una vez equilibrado un proceso de producción, su replicación en un número no exacto de veces, incurre en ineficiencia y mayores costos.
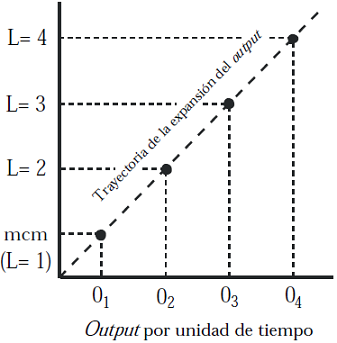
Como se ilustra en la Figura 8, el nivel de producción crece según lo hace el parámetro Λ. Hay que señalar que, sólo los puntos resaltados de la trayectoria de expansión del output tienen significado: indican el nivel de replicación en paralelo del proceso elemental múltiple perfectamente equilibrado. Los diferentes niveles de output por unidad de tiempo resultantes (O1, O2, …) tienen los mismos costos medios totales. Entre dos niveles consecutivos de output, el costo total por unidad de producto será superior debido a la falta de equilibrado temporal o de capacidades.
Para terminar, los diversos conceptos referidos, de una forma u otra, al tamaño de la actividad productiva, pueden ser clasificados de la siguiente manera:
La medida del proceso en línea (M p ) o número de procesos elementales simultáneamente activos. Cuando está activo un proceso elemental múltiple, M p crece proporcionalmente. Lo mismo ocurre si coexisten varias líneas de producción en una misma planta.
La escala (scale) es la cantidad de output, por unidad de tiempo. Obviamente, el concepto se refiere a un mismo tipo de output, aunque también pueda aplicarse al caso de lotes con diferencias menores. Esta variable está directamente afectada por la indivisibilidad de los fondos, el ritmo de trabajo, la duración de la jornada, etcétera.
La capacidad productiva de una planta resulta de multiplicar su escala por el número de horas (anuales) de actividad.
El tamaño (size) de una empresa se mide, dada la heterogeneidad de sus productos y servicios, en términos de valor. Una medida a la que, a menudo, hay que añadir los ingresos por actividades atípicas, dando lugar al volumen de negocios de la empresa. Como resulta lógico, los cambios en el tamaño de la empresa pueden responder a multitud de factores. De ahí que su relación con la eficiencia de la actividad productiva sea muy incierta.
El uso indiscriminado de términos relativos a la magnitud o dimensión de un proceso productivo o planta es fuente de ambigüedades y da pie a numerosas confusiones.
Conclusiones
El modelo de los fondos y los flujos como alternativa a la función de producción convencional
La modelización de los procesos productivos cuenta con dos opciones: considerar flujos a todos los elementos participantes, o bien combinar flujos y fondos. La primera alternativa la han adoptado enfoques tan diametralmente opuestos como los modelos de von Neumann o de Sraffa y la función de producción neoclásica y el análisis de la actividad de Koopmans. La segunda opción fue la preferida por Georgescu-Roegen.
Los modelos con sólo flujos, hayan sido diseñados para el análisis de equilibrio general o para el parcial, han alcanzado un enorme grado de desarrollo y difusión. Con ellos se han abordado temas clave de la teoría económica como, por ejemplo, la distribución del producto neto. No obstante, tales modelos caracterizan los elementos participantes en el proceso y tratan su dimensión temporal de forma insatisfactoria. En este punto, el modelo de fondos y flujos permite un análisis mucho más pormenorizado de la organización de los procesos productivos. En concreto, la propuesta de Georgescu-Roegen presenta los siguientes rasgos metodológicos:
Mantiene la visión unidireccional del proceso productivo (desde los inputs hacia el output) típica de los modelos de equilibrio parcial.
Rechaza el convencionalismo extremo de los modelos neoclásicos. Así, por ejemplo, no contiene ningún supuesto relativo a la productividad inmanente de los factores.
Insiste en el cuidadoso inventario de todos los elementos participantes en el proceso productivo y convierte la dimensión temporal en uno de los pilares analíticos del modelo.
La propuesta de Georgescu-Roegen nació de su crítica de los atributos metodológicos y del diseño conceptual básico de la función de producción. Como es sabido, la función de producción surgió como una extensión mutatis mutandis del corpus conceptual creado para la maximización de la utilidad (Mirowski, 1989, pp. 309 y ss.). Con el paso del tiempo, la función de producción se desplegó en múltiples versiones, siempre en pos del objetivo de elaborar recetas resolutivas para la maximización de las ganancias del productor. La estimación masiva de funciones de producción se consolidó en los cincuenta, gracias tanto a los avances de la econometría, como a la mejora de los sistemas de cálculo. No obstante, en la década siguiente, el modelo fue puesto en duda debido a los problemas de consistencia de la teoría de la productividad marginal.13 A pesar de ello, el concepto de función de producción nunca ha dejado de ser masivamente divulgado y utilizado. Basta con abrir cualquier manual o rastrear los contenidos de las principales revistas.
La definición de una función de producción microeconómica suele ir acompañada de una larga relación de supuestos, no siempre explicitados, como son el carácter instantáneo del proceso de transformación, la naturaleza continua y sin atisbo de complementariedad entre los factores, la existencia de un agente que busca maximizar sus beneficios en un entorno perfectamente competitivo y ciertas propiedades matemáticas que apoyan la elección de la forma funcional.
Los procesos productivos son contemplados como una caja negra. En efecto, se abordan como si fueran unidades simples desprovistas de estructura interna. A pesar de la antigüedad del modelo, muy poco se ha hecho para rebajar su grado de opacidad. Así, continúan manteniéndose supuestos como la instantaneidad del proceso, la variedad de factores se reduce a unos pocos (capital, trabajo, tierra), las combinaciones más dispares de éstos se suponen referidas a un mismo proceso productivo y un largo etcétera. Por todo ello, la función de producción peca de un excesivo grado de convencionalismo, esto es, su diseño contiene una proliferación inaceptable de supuestos ad hoc. El modelo aparece blindado por una multitud de supuestos que constituyen ficciones sobre la naturaleza del proceso productivo y los elementos implicados. Se trata de una protección que garantiza que los resultados obtenidos cumplan con los principios de la axiomática de la elección del productor. Así, la estimación de funciones a partir de datos reales, se limita a cuantificar variables cuyo comportamiento económico está ya prefigurado en el formato matemático. De hecho, existe una larga tradición de buscar formatos que presenten las mejores expectativas de buen comportamiento económico. De esta forma, la especificación de una función está al servicio de las conclusiones que se desean obtener. Con ello, el convencionalismo se manifiesta como artificio y conduce al apriorismo.
Algunos autores defienden la función de producción por su capacidad instrumental que, si bien nació como una pura abstracción a imagen y semejanza de los postulados de la utilidad,14 terminó por converger con las funciones de respuesta y otros métodos de optimización desarrollados por los ingenieros. Así, por ejemplo, las funciones de reacción de las cosechas a las dosis de abonado, formalmente justificadas por la continuidad del crecimiento de plantas, así como la divisibilidad de muchos de los inputs agrarios, fundamentan, con pequeñas adaptaciones, las funciones de producción económicas. Esta confluencia, no obstante, supone perder de vista que las investigaciones de los ingenieros operan en un plano epistemológico diferente del correspondiente al análisis económico. Por seguir con el anterior ejemplo, las curvas de respuesta sólo pretenden detectar la existencia de relaciones sistemáticas entre las muy concretas variables seleccionadas para, posteriormente, intentar explicar tales regularidades estadísticas a partir de los conocimientos sobre los procesos bioquímicos subyacentes. Son modelos correctos en la medida que resultan útiles. Esta práctica tecnológica está muy alejada de la funciones económicas que dan cabida a una amplia amalgama de factores técnicos y económicos, con el objetivo de corroborar presuntas leyes acerca de los rendimientos de los procesos productivos.
La función de producción ignora también el elevado grado de complementariedad que existe entre los factores. En este punto, habría cuando menos que recuperar la vieja noción de factor limitacional (Georgescu-Roegen, 1966): aquel cuyo aumento es una condición necesaria, aunque no suficiente, para que crezca la cantidad de producto. Ello es debido a que el incremento de las cantidades usadas sólo incide sobre el output si crece la cantidad de, al menos, algún otro factor. Así se reconocen las complementariedades entre los inputs: los distintos tipos de trabajo se combinan, inextricablemente, con el uso de máquinas específicas y ciertas necesidades de flujos.15 Las dificultades para separar los factores conlleva, pues, que sus respectivas productividades marginales sean nulas (Pasinetti, 1985, pp. 201-206).16
Otro problema tiene que ver con la “ley” de los rendimientos decrecientes de los factores. Este postulado lo estableció Ricardo a tenor de lo que observaba en la agricultura de su tiempo, en conexión con el problema de la renta del suelo (o de la distribución del ingreso): una capacidad de producción progresivamente por debajo de las necesidades de la creciente población (urbana) y los requerimientos de la industria. Piero Sraffa (1986a y b) distinguió entre rendimientos crecientes con un factor constante y rendimientos crecientes de escala. Los primeros aparecen sólo cuando el input constante (esto es, aquel cuya cantidad, por la razón que sea, no puede cambiarse a voluntad) es indivisible. En este caso, un aumento en las cantidades de los inputs denominados variables significa alcanzar proporciones progresivamente más eficientes en relación al input indivisible, lo que conlleva rendimientos crecientes hasta alcanzar la proporción óptima entre ambos, resultado que queda bien fundamentado en el modelo de fondos y flujos. Sin embargo, si el factor constante es divisible, como sucede con la tierra de cultivo, no emergerán rendimientos crecientes ya que se produce un ajuste sistemático entre la tierra y los factores variables. Por otra parte, los rendimientos crecientes de escala están asociados con incrementos de todos los inputs. En este punto, suele apelarse a las deseconomías de escala como factor que limita el tamaño de las empresas. Si bien la expansión de una empresa complica su gestión, justo es reconocer que la causa de tales problemas no es tanto el tamaño absoluto como el ritmo de crecimiento.
Si bien los problemas metodológicos y teóricos apuntados,17 no afectan el modelo propuesto por Georgescu-Roegen, hay que reconocer que en éste persisten algunos otros. Así, este autor supuso que la eficiencia del capital fijo se mantiene inalterable a lo largo de los sucesivos ciclos productivos, a la vez que indicó que tampoco el trabajador perdería su buena condición para el trabajo. También sugirió ignorar los subproductos nocivos.
Georgescu-Roegen (1976, p. 64) propone no incluir la máquina usada y el trabajador cansado dentro de la lista de outputs del proceso productivo, ya que la finalidad de éste no es producir tales outputs. Esta justificación no es aceptable: la inclusión de los fondos entre los outputs sería oportuna porque los fondos no se incorporan físicamente al output y sus capacidades productivas se extienden más allá de un único ciclo de producción. En efecto, la conexión objetiva entre un fondo fijo (una máquina) y sus servicios puede establecerse según el esquema conceptual siguiente (Barceló, 2003: 21):
En el lado de las entradas, se ubican la máquina nueva más los servicios de mantenimiento y reposición necesarios para sostener su capacidad productiva lo más próxima posible a la de sus momentos iniciales. En el lado de las salidas, aparece la máquina una vez envejecida más las horas de servicios productivos que ha ido suministrando ciclo tras ciclo. De acuerdo con este esquema, el concepto de preservación intacta del capital tiene que ser interpretado como la capacidad de un fondo fijo para generar, en los sucesivos ciclos de la producción, servicios productivos suficientemente similares. Sin embargo, la eficiencia de los fondos fijos declina con el paso del tiempo. Por ello, hay que llevar a cabo operaciones de mantenimiento y reposición cuya intensidad crece progresivamente y, por consiguiente, el gasto en este capítulo. No hay que olvidar que existen barreras físicas o restricciones económicas que impiden la perfecta recuperación de la eficiencia productiva de los fondos fijos. Tampoco hay que dejar a un lado el hecho de que la vida técnica de un fondo fijo consta de un tiempo máximo absoluto: cuando la máquina es incapaz de prestar más servicios y su reparación resulta muy difícil (por su alto costo por los problemas técnicos observados -como el caso de la bombilla cuyo filamento se rompió-, por falta de suministro de piezas de recambio, por la ausencia de personal especialista, etc.). A pesar de lo indicado, el severo supuesto de eficiencia constante puede aceptarse porque el modelo de los fondos y los flujos pertenece a la familia de los modelos de equilibrio parcial.18
En el caso del fondo del trabajo, el punto de vista de Georgescu-Roegen coincide con el resto de modelos económicos sobre la producción: se dejan fuera del modelo las actividades de cuidado, formación y sostenimiento de la fuerza de trabajo. Su naturaleza a la vez social y económica, es la justificación para considerar tales actividades como exógenas.
Por lo que se refiere a los subproductos nocivos, la recomendación de Georgescu-Roegen de ignorarlos porque carecen de valor, merece las tres puntualizaciones siguientes: 1) todo subproducto es necesariamente producto conjunto de otro output; 2) un residuo de un proceso puede ser input de otro, circunstancia que le otorga un valor de uso; 3) como regla general, cuando sólo se toma en cuenta el proceso que lo genera, es imposible decidir si un subproducto es o no un residuo. Este último atributo solamente puede concederlo el sistema económico como un todo. Así, la cuestión del precio de los subproductos no puede ser resuelta sin tomar en consideración las exigencias de los requerimientos reproductivos del sistema. En este punto, el modelo de los fondos y los flujos también está completamente desarmado, como sucede con cualquier otra propuesta de equilibrio parcial.
La propuesta de Georgescu-Roegen merece ser sobre todo destacada por su capacidad para describir y clarificar la organización interna y temporal de los procesos de producción. Con ello, como se ha demostrado en este breve trabajo, se pueden refinar conceptos como la escala de producción y obtener, como si de un resultado derivado de la propia naturaleza del proceso productivo se tratase, principios organizativos y de gestión universalmente conocidos y aplicados.











 nova página do texto(beta)
nova página do texto(beta)