1. Introduction
This paper continues a series on orbits of comets with catalogued parabolic orbits (Marsden and Williams 2003), but which nevertheless possess sufficient observations to do a better calculation. Various reasons exist for studying these comets. A comet with a parabolic orbit may be, depending on factors such as perihelion distance, a Near Earth Object (NEO). A non-parabolic orbit decides the matter. If a more refined orbit proves to be a hyperbola, the comet might potentially be of extra-solar origin. This should be addressed. Many, perhaps most, parabolic orbits were calculated by the method of Olbers (Dubyago 1961, Ch. 8) as a computational convenience and used normal places. With modern computers normal places are an anachronism that degrades, if only slightly, the solution. Better can be done. And better orbits mean better statistics for studying the origin of comets. But perhaps most importantly is professionalism. It is disconcerting that a great comet should be catalogued with an orbit calculated in 1873. We can do much better with modern computational techniques.
Why study Comet C/1830 F1 (Great March comet), hereafter simply “the comet”, in particular? Numerous observations, over 400, are available. The perihelion distance of 0.9210 au and eccentricity of 0.99792 mean that the object could be an NEO, but the calculation of the orbit, given shortly, shows that the comet never comes closer than 0.147 au from the earth. Its period of over 9,000 yr renders nugatory any preoccupation over a possible close approach. The comet, nevertheless, was observed for five months and professionalism dictates a better than 19th century orbit.
2. Preliminary Data Reduction and Ephemerides
Gambart (1830) discovered the comet in Marseille on 22 April, although it had apparently been seen previous to perihelion passage near the south equatorial pole (Schulze 1873). I conducted a literature search of the journals published in the 19th century that include comet observations and also annual reports of some of the major observatories. The search proved vexing, not only because the 1830 date precluded use of a number of journals that were founded later, such as The Astronomical Journal, but also because some of the formats were unusual. Mayer in Vienna, for example, refers to “observation lines” “Beobachtungsreihen” to which corrections in α and δ are made. It is unclear to me exactly how he is reducing the observations, which are neither ring nor filar micrometer observations. Likewise, the Florence observations contain times of entry and egress from the inner and outer rings of a ring micrometer for the comet, but also for an accompanying star. This star cannot be a reference star because insufficient information is given to calculate the comet’s position from the reference star’s position; see Chauvenet (1962, Vol. 2, pp. 436-438). It appears as if the observer merely wished to publish the comet’s position along with that for a star. Schulze mentions that three transit circle observations of the comet were made at the Cape Observatory before perihelion passage, but he does not publish the original observations, only a normal place based on the three. I could find no reference to the original observations in the literature and therefore treated the normal place as a genuine observation.
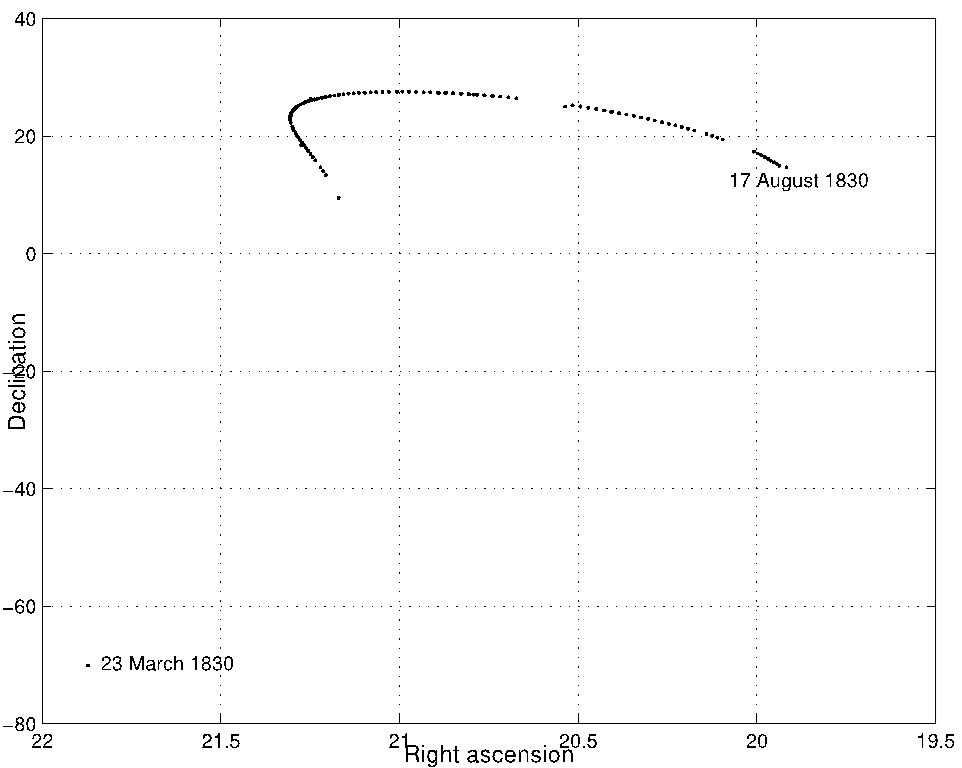
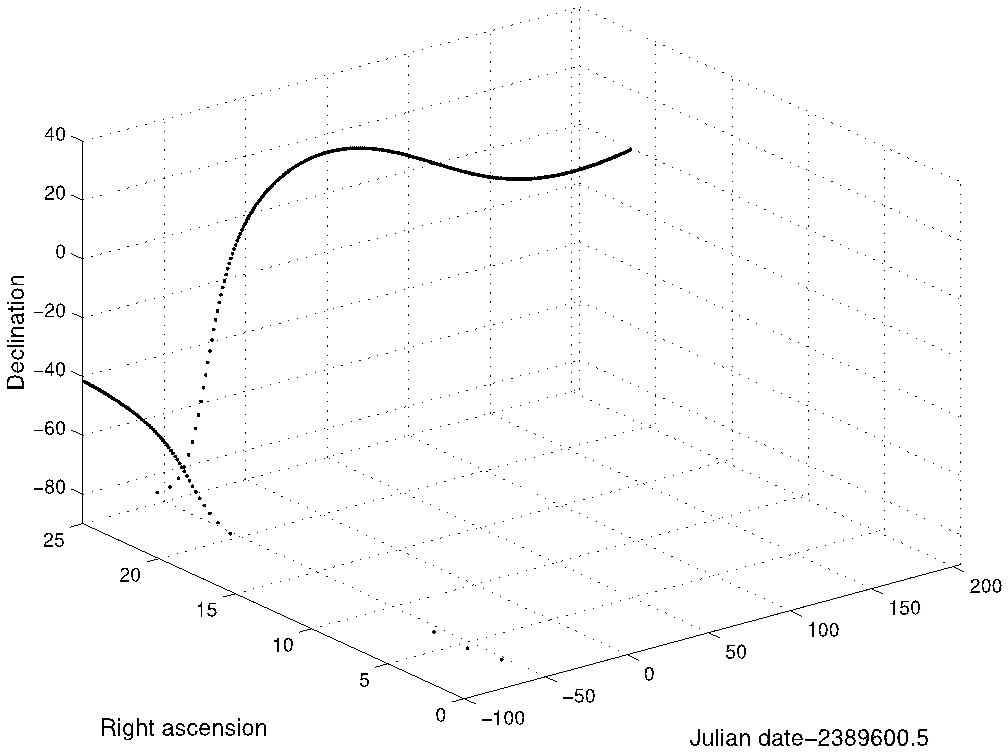
This search yielded a total of 428 observations in right ascension (α) and 424 in declination (δ). Some observations were made in one coordinate only. Two observations, the Cape normal place and one of the Vienna observations, were made with a transit circle. Their data processing differs slightly from the others because transit circle observations are traditionally reduced to the geocenter rather than to the topocenter and of course the time of observation is the same as α. Table 1 summarizes the observations for each observatory and Figure 1 graphs them. One notices that the Cape observation, really three observations, lies far from the others, but nevertheless seems to follow the general pattern of the post-perihelion observations if one projects them backwards. This is shown in Figure 2, where one sees that near an x-axis value of −65 the value for α is ≃ 21h and the value for δ ≃ −70°0.
Table 1 Observations by Observatory
| Observatory | Obs. in α | Obs. in δ | Reference1 |
|---|---|---|---|
| Altona, Germany | 7 | 4 | AN, 1830, 8, 365 |
| Bremen, Germany | 7 | 6 | AN, 1830, 8, 285 |
| Cape, South Africa | 1 | 1 | AN, 1873, 82, 975 |
| Crakow, Poland | 84 | 87 | AN, 1830, 8, 477 |
| Florence, Italy | 132 | 132 | AN, 1831, 9, 149 |
| Göttingen, Germany | 3 | 3 | AN, 1830, 8, 253 |
| Königsberg, Germany | 21 | 21 | AN, 1831, 9, 165 |
| Kremsmünster, Austria | 16 | 16 | AN, 1831, 9, 291 |
| Mannheim, Germany | 18 | 18 | AN, 1830, 8, 337 |
| MN, 1830, 1, 180 | |||
| Marseilles, France | 7 | 7 | AN, 1830, 8, 319 |
| AN, 1830, 8, 251 | |||
| Padua, Italy. | 66 | 66 | AN, 1831, 9, 285 |
| Prague, Czech Rep | 16 | 16 | AN, 1830, 8, 285 |
| AN, 1830, 8, 315 | |||
| Speyer, Germany | 10 | 7 | AN, 1830, 8, 299 |
| Vienna, Austria | 40 | 40 | AN, 1830, 8, 437 |
1AN: Astron. Nachr.; MN: Monthly Notices RAS
Because most of the observers use local mean or sidereal time and some express α in degrees rather than hours, minutes, and seconds all of the observations were reduced to the common format of Terrestrial Time, α, and δ. None of the observations employed north polar distance in lieu of δ. Whenever a specific reference star was given to which the comet observation had been referred, as happened for 53 observations, its position was recalculated, with modern positions taken from the Tycho-2 catalog (Høg et al. 2000), using the algorithm in Kaplan et al. (1989). If differences in α and δ from the reference star, ∆α and ∆δ, were given, they were applied, corrected for differential aberration and refraction, to the new position. Sometimes it was not evident if an observation had already been corrected for differential aberration or refraction. I calculated two final sets of residuals, both with and without these corrections, but the results were nearly the same. If ∆α and ∆δ were not given but a reference star was (21 observations) the differences in the positions between the older catalog and Tycho-2 were applied to the published positions of the comet. Observations for which no reference star was given, the remaining observations, were taken as published. Because the observations are 19th century, they were corrected for the E-terms of the aberration if the observation was derived from a mean position. See Scott (1964) for a discussion of the E-terms.
Rectangular coordinates needed to calculate observed minus calculated positions, (O C)’s, were initially generated, along with numerically integrated partial derivatives to correct the comet’s orbit, from a 12th order predictor-corrector integrator. This is generally referred to as Moulton’s method, for which Branham (1979) gives more detail. The coordinates are heliocentric and the Moon is carried as a separate body.
3. Errors or Missing Information in the Observations
Processing 19th century observations is a far from trivial task because the observations are published in different languages, English, French, German, Italian, and even Latin, do not conform to a standard format, and contain many errors. The reader may refer to an article of mine that discusses the matter in detail (Branham 2011a) and includes various examples. Common errors include mistaking a 3 for a 5 or 8, a 2 for a 7, transposing numbers, 35 for 53, misidentifying a reference star, or an error in time that affects both the (O C), observed minus calculated position, in α and also in δ in such a manner that one can identify the error in time. With previous comets that I have studied over half of the bad (O C)’s could be corrected to produce reasonable values. Unfortunately, for the Great March comet this turned out not to be the situation. For example, an observation made at Marseilles on 11 May gave an (O C)δ close to 120’’. A change in the minutes of the observation from 56 to 54 would eliminate this large (O C), but misreading a 6 for a 4 seems unlikely, and I left the observation alone. Likewise, declination observations, two made on 11 July and another two on 13 July in Florence, had (O C)δ ’s between 120'' and 134''. These are close to a two arc-minute error, but it seems unlikely that all of the observations would have this sort of error. In any event there is insufficient evidence in the observations themselves to suggest a possible source of error and thus the observations remain untouched. Therefore, unlike all of my previous studies of 19th century comets, no changes were made to the observations as published.
4. Treatment of the Observations
The observations of Table 1 result in 852 equations of condition, calculated from the numerically integrated partial derivatives, and hence the residuals necessary to correct the orbit. Assigning weights to the observations, necessary because of the disparity in their quality, remains similar to that of my previous publications on comet orbits. The first orbits were calculated by use of the robust L1 criterion (Branham 1990, Ch. 6) to minimize the effect of discordant observations. Then the final orbit came from weighting the residuals with the biweight function. If r represents the vector of the post-fit residuals, scale an individual residual ri by the median of the absolute values of the residuals, ri = ri/median(|r|). Then calculate weighting factors wi by:
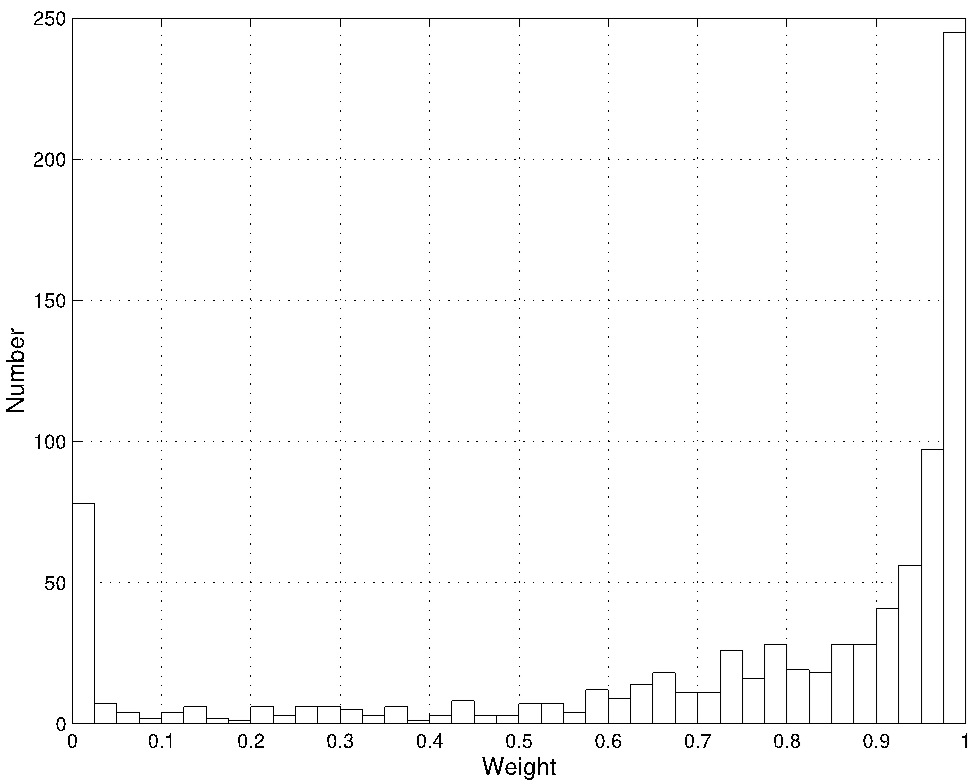
Equation (1) incorporates the advantages of being impersonal, recognizes that smaller residuals are more probable than larger ones, and assigns them higher weight. Figure 3 shows a histogram of the weights. The amount of trimming, 8.1% of the weights, lower than the machine epsilon of 2.22 10−16, is acceptable, especially considering that 81.6% of the weight are greater than 0.5 and 51.5% great than 0.9. With the biweight the final mean error of unit weight becomes σ(1)=14.’’77, a value that falls somewhat on the high side compared with other 19th century comets, but is still acceptable. The Windsor, Australia, observations of the Great Southern comet (Branham 2018), for example, have σ(1) = 16.’’ 47, although with all of the observations for that comet we find σ(1) = 10.’’80. Other 19th century comets have mean errors over 10’’. Comet C/1819 N1 (Great comet of 1819) has σ(1) = 11.’’23 (Branham 2017) and comet C/1857 D1 (d’Arrest) has σ(1) = 10.’’25 (Branham 2011b). If the 11 and 13 July observations in Florence could be corrected by 120’’, or simply eliminated, the mean error would undoubtedly decrease. But in lieu of unavailable specific details there remains no justification for such an arbitrary action, and one must accept the observations as given. Such a procedure seems more objective than that adopted by Peck for his 1904 computation of a parabolic orbit of comet C/1845 L1 (Great June comet) (Branham 2009), where observations from Kremsmünster, Austria, and Modena and Padua in Italy were discarded as being “worthless”, “poor quality”, and “untrustworthy”, but no statistical evidence was offered for such pejorative adjectives.
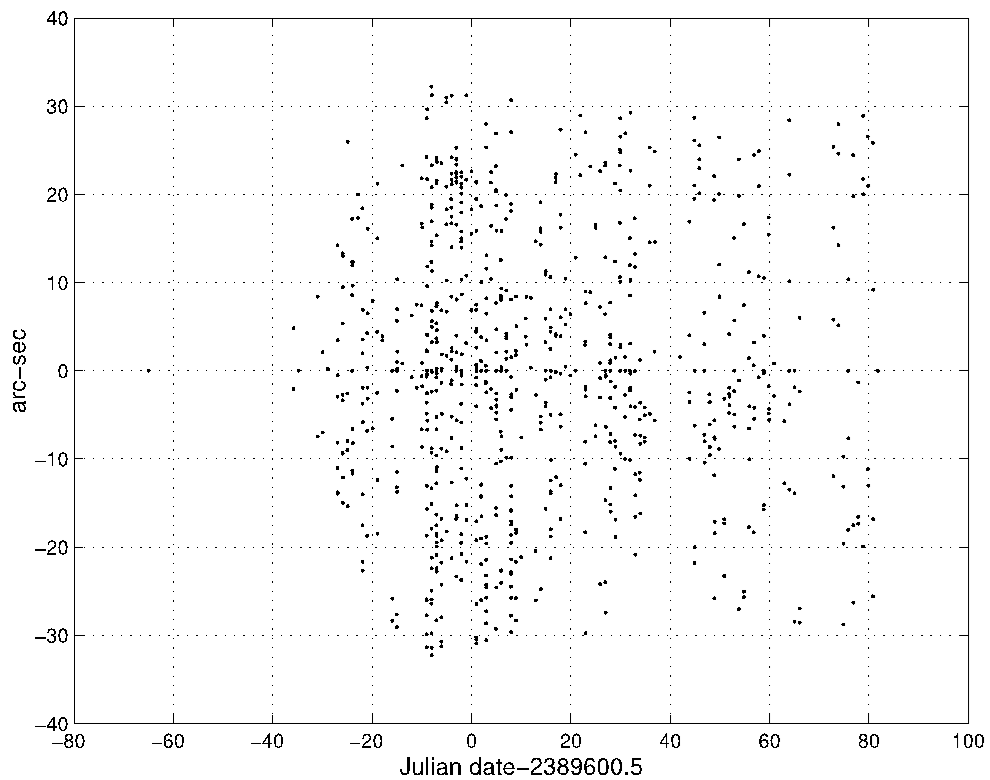
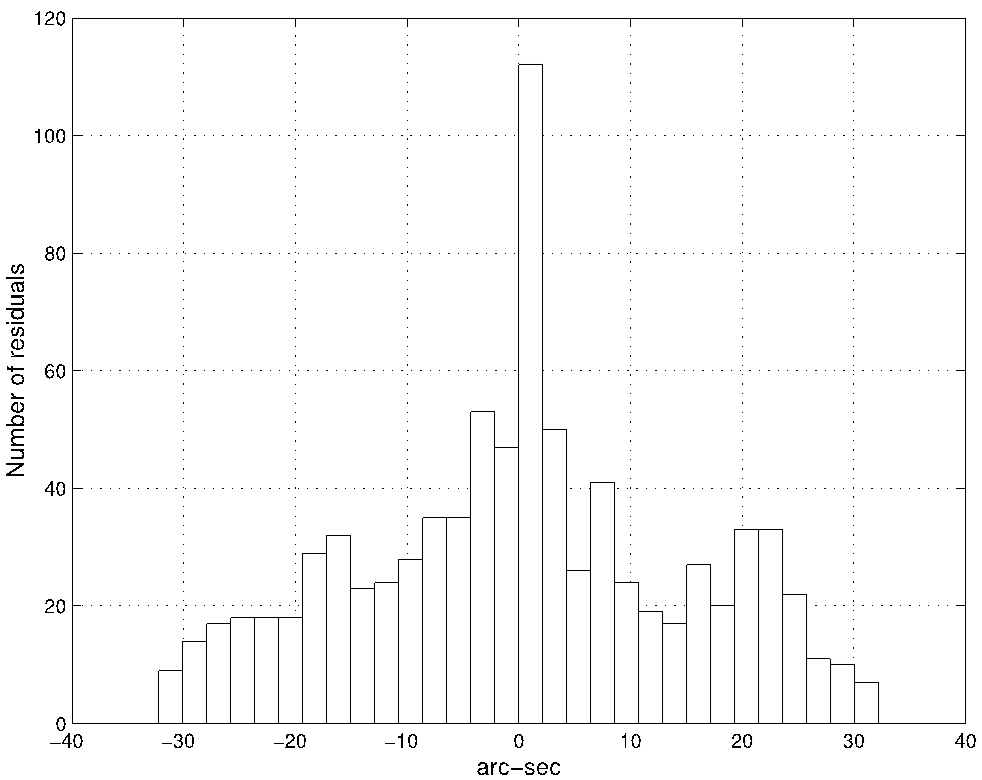
Figure 4 shows the distribution of the residuals from the final solution and Figure 5 a histogram of the residuals. The distribution appears far from Gaussian (normal, bell shaped): a skewness of -1.12, (0 for a normal distribution), indicating an excess of negative residuals; a kurtosis of -0.25 (0 for the normal) shows a platykurtic distribution, and the Q factor of 0.15 (2.54 for the normal), shows tails not too heavy considering the height of the distribution near 0. Thus, the distribution is far from normal, but nevertheless random. Application of a runs test for randomness of the non-zero residuals, eliminated by the biwright function, (Wonnacott & Wonnacott 1972, pp. 409-411) indicates 363 runs out of an expected 365, or an 84.2% chance of being random. Randomness remains more important than normality for the goodness of fit of a distribution.
5. The Solution
Table 2 shows the final solution for the rectangular coordinates, x0, y0, z0, and velocities, ẋ0, ẏ0, ż0, along with their mean errors for epoch JD 2389600.5 and the mean error of unit weight, σ(1).
Table 2 Rectangular Coordinates and Velocities: (EPOCH JD 2389600.5, EQUINOX J2000)
| Unknown | Solution | Mean Error |
|---|---|---|
| x0 | 9.088867e-02 | 3.801770e-06 |
| y0 | -1.239522e+00 | 3.387994e-06 |
| z0 | -8.837712e-02 | 6.926546e-04 |
| ẋ0 | 1.921819e-02 | 1.514776e-07 |
| ẏ0 | -9.942274e-03 | 2.259179e-07 |
| ż0 | 2.475755e-03 | 7.067256e-05 |
| σ(1) | 14.’’73 |
Table 3 shows the covariances and the correlations. Some correlations are high, but the condition number of the matrix of the equations of condition, 4.67 × 107, remains moderate. Moreover, Eichhorn’s efficiency of 0.52 implies that the linear system seems well-conditioned and should result in a reliable solution. Eichhorns’s efficiency (Eichhorn 1990) varies from 0 for completely dependent columns of a linear system to 1 for completely independent columns.
Table 3 Covariance (Upper Triangle) and Correlation (Subdiagonal) Matrices
| 0.0028 | -0.0006 | 0.0735 | -0.0000 | -0.0000 | 0.0093 |
| -0.2422 | 0.0023 | -0.2986 | -0.0000 | 0.0000 | -0.0192 |
| 0.1423 | -0.6489 | 94.0689 | 0.0025 | -0.0228 | 8.3848 |
| -0.1563 | -0.0352 | 0.1203 | 0.0000 | -0.0000 | 0.0001 |
| -0.0878 | 0.2829 | -0.7436 | -0.1261 | 0.0000 | -0.0027 |
| 0.1774 | -0.4099 | 0.8736 | 0.0365 | -0.8784 | 0.9793 |
Table 4 gives the orbital elements corresponding with the rectangular coordinates of Table 3: the mean anomaly of perihelion passage, M0; the eccentricity, e; the semi-major axis, a; perihelion distance, q; the inclination, i; the node, Ω; and the argument of perihelion, ω. Rice’s procedure (1902), expressed in modern notation, calculates the mean errors for the elliptical elements and uses C, the covariance matrix from the least squares solution for the rectangular coordinates and velocities.
| Unknown | Value | Mean Error |
|---|---|---|
| 0.°0050907 | ||
| M0 | JD 2389552.20502 | 0.0039517 |
| (1830 April 09.70502) | ||
| a | 443.80734 | 229.34518 |
| e | 0.99792 | 0.00107 |
| q | 0.92100 | 0.25039 |
| Ω | 295.◦ 97864 | 27.°96157 |
| i | 104.◦ 94660 | 0.°72621 |
| ω | 227.◦ 85682 | 11.◦ 62836 |
Identify the errors in a quantity such as the node Ω with the differential of the quantity, dΩ. Let V be the vector of the partial derivatives (∂Ω/∂x0 ∂Ω/∂y0 … ∂Ω/∂ż). Then the error can be found from
The partial derivatives in equation (2) are calculated from the well known expressions linking orbital elements, whether elliptical or hyperbolic, with their rectangular counterparts. The solution shows a highly elliptical orbit, and the mean errors indicate that the ellipse is statistically distinguishable from a parabola.
The comet’s period P comes from the relation
where k is the Gaussian gravitational constant. From equation (2), equation (3), and the values in Table 3 we calculate P = 9351 ± 7098 yr, a large formal mean error but one consistent with the substantial error in the semi-major axis. It also seems evident that no close approach to the earth will take place in the future.
Given that the orbit is highly elliptic, could the comet possibly be of extra-solar origin, an initially hyperbolic orbit converted by planetary perturbations to elliptical? To check this possibility I integrated the orbit backwards to JD -5805999.5, an interval of a little over 22,400 years. The integration uses once again heliocentric coordinates. Such long integrations generally employ barycentric coordinates because they permit a longer time interval. But given the speed of modern computers such a concern becomes secondary. Barycentric coordinates are needed for calculations involving stellar aberration such as the determination of aberration day numbers.
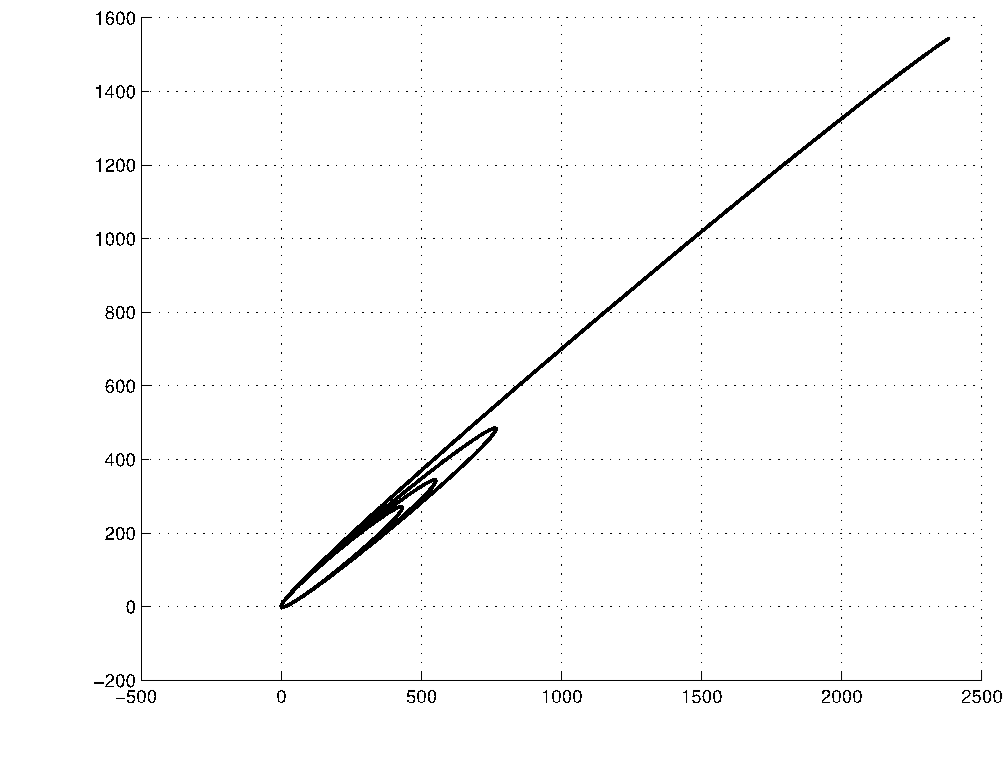
Figure 6 shows the results of the integration in the x-y plane. The comet finds itself 2889 au from the Sun at JD -5805999.5 with a still elliptic orbit, a = 1494 au. Thus, the comet is not hyperbolic and comes from the Oort cloud. The closest approach to the Earth is 0.147 au at JD 9736510.5, and thus the comet represents no threat in the future. It is evident that the orbit has become substantially modified over thousands of years as Figure 6 shows. Something similar occurred with comet C/1857 D1 (d’Arrest); see Figure 5 in Branham (2011b). This is most likely caused by the effects of the Jovian planets, but the Great March comet’s mediocre orbit quality hardly justifies an intensive investigation.
6. Conclusions
An orbit for Comet C/ 1830 F1 (Great March comet), based on available observations, 428 in α and 424 in δ, is given. The orbit is highly elliptical and statistically different from a parabola. The comet cannot be considered a NEO. Nor is it likely that the comet has an extra-solar origin, but rather originated in the Oort cloud.











 nova página do texto(beta)
nova página do texto(beta)