1. Introduction
Observations of the remarkable, mildly relativistic bipolar outflow from SS 433 (see the early papers of Ryle et al. 1978 and Margon et al. 1979) showing an unusual precession signature (Hjellming & Johnston 1981a), led to the study of the dynamics of ballistic, “corkscrew” (i.e., precessing) jets. This simple problem was lucidly addressed by Hjellming & Johnston (1981b) and Gower et al. (1982).
The analytic treatment of relativistic, corkscrew jets has been extended including the effect of a magnetic field (Kochanek 1991) and considering a “ram pressure braking term” (Panferov 2014). Also, more complex time evolutions of the ejection direction (e.g., including a “nodding” superposed on the precession) have been explored (e.g., Stirling et al. 2002). Relativistic gasdynamical simulations have also been done (see, e.g., Horton et al. 2020; Barkov & Bosch-Ramon 2021).
These models are naturally relevant for modelling SS 433, which has continued to be actively observed through the years (see, e.g., Bell et al. 2010; Jeffrey et al. 2016; Martí et al. 2018; Blundell et al. 2018), and for other galactic “microquasars” with precessing jets (see, e.g., Luque-Escamilla et al. 2015; Coriat et al. 2019). Also, some of the early papers on models of relativistic corkscrew jets were directed to outflows from quasars or from AGN (Gower et al. 1982; Baryshev 1983), and observations of such jets have naturally continued over the years (see, e.g., An et al, 2010; Kharb et al. 2019).
Our present paper studies a specific feature of the ballistic corkscrew jet model. As pointed out by Gower et al. (1982), an increase in v/c has the effect of an apparent rotation of the precession axis, with the projected (i.e., blueshifted) jet lobe appearing to lie closer to the plane of the sky. Through an analysis of the ballistic, precessing jet equations we show that this is indeed the case, and obtain the value of the rotation angle as a function of the flow parameters.
The paper is organized as follows. In § 2, we present the ballistic, precessing jet model of Hjellming & Johnston (1981b) and Gower et al. (1982). In § 3, we derive the conditions under which a “classical jet spiral” (projected onto the plane of the sky without considering time-delay effects) approximately coincides with the projection of a relativistic, corkscrew jet. In § 4 we explore the parameter space of the problem, and derive the range of parameters in which the “equivalent, rotated spiral model” is an appropriate description of the relativistic jet. Finally, the results are summarized in § 5.
2. Relativistic, Free-Streaming Equations
Let us consider a bipolar jet source located at the origin of the (x, y, z) coordinate system, with (x, y) on the plane of the sky and z pointing towards the observer. The ejection axis precesses on a cone of half-opening angle α, and the axis of the cone lies at an angle φ from the plane of the sky towards the observer, as shown in the schematic diagram of Figure 1. The precession phase (with origin on the xz-plane) is:
where τ is the time of ejection, θ0 is the precession phase at τ = 0 and Ω = ± 2π/τp, with τp being the precession period (the positive sign corresponding to a counterclockwise and the negative sign to a clockwise precession).
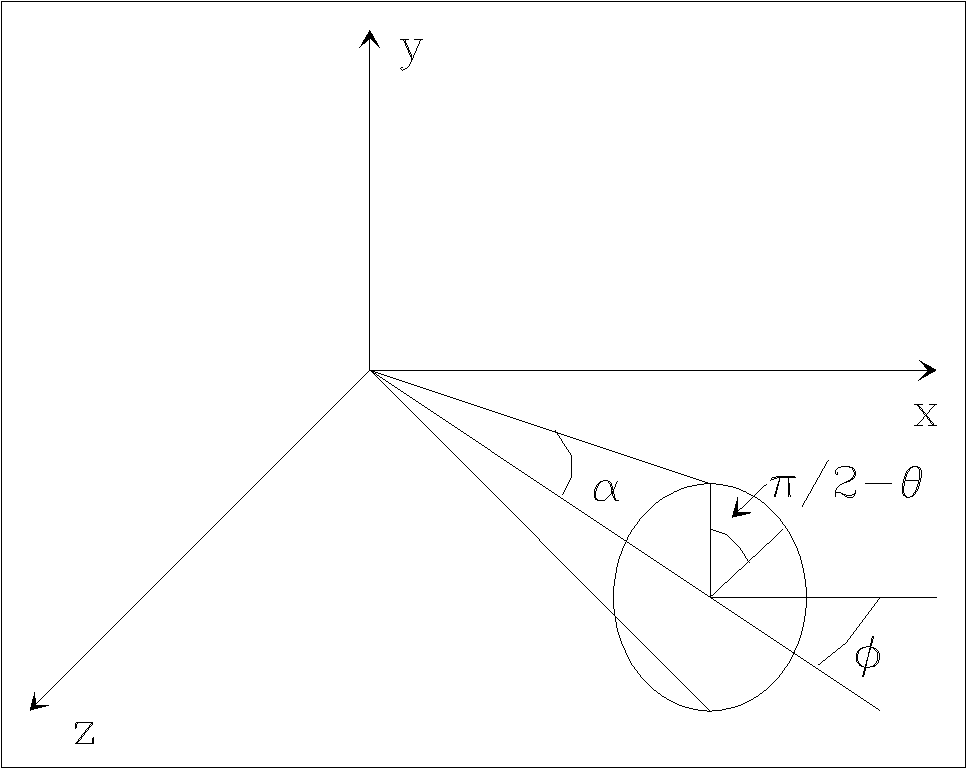
Fig. 1 Schematic diagram showing the precession cone of the ballistic jet model. The xy-plane is parallel to the plane of the sky, and the z-axis points towards the observer. The half-opening angle of the cone is α, and the precession axis points towards the observer at an angle φ from the plane of the sky. There is also an oppositely directed counterjet which is not shown in the figure.
The ballistic trajectory of the ejected fluid parcels is given by:
where t' is the evolutionary time of the jet, τ ≤ t' is the time at which the fluid parcels were ejected and v is the (constant) ejection velocity. The locus of the oppositely directed couterjet is obtained with the v → -v change in equations (2-4).
An observation of the shape of the precessing jet (projected onto the plane of the sky), is done at a fixed arrival time t (of the emitted light at the observer). Setting t = 0 for t’ = 0 these two times obey the relation:
where c is the speed of light and z is given by equation (4).
Combining equations (2-5) one obtains the plane of the sky jet locus
with
The locus of the counterjet is obtained by setting a negative v.
Equations (6-8) give the plane of the sky locus of the jet in a parametric way, with the parameter being the ejection time τ (with τ ≤ t). These equations have been derived and explored by Hjellming & Johnston (1981b) and by Gower et al. (1982).
Interestingly, the y/x ratio is independent of v and v/c (see equations 6-7). This ratio has a series of alternative maxima and minima, which correspond to the maximum excursions from the projected precession axis of the projected spiral. These maxima fall at rotation angles:
and all have the same value
Therefore, the observed path of the projected jet lies within a triangle of half-opening angle α 0 (given by equation 10), regardless of the value of v/c. One should note that these successive maxima in y/x only appear if the α + φ ≤ π/2 condition is met.
3. The Equivalent Classical Spiral
A classical, v << c precessing jet has a projected path given by equations (6-7) with v/c = 0 in the denominator. In this section we search for a “classical jet spiral” with velocity v1, half-opening angle α1 and orientation φ1 (with respect to the plane of the sky) that produces the same plane of the sky locus as a relativistic jet (of arbitrary v/c) with corresponding parameters v, α and φ.
Setting φ 1 = φ + ∆φ, the v/c = 0 limit of equations (6-7) can be written as:
with θ given by equation (1) and A(τ) by equation (8) with α = α1.
It can be straightforwardly shown that if one chooses:
then equations (6-7) coincide with equations (11-12) to first order in the terms of
Therefore, for small values of β and ϵ the plane of the sky projection of a relativistic, precessing jet corresponds to the projection of a spiral with an orientation φ1 = φ + ∆φ, half opening angle α1 and velocity v 1 (see equations 13-15) that differ from the φ, α, v values of the relativistic flow.
The “rotated spiral” description (equations 11-15) is appropriate for v/c << 1 and/or ϵ << 1 (see equation 16). This latter condition can be obtained by having α 1 and/or φ 1, as the cos θ(τ) term adopts all values from -1 to 1 along the jet locus. In the following section, we explore quantitatively the agreement of equations (11-12) with equations (6-7) for different values of the parameters of the precessing jet flow.
4. Exploration of Parameter Space
We now carry out a comparison between the rotated spiral description and the relativistic plane of the sky projection of corkscrew jets for a range of model parameters. We have chosen the 21 parameter combinations listed in Table 1. The first column of this table gives the number of the figure in which each model is displayed. Columns 2-4 give the v/c, orientation angle φ and half-opening angle α that fix each of the models. The remaining columns give the values that determine the rotated spiral description: ∆φ (equation 13, the value for the jet is given, the counterjet having a positive ∆φ with the same module), ∆α = α1 - α (see equation 14, the first value corresponding to the jet and the second one to the counterjet) and v1/v (see equation 15, the counterjet having a negative value with the same module).
Table 1 Physical Conditions for the Numerical Simulations.
| Fig. | v/c | φ | α | Δφ | Δα | v1/v | |
|---|---|---|---|---|---|---|---|
| 2 | 0.1 | 0 | 10 | −5.62 | −0.05, | −0.05 | 1.00 |
| 2 | 0.1 | 20 | 10 | −5.29 | 0.30, | −0.38 | 1.00 |
| 2 | 0.1 | 40 | 10 | −4.31 | 0.61, | −0.67 | 1.00 |
| 2 | 0.1 | 60 | 10 | −2.82 | 0.85, | −0.87 | 1.00 |
| 2 | 0.1 | 80 | 10 | −0.98 | 0.98, | −0.98 | 1.00 |
| 3 | 0.2 | 0 | 10 | −11.14 | −0.19, | −0.19 | 1.02 |
| 3 | 0.2 | 20 | 10 | −10.49 | 0.50, | −0.83 | 1.02 |
| 3 | 0.2 | 40 | 10 | −8.58 | 1.15, | −1.38 | 1.01 |
| 3 | 0.2 | 60 | 10 | −5.62 | 1.67, | −1.76 | 1.00 |
| 3 | 0.2 | 80 | 10 | −1.96 | 1.96, | −1.96 | 1.00 |
| 4 | 0.26 | 10 | 20 | −13.53 | 0.28, | −1.43 | 1.03 |
| 5 | 0.2 | 10 | 20 | −10.49 | 0.32, | −1.01 | 1.02 |
| 5 | 0.4 | 10 | 20 | −20.31 | −0.02, | −2.55 | 1.07 |
| 5 | 0.6 | 10 | 20 | −29.04 | −0.83, | −4.35 | 1.14 |
| 5 | 0.8 | 10 | 20 | −36.52 | −1.89, | −6.17 | 1.24 |
| 6 | 0.26 | 10 | 30 | −12.50 | 0.48, | −2.03 | 1.02 |
| 6 | 0.26 | 10 | 50 | −9.35 | 1.06, | −2.78 | 1.01 |
| 6 | 0.26 | 10 | 70 | −5.00 | 61.91, | −2.83 | 1.00 |
| 6 | 0.26 | 45 | 30 | −9.05 | 4.92, | −5.47 | 1.01 |
| 6 | 0.26 | 45 | 50 | -6.74 | 8.28, | −7.87 | 1.01 |
| 6 | 0.26 | 45 | 70 | −3.60 | 15.42, | −8.49 | 1,00 |
*The values of ∆φ and v1 correspond to the jet (directed towards the observer). The oppositely directed counterjet has a ∆φ equal to (−1)× the values given in this table. The two values given for ∆α correspond to the jet and the counterjet. All of the angles are given in degrees.
We first consider a jet with v/c = 0.1 and α = 10°. In Figure 2 we show the locus of the jet projected on the plane of the sky for different orientation angles φ. We have assumed that the ejection direction has a θ0 = 0 initial phase (see equation 1). In the plots, we have the jet (directed towards the observer) for x > 0 and the counterjet (directed away from the plane of the sky) for x < 0.
From Figure 2 we see that (at the resolution of the plots), the “rotated spiral” description of the flow (equations 11-15) coincides with the relativistic jet (equations 6-7) except for φ = 80° for which small differences between the two solutions are seen.
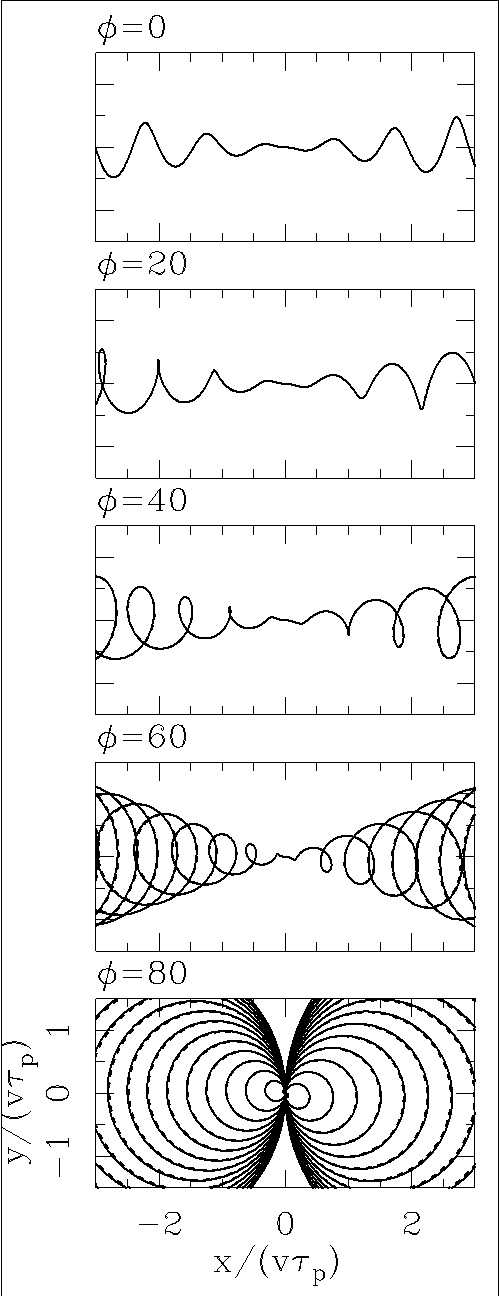
Fig. 2 The projection of the jet locus onto the plane of the sky for jet/counterjet systems with v/c = 0.1, α = 10° and different values of the angle φ between the precession axis with respect to the plane of the sky. The blueshifted jet is shown with x > 0 and the redshifted counterjet with x < 0. The exact solution to the relativistic problem is shown with a solid line, and the approximate “rotated spiral description” is shown with a dashed line. Both solutions almost coincide at the resolution of the plots. The plane of the sky coordinates are normalized with the product vτp of the outflow velocity times the precession period. An initial θ0 = 0 phase for the precession has been assumed.
In Figure 3, we show the projected locus of a jet with v/c = 0.2 and α = 10°. As expected, we see that there are somewhat larger deviations between the “rotated spiral” and the relativistic solutions. However, a reasonable qualitative agreement is obtained for all values of φ (the largest deviations appearing in the φ = 80◦ projection).
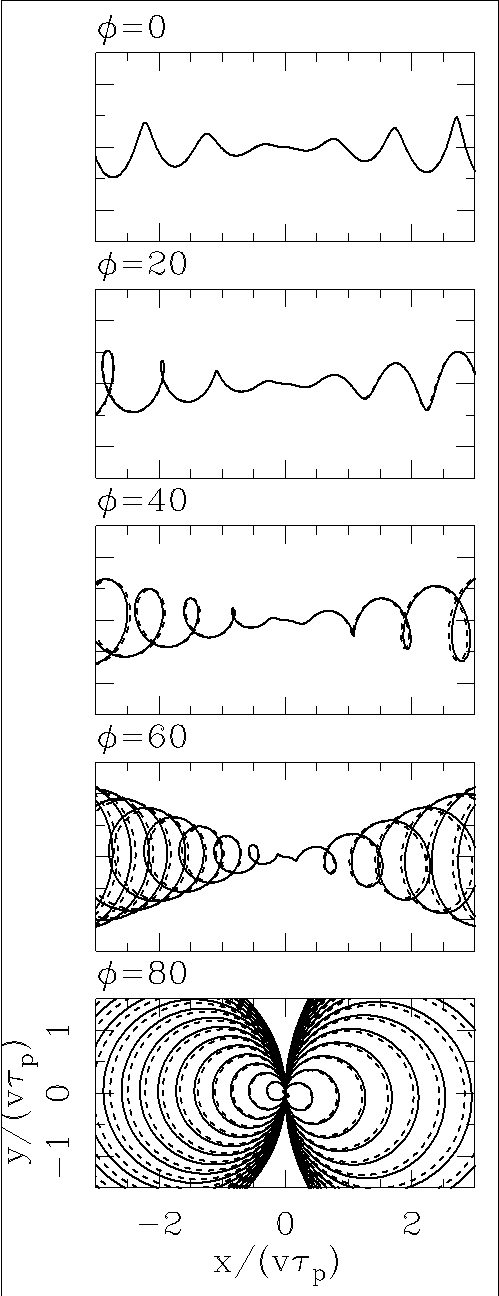
Fig. 3 The same as Figure 2 but for flows with v/c = 0.2. Larger differences between the full solution (solid lines) and the “rotated spiral description” (dashed lines) are seen.
The results shown in Figures 2 and 3 demonstrate that for relatively low values of v/c and α (so that β and ϵ are small, see equation 16) there is a good agreement between the “rotated spiral” and relativistic solutions for all orientation angles φ ≤ 80°.
We now choose the v/c = 0.26, α = 20°, φ = 10° parameters derived by Hjellming & Johnston (1981) for the SS 433 outflow. It is clear that this jet indeed corresponds to our “rotated spiral” solution (see Figure 4).

Fig. 4 Outflow with the “SS 433 parameters” v/c = 0.26, α = 20°, φ = 10° parameters derived of Hjellming & Johnston (1981). A good agreement is found between the full solution (solid line) and the “rotated spiral description” (dashed line). Again a θ0 = 0 initial phase has been assumed.
In order to further explore the limits of our approximate rotated spiral solution, we now fix the α = 20° and φ = 10° “SS 433 parameters” and play with the value of v/c. The results of this exercise (see Figure 5) show that while for v/c = 0.2 and 0.4 we obtain a good quantitative agreement between the relativistic and “rotated spiral” solutions, for v/c = 0.6 and 0.8 the two solutions only show a qualitative resemblance. Therefore, we see that the rotated spiral solution provides a good description of the jet solution only for velocities smaller than v ≈ 0.5.
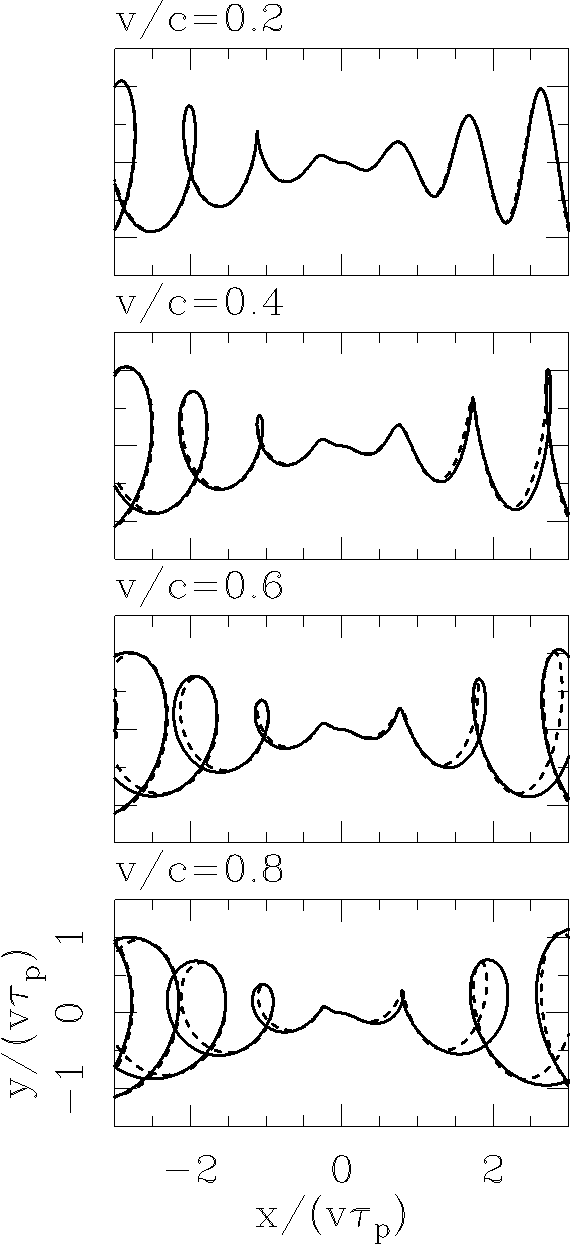
Fig. 5 Precessing jet flows with α = 20° and φ = 10°, and with different values of v/c (given by the labels at the top left of each frame. The full solution (solid lines) and the “rotated spiral description” (dashed lines) show a good agreement for v/c ≤ 0.5.
Finally, we calculate models with v/c = 0.26, two orientation angles φ = 10 and 45° and half-opening angles α = 30, 50, and 70◦. The results of this exercise (see Figure 6) show that while the discrepancies between the relativistic and “rotated spiral” solutions grow with increasing α, a reasonable qualitative agreement is obtained except for the α = 70◦, φ = 45° model.
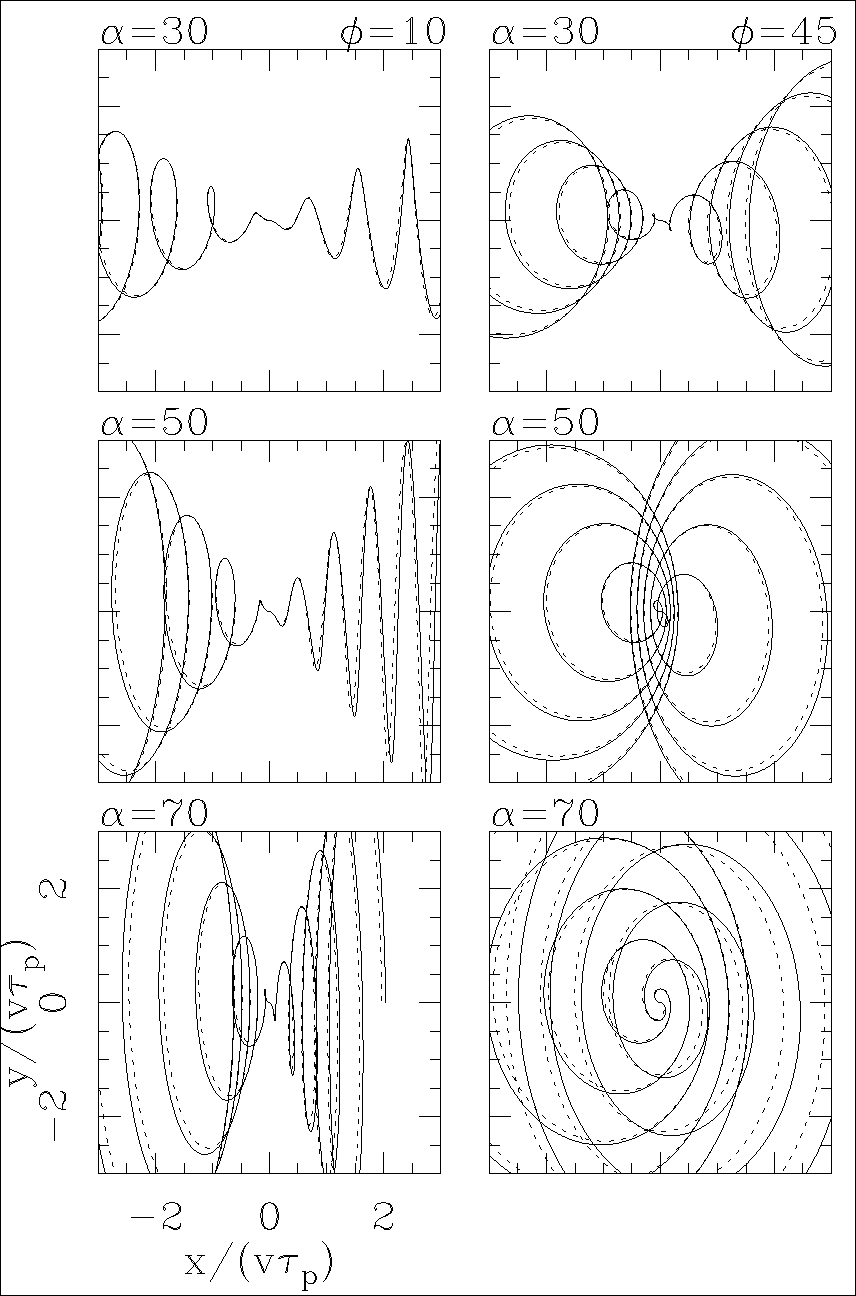
Fig. 6 Jet flows with v/c = 0.26, two orientations (φ = 10° for the left and φ = 45° for the right column) and three half-opening angles (top: α = 30°; center: α = 50°; bottom: α = 70°). One can appreciate the increasing differences for larger α values between the full solution (solid lines) and the “rotated spiral description” (dashed lines). To avoid confusion, we only show the locus of the material ejected during five precession periods.
5. Summary
We find that, independent of the v/c value, the projection of a precessing jet on the plane of the sky lies within a triangle of half-opening angle α0 given by equation (10), provided that the α + φ ≤ π/2 condition is met (where α is the precession halfopening angle and φ the angle between the precession axis and the plane of the sky).
We also find that mildly relativistic precessing jet/counterjet systems on the plane of the sky correspond to the (classical) projection of a spiral with an orientation angle φ1 = φ+∆φ, half-opening angle α1 = α + ∆α and flow velocity v1 which differ from the corresponding φ, α and v of the outflow.
As can be seen in Table 1, the rotated spiral has:
velocity correction: generally v1/v ≈ 1, except for the v/c = 0.6, 0.8 models (see Figure 5), for which the “rotated spiral” description does not work well;
opening angle correction: ∆α = α1α is generally small (< 2°), except for the higher v/c and α models (see figures 5 and 6);
rotation: this is clearly the main correction that has to be done so that the classical plane of the sky projection of a spiral agrees with the relativistic, time-delayed projection. The axes of the jet and the counterjet are both rotated (by the same ∆φ) away from the observer. Because of this, in the models with φ ≥ 10◦ the counterjet axis (directed away from the observer) increases its angle with respect to the plane of the sky, and the jet axis (directed towards the observer) approaches the plane of the sky.
Even though the “rotated spiral” description is based on a linearization of the relativistic free-streaming equations (with respect to the β and ϵ variables, see equation 16), we find that it provides a qualitatively correct approximation to the projected, relativistic corkscrew when v/c < 0.5 (see § 4 and Figure 5). Provided that this condition is met, the rotated spiral description is good approximation for all orientation angles (see Figures 2 and 3), and for half-opening angles α ≤ 50° (see Figure 6). Also, it is a definitely good approximation for the parameters of the SS433 flow (see Figure 4).
These results are clearly not of ground-breaking importance. However, we think that they provide an interesting advance in the qualitative understanding of the observed morphologies of mildly relativistic, corkscrew jets.











 nueva página del texto (beta)
nueva página del texto (beta)


