1. Introduction
Pulsars are spinning magnetized neutron stars (Gold 1968). The spin rates of these objects are highly stable due to the huge moment of inertia they possess (≈ 1045 g cm2). In spite of this, the spin rate of some pulsars is occasionally perturbed during events known as glitches. Pulsar glitches are impulsive increases in the pulsar spin frequency,
Pulsar glitch models involving a superfluid component view the neutron star as a system in which its components rotate differentially. The main components are: the solid crust, the interior superfluid neutrons (inner crust and outer core), and the core (Takatsuka & Tamagaki 1989). In this model, the solid crust and the core are coupled electromagnetically. The inner crust superfluid component viewed as a momentum reservoir, rotates via an array of quantized vortices whose areal density is proportional to the fluid velocity. These vortices are pinned in the ion lattice of the inner crust, leading to partial decoupling of the inner crust superfluid component from the other components (Anderson & Itoh 1975; Alpar et al. 1984). As the coupled components spin down electromagnetically, the inner crust superfluid maintains its own velocity. In this situation, the superfluid at a higher velocity stores angular momentum, which is occasionally released in glitches. For the superfluid to spin down, the vortex areal density must decrease. This could happen either by reduction of the vortex number, or by outward migration of vortices. Such processes are prevented by the pinning force on the vortices. As long as the vortices remain in their pinned position, the superfluid angular momentum is conserved.
Meanwhile, as the solid crust lags behind the superfluid component, the rotation lag (i.e. the magnitude of the velocity difference between the two components) increases with time. The lag is not sustainable over the pulsar life time. At a critical lag, unclear mechanisms unpin some of the vortices (or all of them). The vortices migrate outward transferring their momentum to the crust; the superfluid spins-down and the crust spins-up (Anderson & Itoh 1975; Alpar et al. 1984). The magnitude of the crustal spin-up,
A glitch model involving angular momentum transfer has been standard for discussing pulsar glitches for decades. This is partly due to its ability to explain post glitch features such as exponential recoveries and long recovery times (Baym et al. 1969; Alpar et al. 1984), and mainly due to the agreement between the theoretical prediction of neutron star crustal thickness and the pulsar glitch size (Ravenhall & Pethick 1994; Link et al. 1999). Recently, most aspects of the Vela pulsar glitches have been fully described based on this model (Haskell et al. 2012). Plausibly, the angular momentum transfer model is becoming the most widely accepted theory. In the work of Link et al. (1999), the moment of inertia of the superfluid component involved in the Vela glitches is just about 1.4% of the stellar moment of inertia. This amount of superfluid can conveniently reside in the inner crust of the star. In view of the inner crust superfluid involvement in pulsar glitches, the regularity of the glitches of the Vela pulsar and of PSR J0357 − 6910, is seen as a consequence of recycling a reservoir that is exhausted at each event (Andersson et al. 2012).
However, following the recent involvement of crustal entrainment in pulsar glitch size (Andersson et al. 2012; Chamel 2013), angular momentum transfer models are under a serious challenge. Basically, entrainment increases the inertia of superfluid neutrons, thereby reducing the mobility of the fluid (Chamel 2005; Chamel & Carter 2006; Chamel 2012). For this reason, the superfluid confined in the inner crust is not sufficient to produce Vela-like glitches; unless glitching pulsars are low mass neutron stars
On the other hand, recent works (Piekarewicz et al. 2014; Steiner et al. 2015) have argued that the inner crust superfluid could sufficiently produce the observed glitches. The argument is based on exploring the uncertainties of the equation-of-state (EoS) of the nuclear matter, which models the structure of the neutron star. With this approach, Piekarewicz et al. (2014) obtained a crust thick enough to contain a fluid with up to 7% of the stellar moment of inertia, given a neutron star mass < 1.6 M⊙. Similarly, for a neutron star mass of 1.4 M⊙, Steiner et al. (2015) obtained a thicker crust with up to 10% of the stellar moment of inertia. Large crustal thickness implies large stellar radius and small stellar mass. In this framework, there is a limit for how much one can extend the crust irrespective of the magnitude of the uncertainty of the EoS, else one would approach a white dwarf.
In the previous analyses, the approach has been to calculate the fractional moment of inertia (FMI) (i.e. the ratio of inner crust superfluid moment of inertia to that of the coupled components) of the neutron star components participating in the glitch based on the average glitch size of a given pulsar. The result is then compared with the theoretical magnitude of neutron star crustal thickness. However fair this approach is, it hides the intrinsic size of the inner crust fluid. Efforts should be channelled towards calculating the FMI based on individual glitches, as this will show the possible range of crustal thickness. This paper treats each glitch as a unique event, and calculates the FMI for each glitch in three pulsars that exhibit strong linear transfer of angular momentum with time. The linearity of glitches in these pulsars is believed to be a consequence of a reservoir that is exhausted at each event, thereby making each glitch independent of others. In such a situation, the FMI for each glitch is a measure of a distinct momentum reservoir. The result shows that some glitches exceed the initial inner crust moment of inertia as constrained in Link et al. (1999) even without the entrainment factor. In addition, if the entrainment factor stands at 4.3, the present neutron star crustal thickness (≈ 10%) is not sufficient to produce some glitches.
2. Rotation lag and fractional moment of inertia
For a spinning neutron star, the standard rotation lag between the momentum reservoir4 and the observable solid crust, which leads to accumulation of transferable momentum, is
where
where
In a glitching pulsar, at a time-interval (
at a rate of
where
at a rate of
In this framework, if the rate of accumulation of angular momentum by the reservoir is directly proportional to the rate angular momentum is transferred, the cumulative glitch spin-up sizes (
Such an expression for the FMI has been obtained earlier (Eya et al. 2017). The magnitude of FMI gives an insight on the magnitude of the momentum reservoir.
3. Entrainment factor and the magnitude of FMI/glitch size
It is known that a superfluid flows with zero viscosity. The superfluid neutrons in the inner crust of a neutron star also flow with zero viscosity, but they are still entrained by the crust (Pethick et al. 2010). The entrainment is non-dissipative, it occurs due to the elastic scattering of free neutrons by the crustal lattice (Chamel 2013). The magnitude of the entrainment in the inner crust is quantified by either the density of conduction neutrons in the crust or by the effective mass of the neutron (Andersson et al. 2012; Chamel 2013). In this paper, the interest is on how the entrainment factor constrains the observed glitch sizes.
For a sphere spinning down, such as pulsars, the loss in rotational energy is
This loss in rotational energy results in the observed radiation from the pulsar, which can be approximated to that of a dipole radiator in a vacuum,
where
Equation (10) is the standard spin-down law of pulsars, where
As entrainment is non-dissipative,
Therefore, the effective torque on the pulsar is
where
Let us determine the effective moment of inertia associated with the glitch event. Based on the two component model, the total angular momentum of the system is
where
where
The term in parentheses is the differential rotational lag,
The interpretation of this result is quite simple; the observed glitch sizes should be less by a factor of
4. Data and results
The glitches for this analysis are taken from Espinoza et al.
(2011), and updated with JBO glitch tables and references therein7 to include more recent events, up to
the time of this analysis. Three pulsars in which glitch spin-up sizes
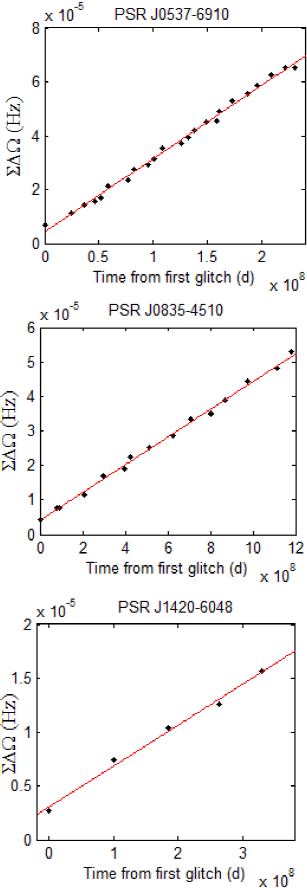
For nearly two decades, the constraint on crustal thickness estimated from glitch data was based on comparing the moment of inertia of the inner crust superfluid obtained from a linear fit to glitch points in plots such as Figure 1. With the slope of the linear fits in Figure 1 and the mean spin down rate of the corresponding pulsar, the mean FMI for each of the pulsars are: 0.85% for PSR J
The FMIs for each glitch are shown in Table 1. The FMI corresponding to the first glitch in a given pulsar could not be calculated since the time interval preceding the glitch is not available. The distribution of FMIs is shown in the top panel of Figure 2, while the bottom panel shows the distribution of FMIs scaled with the entrainment factor (4.3). From the top panel, it is clear that an
Table 1 Characteristic FMI in the pulsars.
| Ng | J0537-6910 | J0835-4510 | J1420-6048 |
| 1 | - | - | - |
| 2 | 0.763 | 1.851 | 1.660 |
| 3 | 1.067 | 0.080 | 1.241 |
| 4 | 0.724 | 1.448 | 0.959 |
| 5 | 0.964 | 2.605 | 1.685 |
| 6 | 2.182 | 0.792 | - |
| 7 | 0.595 | 5.570 | - |
| 8 | 21.267 | 1.244 | - |
| 9 | 0.418 | 1.184 | - |
| 10 | 1.156 | 2.395 | - |
| 11 | 1.449 | 0.627 | - |
| 12 | 0.301 | 5.116 | - |
| 13 | 1.165 | 2.241 | - |
| 14 | 1.234 | 2.145 | - |
| 15 | 1.025 | 1.093 | - |
| 16 | 0.057 | 2.812 | - |
| 17 | 6.804 | 1.095 | - |
| 18 | 0.944 | 2.225 | - |
| 19 | 0.612 | 0.001 | - |
| 20 | 1.089 | - | - |
| 21 | 0.990 | - | - |
| 22 | 0.492 | - | - |
| 23 | 0.067 | - | - |
Note: The FMIs are measured in percent (%), Ng denotes the glitch number.
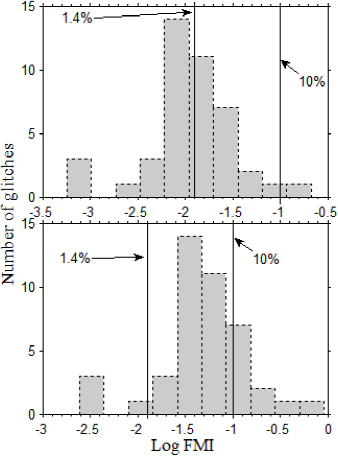
Fig. 2 Distribution of FMIs calculated from equation (7); bottom panel is the distribution of FMIs scaled with an entrainment factor as suggested by equation (17).
5. Discussion
The FMI in this analysis is a measure of distinct reservoir moment of inertia. The upper limit
in the range of FMIs in a given pulsar gives an insight on the minimum size of the
neutron star crustal thickness. Without the entrainment factor, the: 6th, 8th and
17th glitch in PSR J
Finally, pulsar glitch models relying on an inner crust superfluid and nuclear matter EoS are under serious challenge unless the vortex unpinning trigger mechanism, which is still elusive, has the ability to squeeze angular momentum and liberate it at the onset of the glitch.











 nueva página del texto (beta)
nueva página del texto (beta)