1. Introduction
Pulsars are spinning magnetized neutron stars (Gold 1968). The spin rates of these objects are highly stable due to the huge moment of inertia they possess (≈ 1045 g cm2). In spite of this, the spin rate of some pulsars is occasionally perturbed during events known as glitches. Pulsar glitches are impulsive increases in the pulsar spin frequency, Δν (Radhakrishnan & Manchester 1969; Wang et al. 2000; Espinoza et al. 2011; Yu et al. 2013). These events are sometimes associated with changes in the pulsar spin-down rate, Δ˙v (Lyne et al. 1993). In most of the pulsars, glitch events are believed to involve superfluid neutrons in the inner crust of the neutron star (Baym et al. 1969; Anderson & Itoh 1975; Alpar et al. 1984). Firstly, this is due to the long time it takes a pulsar to recover to a steady spin frequency after a glitch (days to months) and, secondly, due to the recovery phase, which is exponential in nature for most pulsars. Recently, studies of the interior of neutron stars containing superfluids have gained observational support by the cooling of young neutron stars (Page et al. 2011; Shternin et al. 2011). So there is no doubt that neutron stars contain a superfluid component.
Pulsar glitch models involving a superfluid component view the neutron star as a system in which its components rotate differentially. The main components are: the solid crust, the interior superfluid neutrons (inner crust and outer core), and the core (Takatsuka & Tamagaki 1989). In this model, the solid crust and the core are coupled electromagnetically. The inner crust superfluid component viewed as a momentum reservoir, rotates via an array of quantized vortices whose areal density is proportional to the fluid velocity. These vortices are pinned in the ion lattice of the inner crust, leading to partial decoupling of the inner crust superfluid component from the other components (Anderson & Itoh 1975; Alpar et al. 1984). As the coupled components spin down electromagnetically, the inner crust superfluid maintains its own velocity. In this situation, the superfluid at a higher velocity stores angular momentum, which is occasionally released in glitches. For the superfluid to spin down, the vortex areal density must decrease. This could happen either by reduction of the vortex number, or by outward migration of vortices. Such processes are prevented by the pinning force on the vortices. As long as the vortices remain in their pinned position, the superfluid angular momentum is conserved.
Meanwhile, as the solid crust lags behind the superfluid component, the rotation lag (i.e. the magnitude of the velocity difference between the two components) increases with time. The lag is not sustainable over the pulsar life time. At a critical lag, unclear mechanisms unpin some of the vortices (or all of them). The vortices migrate outward transferring their momentum to the crust; the superfluid spins-down and the crust spins-up (Anderson & Itoh 1975; Alpar et al. 1984). The magnitude of the crustal spin-up, Δν, is the glitch spin-up size. Large glitches, such as that of the Vela pulsar, are characterised by Δν > 10−6 Hz. Such a glitch size is one of the reasons why scholars believed that there is an angular momentum reservoir somewhere in the neutron star interior.
A glitch model involving angular momentum transfer has been standard for discussing pulsar glitches for decades. This is partly due to its ability to explain post glitch features such as exponential recoveries and long recovery times (Baym et al. 1969; Alpar et al. 1984), and mainly due to the agreement between the theoretical prediction of neutron star crustal thickness and the pulsar glitch size (Ravenhall & Pethick 1994; Link et al. 1999). Recently, most aspects of the Vela pulsar glitches have been fully described based on this model (Haskell et al. 2012). Plausibly, the angular momentum transfer model is becoming the most widely accepted theory. In the work of Link et al. (1999), the moment of inertia of the superfluid component involved in the Vela glitches is just about 1.4% of the stellar moment of inertia. This amount of superfluid can conveniently reside in the inner crust of the star. In view of the inner crust superfluid involvement in pulsar glitches, the regularity of the glitches of the Vela pulsar and of PSR J0357 − 6910, is seen as a consequence of recycling a reservoir that is exhausted at each event (Andersson et al. 2012).
However, following the recent involvement of crustal entrainment in pulsar glitch size (Andersson et al. 2012; Chamel 2013), angular momentum transfer models are under a serious challenge. Basically, entrainment increases the inertia of superfluid neutrons, thereby reducing the mobility of the fluid (Chamel 2005; Chamel & Carter 2006; Chamel 2012). For this reason, the superfluid confined in the inner crust is not sufficient to produce Vela-like glitches; unless glitching pulsars are low mass neutron stars (≤1.0 M⊙), or the core fluid is involved in the glitch (Andersson et al. 2012). Consequently, in Link et al. (1999) the inner crust superfluid moment of inertia is underestimated by a factor of 4.3 (Andersson et al. 2012; Chamel 2013), which is the likely value of the entrainment factor. Physically, this means that the moment of inertia of the superfluid contained in the inner crust should be above 6% of the stellar moment of inertia for it to produce the observed glitches (i.e. 4.3 × 1.4%).
On the other hand, recent works (Piekarewicz et al. 2014; Steiner et al. 2015) have argued that the inner crust superfluid could sufficiently produce the observed glitches. The argument is based on exploring the uncertainties of the equation-of-state (EoS) of the nuclear matter, which models the structure of the neutron star. With this approach, Piekarewicz et al. (2014) obtained a crust thick enough to contain a fluid with up to 7% of the stellar moment of inertia, given a neutron star mass < 1.6 M⊙. Similarly, for a neutron star mass of 1.4 M⊙, Steiner et al. (2015) obtained a thicker crust with up to 10% of the stellar moment of inertia. Large crustal thickness implies large stellar radius and small stellar mass. In this framework, there is a limit for how much one can extend the crust irrespective of the magnitude of the uncertainty of the EoS, else one would approach a white dwarf.
In the previous analyses, the approach has been to calculate the fractional moment of inertia (FMI) (i.e. the ratio of inner crust superfluid moment of inertia to that of the coupled components) of the neutron star components participating in the glitch based on the average glitch size of a given pulsar. The result is then compared with the theoretical magnitude of neutron star crustal thickness. However fair this approach is, it hides the intrinsic size of the inner crust fluid. Efforts should be channelled towards calculating the FMI based on individual glitches, as this will show the possible range of crustal thickness. This paper treats each glitch as a unique event, and calculates the FMI for each glitch in three pulsars that exhibit strong linear transfer of angular momentum with time. The linearity of glitches in these pulsars is believed to be a consequence of a reservoir that is exhausted at each event, thereby making each glitch independent of others. In such a situation, the FMI for each glitch is a measure of a distinct momentum reservoir. The result shows that some glitches exceed the initial inner crust moment of inertia as constrained in Link et al. (1999) even without the entrainment factor. In addition, if the entrainment factor stands at 4.3, the present neutron star crustal thickness (≈ 10%) is not sufficient to produce some glitches.
2. Rotation lag and fractional moment of inertia
For a spinning neutron star, the standard rotation lag between the momentum reservoir4 and the observable solid crust, which leads to accumulation of transferable momentum, is
where Ωres=2πνres is the reservoir’s angular frequency, Ωc=2πνc the angular frequency of the solid crust and any other component coupled to it. The stellar moment of inertia is
where Ires and Ic are the moments of inertia of the momentum reservoir and that of the coupled components, respectively. In this model, Ic makes up at least 90% of the neutron star moment of inertia (Link et al. 1999, and references therein), implying Ic≈I.
In a glitching pulsar, at a time-interval (ti) preceding a glitch, the reservoir accumulates transferable momentum due to the rotation lag, which can be quantified by
at a rate of
where ˙Ωic(t)=2π˙νic is the spin-down rate of the crust at a time-interval preceding the glitch. Here, it is assumed that the momentum accumulated over a period ti, results in a spin-up of the crust ΔΩic. A measure of ΔΩc is an indirect way of estimating the transferred momentum. In this, for a given glitch, the transferred momentum is
at a rate of
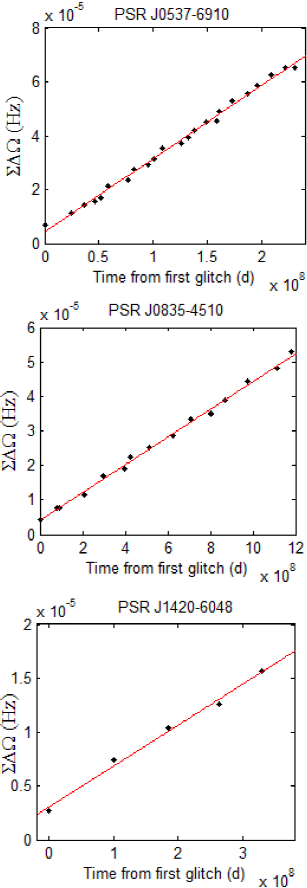
In this framework, if the rate of accumulation of angular momentum by the reservoir is directly proportional to the rate angular momentum is transferred, the cumulative glitch spin-up sizes (ΣΔΩic) should be linear over time if the momentum reservoir is exhausted at each glitch. Such pulsars of linear transfer of angular momentum over time are shown in Figure 1. This kind of behaviour has been reported in PSRs J0835-4510 (Vela pulsar) (Link et al. 1999; Marshall et al. 2004; Eya & Urama 2014), J0537-6910 (Middleditch et al. 2006), and J1420-6048 (Eya et al. 2017). Hence, equations (4) and (6) give the individual glitch FMI
Such an expression for the FMI has been obtained earlier (Eya et al. 2017). The magnitude of FMI gives an insight on the magnitude of the momentum reservoir.
3. Entrainment factor and the magnitude of FMI/glitch size
It is known that a superfluid flows with zero viscosity. The superfluid neutrons in the inner crust of a neutron star also flow with zero viscosity, but they are still entrained by the crust (Pethick et al. 2010). The entrainment is non-dissipative, it occurs due to the elastic scattering of free neutrons by the crustal lattice (Chamel 2013). The magnitude of the entrainment in the inner crust is quantified by either the density of conduction neutrons in the crust or by the effective mass of the neutron (Andersson et al. 2012; Chamel 2013). In this paper, the interest is on how the entrainment factor constrains the observed glitch sizes.
For a sphere spinning down, such as pulsars, the loss in rotational energy is
This loss in rotational energy results in the observed radiation from the pulsar, which can be approximated to that of a dipole radiator in a vacuum,
where B is the magnetic field strength, R is the stellar radius, and c is the speed of light. Comparing equations (8) and (9) (with Ω≡Ωc) leads to
Equation (10) is the standard spin-down law of pulsars, where K=6-1B2R6 c-3sin2α is assumed to be constant. For the two components model and owing to the pinned vortices,
As entrainment is non-dissipative, Ires˙Ωres is not expected to affect the spin down of the pulsar. In the frame of perfect pinning and expressing entrainment in terms of the coefficient, en, (Andersson et al. 2012, and references therein),
Therefore, the effective torque on the pulsar is
where Ief=Ic-(en1-en)Ires is the effective moment of inertia of the pulsar due to entrainment, and (en1-en)=En is the entrainment factor. If the entrainment coefficient is zero, the standard spin-down law is recovered.
Let us determine the effective moment of inertia associated with the glitch event. Based on the two component model, the total angular momentum of the system is
where IresΩres is the angular momentum of the momentum reservoir (neutron superfluid), and IcΩc is the observable angular momentum of the star. However, owing to entrainment, the angular momentum of the superfluid is a function of both the superfluid angular velocity and the angular velocity of the star, Ωc, (Chamel 2013), which is expressed as (Chamel & Carter 2006; Chamel 2013)
where Iss is the moment of inertia associated with the entrained neutrons. Hence, the total angular momentum of the system as a result of entrainment is5
The term in parentheses is the differential rotational lag, ω(t). The implication of this is that the effective moment of inertia associated with the transferred momentum is that of the entrained neutron, and Ires in equation (7) could be safely replaced with Iss. From equation (16), the effective torque is (I-Iss)˙Ωc and with equation (13) 6 Iss=EnIres. Hence incorporating the entrainment factor in the expression of FMI leads to
The interpretation of this result is quite simple; the observed glitch sizes should be less by a factor of 1/En, or equivalently, the moment of inertia of the momentum reservoir should be enhanced by a factor of En for the observed glitch sizes. Though this argument is not new, it has not been extended to individual glitch FMI.
4. Data and results
The glitches for this analysis are taken from Espinoza et al. (2011), and updated with JBO glitch tables and references therein7 to include more recent events, up to the time of this analysis. Three pulsars in which glitch spin-up sizes (Δν) are quite regular over time were selected for this analysis (Figure 1). Concentrating on such pulsars is a precaution to avoid glitches that may originate from any component other than the crustal superfluid, which is the basis for the regularity of the glitches. In addition, pulsars in which glitches follow this trend are believed to possess a reservoir that is exhausted at each glitch. In this view, each of the glitches is a unique event independent of others.
For nearly two decades, the constraint on crustal thickness estimated from glitch data was based on comparing the moment of inertia of the inner crust superfluid obtained from a linear fit to glitch points in plots such as Figure 1. With the slope of the linear fits in Figure 1 and the mean spin down rate of the corresponding pulsar, the mean FMI for each of the pulsars are: 0.85% for PSR J0537-6910, 1.55% for PSR J0835-4510 and 1.29% for PSR J1420-6048. These values are in line with other analyses (Link et al. 1999; Andersson et al. 2012; Eya et al. 2017). A constraint of this kind is based on the average glitch sizes in a pulsar. This approach does not allow for the extreme values.
The FMIs for each glitch are shown in Table 1. The FMI corresponding to the first glitch in a given pulsar could not be calculated since the time interval preceding the glitch is not available. The distribution of FMIs is shown in the top panel of Figure 2, while the bottom panel shows the distribution of FMIs scaled with the entrainment factor (4.3). From the top panel, it is clear that an 1.4% crustal thickness moment of inertia could not accommodate the observed glitches, even without the entrainment factor. The relevant glitches are the glitches with FMIs at the right side of the 1.4% line. These glitches make up ≈52% of the total glitches in these pulsars. Interestingly, when the FMIs are scaled by the entrainment factor, ≈93% of the glitches require crustal thickness that are more than 1.4% of the stellar moment of inertia, as seen in the bottom panel of Figure 2. In addition, with the entrainment factor, ≈26% of the glitches require a crust beyond the possible 10% stellar moment of inertia proposed by Steiner et al. (2015).
Table 1 Characteristic FMI in the pulsars.
| Ng | J0537-6910 | J0835-4510 | J1420-6048 |
| 1 | - | - | - |
| 2 | 0.763 | 1.851 | 1.660 |
| 3 | 1.067 | 0.080 | 1.241 |
| 4 | 0.724 | 1.448 | 0.959 |
| 5 | 0.964 | 2.605 | 1.685 |
| 6 | 2.182 | 0.792 | - |
| 7 | 0.595 | 5.570 | - |
| 8 | 21.267 | 1.244 | - |
| 9 | 0.418 | 1.184 | - |
| 10 | 1.156 | 2.395 | - |
| 11 | 1.449 | 0.627 | - |
| 12 | 0.301 | 5.116 | - |
| 13 | 1.165 | 2.241 | - |
| 14 | 1.234 | 2.145 | - |
| 15 | 1.025 | 1.093 | - |
| 16 | 0.057 | 2.812 | - |
| 17 | 6.804 | 1.095 | - |
| 18 | 0.944 | 2.225 | - |
| 19 | 0.612 | 0.001 | - |
| 20 | 1.089 | - | - |
| 21 | 0.990 | - | - |
| 22 | 0.492 | - | - |
| 23 | 0.067 | - | - |
Note: The FMIs are measured in percent (%), Ng denotes the glitch number.
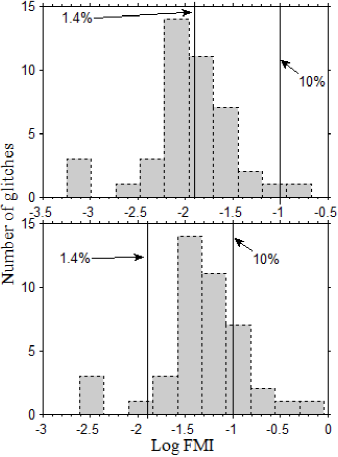
Fig. 2 Distribution of FMIs calculated from equation (7); bottom panel is the distribution of FMIs scaled with an entrainment factor as suggested by equation (17).
5. Discussion
The FMI in this analysis is a measure of distinct reservoir moment of inertia. The upper limit in the range of FMIs in a given pulsar gives an insight on the minimum size of the neutron star crustal thickness. Without the entrainment factor, the: 6th, 8th and 17th glitch in PSR J0537-6910; 5th, 7th, 10th, 12th, 13th, 14th, 16th and 18th glitch in the Vela pulsar require a crustal thickness that is above 2%, of the stellar moment of inertia. Only the glitches in PSR J1420-6048 are exempt from this anomaly. Owing to this, the earlier theoretical calculations of the neutron star crust (Ravenhall & Pethick 1994; Link et al. 1999) could not account for some of the glitches, even without entrainment factor. This effect is more severe with the entrainment factor, where some of the glitches will require a crust thickness that is above 10% of the stellar moment of inertia. The FMI could be as large as 90% and 24% for the 8th and 7th glitches in PSRs J0537-6910 and J0835-4510 respectively8. As at present, no EoS provides a neutron star crust that could contain a crustal fluid for such a reservoir. This result is quite disturbing if one recalls that these glitches are from pulsars which deplete their reservoir at each glitch. There is no evidence of radiative change in these pulsars during the glitch, which might have suggested that glitches are enhanced by magnetospheric activity. The 7-10% crustal thickness moment of inertia (Piekarewicz et al. 2014; Steiner et al. 2015) is an upper limit in the current theoretical calculation of the neutron star structure. The actual value could be lower, since the authors neglected superfluidity. In particular, for such a crustal thickness, the neutron star radius should be as large as ≈14.0±0.5 km. Clearly this value is in contrast with the recent analysis of low mass X -ray binaries, with predicted small radii of ≈11.8±0.9 km (Lattimer & Steiner 2014), or even smaller from the analysis of Guillot et al. (2013).
Finally, pulsar glitch models relying on an inner crust superfluid and nuclear matter EoS are under serious challenge unless the vortex unpinning trigger mechanism, which is still elusive, has the ability to squeeze angular momentum and liberate it at the onset of the glitch.











 text new page (beta)
text new page (beta)