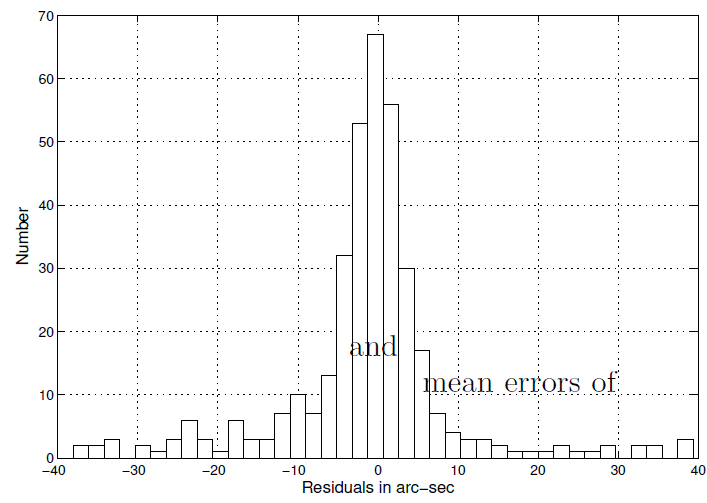1. Introduction
I have explained previously (Branham 2003) reasons for calculating an orbit for a comet catalogued as parabolic, which remain germane but perhaps merit repetition. A parabolic orbit usually represents a compromise between a precise orbit and computational convenience. This was almost mandatory before the era of the computer because a parabolic orbit is easier to compute than an elliptical or hyperbolic orbit and normal places greatly reduce the size of the linear system needed for differential corrections. Use of all of the observations, however, almost never results in a parabolic orbit. Thus, comets with catalogued parabolic orbits, such as those in the Marsden and Williams catalog (2003), should be re-examined to see if the orbit, given the calculated mean errors, is other than a parabola. A parabolic orbit, moreover, may, depending on factors such as perihelion distance, represent a near earth object (NEO) should the final orbit be elliptic and the object return. Even a remote possibility of a collision with such an object merits investigation.
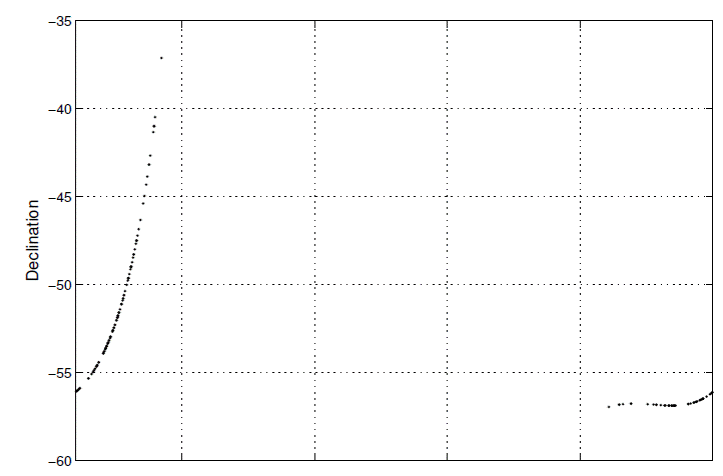
Comet C/1865 B1 (Great Southern Comet of 1865), which I now refer to as merely “the comet”, represents a particularly intriguing object. It was discovered at declination −37° and moved further south, see Figure 1, and thus was observed only in the southern hemisphere. Because northern hemisphere observatories were excluded and important southern hemisphere observatories such as Argentina’s Cordoba and La Plata not yet established, the number of observations is sparse compared with that of other great comets. Körber published an orbit in 1887 according to the Marsden and Williams catalog (2003). (A more recent version of the catalog was published in 2008, but I have the 2003 version. Both versions agree on the orbit for Comet C/1865 B1 as confirmed by the NASA JPL Small-Body Database Browser, https://ssd.jpl.nasa.gov/sbdb.). The orbit is parabolic and shows a small perihelion distance, 0.026 AU.; only 2% of the comets in the catalog have a smaller perihelion distance. Given that the orbit is 130 years old this particular comet merits study using modern techniques.
2. The observations and ephemerides
Both Abbott in Hobart, Tasmania, (Abbott 1865) and Ellery in Melbourne (Ellery 1865) discovered the comet on the night of 17 Jan. 1865; Ellery’s original position is too crude for precise orbit calculations. The comet was apparently also seen in Brazil, South Africa, and Chile. Precise astrometric observations were made at the Cape Observatory, Melbourne, Santiago, and Windsor, shown in Table 1. According to Tebbutt (1865) the comet was also observed in Port de France. It is unclear what he means by “Port de France”, but presumably Fort-de-France in Martinique. Although Fort-deFrance lies in the northern hemisphere, it is close to the equator (+14°26´) and thus an observation from there is possible, although I could find none in either the ADS database (http://adswww.harvard.edu/) or the Comptes rendus hebdomadaires des séances de l’Académie des sciences (http://gallica.bnf.fr). If observations were made from Martinique they could not have been precise astrometric observations. Copsey (1865) mentions observations made in San Joao d’el Rei, Brazil. These turn out to be two crude sextant observations unsuitable for precise orbit computation.
Table 1 Observations of comet C/1865 B1 (Great Southern Comet)
| Observatory | Obsns. in α | Obsns. in δ | Reference1 |
|---|---|---|---|
| Melbourne, Australia | 30 | 30 | MN, 1865, Vol. 25, pp. 30, 196-197 |
| Windsor, Australia | 68 | 62 | MN, 1865, Vol. 25, pp. 195, 258 |
| Santiago, Chile | 27 | 24 | AN, 1866, No. 64, p. 111-112, 251-252 |
| Cape Town, South Africa | 77 | 49 | MmRAS, 1866, Vol. 34, pp. 35-41 |
| Total | 202 | 165 |
1AN: Astronomische Nachrichten; MmRAS: Memoirs Royal Astronomical Society; MN: Monthly Notices Royal Astronomical Society.
The lack of observations from the Imperial Observatory in Rio de Janeiro is somewhat surprising. As the oldest professional observatory in the southern hemisphere, founded in 1827, it has contributed numerous southern hemisphere cometary observations, such as those used in the computation of the orbit of the Great comet of 1861 (Branham 2014). But my literature search yielded none.
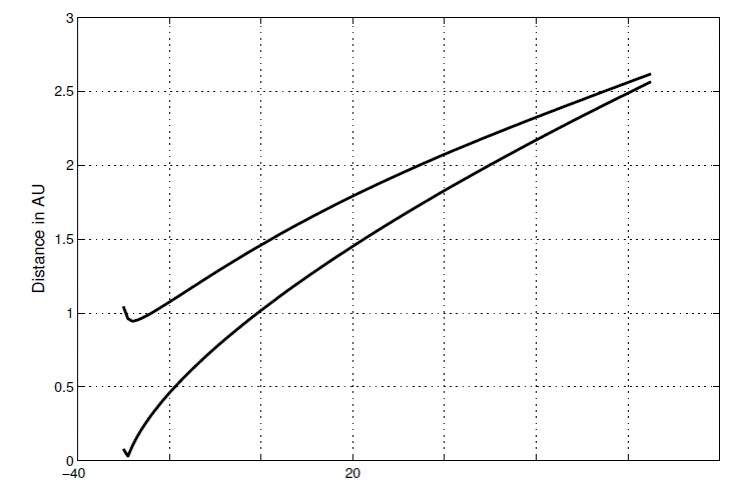
There are altogether 202 astrometric observations in right ascension (α) and 165 in declination (δ) for the comet as gleaned from the literature search and shown in Table 1, graphically in Figure 1. Figure 2 shows the distance of the comet from the Earth and from the Sun. Although the comet passes close to the Sun, it never comes closer than 0.94 AU from the Earth. The Marsden and Williams catalog (2003) lists 198 observations for this comet, a number coming from Köber’s doctoral thesis for the University of Breslau. I, therefore, use slightly more observations, another reason for a rediscussion of the orbit. If the observation was given in the form of a differential measurement ∆α and ∆δ with respect to a reference star, the reference star position was recalculated from the Tycho-2 catalog (Høg et al. 2000) using the algorithm in Kaplan et al. (1989) and the differences applied to the new star position. Unless the observer mentioned that differential aberration and refraction had been specifically calculated, these small corrections were applied. If no differences were given, but the reference star mentioned, the difference between the original catalog and Tycho-2, with the reference star position also calculated by the Kaplan et al. algorithm, was applied to the published α and δ. If no reference star was mentioned, the observation had to be taken as given. The observations were reduced to the common format of: Julian Day (JD), referred to Terrestrial Time (TT), right ascension, and declination. Of the 202 α−only observations, 132 were differential, 29 were not, but could be associated with a reference star, and 41 taken as is; the respective numbers for the δ−only observations are 97, 27, and 41.
There seem to be few errors in the observations and for those that are I can find no reasonable explanation to convert a bad observation to a good one, e.g., wrong reference star or transposed digits. There are, however, numerous reference stars not identified by the observer. Because the bulk of these are from the Cape Observatory, I give these in a separate table, Table 2, and the remaining in Table 3.
Table 2 Star identifications for cape observations
| Ref. star | Tycho | Ref. star | Tycho |
|---|---|---|---|
| 2 | 7970 00450 1 | 3 | 7970 00450 1 |
| 4 | 8437 00047 1 | 5 | 8437 00047 1 |
| 6 | 8437 00047 1 | 7 | 8440 00966 1 |
| 8 | 8440 00966 1 | 9 | 8441 00991 1 |
| 10 | 8441 00991 1 | 11 | 8441 00991 1 |
| 12 | 8441 00991 1 | 13 | 8441 00991 1 |
| 14 | 8441 01639 1 | 15 | 8441 00497 1 |
| 17 | 8441 01639 1 | 18 | 8441 01639 1 |
| 19 | 8441 00497 1 | 20 | 8441 01088 1 |
| 21 | 8441 01336 1 | 22 | 8445 00577 1 |
| 23 | 8445 00577 1 | 24 | 8452 01211 1 |
| 25 | 8452 01211 1 | 26 | 8452 01211 1 |
| 27 | 8452 00617 1 | 28 | 8452 00617 1 |
| 29 | 8452 00617 1 | 30 | 8453 00851 1 |
| 31 | 8453 00851 1 | 32 | 8453 00851 1 |
| 33 | 8824 00409 1 | 34 | 8824 00033 1 |
| 35 | 8824 00409 1 | 36 | 8824 00033 1 |
| 37 | 8824 00409 1 | 38 | 8824 00033 1 |
| 39 | 8824 00062 1 | 40 | 8824 00062 1 |
| 41 | 8824 00062 1 | 42 | 8824 00062 1 |
Table 3 Reference star identification for other observatories
| Reference | Date | Identi cation |
|---|---|---|
| AN, No. 64, pp. 111-112 | Jan. 23 | Star a is Tycho 7987 00843 1 |
| AN, No. 64, pp. 111-112 | Jan. 23 | Star b is Tycho 7987 00280 1 |
| AN, No. 64, pp. 111-112 | Jan. 24 | Star c is Tycho 7978 01128 1 |
| AN, No. 64, pp. 111-112 | Jan. 25 | Star d is Tycho 7993 01015 1 |
| AN, No. 64, pp. 111-112 | Jan. 27 | Star An(1)Tycho 8424 00554 1 |
| AN, No. 64, pp. 111-112 | Jan. 28 | Star An(2) is Tycho 8437 00445 1 |
| AN, No. 64, pp. 111-112 | Jan. 30 | Star An(3) is Tycho 8440 00738 1 |
| AN, No. 64, pp. 111-112 | Jan. 31 | Star An(4) is Tycho 8441 00214 1 |
| AN, No. 64, pp. 221-222 | Febr. 3 | Star is Tycho 8445 01396 1 |
| AN, No. 64, pp. 221-222 | Febr. 1 | Star a is Tycho 8441 01336 1 |
| AN, No. 64, pp. 221-222 | Febr. 3 | Star An(1) is Tycho 8445 00330 1 |
| AN, No. 64, pp. 221-222 | Febr. 4 | Star An(2) is Tycho 8445 00963 1 |
| AN, No. 64, pp. 221-222 | Febr. 8 | Star An(3) is Tycho 8824 01503 1 |
| AN, No. 64, pp. 221-222 | Febr. 14 | Star An(4) is Tycho 8832 00251 1 |
| AN, No. 64, pp. 221-222 | Febr. 23 | Star An(5) is Tycho 8467 00826 1 |
| MNRAS, 25, p. 258 | Mar. 16 | Star is Tycho 8478 00902 1 |
| MNRAS, 25, p. 258 | Mar. 17 | Star is Tycho 8478 00902 1 |
| MNRAS, 26, p. 30 | Jan. 26 | Ref. star cannot be identified |
| MNRAS, 26, p. 30 | Jan. 30 | Ref. star cannot be identified |
| MNRAS, 26, p. 30 | Feb. 27 | Ref. star probably Tycho 8023 00900 1 |
| MNRAS, 26, p. 30 | Mar. 1 | Ref. star probably Tycho 8023 00713 1 |
| MNRAS, 26, p. 30 | Mar. 6 | Ref. star probably Tycho 8031 00566 1 |
The rectangular coordinates and velocities of the comet and the Earth were calculated by a program, used in numerous investigations previously, that treats the solar system as an n-body problem. The program is a 12-th order Lagrangian predictor-corrector that incorporates relativity by a Schwarzschild harmonic metric. To obtain coordinates and velocities for the Earth, the Moon is carried as a separate body. This means a small step-size, 0.d25. All planets Mercury-Pluto were included in the perturbations. Yes, I am considering Pluto a planet, at least for the perturbation calculations. Starting coordinates were taken from the JPL DE 405 (ftp://ssd.jpl.nasa.gov/eph/planets/ascii). The Marsden and Williams catalog (2003), with parabolic orbital elements converted to rectangular coordinates, provided the comet’s starting coordinates. To correct the comet’s orbit partial derivatives are calculated by Moulton’s method (Herget 1968), which integrates the partial derivatives to correct for the osculating rectangular coordinates and velocities the epoch, JD2402280.5, along with the coordinates and velocities. The rectangular coordinates, after interpolation to the moment of observation for the Earth and to the moment of observation antedated by the light time correction to allow for planetary aberration, are then converted to a unit vector that is transformed to a mean or apparent place in α and δ by application of precession, nutation, annual aberration, relativity, and so forth. All observations were given as apparent place, and thus one need not be concerned with the E-terms. The final step calculates an observed minus a computed place, (O-C), in α and δ.
To assign weights to the observations I use the biweight, which assumes nothing as to the quality of a given type of observation, but rather assigns weight based on the magnitude of the post-fit residual (Branham 1990). Other weights are possible, but the final results depend little on the particular weight used. The biweight, as Shane says in a different context in the classic 1953 movie, is as good as any and better than most. It recognizes two features from statistical analysis of data: smaller residuals are more probable than larger residuals and hence assigns them higher weight; extremely large residuals are errors, not genuine but improbable residuals, and assigns them zero weight. One scales the post-fit residual ri by the median of the absolute values of the residuals and assigns a weight wt as
I use a preliminary least squares solution with equal weights, calculate the residuals from this solution, compute the weights, and then recalculate a least squares solution. Further iterations become unnecessary because they produce scant difference in the solution.
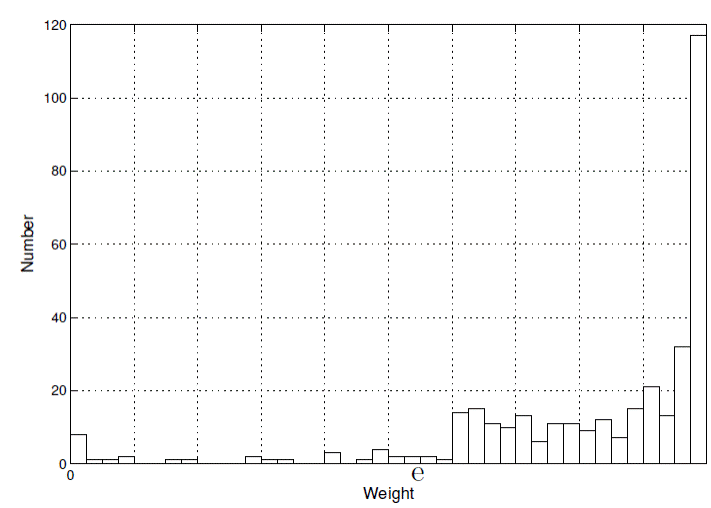
Figure 3 shows a histogram of the weights, only 8 of which are lower than the machine ε of 2.2·10-16 but of which the others exhibit slight bimodality. 93% of the weights are greater than 0.5.
3. The solution
Table 4 shows the final solution for the rectangular coordinates, x0, y0, z0, and velocities, x0, ẏ0, z0, along with their mean errors and also the mean error of unit weight σ(1) for the comet; Table 5 gives the corresponding covariance and correlation matrices. The σ(1) is relatively high, but lower than mean errors for some other 19th century comets; 11.´´23 for comet C/1819 N1 (Great Comet of 1819) (Branham 2017) and 12.´´11 for Comet C/1845 D1 (de Vico) (Branham 2010). If one breaks down the mean error to the observations recalculated by application of differences in α and δ to star positions, those calculated from the Tycho-2 catalog have the best mean errors, 6.´´04 with a median for the biweights of 0.96; for the other observations the respective numbers are 17.´´48 and 0.93 for the original observation plus catalog corrected for the catalog-Tycho-2 difference and 15.´´69 and 0.95 for the as is observations. That the corrected observations are slightly worse than the as is observations seems surprising, but what can one say? The data give what they give. Re-reducing an observation when it is possible to do so evidently greatly improves the mean error. The mean errors on an observatory basis show: Cape 3.´´42, Melbourne 8.´´12, Santiago 6.´´65, and Windsor 16.´´47. Why the Windsor observations are worse than the others may be explained by the Cape using a filler micrometer and Windsor, according to Tebbutt, a ring micrometer. Ellery at Melbourne mentions a spider-wire micrometer, but Mösta at Santiago makes no mention of what type of micrometer was used. Regarding the ring micrometer Janiczek (1971) writes, “The ring micrometer was never considered an accurate device; its continued favor was probably due to simplicity and ease of use.” Chauvenet (1960, p. 436) states, “Although inferior in accuracy to the filar micrometer and the heliometer, it [the ring micrometer] possesses the advantage [of not requiring illumination or an equatorial mounting].”
Table 4 Solution for rectangular coordinates and velocities*
| Unknown | Value | Mean Error |
|---|---|---|
| x0 (AU ) | 2.712920e-02 | 2.270830e-05 |
| y0 (AU ) | 3.399232e-01 | 1.168575e-05 |
| z0 (AU ) | -9.587848e-01 | 1.910186e-05 |
| x˙ 0 (AU day−1) | -3.800226e-04 | 5.940780e-07 |
| y˙0 (AU day−1) | 4.474304e-03 | 4.894366e-07 |
| z˙0 (AU day−1) | -2.370289e-02 | 6.868151e-07 |
| σ(1) | 10.′′80 |
*For the Great Southern Comet; JD 2402280.5
Table 5 Correlation (upper triangle) and covariance (diagonal, lower triangle)*
| 1.880921e-01 | -78.0003 | -85.9097 | -29.5470 | 64.1266 | 21.3563 |
| -7.549862e-02 | 4.980979e-02 | 68.9731 | 45.6372 | -53.8062 | -21.0254 |
| -1.359264e-01 | 5.615825e-02 | 1.330922e-01 | 27.8630 | -43.0971 | -5.9224 |
| -1.453929e-03 | 1.155634e-03 | 1.153314e-03 | 1.287325-04 | -12.2504 | -52.9166 |
| 2.599683e-03 | -1.122501e-03 | -1.469674-03 | -1.299250e-05 | 8.737639e-05 | 30.3620 |
| 1.214933e-03 | -6.15520e-04 | -2.834102e-04 | -7.875471e05 | 3.722786e-05 | 1.720604-04 |
*Matrices for the Great southern comet.
For the comet none of the correlations is high, where “high” is considered greater than 90%, and the condition number of 98 for the data matrix shows that the solution is stable.
Tables 6 give the orbital elements corresponding to the rectangular coordinates of Table 4: the time of perihelion passage, T0; the eccentricity, e; the semi-major axis, α; the perhelion distance, q; the inclination, i; the node Ω; and the argument of perihelion, w. The calculation of the mean errors of the orbital elements proceeds via Rice’s procedure (1902). Let Cbc the covariance matrix for the least squares solution for he rectangular coordinates and velocities.
Table 6 Hyperbolic orbital elements and mean errors.*
| Unknown | Value | Mean Error |
|---|---|---|
| T0 | JD 2402251:32562 | 2.d90230e-04 |
| 4:82562Jan:1865 | ||
| α(AU) | -714.602266 | 58.143698 |
| e | 1.0000361 | 0.0000029 |
| q (AU) | 0.0258001 | 0.0006140 |
| Ω | 255.◦028896 | 0.◦762355 |
| i | 86.◦323634 | 0.◦190231 |
| w | 89.◦087204 | 0.◦0.220716 |
*For the Great Southern Comet.
Identify the errors in a quantity such as the node Ω with the differential of the quantity, dΩ. The error can be found from:
The partial derivatives in Equation (2) are calculated from the well known expressions linking elliptical or hyperbolic orbital elements with their rectangular counterparts. The comet’s orbit is hyperbolic and statistically distinguishable from a parabola. To be precise given the mean error of the eccentricity the hyperbola lies over 12 standard deviations from a parabola if we assume a Gaussian distribution for the error. The Great Southern Comet, therefore, represents no NEO threat.
4. Discussion
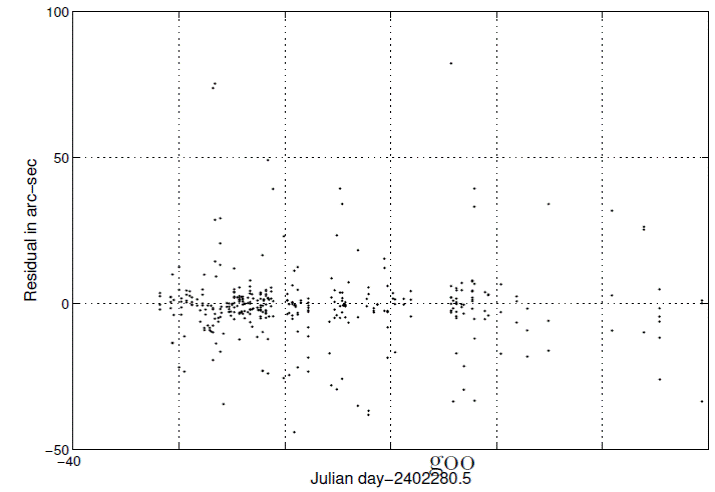
Although a nonparabolic orbit has been calculated for the comet, how good is it? Figure 4 shows a histogram of the residuals and Figure 5 the residuals themselves. The skewness of the residuals is 0.03, their kurtosis 1.94, and Q factor of 0.44. Because a normal distribution has a kurtosis of 3, a Q factor of 2.11, and 0 skewness we see a flatter distribution with lighter tails and somewhat skewed. Thus, the residuals are platykurtic and lighter tailed than the normal distribution. What about randomness for determining the goodness of the solution, even more important than the hardly ever achieved in reality normality? A runs test (Wonnacott and Wonnacott 1972, pp. 409-411) calculates a 39.2% chance that the residuals are random. Another test of randomness, the Durbin-Watson statistic, also called the mean-square difference test, (Wonnacott & Wonnacott 1972, pp. 411-413) gives the residuals a 78.6% chance of being random. The two tests measure different properties of the residuals: the runs test the tracking above and below 0 and Durbin Watson the serial correlation of a residual with its successor. The residuals, therefore, are random and evince no indication of serious systematic error. One may conclude that the least squares solution seems satisfactory.
Given, nevertheless, the small perihelion distance one cannot help but wonder if perhaps outgassing occurred, giving rise to nongravitational forces. Perhaps the randomness of the residuals can be improved? The nongravitational force model I use is
where r is the radial component measured positive outward from the Sun, f(r) the resulting force, and A1 a parameter to be determined or assumed. The transverse component becomes Equation (3) with A1 replaced by A2. One assumes that the component normal to the orbital plane may be considered negligible. For A1 I used the mean of the values for this quantity given in Marsden, Sekanina, and Yeoman’s (1973) Table I, or A1 = 0.2 × 10-8. The transverse component has a value, from the same table, of A2 = −0.5 · 10-10, probably not large enough to produce a significant effect. To apply the nongravitational accelerations one must transform from the x − y − z coordinates to the radial-transversenormal coordinate system (McCuskey 1963); calculate the nongravitational accelerations; rotate back to the x − y − z system, and apply the accelerations to the cometary equations of motion. The effect on the residuals, however, was negligible, with the runs test still giving a 39.2% probability of randomness. If one had pre-perihelion observations to check the randomness of both the preand post-perihelion residuals there might be a better indication of possible nongravitational effects.
One would also like to know if the comet might perhaps have had an origin outside of the solar system. To test this idea the orbit was integrated backwards to a distance of 200,000 AU, beyond the outer edge of the Oort cloud. Rather than integrate separately the Earth and the Moon for this backwards integration, I used the Earth-Moon barycenter and included Galactic tidal forces. At this distance the orbit is still hyperbolic, a = −0.00020 ± 0.01061, but only slightly so and given the mean error indistinguishable from a high eccentricity ellipse. Given this plus the high value for the inclination one may infer that the comet was born in the Oort cloud.











 text new page (beta)
text new page (beta)