1. Introduction
The study presented in this paper was motivated by the use of low-thrust propulsion systems in new space missions. The two pioneer missions were NASA-JPL Deep Space 1 and ESA-SMART1. Deep Space 1 was the first interplanetary spacecraft to utilize Solar Electric Propulsion. It was launched on October 24, 1998, and its mission terminated on December 18, 2001, when its fuel supply was exhausted. SMART-1 was developed by ESA. It was launched on September 27, 2003, and its mission ended on September 3, 2006, when the spacecraft, in a planned maneuver, impacted the lunar surface. Interesting details of the these pioneer missions can be found in Rayman et al. 2000; Racca et al. 2002; Camino et al. 2005.
Low-thrust electric propulsion systems are characterized by high specific impulse and low thrust capability (the ratio between the maximum thrust acceleration and the gravity acceleration on the ground is small, between 10-4and 10-2) and show greatest benefits for high-energy planetary missions (Marec 1979; Racca 2003). Numerical and analytical solutions have been developed in the last fifty years for several maneuvers involving specific initial and final orbits, and specific thrust profiles (Gobetz 1964, 1965; Edelbaum 1964, 1965, 1966; Marec and Vinh 1977, 1980; Haissig et al. 1993; Geffroy and Epenoy 1997; Sukhanov 2000; Kiforenko 2005; Bonnard et al. 2006; da Silva Fernandes and Carvalho, 2008; Jamison and Coverstone 2010; Jiang et al. 2012; Huang 2012; Quarta and Mengali 2013).
In previous works (da Silva Fernandes and das Chagas Carvalho 2008; da Silva Fernandes et al. 2016; das Chagas Carvalho et al. 2016) the authors presented complete first order analytical solutions based on canonical transformation theory for the problem of optimal time-fixed low-thrust limited-power transfers between arbitrary elliptic coplanar orbits, and for the problem of optimal time-fixed low-thrust limited-power transfers between coplanar orbits with small eccentricities. In the last study, non-singular orbital elements were used as state variables, and the maximum Hamiltonian and the optimal thrust acceleration were developed up to the first order in the eccentricity. It was observed that the analytical first order solution expressed in non-singular elements provides a good approximation when compared to a numerical solution obtained through a neighboring extremals algorithm considering large time of flight, moderate ratio of semi-major axis and arbitrary, very small, eccentricities. However, for a maneuver in which the radius of the final orbit is three times the radius of the initial orbit, the time behaviour of the eccentricity given by the analytical solution differs considerably from the behaviour given by the numerical solution. In that study, the numerical solution, used as exact solution, was obtained for the optimal transfer problem formulated as a Mayer problem with the radial distance and the components, radial and circumferential, of the velocity vector as state variables.
The main purpose of this paper is to develop a numerical-analytical procedure to solve the problem of optimal time fixed low-thrust limited power transfers (no rendezvous) between coplanar orbits with small eccentricities in an inverse-square force field, in which second order terms of the eccentricity are considered in the development of state equations such that solution can be applied to a larger class of maneuvers. The proposed procedure involves the development of a two-stage Newton-Raphson algorithm based on an infinitesimal canonical transformation. In the first stage of the algorithm, a two-point boundary value problem, defined by an average canonical system describing the secular behaviour of the optimal trajectories, is solved. The maximum Hamiltonian governing the average canonical system is derived by applying Hori (1966) method. So, an infinitesimal canonical transformation is built, and the short periodic terms are included in the solution by computing the Poisson brackets of the generating function with state variables. This technique provides an approximation to the numerical integration of the complete canonical system. However, when the short periodic terms are included in the solution of the two-point boundary value problem obtained in the first stage, small deviations from the prescribed final conditions arise, and the initial values of the adjoint variables computed in the first stage must be adjusted. The main advantage of this procedure is that the average canonical system is much simpler than the complete canonical system with periodic terms. Moreover, the average canonical system has a first integral, namely the new Hamiltonian, which is used to reduce the order of the system of differential equations and then to simplify the determination of the new values for the initial adjoint variables.
Numerical results are presented for the same transfers between circular coplanar orbits, including EarthVenus and Earth-Mars missions, discussed in the previous work (das Chagas Carvalho et al. 2016) and a comparison with the exact solution previously obtained is performed.
The paper is organized as follows. In § 2, the optimization problem for time-fixed low-thrust limited power transfer between coplanar orbits with small eccentricities is formulated as a Mayer problem of optimal control with a set of non-singular variables as state variables. In § 3, a numerical-analytical procedure to solve the two-point boundary value problem defined by the maximum Hamiltonian is described. In § 4, the Hori method is applied to eliminate the short periodic terms, and an infinitesimal canonical transformation is built. In § 5, the solution of the two-point boundary value problem of going from a initial orbit to a final orbit described by the average canonical system is presented. In § 6, numerical results are presented for some maneuvers, including Earth-Mars and Earth-Venus missions.
2. Formulation of the optimization problem
A low-thrust limited-power propulsion system - LP system - is characterized by low thrust acceleration level and high specific impulse. For such a system, the fuel consumption is described by the variable J defined as (Marec 1979).
where Γ is the magnitude of the thrust acceleration vector Γ, used as a control variable. The consumption variable J is a monotonic decreasing function of the mass m of the space vehicle,
where Pmax is the maximum power and m0 is the initial mass. The minimization of the final value of the fuel consumption, Jf , is equivalent to the maximization of mf .
Consider the motion of a space vehicle M, powered by a limited-power engine in an inverse-square force field. Since the terminal orbits are coplanar, the entire motion of the space vehicle is confined in a plane. So, at time t, the state of the space vehicle can be defined by the following set of non-singular orbital elements:
and the fuel consumption is defined by variable J. Here, a is the semi-major axis, e is the eccentricity, ω is the argument of pericenter and M is the mean anomaly.
The optimization problem can be formulated as a Mayer problem of optimal control as follows: It is proposed to transfer the space vehicle M from initial state (a0,h0,k0,l0,0) at time t0 = 0 to the final state (af , hf , kf , lf , Jf ) at time tf , such that the final consumption variable Jf is a minimum. The duration of the transfer tf − t0 is specified, and the final position of the vehicle is free, since only simple transfers (no rendezvous) are considered in this study.
The state equations, expressed up to the second order in eccentricity, are given by:
when
The performance index is defined by
For limited power system, it is assumed that there are no constraints on the thrust acceleration vector (Marec 1979).
According to the Pontryagin Maximum Principle (Pontryagin, et al, 1962), the adjoint variables pa, ph, pk, pl and pJ are introduced and the Hamiltonian function H(a, h, k, l, -, pa, ph, pk, pl, pJ , R, S) is formed:
where fi, i = 1, 2, 3, 4, 5 denotes the right-hand side of each differential equations in Equations (4), (5), (6), (7), (8), respectively.
The control variables, R and S, must be selected from the admissible controls such that the Hamiltonian function reaches its maximum along the trajectory. So, one finds
These equations can be simplified if it will be taken into account that the adjoint variable pJ is a first integral of the canonical system governed by the maximum Hamiltonian; that is, pJ is a constant whose value is obtained from the transversality condition, pJ (tf ) = −1. Accordingly, pJ (t) = −1. So, introducing this result into Equations (11)-(12), one finds the expressions for the components of the optimal thrust acceleration.
From Equations (10), (11) and (12) one finds that the expression of the Hamiltonian, taking into account only terms up to the second order in eccentricty, is given by:
where
denotes the undisturbed Hamiltonian and Hγ * is the part related to the optimal thrust acceleration,
It should be noted that in the development of Hγ *higher order terms in eccentricity are neglected, since such terms that arise from R*2 and S*2 are incomplete (they do not appear in R* and S*).
3. Numerical-analytical procedure to solve the two point-boundary value problem
In this section, a numerical-analytical procedure is described to solve the two-point boundary value problem of going from an initial orbit O0 at time t0 = 0 to a final orbit Of at a prescribed final time tf = T .
This two-point boundary value problem is defined by the canonical system of differential equations governed by the maximum Hamiltonian H* and the terminal constraints defining the initial orbit O0 and the final orbit Of ; that is,
with
In above equations, x denotes the state vector x = (a, h, k), p denotes de adjoint vector p = (pa, ph, pk), and are 3x1 matrices of partial derivatives of the maximum Hamiltonian with respect to the state vector and adjoint vector, respectively. For simple transfers, the final position of the space vehicle is free; so, variable l plays no special role in the two-point boundary value problem. Therefore, the differential equations for l and pl are not included in the set of differential equations above.
It should be noted that the explicit forms of the state and adjoint equations are relatively extensive due to the short periodic terms in the maximum Hamiltonian (see Eqn.(14)).
A two-stage Newton-Raphson algorithm is then proposed to solve the two-point boundary value problem described by Equations (15) (17). This algorithm has two distinct phases: in the first one, a two-point boundary value problem, defined by the average canonical system describing the secular behavior of the optimal trajectories, is solved. The maximum Hamiltonian governing the average canonical system is derived by applying the Hori (1966) method. So, an infinitesimal canonical transformation is built, and the short periodic terms are included in the solution by computing the Poisson brackets of the generating function with the state variables. This technique provides an approximation, to first order in a small parameter closely related to the magnitude of the optimal thrust acceleration, to the time behavior of the state variables considering the complete maximum Hamiltonian. In other words, it provides an approximation to the solution obtained by numerical integration of the complete canonical system. However, when the short periodic terms are included in the solution of the two-point boundary value problem obtained in the first stage, small deviations from the prescribed final conditions arise. Accordingly, the initial values of the adjoint variables computed in the first stage must be adjusted by a second Newton Raphson algorithm. The advantage of this procedure is that the average canonical system is much simpler than the complete system and it has a first integral used to reduce the order of the system of differential equations, making easier the numerical integration and the determination of the initial value for the adjoint variables.
In the next section, the Hori method is applied to obtain the infinitesimal canonical transformation and the average canonical system. In § 5, the solution of the two-point boundary value problem described by the average canonical system is briefly defined.
4. Infinitesimal canonical transformation
In order to eliminate the short periodic terms from the maximum Hamiltonian H*, an infinitesimal canonical transformation is built by means of the Hori (1966) method. It is assumed that the undisturbed Hamiltonian H0 is of zero order and the remaining part H* is of first order in a small parameter associated to the magnitude of the optimal thrust acceleration (da Silva Fernandes and das Chagas Carvalho, 2008; da Silva Fernandes et al, 2016; das Chagas Carvalho et al, 2016).
Consider an infinitesimal canonical transformation,
The new variables are denoted by the symbol “´”.
Following the algorithm of the Hori method, one finds from the zero-th order equation of the algorithm that the new undisturbed Hamiltonian is given by
with F0 expressed in terms of the new canonical variables.
Now, consider the canonical system described by F0:
The general solution of this system is very simple and it is given by
The subscript ’0’ denotes the constants of integration.
Introducing the general solution defined above into the equation of order 1 of the algorithm of the Hori method results in
Following the integration theory for the Hori method proposed by da Silva Fernandes (2003), one finds that the new (average) Hamiltonian function F1 and the generating function S1 are given, respectively, by:
and
Terms factored by pl i have been omitted in equations above, since only transfers (no rendez-vous) are considered. Note that pl i is a first integral of the average canonical system; that is, pl i is constant and its value is computed from the transversality condition which gives pl(tf) = 0 for simple transfers (the final position of the space vehicle is free). This result simplifies the expressions of the new Hamiltonian and the generating function as given by equations above.
By computing the Poisson bracket of the generating function with the state variables a, h, k -, one finds that the infinitesimal canonical transformation built by means of the Hori method is then defined by the following equations:
Equations (23), (24) and (25) can be applied to get an approximation of the time evolution of the state variables if the solution of the average canonical systems governed by the new Hamiltonian F1 is known. In other words, they provide an approximation to the numerical solution obtained by integrating the complete canonical system governed by the maximum Hamiltonian H*. Note that l´ is given by numerical integration of the differential equation
The second term of right-hand side of Equation (26) is obtained from the terms factored by pl in the new Hamiltonian, that dissapear when one takes pl = 0 for the case of simple transfers. Recall that pl is a constant, whose value obtained from the transversality condition for simple transfers is zero.
Equations (23) (25) can be put in the following compact form
where δa, δh and δk denotes the periodic terms in the right-hand side of Equations (23), (24) and (25). Applying the initial conditions one finds that the time evolution of the state variables is written in a compact form as
where δa(t), δh(t) and δk(t) are calculated at time t, with a´,h´, k´, pa´, ph´, pk´ obtained by numerical integration of the average canonical system from the initial conditions a0, h0, k0, pa0 , ph0 and pk0 . δa(t0), δh(t0), δk(t0) are calculated in terms of the initial conditions at t = t0. Accordingly, the solution with periodic terms and the average solution satisfy the same initial conditions.
Note that if the two-point boundary value problem governed by the average canonical system is solved by means of a Newton-Raphson algorithm, that is, pa0 , ph0 and pk0 are determined such that the final conditions are satisfied, then the periodic terms expressed by δa(t) − δa(t0), δh(t) − δh(t0) and δk(t) − δk(t0) provide small deviations from the final conditions, and pa0 , ph0 , pk0 must be adjusted in order to satisfy these conditions. This adjustment is made by another Newton-Raphson algorithm in the second stage of the proposed algorithm.
5. The average two-point boundary value problem
In what follows is described the first stage of the proposed algorithm, in which the two-point boundary value problem defined by the average canonical system is solved. The Newton-Raphson algorithm developed in this first stage uses a first integral generated by the Hori method, namely the new Hamiltonian, to reduce the order of the canonical system and to simplify the determination of new values for the initial adjoint variables.
The two-point boundary value problem defined by the average canonical system governed by the new Hamiltonian F1 is then given by the following set of differential equations
with the boundary conditions given by
As before, the symbols denoting the new canonical variables are omitted.
According to the Hori method, the new Hamiltonian F1 is a first integral of the canonical system defined above and can be used to reduce the order of the system. From the differential equations for a and pa one finds = −E.
Thus,
The constant E denotes the value of new Hamiltonian, that is, F1 = E.
Finally, using the above result, the differential equation for a can be integrated. After simplifications, one finds
where B = a0pa0 .
Equations (31) and (33) can be used to simplify the algorithm of the Newton-Raphson method, since only four differential equations have to be integrated. Note that three unknowns - pa0 , ph0 , pk0 - are iterated at each step of the algorithm.
We note that the average canonical system has two other first integrals:
But, they do not allow further simplifications to the algorithm.
6. Results
In this section, the numerical-analytical procedure based on canonical transformation proposed to compute optimal time-fixed low-thrust limited power transfers (no rendezvous) between coplanar orbits with small eccentricities in an inverse-square force field is applied in a preliminary analysis of some transfers discussed in the previous work (das Chagas Carvalho et al. 2016).
As noted in the previous work, the complete first order analytical solution, with terms of first order in eccentricity, does not provide accurate results for the time behaviour of the eccentricity along the optimal trajectory, considering transfers between circular coplanar orbits with moderate amplitude (radius of the final orbit three times the radius of the initial orbit). Accordingly, the present analysis considers some values of the radius ratio
Table 1 Consumption variable J
|
|
Tf-t0 | J1 | J2 |
|---|---|---|---|
| 0.7270 | 25.0 | 5.9852 × 10−4 | 6.0010 × 10−4 |
| 125.0 | 1.1949 × 10−4 | 1.1950 × 10−4 | |
| 1.5236 | 25.0 | 7.2468 × 10−4 | 7.3362 × 10−4 |
| 125.0 | 1.4421 × 10−4 | 1.4428 × 10−4 | |
| 2.0000 | 100.0 | 4.2976 × 10−4 | 4.3134 × 10−4 |
| 200.0 | 2.1462 × 10−4 | 2.1485 × 10−4 | |
| 2.5000 | 100.0 | 6.7826 × 10−4 | 6.8525 × 10−4 |
| 200.0 | 3.3811 × 10−4 | 3.3894 × 10−4 | |
| 3.0000 | 100.0 | 9.0260 × 10−4 | 9.2706 × 10−4 |
| 200.0 | 4.4776 × 10−4 | 4.4505 × 10−4 |
The orbits of the planets are circular;
The orbits of the planets lie in the plane of the ecliptic;
The flight of the space vehicle takes place in the plane of the ecliptic;
Only the heliocentric phase is considered; that is, the attraction of planets on the spacecraft is neglected.
All results in the Table 1 are expressed in canonical units. The starting guess for the adjoint variables is given by the first order solution in eccentricity developed in previous works (da Silva Fernandes et al. 2016; das Chagas Carvalho et al. 2016). Note that the consumption variable J2 is computed as described in previous works; that is,
where ∆S1 = S1(tf ) − S1(t0), with, S1 given by Equation (22).
It should be noted that the numerical results computed through the proposed algorithm (Method 2) for the consumption variable have almost the same accuracy as those of the numerical approach based on the neighbouring extremals algorithm (Method 1). This good agreement between the results is closely related to the excellent accuracy obtained by the proposed algorithm (Method 2) for the time behavior of the semi-major axis, which represents the main parameter in transfers between coplanar circular orbits (the fuel is mainly spent to satisfy the imposed change in the semi-major axis).
The time evolutions of semi-major axis and eccentricity are presented in Figures 1, 2, 3, 4, 5, 6, 7, 8, 9 and 10; as well as the difference between the solutions obtained by the methods. From Figures 1 to 10 and Table 1, note that the excellent agreement between the results for all variables semi-major axis, eccentricity and consumption variable for all values of ρ and T presented in Table 1. The solution considering second order terms in eccentricity in the development of the state equations obtained by means of the proposed algorithm (Method 2) has almost the same accuracy as Method 1: in the worst case (ρ = 3.0000 DU and tf − t0 = 100.0 TU) the difference for the semimajor axis does not exceed 10-2DU, and the difference for the excentricity does not exceed 8 × 10-3.
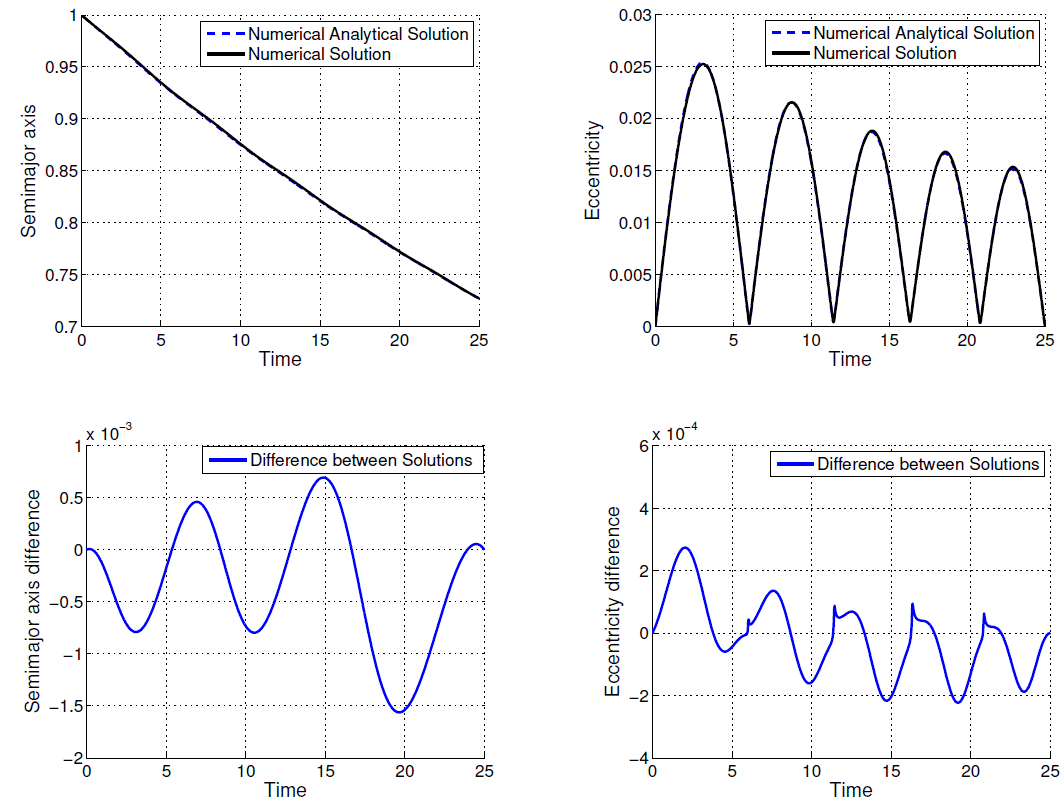
Fig. 1 Comparison between numerical-analytical solution and numerical solution for ρ = 0.7270 DU and tf − t0 = 25.0 TU.
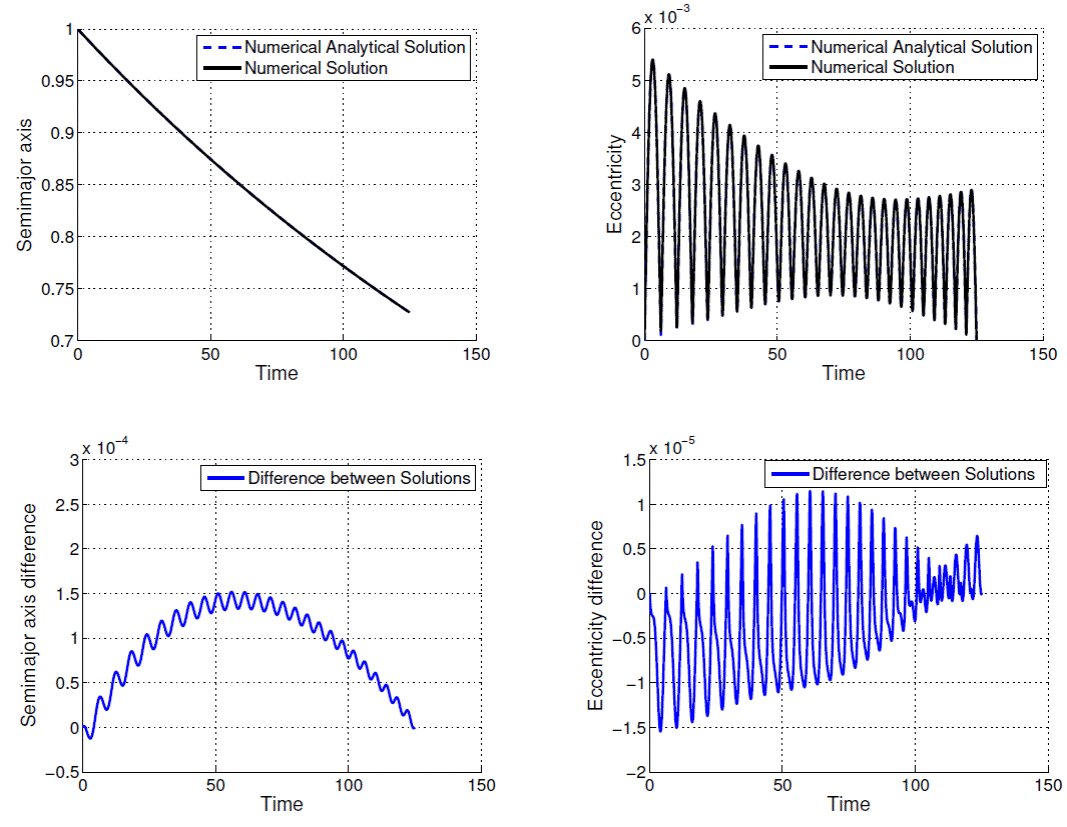
Fig. 2 Comparison between numerical-analytical solution and numerical solution for ρ = 0.7270 DU and tf − t0 = 125.0 TU.
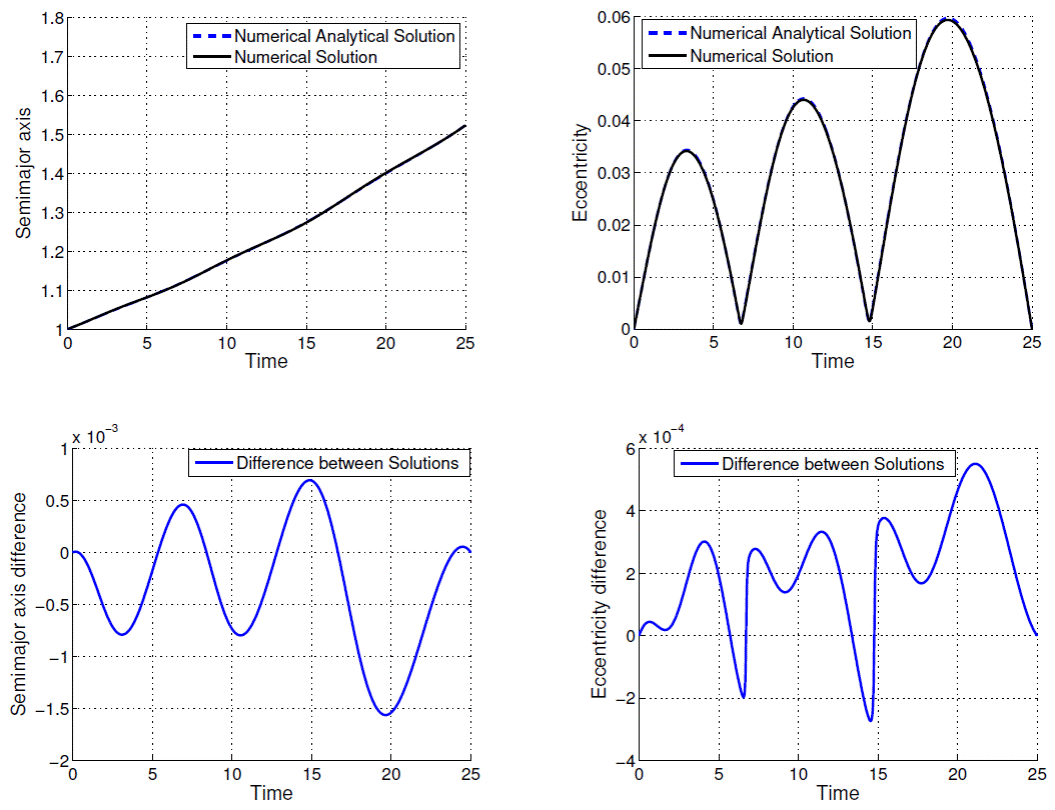
Fig. 3 Comparison between numerical-analytical solution and numerical solution for ρ = 1.5236 DU and tf − t0 = 25.0 TU.
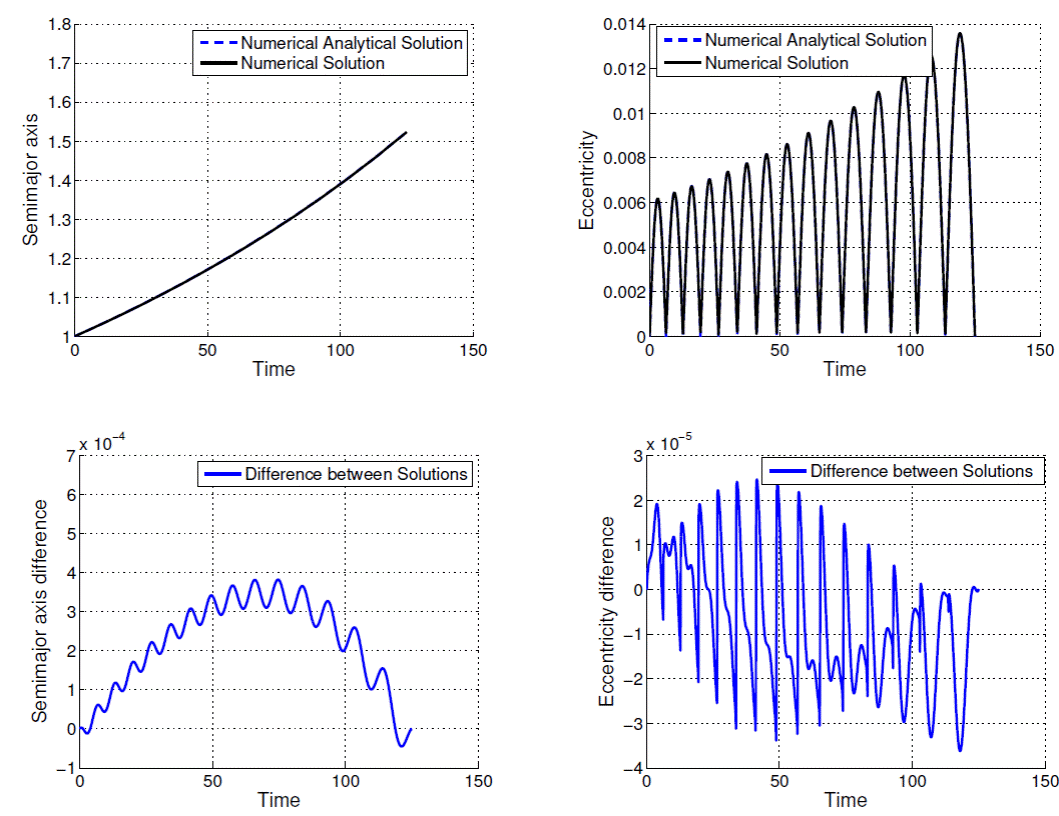
Fig. 4 Comparison between numerical-analytical solution and numerical solution for ρ = 1.5236 DU and tf − t0 = 125.0 TU.
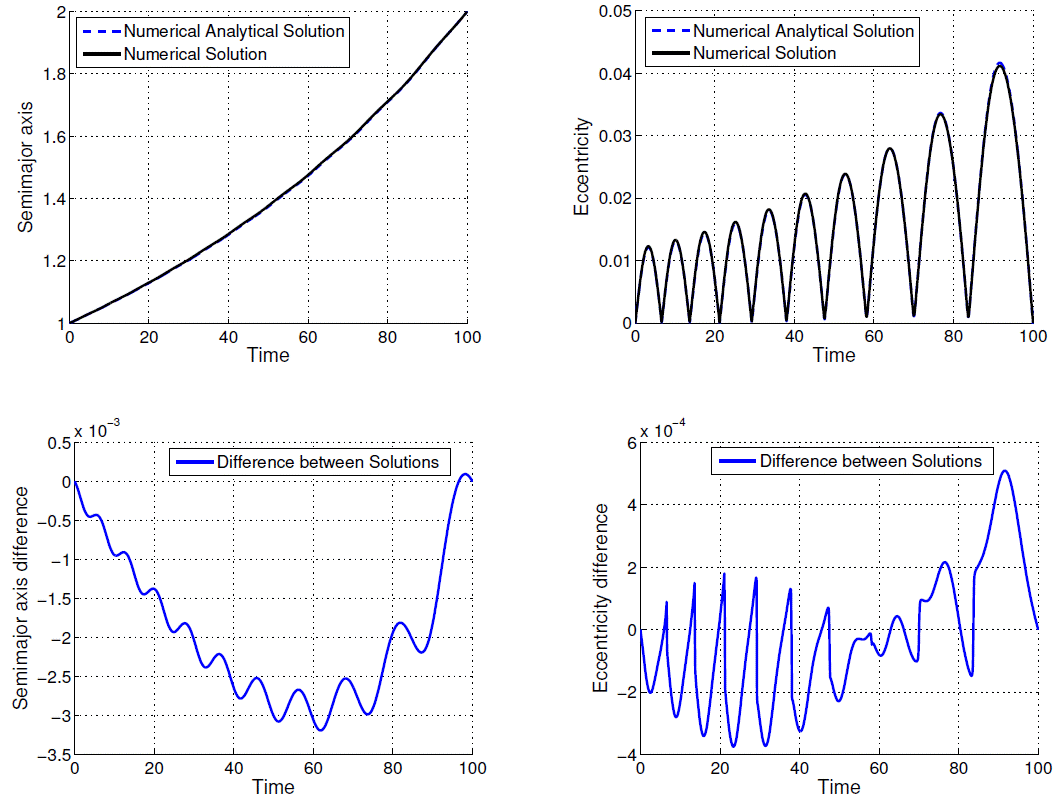
Fig. 5 Comparison between numerical-analytical solution and numerical solution for ρ = 2.0000 DU and tf − t0 = 100.0 TU.
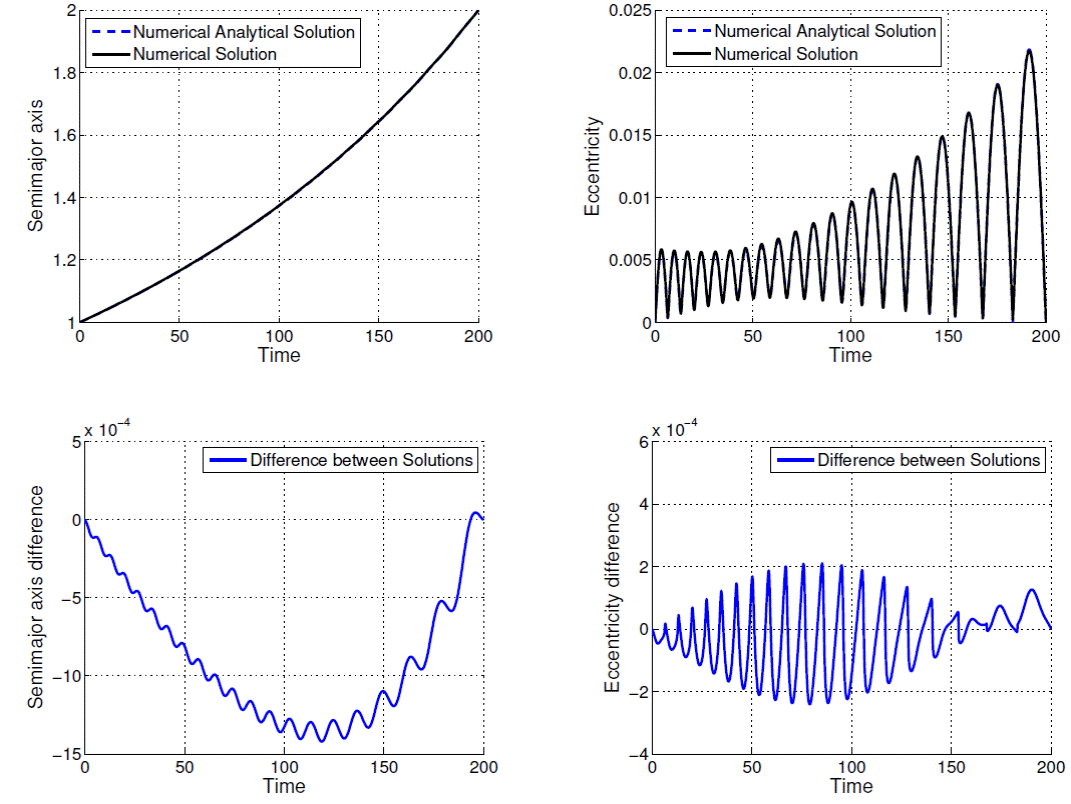
Fig. 6 Comparison between numerical-analytical solution and numerical solution for ρ = 2.0000 DU and tf − t0 = 200.0 TU.
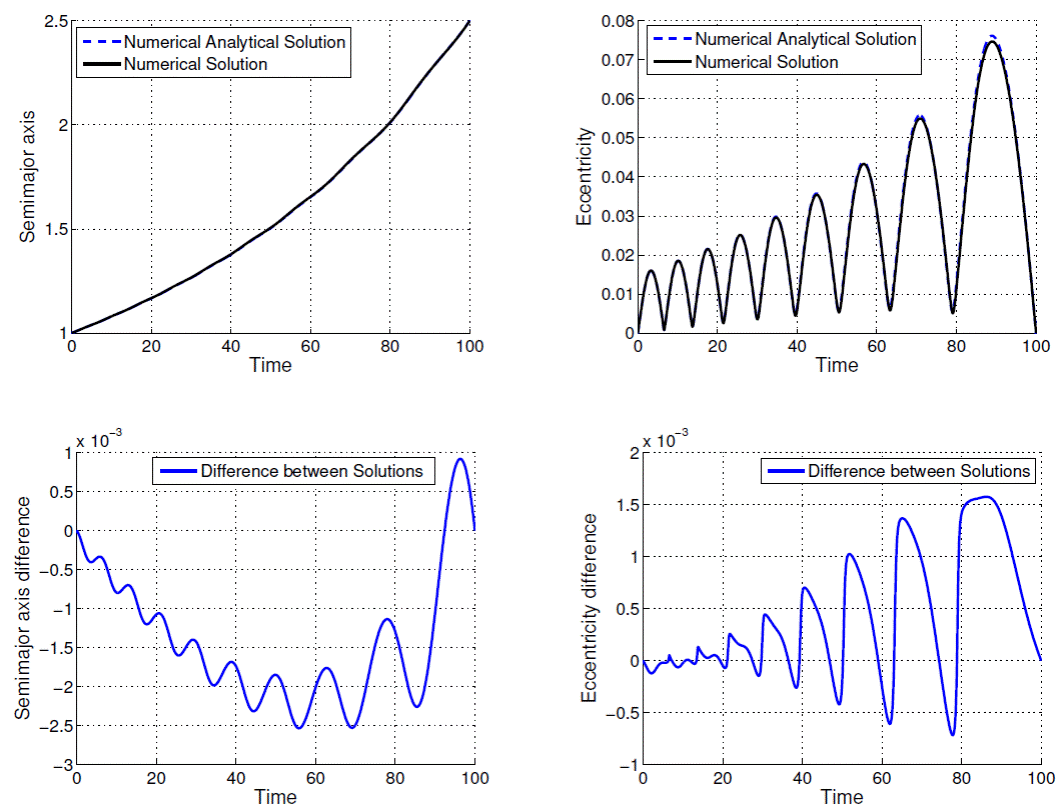
Fig. 7 Comparison between numerical-analytical solution and numerical solution for ρ = 2.5000 DU and tf − t0 = 100.0 TU.
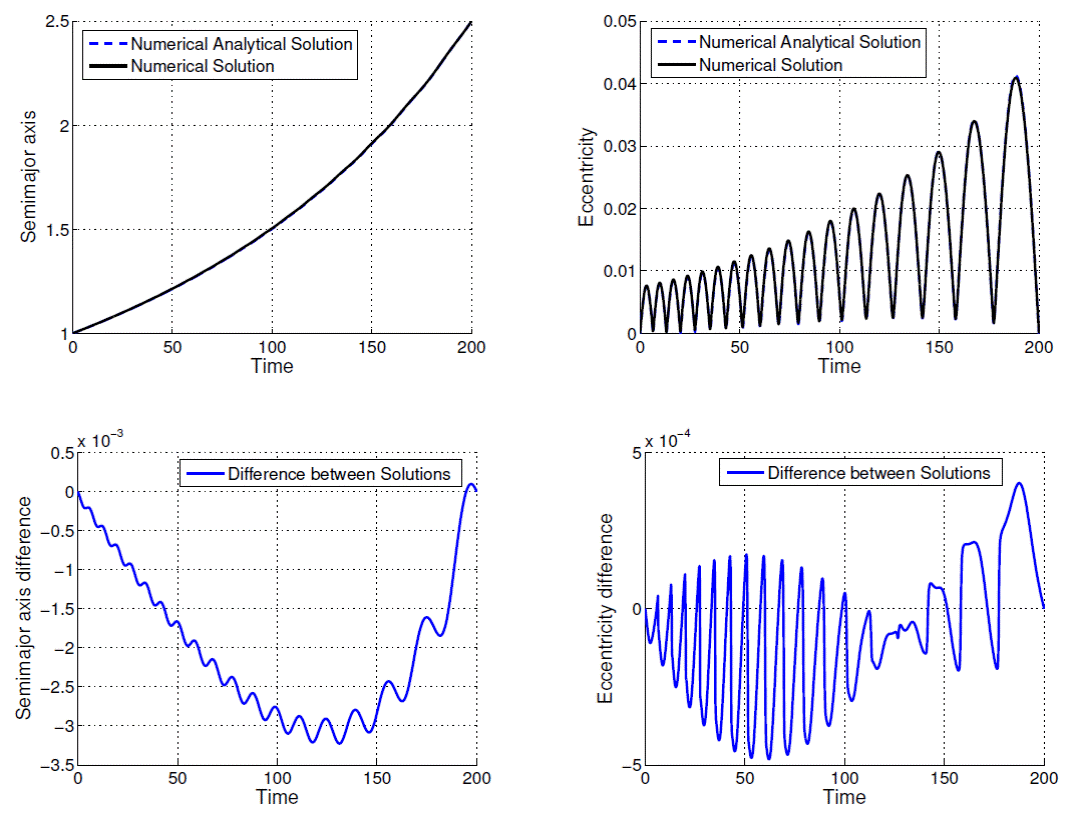
Fig. 8 Comparison between numerical-analytical solution and numerical solution for ρ = 2.5000 DU and tf − t0 = 200.0 TU.
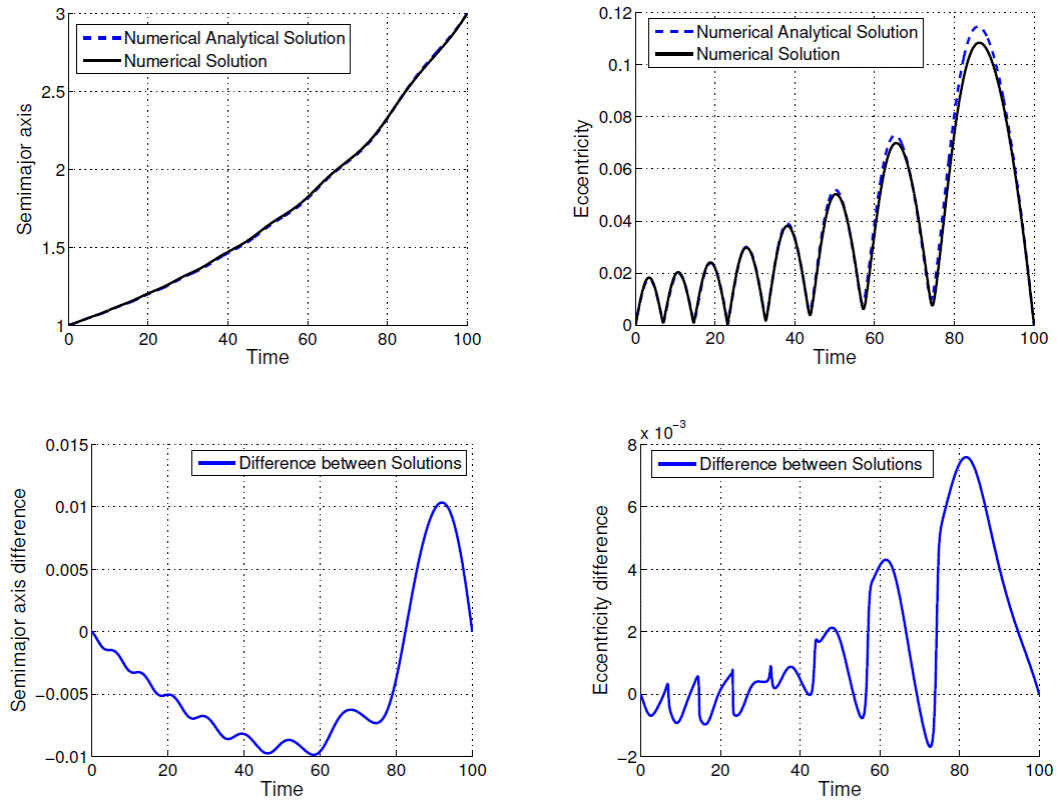
Fig. 9 Comparison between numerical-analytical solution and numerical solution for ρ = 3.0000 DU and tf − t0 = 100.0 TU.
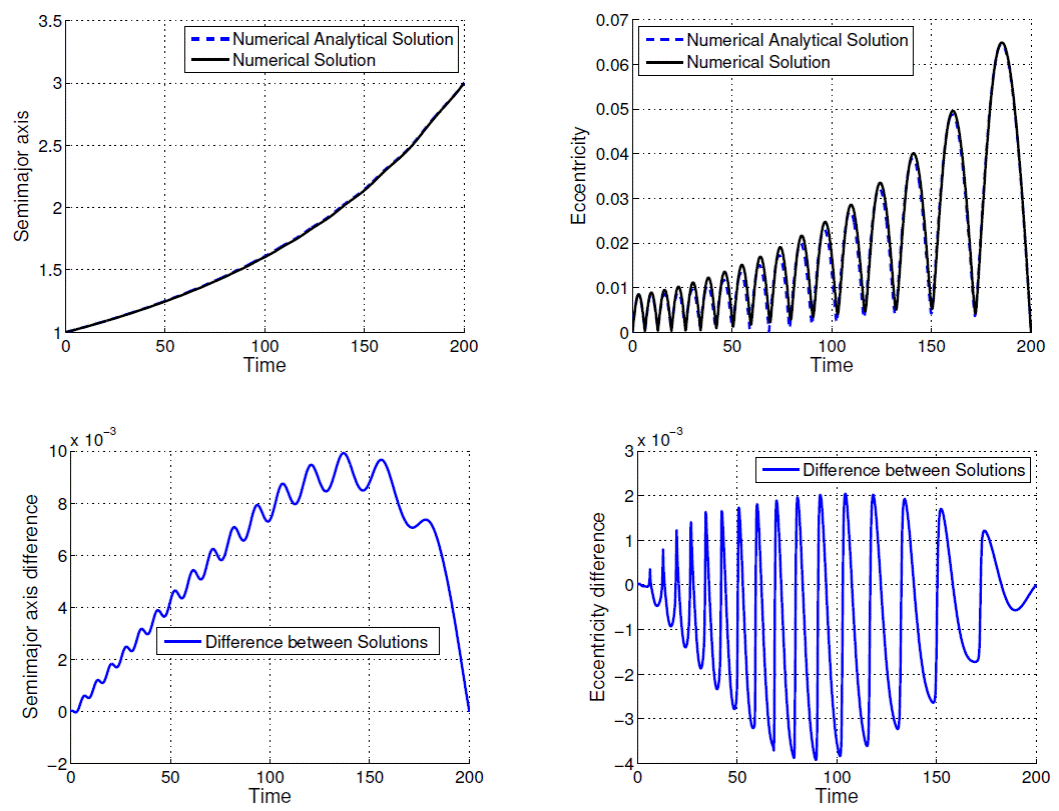
Fig. 10 Comparison between numerical-analytical solution and numerical solution for ρ = 3.0000 DU and tf − t0 = 200.0 TU
In Figures 1-10 the contribuition of the periodic terms in the time behavior of the orbital elements, mainly, of the eccentricity should be noted. The analytical-numerical solution given by Equations (23), (24), (25) provides a good description for the solution of the two-point boundary value problem governed by the maximum Hamiltonian defined by Equations (13) and (14).
The optimal trajectories with amplitudes ρ = 0.7270 DU and ρ = 1.5236 DU and time of flight tf − t0 = 25.0 TU are depicted in Figure 11, and the optimal trajectories with amplitudes ρ = 2.0000 DU and ρ = 2.5000 DU and time of flight tf − t0 = 100.0 TU are depicted in Figure 12. Finally, the optimal trajectory with largest amplitude ρ = 3.0000 DU and time of flight tf − t0 = 100.0 TU is shown in Figure 13. As mentioned before, the optimal trajectories computed through the proposed algorithm (Method 2) give a good description for the solution of the two-point boundary value problem of going from an initial orbit to a final orbit when compared to the trajectories computed by means of the numerical approach based on the neighboring extremals algorithm (Method 1).
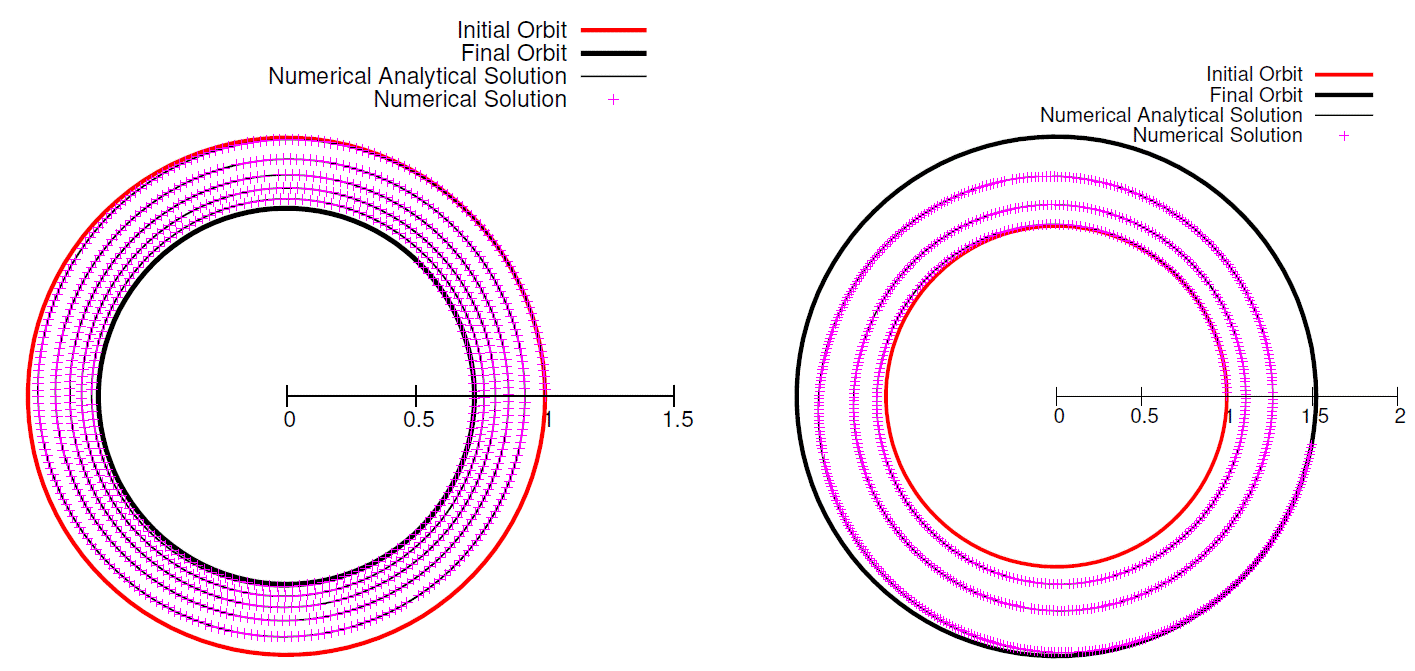
Fig. 11 Trajectory of comparison between numerical-analytical solution and numerical solution for ρ = 0.7270 DU and ρ=1.5236DUwithtf −t0 =25.0TU.
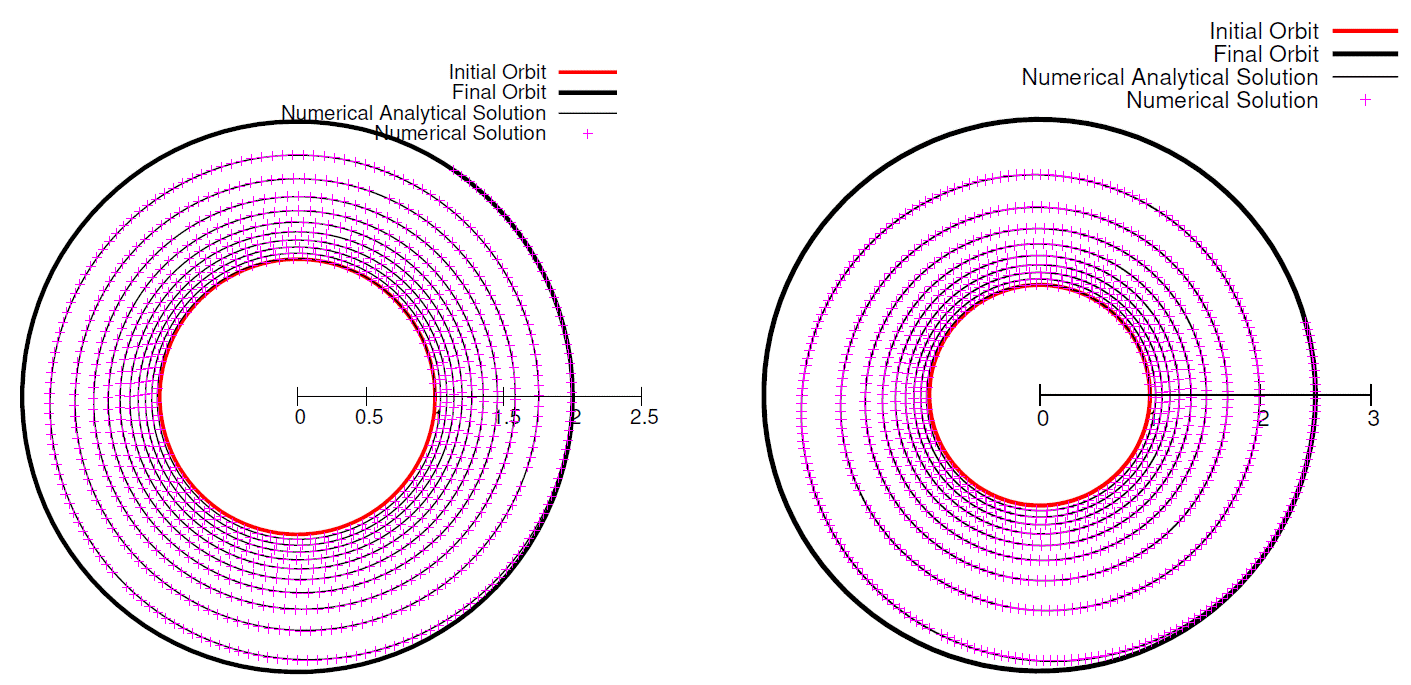
Fig. 12 Trajectory of comparison between numerical-analytical solution and numerical solution for ρ = 2.0000 DU and ρ=2.5000DUwithtf −t0 =100.0TU.
7. Conclusion
In this paper, a numerical-analytical procedure for computing optimal time-fixed low-thrust limited power transfers between coplanar orbits with small eccentricities in an inverse-square force field is presented. Second order terms in eccentricity are considered in the development of the state equations. The proposed procedure is based on an infinitesimal canonical transformation built by applying Hori method. A two-stage NewtonRaphson algorithm is described to solve the two-point boundary value problem of going from an initial orbit to a final orbit. The proposed algorithm is applied in a preliminary analysis of some interplanetary missions discussed in previous work. Numerical results show the very good agreement between the results provided by the proposed algorithm and the numerical results previously obtained through a different approach of the transfer problem. The time behavior of the eccentricity along the optimal trajectory shows excellent agreement with previous results, including maneuvers with larger radius ratio and time of flight.
Finally, we note that the procedure described in this paper can be extended to more general low-thrust limited power transfers.











 nueva página del texto (beta)
nueva página del texto (beta)



