1. Introduction
Important efforts have been made in order to determine proper motions with the highest accuracy because they provide valuable information for many astronomical matters, for instance the determination of membership probabilities of stars to clusters (Kharchenko et al. 2012), the separation of nearby stellar populations from more distant objects by measuring their tangential motion on the sky, the investigation of kinematically distinct populations within our Galaxy (Theissen et al. 2016), the accurate astrometry of asteroids (Tholen et al. 2013), and the subsequent determination of their orbital elements (Farnocchia et al. 2015).
The usual way to obtain the proper motion of a star consists in a linear fitting to a set of positions for different epochs with the largest possible time span. This requires having accurate stellar positions if one wants to get accurate proper motions. These optimal requirements are not always fulfilled: the positions of faint stars are not the most accurate, and the epochs of available all-sky catalogs are not well separated in time.
There are some astrometric all-sky surveys that provide the proper motions of bright stars
If proper motions were derived from the 2MASS positions, these systematic differences would cause systematic errors in the resulting proper motions. This is the case of the proper motions in the catalog PPMXL (Roeser et al. 2010) and more recently in the catalog URAT1 (Zacharias et al. 2015). Although other authors have studied the systematic differences in positions and proper motions of PPMXL with other astrometric catalogs, Chesley et al. (2010), Farnocchia et al. (2015), Vityazev & Tsvetkov (2015), they searched for large scale systematics (length-scales ∼1°) and therefore the high spatial frequency systematics that are analyzed in this work were not noticed before.
2. Comparison of proper motions
In order to find evidence of the suspected systematics we have compared the proper motions in catalogs derived from the 2MASS positions, namely PPMXL and URAT1, with other proper motions that were not derived from the 2MASS positions, namely the astrometric catalogs UCAC4, SPM4 and USNO-B1 (Monet et al. 2003).
The comparisons were performed in square fields of 3°×3° that were previously analyzed in BF&C16 in order to evaluate systematic differences in the 2MASS positions with respect to UCAC4. In this work we selected the two fields with the highest densities, one in the northern hemisphere: Zone1 (RA 70.572°, DEC 22.587°); and the other in the southern hemisphere: Zone1+180 (RA 249.555°, DEC − 21.223°).
2.1. Zone1
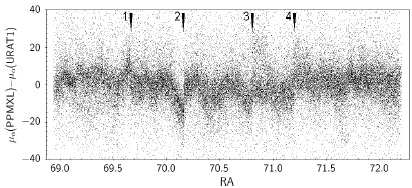
This field in the northern hemisphere is covered by two catalogs with proper motions derived from the 2MASS positions: PPMXL and URAT1. These proper motions were compared with the ones from UCAC4 that are independent of 2MASS. In BF&C16 it was noticed that the systematic differences in the positions depending on RA are more easily recognizable than those depending on DEC. Therefore, only the differences depending on RA will be shown in this work. In order to evaluate if there exists any correspondence between the systematic differences in proper motions and the previously found systematic differences in positions we reproduce Figure 3(a) from BF&C16 as Figure 1(a). In all the figures shown hereafter there are arrows numbered 1 through 4 pointing to some characteristic features of the systematics that are easily recognized. All the proper motions and their differences are expressed in mas yr−1.

Fig. 1 (a) Differences of positions 2MASS−UCAC4 in mas from BF&C16 (by permission from RMxAA). (b) Differences of proper motions PPMXL−UCAC4. (c) Differences of proper motions URAT1−UCAC4. (d) Differences of proper motions URAT1−USNO-B1.
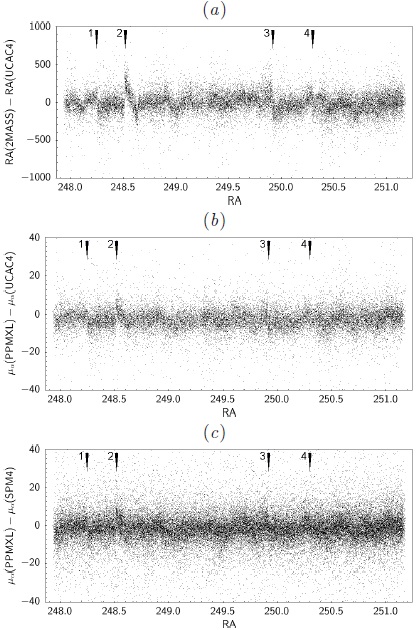
Fig. 3 (a) Differences of positions 2MASS−UCAC4 in mas from BF&C16 (by permission from RMxAA). (b) Differences of proper motions PPMXL−UCAC4. (c) Differences of proper motions PPMXL−SPM4.
Figure 1(b) shows the differences between the proper motions in RA in PPMXL and UCAC4. Here it is possible to appreciate a high spatial frequency systematic pattern in the proper motions whose appearance corresponds roughly to that found in the 2MASS positions. Besides this correspondence the positions of the features that are pointed with arrows numbered 1 to 4 match in all the panels of Figure 1.
Figure 1(c) shows the differences between the proper motions in RA in URAT1 and UCAC4. Also in this figure it is possible to appreciate a high spatial frequency systematic pattern in the proper motions whose features match those found in the 2MASS positions. In this comparison the signs of the features in the URAT1 proper motions are inverted with respect to those in the 2MASS positions because of the use of 2MASS as the first epoch, unlike in PP-MXL where 2MASS is used as the last epoch. It is worth noting that the systematic differences in 2MASS positions introduce systematic differences in proper motions that are larger in URAT1 than in PPMXL due to the smaller epoch difference and the use of only two epochs in URAT1. For example, an error of 200 mas in the position of 2MASS will produce an error of 15 mas yr−1 in a proper motion determined with two epochs separated by about 13 years, as can be seen in the feature number 2.
Figure 1(d) shows the differences between the proper motions in RA in URAT1 and USNO-B1. As in Figures 1(b) and 1(c) it is possible to appreciate a high spatial frequency systematic pattern in the proper motions whose features match those found in the 2MASS positions. In a similar manner to Figure 1(c) the sign of the features in the URAT1 proper motions are inverted with respect to those in the 2MASS positions because of the use of 2MASS as the first epoch.
As an additional confirmation that the systematic differences found in the proper motions are caused by the 2MASS positions, we subtracted the proper motions in URAT1 from the ones in PPMXL. Since 2MASS is the last epoch in PPMXL and the first epoch in URAT1, this subtraction is expected to enhance the systematic pattern. This occurs in fact, as shown in Figure 2.
2.2. Zone1+180
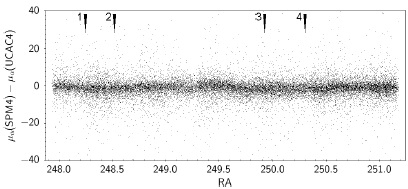
This zone is located in the southern hemisphere. Unlike Zone1 this field is covered by only one catalog with proper motions derived from the 2MASS positions, PPMXL. These proper motions were com-pared with the ones from UCAC4 and SPM4 that are independent of 2MASS positions. In order to evaluate if there exists any correspondence between the systematic differences in proper motions and the previously found systematic differences in positions, in Figure 3(a) we reproduce Figure 7 (upper-left) from BF&C16.
Figure 3(b) shows the differences between the proper motions in RA in PPMXL and UCAC4. In a similar way to Zone1, here it is possible to appreciate a systematic pattern that corresponds to that found in the 2MASS positions, as well as the match of the positions of the features pointed with arrows in all the panels of Figure 3.
Figure 3(c) shows the differences between the proper motions in RA in PPMXL and SPM4. Also in this figure it is possible to appreciate a behavior similar to that shown in Figure 3(b). Although the great number of points in this plot makes the pointed features less noticeable, they are still clearly recognizable.
Figure 4 displays the differences between the proper motions in RA in SPM4 and UCAC4 which do not show the systematic pattern previously found. For instance, in the positions pointed by the arrows the features that were clearly noticed in the previous comparisons are not seen. This provides an additional confirmation that the patterns found in the previous comparisons are due to the use of 2MASS positions for the determination of proper motions in PPMXL. It is worth noting that the small dispersion of these differences (median absolute deviation 2 mas yr−1) shows the excellent agreement between the proper motions in these catalogs.
3. Proper motions derived from rectified 2MASS
As concluded in BF&C16, the 2MASS catalog rectified with the method proposed in that work, hereafter mentioned as Rectified 2MASS or 2MASSr, can be regarded as an extension of UCAC4 with negligible systematic errors. Therefore, it is better suited for the determination of proper motions.
With the aim of profiting from the high density and depth of 2MASS as well as the small random errors of its positions for the determination of proper motions free from their local systematic errors, we recalculated the proper motions in Zone1 using first epoch positions from 2MASSr instead of 2MASS, and second epoch positions from URAT1. We call these proper motions µα(2MrUR1), µδ(2MrUR1) and they are defined by:
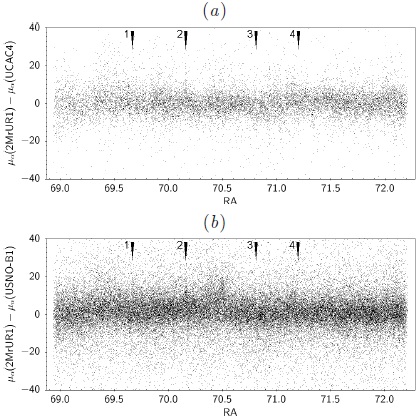
In order to evaluate if the proper motions calculated this way are free from the local systematic differences previously found, we computed the differences between them and the proper motions in UCAC4 and USNO-B1. These differences are shown in Figure 5, where it can be seen that the systematic differences are greatly reduced when compared with Figures 1(c) and 1(d) which correspond to the same zone; see for instance the positions pointed by the arrows.
4. Conclusions
By comparing proper motions of catalogs PPMXL and URAT1, which use 2MASS positions in order to derive proper motions, with those of UCAC4, SPM4, and USNO-B1, which do not use 2MASS to derive the proper motions, we have proved that those of PPMXL and URAT1 are strongly affected by the systematic differences in positions observed in 2MASS in Bustos Fierro & Calderón (2016). It is more noticeable in URAT1 than in PPMXL because in the first catalog the proper motions were calculated with only two epochs -one of them 2MASS- which are less than fifteen years apart, while in the last one the proper motions were calculated with several epochs, which reduces the weight of the 2MASS positions.
We have shown that using Rectified 2MASS as first epoch and URAT1 as second epoch for the determination of proper motions, in a similar way to the determination in URAT1, the systematic effects become negligible. Therefore, we propose the use of Rectified 2MASS (the all-sky catalog is in preparation, to be available late 2016) instead of 2MASS without rectification in order to derive proper motions free from the local systematics due to 2MASS positions.











 nueva página del texto (beta)
nueva página del texto (beta)