1. Introduction

In ^{Cisneros et al. I (2015}) equilibrium figures were obtained from a self-gravitating homogeneous liquid mass endowed with an internal motion of differential vorticity, whose surface equation was that of either a distorted ellipsoid or a distorted spheroid; however, as we noticed a posteriori, the figures, called ellipsoidal and spheroidal after Jeans (1920), were erroneously deduced, although their qualitative features remained more or less unaffected (see § 5.1). In the current paper, we investigate the equilibrium of a heterogeneous model consisting of two concentric homogeneous spheroidal masses of different density, the ‘nucleus’ and the ‘atmosphere’ (whose semi-axes are not correlated) through a simple and precise rotation law. Affixing sub indexes n and a to the pertinent quantities, the body’s relative density, (ρ_n− ρ_a)/ρ_a , is denoted by ε, with ρ_n > ρ_a, so that the distribution of density is somewhat closer to that prevailing in real stars. The quantities in our development are normalized as explained in ^{Cisneros et al. I (2015)}.

2.Bernoulli’s theorem, the classical homogeneous figures and ours

Before going on with our heterogeneous model, we wish to discuss Bernoulli’s theorem as is commonly employed for obtaining the classical homogeneous figures (^{Lyttleton 1953}; ^{Dryden 1956}), particularly the Dedekind ellipsoids which, along with our models, are static. The steady-state equations of motion for a self-gravitating fluid are

where v is the velocity field, V is the potential and p is the pressure. These equations can also be written as

For a streamline (tangent to v) we get, after taking the dot product of v in the first equation (2),

that is

k being constant on a streamline. Commonly, k changes from one streamline to another, being an overall constant only when rot v = 0. The changes in k are dictated by [cf. equations (2) and (4)]

The Maclaurin and Jacobi figures are characterized by the rotational velocity field

where ω is the constant angular velocity. We can see that relation (6) satisfies the continuity equation div v = 0. According to equation (6), the k in Bernoulli’s equation is given by

that is

From which we deduce

c being any constant. Therefore, Bernoulli’s equation (4) becomes

which agrees with the well-known equation.¹

While the Jacobi and the Maclaurin figures rotate as a rigid body, a Dedekind ellipsoid (1, e₂, e₃ are the major, middle, and minor semi-axes) remains fixed in space, its equilibrium being due to an internal motion of uniform vorticity ζ, its velocity field being

We can convince ourselves that V is tangent to ellipses x² + y²/e²₂ = const.. Hence, streamlines are ellipses perpendicular to the z-axis. For ζ constant, the velocity field satisfies the continuity equation, and k obeys the relation

so that

The solution of the partial differential equations (13) is

where c is an arbitrary constant. In this case, Bernoulli’s equation

reduces to

This is essentially equation (10) for obtaining the Jacobi ellipsoids if we put

a known result that establishes the equivalence between Jacobi’s angular velocity and Dedekind’s vorticity (^{Chandrasekhar 1969}). Of course, if we had assumed from the beginning that k = const., it would have been impossible to reach equation (15).

3. The heterogeneous spheroidal mass

The composite model consists of a core, or nucleus, of density ρ_n, whose shape is

surrounded by an envelope, or atmosphere, of density ρ_a, of the form

Here e₁ is the ratio of the nucleus and atmosphere major axes; e_n and e_a are proportional to the rotation semi-axes, which are

The net potentials at any point of the nucleus and the atmosphere are (^{Montalvo et al. 1983}),

respectively, where V_nn is the self-potential of the nucleus; V_na is the potential on the nucleus due to the atmosphere; V_an is the potential on the atmosphere due to the nucleus; V_aa is the self-potential of the atmosphere; ε is the body’s relative density difference:

Let us now suppose that core and envelope rotate with (variable) angular velocities ω_n and ω_a , so that their velocity fields are

Both fields must obey the continuity equation div v = 0. Thus, according to equation (20), we have

In the equilibrium state the angular velocities (42) must fulfill Bernoulli’s equation:

where f_n and f_a are functions to be determined. f_n and f_a are established from the surface conditions p_n = p_a (core surface) and p_a =0 (envelope surface), where p_n and p_a are pressures on points of the nucleus and the atmosphere:

Using equation (31), these relations can be written as

where r = x² + y² and V_N, V_A are potentials on core and envelope surfaces, taken as functions of r only. Thus, for establishing ω_a and ω_n, the potential derivatives must be available at each point of the surface. Since the potential is given numerically, its derivative must be numerically computed. For a homogeneous body (only interior points are needed), we find that a reasonable good approximated expression for the potential at points on the surface is:

where α_i are parameters to be fixed by fit procedures, and thus the angular velocity is given by equation (35)

In the case of our heterogeneous mass, equation (46) is not acceptable, especially at points where external potentials are needed (they must approach 0, as r →∞). To obtain equilibrium figures for the heterogeneous case, the potential derivatives will be established by numerical means. For this purpose, we use the approximation

where h is a small quantity. The precision of expression (47) is of order h². A not too small value for h will be used, since potentials are calculated with an accuracy of about 10⁻⁷; a reasonable h could be ≈ 5 × 10⁻³.

4. Model geometry

The heterogeneous mass can easily be built by making the two surfaces similar: coordinates of corresponding surface points are proportional, so that

for all (x, y, z), from what it follows that c = 1/e₁, e_n = e₁ e_a and d_n = d_a. Thus, the whole mass is characterized by only two parameters, say, e_a and d_a (and, of course, the relative size e₁ of major semi-axes, and the relative density difference ε). Hence, the series, should they exist, would be relatively simple to handle. Yet we prefer to explore a more general case, and let e_n, e_a, d_n, d_a vary freely, thus leading to more involved series (actually, six-parametric, if we take into account the parameters e₁ and ε). The model effectively yields series which are subject to certain limits, both physical and geometrical; for instance, the major semi-axis of the atmosphere must be greater than that of the nucleus: e₁ < 1; besides, the rotation semi-axes z_Mn, z_Ma must be smaller than the corresponding major semi-axes:

or [cf. equation (38)]

Finally, the rotation semi-axis of the atmosphere must not be smaller than that of the nucleus, otherwise the atmosphere would intrude in the nucleus, and the present equilibrium conditions would not apply:

The particular configuration for which z_{M n} = z_Ma (e₁ ≠ 1), i. e., when the poles coincide, is termed a ‘contact figure’; e_a and e_n are related by

5. Numerical results

5.1. The homogeneous spheroidal mass

Clearly, our calculations of (^{Cisneros et al. 2015}, Paper I) must be affected if the right k in Bernoulli’s equation (4) is used, but the qualitative features of the new figures remain more or less alike. In the case of homogeneous figures for which the surface equation is

x2+y2+z2e32+dz4e34=1

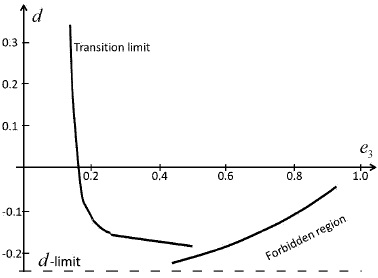
we come as before to continuous e₃ -series for each d value and, furthermore, we again find limits. For d positive, and low e₃ -values up to a definite limit, ω² increases from pole to equator; thereafter, the tendency is inverted (Figure 1). For d negative (but greater than −1/4), another limit appears: as d becomes more and more negative, the e₃ -series becomes shorter, because ω² takes negative values, and the figures come into a forbidden region (Figure 1), a behavior that was also noticed in previous work.

Fig. 1 Limiting e₃ -d curves for the ω² tendency transition (left) and the forbidden region (right) where ω² is partially negative. In fact, the last figure is plotted from the condition that ω² is 0 at the pole. 

5.2. The Heterogeneous Spheroidal Mass

The present series are more involved than those for the homogeneous case, so we must proceed care-fully and not try to get an overwhelming bulk of models that would render it difficult to give a clear panorama of their regularities. For this purpose, a basic series is constructed by fixing five parameters: ε= 1, e₁ = 0.5, e_n = 0.1 and d_n = d_a = −1/8, while the remaining one e_a is let to vary in its allowed range.

5.2.1. The Case d_n= d_a= −1/8

First, we take d_n = d_a = −1/8 and allow e_a to vary from 0.1 up to its maximum value, finding that equilibrium is possible for the angular velocity distribution given by equation (31) for the envelope and core. In Figure 2 we plot the angular velocity distribution in the nucleus (R < 0.5), and the atmosphere (R < 1); Figure 3 is a sketch of the model geometry.

Fig. 2 Angular velocity distribution between pole (R = 0) and equator for the nucleus (shorter line) and atmosphere as e_a varies from 0.1 (contact figure) to the limiting value 0.78. Fixed parameters are: e₁ = 0.5, e_n = 0.1, d_n = d_a = −1/8, ε = 1. 

Fig. 3 Heterogeneous equilibrium figures as e_a varies from 0.1 (contact figure) to the limiting value 0.78. Poles are suggested by a thick dot. Fixed parameters are: e₁ = 0.5, e_n = 0.1, d_a = d_n = −1/8, ε = 1. 

In Figure 2 (see also Figure 3), the series begins with a contact figure in which the poles of core and envelope touch each other, but not the equators, since the equator of the atmosphere is twice as large as that of the nucleus (e₁ = 0.5). We see that the core rotates slower than its envelope, even at the pole. In both, the angular velocity decreases from pole to equator, i. e., the central parts rotate faster than the outer ones. As e_a increases (the atmosphere expands), ωa2 decreases, until a point is reached where the tendency is reversed: the angular velocity now increases from pole to equator, remaining so up to the end; we say that a transition figure occurs. For larger e_a -values, ωa2 steadily decreases, reaching a zero value at the pole; thereafter, it is negative and unacceptable. The limit is achieved at e_a = 0.78 (z_M = 0.84). At the same time, less dramatic changes in the core occur with increasing e_a : the pole ωa2 increases a little, until the angular velocity decreasing tendency ends: a transition figure occurs. Subsequently, ωa2 monotonically increases from pole to equator. Both angular velocity distributions have, therefore, two limits: one for which ω² becomes zero at a point, and the other, less drastic, where the angular velocity reverses its tendency from monotonically decreasing to increasing. Certainly, the change takes place gradually, and we refer to a limit when ω² increases monotonically for the first time. Still another limit might be disclosed by building more series for larger e_n values. Indeed, we find similar series starting with a contact figure and ending up with a top figure (e_a ≈ 0.78) if e_n ≤ 0.3975 (z_Mn = 0.43). For the small interval 0.4004 > e_n > 0.3975 there are series that do not be-gin with a contact figure and end with a one-member series at e_n = 0.4004, e_a = 0.969.

5.2.2. The Case d_n = d_a = 1/8

Here we take d_n = d_a = 1/8 and let e_a vary from 0.1 (contact figure) up. Once more, we get a set of series somewhat different from the former one (Figure 2), but also sharing several properties:

1. The series begins with a contact figure with the atmosphere rotating faster than the nucleus, as formerly.

2. Both differential angular velocities always monotonically decrease from pole to equator. In other words, there are not transition figures.

3. The limiting figure occurs at e_a = 0.967 (z_Ma = 0.917).

4. The contact figure has a limit for e_n = 0.398 (cf. § 2.1.1).

5. The series do not end at e_n = 0.398; they continue for larger e_n and are more and more narrow, ending with an isolated figure with e_n = 0.4827, e_a = 0.969 (z_Mn = 0.457) (see Figure 4).

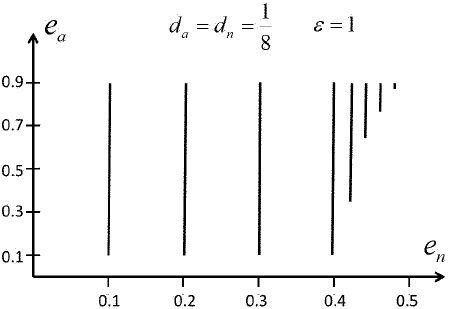
Fig. 4 Sketch of e_n -series for d_a = d_n = 1/8, ε = 1. The series begin with a contact figure for e_n < 0.3975 and end at an e_a around 0.9. After e_n = 0.3975 they become narrower and begin without a contact figure. 

Hence, the plus sign of d_a, d_n hinders the monotonous property of the angular velocity, and raises the upper limit of e_a. Additionally, the series does not disappear after a last contact figure, but at a higher e_n limit.

5.2.3. The Case d_n= 1/8, d_a= −1/8

This time, only d_n sign is modified, so that our set of parameters is

e1=12, en=110, dn=18, da=-18, ε=1

Once more, the series starts with the contact figure e_a = 0.0876; e_a is established by z_Ma = z_Mn condition (equation (51)). The series resembles more the d_a = d_n = −1/8 case than the d_a = d_n = 1/8 one, in the sense that it has angular velocity transition limits and a limiting contact figure at e_n ≈ 0.4 (z_Mn = 0.38). For greater e_n values, there are, however, more series without an initial contact figure, which become narrower as e_n → 0.5 (z_Mn = 0.47). For e_n = 0.5 there only exists a series with the member e_a = 0.97 (z_Ma = 0.92).

5.2.4. The Case d_n = −1/8, d_a = 1/8

Here, d_a alone is modified relative to first case, so that the parameters values are now

e1=12, en=-110, dn=-18, da=18, ε=1

With these parameters, we also establish series starting with a contact figure, when e_n < 0.4 (z_Mn = 0.43). Series without a contact figure are possible when 0.4 < e_n < 0.421; for e_n = 0.421 (z_Mn = 0.46) the series has a unique member at e_a = 0.97. The atmosphere does not present angular velocity transition limits, and the nucleus has only one, at e_n = 0.2, e_a = 0.6.

5.3. Consequences of the ε-value

To study the ε impact on our series, we assumed values for the parameters according to

e1=12, dn=-18, 18, da=18,-18,ε=1,2,4,9,24.

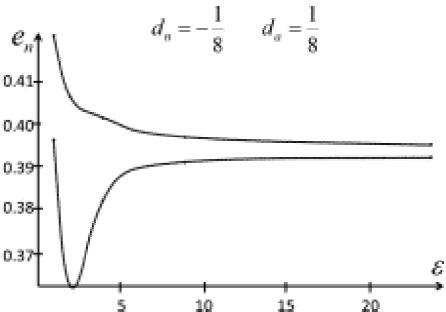
and constructed the series changing e_a for a given e_n of a set 0.1 . . . 0.5, as formerly done. As an illustration, only cases d_n = ∓1/8, d_a = ±1/8 were considered, and cases with d_n = d_a = −1/8, 1/8 were disregarded. We refer briefly to these d-values as −+, +−, −−, and ++ (first sign for d_n, second for d_a). Generally speaking, we did not find any new property, (other than those recognized above) when ε was modified, i. e., for each ε, the set of series can or cannot show angular velocity distribution ‘turning points’ (transition to monotonically increasing distribution), there is a final series having a contact figure, and there is a last (one-member) series. Clearly, as ε changes, the values characterizing a last contact figure, a last series, and a transition figure, must suffer modifications. The contact limiting figure has an e_n -value that first decreases and then increases, as ε increases from 1 to 24 (see Figure 5). On the other hand, e_n in the last series continually decreases as ε increases. The e_n span between last contact figure series and last series initially increases and thereafter continuously decreases (Figure 5).

Fig. 5 As ε increases, the last contact figure e_n (lower curve) first decreases and then increases slowly; on the contrary, for the last one-member series e_n decreases continually. Both curves tend to the same point, i. e., the last contact figure is at the same time the last one-member series. 

5.4. Consequences of the e ₁ -value

To study changes of our basic series (Figure 2) regarding the nucleus and atmosphere relative size e₁, we varied it in steps of 0.1 from 0.9 down. We fixed d_a = ±1/8, d_n = ±1/8, ε = 1 and constructed e_n series varying e_a for each e₁ value of the set. For example, when e₁ = 0.9 we built the series for e_n = 0.1, 0.2, . . . . Qualitatively again, we found series with or without transition limits, e_a upper limits, last contact figure for e_n series, and final one-member series. Quantitatively, there are differences regarding the above results. The ω² magnitudes and the variation range change; the e_n gap between last contact figure and last one-member series grows as e₁ decreases, starting at e₁ = 0.5; likewise, beyond e₁ = 0.5 the gap approaches 0 (see Figures 6 and 7). This behavior is somewhat similar to the ε-effect (Figures 4 and 5): as e₁ or ε increases the gap be-comes narrower, and finally it disappears.

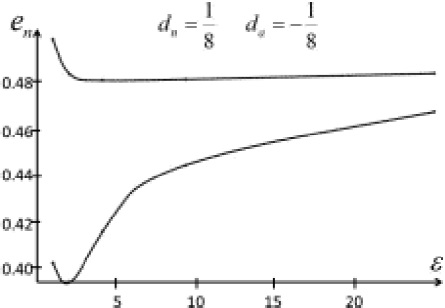
Fig. 6 As ε increases, the last contact figure e_n (lower curve) first decreases and then increases slowly; on the contrary, last one-member series e_n decreases continually. Both curves tend to the same point, i. e., last contact figure is at the same time last one-member series. 

Fig. 7 As e ₁ increases, the last contact figure e_n /e₁ (lower curve) increases continuously, practically for all e₁ values; on the contrary, for the last one-member series e_n /e₁ remains constant up to about e₁ = 0.5. Both curves coincide after about e₁ = 0.5. The curves were plotted for d_n , d_a = −1/8. 

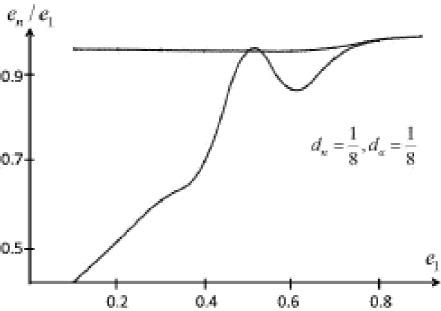
Fig. 8 As e₁ increases, the last contact figure e_n /e₁ (lower curve) increases continuously with some small oscillation, for all e₁ values; on the contrary, the last one-member series e_n /e₁ remains constant (≈ 0.98) practically all the way. Both curves coincide after about e₁ = 0.7. The curves were plotted for d_n , d_a = 1/8