1. INTRODUCTION
We are currenty working to obtain astrometrie positions on deep CCD images each covering a field 6׳ x 14׳. This is a small field; therefore, an optimal astrometrie reduction is difficult to obtain, either because of the small number of reference stars or because their spatial distribution on the image is non-uniform. This situation is common to most CCDs of similar or larger size. In deep CCD images-such as in our case-"bright" stars are saturated and they have to be discarded as reference stars.
All-sky reference catalogs dense and precise enough to enable the astrometrie reduction of deep CCD images do not exist. The only available all-sky dense astrometrie catalog is UCAC4; its average density is over 2000 stars per square degree (Zacharias et al. 2013) with large variations among different regions of the sky. Its limiting magnitude is ≈ 16. Since in our images the stars with the highest positional accuracy are saturated they cannot be used as reference stars. On the other hand, non-saturated stars have magnitudes at the faint end of the catalog and their positional accuracy is lower. Another available catalog is the 2MASS All-Sky Catalog of Point Sources. The more precise positions of this catalog have a K s magnitude range between 13.5 and 15.5, with a positional accuracy of 70-90mas (Skrutskie et al. 2006).
Figure 1 shows that using 2MASS as a reference catalog would overcome the lack of reference positions for the astrometrie reduction of small fields in regions with poor coverage in UCAC4. For instance, in the interval 14.5 < K s < 15.0 the number of sources in 2MASS is four times larger than in UCAC4, and in the interval 15.0 < K s < 15.5 it is fifteen times larger. In addition Figure 2 suggests that the sources brighter than K s = 13.5 have better astrometrie positions in UCAC4 than in 2MASS, while the opposite occurs for the fainter sources. Therefore 2MASS seems to be a good choice as a reference catalog in small deep fields, but it is not an astrometrie catalog because of severe systematic errors in its positions.
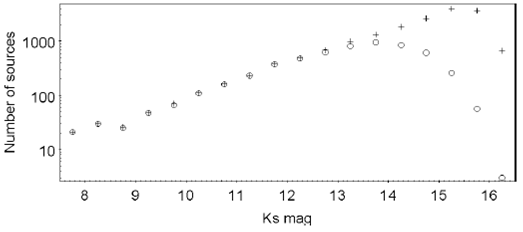
Fig. 1 Number of sources within a typical 3°x3° field far from the galactic plane as a function of K s magnitude. Circles: UCAC4. Crosses: 2MASS.
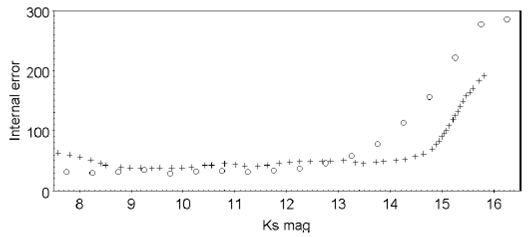
Fig. 2 Circles: median of UCAC4 internal errors within a typical 3°x3° field far from the galactic plane as a function of K s magnitude. Crosses: internal estimation of positional uncertainty in 2MASS from Skrutskie et al. (2006).
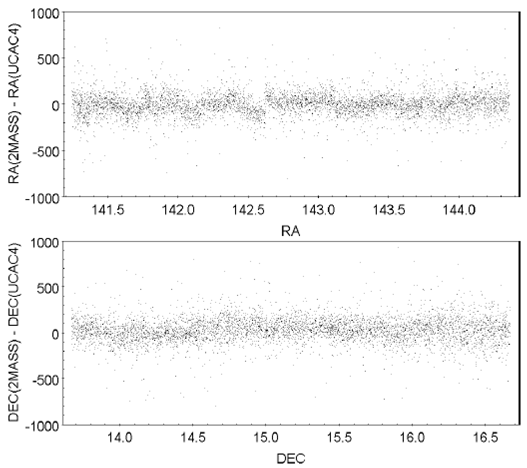
The systematics can be seen in Figure 3 where we display position differences between 2MASS and other catalogs for different fields. The observed amplitudes of the systematic differences are hundreds of milliarcseconds. These differences are well above the 2MASS dispersion given by the authors of this catalog.
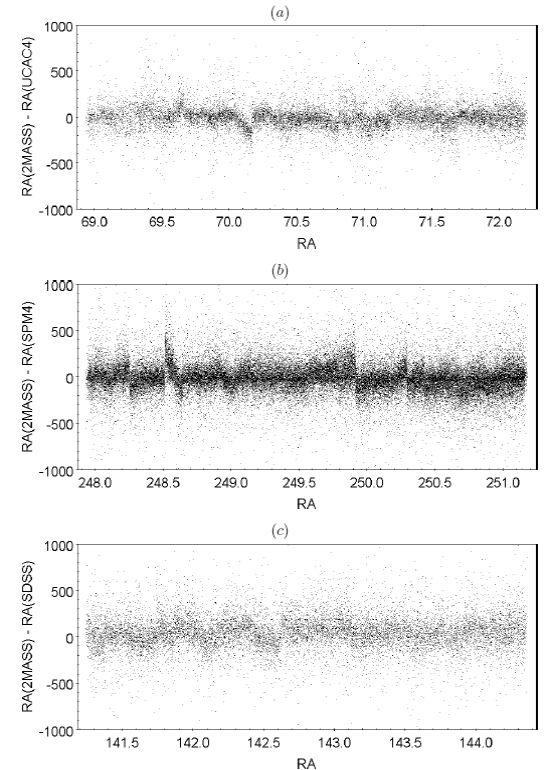
Fig. 3 Comparison of 2MASS positions with different catalogs over fields of 3° x 3°. (a) UCAC4, (b) SPM4, (c) SDSS-DR9.
When 2MASS is used as a reference catalog these systematic errors appear in the results of the astrometrie reduction. In this work we propose to improve the quality of the 2MASS positions with respect to UCAC4 by means of a rectification method that removes the systematic differences between these catalogs. The proposed rectification of 2MASS would extend the range of accurate positions up to K s = 15 and with a lower accuracy up to K s = 15.5. After this correction the astrometrie reduction of small field CCD images could rely on 2MASS as a reference catalog.
Since we are interested in obtaining astrometrie positions on the ecliptical zone from deep CCD images, we plan to apply this rectification method to 2MASS in a strip a few degrees wide along he Ecliptic. The rectified 2MASS will also be useful for studies of Solar System objects, mainly for precise astrometry of small bodies.
2. THE METHOD
Figures 3 and 4 show that the systematics in RA are very different from those in DEC: the RA systematics show strong discontinuities with abrupt changes in the value of the mean, a behaviour very different from that of the DEC systematics, which vary continuously in a smooth way, with a longer period of variation. Thus, the RA systematics have a higher spatial frequency than the DEC systematics.
We propose to locally rectify 2MASS with respect to UCAC4 in order to diminish the systematic differences 2MASS-UCAC4. Similar efforts were done with other catalogs by Stock & Abad (1988) for example. The different behavior in both coordinates is related to the 2MASS tiling strategy of observations in scans covering a sky region 8.5' wide in RA and 6° long in DEC.
We define a working field of 3° x 3° on the sky. This size is selected in order to include several 2MASS tiles, because their systematic errors change from tile to tile. On that field we match the catalogs UCAC4 and 2MASS with a coincidence radius of 1״; a proper motion correction to the UCAC4 positions is not necessary because the epochs of these catalogs are quite close. We calculate the differences (α 2MASS - α UCAC4, δ 2MASS - δ UCAC4 ) for the stars in common.
On the working field we define a square grid of step ρ, aligned with the coordinate axes RA and DEC. On each node of the grid (α g, δg) we calculate the weighted mean difference (α2MASS - α UCAC4, δ 2MASS - δ UCAC4 ) inside a smoothing area centered on that node. As result of this procedure we obtain the mean systematic differences between 2MASS and UCAC4 evaluated on the nodes of a grid of size 3° x 3° that will be used for the rectification of 2MASS.
In order to decide the size of the grid step ρ, we performed the rectification of one field using values for ρ ranging from 0.75' to 2'. We finally adopted ρ = 1' because we found that with ρ < 1' there was no noticeable improvement in the rectification, and with ρ > 1' the differences with the highest spatial frequency were not properly corrected.
We also tested the effect on the rectification of the grid shift and we found that 90% of the differences between the corrections performed with the grid shifted in both coordinates are smaller than 7 mas, and less than 0.7% of them are larger than 30 mas. Therefore the effect of the grid shift is not significant, since it is well below the errors of UCAC4 positions.
We use as weight function a two-dimensional Gaussian
where
are computed as
The constant K was selected in such a way that ω x(x) = 0 for x =
In order to perform the rectification, for each position (α 2MASS , δ 2MASS ) we compute the correction (∆α, ∆δ ) by means of a two-dimensional cubic spline interpolation of the mean differences on the nodes of the grid. The corrected coordinates (α 2MASS -r , δ 2MASS -r ) are computed by
Notice that although the size of the working field is 3° x 3°, the useful area is smaller because close to the borders the correction is erroneously estimated due to the asymmetry in the calculation of the mean differences and in the interpolation, since part of the smoothing area is outside the working field.
3. APPLYING THE METHOD
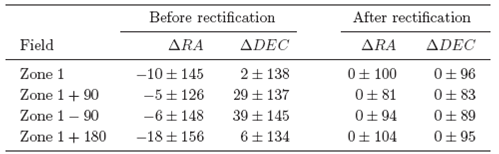
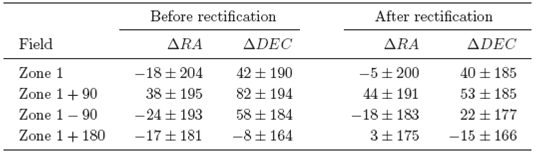
In order to evaluate the quality of the proposed procedure we applied the rectification method on four fields 3° x 3° in the ecliptical region (our region of interest). The coordinates of the center of Zone 1 were arbitrarily selected. The other three fields were selected approximately at ecliptic longitude +90°, -90° and +180° from Zone 1, and they were called Zone 1 + 90, Zone 1-90 and Zone 1 + 180 respectively. The centers of these fields and the number of sources on each one are listed in Table 1.
Figure 5 shows the differences between the 2MASS coordinates and UCAC4 before and after rectification in Zone 1 + 90. This is the field with the lowest density. Notice that the differences that depend on RA are more easily recognizable than those that depend on DEC. Therefore in subsequent comparisons only the differences that depend on RA will be shown.
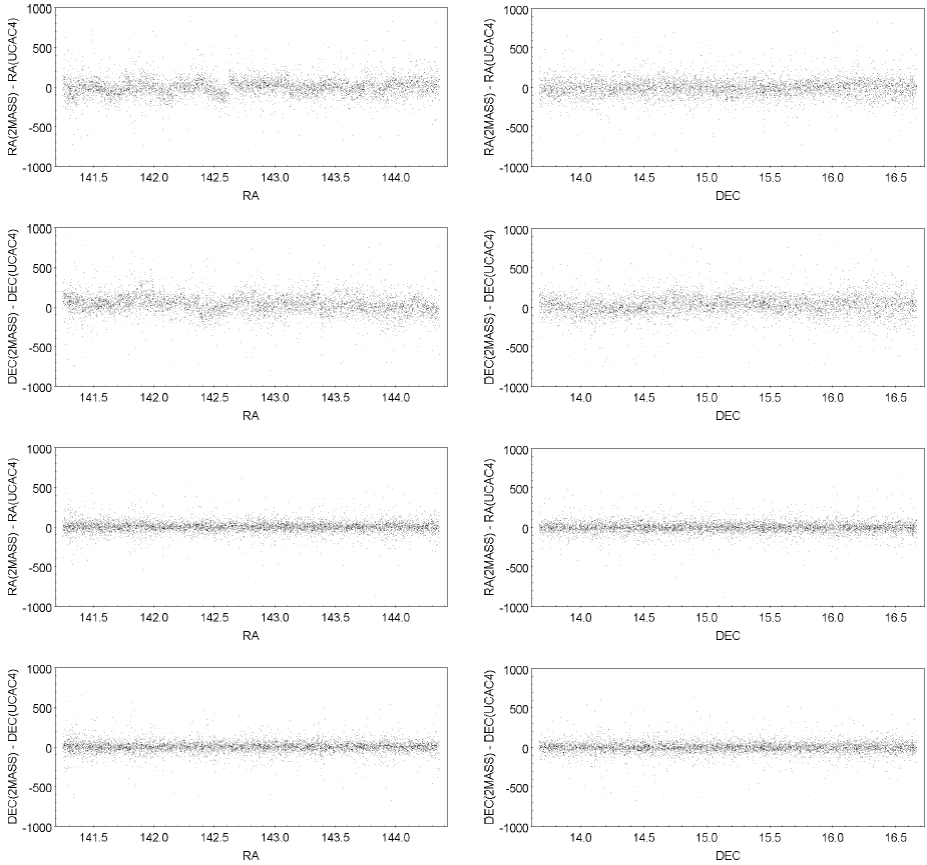
Fig. 5 Differences 2MASS-UCAC4 in RA and DEC, depending on both coordinates in Zone 1 + 90. Upper two panels: before rectification. Lower two panels: after rectification.
Since UCAC4 was the reference catalog for the rectification, we also evaluated it by comparison with an external catalog. We computed the differences between 2MASS and SDSS-DR9 (Ahn et al. 2012) in the same field, before and after rectification; the results are shown in Figure 6.
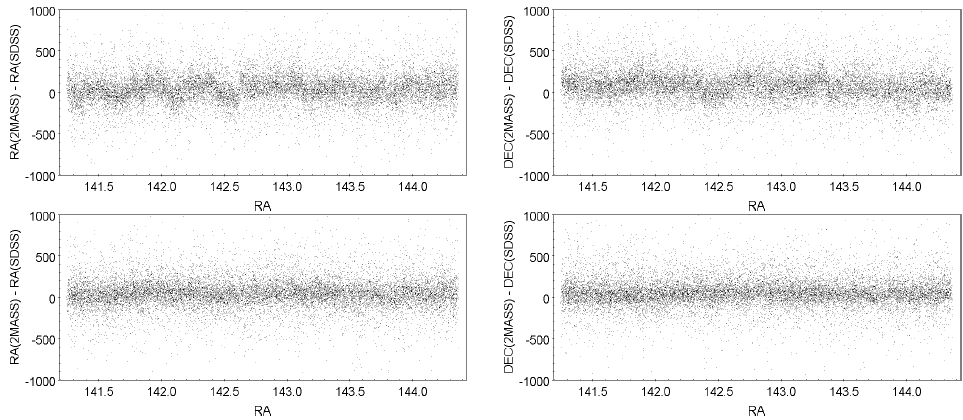
Fig. 6 Differences 2MASS-SDSS-DR9 in RA and DEC, depending on RA in Zone 1+90. Upper panel: before rectification. Lower panel: after rectification.
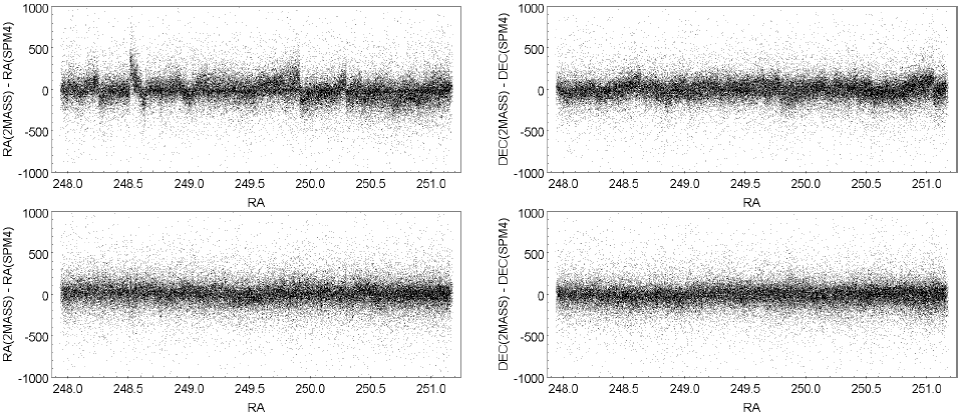
Figure 7 shows the differences between 2MASS coordinates and UCAC4 before and after the rectification in Zone 1+180. This is the field with the highest density. Figure 8 shows the comparison with another catalog, SPM4 (Girard et al. 2011) for the same field. Zone 1 and Zone 1 - 90 are not displayed because the results of the rectification method were very similar to those found for the other fields.
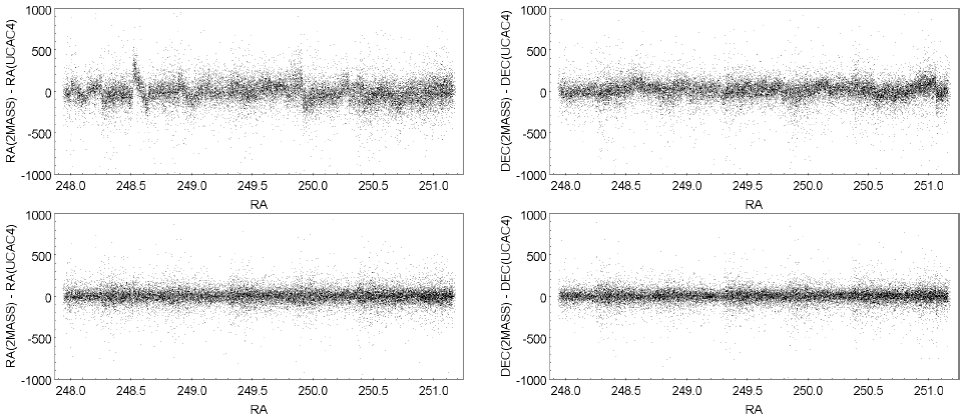
Fig. 7 Differences 2MASS-UCAC4 in RA and DEC, depending on RA in Zone 1+180. Upper panel: before rectification. Lower panel: after rectification.
4. EVALUATION OF THE METHOD
Tables 2 and 3 contain a brief statistical summary of the four fields analyzed in this work. The comparisons with UCAC4-regarded as an internal check-shown in Figures 5 and 7 demonstrate that the remarkable systematic differences between 2MASS and UCAC4 become negligible after the proposed rectification method is applied. As a consequence, it can be seen in Table 2 that the mean differences become null and the dispersions are significantly reduced, down to ≲100mas, the typical positional uncertainty of 2MASS (Skrutskie et al. 2006).
Table 3 Comparisons with external catalogsa
aSDSS-DR9 in Zone 1, Zone 1 + 90, Zone 1 - 90; SPM4 in Zone 1 + 180. Mean differences and standard deviations in mas.
The comparisons with external catalogs shown in Figures 6 and 8 demonstrate that prior to rectification the systematic differences are very similar to those found with UCAC4, although the dispersions are noticeably larger. After rectification the systematic differences are greatly reduced. However, slight systematic differences may still persist. In addition, the reduction of the dispersions and the variation in the mean differences shown in Table 3 are very slight. Since the dispersions are large, they are not significant.
Although in the above figures there are no visible systematic differences after rectification, some small ones could survive under the scattering of the data. In order to quantify these residual systematic differences, we calculated the grid of mean differences between the rectified 2MASS and UCAC4 (referred to as "second grid" hereafter), and we compared it with the grid used for rectification ("first grid"). Figure 9 shows the values of the first and the second grid along one grid line in the center of Zone 1+180. The statistics of the values for the first grid are: ∆RA = (-18 ± 104) mas, ∆DEC = (3 ± 83) mas, and for the second grid they are: ∆RA = (0 ± 28) mas, ∆DEC = (0 ± 25) mas. The dispersions are similar to the smallest errors in the UCAC4 positions, and they can be regarded as a measure of the error of the rectification method.
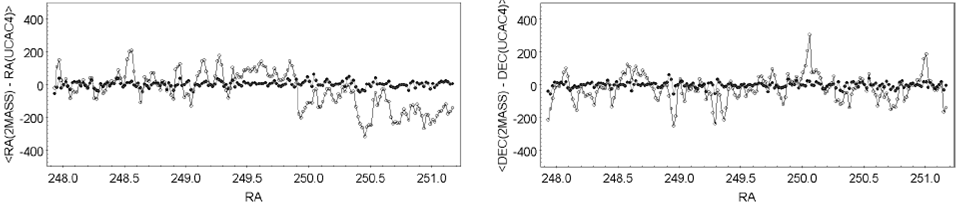
Fig. 9 Mean differences 2MASS−UCAC4 in RA and DEC along one grid line in Zone 1+180. Open circles: before rectification. Filled circles: after rectification.
Figure 10 displays the VPD of second grid values versus first grid values in both coordinates. The correlation between them provides information on the residual systematic differences after the rectification. As a first approximation they can be quantified by means of the slopes of the displayed distributions computed by linear least squares fits. The resulting slope in RA is 0.101 ± 0.001 and in DEC it is 0.137 ± 0.001. These values suggest that the residual systematic differences are approximately 10% of the corrected ones.
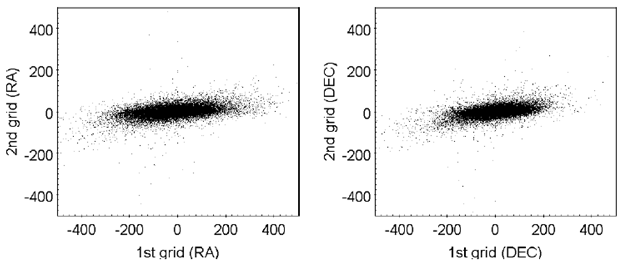
Fig. 10 VPD of second grid values versus first grid values in right ascension (left) and declination (right), in mas.
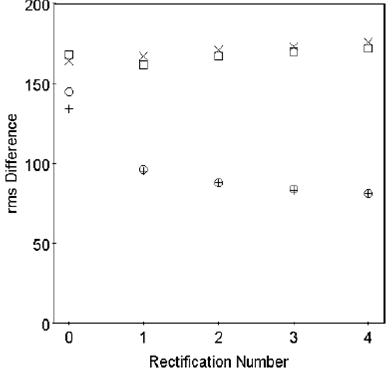
We also analyzed the resulting rms differences obtained with UCAC4 and SPM4 after successive applications of the rectification method in Zone 1+180; they are displayed in Figure 11. It can be seen that the rms differences obtained with UCAC4 always decrease while those with SPM4 decrease after the first rectification, but they increase after the next ones.
5. CONCLUSIONS
The proposed method was able to reduce the systematic differences between 2MASS and UCAC4 well below the random differences in all the fields analyzed in this work, despite their very different densities (from 0.182 to 0.774 sources per square arcminute).
As expected, after rectification the mean differences 2MASS-UCAC4 are null, and the rms differences are reduced from ≈ 140 mas to ≈ 90 mas. If we assume that the average error of positions in UCAC4 is ≈ 30 mas and that in 2MASS ≈ 85 mas, then the resulting rms differences are ≈ 90 mas, as obtained.
The application of successive rectifications was tested only on Zone 1 + 180. It was found that the differences with UCAC4 always decreased, while the rms differences with an external catalog decreased after the first application, but they increased after further rectifications. This behavior suggests that successive rectifications could cause the rectified 2MASS to approach UCAC4 and its random errors. Therefore, they are not recommended.
The 2MASS catalog rectified with the proposed method can be regarded as an extension to magnitude Ks = 15 of UCAC4. It is suited for astrometry with an accuracy around ≈ 90 mas in the positions and with a lower accuracy to magnitude Ks = 15.5, with negligible systematic errors. While our primary goal was to rectify 2MASS in the ecliptical zone to enable its use as a reference catalog for the astrometric reduction of deep CCD images, we are considering performing the rectification of the complete 2MASS catalog. In the meantime we can perform on demand rectifications of particular fields requested by other authors.
Despite the fact that the rectification method was developed in the ecliptical zone, the method itself is not dependent on the region of the sky, so it could be applied in any other region if necessary, after adequate adaptation for regions close to the celestial poles.
This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation.











 nueva página del texto (beta)
nueva página del texto (beta)