Introducción
La eficiencia de un modelo en los programas especializados de análisis depende de la eficacia con la que reproduce y evalúa la respuesta física de la estructura en condiciones reales. En el caso de sistemas con pocas redundantes, la evaluación correcta de las capacidades de los elementos es fundamental, debido a que la formación de la primera incursión inelástica influye en la predicción del mecanismo de colapso y las capacidades de toda la estructura. Específicamente, la respuesta inelástica de edificios estructurados con marcos de acero contraventeados ante excitaciones laterales es altamente dependiente de las capacidades y de la respuesta inelástica de los contravientos (Tremblay y Robert 2001; Tapia y Tena 2011; D'Aniello et al. 2015).
En el caso típico de marcos de acero con contravientos, la demanda de distorsión queda restringida a la capacidad de algunos entrepisos después del pandeo por compresión en marcos con contravientos concéntricos (Marino y Nakashima 2006; Lacerte y Tremblay 2006; Tapia y Tena 2014; D'Aniello et al. 2015) y también en marcos con contravientos excéntricos después de la fluencia de la viga enlace (Rozon et al. 2008; García 2015). Por esto, la predicción adecuada de las capacidades del contraviento trasciende a la estimación adecuada de la capacidad de deformación de los entrepisos y, en consecuencia, en la evaluación de la rigidez lateral de todo el sistema.
Este artículo discute los resultados de estudios paramétricos de la formulación geométrica no lineal para elementos viga-columna de contravientos con respuesta dúctil en tres dimensiones ante cargas estáticas y dinámicas con el propósito de:
Establecer aproximaciones óptimas del modelado.
Estimar la influencia de la discretización de la sección transversal con fibras, el número de elementos y las imperfecciones geométricas iniciales en la respuesta de los modelos.
Comparar la respuesta sísmica entre diferentes modelos de la placa de conexión.
Evaluar la influencia de la respuesta del material (fatiga, sobrerresistencia y endurecimiento por deformación).
Modelado inelástico
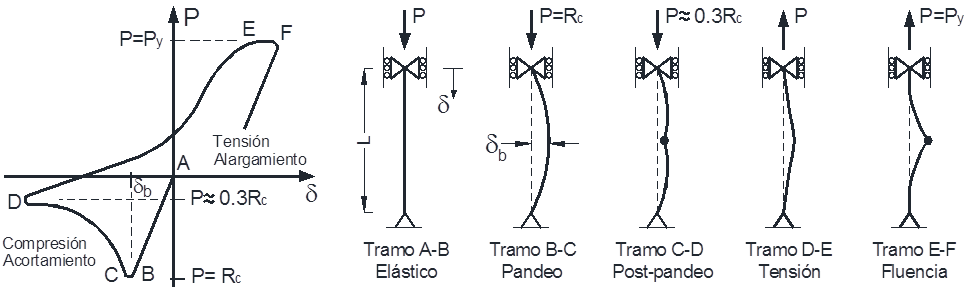
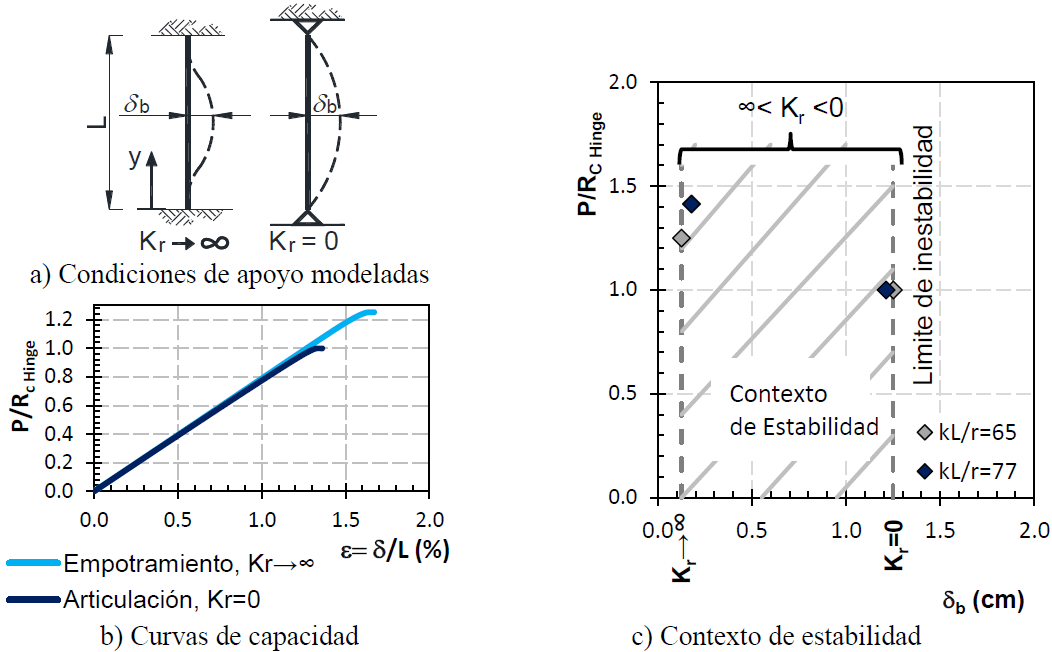
Los marcos dúctiles de acero con contravientos son comúnmente usados como sistema sismo-resistente en edificaciones. Durante demandas sísmicas intensas (Figura 1), se espera que el inicio del daño se presente por pandeo global de los contravientos en compresión (P= Rc), donde las deformaciones inelásticas de los contravientos deben ser redistribuidas en demandas a las trabes, columnas y conexiones. Después del pandeo, la resistencia a compresión disminuye hasta una resistencia a compresión post-pandeo (P ≈ 0.3Rc ), donde se forma una articulación al centro del claro. Luego, ante el cambio de dirección de la fuerza a tensión, se espera que un contraviento dúctil fluya por tensión (P= Py ).
En los programas de análisis no lineales es posible modelar la respuesta inelástica de edificios en zonas sísmicas a través del modelado de elementos estructurales detallados y la interacción entre ellos. Sin embargo, las suposiciones, simplificaciones, omisiones y los errores relacionados con las formulaciones representan una fuente de incertidumbre en la evaluación del desempeño sísmico de las edificaciones; especialmente, las estructuradas con marcos con contravientos debido a la complejidad de su respuesta (Figura 1).
En este estudio, se evalúan las formulaciones para el modelado de la respuesta inelástica de contravientos mediante el programa de análisis no lineal OpenSees (Mazzoni et al. 2006). Los resultados son fácilmente extrapolables a algún otro de los múltiples programas y herramientas de análisis no lineal que existen en la actualidad. OpenSees es un programa orientado a objetos con código abierto para simular la respuesta sísmica de sistemas estructurales y geotécnicos. La estructura de programación permite la selección del elemento viga-columna y la transformación geométrica para cada contraviento. En los casos en estudio, se usa un material Steel02 del modelo Giuffré-Menegotto-Pinto, que permite incluir un endurecimiento isotrópico por deformación e incluye el efecto Bauschinger bajo cargas ciclas para proporcionar una representación más realista de la respuesta de los elementos estructurales comparada con elementos bilineales.
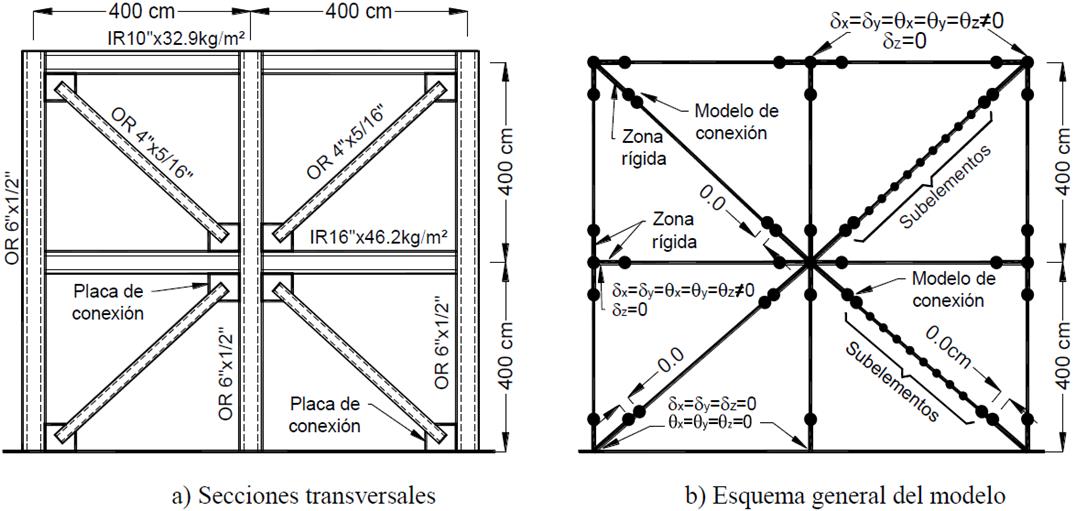
Cuando dos o más elementos estructurales convergen a un mismo punto, como el caso de vigas y columnas, se considera una superposición de las secciones transversales, donde no hay deformaciones (Figura 2). Con el propósito de definir correctamente la longitud de esa zona rígida, las conexiones se diseñaron cuidadosamente, especialmente la placa de conexión de los contravientos en cada caso. Las zonas rígidas de la conexión de columnas, vigas y contravientos se modelan mediante elementos elásticos cuya área es diez veces la transversal y diez veces el momento de inercia de cada elemento.
En los perfiles estructurales se usó acero tipo A572 Gr. 50 con un esfuerzo de fluencia Fy = 3,515 kg/cm2, un factor de sobrerresistencia del material Ry igual a 1.0 y una sobrerresistencia por endurecimiento por deformación b igual a 0.003, excepto en los modelos donde explícitamente se indican otras magnitudes. La respuesta de los modelos de los contravientos se evaluó a través de análisis estáticos no lineales ante carga monótonamente creciente y análisis dinámicos no lineales. En los análisis estáticos, la capacidad del contraviento se estudió como elemento aislado aplicando una carga en compresión que se incrementó monótonamente.
La respuesta en ciclos histeréticos de los contravientos se evaluó mediante análisis dinámicos usando un marco de dos niveles, que se diseñó siguiendo criterios de capacidad (AISC 341-10 2010). En la Figura 3, se muestran las secciones del diseño y las principales características del modelo. En los análisis dinámicos, la sección transversal de todos los elementos se discretizó por medio de fibras para incluir la plastificación progresiva de la sección. Además, los contravientos se modelaron usando diez subelementos con cinco puntos de integración cada uno, una deformación inicial al centro del claro igual a 0.002L en configuración parabólica hacia afuera del plano del marco, una transformación geométrica P-delta en columnas y trabes y una transformación corrotacional en contravientos. La justificación y conveniencia de usar estos parámetros se discutirá a lo largo del artículo, donde la discusión se centra en la respuesta del contraviento de la crujía izquierda de planta baja, aunque los resultados de los otros elementos son equivalentes. Igualmente, se prevé que los modelos de contravientos que formen parte de edificaciones más complejas y que consideren las recomendaciones discutidas más adelante desarrollarán una respuesta analítica equivalente.
Efectos de segundo orden
Los efectos de segundo orden se incluyen comúnmente mediante una subdivisión del contraviento en subelementos, lo que pretende estimar la capacidad de pandeo e incluir la variación de la deformación a lo largo del elemento (Tapia y Tena 2013). Una cantidad pequeña de subelementos podría estar asociado a una imprecisión de la respuesta del elemento, mientras que una cantidad grande de subelementos requiere un trabajo computacional exhaustivo e innecesario. Así, el tiempo de cómputo requerido para desarrollar los cálculos en el programa es proporcional al número de subdivisiones de los elementos estructurales.
Para evaluar esto, en la Figura 4 se muestran las curvas de capacidad de análisis no lineales ante carga en compresión monótonamente creciente de un contraviento biarticulado con una relación de esbeltez kL/r= 52. Así, el contraviento modelado con dos subelementos está relacionada con la mayor imprecisión (1- Pmax /Rc = 0.02683); mientras que la solución exacta se obtiene a partir de contravientos modelados con ocho subelementos. Pese a esto, en la literatura es común encontrar investigaciones (Lacerte y Tremblay 2006; Terzic 2013; Tapia y Tena 2013; García y Tapia 2015) que han usado subdivisiones del contraviento entre 10 y 20 subelementos; la razón está fundamentada con el cálculo de las transformaciones geométricas de los desplazamientos.
Las curvas de capacidad son sensibles al criterio para la transformación de los desplazamientos que están disponibles en los programas de análisis no lineal. Esto es, en los programas como OpenSees (Mazzoni et al. 2006), los desplazamientos en ejes globales se calculan a través de una transformación geométrica de las condiciones locales que usualmente puede ser a) lineal, b) con efectos P-Δ y c) corrotacional (por ejemplo, en los análisis de la Figura 4 se usó una transformación corrotacional). La transformación P- Δ actualiza en cada paso los desplazamientos de los grados de libertad del nodo extremo del elemento; mientras que la transformación corrotacional, además actualiza en cada paso la orientación del eje local del elemento ante la aplicación de la carga lo que teóricamente proporciona resultados más precisos.
Denavit y Hajjar (2013) desarrollaron un estudio comparativo de la determinación de los desplazamientos en ejes globales a partir de análisis no lineales con carga estática monótona creciente de contravientos sometidos a carga axial usando tres tipos de transformaciones geométricas en un elemento biarticulado de 152 cm de longitud. Los resultados se muestran en la Figura 5 en escala logarítmica en función de la carga crítica de Euler Pcr para contravientos conformados desde 2 hasta 100 subelementos. Con base en los resultados, la estimación correcta de la capacidad de pandeo se obtiene con un mínimo de 10 elementos que está asociado a un porcentaje de error P/Rcr -1= 0.09% y se nota poca o nula diferencia entre los dos tipos de transformaciones consideradas cuando el estudio centra su atención en análisis estáticos crecientes.
Ciclos histeréticos
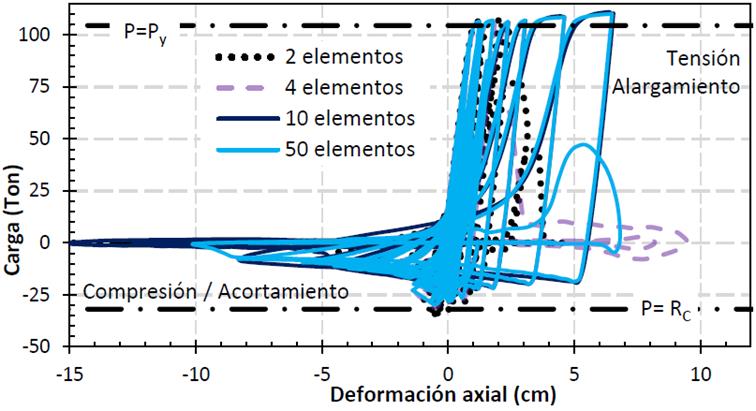
En la Figura 6 se muestran los resultados sobre la influencia de la cantidad de subelementos en el comportamiento de los ciclos histeréticos de un contraviento. El elemento analizado tiene sección cajón cuadrada OR 15.2 cm ( 1.27 cm con una longitud no arriostrada de 453 cm y una relación de esbeltez kL/r igual a 128.4 con apoyo articulados y cinco puntos de integración.
Con base en los resultados (Figura 6), se nota que la cantidad de subelementos tiene poca influencia en la modelación de la carga de pandeo en el primer ciclo de carga. Sin embargo, en los ciclos subsecuentes, los modelos con pocas subdivisiones tienen diferencias en la deformación significativas. De hecho, Salawdeh y Goggins (2013) encontraron que son necesarios al menos ocho subelementos para describir satisfactoriamente el comportamiento no lineal del contraviento en ciclos posteriores al pandeo e identificaron que un incremento de la cantidad de puntos de integración facilita el proceso de modelado y disminuye el esfuerzo computacional.
Así, la cantidad de subelementos necesarios depende del objetivo del análisis: ocho elementos son suficientes para modelar correctamente la capacidad de pandeo, pero es necesario considerar al menos diez si se desea modelar correctamente la respuesta inelástica en ciclos histeréticos en contravientos dúctiles.
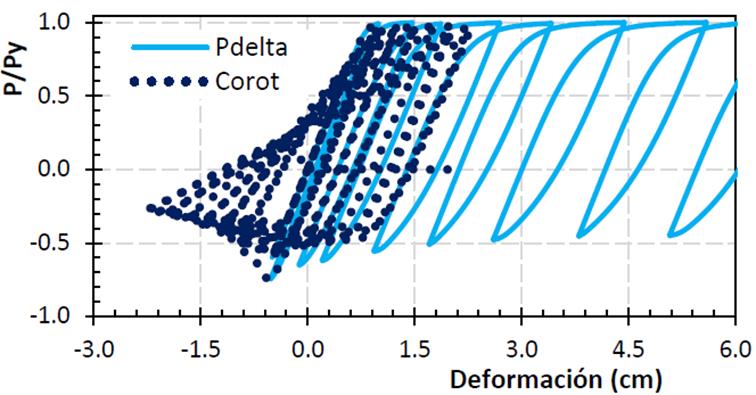
Es valioso hacer notar que en análisis dinámicos cuando se usa una transformación geométrica con efectos P-delta, es posible que los elementos reporten ciclos histeréticos estables asociados a deformaciones que difícilmente se pueden reproducir en la realidad. Con el propósito de ampliar la información, en la Figura 7 se muestra el comportamiento de la carga axial P normalizada con la carga de fluencia por tensión Py (=AFy ) y la deformación axial (acortamiento o alargamiento). Los resultados se basan en la respuesta dinámica de un contraviento con relación de esbeltez kL/r= 63 de sección cajón, subdividido en veinte elementos, sin endurecimiento por deformación y diez puntos de integración. Note que las respuestas entre la transformación P-delta y la transformación corrotacional son similares cuando se pretende estudiar los primeros ciclos inelásticos; sin embargo, en ciclos superiores los resultados con modelos con transformación con desplazamientos pequeños (P-delta) podrían estar relacionados con un colapso matemático; es decir, aunque el programa es capaz de armar la matriz de rigideces (el determinante es diferente de cero), los resultados no están asociados con un fenómeno físicamente posible.
Deformación inicial en el centro del Claro
Los perfiles de acero estructural no son perfectamente rectos debido al proceso de fabricación, transporte, almacenaje y montaje. La deformación máxima permisible al centro de la longitud no arriostrada L en los manuales especializados es igual a δ i = L/1000= 0.001L (AISC-303-10 2010; IMCA 2014) y se modelan con una configuración deformada en forma parabólica, usualmente.
En la Figura 8a se muestra el comportamiento de un contraviento de sección cajón cuadrada OR 25.4 cm ( 0.635 cm con una relación de esbeltez kL/r= 83 bajo un análisis no lineal ante carga estática en compresión monótona creciente. En los análisis se consideraron modelos con deformaciones iniciales δi en el centro del claro en función de la longitud del contraviento desde δi = L/∞→0.0 hasta δi = L/200= 0.005L.
Con base en los resultados, cuando los modelos no consideran una deformación inicial δi, la carga máxima resistente del elemento tiende a la fuerza axial que ocasiona la plastificación del contraviento (P→Py= AFy). Esto implica que los programas de análisis no lineal usualmente son incapaces de identificar el pandeo elástico por compresión, tal que debe ser incluido en el modelo a través de una deformación inicial δi que propicie la inestabilidad. Sin embargo, la deformación inicial (δi = L/w) debe limitarse para evitar que la capacidad del contraviento en compresión se subestime como ocurre en el modelo con δi = L/200 (Figura 8a). De hecho, es concluyente que la magnitud de la deformación inicial δi es un parámetro que gobierna la predicción numérica de la capacidad de los contravientos y, por consiguiente de toda la estructura.
Además, nótese que la magnitud de la deformación inicial δi que está asociada con una representación adecuada de la capacidad de carga teórica en compresión del contraviento Rc no puede generalizarse para todos los contravientos, puesto que es función de la relación de esbeltez kL/r como se nota en la fFigura 8b. Cuando la relación de esbeltez es pequeña en contravientos robustos (kL/r= 32.98), la capacidad tiende a la carga de pandeo teórica (P→Rc) en un intervalo más grande de deformaciones iniciales δi. Sin embargo, cuando el contraviento es esbelto con relaciones de esbeltez más grandes (kL/r= 83.5), la carga modelada tiende a la carga de pandeo P→Rc sólo cuando la deformación inicial es lo suficientemente grande.
Algunos autores (Dicleli y Calik 2008; D'Aniello et al. 2015) han intentado establecer intervalos de la magnitud de la deformación inicial δi que estiman adecuadamente la capacidad de elementos sometidos en compresión, con base en correlaciones entre la capacidad teórica estimada y su comportamiento físico en pruebas experimentales. Los resultados se basan en modelos de elementos articulados en sus extremos únicamente y concluyen que la deformación inicial δi afecta mayormente la demanda de distorsión y el mecanismo de colapso a estructuras con marcos con contravientos en configuración chevrón, lo que afecta a marcos con contravientos en cruz.
Específicamente, la propuesta de Dicleli y Calik (2008) establece un método para determinar analíticamente la deformación de pandeo δb para considerarla en el desarrollo del modelo; de manera que la deformación inicial se debe definir en el intervalo 0< δi < δb. La fórmula (ecuación 1) se obtiene a través del método de carga ficticia, donde se considera que la configuración deformada del contraviento se aproxima a una función sinusoidal. A partir de esto, la ecuación se integra para la mitad del claro y=L/2 cuando la carga axial tiende a la carga de pandeo (P→Rc ).
En la ecuación 1, Rc es la carga a compresión de pandeo (Figura 1), E es el módulo de elasticidad del material, I es el momento de inercia en la dirección del pandeo, δb es la deformación en el centro del claro relacionada con la carga Rc y e una excentricidad en la aplicación de la carga P. Así, en la Figura 9 se muestra el intervalo sugerido para la identificación de deformaciones, que tiene una alta dependencia de la relación de esbeltez de los contravientos kL/r. Los contravientos robustos se pandean con una magnitud pequeña de deformación en el centro del claro, por lo que la incertidumbre en la definición de la deformación inicial δi es menor como se había demostrado anteriormente (Figura 8b). Sin embargo, el intervalo aumenta con el incremento de la relación de esbeltez kL/r.
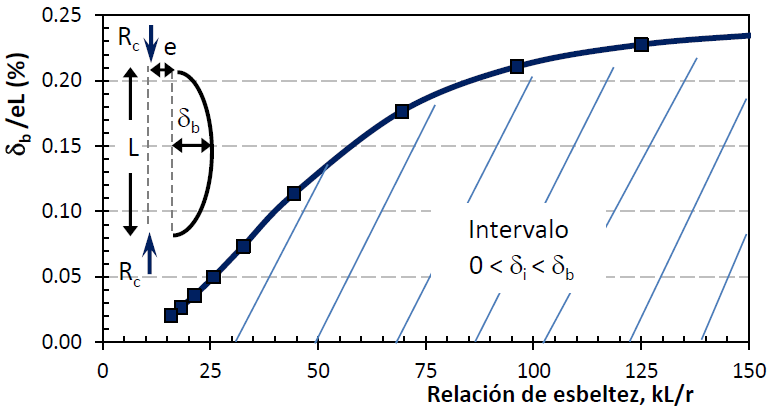
Figura 9 Evaluación del intervalo de deformación inicial δi con la ecuación de Dicleli y Calik (2008)
Ciclos histeréticos
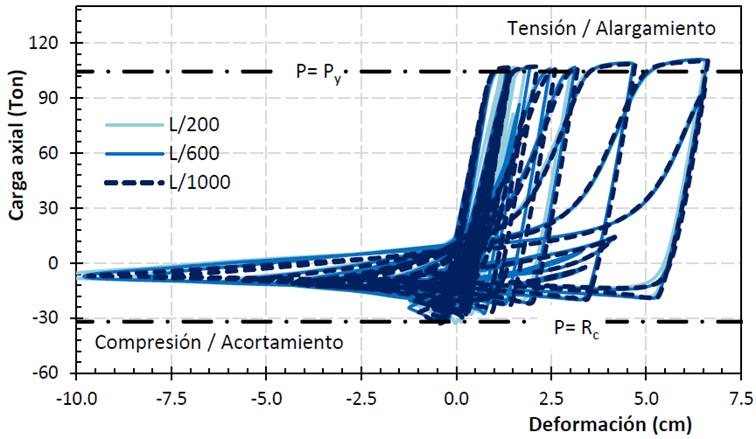
En la Figura 10 se muestran los resultados carga axial contra deformación axial (acortamiento ó alargamiento) de análisis dinámicos no lineales de contravientos (Figura 3), que fueron modelados para distintas magnitudes de la deformación inicial δi en función de la longitud no arriostrada L del contraviento (δ i= L/w). En los análisis se nota poca influencia sobre la magnitud de la deformación inicial δi en los primeros ciclos (Figura 10); pese a esto, algunos autores han señalado que en análisis dinámicos la imperfección inicial modelada δi afecta la demanda de distorsión, el mecanismo de colapso y tiene impacto en los parámetros de respuesta sísmica (Uriz et al. 2008; D'Aniello et al. 2015).
La influencia de la deformación inicial δi puede ser significativa en los ciclos posteriores al pandeo dependiendo de la relación de esbeltez kL/r (Terzic 2013). Igualmente, en análisis dinámicos cuando no se modela una deformación inicial (δi →0), la carga axial tiende a la carga de plastificación, la que a su vez tiende a la carga de fluencia por tensión (P→Py= AFy), como ocurre en los análisis estáticos no lineales (Figura 8a).
Discretización de la sección transveresal
Estudios recientes (Izvernari 2007; Rozon et al. 2008; Tapia y Tena 2011; Chen y Tirca 2013) han hecho notar la trascendencia de la discretización de fibras de los contravientos en la respuesta inelástica de los modelos (Figura 11). La discretización de la sección transversal permite modelar la plastificación progresiva de la sección transversal a lo largo de los análisis inelásticos. Sin embargo, una mayor cantidad de fibras está relacionada con un mayor tiempo y trabajo de cómputo.
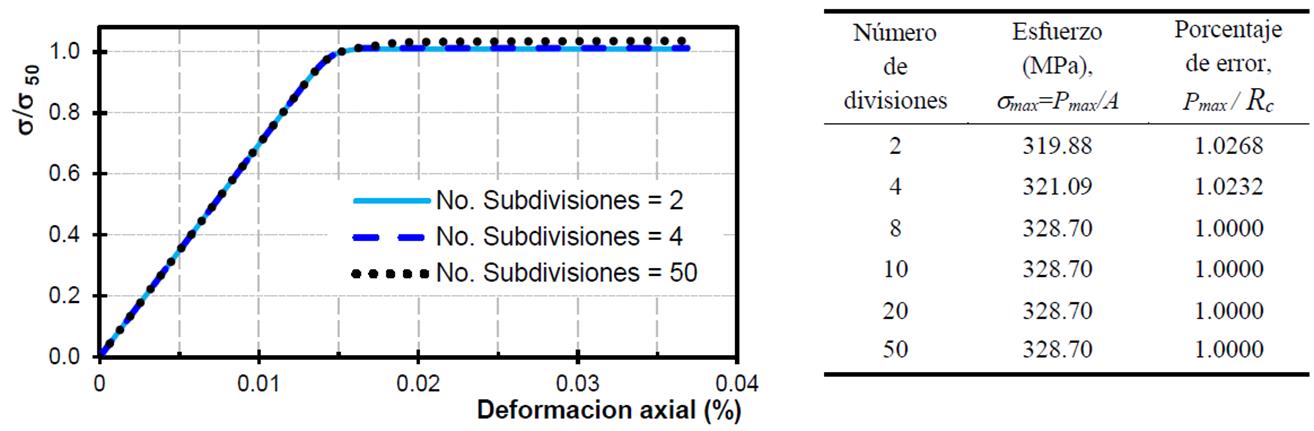
Con el propósito de hacer notar la influencia de la discretización con fibras, se realizó un análisis ante carga axial en compresión estática monótona creciente en contravientos de sección transversal en cajón OR 254 mm ( 12.7 mm, una longitud no arriostrada de L= 360 cm y una relación de esbeltez kL/r= 52. En los análisis se modeló una transformación geométrica corrotacional y se usó como variable la cantidad de fibras que conforman la sección transversal del elemento (Figura 11).
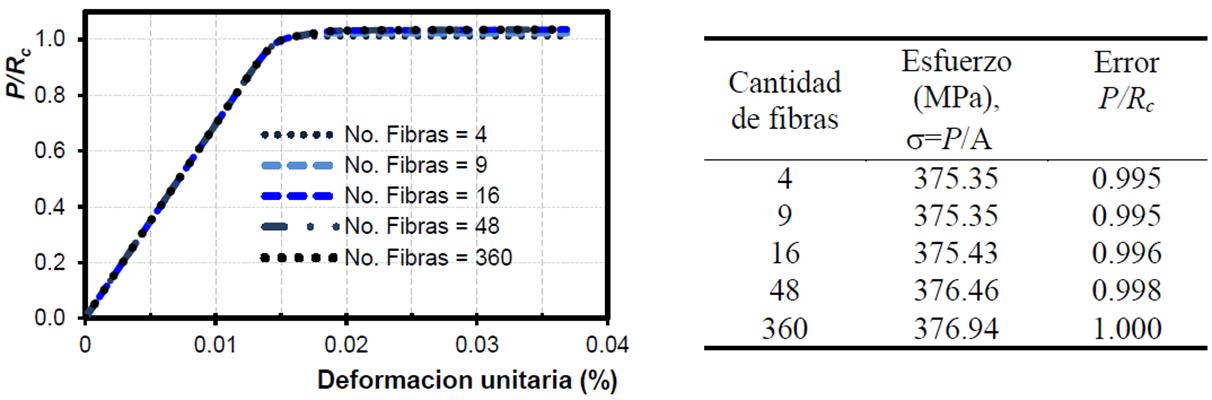
En la Figura 12 se muestran las curvas esfuerzo - deformación unitaria ε, donde la carga axial P está normalizada con la capacidad teórica en compresión Rc . Aunque los resultados reportan pocas diferencias, el contraviento modelado con cuatro fibras está relacionado con el mayor porcentaje de error (0.50%). Los resultados convergen a la capacidad objetivo cuando se modelan placas con al menos cuatro fibras por lado (modelo con 16 fibras). Este resultado coincide con criterios considerados en algunas investigaciones recientes (Lacerte y Tremblay 2006; Izvernari 2007; Tapia y Tena 2011).
En general, el modelo de la discretización de fibras no afecta la respuesta global de estructuras con contravientos (Izvernari 2007; Chen y Tirca 2013; García y Tapia 2015), por lo que no amerita usar el tiempo de cómputo en un detallado exhaustivo de la sección transversal.
Condiciones de apoyo en los extremos
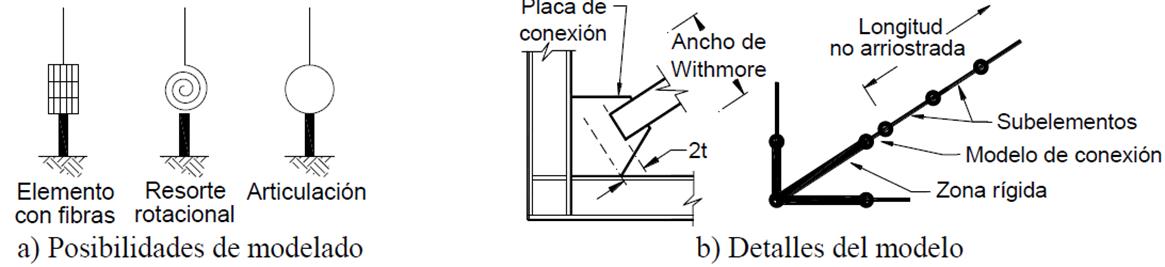
Investigaciones recientes como Rozon et al. (2008), Chen y Tirca (2013), Tapia y Tena (2013) y García (2015) han desarrollado modelos complejos usando una conexión en los extremos del contraviento con resortes rotacionales. En los programas de análisis no lineal, el modelado de las placas puede realizarse en tres formas (Figura13a):
Mediante resortes rotacionales como una representación de la rigidez de la placa.
Con elementos de longitud finita con una sección transversal modelada con fibras.
Usando una articulación en los extremos.
Algunos investigadores (Tapia y Tena 2013; Wijesundara et al. 2014), que estudiaron la influencia de usar apoyos modelados con elementos fibra, recomiendan usar elementos con una longitud de dos veces el espesor de la placa (Figura 13b), con el propósito de tomar en cuenta la posibilidad de que la articulación plástica se desarrolle en la placa de conexión. Terzic (2013) demuestra que el modelo de conexiones con elementos fibra y resortes rotacionales determinan con precisión la capacidad de los contravientos; sin embargo, hace notar que los modelos con elementos fibra tienen la ventaja de ser más fáciles de modelar.
Con excepción del modelado de la placa de conexión con una articulación, los modelos (elementos fibra y resortes) pueden conectarse por medio de un elemento de longitud-cero (ZeroLength), el cual debe contener las propiedades mecánicas de la placa de conexión (Figura 13b).
La relación entre la rigidez a flexión del contraviento KC y la rigidez de la placa de conexión Kr se suele determinar usando las ecuaciones 2 y 3 (Hsiao et al. 2012), lo que permite estimar el factor de longitud efectiva k (ecuación 4) cuando se modelan conexiones semi-rígidas mediante resortes.
En las ecuaciones 2 a 4, E es el módulo de elasticidad; IC y L es el momento de inercia y la longitud no arriostrada del contraviento; IPL y Lprom son el momento de inercia de la placa de conexión y la longitud promedio en la sección de Whitmore. Es posible conocer más información sobre la sección de Whitmore en placas de conexión de contravientos de acero en Tapia y Tena (2013); García (2015) y Del Rincón (2016). El parámetro µ es una variable que se determinó empíricamente de un conjunto de pruebas experimentales, que puede tomar magnitudes entre 0.5( y ( se determina como sigue:
En la Figura 14 se muestra una representación esquemática del modelo de contraviento, donde las opciones de modelado de la conexión discutidas permiten modelar el pandeo del contraviento en el plano o fuera del plano de la placa de conexión y considerar la posibilidad de que se desarrollen articulaciones plásticas en el contraviento y/o en la placa de conexión.
Rigidez de la placa de conexión
Estudios experimentales recientes sobre la capacidad de pandeo de elementos de acero sometidos a carga axial han demostrado que las longitudes teóricas kL que deben relacionarse con la determinación de la capacidad de los elementos son menores que las que actualmente se usan en la práctica. Lo anterior se debe a que, en contravientos concéntricos, la restricción del contraviento adyacente en tensión aumenta la rigidez de la conexión del contraviento en compresión (Metelli 2013). Otros estudios (Jankowska-Sandberg y Kolodziej 2013; Da Silva et al. 2005) explican la disminución de la longitud (estabilidad del contraviento) al hecho que la placa de conexión se aproxima más a una conexión semi-rígida, en lugar de la articulación que se asume usualmente. Estas fuentes de capacidad adicionales, no están actualmente incluidas en los reglamentos y son usualmente ignoradas en el análisis estructural de la capacidad de los contravientos.
Aquí, la influencia de la rigidez de la placa de conexión Kr en la capacidad del sistema de contravientos se estudió como una función de la deformación máxima en el centro del claro v (Figura 15a). El modelo de una conexión con una rigidez muy alta (Kr →∞) representa el caso de un apoyo empotrado (conexión rígida), mientras que el modelo de una conexión sin rigidez (Kr = 0) representa el caso de un apoyo articulado. Así que el intervalo de rigidez 0< Kr <∞ representa el universo de conexiones semi-rígidas que podrían diseñarse.
Siguiendo este razonamiento, se realizaron análisis inelásticos a dos modelos de contravientos con una relación de esbeltez kL/r igual a 65 y 77, respectivamente. Los modelos se analizaron ante una carga axial en compresión estática monótona creciente, considerando las condiciones extremas de rigidez de la placa de conexión discutidas anteriormente (Kr →∞ y Kr = 0). La Figura 15b muestra las curvas de capacidad, donde la carga axial se normalizó con la resistencia de la conexión articulada Rc Art contra la deformación unitaria (. En los análisis se determinó la deformación máxima δb (deformación de pandeo) en el centro de la longitud no arriostrada (y= L/2) que se desarrolló a lo largo del análisis con el propósito de identificar la condición de estabilidad de los modelos.
Así, en la Figura 15c se muestra la influencia de la rigidez de la placa de conexión de los contravientos Kr en la capacidad axial del elemento en función de la máxima δb en el centro de la longitud no arriostrada (y= L/2). Con base en los resultados, la condición modelada como articulación Kr = 0 representa el límite de inestabilidad. De manera que, a pesar de que existe un amplio intervalo de posibles conexiones semi-rígidas (0< Kr <∞) que podrían guiar a una respuesta diferente, el modelo con la conexión articulada representa la condición más crítica físicamente posible.
Influencia del tipo de conexión en los ciclos histeréticos
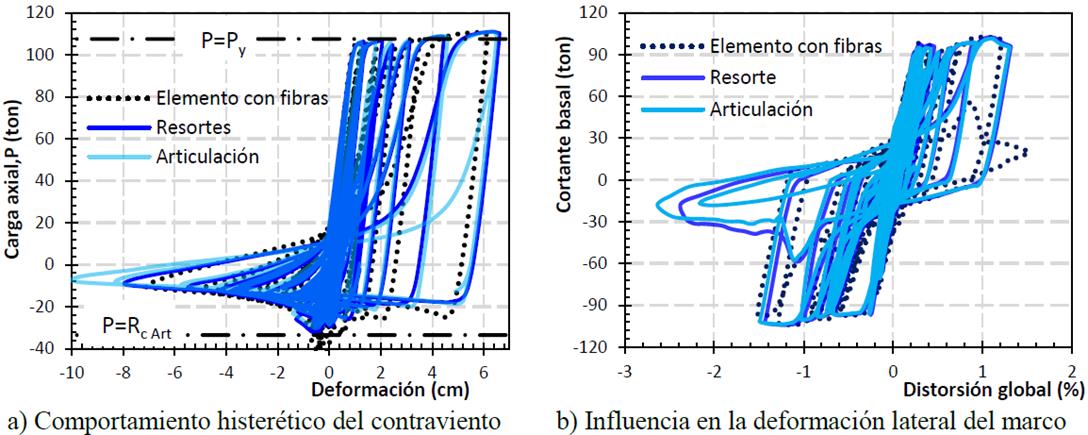
En la Figura 16 se muestra el comportamiento del contraviento (Figura 3) en análisis dinámicos no lineales cuando se estudia la influencia del modelado del apoyo. Los contravientos estudiados están divididos en diez subelementos, con las mismas condiciones de modelado en la zona rígida, una transformación corrotacional y una deformación inicial igual a δi = L/500= 0.002L.
En las curvas de histéresis (Figura 16a), la capacidad teórica del contraviento en compresión se calculó usando un factor de longitud efectiva k igual a 1.0, aplicable al modelo con articulaciones Rc Art . Por esta razón, la capacidad del modelo con resortes y elemento con fibras sobrepasa la resistencia a compresión Rc Art , especialmente cuando la conexión se modela con un elemento con fibras; debido a que el factor de longitud efectiva para esas condiciones es menor a uno (k<1.0).
Pese a que la deformación post-pandeo del contraviento con conexión articulada es más grande, en general, la respuesta y cantidad de ciclos no se ve influenciada por el tipo de conexión modelada (Figura 16a). Sin embargo, cuando se evalúa la influencia del tipo de conexión en la rigidez lateral del marco (Figura 16b), la conexión modelada mediante un elemento con fibras desarrolla ciclos más estables con una magnitud de distorsión menor. Este resultado es relevante cuando los modelos se usan en análisis que pretenden establecer la capacidad lateral de los edificios, puesto que los modelos con articulaciones (y resortes) podrían relacionarse con demandas laterales que no forzosamente desarrollarían la estructura en realidad.
Propiedades del material
En el programa de análisis no lineal considerado (Mazzoni et al. 2006), el modelo del material considera los efectos de ciclos de fatiga acumulando el daño en el elemento a partir de las amplitudes de la deformación unitaria. La acumulación de la deformación en cada ciclo utiliza un modelo lineal usando relaciones que describen la falla por fatiga. Entonces, el modelo de fatiga del material envuelve al modelo del material fuente sin afectar su relación esfuerzo - deformación. Una vez que el modelo del material con fatiga alcanza un nivel de daño igual a 1.0, la fuerza (o esfuerzo) del material fuente tiende a cero. La magnitud de los parámetros por defecto en OpenSees se calibró en el programa mediante los resultados de pruebas experimentales de fatiga en perfiles de acero europeos como se discute en Uriz (2005).
En la Figura 17 se muestran los resultados de un estudio comparativo de la respuesta del contraviento (Figura 3) en función del tipo de conexión modelada. Como se comentó antes, los contravientos cuyas conexiones son modeladas mediante elementos más rígidos son capaces de desarrollar una carga axial de pandeo que supera la carga teórica calculada con un factor de longitud efectiva k= 1.0 que corresponde al modelo del contraviento biarticulado (Rc Art ).
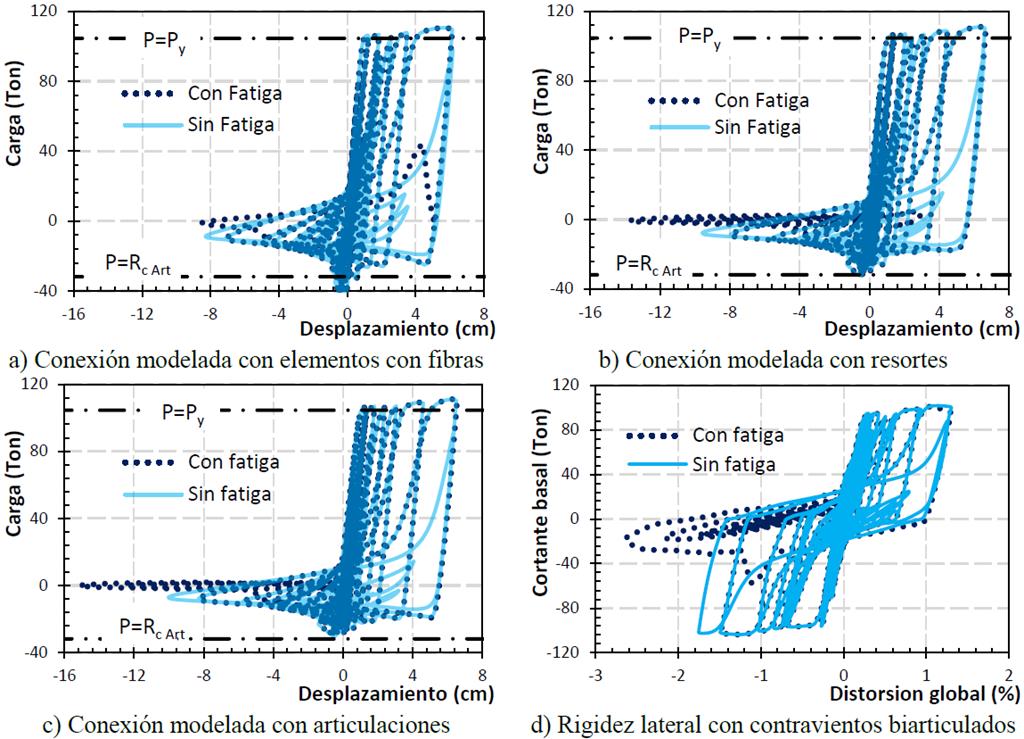
Figura 17 Influencia de la fatiga en los ciclos histeréticos en función del tipo de conexión modelada.
Con base en los resultados (Figura 17a, 17b y 17c), la mayoría de los ciclos histeréticos de los contravientos son significativamente similares independientemente del tipo de conexión modelada. Hacia el final de los análisis, los modelos con fatiga en el material son incapaces de desarrollar ciclos adicionales estables y están relacionados con deformaciones por acortamiento mucho más grandes que los elementos sin modelos de fatiga del material. Además, se hace notar que la fatiga tiene poca o nula influencia en los contravientos que tienen conexiones modeladas mediante un elemento con fibras.
En la Figura 17d se muestra el comportamiento del cortante basal contra distorsión global del marco con contravientos biarticulados. En ella, se aprecia que el incremento de la deformación axial en los últimos ciclos del contraviento (Figura 17c) modifica significativamente el desplazamiento lateral máximo que desarrolla el marco. Este resultado es relevante cuando los modelos se usan para evaluar la capacidad de desplazamiento de las estructuras (ductilidad, límites de distorsión, rotaciones, etc.), puesto que los marcos con contravientos biarticulados desarrollaran deformaciones laterales significativamente mayores, que los modelados con elementos con fibras.
Endurecimiento por deformación
En el intervalo inelástico a nivel microscópico, los elementos de acero sometidos a una deformación plástica desarrollan dislocaciones en el material. De manera que la resistencia del material a la formación y movimiento de las dislocaciones en el intervalo inelástico se manifiesta a nivel macroscópico como un incremento en la resistencia (FEMA 355A 2000). Así, la magnitud de la plastificación por fluencia en tensión en ciclos posteriores al pandeo podría ser mayor a la que se desarrolla en los primeros ciclos.
En los programas de análisis, en la definición de la curva esfuerzo - deformación, la pendiente Esh que establece el incremento de resistencia por el endurecimiento por deformación se define mediante el módulo de elasticidad del intervalo elástico E afectado por una variable b (Esh= bE).
En FEMA 355A (2000) se muestran los resultados de una investigación experimental que pretende establecer una referencia del parámetro b= Esh/E basados en perfiles laminados. Con base en los resultados de las 38 probetas, la magnitud promedio bprom recomendada es igual a 0.0131; el límite inferior resultó ser igual a bmín = 0.0075 y el límite superior fue bmax = 0.0165.
El intervalo de magnitudes propuestas en investigaciones recientes para este parámetro b es bastante amplio. Algunas investigaciones como Terzic (2013); García y Tapia (2014) han usado factores conservadores igual a 0.003. En otros casos, investigaciones como Lacerte y Tremblay (2006) y Izvernari (2007) han desarrollado sus estudios usando magnitudes similares a las recomendadas en FEMA 355A (2000) igual a 0.01. Mientras que en otros casos, como Tapia y Tena (2011, 2013) se usó una magnitud significativamente mayor (b= 0.03) para considerar indirectamente la sobrerresistencia del material (Ry= Fy real/Fy teórico >1.0), que se discutirá más adelante.
En este estudio, se evaluó la influencia del endurecimiento por deformación, a través de la variable b, en el marco estudiado (Figura 3). Los resultados indican que el endurecimiento por deformación tiene una influencia proporcional a la magnitud de la variable b, especialmente en los últimos ciclos en tensión cuando se estudia la respuesta del elemento aisladamente (Figura 18a) y también cuando se evalúa la rigidez lateral del marco (Figura 18b). El modelo con un menor endurecimiento por deformación b= 0.001 desarrolla la mayor deformación axial, puesto que tiene una menor capacidad en los últimos ciclos (Figura 18a); esto ocasiona que el marco en su conjunto desarrolle un mayor desplazamiento lateral. En contraparte, el modelo con b= 0.03 tiene ciclos más estables, pero representa un escenario poco conservador de la respuesta del material. Con el propósito de evitar sobreestimar la resistencia, se sugiere limitar la influencia del endurecimiento a magnitudes conservadoras en el intervalo 0.001 < b < 0.01.
Influencia de los puntos de integración
En los programas de análisis para determinar las fuerzas internas de los contravientos es necesario definir un número de puntos de integración a través del elemento. Los puntos de integración establecen la integración numérica para representar la distribución de la plasticidad a través del dominio de todo el elemento [0, L]. Algunos estudios (Uriz 2005) han demostrado que la cantidad de puntos tiene poca influencia en el comportamiento histerético de los contravientos y que tres puntos de integración son suficientes para simular adecuadamente la respuesta inelástica.
En contraparte, otros estudios (Wijesundara et al. 2014; D'Aniello et al. 2015) han hecho notar una aparente similitud en el efecto que ocasiona la cantidad de puntos de integración y los subelementos que conforman el contraviento en la estimación de la carga resistente en compresión. De hecho, Salawdeh y Goggins (2013) demostraron proporciones de estas variables mediante las que es posible obtener respuestas inelásticas equivalentes. De manera que un incremento en los puntos de integración modelados podría asociarse a una menor cantidad de subelementos para reproducir adecuadamente la capacidad del contraviento y viceversa.
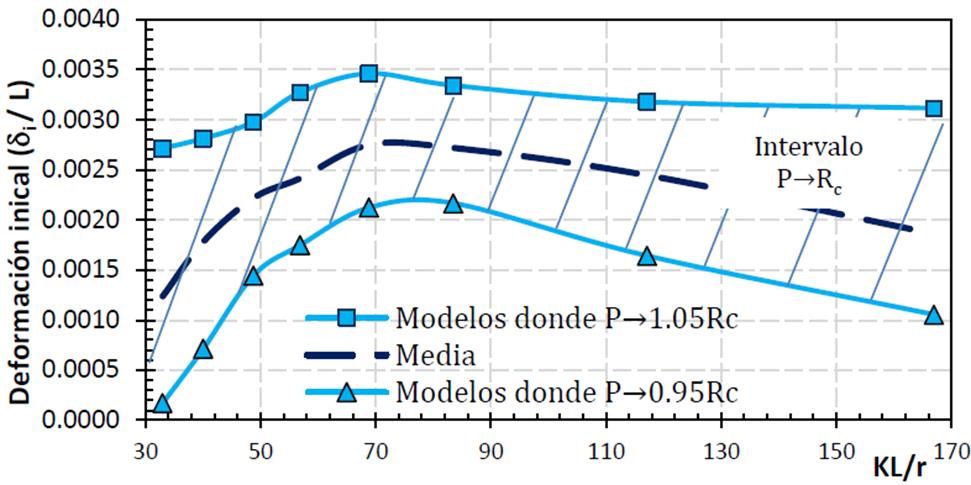
La trascendencia de lo anterior, radica en que los contravientos que sean modelados con una limitada cantidad de puntos de integración y que estén conformados por pocos subelementos podrían estar asociados con incongruencias físicas. Con el propósito de ampliar la discusión, en la Figura 19 se muestran los resultados de análisis no lineales ante carga estática monótona creciente en compresión de contravientos, donde se determinó la deformación inicial δi en el centro del claro que era necesaria para que la carga axial resistente del modelo se aproximara a la resistencia en compresión teórica (P→Rc ). Los resultados se muestran en función de la relación de esbeltez kL/r de los contravientos que fueron modelados con sólo cuatro subelementos con cinco puntos de integración cada uno. En la Figura 19 la deformación inicial (i se muestra normalizada con respecto a la longitud del elemento L y se identificó un intervalo con magnitudes recomendadas para la deformación inicial δi (0.95Rc < P < 1.05Rc).
Los resultados (Figura 19) denotan una tendencia que depende de la relación de esbeltez de los contravientos kL/r que había sido previamente identificada y discutida (Figura 8b y 9). Ahora, teniendo en consideración que la deformación permisible al centro de la longitud no arriostrada L con base en reglamentos especializados es igual a L/1000= 0.001L (AISC 360-10 2010; IMCA 2014), implica que los modelos de los contravientos requieren una deformación inicial δi mucho mayor a la permisible para estimar correctamente la capacidad en compresión, lo que es físicamente poco convencional. Este efecto no debe considerarse como una magnitud incorrecta de la deformación inicial δi, sino como la necesidad de mejorar el modelo mediante un incremento de la cantidad de puntos de integración y de los subelementos que conforman el contraviento.
Sobrerresistencia del material
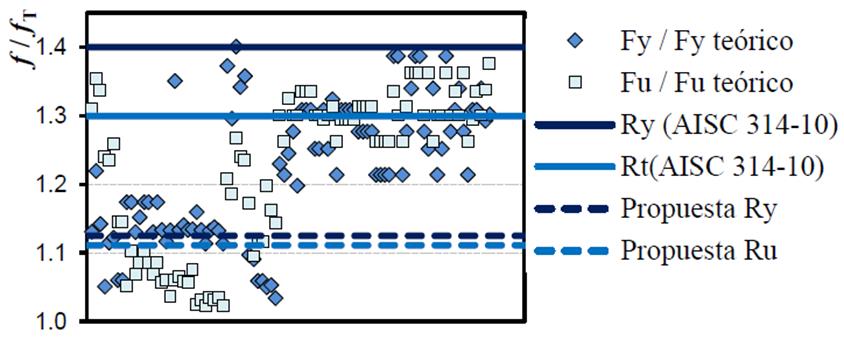
El material puede aportar una sobrerresistencia adicional por el efecto de la diferencia que hay entre el esfuerzo teórico y el esfuerzo que realmente alcanza el acero. En las previsiones sísmicas AISC 341-10 (2010), los esfuerzos se modifican a través de los factores Ry y Rt (Tabla 1), que fueron obtenidos de ensayes a perfiles laminados y placas de diferentes tipos y grados de acero. Sin embargo, las condiciones del mercado de estructuras metálicas no es equivalente de un país a otro, por lo que aplicar los factores del AISC 341-10 (2010) en las condiciones locales podría guiar a resultados poco conservadores.
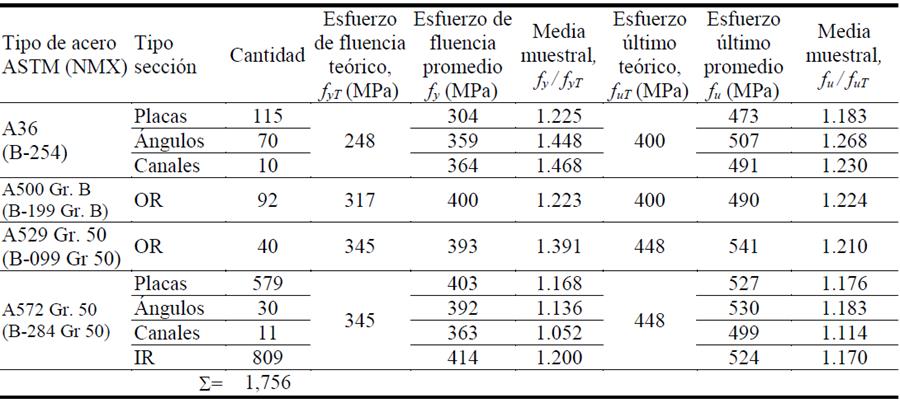
Tabla 1 Magnitudes de Ry y Rt de acuerdo con el AISC 341-10 (2010) y las propuestas de este estudio.
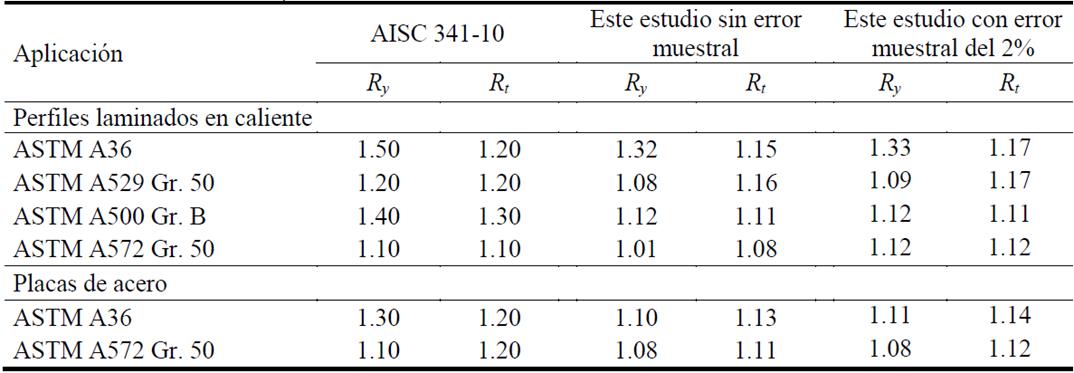
Por esto, se realizó un estudio estadístico sobre los esfuerzos de fluencia y último de perfiles laminados (sección IR, ángulos y canales) y placas de acero reportados en 1,756 certificados de calidad de laboratorios de fabricantes de aceros nacionales e importados con el propósito de desarrollar una estimación conservadora de la sobrerresistencia del material en México. El estudio considera varios tipos de tipos de acero (A36; A500 Gr. 50; A529 Gr 50; A572 Gr. 50), donde se distingue entre los resultados de perfiles laminados y los resultados de placas de acero para incluir los casos cuando el contraviento se forma con placas soldadas.
En el estudio, el 68% de los perfiles fueron de fabricación nacional (Gerdau, Altos hornos de México, entre otros) y el 32% fueron de fabricación extranjera (Alemania, Corea, España, Estados Unidos y Ucrania). La media muestral de la proporción de los esfuerzos de fluencia y último resultó ser igual a fy /fu = 0.805 para aceros de fabricación nacional e igual a fy /fu = 0.775 para aceros importados; en otras palabras la calidad de los perfiles no tiene dependencia del país de procedencia. Otros detalles sobre los pormenores del estudio y la influencia del país de origen pueden ser consultados en García y Tapia (2014)) y García (2015).
Características de la muestra
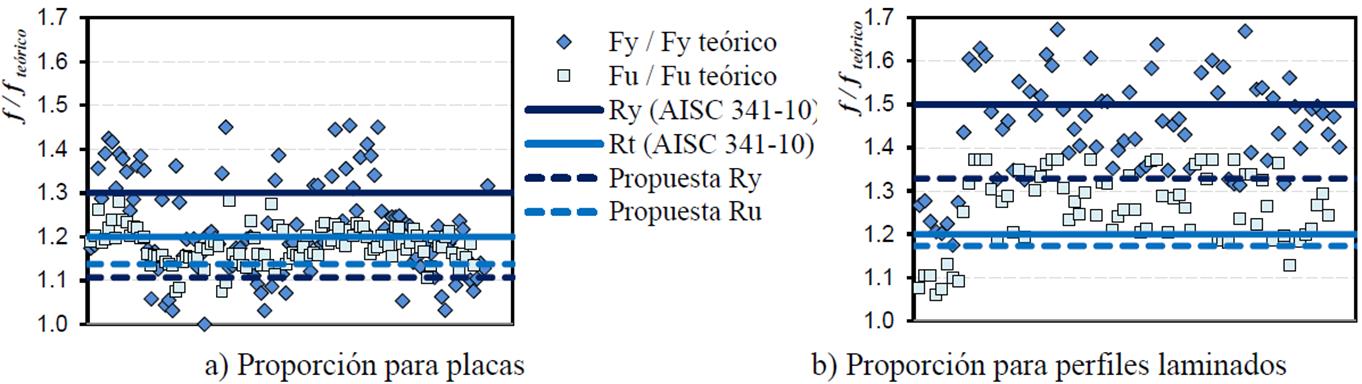
El acero tipo ASTM A36 (NMX B-264) está disponible en México en placas y perfiles laminados en caliente: ángulos, canales, perfiles IR y redondos (IMCA 2014). Sin embargo, su demanda está disminuyendo, puesto que los constructores y diseñadores en México prefieren usar perfiles y placas que soporten mayores esfuerzos para reducir el costo de la estructuras. De los 195 ensayes de procedencia nacional, 115 corresponden a certificados de placas de acero con espesores de 0.625 mm (0.25") hasta 63.5 mm (2.5"); 70 son certificados de perfiles tipo ángulo que van desde LI 1 1/2" ( 1/8" hasta LI 6" ( 1/2" y diez son certificados de canales de peraltes desde CE 3" hasta CE 6". En la Figura 20 se muestran los esfuerzos de fluencia y último de los certificados normalizados con los esfuerzos de fluencia y último teórico, donde se han incluido la magnitud propuesta del AISC 341-10 (2010).
El acero tipo ASTM A500 es comúnmente especificado para perfiles laminados en frío tubulares circulares o rectangulares como contravientos en México (IMCA 2014). Tiene cuatro grados basados en su composición química, resistencia a la tensión y tratamiento térmico, donde el más usado con fines estructurales es el ASTM A500 Gr. B (NMX B-199 grado B). Aquí se consideraron 92 certificados de laboratorio de secciones OR cuadrados y rectangulares, desde un OR 25.4 mm ( 25.4 mm ( 0.476 mm (HSS 1" ( 1" ( 0.1875") hasta un OR 406.4 mm ( 406.4 mm ( 12.7 mm (HSS 16" ( 16" ( 1/2"). La mayor parte de los certificados son de procedencia extranjera: China, Corea y Estados Unidos, siendo China con el mayor número de certificados; mientras que sólo el 35% son de fabricación nacional. En la Figura 21 se muestran los esfuerzos normalizados con los esfuerzos teóricos.
Por otra parte, el acero tipo ASTM A529 (NMX B-099 Gr. 50) puede ser usado en contravientos mediante ángulos, canales, perfiles IR y redondos. El análisis estadístico consideró 40 certificados para perfiles tipo ángulo que van desde LI 1 1/2" ( 1/8" hasta LI 4" ( 5/16". No fue posible tener acceso a muestras de procedencia extranjera, por lo que en este caso todos los certificados fueron de fabricación mexicana. En la Figura 22 se muestran los esfuerzos de fluencia y últimos de los certificados de perfiles laminados ASTM A529 grado 50 normalizados con el esfuerzo teórico.
Finalmente, se consideraron 1,429 ensayes de laboratorio de acero tipo ASTM A572 grado 50, el 78% corresponde a fabricantes de aceros nacionales (Gerdau y Altos Hornos de México, principalmente) y el 22% corresponde a fabricantes de acero provenientes de Alemania, China, Corea, España, Estados Unidos, Japón y Ucrania. De ellos, 579 corresponden a certificados de placas de acero con espesores de 0.305 mm (0.12") hasta 101.6 mm (4.0"). Treinta certificados son de perfiles tipo ángulo que van desde LI 1 1/4" ( 1/8" hasta LI 6" ( 1/2"; once certificados son de canales de peraltes desde CE 10" hasta CE 15" y, finalmente, 809 son certificados de perfiles tipo IR que van desde IR 102 mm ( 22.3 kg/m hasta IR 762 mm ( 147.4 kg/m. En la Figura 23 se muestran los esfuerzos de los certificados normalizados con los esfuerzos de fluencia y últimos teóricos parra placas y perfiles laminados. En el caso de perfiles laminados (Figura 23b) el criterio del AISC 341-10 para Ry y Rt tiene la misma magnitud. Este es el único caso (Figura 23) donde la magnitud de los esfuerzos de fluencia promedio coincide aproximadamente con la propuesta del AISC 341-10 (2010); sin embargo, esta tendencia no es conservadora si se analizan los esfuerzos últimos.
En la Tabla 2 se muestran los promedios de los esfuerzos de fluencia y esfuerzo último obtenidos del muestreo en función del tipo de acero y del tipo de sección. Así, el criterio del Manual AISC 341-10 (2010) no es conservador para todos los tipos de acero del mercado mexicano.
Desarrollo del estudio estadístico
A partir de lo anterior, se desarrolló un análisis que pretende establecer una magnitud conservadora de la sobrerresistencia del material mediante dos métodos: a) un escenario sin error muestral (nivel de confianza del 100 por ciento) y b) un escenario considerando por porcentaje de error muestral del 2 por ciento (nivel de confianza del 98 por ciento).
El valor característico µ obtenido del estudio (media muestral), que se mostró en la Tabla 1 y se graficó en las Figuras 20, 21, 22 y 23 se obtuvo considerando que se trata de un conjunto finito de magnitudes y partiendo del principio de la esperanza matemática o valor esperado sin error muestral. Su magnitud se calculó mediante la suma de todos sus valores dividida entre el número total de certificados n para cada tipo de acero (ecuación 6). En ella, Fi es la magnitud del esfuerzo (de fluencia ó último) recopilado de los certificados de calidad de laboratorio.
Ahora, se determinó la desviación estándar ( para considerar una medida de dispersión respecto a la media muestral µ con el propósito de desarrollar una propuesta conservadora y acorde a las tendencias actuales de los tipos de acero existentes en México. Esta desviación estándar, que es una medida estable muy usada en estadística, debe ser interpretada como una referencia de la incertidumbre en el modelo teórico. Ahora dado que en el estudio interesa realizar inferencias del muestreo, se consideró la corrección de Bessel (n/n-1) para corregir el posible sesgo estadístico en la estimación de la varianza mediante la ecuación 7.
Así, la propuesta de este estudio sugiere usar una magnitud del esfuerzo R como se propone en la ecuación 8. Esta propuesta para estimar los esfuerzos de fluencia y últimos se han incluido en las Figuras 20, 21, 22 a 23 y en la Tabla 1 para compararlo con la propuesta del manual AISC 341-10 (2010). En la Tabla 3, se muestran los pormenores para la determinación de las magnitudes propuestas cuando se consideró un error muestral igual a cero; es decir, considerando todos los módulos.
Aunado a lo anterior, con el propósito de asegurar que los valores sean representativos se recurrió a la eliminación de algunos datos que puedan generar errores. Esto se logra estableciendo un nivel de confianza para eliminar valores que pueden no ser representativos de la muestra (Bejamin y Cornell, 1970) de la cola inferior y superior de la distribución de probabilidades. El nivel de confianza (ecuación 9) se calculó con un nivel de significancia igual a α= 0.02.
Con el nivel de confianza propuesto, se determinaron las magnitudes máximas X*M y mínimas x*m probables de los esfuerzos de fluencia y último de los certificados normalizados con la magnitud teórica (ecuaciones 10 y 11), a partir de la distribución de probabilidades; es decir, se elimina un 2% de las colas inferior y superior de la distribución de probabilidad.
En las ecuaciones anteriores, Cx es el coeficiente de variación que determina la dispersión que puede tener una variable de un estudio estadístico y se define como el cociente de la desviación estándar y la media (ecuación 12).
En la Tabla 4 se muestran los resultados para la determinación del factor de sobrerresistencia del material usando un error muestral. Con base en los resultados (Tablas 3 y 4 ), considerar un error porcentual igual al 2% tiene una ligera influencia únicamente en los resultados del acero A572 Gr. 50. Esta observación implica que los resultados considerados en el estudio estadístico son una buena representación de las condiciones promedio del mercado.
Los factores obtenidos se incluyeron en la Tabla 1, donde se nota que el criterio del AISC 341-10 (2010) difiere al menos en un 10 por ciento, en prácticamente en todos los casos, independientemente si se trata de perfiles laminados ó placas laminadas.
Finalmente, es valioso hacer notar que la sobrerresistencia del material no es la única fuente de sobrerresistencia en estructuras acero (Mitchel et al. 2003; García y Tapia 2014), por lo que en el análisis de modelos complejos es útil incluir otras fuentes de sobrerresistencia.
Conclusiones
En este artículo se evalúa la influencia de parámetros que intervienen en el modelado de la respuesta inelástica de contravientos de acero. La formulación geométrica se evalúa mediante análisis estáticos y dinámicos no lineales con el propósito de: a) establecer las aproximaciones óptimas del modelado; b) estimar la influencia en la respuesta de la discretización de la sección transversal con fibras, del número de elementos y las imperfecciones geométricas iniciales; c) comparar la respuesta sísmica entre modelos de la placa de conexión y d) evaluar la influencia de la respuesta del material (fatiga y endurecimiento por deformación).
En los análisis estáticos no lineales, la capacidad del contraviento se estudió mediante una carga en compresión que se incrementó monótonamente; mientras que la respuesta en ciclos histeréticos de los contravientos se evaluó mediante análisis dinámicos a un marco de dos niveles, que se diseñó siguiendo criterios de capacidad. Las principales contribuciones de esta investigación son las siguientes:
La división de los contravientos en subelementos es una técnica que permite estimar correctamente la capacidad de pandeo e incluir la variación de la deformación. La cantidad de subelementos tiene poca influencia en la precisión cuando se evalúa la carga por pandeo en análisis estáticos no lineales y cuando se estudia el primer ciclo de carga en análisis dinámicos. Sin embargo, se recomienda usar al menos diez elementos si se pretende representar correctamente la respuesta histerética del contraviento en ciclos posteriores al pandeo.
Los programas de análisis no lineales son incapaces de identificar el pandeo elástico por compresión, por lo que se debe recurrir a modelar una deformación inicial δi al centro del claro para propiciar la inestabilidad. Una deformación inical δi pequeña ocasiona que la carga resistente tienda a la capacidad de fluencia por tensión (P→Py= AFy); mientras que una deformación δi grande subestima la capacidad a compresión (P<Rc). Así, la magnitud de la deformación inicial δi es un parámetro que gobierna la predicción numérica de la capacidad de los contravientos, por lo que se sugiere que su magnitud se limite al intervalo 0< δi < δb ; donde δb es la deformación teórica del pandeo. Además, se demostró que la magnitud de la deformación inicial δi que está asociada con una representación adecuada de la capacidad de carga teórica en compresión del contraviento Rc es función de su relación de esbeltez kL/r.
En el amplio intervalo de posibles conexiones de contravientos (0< Kr <∞), la conexión articulada representa la condición más crítica físicamente posible. El modelo de la placa de conexión no tiene una influencia concluyente en la respuesta de histéresis del contraviento como elemento aislado. Sin embargo, cuando se estudia la influencia del modelo de la conexión del contraviento en la respuesta global de un marco, el modelo con elementos con fibras desarrolla ciclos más estables con una magnitud de distorsión menor, lo que es relevante cuando los modelos se usan en análisis que pretenden evaluar la capacidad de rigidez lateral de los edificios.
Cuando se estudian modelos con fatiga del material, la mayoría de los ciclos histeréticos son similares independientemente del tipo de conexión modelada. En contravientos biarticulados, las deformaciones de los últimos ciclos son más grandes que la respuesta de contravientos con otros tipos de conexiones (resortes y elementos con fibras). Este resultado afecta los resultados de análisis, puesto que los marcos podrían relacionarse con desplazamientos laterales mucho mayores a las que es capaz de soportar una estructura en realidad.
Se demostró que el incremento de resistencia por endurecimiento por deformación tiene influencia en la respuesta de los ciclos de histéresis del contraviento. Se sugiere considerar la sobrerresistencia por endurecimiento por deformación en el intervalo 0.001< b <0.01.
Con base en los resultados de un estudio estadístico de certificados de calidad de laboratorio de varios tipos de acero se propuso un factor que estima la sobrerresistencia del material que varía entre l.01 hasta 1.33, que es función del tipo de acero y el perfil estructural.











 nueva página del texto (beta)
nueva página del texto (beta)