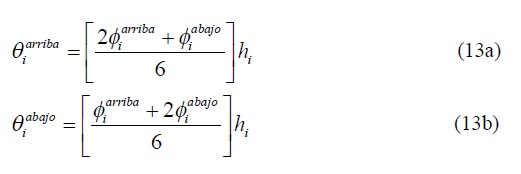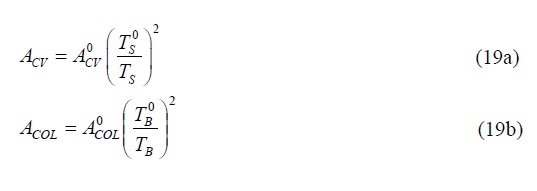Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería sísmica
versión impresa ISSN 0185-092X
Ing. sísm no.90 Ciudad de México ene./jun. 2014
Artículos
Dimensionado preliminar basado en rigidez de edificios altos con estructura de acero rigidizados con diagonales concéntricas*
Stiffness-based preliminary sizing of tall buildings having a steel structure with concentric braces
Amador Terán Gilmore1, Guillermo Coeto Galaz2
1 Profesor, Departamento de Materiales, Universidad Autónoma Metropolitana, Av. San Pablo 180, Col. Reynosa Tamaulipas, México, D.F., México, C.P. 02200. tga@correo.azc.uam.mx
2 Gerente Técnico, CoreBrace México, Tintoreto 92 Desp. 501, Col. Ciudad de los Deportes, México, D.F., México, C.P. 03710. +52(55) 5563-3783. guillermo.coeto@corebracemexico.com
Artículo recibido el 8 de enero de 2013.
Aprobado para su publicación el 24 de marzo de 2014.
Resumen
Se presenta una metodología para el dimensionado preliminar de un sistema resistente a sismos estructurado con base en marcos de acero rigidizados con diagonales concéntricas. La metodología aplica para el caso de edificios altos, cuya respuesta queda influida por componentes de deformación global en flexión y por el efecto de modos superiores de vibrar. Se presenta el dimensionado preliminar de los elementos estructurales de diferentes versiones de un sistema de contraventeo para un edificio de 24 pisos. A partir de la evaluación de las características dinámicas de las diferentes versiones del sistema de contraventeo, se concluye que la metodología propuesta conduce a un dimensionado adecuado durante el diseño preliminar basado en desempeño de edificios altos de acero contraventeados.
Palabras clave: dimensionado basado en rigidez; diseño basado en desplazamientos; sistemas de contraventeo; deformación lateral global en corte; deformación lateral global en flexión.
Abstract
A methodology for the preliminary sizing of an earthquake-resistant system composed of steel frames and concentric braces is discussed. The methodology applies to the case of tall buildings, whose dynamic response is influenced by global bending deformations and the effect of higher modes of vibration. The preliminary sizing of the structural members of different versions of a bracing system for a 24-story building is presented. From the evaluation of the dynamic characteristics of the different versions of the bracing system, it is concluded that the use of the proposed methodology yields an adequate sizing during the preliminary performance-based design of tall braced steel buildings.
Key words: stiffness-based design; displacement-based design; bracing system; global shear lateral deformation; global bending lateral deformation.
INTRODUCCIÓN
Algunos centros urbanos del mundo situados en zonas de alta sismicidad, como los ubicados en la costa oeste de los Estados Unidos y la Zona del Lago de la Ciudad de México, han visto un crecimiento importante en el número de sus edificios altos con estructura de acero. Conforme a lo discutido por Moehle (2008), los requisitos prescritos por los códigos actuales de diseño restringen de manera innecesaria el diseño de este tipo de edificios. Como consecuencia de esto, los ingenieros dedicados a la práctica de la ingeniería estructural han recurrido cada vez más al uso de metodologías de diseño basado en desempeño. Dentro de este contexto, se ha considerado que un diseño adecuado solo será posible a partir de: A) La definición correcta de los objetivos de desempeño; B) La selección adecuada de los registros sísmicos a usar; y C) El planteamiento y uso apropiado de modelos no lineales de análisis complementados por una interpretación juiciosa de sus resultados. Como consecuencia, la atención de los ingenieros estructurales empieza a enfocarse en el planteamiento de modelos no lineales con alto grado de refinamiento que les permita identificar las características de la respuesta dinámica del edificio alto, tal como los mecanismos de fluencia, las fuerzas internas asociadas y las demandas de deformación. Un posible problema dentro de este esquema consiste en caer en la tentación de usar modelos refinados de análisis para ajustar de manera iterativa el tamaño de los elementos estructurales de una propuesta estructural inicial mal concebida. Una solución preliminar deficiente puede fácilmente resultar en un diseño final limitado que quede lejos de representar una solución eficiente y confiable (incluso si dicho diseño satisface requisitos particulares de desempeño); de tal manera que la adecuada concepción complementada con un buen dimensionado preliminar de los elementos estructurales se constituye en una medida esencial para un diseño basado en desempeño.
El diseño estructural de edificios altos sujetos a carga lateral suele quedar regido por el control de distorsiones laterales. Con base en esta consideración, ha llegado a plantearse que la propiedad estructural más importante de este tipo de sistemas es su rigidez lateral (Park et al., 2002; Moon et al., 2007; Moon, 2008); y que los marcos rígidos por sí solos no son capaces de aportar la rigidez lateral necesaria para un adecuado control de desplazamientos. No es sorpresivo entonces que los marcos de los edificios altos hayan sido contraventeados para aportarles la rigidez lateral suficiente para controlar sus distorsiones laterales dentro de límites aceptables (Liang et al., 2000; Kameshki y Saka, 2001).
En las últimas dos décadas se han desarrollado varios métodos para el dimensionado de los elementos estructurales de los edificios altos con estructura de acero. La mayoría de estos tienen una naturaleza evolutiva o iterativa, de tal manera que una solución inicial se refina en búsqueda de una solución óptima que satisfaga una serie de restricciones planteadas en términos de distorsión y resistencia. En muchos casos, se usa un parámetro estructural o de desempeño para formular un problema de optimización que a menudo requiere de herramientas analíticas complejas y de una formulación cuidadosa de restricciones complementarias.
Inicialmente, los métodos de dimensionado para marcos contraventeados se orientaron a optimizar el peso y otros parámetros del sistema estructural (Baker, 1990; Chan y Grierson, 1993). Al paso del tiempo, se identificó a la rigidez lateral como la propiedad estructural más relevante del edificio, y esto llevó al planteamiento de varias propuestas basadas en rigidez enfocadas al caso de modelos estructurales que permanecen elásticos y que son sujetos a cargas laterales constantes y a restricciones varias en términos de resistencia y distorsión (Kim et al., 1998; Kameshki y Saka, 2001). En algún momento, los investigadores fueron más allá del dimensionado de elementos estructurales para una configuración dada, y propusieron métodos evolutivos basados en desempeño para establecer la topología óptima para el sistema de contraventeo de edificios de acero de varios pisos que permanecen elásticos bajo la acción de cargas laterales estáticas (Liang et al., 2000; Baldock y Shea, 2006). Además, se llegaron a proponer metodologías basadas en el control de las distorsiones que toman en cuenta la interacción que se da entre las propiedades dinámicas del sistema estructural y las del movimientos del terreno (Park y Kwon, 2003; Zou y Chan, 2005). Dentro de un contexto así, la complejidad de la matemática y la necesidad de amplios recursos computacionales resultaron en una excesiva simplificación del modelo estructural, en dificultades para interpretar los resultados finales del proceso de optimización, y en la necesidad de plantear restricciones adicionales para el dimensionado y para promover la convergencia del procedimiento planteado.
En términos de la resistencia a sismo de los edificios altos rigidizados con un sistema de contraventeo, todavía hay varias cuestiones que requieren de un tratamiento conceptual adecuado. En primer lugar, las diagonales no solo proveen rigidez lateral al edificio, sino capacidad de disipación de energía. Mientras que en algunos casos se aporta la disipación de energía por medio de amortiguadores viscosos, otros casos requieren el uso de dispositivos basados en la fluencia del acero (Soong y Spencer, 2002). En cualquier de estos casos, la estabilidad del mecanismo resistente a sismo suele requerir que la disipación de energía se concentre en las diagonales (Montiel-Ortega y Terán-Gilmore, 2013). Debe notarse que dentro de este contexto, el sistema de contraventeo se comporta como una enorme armadura en voladizo (Kim et al., 1998). Mientras que las columnas del sistema de contraventeo actúan como las cuerdas de la armadura, las diagonales y las vigas constituyen un alma que toma, mediante carga axial en los miembros, la cortante lateral. Dentro de un contexto así, la deformación lateral total del sistema de contraventeo puede estimarse de manera razonable al sumar la deformación lateral global en flexión producto de la deformación axial de las columnas que forman parte del sistema de contraventeo y la deformación lateral global en corte asociada a la deformación axial de las diagonales (Terán-Gilmore y Coeto, 2011). Así, una propiedad importante (disipación de energía) de una gran cantidad de sistemas estructurales altos ubicados en zonas de alta sismicidad no depende de las demandas totales de desplazamiento lateral, tal como ha sido presumido por metodologías previas de dimensionado, sino del comportamiento global en corte del sistema de contraventeo.
En segundo lugar, un diseño basado en el control de desplazamientos representa un reto mayor que uno basado en resistencia, ya que el desplazamiento lateral es un criterio asociado a todo el sistema estructural, lo que implica la consideración simultánea de todos los elementos estructurales del edificio. Aunque es posible obtener información valiosa a partir del uso de técnicas refinadas de optimización, el diseño sismorresistente requiere de sistemas estructurales adecuados que incorporen el buen juicio y conocimiento del diseñador. Dentro de este contexto es importante considerar que la resistencia a sismo debe aportarse dentro de un marco de alta incertidumbre. Esto implica que, independientemente de las características de la excitación sísmica real y de sus diferencias con aquellas presumidas por su representación de diseño, el sistema estructural del edificio debe aportar un mecanismo resistente estable. Si no se conforman a reglas básicas en términos de redundancia y configuración estructural, las topologías óptimas obtenidas con varias de las metodologías propuestas pueden fácilmente resultar en sistemas resistentes a sismo altamente inestables y poco confiables. El ajuste iterativo o evolutivo de las dimensiones de los miembros estructurales de un sistema mal concebido puede fácilmente resultar en sistemas resistentes a sismo deficientes, de tal manera que cualquier metodología que se proponga debe incluir el desarrollo conceptual de soluciones preliminares adecuadas que lleven, a través de unas cuantas iteraciones que sean fácilmente entendibles, al dimensionado óptimo de los elementos estructurales.
Este artículo plantea una metodología conceptual simple para el pre-dimensionado basado en rigidez de los elementos estructurales (diagonales y columnas) de un sistema de contraventeo para edificios altos resistentes a sismo. Con base en principios básicos de la mecánica, la metodología estima dimensiones para diagonales y columnas capaces de promover un desempeño estructural adecuado por medio del control explícito de las demandas de desplazamiento lateral del edificio. El uso de la metodología resulta en sistemas estructurales altamente eficientes que pueden usarse directamente para obtener el diseño final del edificio, o como una solución inicial que promueva el uso racional de planteamientos analíticos enfocados a optimizar el sistema estructural resistente a sismo.
DISEÑO BASADO EN DESPLAZAMIENTOS
Después de analizar las razones por las que muchos de los eventos sísmicos recientes han resultado en pérdidas económicas excesivas, la comunidad internacional de ingeniería sísmica ha concluido que el nivel de daño estructural y no estructural en un edificio es consecuencia directa de un excesivo nivel de deformación lateral. La innovación en el ámbito del diseño sismorresistente se ha enfocado a la concepción, diseño y construcción de sistemas estructurales, ya sean tradicionales o innovadores, que sean capaces de controlar adecuadamente su daño por sismo por medio del control explícito de su deformación lateral durante eventos sísmicos con diferente intensidad. Esto ha llevado a la formulación de metodologías de diseño enfocadas explícitamente a controlar el nivel de deformación lateral de los edificios resistentes a sismo (Bertero y Bertero, 1992; Priestley, 2000). Los países que encabezan el avance del diseño sismorresistente (como Estados Unidos y Japón) empiezan a cambiar su paradigma de diseño por medio de la formulación de formatos y códigos de diseño basados en desplazamientos (como por ejemplo, el considerado por la Federal Emergency Management Agency, 2000).
Conforme a lo mostrado en la figura 1, varias metodologías basadas en desplazamiento consideran los cinco pasos siguientes:
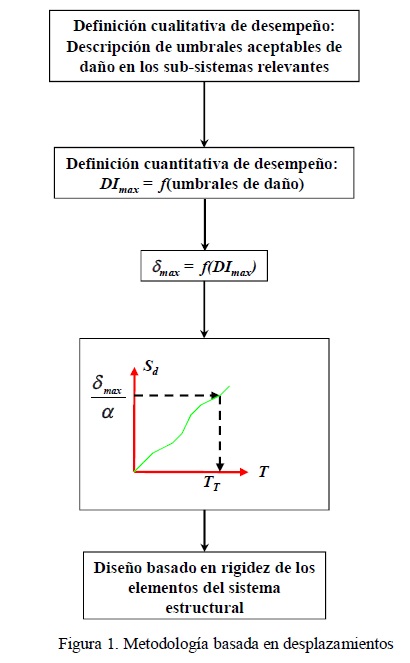
A) Se establece una definición cualitativa de lo que se considera un desempeño adecuado por medio de la consideración explícita de los niveles aceptables de daño para los diferentes sub-sistemas que componen el edificio (estructural y no estructural).
B) Se cuantifica el desempeño por medio de establecer umbrales de respuesta que son congruentes con el nivel de daño considerado aceptable para los diferentes sub-sistemas. Normalmente los umbrales se formulan en términos de la distorsión máxima de entrepiso permitida en el edificio (DImax) y deben considerar el desempeño de los sub-sistemas estructural (que a su vez puede estar constituido por sub-sistemas gravitacional y resistente a sismo) y no estructural.
C) Se usa el umbral de distorsión de entrepiso para establecer el umbral para la demanda máxima de desplazamiento de azotea (δmax).
D) Se establece un valor objetivo para el periodo fundamental de vibración del edificio (TT, que cuantifica los requisitos de rigidez lateral a nivel global) por medio del uso de un espectro de diseño de desplazamientos. Conforme a lo mostrado en la figura 1, es necesario ajustar con este fin el desplazamiento lateral de azotea para tomar en consideración los efectos de múltiples grados de libertad. De acuerdo con lo discutido con anterioridad, un diseño basado en el control de distorsiones es una tarea difícil debido a que se establece un criterio de revisión para todo el sistema estructural, lo que requiere la consideración simultánea de todos los elementos estructurales del edificio. Para simplificar el dimensionado de estos elementos, varios investigadores han propuesto el uso de un valor objetivo para el periodo fundamental de vibración (Bertero y Bertero, 1992; Priestley, 2000). Varios estudios han mostrado que el uso de este criterio para el diseño basado en desplazamientos de edificios de acero contraventeados puede considerar la interacción que se da entre las propiedades mecánicas del sistema estructural, y los contenidos de frecuencia y energía del movimiento del terreno, para dar lugar a sistemas estructurales eficientes y confiables (Terán-Gilmore y Ruiz-García, 2010; Terán-Gilmore y Coeto, 2011; Montiel-Ortega y Terán-Gilmore, 2013).
E) Las dimensiones de los elementos estructurales del sub-sistema resistente a sismo se establecen de manera que el periodo fundamental de vibración real del sistema estructural esté lo más cerca posible de TT. Las dimensiones de estos elementos definen la capacidad disponible del sistema estructural en términos de la rigidez a nivel local. La metodología de dimensionado basada en rigidez introducida en este trabajo se contextualiza en este paso de un enfoque basado en desplazamientos.
DIAGONALES RESTRINGIDAS CONTRA PANDEO
Una diagonal restringida contra pandeo es un elemento estructural que trabaja a compresión sin exhibir problemas de pandeo. Dado que una diagonal suele trabajar de una manera estable a tensión, lo que se logra es un dispositivo capaz de disipar energía de manera estable en presencia de varias reversiones de carga. La figura 2 muestra esquemáticamente el concepto de diagonal restringida contra pandeo, e ilustra sus diferentes componentes: A) Un núcleo de acero que disipa energía a través de su extensión o contracción axial, B) Material confinante que restringe el pandeo del núcleo, y C) Camisa de acero que mantiene la integridad del material confinante y aporta mayor restricción contra pandeo. Bajo la acción de un sismo severo, se espera que fluya el núcleo de la diagonal. El núcleo de acero se desadhiere del mortero o concreto confinante; es decir, se minimiza cualquier contacto en la interface entre ambos materiales. Esto con el fin de evitar que la resistencia a compresión de la barra sea significativamente mayor que su resistencia a tensión. Una discusión más detallada del concepto y uso de diagonales restringidas contra pandeo puede encontrarse en Uang y Nakashima (2003) y Tremblay et al. (2006). Las pruebas experimentales llevadas a cabo en diagonales restringidas contra pandeo indican un comportamiento altamente estable ante la presencia de deformaciones plásticas severas. En Japón se han desarrollado varios tipos de diagonales, y se cuenta con múltiples patentes. De hecho, en ese país existen varias centenas de edificios cuyo sistema sismorresistente principal consiste en sistemas de diagonales restringidas contra pandeo. En Taiwán, Canadá y EE.UU. también ha habido desarrollos experimentales de importancia y se han construido decenas de edificios que utilizan este tipo de dispositivo.
La rigidez lateral que aporta una diagonal restringida contra pandeo a un entrepiso dado (KL) se relaciona con el área de su núcleo (A) por medio de la siguiente ecuación (Tremblay et al., 2006):
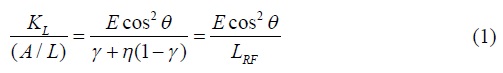
donde L es la longitud total de la diagonal, E su módulo de elasticidad, y θ su ángulo de inclinación (ver figura 3). γ es el cociente entre la longitud del núcleo (Lc en la figura 3) y L, η el cociente entre los esfuerzos axiales promedio fuera del núcleo y en el núcleo de la diagonal, y LRF un factor usado para considerar las zonas de mayor rigidez axial en los extremos de la diagonal. La ecuación 1 hace posible establecer al área requerida de diagonales en un entrepiso en función de la geometría del sistema de contraventeo y de la rigidez lateral que debe aportar a ese entrepiso.

En cuanto a la distorsión de entrepiso en la que se presenta la fluencia de la diagonal, puede establecerse lo siguiente:

donde ΔL y h son el desplazamiento lateral relativo y la altura del entrepiso, respectivamente (figura 3); y fy el esfuerzo de fluencia de la diagonal. El subíndice y indica fluencia.
ESTRUCTURAS TOLERANTES A DAÑO
Un enfoque prometedor para la concepción de edificios ligeros y seguros es el de sistema tolerante a daño (Wada et al., 2003). En uno de estos sistemas, el daño inducido por sismo se concentra en elementos estructurales específicos, conocidos como elementos de sacrificio. Su papel es funcionar como fusibles estructurales que protegen contra daño excesivo al sub-sistema principal o gravitacional del edificio, así como al sub-sistema no estructural. Debido a esto, la rehabilitación estructural del sub-sistema resistente a sismo después de la ocurrencia de un sismo severo se reduce a la sustitución de los fusibles dañados. El uso de este tipo de sistema en Japón ha resultado en edificios ligeros, y promete grandes ahorros en términos de costo y tiempo de rehabilitación estructural.
Terán-Gilmore y Coeto (2011) propusieron, dentro del contexto planteado en la figura 1 y el concepto de estructuras tolerantes a daño, una metodología de diseño basado en desempeño para la concepción y diseño preliminar de edificios altos. La metodología requiere que la carga vertical sea soportada en su totalidad por marcos momento-resistentes flexibles, y que la resistencia lateral del edificio sea provista por un sistema de diagonales restringidas contra pandeo. En términos de modelado, la metodología supone que: A) Las losas del sistema de piso actúan como diafragmas rígidos; B) La rigidez lateral total del edificio puede estimarse como la suma de las rigideces suministradas por el sub-sistema gravitacional y por el sub-sistema de contraventeo y C) Las distorsiones debidas al comportamiento global en corte y flexión del sub-sistema de contraventeo se consideran independientes y corresponden, respectivamente, a la deformación axial de diagonales y columnas. Note que la presencia de diafragmas rígidos restringe la deformación axial de las vigas y por tanto, reduce considerablemente la posible contribución de esta deformación al comportamiento global en corte del sistema de contraventeo.
Bajo estas tres suposiciones, es posible formular, conforme a lo mostrado en la figura 4, un modelo simple que considera que el sistema estructural del edificio puede ser modelado por medio de dos subsistemas paralelos. A su vez, el sub-sistema de contraventeo puede modelarse como dos sub-sistemas que trabajan en serie: uno que representa la rigidez global en corte proporcionada por las diagonales; y otro que representa la rigidez global en flexión proporcionada por las columnas del sistema de contraventeo.
Terán-Gilmore y Coeto (2011) discuten, dentro de un formato que considera explícitamente el comportamiento estructural de las diagonales y columnas del sistema de contraventeo y del sub-sistema gravitacional, la estimación del valor objetivo para el periodo fundamental de vibración de edificios altos. Explican que bajo la suposición de que los sub-sistemas gravitacional y sismorresistente trabajan en paralelo, el periodo fundamental de vibración que define los requisitos de rigidez para el sub-sistema de contraventeo (TCV) puede determinarse como:

donde TSG es el periodo que tendría el edificio si sólo su sub-sistema gravitacional contribuyera a su rigidez lateral.
Es importante mencionar que aunque la metodología desarrollada por Terán-Gilmore y Coeto fue planteada para sistemas de contraventeo con diagonales restringidas contra pandeo, es posible aplicarla a sistemas con cualquier tipo de diagonales. Al respecto, una diferencia sería la definición de los espectros de diseño, ya que mientras que el diseño de un sistema restringido contra pandeo requiere de espectros establecidos a partir de comportamiento elasto-plástico; el caso de diagonales que se pandean debe considerar un comportamiento histerético degradante que pueda modelar el pandeo y su impacto en las propiedades mecánicas del sistema estructural. Conforme a los requisitos planteados por la Sección 3.2.2 de las Normas Técnicas Complementarias para el Diseño y Construcción de Estructuras Metálicas, dicho pandeo depende de parámetros tales como la relación de esbeltez y esfuerzo de fluencia de la diagonal. Otra consideración sería el uso de valores de γ y η (ver ecuación 1) que correspondan apropiadamente a la geometría de la diagonal bajo consideración.
Dentro del contexto de un medio profesional acostumbrado a utilizar formatos basados en resistencia, es necesario aclarar que no se requiere revisar la capacidad resistente de diagonales dimensionadas conforme a un formato basado en desplazamientos. Aunque esto se discute en detalle en Terán-Gilmore y Coeto (2011), el apéndice de este artículo ofrece una demostración simple de lo anterior para un sistema de un piso rigidizado con una diagonal. Note además que el enfoque de estructura tolerante a daño considera que las diagonales deben constituirse en fusibles estructurales, de tal manera que es necesario revisar el dimensionado basado en rigidez para asegurarse que las vigas y columnas del sistema de contraventeo tengan suficiente resistencia como para que el comportamiento plástico se concentre en las diagonales y en menor medida, en sus conexiones.
DIMENSIONADO BASADO EN RIGIDEZ
Como complemento a la metodología discutida por Terán-Gilmore y Coeto (2011), este trabajo discute en detalle un procedimiento basado en rigidez que puede utilizarse durante el quinto paso de la figura 1. Dentro de este contexto, debe mencionarse que aunque el valor de TCV derivado de la ecuación 3 proporciona información acerca de los requisitos locales de rigidez que deben ser satisfechos por las dimensiones de las diagonales y columnas del sistema de contraventeo, es necesario definir primero las rigideces relativas en corte y flexión requeridas por el sub-sistema de contraventeo. La metodología propuesta por Terán-Gilmore y Coeto atiende esta cuestión mediante la definición de periodos independientes capaces de controlar a nivel global las deformaciones laterales en corte y flexión (TS y TB, respectivamente) del sub-sistema de contraventeo, que necesitan satisfacer la condición siguiente:

El dimensionado basado en rigidez de los diagonales y las columnas del sistema de contraventeo debe resultar en que los periodos fundamentales de vibración asociados a los comportamientos globales en corte y flexión del sub-sistema de contraventeo estén cerca de TS y TB, respectivamente. Esto debe ocasionar que el periodo fundamental de vibración del sub-sistema de contraventeo este muy cerca de TCV-Note que TS menor que TB implica una mayor rigidez lateral asociada al comportamiento global en corte que la asociada al comportamiento global en flexión. En términos cualitativos, el resultado final de disminuir el valor de Ts (y el respectivo aumento en el valor de TB de acuerdo con la ecuación 4 para un valor dado de TCV) son áreas más grandes para las diagonales que las consideradas para las columnas del sistema de contraventeo.
Una alternativa para el dimensionado de las diagonales y columnas del sistema de contraventeo inicia con el planteamiento de un patrón de cargas laterales en altura:

donde Vb es la cortante basal; wi y hi el peso y la altura con respecto al nivel del terreno, respectivamente, del sistema de piso correspondiente al i-ésimo nivel; y n el número de pisos. De acuerdo con las sugerencias hechas por FEMA 356 (Federal Emergency Management Agency, 2000), k puede estimarse como:

En algún momento, el ingeniero estructural debe tomar decisiones en cuanto a los materiales estructurales y la configuración geométrica del sistema de contraventeo. Estas decisiones deben basarse en el entendimiento sólido y conceptual del comportamiento no lineal de un sistema de contraventeo sujeto a deformación lateral, y deben tener en cuenta el número de diagonales por nivel (N) en la dirección de análisis, la longitud total de cada diagonal (L) y el módulo de elasticidad de diagonales y columnas del sistema de contraventeo (ECV y ECOL, respectivamente). Una vez que se establecen los valores de TCV, TS y TB para el edificio (un ejemplo de cómo determinar estos valores puede encontrarse en Terán-Gilmore y Coeto, 2011), las dimensiones de diagonales y columnas pueden determinarse de la siguiente manera:
1) Se establece una distribución de fuerzas laterales en altura, y en función de estas, las distribuciones correspondientes de fuerzas cortantes y momentos de volteo de entrepiso.
donde Fj es la fuerza lateral calculada con la ecuación 5 para el j-ésimo entrepiso; hj la altura de dicho entrepiso; y mB y mS, las masas asociadas a los modos fundamentales de vibración correspondientes a los comportamientos globales en flexión y corte, respectivamente, del subsistema de contraventeo. La tabla 1 resume valores de mB y mS que pueden usarse para el dimensionado basado en rigidez de edificios altos que exhiben regularidad estructural en altura. En la tabla, m es la masa total del edificio. La tabla se estableció a partir del estudio de las propiedades dinámicas de sistemas de contraventeo cuyas diagonales y columnas exhibían diferentes variaciones en altura de dimensiones de sus secciones transversales.
2) Se asigna un valor inicial para las áreas de las diagonales (A°CV) y las columnas del sistema de contraventeo (A°COL). A estas alturas, la única condición que debe ser satisfecha por las áreas de las diagonales es que su variación en altura sea proporcional a la de la fuerza cortante de entrepiso de acuerdo con las ecuaciones 5 y 7. En el caso de las columnas, su área debe variar en altura proporcionalmente a los momentos de volteo de entrepiso, de acuerdo a las ecuaciones 5 y 8.
3) Una vez que se cuenta con un dimensionado preliminar para las diagonales, se estiman las deformaciones laterales en el sub-sistema de contraventeo debidas a su comportamiento global en corte. Con este propósito, es razonable suponer que la deformación lateral en corte es consecuencia de la deformación axial de las diagonales. Dentro de este contexto, es importante mencionar que la presencia de diafragmas rígidos provistos por las losas de entrepiso restringen las deformaciones axiales de las vigas, y que la rigidez lateral en corte proporcionada por las diagonales puede estimarse como:
donde Ni es el número total de diagonales ubicadas en el i-ésimo entrepiso en la dirección de análisis; A°CVi, el área inicialmente propuesta para cada diagonal; θh su ángulo de inclinación; Li su longitud total, y LRFi un factor de ajuste de rigidez (ver ecuación 1).
El desplazamiento lateral relativo en el i-ésimo entrepiso puede estimarse como:
y el desplazamiento lateral en el i-ésimo nivel como:
4) Una vez que se cuenta con un dimensionado preliminar para las columnas, se estiman las deformaciones laterales en el sub-sistema de contraventeo debidas a su comportamiento global en flexión. Con este propósito, es razonable suponer que el sistema de contraventeo se comporta como una gran viga en voladizo y, por tanto, que la deformación lateral en flexión es consecuencia de la deformación axial de las columnas de soporte. Dentro de este contexto, la rigidez lateral en flexión del sub-sistema de contraventeo en el i-ésimo entrepiso (IBi) puede estimarse considerando las áreas transversales de las columnas y las distancias que las separan. La figura 5 ilustra la estimación de IB para sistemas de contraventeo con diferentes configuraciones.
5) Las curvaturas en los extremos superior e inferior de la porción del sub-sistema de contraventeo ubicada en el i-ésimo entrepiso pueden estimarse como:
Las rotaciones en esos mismos extremos pueden estimarse al integrar las curvaturas:
El incremento total de rotación en la losa situada en el i-ésimo nivel debido al comportamiento global en flexión puede estimarse como la suma de las contribuciones de las porciones del subsistema de contraventeo situadas por encima y por debajo de ella:
La rotación total de la losa ubicada en el i-ésimo nivel puede establecerse al acumular las contribuciones de todos los entrepisos ubicados debajo de ella:
Finalmente, el desplazamiento relativo del i-ésimo entrepiso debido al comportamiento global en flexión puede estimarse como:
Y el desplazamiento lateral en el i-ésimo nivel como:
6) Una vez que se han establecido los desplazamientos laterales debidos a los comportamientos globales en corte y flexión del sub-sistema de contraventeo, se hace una estimación inicial de los valores de TS y TB conforme a lo que sigue:
donde g es la aceleración debida a la gravedad. Note que δSi y δBi se estiman a partir de la distribución de la fuerza lateral planteada por la ecuación 5, y que con este propósito y dentro del contexto de un dimensionado basado en rigidez, es posible considerar un valor arbitrario para el cortante basal.
7) Una vez que se han estimado valores iniciales para TS y TB (TS° y TB°, respectivamente) con las ecuaciones 18, las áreas definitivas para las diagonales y las columnas se estiman como:
SISTEMA DE CONTRA VENTEO: EJEMPLO
Para ilustrar la aplicación de la metodología, se seleccionó el edificio de 24 niveles con estructura de acero mostrado en la figura 6, el cual tiene dimensiones en planta de 45 x 45 m. La altura de entrepiso es de 4.5 m; excepto en los primeros 4 entrepisos que tienen alturas de 4.0, 5.65, 5.65 y 6.0 metros; y en los dos superiores, de 6.0 y 6.5 metros. En total, el edificio tiene una altura de 114.8 m. El edificio tiene 4 crujías centrales de 9 m, dos crujías laterales de 4.5 m y 7 marcos en cada una de las dos direcciones principales de análisis. Los tres primeros pisos tienen un peso de 1916 ton cada uno, el último de 1355 ton, y los demás de 1340 ton. Conforme a lo mostrado, el edificio requiere de un sub-sistema de contraventeo de acero que incluye las dos crujías centrales de los tres marcos centrales en cada dirección de análisis (por ejemplo, los marcos C, D y E). Para ilustrar el alcance de la metodología de dimensionado basada en rigidez, se consideran a continuación los cuatro casos resumidos en la tabla 2.

Como una restricción, el área de las diagonales y columnas se varía cada 4 niveles. La tabla 3 resume, para las diferentes versiones del sub-sistema de contraventeo, las dimensiones de diagonales y columnas. Las áreas de diagonales se estimaron bajo la consideración de un LRF = 1.5 (ver ecuaciones 1 y 9).
CARACTERÍSTICAS DINÁMICAS DE LOS SISTEMAS DE CONTRAVENTEO
Los periodos fundamentales de vibración de las cuatro versiones del sub-sistema de contraventeo se estimaron con el software SAP2000. El área transversal de las diagonales se ajustó en los modelos analíticos de acuerdo con el valor de LRF utilizado durante el dimensionado (1.5). Se establecieron tres periodos fundamentales de vibración para cada versión del sub-sistema de contraventeo: A) Uno asociado al comportamiento global en corte (TS); B) Otro asociado al comportamiento global en flexión (TB); y, finalmente, C) Uno asociado al comportamiento global total (TCV). TCV se estimó mediante un modelo analítico que asignó a las diagonales y columnas las áreas resumidas en la tabla 3; y TS al modificar dicho modelo por medio de asignar áreas muy grandes a las columnas de soporte (columnas con rigidez axial "infinita"). En el caso de TB, el modelo fue modificado al asignar áreas muy grandes a las diagonales, de tal manera de plantear diagonales con rigidez axial "infinita". El momento de inercia de las columnas para todos los modelos analíticos se estableció al considerar para ellas una sección transversal cuadrada correspondiente a las áreas resumidas en la tabla 3 (estas inercias no se modificaron en los modelos con columnas con rigidez axial "infinita").
La tabla 4 resume y compara los periodos fundamentales de vibración objetivo y estimado para las diferentes versiones del sub-sistema de contraventeo. Conforme a lo discutido con anterioridad, un menor valor de TS con respecto a TB implica mayores dimensiones de las diagonales que de las columnas. Note que la metodología propuesta aporta estimaciones razonables de TB para las diferentes versiones del subsistema de contraventeo. En el caso de TS, la metodología arroja mejores estimaciones conforme decrece el valor objetivo para este periodo (es decir, se obtiene una mejor estimación de TS para el Caso 1 que para el Caso 4). Esto puede explicarse por el hecho de que la metodología no considera la rigidez lateral en corte proporcionada por las columnas (siempre que su momento de inercia sea mayor que cero, con algo contribuirán esas columnas a la rigidez lateral de entrepiso), y que el momento de inercia de las columnas aumenta con un incremento en el valor de TS. En general, la metodología establece dimensiones para el sub-sistema de contraventeo que reflejan adecuadamente los requisitos de diseño planteados en términos de rigidez lateral. En caso de considerarlo conveniente, el diseñador podría iterar y reducir ligeramente las dimensiones de las diagonales para compensar la contribución de las columnas del sistema de contraventeo a la rigidez lateral del sub-sistema de contraventeo.
La figura 7 muestra los modos fundamentales de vibración para las cuatro versiones del sub-sistema de contraventeo. Note la creciente influencia del comportamiento global en flexión conforme disminuye el valor de TS (y, por tanto, conforme se reducen las deformaciones globales en corte con respecto a las deformaciones globales en flexión).
Mientras que la figura 8 muestra los modos fundamentales de vibración asociados al comportamiento global en corte para las diferentes versiones del sub-sistema de contraventeo, la figura 9 hace lo propio para los modos fundamentales de vibración asociados al comportamiento global en flexión. Independientemente de los tamaños relativos de diagonales y columnas, los modos fundamentales de vibración debidos al comportamiento global en corte son prácticamente iguales entre sí. Puede hacerse una observación similar para el caso de los modos fundamentales de vibración debidos al comportamiento global en flexión.
Las figuras 8 y 9 aportan un soporte gráfico para la condición de independencia implícita en la figura 4 y la ecuación 4 para los comportamientos globales en corte y flexión del sub-sistema de contraventeo. Esto implica que una metodología como la planteada en este documento para el dimensionado basado en rigidez, puede establecer dimensiones para las diagonales y columnas por medio de formulaciones numéricas independientes. En términos de esta independencia, es necesario discutir la posibilidad de que un sistema de contraventeo exhiba una respuesta lateral que quede caracterizada por una interacción entre sus comportamientos globales en corte y flexión. Normalmente una interacción así, ya sea que se de en elementos estructurales de mampostería, concreto o acero, se da a partir de un daño a corte que aparece en el elemento estructural después de un comportamiento no lineal a flexión; y por lo general ocurre por la elevada sobrerresistencia asociada a la capacidad resistente a flexión. Dado que el enfoque de estructura tolerante a daño utiliza el diseño por capacidad para fomentar que el comportamiento plástico se concentre en las diagonales, y que éstas exhiben un bajo nivel de sobrerresistencia para los niveles de deformación implícitos en lo de tolerante a daño, resulta probable que, conforme a lo planteado por Terán-Gilmore y Coeto (2011), el mecanismo global en flexión permanezca sin daño y por tanto que no se presente una interacción flexión-corte de importancia.
DISCUSIÓN
La metodología planteada en este artículo ha sido aplicada con éxito para el dimensionado de los elementos estructurales de un sub-sistema de contraventeo que tiene el mismo número de diagonales (con longitud y configuración estructural similares) en todos los entrepisos, y que, por tanto, puede ser idealizado como una gran armadura de acero en voladizo. Al respecto, la metodología puede ser fácilmente programada en una hoja de cálculo electrónico para que pueda ser aplicada a sistemas de contraventeo con otras características geométricas (por ejemplo, número diferente de diagonales en los diferentes entrepisos).
La existencia de cinturones (armaduras) rigidizantes en algunos de los entrepisos del edificio puede modificar significativamente el comportamiento global en flexión del sistema de contraventeo. Mientras que bajo estas circunstancias, el dimensionado de las diagonales sigue las mismas consideraciones planteadas en este artículo, el dimensionado de las columnas tendría que considerar las restricciones que las armaduras rigidizantes imponen al giro global de los entrepisos donde se ubican (como consecuencia, la distribución de momentos de volteo en altura cambiaría con respecto a lo planteado por la ecuación 8). En cuanto a los efectos de modos superiores, es posible refinar el dimensionado de diagonales y columnas si las ecuaciones 5 y 6 se ajustan para explícitamente reflejar la influencia de dichos modos en la distribución en altura de fuerzas laterales.
La tabla 5 resume el peso de los elementos estructurales de las cuatro versiones del sub-sistema de contraventeo. Mientras que el peso de las columnas se calcula como el producto de su área, longitud, y el peso específico del acero; en el caso de las diagonales este producto se multiplicó por 1.5 para considerar el peso de las conexiones. Note que en términos de peso, las soluciones más eficaces son aquellas en que TS es similar o ligeramente menor que TB. De todos los casos bajo consideración, los Casos 1 y 4 pueden ser considerados como inadecuados. Mientras que en el primer caso, las fuerzas axiales desarrolladas por las diagonales no pueden ser resistidas adecuadamente por las columnas; el último caso requiere de dimensiones demasiado grandes para las columnas, de tal manera que el peso total resulta demasiado grande cuando se le compara con el correspondiente a los Casos 2 y 3.
Finalmente, debe mencionarse por un lado que el dimensionado derivado del uso de la metodología conceptual propuesta puede ser utilizado directamente por el ingeniero estructural para establecer el diseño final del sistema estructural, o puede utilizarse como un estado inicial dentro del contexto de una metodología refinada enfocada a la optimización del peso estructural del edificio.
CONCLUSIONES
Se ha planteado una metodología simple para el dimensionado basado en rigidez de los elementos estructurales de un sistema de contraventeo para edificios altos sismorresistentes. Con base en conceptos básicos de la mecánica, y bajo el supuesto de independencia entre los comportamientos globales en corte y flexión del sistema de contraventeo, la metodología plantea una serie de pasos sencillos que permiten, de manera independiente, el dimensionado basado en rigidez de las diagonales y columnas.
La aplicación de la metodología para el dimensionado de diagonales y columnas de cuatro versiones de un sistema de contraventeo de 24 pisos dio lugar a diseños adecuados en términos de rigidez lateral. Aunque el uso de la metodología se ilustró para un sistema de contraventeo sin cinturones rigidizantes, y que tiene el mismo número de diagonales en todos sus entrepisos y puede suponerse empotrado en la base; dicha metodología puede ser fácilmente adaptada para considerar otras configuraciones estructurales y geométricas.
Metodologías como la planteada y discutida en este trabajo se constituyen en herramientas esenciales y útiles para la concepción y dimensionado preliminar de sistemas estructurales para edificios altos ubicados en zonas de alta sismicidad, que lleven a diseños eficientes y confiables dentro del contexto de un diseño basado en desempeño.
AGRADECIMIENTOS
Los autores desean expresar su agradecimiento a la Universidad Autónoma Metropolitana por el apoyo otorgado al trabajo que aquí se reporta.
REFERENCIAS
Baker, W (1990), "Sizing technique for lateral systems in multi-story steel building," 4th World Congress on Tall Buildings, pp. 868-875, Hong Kong, China. [ Links ]
Baldock, R y K Shea (2006), "Structural topology optimization of braced steel frameworks using genetic programming," Intelligent Computing in Engineering and Architecture, Lecture Notes in Computer Science, vol. 4200/2006, pp. 54-61. [ Links ]
Bertero, R y V V Bertero (1992), "Tall reinforced concrete buildings: conceptual earthquake-resistant design methodology," Reporte UCB/EERC-92/16, Universidad de California en Berkeley. [ Links ]
Chan, C M y D E Grierson (1993), "An efficient resizing technique for the design of tall buildings subject to multiple drift constraints," The Structural Design of Tall and Special Buildings, vol. 2 (1), pp. 17-32. [ Links ]
Federal Emergency Management Agency (2000), "FEMA 356, Prestandard and commentary for the seismic rehabilitation of buildings. [ Links ]"
Kameshki, E S y M P Saka (2001), "Genetic algorithm based optimum bracing design of non-swaying tall plane frames," Journal of Constructional Steel Research, vol. 57, pp. 1081-1097. [ Links ]
Kim, C K, H S Kim, J S Hwang y S M Hong (1998), "Stiffness-based optimal design of tall steel frameworks subject to lateral loading," Structural Optimization, vol. 15, pp. 180-186. [ Links ]
Liang, Q Q, Y M Xie y G P Steven (2000), "Optimal topology design of bracing systems for multi-story steel frames," ASCE Journal of Structural Engineering, vol. 126 (7), pp. 823-829. [ Links ]
Moehle, J P (2008), "Performance-based seismic design of tall buildings in the U.S.," 14th World Conference on Earthquake Engineering (CD), Beijing, China. [ Links ]
Montiel-Ortega, M A y A Terán-Gilmore (2013), "Comparative reliability of two twenty-four story braced buildings: traditional versus innovative," The Structural Design of Tall and Special Buildings, vol. 22 (8), pp. 635-654. [ Links ]
Moon, K-S, J J Connor y J E Fernandez (2007), "Diagrid structural systems for tall buildings: characteristics and methodology for preliminary design," The Structural Design of Tall and Special Buildings, vol. 16, pp. 205-230. [ Links ]
Moon, K-S (2008), "Sustainable structural engineering strategies for tall buildings," The Structural Design of Tall and Special Buildings, vol. 17, pp. 895-914. [ Links ]
Park, H S, K Hong y J H Seo (2002), "Drift design of steel-frame shear-wall systems for tall buildings," The Structural Design of Tall Buildings, vol. 11, pp. 35-49. [ Links ]
Park, H S y J H Kwon (2003), "Optimal drift design model for multi-story buildings subjected to dynamic lateral forces," The Structural Design of Tall and Special Buildings, vol. 12, pp. 317-333. [ Links ]
Priestley, M J N (2000), "Performance based seismic design," 12th World Conference on Earthquake Engineering (CD), Auckland, Nueva Zelanda. [ Links ]
Soong, T T y B F Spencer (2002), "Supplemental energy dissipation: state-of-the-art and state-of-the practice," Engineering Structures, vol. 24, pp. 243-259. [ Links ]
Terán-Gilmore, A y J Ruiz-Garcia (2010), "Comparative Seismic Performance of Steel Frames Retrofitted with Buckling-Restrained Braces through the Application of Force-Based and Displacement-based Approaches," Soil Dynamics and Earthquake Engineering, vol. 31, pp. 478-490. [ Links ]
Terán-Gilmore, A y G Coeto (2011), "Displacement-Based Preliminary Design of Tall Buildings Stiffened with a System of Buckling-Restrained Braces," Earthquake Spectra, vol. 27 (1), pp. 153-182. [ Links ]
Tremblay, R, P Bolduc, R Neville y R DeVall (2006), "Seismic testing and performance of buckling-restrained bracing systems," Canadian Journal of Civil Engineering, vol. 33, pp. 183-198. [ Links ]
Uang, C M y M Nakashima (2003), "Steel buckling-restrained braced frames," Earthquake Engineering: Recent Advances and Applications, Capítulo 16, CRC Press. [ Links ]
Wada, A, Y Huang y V V Bertero (2003), "Innovative strategies in earthquake engineering," Earthquake Engineering: Recent Advances and Applications, Capítulo 10, CRC Press. [ Links ]
Zou, X-K y C-M Chan (2005), "An optimal resizing technique for seismic drift design of concrete buildings subjected to response spectrum and time history loadings," Computers and Structures, vol. 83, pp. 1689-1704. [ Links ]
* Se aceptarán comentarios y/o discusiones hasta cinco meses después de su publicación.