Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería sísmica
versión impresa ISSN 0185-092X
Ing. sísm no.86 Ciudad de México ene./jun. 2012
Artículo
Una medida de intensidad sísmica basada en un parámetro para caracterizar la forma espectral denominado Np
Edén Bojórquez Mora1, Iunio Iervolino2, Alfredo Reyes Salazar1, Héctor Rodríguez Lozoya1 y Luz Rivera Salas1
1 Facultad de Ingeniería, Universidad Autónoma de Sinaloa, Calzada de las Américas y Boulevard Universitarios S/N, Ciudad Universitaria, Culiacán, Sinaloa, México, C.P. 80040. ebojorq@uas.uasnet.mx eden_bmseg@hotmail.com reyes@uas.uasnet.mx
2 Dipartimento di Ingegneria Strutturale, Università degli Studi di Napoli Federico II, Via Claudio 21, 80125 Napoli Italia. iunio.iervolino@unina.it
Recibido el 29 de noviembre de 2010
Aprobado el 28 de bre de 2011
Resumen
En este trabajo se analizan diversas medidas de intensidad sísmica (IS) representativas de la forma espectral. En primer lugar, se introduce una nueva medida de IS vectorial basada en la pseudo-aceleración en el periodo fundamental de vibración de la estructura Sa(T1), y un parámetro que caracteriza la forma espectral denominado Np. Se compara la eficiencia del vector <Sa(T1), Np> con diversas medidas de intensidad sísmica mediante el análisis de sistemas de un grado de libertad (S1GL), marcos de concreto reforzado y acero, los cuales se someten a la acción de movimientos sísmicos con distintas características (que incluyen registros cercanos al epicentro y de banda angosta). Se demuestra que el vector propuesto tiene una mejor relación con las demandas máximas y de energía, por lo que su uso reduce las incertidumbres asociadas a la respuesta estructural, que es pieza fundamental en la selección de acelerogramas para el análisis dinámico no-lineal de estructuras, y para evaluar la confiabilidad estructural. Finalmente, se analiza una medida de intensidad sísmica escalar basada en Sa(T1) y Np, y se demuestra que el análisis del peligro sísmico para la medida escalar puede efectuarse mediante herramienta actualmente disponible.
Palabras clave: marcos dúctiles contraventeados, contraventeo metálico chevrón, diseño por capacidad, distorsiones de diseño, factor de reducción por sobrerresistencia, desempeño estructural.
Abstract
Several spectral-shape based ground motion intensity measures (IMs) are analyzed. Firstly, a new vector-valued IM based on the spectral acceleration at first mode of vibration Sa(T1), and a parameter proxy for the spectral shape named Np is introduced. The efficiency of the vector <Sa(T1), Np> is compared with other IMs by dynamic analysis of single degree of freedom (SDOF), reinforced concrete and steel frames. The structures are subjected to ground motion records with different characteristics (including near-fault and narrow-band motions). It is shown that the vector here proposed has better relation with maximum and energy demands, reducing the uncertainties associated with the structural response, which is fundamental piece in record selection for nonlinear dynamic analysis, and for structural reliability assessment. Finally, a scalar intensity measure based on Sa(T1) and Np is analyzed, and it is illustrated the possibility to compute seismic hazard analysis for the new scalar parameter with tool currently available.
Keywords: ductile braced frames, chevron steel bracing, capacity design, design drifts, overstrength factor, structural performance.
INTRODUCCIÓN
La definición de un parámetro que pueda describir la severidad de un movimiento sísmico y tenga buena relación con la respuesta estructural, ha sido constantemente estudiada. Uno de los objetivos principales de dicho parámetro que se conoce como medida de intensidad sísmica, es estar íntimamente relacionado con la demanda sísmica (DS), lo cual permite reducir las incertidumbres en la respuesta sísmica. Las incertidumbres asociadas a la respuesta de estructuras sujetas a la acción de los sismos, hacen que el problema sísmico se defina en términos probabilísticos. Por tal motivo, uno de los objetivos fundamentales de la ingeniería sísmica es cuantificar que tan confiable es una estructura considerando todo el posible peligro sísmico al cual será sometida durante su vida útil. Una herramienta para estimar la confiabilidad de estructuras sujetas a acciones sísmicas es través de la evaluación de la tasa media anual de excedencia (TAE) de un parámetro asociado a la demanda sísmica, por ejemplo: la distorsión máxima de entrepiso, la energía histerética disipada, o el índice de daño de Park y Ang (Park y Ang, 1985). Mediante el teorema de la probabilidad total, la TAE se puede obtener a través de la siguiente expresión:

donde λDS(x) es la tasa media anual de que DS exceda un valor x, vi es la tasa de sismos para un fuente específica que afecta el sitio de interés, f(IS | M, R) es la función de de densidad de probabilidades de la medida de intensidad sísmica utilizada dados la magnitud (M) y la distancia (R) (ley de atenuación sísmica). f(M, R) es la función de densidad de probabilidad conjunta de M y R. Finalmente, P(DS > x | IS, M, R) es la probabilidad de excedencia de DS dados IS, M y R. Si P(DS > x | IS, M, R) = P(DS > x | IS) se dice que la medida de IS es suficiente (Bazzurro, 1998; Shome, 1999; Luco, 2002) debido a que la predicción de la respuesta estructural es independiente de M y R cuando se utiliza cierta medida de IS, y por lo tanto, la ecuación 1 se puede escribir de la siguiente forma:

En la ecuación 2, dλIS(is) = λIS(is) - λIS(is + dis) representa la diferencia de la curva de peligro sísmico en función de cierta medida de IS. Si la medida de IS muestra una buena relación con la respuesta estructural se dice que ésta es eficiente (Bazzurro, 1998; Luco, 2002). Es decir, una medida de IS eficiente, es aquella que permite reducir las incertidumbres asociadas a la respuesta sísmica. En general, las propiedades deseables para una medida de IS son: suficiencia, eficiencia y robusta al escalamiento (Bazzurro, 1998).
La importancia de contar con una medida de IS que represente de manera razonable el potencial destructivo de un movimiento sísmico, ha provocado que muchos estudios se hayan orientado en esa dirección. En 1952, Housner propuso utilizar el área del espectro de pseudo-velocidad como medida de IS; algunos años después (Von Thun et al., 1988) sugiere el uso del área encerrada en el espectro de pseudo-aceleración en un intervalo de periodos de 0.1 a 0.5s para el análisis sísmico de presas. En los últimos años, la aceleración espectral en el periodo fundamental de vibración Sa(T1) (también nombrado en este trabajo como Sa) ha sido muy popular como medida de IS, pero debido a su insuficiencia en algunos casos para predecir la DS (Baker y Cornell, 2005); recientemente, otras medidas de intensidad más avanzadas se han propuesto. En particular, el vector <Sa, ε> que está relacionado con la forma espectral elástica ha resultado suficiente y eficiente en varios casos analizados (Baker y Cornell, 2005). Sin embargo, Tothong y Luco (2007) mostraron la ineficacia de <Sa, ε> como predictor de la respuesta estructural para el caso de registros de fuente cercana que presentan pulsos de velocidad, y propusieron una medida de IS escalar avanzada basada en el desplazamiento espectral inelástico. Esta resulta adecuada para registros ordinarios y de fuente cercana, al menos en la predicción de la distorsión máxima de entrepiso, pero su aplicación es más compleja y no resulta tan adecuada para fines prácticos. Otra medida de IS vectorial <Sa, RT1,T2> (basada en una medida escalar propuesta por Cordova et al. (2001); donde RT1,T2 es la relación entre la aceleración espectral en el periodo T2 dividida entre la aceleración espectral en T1, y T2 representa un periodo mayor que T1) ha resultado eficiente para predecir la respuesta de estructuras sujetas a movimientos de fuente cercana (Baker y Cornell, 2008). Baker y Cornell (2006) también exploraron de manera preliminar la media geométrica de la aceleración espectral en un intervalo de periodos Saavg(T1...TN) para evitar que se produjeran valles o picos en la forma espectral elástica. En todos los trabajos mencionados puede observarse un aspecto importante: los esfuerzos en plantear parámetros para definir una medida de IS alternativa se concentran en la forma espectral debido a su relación con la respuesta estructural. En otras palabras, existe evidencia importante que soporta el uso de la forma espectral elástica como medida de IS. Si la información necesaria para predecir la respuesta sísmica de estructuras se encuentra en la forma espectral, el primer paso es tratar de encontrar un parámetro capaz de representar con la mejor aproximación la forma espectral. Por este motivo, en el presente trabajo se introduce un parámetro denominado Np, cuyo objetivo es caracterizar con buena aproximación la forma espectral. Para observar la importancia del parámetro propuesto y su relación con la respuesta estructural, se hace una revisión de varias medidas de intensidad sísmica comúnmente utilizadas. En particular, se discute el uso del escalar Sa(T1) que a pesar de ser uno de los parámetros más utilizados como medida de intensidad y para realizar análisis de peligro sísmico, éste no resulta en algunos casos eficiente. Además, se muestra la ventaja de utilizar medidas de IS vectorial tales como <Sa, RT1,T2> ó <Sa, Np>. Finalmente, se propone una medida de intensidad sísmica escalar basada en Sa(T1) y Np, y se discute la posibilidad de realizar análisis de peligro sísmico para dicho parámetro. Se concluye que, los parámetros basados en Sa(T1) y Np son buenos candidatos para reflejar el potencial destructivo de movimientos sísmicos de suelos rígidos, de fuente cercana y de banda angosta, y presentan mejor relación con la respuesta estructural en términos de ductilidad, distorsiones máximas de entrepiso, energía histerética e índice de daño de Park y Ang. Además, su uso reduce la importancia de los cuidados especiales en la selección de acelerogramas para análisis, diseño y evaluación de la confiabilidad estructural.
PARÁMETROS PARA CARACTERIZAR LA FORMA ESPECTRAL
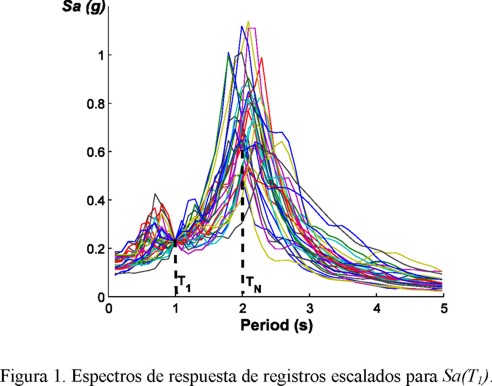
Debido a la importancia de la forma espectral como predictor de la respuesta estructural, recientemente se han propuesto diversas medidas de IS que se basan en esta peculiar característica. Sin embargo, en varios casos dichas medidas podrían no representar con suficiente aproximación la forma espectral; en particular, del espectro de pseudo-aceleraciones. Por ejemplo, escalar registros sísmicos para Sa(T1), aunque resulta en un perfecto predictor de la respuesta de S1GL elásticos, no da información en otras zonas espectrales, que son importantes para predecir el comportamiento no-lineal de estructuras o de aquellas dominadas por modos superiores. En el caso de estructuras que exhiben comportamiento no-lineal, el periodo estructural puede sufrir un alargamiento importante. Las implicaciones de lo anterior quedan más claras al suponer una estructura con un periodo fundamental de vibración T1=1s que se somete a diferentes registros escalados para un nivel específico de Sa(T1). La figura 1 ilustra los espectros de respuesta de varios registros de suelo blando del valle de México escalados. Debido al comportamiento no-lineal de la estructura, está sufrirá un alargamiento en el periodo de vibración que en la figura por ejemplo se define como TN, y que se supone igual a 2. En primer lugar, se observa que el escalar en términos de Sa(T1) no aporta información en otras zonas espectrales que pueden influir en la respuesta no-lineal. De hecho, se puede observar una dispersión muy grande en las ordenadas espectrales en el periodo TN. Esto implica que la demanda sísmica sobre la estructura que le provoca cada registro en un intervalo de comportamiento no-lineal es completamente diferente, lo que resultará en incrementos importantes en la incertidumbre asociada a la respuesta estructural. Sin embargo, estudios han encontrado que Sa(T1) es suficiente con respecto a la magnitud y la distancia (Shome, 1999; Iervolino y Cornell, 2005). Actualmente, con la finalidad de proveer de información en otras zonas espectrales, Baker y Cornell (2008) exploraron un vector de la forma <Sa, RT1,T2>, y encuentran muy buena relación de este parámetro con la respuesta de estructuras sujetas a registros sísmicos de fuente cercana. El uso de este vector consiste en escalar los registros para un mismo nivel de Sa(T1) y observar la relación entre RT1,T2 y la respuesta estructural para ese nivel de escalamiento. La ventaja de este vector es que aporta información en dos puntos del espectro, en lugar de Sa(T1) que solo lo hace en uno. La idea de incorporar información en T2 es para considerar el comportamiento no-lineal de la estructura. Baker y Cornell (2006) también exploraron la posibilidad de utilizar la media geométrica Saavg(T1...TN) como medida de IS, que en realidad se trata de una extensión de la medida propuesta por Von Thun et al. (1988). Ambas medidas de IS <Sa, RT1,T2> y Saavg(T1...TN tienen el potencial de caracterizar la forma espectral con suficiente aproximación. Sin embargo, la información dada por dos puntos del espectro podría ser insuficiente, especialmente para registros de banda angosta, donde información relevante podría ser excluida. Más aún, en el caso de Saavg(T1...TN que considera varios puntos del espectro, esta puede dar lugar a distintas formas espectrales o trayectorias del espectro en el intervalo T1 y TN para valores similares de Saavg(T1...TN. Por esta razón, una manera más apropiada de aproximar la forma espectral es mediante el uso de la media geométrica Saavg(T1...TN normalizada por Sa(T1). Con base en esto, Bojórquez y Iervolino (2011) propusieron un nuevo parámetro denominado Np (ver ecuación 3), que tiene una clara relación con la característica que tendrá el espectro de respuesta. Esto ayuda a interpretar un espectro a través del conocimiento del parámetro Np.

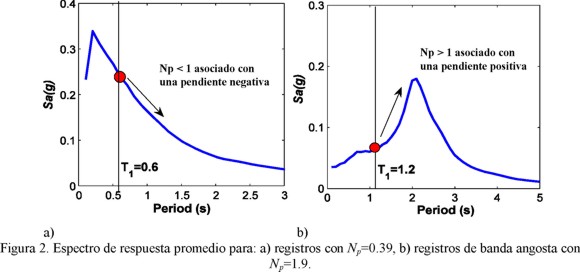
La ecuación 3 indica que si se tienen uno o n registros sísmicos con un valor medio de Np cercano a uno, se puede esperar que el espectro promedio sea constante en el intervalo de periodos T1 hasta TN. Para un valor Np menor que uno, se espera un espectro promedio con pendiente negativa. Como ejemplo, el valor promedio de Np para un conjunto de registros en el intervalo de periodos T1=0.6s hasta TN=2T1 es 0.39. En la figura 2a, se ilustra la gráfica del espectro promedio del conjunto de registros. Se puede observar que el espectro tiene una pendiente negativa para valores de Np menores a la unidad. Si Np es mayor que uno, los espectros tendrán una banda angosta en el intervalo de periodos de interés o una zona espectral creciente, como se ilustra en la figura 2b para un conjunto de registros sísmicos de banda angosta, donde el valor medio de Np es igual a 1.9 en un intervalo de periodos T1=1.2s a TN=2T1. En conclusión, valores de Np mayores que la unidad estarán asociados a una zona de incremento en las ordenadas espectrales (un posible valor mínimo se observará en T1 para el intervalo de interés); mientras que valores menores a la unidad serán representativos de una zona decreciente en las ordenadas espectrales (un posible valor máximo se observará en T1 para el intervalo de interés). Lo anterior permite explicar porque al incrementar Np, aumenta la respuesta estructural como se observará más adelante.
Bojórquez y Iervolino (2011) adoptaron el término Np porque representa la contribución de N puntos del espectro. Además, la normalización entre Sa(T1) permite a Np ser independiente del nivel de escalamiento de los registros para un valor de Sa(T1), y lo más importante mejora sustancialmente el conocimiento acerca de la trayectoria de la estructura desde su comportamiento elástico y durante su incursión en el intervalo de comportamiento no-lineal. En este trabajo se analiza una nueva medida de IS vectorial basada en Sa(T1) y Np, ya que este vector es más representativo de la forma espectral.
El vector <Sa, Np> tiene las siguientes características:
1. El vector es consistente; esto significa que al escalar registros para valores similares de Sa(T1), la respuesta sísmica dependerá de la magnitud del valor de Np.
2. El vector es relativamente más eficiente sin importar las características del movimiento sísmico, o la DS considerada (demandas máximas o parámetros relacionados con la demanda de energía en estructuras).
3. Finalmente, existe una clara relación entre los valores de Np y la forma espectral, lo cual ayuda a interpretar el espectro de pseudo-aceleraciones a través del conocimiento de Np.
Para el caso del vector <Sa, Np>, la tasa media anual de que DS exceda un valor de x puede ser calculada mediante la siguiente ecuación:
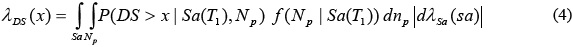
donde f(Np | Sa(T1)) es la función de densidad de probabilidades de Np dado Sa(T1). P[DS > x | Sa(T1), Np] es la probabilidad de que DS exceda x dado Sa(T1) y Np obtenida mediante análisis dinámicos. Finalmente, dλSa(sa) = λSa(sa) - λSa(sa + dsa) es la diferencia entre la curva de peligro sísmico en términos de Sa(T1).
IMPORTANCIA DE LAS MEDIDAS DE INTENSIDAD SÍSMICA VECTORIAL
En varios estudios se han mostrado los beneficios de utilizar medidas de IS vectorial (Shome, 1999; Baker y Cornell, 2005; Baker y Cornell 2007), especialmente por el incremento en la eficiencia que se puede obtener al utilizar dichas medidas. Para ilustrar esto, la figura 3 muestra la relación entre el escalar Sa(T1) y la demanda de ductilidad a través de análisis dinámico incremental (ADI) (Vamvatsikos y Cornell, 2002) para un S1GL con comportamiento no-lineal, y un periodo de 0.6s (el S1GL tiene un comportamiento bilineal con 5% de rigidez de posfluencia y mismo porcentaje de amortiguamiento crítico). La estructura se sometió a 194 registros que se describen más adelante. Se puede observar una gran dispersión para niveles importantes de no-linealidad. Por ejemplo, para un valor de la mediana de la demanda de ductilidad igual a 6 (escalando para Sa=1g), la desviación estándar del logaritmo natural es de (σln(μ)=0.40), y el intervalo de demanda de ductilidad obtenido va desde 2.5 hasta 18 que es demasiado grande. La figura 4 ilustra el potencial de utilizar una medida vectorial. En primer lugar, los registros se escalaron para un valor similar de Sa(T1) igual a 1g, y después se evaluó la relación entre el segundo parámetro del vector y la demanda de ductilidad. La figura 4 muestra la relación entre ε (donde épsilon se determinó con la ley de atenuación de Boore y Atkinson (2007), y se define como la diferencia entre la aceleración espectral de un acelerograma y la calculada con una ley de atenuación para un periodo de interés), RT1,T2 y Np con la demanda de ductilidad. Para RT1,T2 y Np, se utilizaron los valores de T2=2 y TN=2 a 2.5 propuestos por Bojórquez y Iervolino (2011). Se observa una buena relación entre la ductilidad y los vectores formados por RT1,T2 y Np; sin embargo, la eficiencia de Np comparado con RT1,T2 es moderadamente mejor. Para el caso de <Sa, Np>, la dispersión es (σln(μ)=0.228) alrededor de 50% menor comparada con el criterio de escalamiento basado en Sa(T1) (σln(μ)=0.40).
El uso de medidas de intensidad sísmica vectorial es una herramienta importante para reducir no solo el número de registros empleados para análisis dinámico no lineal; también estrategias para la selección de registros sísmicos no serán requeridas si la medida de IS puede predecir con suficiente aproximación la respuesta estructural, sin importar las características de los movimientos sísmicos utilizados en los análisis. Las implicaciones de una medida de intensidad ineficiente pueden resaltarse mediante el siguiente ejemplo. Considere dos ingenieros estructuritas cuya misión es seleccionar un número específico de acelerogramas (en este caso supongamos siete en total) que serán utilizados para diseñar un mismo edificio realizando análisis dinámicos no-lineales. Suponga que el primer ingeniero selecciona siete registros los cuales provocan la mayor demanda y que se ilustran encerrados en un círculo en la figura 3, mientras que el segundo ingeniero selecciona los registros que demandan menor ductilidad a la estructura y que se muestran en un cuadro. Bajo esta consideración, ¿cómo se esperarían los diseños de ambas estructuras? Es claro que los diseños serán bastante diferentes. Por tal motivo, la selección de acelerogramas y en especial las medidas de intensidad sísmica se vuelven cruciales para el diseño sísmico de estructuras en donde se emplea "análisis dinámico no-lineal paso a paso".
EFICIENCIA DE LOS VECTORES <Sa, Np> y <Sa, RT1,T2>
Una medida de intensidad sísmica eficiente puede ayudar considerablemente en la reducción del número de análisis requeridos para estimar la respuesta de estructuras sujetas a la acción de los sismos. Para ilustrar esto, el error estándar asociado a una muestra de tamaño n cuya dispersión de la DS para una medida de intensidad sísmica específica se puede expresar de la siguiente manera (Benjamin y Cornell, 1970):

La ecuación 5 implica que si se reduce la desviación estándar de la demanda sísmica dada una medida de IS, el número de registros empleados para el análisis dinámico también se reduce para un nivel de error. Como ejemplo, en el caso anterior se obtuvo que la dispersión para el vector <Sa, Np> asociado a la ductilidad fue de σln(μ)=0.228 implicando una reducción del 50% de la desviación comparada con el criterio de escalamiento basado en Sa(T1). Para igualar el mismo nivel de error estándar es necesario emplear en el caso de Sa(T1) cuatro veces más registros que en el caso del vector <Sa, Np>, lo cual indica la importancia de utilizar una medida con respecto de la otra.
En la parte precedente del trabajo se mostraron las ventajas de utilizar medidas de intensidad sísmica vectorial, y mediante un ejemplo se observó que los vectores <Sa, RT1,T2> y <Sa, Np> resultaron tener mejor relación con la respuesta estructural que las otras medidas mencionadas. En esta parte, se investiga a <Sa, Np> y la posibilidad de ser un candidato prometedor como predictor de la respuesta estructural, ya sea en términos de demandas máximas o acumuladas, y para movimientos sísmicos con distintas características. Para ello, se compara con Sa(T1), que es la medida de intensidad sísmica más utilizada hasta ahora y otras medidas de IS tales como <Sa, RT1,T2>. Para lograr dicho objetivo, se utilizaron los acelerogramas, modelos estructurales y parámetros de demanda sísmica que se describen en la siguiente parte del trabajo.
ACELEROGRAMAS Y MODELOS ESTRUCTURALES
Para los análisis fueron considerados tres conjuntos de registros sísmicos que se denominaron: registros NGA, cercanos al epicentro y finalmente movimientos sísmicos de banda angosta obtenidos del suelo blando de la ciudad de México. El primer conjunto corresponde a 194 registros que fueron recolectados por Tothong (2007), excepto que los registros provenientes del terremoto de Chi-Chi Taiwán se excluyeron para el presente trabajo. Estos registros fueron originalmente tomados de la base de datos NGA, por está razón en el presente estudio se denominarán "registros NGA". Su distancia más cercana a la falla está en el intervalo de 15 a 95kms, y el intervalo de magnitudes es de 5.65 a 7.90. Los acelerogramas fueron obtenidos de suelo rígido de todos los tipos de falla y se clasifican según la Geomatrix-C3 (Geotechnical Subsurface Characteristics) como clase C y D. Es importante notar que los registros aquí denominados NGA no fueron tomados tan cerca del epicentro y por otro lado no corresponden a movimientos de banda angosta. Para mayores detalles acerca de los registros ver Tothong (2007). Los registros cercanos al epicentro o de fuente cercana consisten en un conjunto de 48 movimientos sísmicos con un valor medio del periodo del pulso de velocidad cercano a 1s (promedio Tp≈1.0s) de acuerdo con Baker (2007). Los registros fueron rotados en la dirección normal a la falla. Se consideró un intervalo de magnitudes entre 5.6 y 7.6, y una distancia más cercana a la ruptura menor que 22kms. El conjunto de registros cercanos al epicentro representa un subconjunto del utilizado por Iervolino y Cornell (2008). Las principales características del conjunto de registros se describen en la tabla 1. Los movimientos sísmicos de banda angosta tienen la característica especial de afectar considerablemente estructuras específicas en un corto intervalo de periodos (especialmente, estructuras que sufren por ablandamiento o con periodos estructurales cercanos al periodo del suelo). De hecho, estos registros demandas grandes cantidades de energía a las estructuras comparados con movimientos de banda ancha (Terán y Jirsa, 2007). Un caso especial donde se generan este tipo de movimientos corresponde a la zona del lago de la ciudad de México. En este estudio, se utilizó un conjunto de 31 movimientos sísmicos obtenidos del suelo blando de la ciudad de México. El intervalo de magnitudes es de 6.9 a 8.1 (incluyendo el registro obtenido en la estación de la Secretaría de Comunicaciones y Transporte durante el evento sísmico del 19 de septiembre de 1985). Los registros utilizados previamente por (Bojórquez et al., 2008a) corresponden a eventos sísmicos de subducción y fueron tomados para un periodo del suelo cercano a 2 segundos, del lugar donde ocurrieron los mayores daños en la ciudad de México durante el temblor del 19 de septiembre de 1985. Mayores detalles de los registros se describen en Bojórquez et al. (2008a).
S1GL con comportamiento no-lineal, marcos de concreto reforzado C/R y acero fueron analizados para el objetivo de este trabajo. Los S1GL corresponden a sistemas con diferentes periodos de vibración, comportamiento bilineal con 5% de rigidez de posfluencia y mismo porcentaje de amortiguamiento crítico. La estructura de C/R consta de tres crujías y cinco niveles, y tiene una altura del primer nivel de 4m, y 3m para el resto de los niveles. El ancho de crujía es de 5m. Se consideró un modelo de comportamiento histerético trilineal con degradación de sus características mecánicas SINA (Saiidi y Sozen, 1979). El periodo de vibración es de T1=0.66s y se utilizó un amortiguamiento crítico de 5%. El marco de acero fue utilizado en un estudio previo por Bojórquez et al. (2007). El periodo del modo fundamental de vibración es de 1.20s, y consta de tres crujías y ocho niveles. La altura de cada nivel es 3.5m, y el ancho de crujía de 8m. Se consideró un modelo de comportamiento histerético bilineal con 3% de rigidez de posfluencia y 3% de amortiguamiento crítico. Los modelos estructurales descritos, fueron utilizados para ilustrar el potencial del vector <Sa, Np> como predictor de la respuesta estructural de S1GL y sistemas de múltiples grados de libertad SMGL. La tabla 2 resume las propiedades principales de cada modelo. Las características geométricas del marco de C/R y acero se muestran en la figura 5.

PARÁMETROS DE DEMANDA SÍSMICA
Se utilizaron como parámetros de DS la demanda de ductilidad D (relación entre el desplazamiento máximo Dm dividido por el desplazamiento de fluencia Dy) y la distorsión máxima de entrepiso. Estos parámetros fueron seleccionados debido a su importancia para propósitos de diseño sísmico; sin embargo, ya que solo capturan información acerca de demandas máximas, también fueron considerados parámetros con una íntima relación con el efecto de la duración del movimiento del terreno en las estructuras. El tercer parámetro de DS utilizado es la energía histerética normalizada EN por el desplazamiento y resistencia a la fluencia Fy (ver ecuación 6), dicho parámetro captura información acerca de los efectos de la duración del movimiento sísmico o de las demandas acumuladas por deformaciones plásticas (Iervolino et al., 2006); además, es un claro indicador del daño que sufren las estructuras (Bojórquez et al., 2010a). Es importante mencionar que en el caso de los SMGL, Fy y Dy se obtuvieron mediante análisis de empuje lateral estático (push-over), y que EH corresponde al total de la energía plástica disipada por la estructura (energía plástica disipada por todos los elementos que integran al marco). Finalmente, la ductilidad se obtuvo como la relación entre desplazamiento máximo de azotea dividido por el desplazamiento de fluencia Dy.

Por último, se consideró el conocido índice de daño de Park y Ang (IDPA). La expresión de IDPA se ilustra en la ecuación 7. En esta ecuación, μ y μD representan la capacidad de ductilidad monotónica del sistema y la demanda máxima de ductilidad respectivamente, y β es un parámetro que representa la contribución de la energía histerética disipada al daño, se consideró un valor de β =0.15 sugerido por Cosenza et al. (1993) para el caso de estructuras con ciclos histeréticos estables.

RESULTADOS
Registros NGA
Se analiza un S1GL con un periodo T=0.6s. El conjunto de 194 registros NGA fueron escalados para valores similares de Sa(T1) igual a 1g, nivel de escalamiento que provoca que la mediana de la ductilidad sea igual a 6. Lo anterior implica que se utilizó un método de escalamiento lineal. Una vez que se obtuvo la respuesta estructural para dicho nivel de escalamiento, se determinó la relación entre el segundo parámetro del vector y la demanda de ductilidad. La figura 6 ilustra la relación entre épsilon, RT1,T2 y Np con la ductilidad. Se observa buena relación entre los parámetros estudiados y la ductilidad, especialmente para Np que resulta relativamente más eficiente comparado con RT1,T2 y mucho más eficiente que épsilon. Estas observaciones también son válidas en la predicción del índice de daño de Park y Ang para el mismo sistema, pero en este caso los registros fueron escalados para valores similares de Sa(T1) igual a 0.7g. La figura 7 ilustra la relación entre épsilon RT1,T2 y Np con IDPA. Se observa buena relación de los parámetros con IDPA, especialmente para Np, y es evidente como la eficiencia de Np comparada con RT1,T2 es moderadamente mayor. Se aprecia menor dispersión para el vector <Sa, Np>.
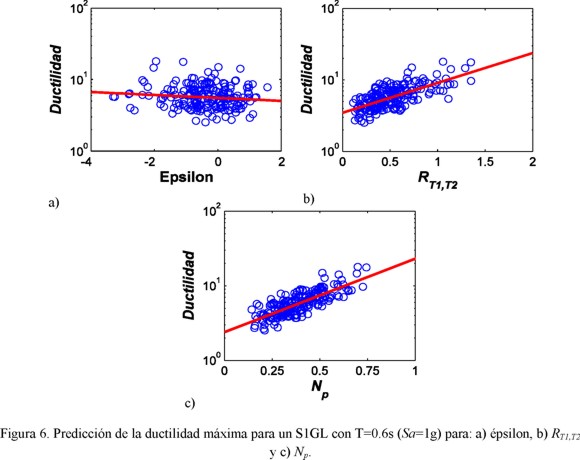

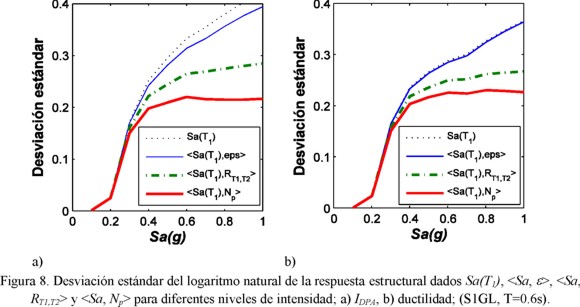
Los resultados ilustrados en la figuras 6 y 7 son válidos para un nivel específico de Sa(T1). Sin embargo, se requiere demostrar que las conclusiones son válidas para un intervalo amplio de niveles de intensidad. Para ello, la figuras 8a y 8b ilustran la desviación estándar del logaritmo natural de IDPA, para Sa(T1), y los vectores <Sa, &epsilon>, <Sa, RT1,T2> y <Sa, Np> para distintos niveles de intensidad sísmica. Se observa que las conclusiones obtenidas anteriormente, son válidas para distintos niveles de IS. Esto es, el vector <Sa, Np> resulta en menor dispersión para los diferentes niveles de intensidad considerados. También puede observarse que, mientras los parámetros analizados tienden a incrementar su dispersión a medida que crece la intensidad, en el caso del vector aquí propuesto <Sa, Np>, la desviación estándar se mantiene constante aún para valores muy grandes de la intensidad sísmica. Note que el vector basado en épsilon resulta en mayores dispersiones comparado con los otros vectores estudiados, y debido a que Tothong y Luco (2007) y Bojórquez et al. (2008b) observaron algunas de sus limitaciones para predecir la respuesta estructural. El presente trabajo se enfoca en Sa(T1) por ser uno de los parámetros más utilizados para estimar el peligro sísmico, así como en <Sa, RT1,T2> y <Sa, Np> por tener mejor relación con la demanda sísmica. Cabe mencionar que épsilon no se calculó para el caso de registros de fuente cercana y banda angosta por dos razones: la primera es por la ineficiencia que ha presentado épsilon, y la segunda por la carencia de modelos de atenuación que permitan estimarlo para este tipo de registros.
Las distorsiones máximas de entrepiso para el marco de C/R sometido a la acción de 40 registros seleccionados de manera aleatoria de los 194 registros NGA escalados para Sa(T1)=1g confirman las conclusiones derivadas para el S1GL (ver figura 9). Los vectores basados en <Sa, Np> y <Sa, RT1,T2> predicen con suficiente aproximación la distorsión máxima de entrepiso para la estructura de C/R, y resulta evidente como el vector aquí propuesto reduce las incertidumbres asociadas a la respuesta estructural. La gráfica para Np ilustra una relación bastante buena con las distorsiones máximas de entrepiso. Esto se debe a que existe una clara interpretación de los resultados basados en Np. Mientras la dispersión en el caso de Np es 0.216, para RT1,T2 es igual a 0.284. Esto implica que el número de registros usados para análisis dinámico no-lineal en el caso de Np se reduce a cerca del 60% si se compara con el número de registros requeridos para RT1,T2. Observaciones similares son válidas para diferentes niveles de intensidad sísmica como se muestra en la figura 10. En general, se concluye que Np resulta mejor predictor de la respuesta de estructuras sujetas a los registros de la base de datos NGA.


Registros cercanos al epicentro
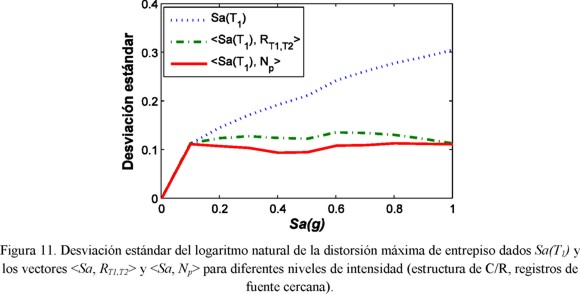
Se ha observado que los registros sísmicos tomados cerca del epicentro se caracterizan por presentar pulsos de velocidad, y tienen una importante influencia en estructuras donde la relación entre el periodo de vibración estructural y el periodo del pulso de velocidad es 0.5 (T1/Tp=0.5) (Mavroeidis et al., 2004; Fu, 2005; Alavi y Krawinkler, 2006). Por ello, se esperan importantes niveles de demanda estructural en el marco de C/R cuando se somete a la acción de los 48 movimientos sísmicos cercanos al epicentro, ya que su periodo de vibración es T1=0.66s, mientras que el periodo promedio de los pulsos de velocidad es (Tp≈1.0s) y por ésta razón se analizó dicha estructura. La figura 11 compara la desviación estándar de la distorsión máxima de entrepiso para distintos niveles de intensidad sísmica y los parámetros de medida de intensidad sísmica estudiados. Tanto Np y RT1,T2 están muy bien relacionados con las demandas de distorsión como se observa en la figura a través de valores bajos de la desviación estándar. De hecho, la figura 11 muestra que la incertidumbre asociada a la respuesta estructural tiende a reducirse a medida que se incrementa el nivel de intensidad sísmica. Para este caso, el parámetro Np presenta solo ligeramente una mejor relación con la respuesta estructural comparado con RT1,T2. Aún así, la consistencia del parámetro Np para predecir la respuesta estructural continúa siendo mejor, y hasta ahora, el parámetro aquí propuesto ha resultado el más apropiado para todos los casos analizados.
Registros sísmicos de banda angosta
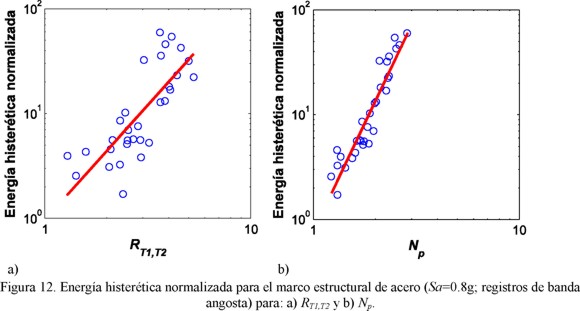
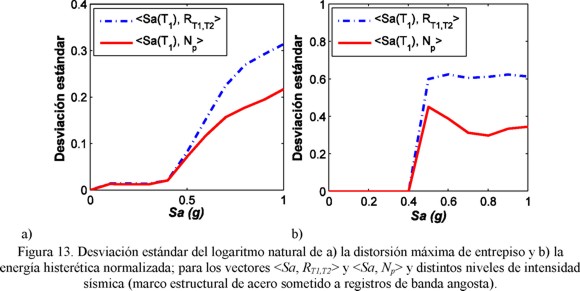
El marco estructural de acero se sometió al conjunto de movimientos sísmicos de banda angosta. La figura 12 ilustra la energía histerética normalizada obtenida para dicho marco de ocho niveles sujeto a los registros sísmicos de banda angosta, los cuales se escalaron para una Sa(T1)=0.8g. Para el caso del vector en estudio, como la figura 12 lo sugiere, la eficiencia del vector <Sa, RT1,T2> comparado con <Sa, Np> es menor, note que <Sa, Np> el cual fue consistente para todos los casos analizados, en la predicción de demandas máximas o de energía plástica en estructuras, y para los registros con tan diversas características empleados; especialmente para movimientos sísmicos de banda angosta como los que ocurren en el valle de México, es más apropiado comparado con <Sa, RT1,T2> o Sa(T1). Además, para evidenciar aún más el potencial de <Sa, Np> para movimientos de banda angosta, el número de registros requeridos para análisis dinámico no-lineal es solo el 28% de los necesarios en el caso de <Sa, RT1,T2>. Finalmente, la figura 13 demuestra que <Sa, Np> es más eficiente que <Sa, RT1,T2> para distintos niveles de intensidad sísmica y para la predicción tanto de la distorsión máxima de entrepiso como de la energía histerética normalizada. Debido a todos los resultados aquí obtenidos, se puede concluir que <Sa, Np> debe ser considerado como un candidato prometedor para la generación de nuevas medidas de intensidad sísmica.
HACIA EL PERFECTO PREDICTOR DE LA RESPUESTA ESTRUCTURAL DE EDIFICACIONES SOMETIDAS A MOVIMIENTOS SÍSMICOS DE BANDA ANGOSTA
De especial interés para la Ingeniería Sísmica Méxicana es contar con un buen predictor de la respuesta estructural de edificios sometidos a movimientos de banda angosta, ya que este tipo de registros son muy comunes en el suelo blando del valle de México donde existe una gran concentración de la población total del país. Sin embargo, dado que se ha observado el efecto que tiene la relación entre el periodo del sistema y el periodo dominante del terreno sobre las demandas sísmicas para el caso de este tipo de movimientos (Miranda, 1993; Terán-Gilmore, 2001; Ruiz-García y Miranda, 2004; Bojórquez y Ruiz, 2004). Es importante analizar estructuras con distintos periodos fundamentales de vibración, con la finalidad de ejemplificar la generalidad de los resultados y de manera implícita tomar en cuenta si las medidas de intensidad sísmica funcionan de manera apropiada para diferentes relaciones de periodos del suelo y la estructura. Por está razón, en esta parte del trabajo se compara la eficiencia de los parámetros aquí considerados como predictores de la distorsión máxima de entrepiso para registros de banda angosta, y utilizando varias edificaciones de acero diseñadas con el Reglamento de Construcciones del Distrito Federal que van desde 4 a 14 niveles y cuyas características se muestran en la tabla 3, y que tienen geometría similar a la figura 5b. Dichas edificaciones son representativas de periodos menores, cercanos e iguales al periodo fundamental del suelo que es de 2s. Note que no se eligieron estructuras con periodos largos mayores al periodo del suelo, ya que este tipo de estructuras requieren un trato especial por la influencia de los modos superiores, efecto que no considera la propuesta aquí presentada, pero que se discute más adelante en el presente trabajo para su posible incorporación en estudios futuros.

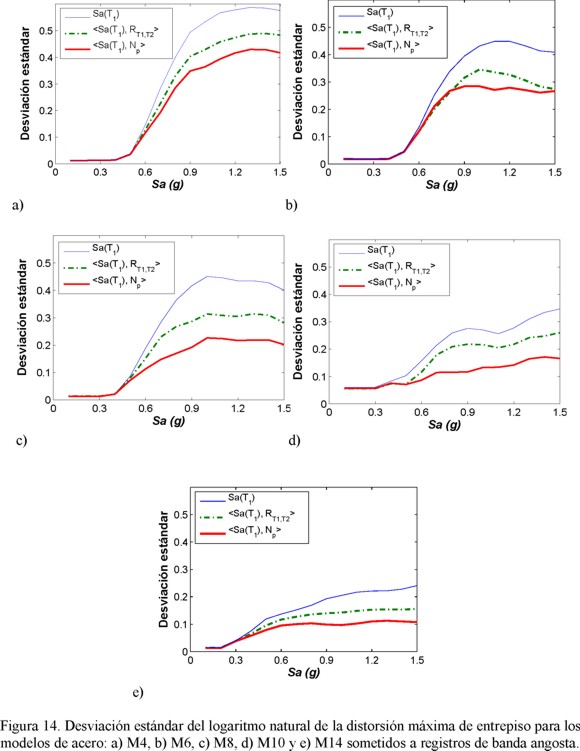
Se decidió evaluar la eficiencia para la distorsión máxima de entrepiso por ser el parámetro que recomienda el Reglamento del Distrito Federal para garantizar un desempeño sísmico satisfactorio. Las figuras 14a, 14b, 14c, 14d y 14e muestran la desviación estándar del logaritmo natural de la distorsión máxima de entrepiso, para Sa(T1), y los vectores <Sa, RT1,T2> y <Sa, Np> para distintos niveles de intensidad sísmica. Se observa que las conclusiones obtenidas anteriormente para el marco de 8 niveles de acero, son válidas para todas las estructuras aquí consideradas. Para todos los marcos de acero analizados, el vector <Sa, Np> resulta en menor dispersión para el intervalo de niveles de intensidad sísmica utilizados. Note que al usar Np y RT1,T2 como segunda componente del vector, se logra incrementar la eficiencia en la predicción de la respuesta estructural de manera considerable comparado con el uso único de Sa(T1), lo cual muestra las ventajas de utilizar las medidas vectoriales. Todo lo anterior permite concluir que la medida de intensidad aquí propuesta estima con buena precisión las distorsiones máximas de entrepiso de edificaciones sometidas a movimientos de banda angosta sin importar el periodo de las estructuras, al menos para estructuras de baja y mediana altura.
UNA MEDIDA DE INTENSIDAD SÍSMICA ESCALAR
Se describieron las ventajas de utilizar medidas de intensidad vectorial, y se demostró que <Sa, Np> es una medida de intensidad sísmica eficiente. Además, debido a la suficiencia de Sa(T1) con respecto a la magnitud y la distancia, el parámetro también resulta suficiente; finalmente, Bojórquez y Iervolino (2011) y Bojórquez et al. (2011) demostraron que es robusto; es decir, el vector <Sa, Np> cumple con las propiedades de suficiencia, eficiencia y robusta al escalamiento. Sin embargo, la evaluación de la tasa media anual de excedencia de una demanda estructural en específico para el caso del vector <Sa, Np> requiere de la ecuación 4, donde es necesario evaluar dos integrales y f Np | Sa T1 que es la función de densidad de probabilidades de Np dado Sa(T1). Por el contrario, para el caso de una medida de IS escalar, la tasa media anual de que DS exceda un valor de x puede ser calculada mediante la ecuación 2, que aquí vuelve a escribirse como ecuación 8:
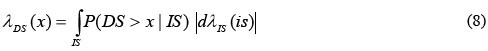
En la ecuación 8, P(DS > x | IS) es la probabilidad de excedencia de DS dada la IS y dλIS(is) = λIS(is) - λIS(is + dis) representa la diferencia de la curva de peligro sísmico en función de cierta medida de IS como se mencionó anteriormente. En otras palabras, el uso de una medida escalar simplifica el cálculo de la tasa media anual de excedencia, además, el uso de una medida de intensidad sísmica escalar permite un entendimiento más claro de su relación con la respuesta estructural. Por esta razón, también se propone un escalar basado en Sa(T1) y Np con características similares al escalar propuesto por Cordova et al. (2001), el cual se muestra en la ecuación 9.

En la ecuación 9, INp es la medida de intensidad sísmica escalar propuesta, y es un parámetro que tiene que ser calibrado dependiendo de la estructura y la medida de demanda sísmica considerada. Se puede observar de la ecuación 9 lo siguiente: 1) la aceleración espectral en el modo fundamental de vibración es un caso particular de INp, el cual ocurre cuando α es igual a cero; 2) Saavg(T1...TN) también representa un caso particular del parámetro propuesto cuando α = 1. Los siguientes análisis demuestran que el valor óptimo de alfa se encuentra en un intervalo de cero a uno; esto implica que se da un peso diferente a la contribución de las ordenadas espectrales para la aceleración espectral en el periodo T1 comparado con las ordenas espectrales para periodos mayores. En realidad el trabajo de consiste en dar una contribución adecuada a Sa(T1) en la respuesta estructural, con respecto a las ordenas espectrales en otros periodos. Con la finalidad de obtener los valores óptimos de α se asumirá TN = 2T1 que es consistente con los resultados obtenidos por Bojórquez y Iervolino (2011). Además, se utilizarán S1GL con distintos periodos de vibración en un intervalo de 0.5 a 2.5s, y se calibrará tanto para la demanda máxima de ductilidad como para el índice de daño de Park y Ang. Para limitar el número de análisis, únicamente se utilizaran tres subconjuntos de 31 acelerogramas obtenidos de los grupos utilizados. Se utilizan todos los registros de banda angosta.
La tabla 4 resume los valores obtenidos de α para las estructuras sujetas a todos lo acelerogramas empleados. Se observan valores similares de dicho parámetro para los distintos grupos de acelerogramas, estructuras analizadas y ambas medidas de demanda sísmica consideradas. Por este motivo, se concluye que α es independiente de las características del movimiento y de la estructura analizada. Los resultados sugieren un valor medio de α igual a 0.4. Es importante observar que el parámetro fue calibrado utilizando el intervalo completo de niveles de intensidad, y por este motivo no se observa la dependencia de α con respecto al nivel de intensidad sísmica.
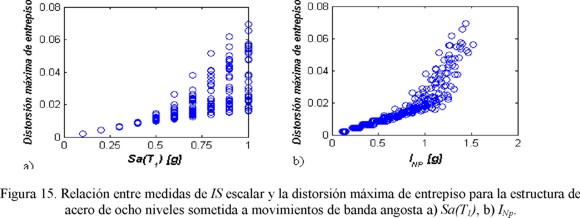
La figura 15 compara para la estructura de acero sometida a los registros de banda angosta, la distorsión máxima de entrepiso para Sa(T1) y INp ambos como fracción de la gravedad. Con la finalidad de comparar valores equiparables, éstos se comparan haciendo análisis dinámico incrementales para Sa(T1), y después los valores específicos del parámetro INp asociados a las distorsiones máximas de entrepiso se incluyeron en el eje horizontal. Los resultados ilustrados en la figura 15 muestran el potencial de la medida escalar aquí propuesta para predecir la respuesta estructural, y por lo tanto su eficiencia. De hecho, se observa una relación muy clara entre INp y las distorsiones máximas de entrepiso para distintos niveles de intensidad sísmica, donde a diferencia de Sa(T1), la dispersión no se incrementa cuando crece la demanda sísmica. Finalmente, no se observa la problemática planteada en la selección de registros para diseño sísmico mediante análisis dinámico no-lineal de estructuras, ya que gracias a la eficiencia del parámetro propuesto, no se requieren cuidados especiales para la selección de acelerogramas si se utiliza el parámetro aquí estudiado.
EVALUACIÓN DEL PELIGRO SÍSMICO EN TÉRMINOS DE INp
La posibilidad de evaluar el peligro sísmico es crucial para cualquier medida de intensidad sísmica que se proponga. Por esta razón, se demuestra que el análisis del peligro sísmico para INp puede efectuarse mediante herramienta actualmente disponible para otras medidas de intensidad sísmica. Sustituyendo la ecuación 3 en la parte derecha de la expresión 9 y aplicando el logaritmo natural en ambos lados se tiene:
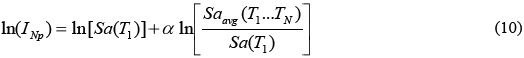
Como Saavg(T1...TN) se determina a partir de la expresión 11, la media y la varianza de ln(INp) se pueden expresar mediante las ecuaciones 12 y 13.
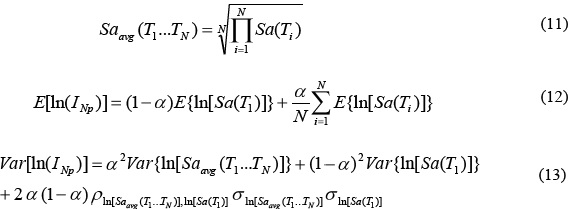
Los valores de ln[Sa(Ti)] se asumen comúnmente con distribución normal (Bazzurro y Cornell, 2002; Stewart et al., 2002), y por esta razón Var ln[Saavg(T1...TN)] también lo es, lo que indica que ρln[Saavg(T1...TN)],ln[Sa(T1)] se puede obtener mediante las ecuaciones 14 y 15 (Baker y Cornell, 2006).
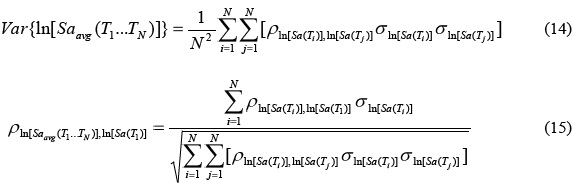
En las ecuaciones anteriores, el coeficiente de correlación ρln[Sa(Ti)],ln[Sa(Tj)] dependerá del tipo de movimientos sísmicos que se consideren, por lo que es necesario establecer ecuaciones que permitan estimar dicho coeficiente para movimientos sísmicos de diferentes características, tal como la relación propuesta por Inoue y Cornell (1990) que se indica en la ecuación 16.
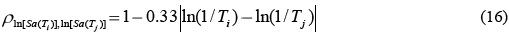
Finalmente, debido a que los valores de ln[Sa(Ti)] se asumen normalmente distribuidos, las ecuaciones 12 y 13 pueden estimarse mediante relaciones de atenuación actualmente disponibles, y estas ecuaciones son suficientes para describir la completa distribución de ln[INp); por último, esto permite el análisis del peligro sísmico tal como se hace para un valor en particular de la aceleración espectral.
Np PARA CARACTERIZAR DIVERSAS FORMAS ESPECTRALES, INCORPORACIÓN DE MODOS SUPERIORES Y ESTUDIOS FUTUROS
Se observó el potencial de un nuevo parámetro para caracterizar el espectro de pseudo-aceleración el cual se denomina Np, ya que representa N puntos del espectro. Aunque el estudio demostró la capacidad de dicho parámetro como predictor de la respuesta estructural. Es necesario observar que pasaría si se utiliza Np para caracterizar un espectro diferente al de pseudo-aceleración; es decir, estudiar la relación entre la respuesta estructural y un vector o un escalar basado en el espectro de pseudo-velocidad NpSV, el espectro de energía de entrada NpE, el espectro de velocidad NpV, el espectro de desplazamiento NpD o incluso de espectros inelásticos representativos de demandas máximas, de energía o índices de daño, etc., ya que éstos parámetros podrían tener una mejor relación con ciertas demandas sísmicas que el Np aquí analizado. Además, una opción podría ser utilizar vectores por ejemplo de la siguiente forma <SV, Npi>, donde el primer parámetro es la pseudo-velocidad en el modo fundamental de vibración y Npi representa un parámetro para caracterizar cualquier tipo de espectro. Actualmente algunos de los autores de este estudio están trabajando en esa dirección.
El trabajo aquí presentado se limitó a predecir la respuesta sísmica no-lineal de estructuras; sin embargo, es necesario contar con una medida de intensidad sísmica capaz de predecir la respuesta de estructuras dominadas por modos superiores. Esto puede efectuarse a través de una modificación al parámetro Np que abarque no solo desde T1 hasta TN sino desde el modo de interés hasta el periodo final. Por ejemplo, evaluar Np desde T2modo hasta TN. Note que la selección de acelerogramas del FEMA se basa en un planteamiento similar, en el cual puede adoptarse el parámetro aquí propuesto para dicha selección. Además, la inclusión de los modos superiores puede realizarse ya sea a través de un vector que incluya tres parámetros <Sa, RT1,T2, RT1,T2modo>, <Sa, Np, RT1,T2modo>, < Sa, INp, RT1,T2modo > o simplemente dando un peso específico a la contribución de la respuesta elástica, nolineal y aquella dominada por modos superiores.
Sería interesante realizar un estudio similar evaluando Np no como la relación entre la media geométrica y Sa(T1), sino con la media geométrica ponderada dividido entre Sa(T1), la cual mejoraría sustancialmente la eficiencia del vector y el escalar aquí propuesto. Puede observarse que existen una amplia gama de posibilidades que podrían incorporarse al estudio aquí presentado con la finalidad de incrementar la eficiencia en la predicción de la respuesta estructural. Además, aunque es necesario comparar otras medidas de intensidad sísmica comúnmente utilizadas que no dependen de la forma espectral. Un estudio reciente desarrollado por Bojórquez et al. (2010b), demostró que la evaluación de la vulnerabilidad sísmica de edificaciones de acero resulta más conveniente si se utiliza <Sa, Np> comparado con medidas vectoriales que dependen de la intensidad de Arias (Arias, 1975), el ID propuesto por Cosenza y Manfredi (1997), la aceleración máxima del suelo, la velocidad máxima del suelo, entre otras. Lo anterior sugiere que la medida vectorial aquí analizada es un buen candidato para reflejar el potencial destructivo de un movimiento sísmico.
Es importante resaltar que la aplicación de la medida de intensidad sísmica propuesta debe limitarse a estructuras con periodos de vibración de 2.5s que están asociadas a TN igual a 5, ya que en los modelos de atenuación para periodos largos la señal registrada por los acelerógrafos está influenciada por ruido que se elimina mediante el proceso de filtrado y que puede afectar considerablemente los valores de las ordenadas espectrales. Uno de los retos para el cálculo de Np es estimar el número de periodos intermedios que deben considerarse. Esto se debe abordar mediante un estudio para encontrar el número de periodos intermedios óptimo que maximiza la eficiencia del parámetro como predictor de la respuesta estructural. Aunque algunos de los autores actualmente están trabajando en esta dirección. En este estudio se decidió utilizar puntos a cada diferencial de periodo igual a 0.1s, indicando que el número de puntos depende del periodo de la estructura. Se debe enfatizar que lo anterior dio lugar a buenos resultados, lo que significa que un estudio de optimación podría todavía mejorar sustancialmente el comportamiento de la medida de intensidad sísmica propuesta.
CONCLUSIONES
Se estudio el potencial de varias medidas de intensidad sísmica basadas en la forma espectral. Se observó que la nueva medida de IS vectorial basada en Sa(T1) y un parámetro relacionado con la forma espectral denominado Np al compararlo con otras medidas de IS comúnmente empleadas resultó más adecuado. En general, los vectores <Sa, Np> y <Sa, RT1,T2> resultaron mejores predictores comparados con <Sa, > y Sa(T1). Se observó como el vector <Sa, Np> mostró mayor eficiencia con respecto al vector <Sa, RT1,T2> para predecir desplazamientos máximos y demandas de energía en S1GL con comportamiento no-lineal, marcos de C/R y acero sujetos a la acción de registros de suelo rígido y de aquellos tomados en las cercanías del epicentro. El incremento en la eficiencia, y por lo tanto reducción en la incertidumbre en la respuesta sísmica a través de <Sa, Np> fue particularmente importante para estructuras sujetas a movimientos sísmicos de banda angosta como los que se presentan en el suelo blando de la ciudad de México con respecto a <Sa, RT1,T2> y las otras medidas de IS empleadas. Reducir la incertidumbre en la respuesta estructural es de importancia relevante para la selección de registros sísmicos sea para análisis y diseño sísmico de estructuras, que para evaluar la confiabilidad sísmica. Mientras que el vector <Sa, RT1,T2> no aporta información acerca de periodos intermedios en el intervalo T1 a T2, la naturaleza del vector <Sa, Np> permite proveer de dicha información que resulta fundamental en registros de banda angosta.
Por otro lado, se propuso una medida de intensidad sísmica escalar basada en Sa(T1) y Np, ya que el uso de medidas escalares es más simple que el caso de las medidas vectoriales, y éstas permiten un mejor entendimiento de su relación con la respuesta estructural. Se observó que existe una relación muy clara entre INp y la respuesta estructural para distintos niveles de intensidad sísmica, y no se requieren cuidados especiales para la selección de acelerogramas. Finalmente, se demostró que el análisis del peligro sísmico para INp puede realizarse con herramienta actualmente disponible para otras medidas de intensidad sísmica.
Se concluye que el vector <Sa, Np> y el escalar INp deben ser considerados como candidatos prometedores para la generación de nuevas medidas de intensidad sísmica.
AGRADECIMIENTOS
Se agradecen los valiosos comentarios de los revisores anónimos, que ayudaron a enriquecer el trabajo aquí presentado. Este trabajo se desarrollo con el apoyo económico brindado por el Consejo Nacional de Ciencia y Tecnología CONACYT, así como a la Universidad Autónoma de Sinaloa dentro del proyecto PROFAPI2011/029.
REFERENCIAS
Alavi, B y H Krawinkler (2001), "Effects of near-field ground motion on frame structures", Report No. 138, John A. Blume Earthquake Engineering Center, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA, http://blume.stanford.edu/Blume/TRList.htm (accessed 5/31/2006) [ Links ]
Arias, A (1970), "A measure of earthquake intensity", Seismic Design for Nuclear Power Plants, edited by R. J. Hansen, MIT Press, Cambridge, MA, pp. 438-483. [ Links ]
Baker, J W (2005), "Vector-valued ground motion intensity measures for probabilistic seismic demand analysis". Ph.D. Thesis, Stanford University. [ Links ]
Baker, J W y C A Cornell (2005), "A vector-valued ground motion intensity measure consisting of spectral acceleration and epsilon", Earthquake Engineering and Structural Dynamics, No 34, pp. 1193-1217. [ Links ]
Baker, J W y C A Cornell (2006), "Spectral shape, epsilon and record selection", Earthquake Engineering and Structural Dynamics, No 35, pp. 1077-1095. [ Links ]
Baker, J W (2007), "Quantitative classification of near-fault ground motions using wavelet analysis", Bulletin of the Seismological Society of America, Vol. 97, No 5, pp. 1486-1501. [ Links ]
Baker, J W y C A Cornell (2008), "Vector-valued intensity measures incorporating spectral shape for prediction of structural response", Journal of Earthquake Engineering, Vol. 12, No 4, pp. 534-554. [ Links ]
Baker, J W y C A Cornell (2008), "Vector-valued intensity measures for pulse-like near-fault ground motions", Engineering Structures, Vol. 30, No 4, pp. 1048-1057. [ Links ]
Bazzurro, P (1998), "Probabilistic seismic demand analysis", Ph.D. Thesis, Stanford University. [ Links ]
Bazzurro, P y C A Cornell (2002), "Vector-valued probabilistic seismic hazard analysis", 7th U.S. National Conference on Earthquake Engineering, Earthquake Engineering Research Institute, Boston, MA, USA. [ Links ]
Benjamin, J R y C A Cornell (1970), "Probability, statistic, and decision for civil engineers", McGraw-Hill, New York. [ Links ]
Bojórquez, E y S E Ruiz (2004), "Strength reduction factors for the valley of Mexico taking into account low cycle fatigue effects", 13th World Conference on Earthquake Engineering, paper 516, Vancouver, Canada 2004 (CD-ROM). [ Links ]
Bojórquez, E, M Díaz, S E Ruiz y F García-Jarque (2007), "Confiabilidad sísmica de varios edificios (cuatro a diez niveles) localizados en suelo blando de la Ciudad de México, diseñados con el RCDF-2004", Revista de Ingeniería Sísmica, No 76, pp. 1-27. [ Links ]
Bojórquez, E, S E Ruiz y A Terán-Gilmore (2008a), "Reliability-based evaluation of steel structures using energy concepts", Engineering Structures, Vol. 30, No 6, pp. 1745-1759. [ Links ]
Bojórquez, E, I Iervolino y G Manfredi (2008b), "Evaluating a new proxy for spectral shape to be used as an intensity measure", The 2008 Seismic Engineering Conference Commemorating the 1908 Messina and Reggio Calabria Earthquake (MERCEA '08). [ Links ]
Bojórquez, E, A Reyes-Salazar, A Terán-Gilmore y S E Ruiz (2010a), "Energy-based damage index for steel structures", Journal of Steel and Composite Structures, Vol. 10, No 4, pp. 343-360. [ Links ]
Bojórquez, E, A Reyes-Salazar, H E Rodriguez, J L Vazquez-Dimas y I Iervolino (2010b), "Evaluation of seismic fragility of steel frames using vector-valued IM", 14th European Conference on Earthquake Engineering, Ohrid, Macedonia. [ Links ]
Bojórquez, E y I Iervolino (2011), "Spectral shape proxies and nonlinear structural response", Soil Dynamics and Earthquake Engineering, Vol. 31, pp. 996-1008. [ Links ]
Bojórquez, E, A Terán-Gilmore, S E Ruiz y A Reyes (2011), "Evaluation of structural reliability of steel frames: interstory drifts versus plastic hysteretic energy", Earthquake Spectra, Vol. 27, No 3, pp. 661-682. [ Links ]
Boore, D M y G M Atkinson (2007), "Boore-Atkinson NGA ground motions relations for the geometric mean horizontal component of peak and spectral ground motion parameter", Pacific Earthquake Engineering Research Center, University of California, Berkeley, PEER Report. [ Links ]
Cordova, P P, G G Dierlein, S S F Mehanny y C A Cornell (2001), "Development of a two parameter seismic intensity measure and probabilistic assessment procedure", The second U.S.-Japan Workshop on Performance-Based Earthquake Engineering Methodology for Reinforce Concrete Building Structures, Sapporo, Hokkaido, pp. 187-206. [ Links ]
Cosenza, E, G Manfredi y R Ramasco (1993), "The use of damage functionals in earthquake engineering: a comparison between different methods", Earthquake Engineering and Structural Dynamics, Vol. 22, pp. 855-868. [ Links ]
Cosenza, E y G Manfredi (1997), "The improvement of the seismic-resistant design for existing and new structures using damage criteria", Seismic Design Methodologies for the Next Generation of Codes, Fajfar P, Krawinkler H (eds). Balkema, Rotterdam, pp. 119-130. [ Links ]
Fajfar, P y H Krawinkler (1997), "Conclusions and recommendations, in: Seismic design methodologies for the next generation of codes", Balkema, Rotterdam. [ Links ]
Fu, Q (2005), "Modeling and prediction of fault-normal near-field ground motions and structural response", Ph.D. Dissertation, Department of Civil and Environmental Engineering, Stanford University, Stanford, CA. [ Links ]
Housner, G W (1952), "Spectrum intensities of strong motion earthquakes", Proceedings, Symposium on Earthquake and Blast Effects on Structures, Earthquake Engineering Research Institute. [ Links ]
Iervolino, I y C A Cornell (2005), "Records selection for nonlinear seismic analysis of structures", Earthquake Spectra, Vol. 21, No 3, pp. 685-713. [ Links ]
Iervolino, I, G Manfredi y E Cosenza (2006), "Ground motion duration effects on nonlinear seismic response", Earthquake Engineering and Structural Dynamics, Vol. 35, pp. 21-38. [ Links ]
Iervolino, I y C A Cornell (2008), "Prediction of the occurrence of velocity pulses in near-source ground motions", Bulletin of the Seismological Society of America, Vol. 98, No 5, pp. 2262-2277. [ Links ]
Inoue, T y C A Cornell (1990), "Seismic hazard analysis of multi-degree-of-freedom structures", Reliability of marine structures, RMS-8, Stanford, CA. [ Links ]
Luco, N (2002), "Probabilistic seismic demand analysis, SMRF connection fractures, and near-source effects", Ph.D. Thesis, Stanford University. [ Links ]
Manfredi, G (2001), "Evaluation of seismic energy demand", Earthquake Engineering and Structural Dynamics, Vol. 30, pp. 485-499. [ Links ]
Mavroeidis, G P, G Dong y A S Papageorgiou (2004), "Near-fault ground motions, and the response of elastic and inelastic single-degree-of-freedom (SDOF) systems", Earthquake Engineering and Structural Dynamics, Vol. 33, No 9, pp. 1023-1049. [ Links ]
Miranda, E. (1993), "Site-dependent strength reduction factors", Journal of Structural Engineering, Vol. 119, No 12, pp. 3503-3519. [ Links ]
Park, Y J y A H Ang (1985), "Mechanistic seismic damage model for reinforced concrete", Journal of Structural Engineering ASCE, No 111(ST4), pp. 740-757. [ Links ]
Ruiz-García, J y E Miranda (2004), "Inelastic displacement ratios for design of structures on soft soils sites", Journal of Structural Engineering ASCE, Vol. 130, No 12, pp. 2051-2061. [ Links ]
Saiidi, M y M Sozen (1979), "Simple and complex models for nonlinear seismic response of reinforced concrete structures", Report UILU-ENG-79-2031, Department of Civil Engineering, University of Illinois, Urbana, Illinois. [ Links ]
Shome, N (1999), "Probabilistic seismic demand analysis of nonlinear structures", Ph.D. Thesis, Stanford University. [ Links ]
Stewart, J P, S J Chiou, J D Bray, R W Graves, P G Somerville y N A Abrahamson (2002), "Ground motion evaluation procedures for performance-based design", Soil Dynamics and Earthquake Engineering; No 22, pp. 765-772. [ Links ]
Terán-Gilmore, A (2001), "Consideraciones del uso de la energía plástica en el diseño sísmico", Revista de ingeniería Sísmica, SMIS, Vol. 65, pp. 81-110. [ Links ]
Terán-Gilmore, A y J O Jirsa (2007), "Energy demands for seismic design against low cycle fatigue", Earthquake Engineering and Structural Dynamics, Vol. 36, pp. 383-404. [ Links ]
Tothong, P y N Luco (2007), "Probabilistic seismic demand analysis using advanced ground motion intensity measures", Earthquake Engineering and Structural Dynamics, Vol. 36, pp. 1837-1860. [ Links ]
Tothong, P (2007), "Probabilistic seismic demand analysis using advanced ground motion intensity measures, attenuation relationships, and near source effects", Ph.D. Thesis, Stanford University. [ Links ]
Vamvatsikos, D y C A Cornell (2002), "Incremental dynamic analysis", Earthquake Engineering and Structural Dynamics, Vol. 31, pp. 491-514. [ Links ]
Von-Thun, J L, L H Rochin, G A Scott y J A Wilson (1988), "Earthquake ground motions for design and analysis of dams, in: Earthquake Engineering and Soil Dynamics II - Recent Advance in Ground-Motion Evaluation", Geotechnical Special Publication 20 ASCE, New York, pp. 463-481. [ Links ]














