Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Salud Pública de México
versión impresa ISSN 0036-3634
Salud pública Méx vol.49 no.3 Cuernavaca may./jul. 2007
ARTÍCULOS DE REVISIÓN
Modelos matemáticos para enfermedades infecciosas
Mathematical models for infectious diseases
Osval Antonio Montesinos-López, M en CI; Carlos Moisés Hernández-Suárez, PhDII
IFacultad de Telemática, Universidad de Colima. Colima, Colima, México
IIFacultad de Ciencias, Universidad de Colima. Colima, Colima, México
RESUMEN
OBJETIVO: Describir la importancia de los modelos matemáticos en la comprensión de la dinámica de transmisión de las enfermedades infecciosas, así como en el diseño de medidas eficaces de control.
MATERIAL Y MÉTODOS: Se revisaron las publicaciones internacionales sobre el tema a través de medios digitales; se identificaron alrededor de 60 artículos, aunque sólo se revisaron 27 de éstos por su estrecha relación con el tema.
RESULTADOS: Este trabajo explica de manera sinóptica los antecedentes, importancia y clasificación de los modelos matemáticos en padecimientos infecciosos. De modo adicional se describen con detalle algunos modelos comunes de transmisión de enfermedades y otros de uso más reciente que se utilizan en la modelación de trastornos infecciosos.
CONCLUSIONES: El empleo de modelos matemáticos ha crecido en grado significativo en los últimos años y son de gran ayuda para idear medidas eficaces de control y erradicación de las enfermedades infecciosas.
Palabras clave: dinámica de transmisión; modelos de transmisión de enfermedades
ABSTRACT
OBJECTIVE: To describe the importance of mathematical models in the understanding of infectious disease transmission dynamics, as well as in the design of effective strategies for control.
MATERIAL AND METHODS: International literature was reviewed on the subject through digital means. Around 60 papers about the subject were identified; nevertheless, this study is based on only 27 of these, due to the fact that they were directly related to the subject.
RESULTS:This work presents a brief explanation of the antecedents, importance and classification of mathematical models for infectious diseases. In addition, a detailed description of some classical models is discussed as well as other more recent models used in the modeling of infectious disease.
CONCLUSIONS: The use of mathematical models for infectious diseases has grown significantly in the last few years and has proven to be of great help in designing efficient strategies for control and eradication of infectious diseases.
Key words: dynamic of spread; models for the transmission of diseases
En términos históricos, las enfermedades infecciosas han constituido una amenaza muy grave para la sociedad. Durante la mayor parte del siglo XX las pandemias (epidemias que se propagan por áreas y poblaciones de enorme tamaño) se habían ya considerado amenazas del pasado; la medicina moderna se había ocupado para siempre de la peste, la viruela y otras catástrofes de carácter contagioso. No obstante, los cambios ambientales actuales han propiciado cambios en las distribuciones geográficas de organismos en general y de parásitos en particular. La resistencia a los agentes antimicrobianos también se ha convertido en un grave problema mundial. Algunas infecciones, antes fáciles de tratar con antibióticos, representan ahora una grave amenaza para la salud en todas partes. El caso de Toronto (Canadá), la única ciudad de un país occidental en la que la epidemia del síndrome respiratorio agudo grave (SRAG) se ha extendido de forma local, es un claro ejemplo de ello. Por lo tanto, en años recientes, las enfermedades infecciosas como malaria, tuberculosis, VIH/SIDA, SRAG y la posibilidad del bioterrorismo han provocado de nueva cuenta un gran efecto económico y de salud, sea en países desarrollados o del tercer mundo, lo cual indica que esta amenaza sigue presente. Por ello, el uso de métodos cuantitativos basados en modelos matemáticos para estudiar la dinámica de transmisión y control de las enfermedades infecciosas ha ganado importancia de forma notoria entre los científicos y profesionales de la salud para idear programas efectivos de control e interpretar patrones epidemiológicos.
En el presente trabajo se revisan los antecedentes, la relevancia y la clasificación de los modelos matemáticos para enfermedades infecciosas; además, se describen de forma detallada algunos modelos típicos y otros esquemas recientes que se utilizan cada vez más para modelar las enfermedades infecciosas.
Material y métodos
Se revisó la bibliografía internacional a través de medios digitales y se identificaron alrededor de 60 artículos, aunque sólo se analizaron 27 por su relación directa con el tema.
Resultados y discusión
Antecedentes
Es probable que el hombre formulara ya teorías acerca de la naturaleza de las enfermedades infecciosas desde mucho tiempo atrás. Por ejemplo, se atribuyó a una lenta nube de aire dañino la difusión de la peste negra en el siglo XIV como una explicación causal.1 D´Alembert fue el primero en describir la propagación de enfermedades infecciosas mediante un modelo matemático en el siglo XVIII.2 Sin embargo, el primer artículo conocido que incluye un modelo explícito para una enfermedad infecciosa apareció en 1760. El documento lo publicó Daniel Bernoulli (1700-82), de nacionalidad suiza, quien tenía conocimientos médicos y matemáticos. Bernoulli propuso varios modelos matemáticos mediante ecuaciones diferenciales para modelar algunas enfermedades infecciosas. Sus resultados parecen válidos aún y el principio de utilizar una técnica matemática de investigación para evaluar medidas alternativas de salud pública es tan aplicable hoy como hace 200 años.3
El segundo desarrollo se debe al famoso epidemiólogo y malariólogo Ronald Ross, quien explicó el ciclo completo de la malaria humana, con la inclusión del mosquito como vector y el parásito Plasmodium; esto le valió la obtención del premio Nobel en 1902.3 Ross fue un competente matemático aficionado y estaba convencido de la necesidad de usar las matemáticas para apoyar las investigaciones epidemiológicas.3
El siguiente gran avance fue el trabajo matemático de Kermack y McKendrick, realizado durante el periodo de 1927 a 1939. En su trabajo también se consideraron las enfermedades endémicas y diversos hallazgos interesantes se relacionaron en datos experimentales con ratones.3 El resultado excepcional fue el célebre teorema umbral, según el cual la introducción de individuos infecciosos dentro de una población de susceptibles podía originar una epidemia sólo si la densidad de susceptibles rebasa un cierto valor crítico o umbral. Si el umbral se excede, entonces sobreviene el brote y, de lo contrario, desaparece. El trabajo pionero atrajo escasa atención y sólo se tomó en cuenta 20 años más tarde cuando se dispuso de métodos efectivos de procesos estocásticos.3
Después de la Segunda Guerra Mundial resultó necesario mejorar el entendimiento de los procesos probabilísticos y muchos nuevos avances se efectuaron a partir de procesos estocásticos. El último de ellos se produjo a finales de la década de 1990, cuando los físicos comenzaron a interesarse por el estudio de las redes complejas al advertir que era vital una perspectiva reticular para entender la dinámica de las enfermedades como el VIH/SIDA. La identificación de las redes es de gran utilidad para comprender la rápida difusión de enfermedades infecciosas, como fue el caso del síndrome respiratorio agudo grave (SRAG) en 2003, que apareció en Hong Kong, se extendió a Norteamérica y Europa y cobró un número elevado de vidas en un plazo de 15 días.4
Importancia de los modelos matemáticos
La construcción de modelos matemáticos es una de las herramientas utilizadas hoy en día para el estudio de problemas en medicina, biología, fisiología, bioquímica, epidemiología, farmacocinética, entre otras áreas del conocimiento; sus objetivos primordiales son describir, explicar y predecir fenómenos y procesos en dichas áreas. Sin embargo, su aplicación se ve limitada con frecuencia por la falta de conocimientos e información acerca de los principios básicos del modelamiento matemático. La relevancia de la construcción de los modelos matemáticos para enfermedades infecciosas es evidente: a) la construcción de modelos revela algunas veces relaciones que no son obvias a primera vista; b) una vez construido el modelo matemático es posible extraer de él propiedades y características de las relaciones entre los elementos que de otra forma permanecerían ocultas; c) en la mayor parte de los problemas de enfermedades infecciosas del mundo real no es factible experimentar con la realidad, ya que puede ser muy costoso, peligroso, inmoral o incluso imposible. Por lo tanto, es natural intentar superar esta dificultad con la construcción de un modelo que describa de manera adecuada las características básicas de la epidemia y entonces usar el modelo para predecir las consecuencias de introducir cambios específicos;5 d) la función principal de un modelo para una enfermedad infecciosa consiste en proveer un medio que posibilita entender la dispersión de una enfermedad infecciosa a través de una población bajo diferentes escenarios.
Es importante resaltar que un modelo está en verdad definido por las relaciones que incorpora. Estas relaciones son independientes de los datos a introducir en el modelo, ya que un modelo puede usarse para diferentes ocasiones y en distintos contextos. Cabe señalar que los modelos matemáticos para enfermedades infecciosas se utilizan como herramienta para tomar decisiones y que deben valorarse en su justa medida, ya que difícilmente es comprensible un problema complejo sin una mínima modelación, aunque también hay que reconocer que no es posible modelar la totalidad de las situaciones reales. En esencia, la función central de crear y analizar modelos matemáticos es mejorar la comprensión de un sistema para prevenir futuras situaciones de enfermedades, determinar la prevalencia e incidencia y coadyuvar a tomar decisiones objetivas para controlar o erradicar las enfermedades.
Clasificación de los modelos matemáticos
Existen dos tipos de modelos matemáticos: determinísticos y estocásticos. En un modelo determinístico se pueden controlar los factores que intervienen en el estudio del proceso o fenómeno y por tanto se pueden predecir con exactitud sus resultados. En un modelo estocástico no es posible controlar los factores que intervienen en el estudio del fenómeno y en consecuencia no produce simples resultados únicos. Cada uno de los resultados posibles se genera con una función de probabilidad que le adjudica una probabilidad a cada uno de éstos, por ejemplo un modelo para predecir el tamaño de una epidemia en una población de N individuos. Para el caso determinístico se proporciona un valor único, C, mientras que el modelo estocástico permite la posibilidad de obtener desde cero hasta N individuos y se adjudica una cierta probabilidad a cada uno de estos sucesos. La diferencia es más grande de lo que parece, ya que en un modelo matemático determinístico en el contexto epidemiológico; un solo sujeto causa una epidemia generalizada, mientras que bajo un modelo estocástico existe la posibilidad de que la epidemia se extinga.
Conceptos básicos de epidemia
Número reproductivo básico. El principal parámetro utilizado en epidemiología es el número reproductivo básico, R0, definido como el número promedio de infecciones causadas por un individuo infeccioso cuando éste es introducido a una población de susceptibles e intenta capturar la capacidad reproductiva de la enfermedad.6 Hernández-Suárez7 propone otra definición de R0 y la expresa en términos de contactos: R0 es el número esperado de contactos que un individuo infeccioso tiene durante su periodo completo de infección, definiendo como un contacto cualquier actividad que pueda causar la infección de un susceptible.
Tamaño de la epidemia. Ésta es una de las propiedades asintóticas más importantes en los modelos epidemiológicos y se define como el número total de individuos infectados en una epidemia.8 Es una medida cuantitativa muy importante porque se relaciona de forma estrecha con los costos de la epidemia.
Principales modelos de transmisión de enfermedades infecciosas
Modelos SI, SIS y SIR
En los modelos epidemiológicos estándar se parte del supuesto de que los individuos se encuentran en uno de varios estados posibles. En función de dichos estados, la población puede incluirse en algunas categorías: individuos susceptibles (S), infectados (I) o removidos (R), etc. Los modelos más importantes son: SI, SIS y SIR, que pueden modelarse en forma determinista o estocástica y en todos ellos se asume que la interacción entre los individuos es aleatoria.9 La mejor manera de modelar las enfermedades infantiles consiste en emplear un modelo SIR puesto que la infección lleva a una inmunidad vitalicia. Para la mayor parte de las enfermedades de transmisión sexual (ETS) resulta más útil el modelo SIS, toda vez que tan sólo un número reducido de ETS confiere inmunidad tras la infección. El VIH es una excepción clara y todavía puede describirse de forma adecuada, al menos en el mundo occidental, mediante el modelo SI. A continuación se describen de modo sinóptico los modelos SI, SIS y SIR bajo sus dos versiones: determinística y estocástica.
La ecuación 1 presenta el modelo SI en su versión determínistica, es decir, como un modelo continuo en su forma más simple, consistente en un sistema de dos ecuaciones diferenciales:

En la ecuación 1 aparecen dos variables dependientes: el número de personas susceptibles (S) y el número de personas infectadas (I). En este modelo, bajo su versión estocástica, cada individuo infeccioso tiene contacto con otro, escogido al azar, a una tasa l (contactos por unidad de tiempo). Por lo tanto, la variable aleatoria tk, tiempo transcurrido entre la infección del individuo k-1 y el individuo k, para k=1,2,3,…, tiene una distribución exponencial con parámetro l, una constante que no cambia con el tiempo. Esto significa que la variable aleatoria X(t), que se refiere al número de susceptibles e infectados al tiempo t, es un proceso Poisson homogéneo. Los estados del proceso al tiempo t se identifican por X(t)={S(t),I(t)}, esto es, el número de susceptibles e infectados al tiempo t. Por consiguiente, cuando hay I infectados y S susceptibles, las probabilidades de transición son:

donde o(d) es una cantidad que tiende a cero cuando d tiende a cero. Para cada valor de tiempo bajo ambos modelos N=S(t)+I(t), donde N es el tamaño de la población. Además, el significado de un contacto es cualquier actividad que resulta en la infección de un susceptible por un individuo infeccioso. También este modelo en ambas versiones es homogéneo para las personas, ya que se presupone que cada individuo tiene el mismo número esperado de contactos, de tal forma que es posible afirmar que el modelo presupone una interacción aleatoria. La solución a este modelo en ambas versiones traza una trayectoria en forma de S, según se muestra en la figura 1, debido a que el número de individuos infectados que puede transmitir la infección es bajo en las primeras etapas del proceso, mientras que el número de individuos susceptibles es bajo en las últimas etapas. Como resultado, el número de infectados experimenta el mayor crecimiento durante la etapa intermedia del proceso.

El modelo SIS puede formularse como un sistema de dos ecuaciones diferenciales, como se ilustra a continuación:

La ecuación para el modelo SIS difiere de la del modelo SI porque se agrega el término µI(t) en la ecuación 3, que describe el ritmo al que los individuos se recuperan de la enfermedad o se convierten en susceptibles, por lo que se aplica en ambas ecuaciones. En el modelo SIS estocástico la tasa de contacto es también l (contactos por unidad de tiempo). De nueva cuenta, la variable aleatoria tiempo transcurrido entre la infección del individuo k-1 y el individuo k, para k=1,2,3,…, tiene una distribución exponencial con parámetro l. Del mismo modo, la variable aleatoria tiempo transcurrido entre la recuperación (el individuo se vuelve otra vez susceptible) del individuo k-1 y el individuo k, para k=1,2,3,…, tiene una distribución exponencial con parámetro µ. Ambas, l y µ, son constantes que no cambian con el tiempo. Por lo tanto, la variable aleatoria X(t), que alude al número de susceptibles e infectados al tiempo t, es un proceso Poisson homogéneo y también N=S(t)+I(t), de manera que los estados del proceso al tiempo t se identifican por X(t)={S(t),I(t)}, es decir, el número de susceptibles e infectados al tiempo t. Aquí, cuando hay I infectados y S susceptibles, las probabilidades de transición son:
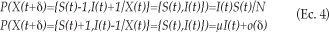
De igual manera, o(d) es una cantidad que tiende a cero cuando también lo hace d. La solución al modelo SIS en ambas versiones también muestra que se debería esperar una trayectoria en forma de S en la cifra de infectados. No obstante, la trayectoria SIS difiere de la SI en que el número de personas infectadas al mismo tiempo nunca alcanza el total de la población (lo que no excluye la posibilidad de que cada uno de los individuos pueda infectarse en algún otro momento). Por el contrario, el proceso alcanza un equilibrio cuando exactamente el mismo número de individuos infecciosos se convierte en susceptible o viceversa.
El último modelo descrito es el SIR, que en su forma más simple puede formularse como un conjunto de ecuaciones diferenciales, tal y como se muestra a continuación:

Por último, en el modelo SIR estocástico cada individuo infeccioso tiene también contacto con otro, escogido al azar, a una tasa l (contactos por unidad de tiempo). A diferencia del modelo SIS, un individuo infectado se recupera y en lugar de susceptible se vuelve inmune a una tasa µ. De nueva cuenta, la variable aleatoria tiempo transcurrido entre la infección del individuo K-1 y el individuo k, para k=1,2,3,…, muestra una distribución exponencial con parámetro l. Del mismo modo, la variable aleatoria tiempo transcurrido entre la recuperación (el sujeto se vuelve inmune) de los individuos k-1 y k, para k=1,2,3,…, tiene una distribución exponencial con parámetro µ. Ambas, l y µ, son constantes que no cambian con el tiempo. Por consiguiente, la variable aleatoria X(t), que denota el número de susceptibles e infectados al tiempo t, es un proceso Poisson homogéneo y aquí N=S(t)+I(t)+R(t); en consecuencia, los estados del proceso al tiempo t pueden identificarse con X(t)={S(t),I(t)}, esto es, el número de susceptibles e infectados al tiempo t. Aquí, las probabilidades de transición son:

También en este caso o(d) es una cantidad que tiende a cero cuando d también lo hace. El modelo SIR describe el proceso en las tres distintas etapas. La solución al modelo SIR muestra asimismo una trayectoria en forma de S en las primeras fases de la epidemia. Este modelo difiere tanto del modelo SI como del SIS porque muestra una propensión a acabar en cero infectados a largo plazo.
Para muchas enfermedades, como el sarampión o la gripe, que se transmiten a través de pequeñas gotas de respiración a partir de una persona infectada, la interacción aleatoria resulta una presunción razonable y probablemente una buena aproximación. En otras palabras, la presunción de interacción aleatoria ofrece una importante ventaja porque puede modelarse con facilidad mediante ecuaciones diferenciales y dichos modelos pueden estudiarse en términos analíticos.10
Estos tres modelos básicos en sus dos versiones pueden adaptarse a las características de las enfermedades específicas. Por ejemplo, resulta posible mostrar a individuos como inmunes durante un determinado intervalo de tiempo, nuevos sujetos que entran en la población mediante nacimientos o emigraciones y personas que la abandonan mediante procesos de migración o muerte. De igual forma, pueden generarse tipos de trayectorias más complejos, como comportamientos cíclicos e incluso dinámicas caóticas, que caracterizan a algunas afecciones infecciosas.
Teoría de redes de transmisión
La presunción de una interacción aleatoria no resulta apropiada para modelar la propagación de ciertos padecimientos. Por ello, a finales de la década de 1990 los científicos empezaron a interesarse por el estudio de redes complejas. Éstas son útiles para estudiar la dinámica en la transmisión de un mensaje, señal, rumor, líquido, moda o enfermedad infecciosa.11 En la actualidad, las redes complejas se emplean en muchos campos de la ciencia; existen redes sociales, económicas, neuronales, computacionales, de sistemas eléctricos, y muchas más.12 En dichas redes, los nodos o vértices se representan en un círculo a través de puntos equidistantes, es decir, los elementos del sistema (seres humanos, empresas, granjas, terminales de computadoras, plantas generadoras de electricidad, etc.) y las ligas que los unen representan las interacciones entre ellos.13 Desde el punto de vista de las matemáticas, el conjunto de los nodos y los enlaces en un sistema social define un grafo y su tratamiento analítico se conoce como teoría de grafos. Tal sistema actúa como catalizador en el desarrollo del análisis de redes sociales, que en la actualidad proporciona las herramientas básicas para el análisis de sociogramas.14 En las redes se describe la dinámica de la población a través de los patrones de contacto.
La importancia del patrón de contacto es una función del grado de contagiosidad de la enfermedad. Las infecciones se transmiten de persona a persona, ya sea directamente o a través del aire, los alimentos o el agua. Cuanto más estrecho sea el contacto para producir la transmisión más importante resulta el patrón de contacto.
La figura 2 muestra algunas enfermedades infecciosas conocidas, ordenadas en una escala unidimensional, de la más contagiosa y de transmisión no cercana en el extremo izquierdo a la menos contagiosa y de transmisión cercana en el extremo derecho. Para los fines de este documento basta decir que cuanto menor sea el grado de contagiosidad mayor atención debe concederse a los patrones sociales de contacto. Por otro lado, si se incrementa la contagiosidad también lo hacen la amenaza y el costo de falsear la importancia de la interacción social a todos los niveles.
La clave del análisis de las redes sociales radica en que el foco de atención del análisis se desplaza de las personas a las relaciones existentes entre ellas y los patrones generales de las relaciones en una población. Estas últimas pueden conectar a los individuos de tal manera que éstos formen díadas, tríadas o, en el presente contexto, redes más amplias. Por lo tanto, es evidente que los patrones de contacto influyen de forma notoria en la dispersión de una enfermedad infecciosa, debido a que éstos se realizan de manera local y a distancia.12
Las redes complejas pueden clasificarse en dos principales grupos, según sean sus propiedades de conectividad. Las redes exponenciales, en las cuales la distribución de conectividad de los nodos (la probabilidad P(k) de que un nodo esté conectado a otros k nodos) se ajusta a una exponencial y la segunda identificada por redes libres de escala (scale-free red) que exhiben una distribución de conectividad de ley de potencia.15
Dentro de las redes del mundo pequeño (figura 3), las más representativas son las siguientes: a) red regular, en la cual cada vértice se comunica con sus k/2 vértices vecinos; b) red aleatoria, en la que cada vértice se conecta con todos los demás; c) el modelo de Watts y Strogats, esto es, una red intermedia entre la regular y la aleatoria en la cual cada vértice se comunica con sus k/2 vértices vecinos, localizados a su lado (unos pocos se comunican con vértices lejanos).16 Todos estos modelos de redes se utilizan hoy en día en modelos de transmisión de enfermedades infecciosas. Sin embargo, en la actualidad el modelo de Watts y Strogats es uno de los más usados para modelar la transmisión de enfermedades infecciosas porque supone un patrón de contactos más real, puesto que en el mundo real cada individuo tiene contactos con un subconjunto de éstos. Por consiguiente, es razonable asumir que cada individuo se comunica con sus k vecinos inmediatos y que de los N individuos, sólo algunos de ellos, además de comunicarse con sus k vecinos inmediatos, se comunican con algunos sujetos lejanos (contactos a distancia). Esto significa que el patrón de contactos entre individuos se lleva a cabo bajo una red del mundo pequeño, donde cada individuo se representa por un nodo o vértice y los contactos entre individuos se representan por ligas y la transmisión de la enfermedad puede tener lugar sólo a través de estos nexos.

Modelos de urnas
Los modelos de urnas proveen un marco natural para analizar modelos de transmisión de enfermedades infecciosas.8 Construirlos y capturar su esencia son aspectos fáciles, ya que consisten en colocar canicas al azar en un conjunto de N urnas vacías. De modo inicial se parte de una urna infectada, la cual impulsa una cantidad aleatoria de canicas sobre las restantes N-1 urnas vacías y cada canica lanzada de la urna infectada se considera una amenaza de infección. Por otro lado, las urnas vacías y ocupadas se refieren como susceptibles e infectadas, respectivamente. Bajo estas condiciones, el proceso de infección puede reproducirse. También con esto es posible calcular el número esperado de infecciones al final del brote. En fecha reciente, estos modelos han provisto una forma de construir modelos de infección que permiten la estimación de parámetros bajo supuestos en algunos casos muy robustos. Un ejemplo muy interesante es el modelo que propusieron Hernández y Castillo17 para determinar la eficacia de las vacunas. Se presupone que un ensayo de eficacia de vacunas se lleva a cabo con N1 individuos vacunados y N0 sujetos no vacunados. Hernández y Castillo17 muestran que para una vacuna all/nothing con eficacia de vacuna, VE=1-b, la variable aleatoria X definida como el número de vacunados infectados en una muestra de tamaño n, total de infectados, sigue una distribución hipergeométrica. Ésta hace posible la derivación de propiedades importantes de este estimador, con lo cual es factible la construcción de intervalos de confianza y pruebas de hipótesis. Asimismo, Hernández y Castillo17 señalan que para la vacuna leaky la distribución de X es hipergeométrica no central, derivada por Wallenius.18 A pesar de que el cálculo analítico de b a través del método de máxima verosimilitud o el método de momentos es en particular difícil, resulta fácil encontrar el estimador de máxima verosimilitud de b con integración numérica o procedimientos de maximización.
Procesos de ramificación
Considérese el caso de un individuo infeccioso que habita en cierto espacio S y que, después de un tiempo de vida aleatorio, contagia y deja tras de sí una descendencia compuesta por y nuevos individuos infecciosos. Aquí y es una variable aleatoria, es decir, una cantidad que se determina mediante una función de densidad de probabilidad. Los nuevos sujetos infecciosos evolucionan de modo independiente, ajustados al patrón de vida de la partícula madre (primer individuo infeccioso): en ellos, que se reproducen, la enfermedad experimenta tiempos de vida aleatorios. A una población como la anterior se la conoce como población ramificada o proceso de ramificación. En este caso, los individuos, además de contagiar (reproducirse), pueden desplazarse en el espacio S o mutar y es posible que haya sujetos provenientes de otras poblaciones o fuentes que se trasladen al espacio S y luego se contagien. La presuposición fundamental en todas estas poblaciones ramificadas es que los individuos se ramifican (contagian) unos de otros de manera independiente. El número de personas infecciosas presentes al principio se denota por X0, esto es, el tamaño inicial de la epidemia (generación cero). Todos los individuos contagiados (descendientes) de la generación cero constituyen la primera generación y se incluyen en X1. En general, Xn denota el tamaño de la n-ésima generación; de igual manera, los Xn individuos en forma independiente producen los números de infecciosos (descendientes) y1(n),y2(n) ,…,yxn(n), por lo que el número de infecciosos al tiempo (generación) n(+1) es:

En consecuencia, los procesos de ramificación se usan en biología, física nuclear o epidemiología como modelos para estudiar el crecimiento, extinción y comportamiento asintótico de una población (seres humanos, animales, bacterias, neutrones, etc.). Cabe aclarar que tanto los modelos de urnas como los procesos de ramificación son enfoques de tipo estocástico.
Conclusiones
El empleo de modelos matemáticos para enfermedades infecciosas ha crecido en grado significativo en los últimos años debido a que proporcionan información útil para tomar decisiones, e instituir medidas operativas en el control o erradicación de una enfermedad infecciosa. Estos modelos son muy útiles porque capturan propiedades esenciales de la dispersión de una enfermedad de una forma simplificada. Además, al modificar los parámetros del modelo se pueden representar o descubrir situaciones que difícilmente se pueden obtener mediante experimentación.5 Por lo tanto, contribuyen a prevenir futuras situaciones patológicas, determinar la prevalencia e incidencia y coadyuvar a tomar decisiones objetivas para el control o supresión de las enfermedades infecciosas.
En fecha reciente, los modelos matemáticos se han utilizado en el establecimiento de políticas de vacunación19 (rubeola, sarampión, polio, entre otras) y cuarentena de granjas ganaderas y seres humanos; además, se han empleado en tareas tan complejas como el manejo de una pesquería durante 50 años. Para modelar la transmisión y el control del SRAG, un considerable número de aproximaciones se ha llevado a cabo en los últimos años.20-25 Por ejemplo, Gjorgjieva y colaboradores26 proporcionan un modelo que incorpora la vacunación como una posible medida para el control del brote del SRAG y encuentra la proporción mínima de individuos susceptibles que necesitan vacunarse exitosamente al inicio del brote para controlar la epidemia. Gjorgjieva y col. concluyen que si se dispone de una vacuna eficaz contra el SRAG, al vacunar a esta proporción mínima tan pronto como los primeros casos de la enfermedad se identifiquen en alguna región del mundo, este modelo permitiría controlar la enfermedad. Otro modelo para el SRAG es el que propusieron Chowell y colaboradores,27 que se ideó para predecir si las medidas de aislamiento y cuarentena podían interrumpir la dispersión de esta enfermedad en Ontario, Hong Kong y Singapore. Se trata de un modelo relativamente sencillo y requiere 11 parámetros. Sin embargo, los autores reconocen que es imposible hacer predicciones exactas con este modelo. Pese a ello, el modelo fue capaz de ilustrar la efectividad de la cuarentena como una medida de control, cuando ésta se aplica a la brevedad.
Cabe mencionar que la adición de elementos más reales al modelo matemático (mayor sofisticación), exige una mayor cantidad de parámetros a calcular y mayor número de supuestos. Infortunadamente, en muchas circunstancias del mundo real no se dispone de datos confiables para realizar las cuantificaciones de los parámetros requeridos, lo cual da lugar a que las predicciones o cálculos de los modelos presenten en muchos casos un considerable margen de error. Por ello, los resultados del modelo deben tomarse en estos casos con cautela. No obstante, a pesar de que muchos modelos matemáticos no pueden realizar predicciones precisas, sobre todo por la falta de datos, éstos son de gran utilidad para medir el efecto de las medidas de control aun antes de iniciar la epidemia.
Asimismo, hay que resaltar que existen diversos modelos epidemiológicos sencillos que modelan algunos fenómenos epidemiológicos de forma adecuada. Estos modelos tienen la ventaja de que no es preciso ser un experto en la materia para hacer un uso apropiado de ellos. Sin embargo, dada la compleja naturaleza de la dinámica de transmisión de algunas enfermedades infecciosas, también existen modelos muy complejos que a menudo son incomprensibles para el profano en la materia. Por lo tanto, para hacer un uso adecuado de ellos se necesitan mayores herramientas matemáticas y computacionales.
Por otro lado, vale la pena mencionar que no existe una metodología sistemática para la modelación y pruebas de hipótesis de enfermedades infecciosas para profesionales de la salud. Por ello es importante que los profesionales de la salud tengan conocimiento de la existencia de estos modelos y fortalezcan su colaboración con modeladores de enfermedades, para diseñar en forma conjunta medidas eficaces de control y erradicación de enfermedades infecciosas. Por último, es prudente mencionar que dado que el actual es un mundo cada vez más interconectado e interdependiente, las amenazas de brotes de epidemias son muy altas, por lo que es sumamente importante fortalecer un sistema de vigilancia epidemiológica para prevenir y combatir la aparición de enfermedades infecciosas capaces de alterar la salud y la economía.
Referencias
1. Ziegler P. The black death. London: Penguin, 1998. [ Links ]
2. Dietz K, Heesterbeek JAP. Daniel Bernoulli's epidemiological model revited. Math Biosci 2002;180:1-21. [ Links ]
3. Bailey NTJ.The role of Statistics in controlling and eradicating infectious diseases. Statistician 1985;34:3-17. [ Links ]
4. Leung PC, Ooi EE. SARS war. Combating the disease. Singapore: World Scientific Publishing, 2003. [ Links ]
5. Becker N. The uses of epidemic models. Biometrics 1979;35:295-305. [ Links ]
6. Diekman O, Heesterbeek JAP, Metz J. On the definition and the computation of the basic reproduction ratio R0 in models of infectious diseases in heterogeneous populations. J Math Biol 1990;28:365-382. [ Links ]
7. Hernández-Suárez CM. A Markov chain approach to calculate Ro in stochastic epidemic models. J Theor Biol 2001;215:83-93. [ Links ]
8. Dietz K. Epidemics and Rumors: A survey. JR Stat Soc [Ser A] 1967;130(4):505-528. [ Links ]
9. Anderson R, May RM. Infectious diseases of humans. Oxford: Oxford University Press; 1991. [ Links ]
10. Diekman O, Heesterbeek JAP. Mathematical epidemiology of infectious disease: model building, analysis and interpretation. New York: John Wiley and Sons, 2000. [ Links ]
11. Watts DC, Strogatz SH. Collective dynamics of 'small-world' networks. Nature 1996;393:440-442. [ Links ]
12. Kretzschmar M, Morris M. Measures of concurrency in networks and the spread of infectious diseases. Math Biosci 1996;133:165-195. [ Links ]
13. Latora V, Marchiori M. Efficient behavior of small-world networks. Phys Rev Lett 2001;87(19):198701-1-198701-4. [ Links ]
14. Wasserman S, Faust K. Social Network Analysis: methods and aplications. Cambridge: Cambridge University Press, 1994. [ Links ]
15. Pastor-Satorras R, Vespignani A. Epidemic dynamics and endemic states in complex networks. Phys Rev E 2001;63:066117. [ Links ]
16. Barabai AL, Albert R. Emergence of scaling in random networks. Nature 1999;401:130. [ Links ]
17. Hernández-Suárez C, Castillo-Chávez C. Urn models and vaccine efficacy estimation. Stat Med 2000;19:827-835. [ Links ]
18. Wallenius KT. Biased sampling: the no central hypergeometric probability distribution. Stanford: PhD thesis, Stanford University, 1963. [ Links ]
19. Ball F, Lyne D. Optimal vaccination policies for stochastic epidemics among a population of households. Math Biosci 2002;177-178:303-354. [ Links ]
20. Riley S, Fraser C, Donnelly CA, Ghani AC, Abu-Raddad LJ, Hedley AJ, et al. Transmission dynamics of the etiological agent of SARS in Hong Kong: impact of public health interventions. Science 2003;300:1961-1966. [ Links ]
21. Lipsitch M, Cohen T, Cooper B, Robins JM, Ma S, James L, et al. Transmission dynamics and control of severe acute respiratory syndrome. Science 2003;300:1966-1970. [ Links ]
22. Lloyd-Smith JO, Galvani AP, Getz WM. Curtailing transmission of severe acute respiratory syndrome within a community and its hospital. Proc Biol Sci 2003;270(1528):1979-1989. [ Links ]
23. Hsieh YH, Chen CWS, Hsu SB. SARS outbreak, Taiwan, 2003. Emerg Infect Dis 2004;10:201-206. [ Links ]
24. Gumel AB, Ruan S, Day T, Watmough J, Brauer F, van den Driessche P, et al. Modelling strategies for controlling SARS outbreaks. Proc Biol Sci 2004; 271(1554):2223-2232. [ Links ]
25. Meyers LA, Pourbohloul B, Newman ME, Skowronski DM, Brunham RC. Network theory and SARS: predicting outbreak diversity. J Theor Biol 2005;232:71-81. [ Links ]
26. Gjorgjieva J, Smith K, Chowell G, Sanchez F, Snyder J, Castillo-Chávez C. The role of vaccination in the control of SARS. Math Biosci Eng 2005;2(4):753-769. [ Links ]
27. Chowell G, Fenimore PW, Castillo-Garsow MA, Castillo-Chávez C. SARS outbreaks in Ontario, Hong Kong and Singapore: the role of diagnosis and isolation as a control mechanism. J Theor Biol 2003;24:1-8. [ Links ]
Solicitud de sobretiros: Mtro. Osval Antonio Montesinos. Facultad de Telemática, Universidad de Colima. Av. Universidad 333, col. Las Víboras. 28040. Colima, Colima, México. Correo electrónico: oamontesl@ucol.mx.














