Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Salud Pública de México
versión impresa ISSN 0036-3634
Salud pública Méx vol.44 no.6 Cuernavaca nov. 2002
Creación de índices de gestión hospitalaria mediante análisis de componentes principales
José Almenara-Barrios, MSP, Dr en MC,(1) Cesáreo García-Ortega, Dr en MC,(1,2) Juan Luis González-Caballero, Dr en Mt,(3) María José Abellán-Hervás, MSP, Dr en MC.(4)
Almenara-Barrios J, García-Ortega C, González-Caballero JL, Abellán-Hervás MJ.
Creación de índices de gestión hospitalaria mediante análisis de componentes principales.
Salud Publica Mex 2002;44:533-540.
El texto completo en inglés de este artículo está disponible en: http://www.insp.mx/salud/index.html
Resumen
Objetivo. Obtener índices útiles para la gestión hospitalaria basados en técnicas estadísticas multivariantes descriptivas. Material y métodos. Durante 1999 y 2000 se recogió información del Hospital de Algeciras correspondiente a los ingresos hospitalarios del periodo 1997-1998. Se estudiaron las variables habitualmente monitorizadas por el Servicio Andaluz de Salud, del Sistema Nacional de Salud Español: número de ingresos, mortalidad, número de reingresos, número de consultas externas, índice case-mix, número de estancias e índice funcional. Las variables se midieron en un total de 22 486 ingresos. Aplicamos la técnica de análisis de componentes principales (ACP), y se utilizó la matriz de correlaciones R. Resultados. Se seleccionaron las dos primeras componentes, con un porcentaje acumulado de variabilidad de 62.67%. Conclusiones. La primera componente puede ser asimilada a un nuevo índice que tiene que ver con la cuantía de personas atendidas, llamado demanda asistencial. La segunda explicaría la dificultad de los casos atendidos; le hemos llamado complejidad asistencial. Ambos índices permiten dar una clasificación de los servicios hospitalarios. El texto completo en inglés de este artículo está disponible en: http://www.insp.mx/salud/index.html
Palabras clave: índices hospitalarios; análisis de componentes principales; epidemiología clínica; gestión; España
Almenara-Barrios J, García-Ortega C, González-Caballero JL, Abellán-Hervás MJ.
Construction of hospital management indices using principal component analysis.
Salud Publica Mex 2002;44:533-540.
The English version of this paper is available at: http://www.insp.mx/salud/index.html
Abstract
Objective. To construct useful indices for hospital management, based on descriptive multivariate techniques. Material and Methods. Data were collected during 1999 and 2000, on hospital admissions occurring during 1997-1998 at Hospital General de Algeciras, part of Servicio Andaluz de Salud (SAS) of Sistema Nacional de Salud Español (Spanish National Health Service). The following variables routinely monitored by health authorities were analyzed: number of admissions, mortality, number of re-admissions, number of outpatient consultations, case-mix index, number of stays, and functional index. Variables were measured in a total of 22486 admissions. We applied the Principal Components Analysis (PCA) method using the R correlation matrix. Results. The first two components were selected, accounting cumulatively for 62.67% of the variability in the data. Conclusions. The first component represents a new index representing the number of attended persons, which we have termed Case Load. The second PC represents or explains the difficulty of the attended cases, which we have termed Case Complexity. These two indices are useful to classify hospital services. The English version of this paper is available at: http://www.insp.mx/salud/index.html
Key words: hospital management indices; principal components analysis; clinical epidemiology; management; Spain
Toda la actividad sanitaria se encuentra condicionada por las características de los enfermos atendidos: edad, diagnóstico, tratamiento, etcétera. Medir dicha actividad ha sido una de las tareas más complejas para los epidemiólogos clínicos, estadísticos y gestores sanitarios, de tal forma que a lo largo de los años muchos han sido los indicadores creados para dicho menester. En la actualidad la actividad de un hospital se mide con indicadores como número de ingresos, camas ocupadas, estancias medias, mortalidad por servicios, reingresos, etcétera, y se unen a estos indicadores clásicos otros que tienen en cuenta la casuística atendida, como son los derivados de los sistemas de clasificación de pacientes (SCP). Un SCP puede analizarse desde una doble perspectiva clínica y estadística. Respecto a la primera, un SCP ha de mostrar una aceptación por los usuarios del mismo (clínicos y gestores), junto a una adecuada validez de contenido y validez de criterio.1 Desde la perspectiva estadística, el rendimiento de los distintos SCP va a estar determinado por su capacidad de captar las diferencias entre los distintos pacientes y, en función de las mismas, predecir un resultado. Se ha demostrado que los grupos relacionados con el diagnóstico (GDR) son los que poseen una mayor fiabilidad.2,3 Los GDR son un sistema de clasificación de pacientes creado por Fetter y colaboradores en la Universidad de Yale en la década de los 70, con el objetivo de obtener una clasificación de episodios de hospitalización en función del consumo de recursos y de la lógica en el manejo clínico de pacientes.4 Los GDR se han convertido en el principal SCP utilizado en Europa para medir el case mix,5 y se utilizan fundamentalmente como un instrumento de gestión hospitalaria, permitiendo identificar la actividad diaria y constituir un lenguaje común entre médicos y gestores para fijar objetivos y monitorizarlos,6 permitiendo efectuar estudios como el EURODRG, que es una acción concertada a escala europea, centrada en tres áreas de trabajo: la producción de información hospitalaria basada en los DRG, la obtención de costos por los DRG y la búsqueda de nuevas aplicaciones de los DRG en Europa.6,7
Dentro del ámbito de la epidemiología clínica, los DRG han servido para definir nuevos indicadores que permiten comparar el funcionamiento global de un hospital o de un servicio. Tales indicadores son la estancia media ajustada por funcionamiento, la estancia media ajustada por casuística, el índice case mix o el índice funcional.8-10
Si se trata de medir la actividad global de los servicios de un hospital en la mayoría de los países europeos se analizan por servicios cada uno de los indicadores mencionados, pero estos sólo permiten la comparación univariante clásica, entendiendo entre los distintos servicios cada indicador como una variable. Esta forma de actuar no ofrece una visión multivariada de la actividad por servicios, no da un modelo de relación funcional entre los indicadores e imposibilita obtener una clasificación de los servicios basada en sus actividades y en sus resultados.
Por ello, en este trabajo se plantea como objetivo generar nuevos índices mediante técnicas multivariantes, en concreto, mediante el análisis de componentes principales (ACP). Dichos índices serán combinaciones lineales de los anteriormente descritos y permitirán establecer una clasificación de los servicios hospitalarios que pueda explicar un cierto modelo subyacente en el conjunto de la información que aportan los indicadores habituales.
Material y métodos
Se estudiaron durante 1997 y 1998 los 22 486 ingresos del Hospital de Algeciras (Cádiz, Andalucía, España), perteneciente al Servicio Andaluz de Salud del Sistema Nacional de Salud Español. Se desagregó la información por servicios, 13 en total, midiendo para cada uno las siguientes variables: (1) número de ingresos (NI), que contabiliza en cada servicio todo nuevo ingreso; (2) mortalidad (MO), entendida como el porcentaje de altas por fallecimiento en el servicio correspondiente para el periodo de estudio; (3) número de reingresos (RE), definido como todo aquel ingreso, por el mismo diagnóstico, en los 30 días posteriores al alta; (4) número de consultas externas (NE), definido como la frecuencia absoluta de consultas ambulatorias; (5) índice case-mix (ICM), definido como el cociente entre la estancia ajustada por funcionamiento (EMFh) y la estancia media de un servicio estándar (EMs). Expresa la complejidad relativa de los pacientes ingresados en un servicio respecto de un patrón de referencia cuyo valor de complejidad media se sitúa en 1. Un índice case-mix superior o inferior a 1 indicará mayor o menor complejidad de los enfermos atendidos en el servicio con respecto al patrón de referencia. La EMFh se calcula como:
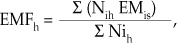
donde Nih es el número de altas en el GDRi del servicio h (representa el número de diagnósticos I, expresados en GDR, que tiene un servicio h determinado) y EMis es la estancia media del GDRi en el estándar. Posteriormente, sumaremos el valor del producto Nih EMis para cada uno de los GDR del servicio en cuestión y dividimos por S Nih, que representa el total de diagnósticos expresados en GDR para cada servicio; (6) número de estancias por servicios (ES),viene dado por la suma del número de días de ocupación de cama en cada servicio por cada ingreso y (7) el índice de funcionalidad (IF), que expresa la eficiencia relativa de un servicio respecto a un patrón de referencia cuyo valor se sitúa en 1. El índice de funcionalidad lo hemos calculado como el cociente entre la estancia media del servicio ajustada por case-mix y la estancia media del estándar.
La matriz de datos obtenida (cuadro I), procedente de medir las variables anteriores, ha sido tratada mediante la técnica multivariante descriptiva de análisis de componentes principales (ACP).

Análisis estadístico
El ACP es quizás la más antigua técnica de análisis multivariante. Su introducción se debe, como tantas veces en estadística, a Pearson (1901),11 pero su verdadero desarrollo y aplicabilidad se la debemos a Hotelling (1933).12 Como ha ocurrido con otras muchas técnicas multivariantes, sus aplicaciones prácticas no se manifestaron hasta que no se desarrollaron los medios informáticos necesarios.
La idea central del ACP es conseguir la simplificación de un conjunto de datos, generalmente cuantitativos, procedentes de un conjunto de variables interrelacionadas. Este objetivo se alcanza obteniendo, a partir de combinaciones lineales de las variables originalmente medidas, un nuevo conjunto de igual número de variables, no correlacionadas, llamadas componentes principales (CP) en las cuales permanece la variabilidad presente en los datos originales, y que al ordenarlas decrecientemente por su varianza, nos permiten explicar el fenómeno de estudio con las primeras CP (Anexo).13-15
Con ello conseguimos: (a) sintetizar la información procedente de un volumen importante de datos recogidos en una investigación en particular; (b) crear nuevos indicadores o índices, representados por las CP, y (c) utilizar el ACP como paso previo a otras técnicas.16
Es necesario revisar los aspectos teóricos del ACP: supongamos que X es un vector de p variables aleatorias, definidas en una población. Y que el vector X se mide en n individuos, generando una matriz de datos con n filas que representan los individuos en los que hemos medido las variables que representan las p columnas. Buscamos combinaciones lineales del tipo:
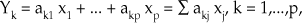
donde ak1,...,akp son constantes numéricas, de tal forma que las nuevas variables Yk o CP tengan varianza máxima en orden decreciente y ausencia de correlación entre sí. Las CP Yk se obtienen diagonalizando la matriz de covarianzas S o la de correlaciones R de las variables medidas originalmente, de forma que las constantes ak1,...,akp se obtienen con las coordenadas de los vectores propios asociados a los valores propios de S o R, ordenados de forma decreciente, que representan las varianzas de las CP.
En definitiva, tras aplicar el ACP creamos unas nuevas variables, las CP. Pero además cada sujeto de la muestra, en nuestro caso los diferentes servicios hospitalarios, obtiene una puntuación en cada una de las CP seleccionadas, que permite resolver un problema frecuente en epidemiología, y no resuelto del todo, como el ordenamiento de sujetos cuando se tiene más de una medición de los mismos. Por otro lado, estas CP ayudan a desentrañar un modelo subyacente en el conjunto de datos iniciales, que logramos en el proceso de nombrarlas.
En nuestro estudio hemos partido de la diagonalización de la matriz de correlaciones, ya que la interpretación de las componentes o factores es más fácil cuando usamos variables estandarizadas.14 Los análisis se realizaron en los programas informáticos BMDP y SPSS.
Resultados
La matriz inicial de datos representada por las puntuaciones obtenidas por los diferentes servicios en las variables medidas se puede observar en el cuadro I. A continuación se obtuvo la matriz de correlaciones entre las variables (cuadro II), previa al proceso de diagonalización propio del ACP. Para verificar si la matriz de correlaciones es una matriz identidad, criterio que desaconsejaría el análisis posterior mediante ACP, se ha utilizado el test de Bartlett, obtenido a partir de la transformación c2 del determinante de la matriz de correlaciones. El test de Bartlett, en este contexto, se lleva a cabo para evaluar la pertinencia estadística de la aplicación del ACP con los datos obtenidos. Si toma un valor alto el valor de p será bajo y más improbable que la matriz sea una matriz identidad.17 En nuestro caso el test de Bartlett toma un valor de 37 371 (p=0.015), por lo que resulta evidente que no estamos ante una matriz identidad y podemos hacer el análisis.
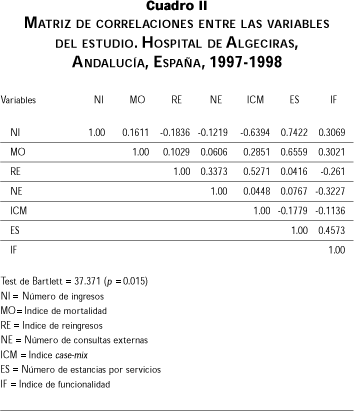
Se seleccionaron los dos primeros valores propios superiores a la unidad, a saber l1=2.558 sólo explica 36.54% de la variabilidad inicial y el l2=1.829 que explica 26.13%; en conjunto explican 62.67% de la variabilidad inicial, criterio suficiente para poder seleccionar las dos primeras componentes asociadas (Y1, Y2). Con la tercera componente se llegaba a explicar 80% de la variabilidad, pero el retener más componentes apenas simplifica la dimensión del problema de crear nuevos índices, objetivo principal de nuestro análisis. Por ello decidimos seleccionar las dos primeras que vienen definidas por:

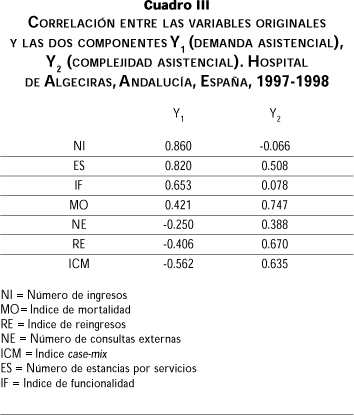
Para poder entender el significado de ambas componentes es necesario estudiar la correlación entre las variables originalmente medidas y las CP seleccionadas, que especifica la intensidad de la contribución de cada variable en la componente seleccionada y nos ayuda a nombrarla facilitando la interpretación del nuevo índice generado. La matriz de correlaciones variables-componentes (cuadro III), nos muestra que la correlación mayor de la primera componente se da con la variable número de ingresos (NI) (r=0.860), seguida de la obtenida con la variable original número de estancias por servicio (ES) (r=0.820). Se observan correlaciones negativas con las variables índice case-mix (ICM) (r=-0.563), número de reingresos (RE) (r=-0.406) y con número de consultas externas (NE) (r=-0.250). Lo que podemos interpretar como un mayor peso en este primer componente Y1 de variables relacionadas con la demanda asistencial que tienen los diferentes servicios, fundamentalmente en términos cuantitativos. Se oponen en ella variables como la ICM o la RE que denotan complejidad asistencial. La mayor correlación con la segunda componente se obtiene con la variable mortalidad (MO) (r=0.747), seguida por la obtenida con la variable reingresos (RE) (r=0.670), y a continuación con la variable índice case-mix (ICM) (r=0.635). Se opone en ella la variable número de ingresos (NI). Podemos interpretar que en esta segunda componente seleccionada Y2 pesan más las variables que señalan una mayor complejidad asistencial, como la mortalidad, los reingresos o el índice case-mix, frente a las variables que denotan sólo demanda en términos cuantitativos, cuya máxima representación es el número de ingresos de un servicio y que en este componente interviene negativamente.
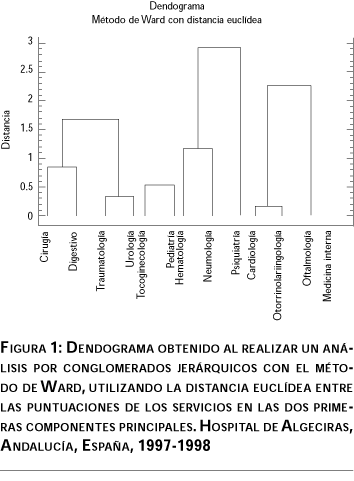
Procede a continuación calcular las puntuaciones que obtienen los servicios del hospital en las dos componentes seleccionadas, para poder dar un ordenamiento de los mismos, que luego interpretaremos. Los resultados obtenidos se pueden ver para todos los servicios en el cuadro IV. Observamos cómo en la primera componente los cinco servicios con puntuación más alta y por orden son, el primero, medicina interna; el segundo, tocoginecología; el tercero, pediatría; el cuarto, cirugía; y el quinto, traumatología. Al final se encuentran hematología, oftalmología y psiquiatría. Son por lo tanto los servicios con una mayor demanda asistencial los que ocupan los primeros puestos sin que esto lleve aparejada una mayor dificultad de los casos atendidos. Si nos centramos en estudiar la segunda componente, la clasificación aportada por la misma es diferente, si bien el servicio de medicina interna continúa siendo el primero, ya en segundo lugar se encuentra el servicio de psiquiatría; la tercera plaza es ocupada por hematología, en la cuarta repite cirugía y cierra este quinteto neumología. Los últimos puestos son ocupados, entre otros, por servicios que puntuaron mucho en la primera componente, como pueden ser pediatría, que ocupa el último lugar, o tocoginecología, que ocupa la posición número 11. Podemos percibir en esta segunda componente que son los servicios con una casuística más compleja los que suben en la clasificación, ocupando los últimos puestos servicios con muchos enfermos atendidos pero con patologías poco complejas o rutinarias dentro de su especialidad. Observamos también cómo cirugía mantiene un cuarto puesto tanto en la primera como en la segunda componente, lo que puede indicar una demanda importante, junto con una casuística relativamente complicada, ambas características propias de un servicio quirúrgico. La posición baja, puesto número 12 en ambas componentes del servicio de oftalmología indica una demanda en número poco frecuente y también de baja complejidad, que se explica por las características del hospital que modelamos y por la existencia en la misma provincia de servicios de oftalmología de elevada especialización. Vemos también plausibles los resultados obtenidos por los servicios en la parte media de la clasificación para ambas componentes.
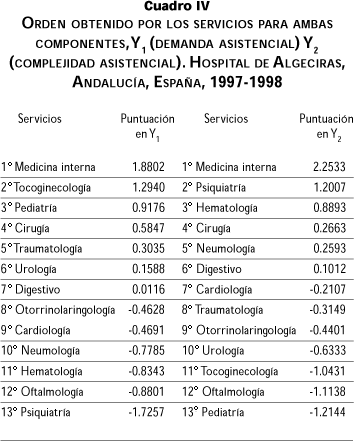
Por último, para obtener una representación gráfica que clarifique lo expuesto realizamos, con las puntuaciones obtenidas de los servicios en las dos CP, un análisis por conglomerados18 utilizando el algoritmo jerárquico de Ward,19 que nos proporciona el dendograma de la figura 1. En ella puede verse cómo pueden clasificarse los servicios en los cinco grupos o conglomerados: a) cirugía, digestivo, traumatología, urología; b) tocoginecología, pediatría; c) hematología, neumología, psiquiatría; d) cardiología, otorrinolaringología, oftalmología, y e) medicina interna.
Discusión
En primer lugar, vamos a interpretar las dos componentes seleccionadas. Hemos observado en los resultados que la primera componente tiene una alta correlación con el número de ingresos, el número de estancias por servicio y el índice de funcionalidad. Por el contrario, su correlación es baja con la mortalidad, e inversa con los reingresos, el número de consultas externas y el índice case-mix. Opone por un lado la carga asistencial y las estancias, indicadores que asimilamos a la demanda, la ocupación del servicio o la presión asistencial y por otro lado, a la mortalidad, los reingresos y el case-mix, indicadores que podemos asumir como de complejidad en la prestación de servicios. Por ello este nuevo índice que representa la primera componente lo hemos nombrado como demanda asistencial, y, pensamos, describe bien esta parcela del trabajo del Hospital de Algeciras. Cuando observamos las puntuaciones obtenidas en esta componente por los distintos servicios son las unidades que podíamos definir como de mayor ocupación las que se encuentran en las primeras plazas: medicina interna, tocoginecología, pediatría o cirugía, y ocupan las últimas plazas hematología, oftalmología y psiquiatría.
Cuando nos ocupamos de estudiar la segunda componente observamos cómo en ella el número de ingresos ha perdido todo el protagonismo y que éste ha pasado a tener una correlación de sentido negativo con la componente, además bajó enormemente la correlación con el índice funcional y bastante con las estancias. El gran protagonismo en esta componente se lo llevan la mortalidad, los reingresos y el índice case-mix, que son las variables con mayor correlación con la componente en estudio. Por ello hemos denominado a este nuevo índice complejidad asistencial. Obtienen las puntuaciones más altas en esta componente los servicios de medicina interna, psiquiatría, hematología o cirugía, y ocupan las plazas inferiores los servicios de tocoginecología, oftalmología o pediatría.
Debido a los pesos de las distintas variables en las dos componentes, y las puntuaciones de los diferentes servicios en las mismas, creemos que el ACP ha generado dos índices eficientes con el propósito de clasificar los servicios y plausibles con el modelo de hospital que monitorizamos, de tipo medio, comarcal y no universitario. Es interesante hacer ver cómo el servicio de medicina interna ocupa en las dos componentes el primer puesto, lo que estaría señalando un servicio con una alta presión asistencial, tanto en términos cuantitativos (gran número de pacientes), como en términos cualitativos (complejidad de los casos tratados); no olvidemos que actúa como filtro en muchas ocasiones y que es a partir de la valoración en este servicio cuando se deriva a otros. También merecen un comentario las puntuaciones obtenidas por los servicios de tocoginecología y pediatría, los que ocupan el segundo y tercer puesto en el primer índice, demanda asistencial. Y los puestos 11 y 13 en el segundo de los índices, complejidad asistencial. Se vuelve a confirmar la eficiencia de los dos nuevos índices, que nos alertan sobre que ambos servicios soportan una gran presión asistencial sólo y exclusivamente numérica pero no compleja. Es fácil de entender que esto sea así, ya que en un hospital de estas características la principal causa de ingreso son los partos normales sin complicaciones y la patología perinatal.20
Por otro lado, señalan también la gran cantidad de ingresos banales en pediatría, que creemos innecesarios y que pueden estar motivados por múltiples factores sociales, demográficos o de práctica médica.
Otro de los propósitos del ACP es utilizarlo como análisis previo a otras técnicas multivariantes. Para ello utilizamos las puntuaciones de los servicios en las dos componentes y hemos efectuado un análisis conglomerado que clarificara gráficamente los resultados.
Es significativa la creación de un cluster que agrupe los servicios de pediatría y tocoginecología, así como el formado sólo por medicina interna, u otro que reúna al resto de servicios que obtenían una puntuación alta en Y2 (psiquiatría, hematología y neumología).
En definitiva, el estudio conjunto multivariante que hacemos de los indicadores clásicos mediante el ACP complementa los numerosos estudios que aparecen en la literatura y que abordan el comportamiento de un solo indicador, ya sea la mortalidad, los reingresos, los DRG, el porcentaje de casos extremos etcétera, o de un conjunto de ellos pero a la manera univariante clásica.7,10,21-25
Pero además, pensamos que la mayor aportación nuestra a la gestión sanitaria con índices multivariantes es la de desentrañar una dimensión subyacente e interpretable con los índices generados (demanda y complejidad) de fenómenos que, en primera instancia, se han medido de múltiples formas (indicadores univariantes clásicos: mortalidad, reingresos, etcétera), incapaces de incorporar toda la estructura del fenómeno y las interrelaciones entre indicadores, lo que creemos conseguir con los dos índices propuestos que, además, permiten ordenar por puntuaciones a los servicios teniendo en cuenta al unísono todos los aspectos útiles en los procesos de gestión.
Hasta el momento han sido pocos los trabajos que abordan la utilización del ACP en esta línea,26 y sus aplicaciones más importantes son en campos tan dispares como la psicología, la educación, el control de calidad, la agricultura, la economía o la anatomía.27 Pero pensamos que dentro de la epidemiología clínica y de la gestión hospitalaria pueden jugar un papel importante en la creación de índices como los presentados.
Estos índices deben ser validados definitivamente mediante su utilización en otros hospitales y en otros escenarios, lo que permitirá continuar con este tipo de investigaciones.
Referencias
1. Argimón JM, Jiménez J. Métodos de investigación aplicados a la atención primaria de salud. Madrid: Mosby/Doyma Libros,1991. [ Links ]
2. Thomas JW, Ashcraft MLF. An evaluation of alternative severity of illness measures for use by university hospitals. Ann Arbor: Department of Health Services Management and Policy, Scholl of Public Health, The University of Michigan, 1986. [ Links ]
3. Thomas JW, Ashcraft MLF. Measuring severity of illness: A comparison of inter-rater reliability among severity methodologies. Inquiry 1989; 26: 483-492. [ Links ]
4. Fetter RB, Shin Y, Freeman JL, Averill RF, Thompson JD. Case mix definition by Diagnosis Related Groups. Medical Care 1980; 18(2 Suppl): 1-53. [ Links ]
5. Wiley MM. Los GRD en Europa: revisión de los proyectos de investigación y experimentación. En: Casas M, ed. Los grupos relacionados con el diagnóstico. Experiencia y perspectivas de utilización. Barcelona: Masson, 1991:85-135. [ Links ]
6. Casas M. Los grupos relacionados con el diagnóstico en Europa. El proyecto EURODRG de la CEE. Todo Hospital 1992; 87: 33-36. [ Links ]
7. Casas M. Issues for comparability of DRG statistics in Europe. Results from EURODRG. Health Policy 1991; 17: 133-149. [ Links ]
8. Casas M. GRD. Una guía práctica para médicos. Barcelona: Iasist, 1995. [ Links ]
9. Freeman JL. Refined DRGs: Trials in Europe. Health Policy 1991; 17: 151-164. [ Links ]
10. Casas M, Tomás R. Descripción de la casuística y el funcionamiento hospitalario. En: Casas M, ed. Los grupos relacionados con el diagnóstico. Experiencia y perspectivas de utilización. Barcelona: Masson, 1991:55-83. [ Links ]
11. Pearson K. On lines and planes of closest fit to systems of points in space. Phil Mag 1901; 2: 559-572. [ Links ]
12. Hotelling H. Analysis of a complex of statistical variables into principal components. J Educ Psychol 1933; 24: 417-441. [ Links ]
13. Jolliffe IT. Principal Component Analysis. Nueva York (NY): Springer-Verlag, 1986. [ Links ]
14. Abraira V, Pérez-de Vargas A. Métodos multivariantes en bioestadística. Madrid: Editorial Centro de Estudios Ramón Areces, 1996. [ Links ]
15. Almenara J, González JL, García C, Peña P. ¿Qué es el análisis de componentes principales? Jano 1998; 1268:58-60. [ Links ]
16. González B. Análisis Multivariante. Aplicación al ámbito sanitario. Barcelona: SG Editores, 1991. [ Links ]
17. Visauta B. Análisis estadístico con SPSS para Windows. Volumen II. Estadística multivariante. Madrid: McGraw-Hill/Interamericana de España, 1998. [ Links ]
18. Everitt BS. Cluster Analysis. 3ª ed. Londres: Edward Arnold, 1993. [ Links ]
19. Ward JH. Hierarchical grouping to optimize an objetive function. J Am Statist Assoc 1963; 58:236-244. [ Links ]
20. García C. Morbi-mortalidad hospitalaria del área sanitaria de Algeciras 1995-1996 Tesis. Cádiz, España: Universidad de Cádiz, 1999. [ Links ]
21. Daley J. Mortalidad y otros datos de resultado. En: Rango DR, Bohr D, ed. Métodos cuantitativos en la gestión de la calidad. Una guía práctica. Barcelona: SG Editores, 1994: 51-85. [ Links ]
22. Rutstein DD, Berenberg W, Chalmers TC, Child CG, Fishman AP, Perrin EB. Measuring the quality of medical care: A clinical method. N Engl J Med 1976; 294:582-588. [ Links ]
23. García C, Almenara J, García JJ. Tasas específicas de mortalidad en el Hospital de Algeciras durante el periodo 1995-1996. Rev Esp Salud Publica 1997;71:305-315. [ Links ]
24. Arce JM, Polo M. Variación en la proporción de outlier por servicio médico en la Fundación Jiménez Díaz entre los años 1992 y 1994.Gestión Hospitalaria 1995;4:50-52. [ Links ]
25. García C, Almenara J, García JJ. Proporción de casos extremos (outlier) por servicio como indicador de gestión. Rev Adm Sanit 1998;8: 123-134. [ Links ]
26. Silva LC. Cultura estadística e investigación científica en el campo de la salud: una mirada crítica. Madrid: Díaz de Santos, 1997. [ Links ]
27. Jackson JE. A user´s guide to principal components. Nueva York (NY): John Wiley & Sons, 1991. [ Links ]
Aspectos parciales del presente trabajo han sido presentados como Ponencia en el IV Congreso de la Sociedad Andaluza de Calidad Asistencial. Cádiz, España, 1999. Y como comunicación a la XVII Reunión Científica de la Sociedad Española de Epidemiología (SEE). Santiago de Compostela, España, 1999.
(1) Area de Medicina Preventiva y Salud Pública. Universidad de Cádiz, España.
(2) Unidad de codificación del Hospital del Servicio Andaluz de Salud de Algeciras. Cádiz, España.
(3) Departamento de Estadística, Universidad de Cádiz, España.
(4) Escuela de Ciencias de la Salud de la Universidad de Cádiz, España.
Fecha de recibido: 10 de enero de 2002 • Fecha de aceptado: 25 de junio de 2002
Solicitud de sobretiros: Profesor José Almenara-Barrios. Escuela de Ciencias de la Salud de la Universidad de Cádiz.
Avenida Duque de Nájera, 18, 11002 Cádiz, España.
Correo electrónico: jose.almenara@uca.es
Anexo
OBTENCIÓN DE LAS COMPONENTES
La idea de obtener índices o indicadores epidemiológicos mediante el ACP es posible gracias a la transformación de las variables originalmente medidas, en un nuevo conjunto de variables llamadas componentes principales, que son incorreladas, y que se presentan ordenadas decrecientemente en cuanto a la variabilidad que son capaces de explicar del conjunto de variables originalmente medidas.
Partimos por lo tanto de X que es un vector de p variables aleatorias, donde se quiere simplificar las varianzas de las p variables y la estructura de covarianzas o correlaciones. Conseguimos nuestro objetivo obteniendo un número más pequeño de variables derivadas que son las CP.
Suponemos que el vector X se mide en n individuos (en nuestro problema servicios hospitalarios) en los que hemos medido las p variables, que vienen representadas por las columnas y donde las filas representan individuos.
Buscamos una función lineal del tipo

que tenga varianza máxima, donde a será un vector de p componentes a1, a2,...,ap tal que
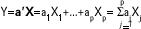
Con las condiciones anteriores, y siendo Spp la matriz de varianzas y covarianzas muestrales de X, se tiene que:
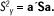
Y definimos la primera componente principal Y1 = a1´X como la combinación lineal de las variables originales, con las restricciones siguientes:
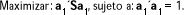
Con estas condiciones, a1 es el vector propio unitario correspondiente al mayor valor propio l1 de S. Siendo,
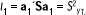
Vemos que a1 es el vector unitario o vector propio de la matriz de covarianzas S asociado al valor propio l1. Además, la inercia "condensada" por la primera CP, es a1´l1a1 = l1 a1´a1 = l1. Es decir, l1 es el primer valor propio de la matriz S y representa la parte de inercia "condensada" por la primera CP.
Esta primera CP es una variable sintética o combinación lineal de variables originales que resume mejor la información que contienen y que en nuestro caso representa un índice, el llamado demanda asistencial.
Podemos buscar otra combinación lineal
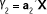
de las variables originales, cuyas proyecciones de los puntos en ella sea la máxima e incorrelada con a1´X para que las varianzas que explican cada una sean independientes. De tal forma que a2 es el vector propio unitario correspondiente al segundo valor propio l2 de S. Y
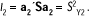
Así, en la k-ésima etapa (hasta p), puede buscarse una función lineal ak´X que tenga varianza máxima, sujeta a la restricción de que sea incorrelada con a1´X, a2´X,...,a´k-1 X. La solución viene dada por el sistema de valores propios y vectores propios ortonormales de la matriz S, es decir, si {(l1,a1), (l2 ,a2),...,(lp ,ap) } son los valores propios ordenados decrecientemente y sus vectores propios asociados, las p componentes principales muestrales vienen establecidas por

En resumen, las componentes se obtienen diagonalizando la matriz de covarianzas S o la matriz de correlaciones R. En virtud de las propiedades de la diagonalización de matrices simétrica, siendo el rango de la matriz S, p ,habrá p componentes asociadas a los p valores propios. Las componentes son los p vectores propios asociados a los p valores propios.














